Quantifying the Variability of Internode Allometry within and between Trees for Pinus tabulaeformis Carr. Using a Multilevel Nonlinear Mixed-Effect Model

Abstract

Allometric models of internodes are an important component of Functional-Structural Plant Models (FSPMs), which represent the shape of internodes in tree architecture and help our understanding of resource allocation in organisms. Constant allometry is always assumed in these models. In this paper, multilevel nonlinear mixed-effect models were used to characterize the variability of internode allometry, describing the relationship between the last internode length and biomass of Pinus tabulaeformis Carr. trees within the GreenLab framework. We demonstrated that there is significant variability in allometric relationships at the tree and different-order branch levels, and the variability decreases among levels from trees to first-order branches and, subsequently, to second-order branches. The variability was partially explained by the random effects of site characteristics, stand age, density, and topological position of the internode. Tree- and branch-level-specific allometric models are recommended because they produce unbiased and accurate internode length estimates. The model and method developed in this study are useful for understanding and describing the structure and functioning of trees.

1. Introduction

Plant allometry has been used extensively to describe the relationship between individual size and other attributes, such as form and process [1,2]. It allows plant organ size to be estimated, commonly from the plant’s biomass, and links plant architecture and physiological activities. It is particularly useful in functional-structural plant models (FSPMs), which explicitly describe the development of the 3D architecture or structure of plants over time as governed by physiological processes and environmental factors [3,4]. In these FSPMs, such as GreenLab [5,6], stem morphology (length and diameter) is an important component because it requires an accurate description of the geometric and topological structure of the plant and canopy. It is well known that plants often display large differences in morphological characters. As a tree grows in response to the local climate, site conditions, and management practices, its components change in size and shape in a coordinated manner. Within a single species, genotypes often vary intrinsically in their phenotypic trait values [7]. The ability to change a phenotype in response to the environment is an important feature of plants, especially for trees living in heterogeneous environmental conditions over both a long generation time and a large geographical area. The 3D architecture of a forest canopy is a highly heterogeneous and dynamic system at all scales. The length, diameter and number of internodes within branches at different levels affect visual appearance but also reflect the resource allocation of a tree, which is driven by the environment and physiological processes. The geometry of tree branches can have a considerable effect on their efficiency in terms of carbon export per unit carbon investment in structure [8].

It has been observed from experiments that there are great variations in internode growth within and between trees, even for branches of similar positions and vigor [9,10,11]. For example, distinct quantitative trait loci between the trunk and branches for internode lengthening were detected in apple hybrids [12]; internode length varies regularly with node order [13]. Numerous empirical works have provided evidence of the variability of structural traits within species, between species, and over time [14,15,16]. Pretzsch and Dieler [17] provided empirical evidence that trees exhibit plastic rather than fixed structural scaling; plastic scaling is relevant for space occupation and competition at the individual tree level. Chen et al. [18] found strong elongation of petioles upon submergence as well as both inter- and intra-population variation. Intraspecific functional variability in terms of the extent, structure, and sources of variation was also investigated [19]. There is increasing evidence challenging the assumption that intraspecific variability is much lower than interspecific variability [20,21]. Moreover, the variability of plant allometric equations (scale laws) for relationships such as metabolic rate-biomass [22], tree height-diameter [23,24,25,26], tree productivity-biomass [27], biomass-diameter [28,29], branch radius-branch length [24,30], and foliage and woody mass in crowns [31] has been extensively examined.

Quantifying the variation in allometric growth is of interest for FSPMs because understanding the variation in allometric internode growth within and between trees should allow us to better understand the underlying tree structure and function. Little is known about the variability in internode allometry; however, such information is essential, both for improving the accuracy of FSPMs and for understanding the mechanisms of tree functioning. It is expected that the allometric relationship of an individual tree deviates from that of a modeled population. Furthermore, the same genetic material occurs within trees; thus, the specification of internodes within trees (i.e. nested random effects) is necessary to model the hierarchical data structure. Internode measurements (length, diameter, and biomass) that are derived from the same tree and branch are not independent. These issues have rarely been described for FSPMs [32,33,34,35,36], with the exception of a single study [37]. There is increasing interest in including the variation among individuals in the modeling of population growth with hierarchical models, in which some parameters are estimated at the level of the population, whereas other parameters are assumed to vary among individuals according to a specific distribution where the mean and the variance of the distribution can be estimated [38,39,40,41]. Recent developments in statistical theory and computational power allow for the specification of multilevel nonlinear mixed-effect models that can generate notable improvements in parameter estimation [42,43]. Analyses of the allometric growth patterns of internodes with mixed-effects models have been limited up until now and could potentially provide valuable biological insights into plant plasticity for FSPMs [37].

Chinese pine (Pinus tabulaeformis Carr.), an important native tree species in China, grows across 14 provinces and plays a significant role in forestry and social development. A Chinese pine tree only produces one internode for both the stem and a branch during one year and is characterized by branches in whorls on each internode. Third-order branches are common and very few fourth-order branches are observed. To better understand inter-tree competition on a source-sink balance, a functional-structural model of Chinese pine was calibrated using the GreenLab framework with the assumption that the internode allometry for the same level branches is identical [43].

The main goal of this study was to examine the variability of internode allometry within and between trees and branches for the Chinese pine. The base allometric model from GreenLab describes the primary growth of the internode. A multi-level nonlinear mixed-effects model approach was adopted based on observed allometric data. We aimed to verify that significant variation exists in internode allometry within and between trees and branches; this needs to be modeled and quantified.

2. Materials and Methods

2.1. Site Description and Data

Data were collected at the Longtoushan forest farm, Weichang county (116°51′–117°45′ E, 41°47′–42°06′ N), Hebei Province, China in April 2011. The mean elevation in the area is 985 m. The mean annual rainfall is 465 mm. Temperatures range from −12.9 °C to 38.9 °C with an average of 2.4 °C. The soil is primarily brown soil.

In this paper, a sampling protocol similar to the one described in the study of Guo et al. [44] was designed to investigate tree architecture and biomass to develop functional-structural models of the Chinese pine. Sixteen Chinese pine trees of different ages and from different sites (S1 to S4) with varying densities (decreased from 1 to 4) were randomly sampled and investigated (Table 1). For each tree, the diameter at breast height (1.3 m) was first measured. After the tree was felled, the total height, the total number of internodes, and their corresponding locations along the stem were measured and recorded. For each internode on the trunk, one representative first-order branch was selected and the length, diameter, fresh biomass, and the corresponding location of each internode on the selected first-order branch were measured. For each internode on the selected first-order branch, one representative second-order branch was selected and the same information was measured as for the first-order branch. The measurements for the third-order branch were the same as for the first and second-order branches. In the GreenLab model, the growth of internodes is described by two processes. The first one is primary growth. The internode grows in length and diameter for a short period and length and diameter are linked by an allometric function during the primary growth. The second one is secondary growth. Internode length is then static but the diameter continues to grow, as long as the branch is alive. For these reasons, the relationships between length and diameter can be linked only for current-year shoots, usually represented by the last internodes of branches [5]. In that sense, we remake allometry only on the last internode of branches, where the secondary growth is negligible. For Chinese pines, the last internode of a branch is commonly used to develop the allometric model, which describes the primary growth of internodes [45,46]. A total of 211 internodes on first-order branches, 969 internodes on second-order branches and 431 internodes on third-order branches were collected. Summary statistics for the last internodes of branches are shown in Table 2. We neglected the fourth order or higher branches because the number of these branches was very limited.

Table 1. Description of 16 sampled Chinese pine trees.

Tree No.	Tree Age (Year)	Age Group	Diameter at Breast Height (cm)	Tree Height (m)	Site Location	Density Group
1	5	A1	1.8 *	0.93	1	1
2	5	A1	1.7 *	0.82	1	1
3	8	A2	2.5	2.06	1	1
4	8	A2	2.2	2.19	1	1
5	47	A3	20.2	13.80	2	4
6	47	A3	17.3	13.02	2	4
7	47	A3	14.4	12.95	2	4
8	47	A3	20.4	16.25	2	3
9	47	A3	15.7	13.80	2	3
10	47	A3	20.4	15.85	2	3
11	21	A4	13.8	7.47	3	2
12	21	A4	12.4	7.29	3	2
13	21	A4	13.4	7.10	3	2
14	11	A5	5.3	4.02	4	1
15	11	A5	3.1	2.85	4	1
16	11	A5	3.4	3.24	4	1

Note: * indicates ground diameter.

Table 1. Description of 16 sampled Chinese pine trees.

Tree No.	Tree Age (Year)	Age Group	Diameter at Breast Height (cm)	Tree Height (m)	Site Location	Density Group
1	5	A1	1.8 *	0.93	1	1
2	5	A1	1.7 *	0.82	1	1
3	8	A2	2.5	2.06	1	1
4	8	A2	2.2	2.19	1	1
5	47	A3	20.2	13.80	2	4
6	47	A3	17.3	13.02	2	4
7	47	A3	14.4	12.95	2	4
8	47	A3	20.4	16.25	2	3
9	47	A3	15.7	13.80	2	3
10	47	A3	20.4	15.85	2	3
11	21	A4	13.8	7.47	3	2
12	21	A4	12.4	7.29	3	2
13	21	A4	13.4	7.10	3	2
14	11	A5	5.3	4.02	4	1
15	11	A5	3.1	2.85	4	1
16	11	A5	3.4	3.24	4	1

Note: * indicates ground diameter.

Table 2. Summary statistics of the last sampled internodes on Chinese pine branches.

Branch Order	Internode Size	Maximum	Minimum	Mean	Standard Deviation	Coefficient of Variation (CV)	Sample Size
1	length (cm)	37.60	0.32	13.33	9.60	0.72	211
	fresh biomass (g)	24.98	0.03	3.96	4.88	1.23
2	length (cm)	18.70	0.10	3.14	2.14	0.68	969
	fresh biomass (g)	3.44	0.01	0.45	0.76	1.69
3	length (cm)	3.01	0.20	1.14	0.60	0.53	431
	fresh biomass (g)	0.60	0.01	0.12	0.10	0.83

Table 2. Summary statistics of the last sampled internodes on Chinese pine branches.

Branch Order	Internode Size	Maximum	Minimum	Mean	Standard Deviation	Coefficient of Variation (CV)	Sample Size
1	length (cm)	37.60	0.32	13.33	9.60	0.72	211
	fresh biomass (g)	24.98	0.03	3.96	4.88	1.23
2	length (cm)	18.70	0.10	3.14	2.14	0.68	969
	fresh biomass (g)	3.44	0.01	0.45	0.76	1.69
3	length (cm)	3.01	0.20	1.14	0.60	0.53	431
	fresh biomass (g)	0.60	0.01	0.12	0.10	0.83

2.2. Base Allometry Model

The base allometry model is from GreenLab; in this study, the internode is represented as a cylinder [47], and a power function is adopted to describe the allometry of internodes with the specification of Equation (1) [45] in the GreenLab model. This has been validated by previous studies [33,34,44], and is also well indicated by most of the scatter plots between internode length and biomass for Chinese pine in this study (Figure 1). The model only accounts for primary growth of the internode.

$$L(K)=\sqrt{{\beta }_1}\cdot Q{(K)}^{\frac{1+{\beta }_2}{2}}+\epsilon$$

(1)

where L(K) and Q(K) are the length and biomass of internode K, respectively; β₁ and β₂ are the shape parameter and geometric parameter of the internode in the GreenLab model, respectively; and ε is an error term.

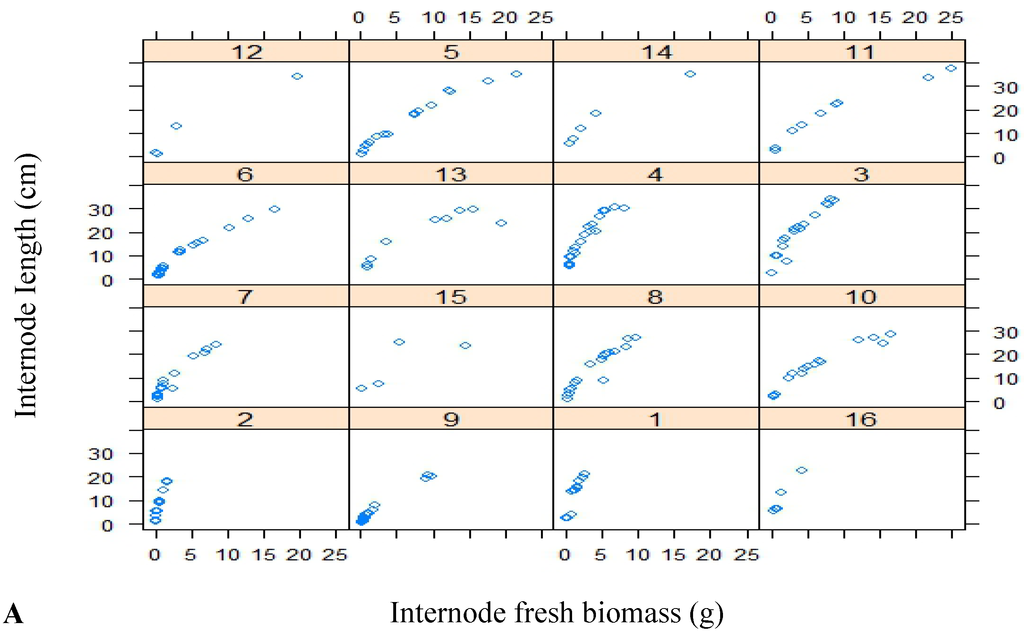
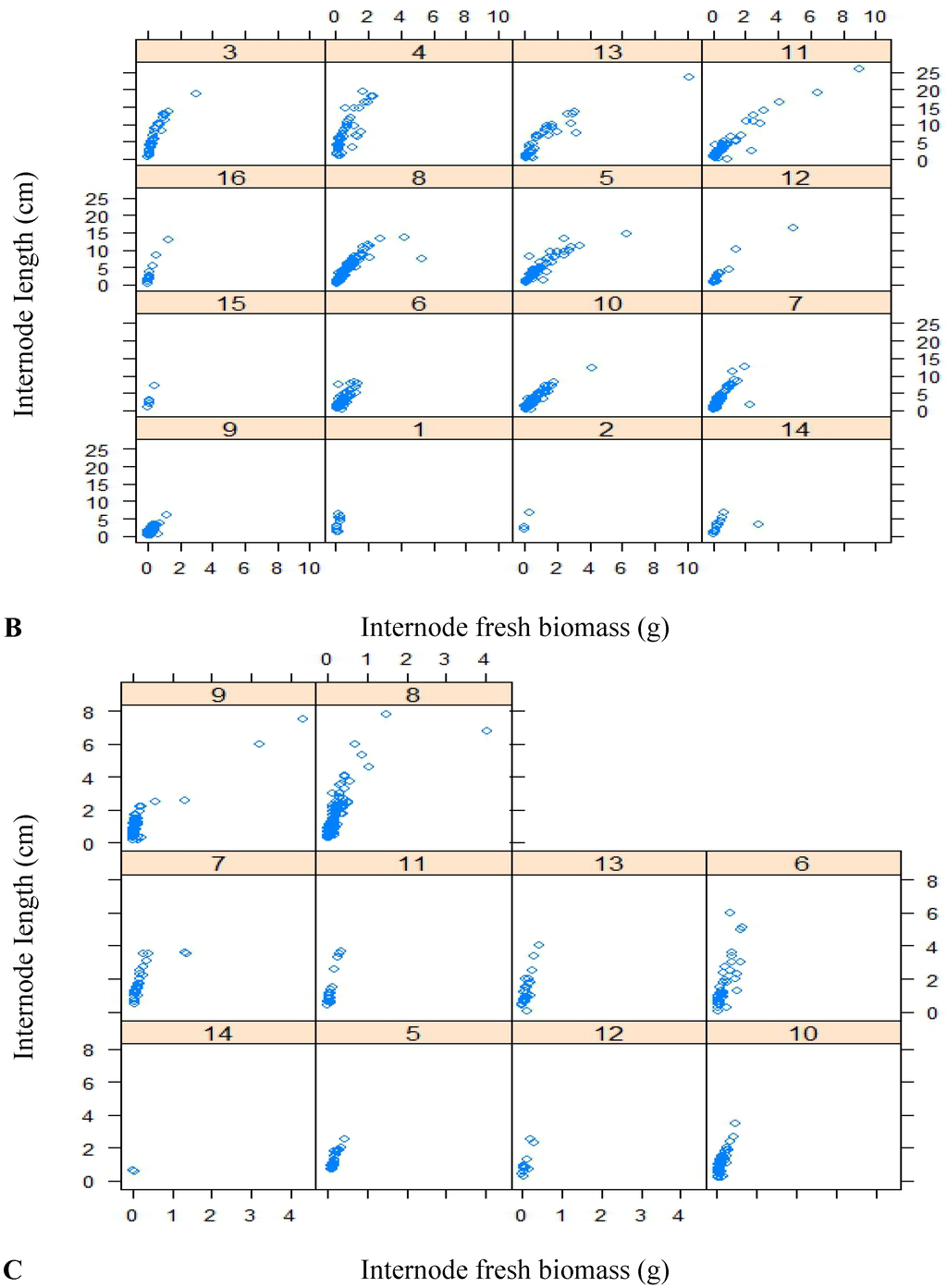
Figure 1. Scatter plots of internode length and biomass for Chinese pine (A: the first-order branches; B: the second-order branches; C: the third-order branches).

Figure 1. Scatter plots of internode length and biomass for Chinese pine (A: the first-order branches; B: the second-order branches; C: the third-order branches).

2.3. Multi-Level Nonlinear Mixed Model

Mixed-effects models can incorporate the hierarchical structure of data into the analysis, and the variation in the parameter estimates is known at each level of the hierarchical sampling structure, thus providing unbiased estimates of model parameters [48]. Using random effects to capture branch-to-branch and tree-to-tree variability allows for modeling the length of the individual tree (subject-specific) as well as the length of the average tree (population-specific). The mixed-effects model for estimating the lengths of internodes on different order branches is specified in Equations (2)–(4):

$$L_{i j}(K)=\sqrt{({\beta }_1+b_{1,i})}\cdot Q_{ij}(K)\frac{1+({\beta }_2+b_{2,i})}{2}+{\epsilon }_{i,j}$$

(2)

$$L_{ijm}(K)=\sqrt{({\text{β}}_1+b_{1,i}+b_{1,ij})}\cdot Q_{ijm}{(K)}^{\frac{1+({\text{β}}_2+b_{2,i}+b_{2,ij})}{2}}+{\text{ε}}_{i,jm}$$

(3)

$$L_{ijml}(K)=\sqrt{({\text{β}}_1+b_{1,i}+b_{1,ij}+b_{1,ijm})}\cdot Q_{ijml}{(K)}^{\frac{1+({\text{β}}_2+b_{2,i}+b_{2,ij}+b_{2,ijm})}{2}}+{\text{ε}}_{i,jml},$$

(4)

where L_ij(K), L_ijm(K), and L_ijml(K) are the lengths of internode K for the first-order branch j, the second-order branch m is located on the first-order branch j, and the third-order branch l is located on the second-order branch m on branch j for tree i, respectively. Q_ij(K), Q_ijm(K), and Q_ijml(K) are the biomasses of internode K for different order branches denoted with the same conventions as for length, β₁ and β₂ are fixed parameters, b_1,i and b_2,i are random parameters specific to tree i describing between-tree random effects, b_1,ij and b_2,ij are random parameters specific to the jth first-order branch of tree i describing between-first-order-branch random effects, b_1,ijm and b_2,imj are random parameters specific to second-order branch m on branch j of tree i describing between-second-order-branch random effects, and ε_i,j, ε_i,jm, and ε_i,jml are model errors. The random parameter vector (b_1,k, b_2,k) and model error ε_i,k, in which k is the object the random parameters are specific to, are assumed to be normally distributed with means of zero and variance-covariance matrices D and R, respectively. R is assumed to be δ_i,k²I, where δ_i,k²I, is the error variance and I is an identity matrix. D is assumed to be an unstructured variance-covariance matrix:

$$D=\left(\begin{array}{cc}{\sigma }_{1,k}^2& {\sigma }_{12,k}\\ {\sigma }_{21,k}& {\sigma }_{2,k}^2\end{array}\right)$$

where ${\text{σ}}_{1,k}^2$ and ${\text{σ}}_{2,k}^2$ are the variance of random parameters b_1,k and b_2,k on the k level, which describe the inter-tree and -branch variability of the parameters; ${\text{σ}}_{12,k}$ and ${\text{σ}}_{21,k}$ are the covariance between random parameters b_1,k and b_2,k in the Equations (2)–(4); and ${\text{σ}}_{12,k}$ = ${\text{σ}}_{21,k}$.

In this study, both shape and geometric parameters (or only one of them in the base model (Equation (1)) were assumed to be mixed, including fixed and random component parameters. They present random effects at the tree, first-order branch, and second-order branch levels. So, in total, we have three, nine, and 27 models to be tested with the combinations of random parameters for internodes on the first-, second-, and third-order branches, respectively (Table 3, Table 4 and Table 5).

Table 3. Values of AIC and BIC of mixed-effect models and the base model for first-order branches.

Model No.	Mixed-Effect Parameters	AIC	BIC
1	β1, β2	891.6	911.2
2	β1	910.3	923.3
3	β2	1100.2	1113.2
Base model		1220.2	1223.0

Table 3. Values of AIC and BIC of mixed-effect models and the base model for first-order branches.

Model No.	Mixed-Effect Parameters	AIC	BIC
1	β1, β2	891.6	911.2
2	β1	910.3	923.3
3	β2	1100.2	1113.2
Base model		1220.2	1223.0

Table 4. Values of AIC and BIC of mixed-effect models and the base model for the second-order branches.

Model No.	Mixed-Effect Parameters		AIC	BIC
	Tree Level	First-Order Branch Level
1	β1, β2	β1, β2	2098.2	2141.7
2	β1, β2	β1	2140.7	2174.6
3	β1, β2	β2	2165.4	2199.3
4	β1	β1, β2	2117.0	2150.9
5	β1	β1	2255.5	2279.7
6	β1	β2	2192.4	2216.6
7	β2	β1, β2	misconvergence
8	β2	β1	2355.0	2379.3
9	β2	β2	3154.1	3178.3
Base model			3376.0	3390.5

Table 4. Values of AIC and BIC of mixed-effect models and the base model for the second-order branches.

Model No.	Mixed-Effect Parameters		AIC	BIC
	Tree Level	First-Order Branch Level
1	β1, β2	β1, β2	2098.2	2141.7
2	β1, β2	β1	2140.7	2174.6
3	β1, β2	β2	2165.4	2199.3
4	β1	β1, β2	2117.0	2150.9
5	β1	β1	2255.5	2279.7
6	β1	β2	2192.4	2216.6
7	β2	β1, β2	misconvergence
8	β2	β1	2355.0	2379.3
9	β2	β2	3154.1	3178.3
Base model			3376.0	3390.5

Table 5. Values of AIC and BIC of mixed-effect models and the base model for the third-order branches.

Model No.	Mixed-Effect Parameters			AIC	BIC
	Tree Level	First-Order Branch Level	Second-Order Branch Level
1	β1, β2	β1, β2	β1, β2	misconvergence
2	β1, β2	β1, β2	β1	misconvergence
3	β1, β2	β1, β2	β2	572.4	613.5
4	β1, β2	β1	β1, β2	misconvergence
5	β1, β2	β1	β1	585.6	618.5
6	β1, β2	β1	β2	616.4	649.4
7	β1, β2	β2	β1, β2	misconvergence
8	β1, β2	β2	β1	558.0	590.9
9	β1, β2	β2	β2	622.9	655.8
10	β1	β1, β2	β1, β2	misconvergence
11	β1	β1, β2	β1	555.7	588.6
12	β1	β1, β2	β2	572.1	605.1
13	β1	β1	β1, β2	misconvergence
14	β1	β1	β1	604.8	629.5
15	β1	β1	β2	637.3	662.0
16	β1	β2	β1, β2	misconvergence
17	β1	β2	β1	564.6	589.3
18	β1	β2	β2	633.6	658.3
19	β2	β1, β2	β1, β2	misconvergence
20	β2	β1, β2	β1	554.0	587.0
21	β2	β1, β2	β2	570.2	603.1
22	β2	β1	β1, β2	misconvergence
23	β2	β1	β1	586.5	611.2
24	β2	β1	β2	621.6	646.3
25	β2	β2	β1, β2	misconvergence
26	β2	β2	β1	569.0	593.7
27	β2	β2	β2	696.5	721.2
Base model				763.8	776.2

Table 5. Values of AIC and BIC of mixed-effect models and the base model for the third-order branches.

Model No.	Mixed-Effect Parameters			AIC	BIC
	Tree Level	First-Order Branch Level	Second-Order Branch Level
1	β1, β2	β1, β2	β1, β2	misconvergence
2	β1, β2	β1, β2	β1	misconvergence
3	β1, β2	β1, β2	β2	572.4	613.5
4	β1, β2	β1	β1, β2	misconvergence
5	β1, β2	β1	β1	585.6	618.5
6	β1, β2	β1	β2	616.4	649.4
7	β1, β2	β2	β1, β2	misconvergence
8	β1, β2	β2	β1	558.0	590.9
9	β1, β2	β2	β2	622.9	655.8
10	β1	β1, β2	β1, β2	misconvergence
11	β1	β1, β2	β1	555.7	588.6
12	β1	β1, β2	β2	572.1	605.1
13	β1	β1	β1, β2	misconvergence
14	β1	β1	β1	604.8	629.5
15	β1	β1	β2	637.3	662.0
16	β1	β2	β1, β2	misconvergence
17	β1	β2	β1	564.6	589.3
18	β1	β2	β2	633.6	658.3
19	β2	β1, β2	β1, β2	misconvergence
20	β2	β1, β2	β1	554.0	587.0
21	β2	β1, β2	β2	570.2	603.1
22	β2	β1	β1, β2	misconvergence
23	β2	β1	β1	586.5	611.2
24	β2	β1	β2	621.6	646.3
25	β2	β2	β1, β2	misconvergence
26	β2	β2	β1	569.0	593.7
27	β2	β2	β2	696.5	721.2
Base model				763.8	776.2

2.4. Statistical Analysis

Model performances for different combinations of random parameters were evaluated using Akaike’s information criterion (AIC) and Schwarz’s Bayesian information criterion (BIC). The smaller the values of AIC and BIC, the better the model fits [49,50]. The significance of random effects was evaluated using the likelihood-ratio test. Comparison of the prediction capacities of the base model and mixed models was based on the graphical and numerical analysis of the residuals and the following goodness-of-fit statistics: average relative error (ARE) and root mean square error (RMSE). These were calculated by Equations (5) and (6):

$$ARE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{y_i-{\widehat{y}}_i}{y_i}}\times 100\%$$

(5)

$$RMSE=\sqrt{{\displaystyle \sum _{i=1}^n\frac{{\left(y_i-{\widehat{y}}_i\right)}^2}{n-k}}}$$

(6)

where y_i is the observed value, ${\widehat{y}}_i$ is the predicted value, n the sample size, and k the number of model parameters.

Among the 16 trees measured, the data for 13 Chinese pine trees were randomly selected for model calibration and the other three trees for model validation. All statistical computations were implemented in R by means of the nlme package [51].

3. Results

3.1. Variability in Internode Size and Biomass within and among Trees

The variability of internode length and biomass was measured by the coefficient of variation (CV). The average CVs of the length and biomass of internodes within trees were 0.664 and 0.709, 0.782 and 1.031, and 1.195 and 1.184 for the first-, second-, and third-order branches, respectively. The biomass of the internodes presented higher variation than the length, and that variation increased with branch order. This indicates that there are obvious size variations within trees. Similar trends were also observed among trees. The average CVs for the length and biomass of internodes among trees were 0.396 and 0.412, 0.754 and 0.593, and 0.588 and 1.717 for the first-, second-, and third-order branches, respectively.

Scatter plots of internode length and biomass for the different branch orders illustrate the variation of the curves (Figure 1). Figure 2 provides the approximate 95% confidence intervals for parameters β₁ and β₂ in Equation (1) for the tree at the first-order branch and second-order branch levels. Substantial variation was noted in the allometric relationships between internode length and biomass within and among trees. We further used box-plots to check the distribution of parameters (Figure 3), which also indicated the difference in the median and mean values among branches. Parameter β₁ is right-skewed, but β₂ is left-skewed or right-skewed. Therefore, parameters β₁ and β₂ can reasonably be considered random effects.

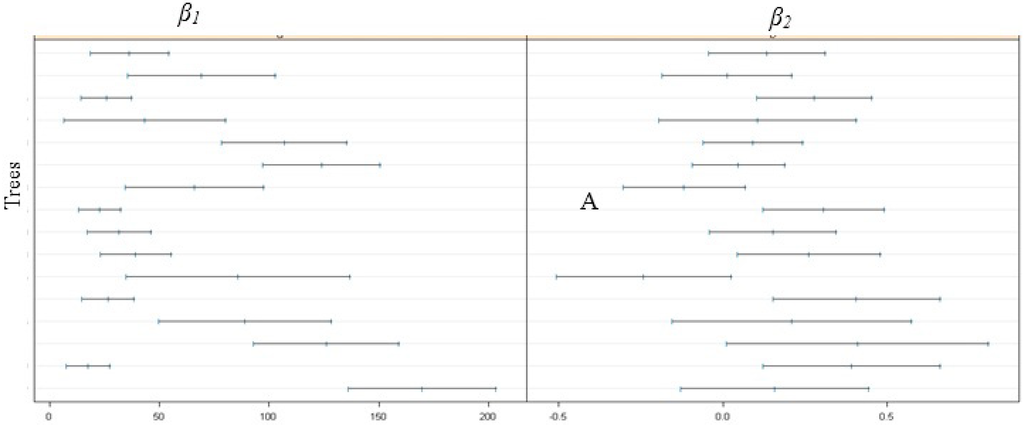
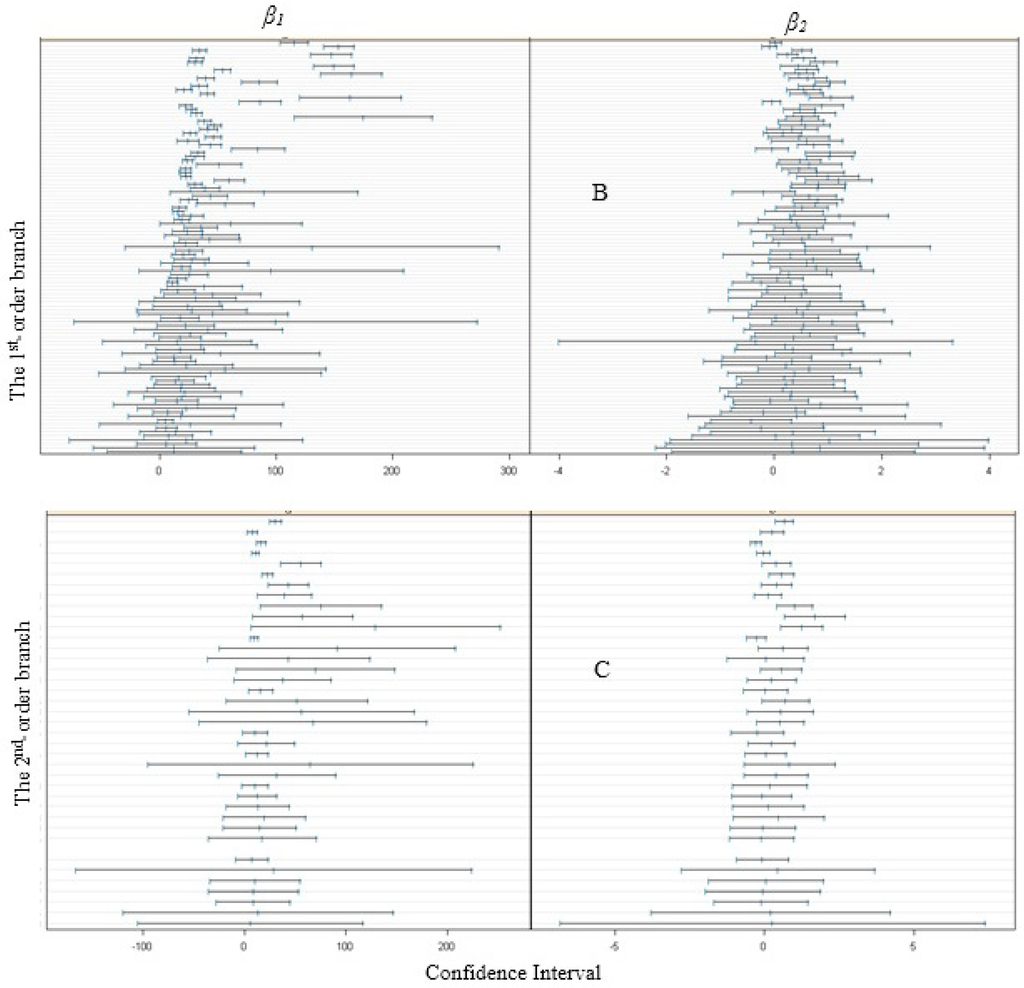
Figure 2. Confidence intervals of parameters β₁ and β₂ for individual Chinese pine trees or for branches (A: trees; B: the first-order branches; C: the second-order branches).

Figure 2. Confidence intervals of parameters β₁ and β₂ for individual Chinese pine trees or for branches (A: trees; B: the first-order branches; C: the second-order branches).

Figure 3. Box-plots of parameters β₁ and β₂ for the first-order branches, the second-order branches, and the third-order branches (dashed line indicates the mean value).

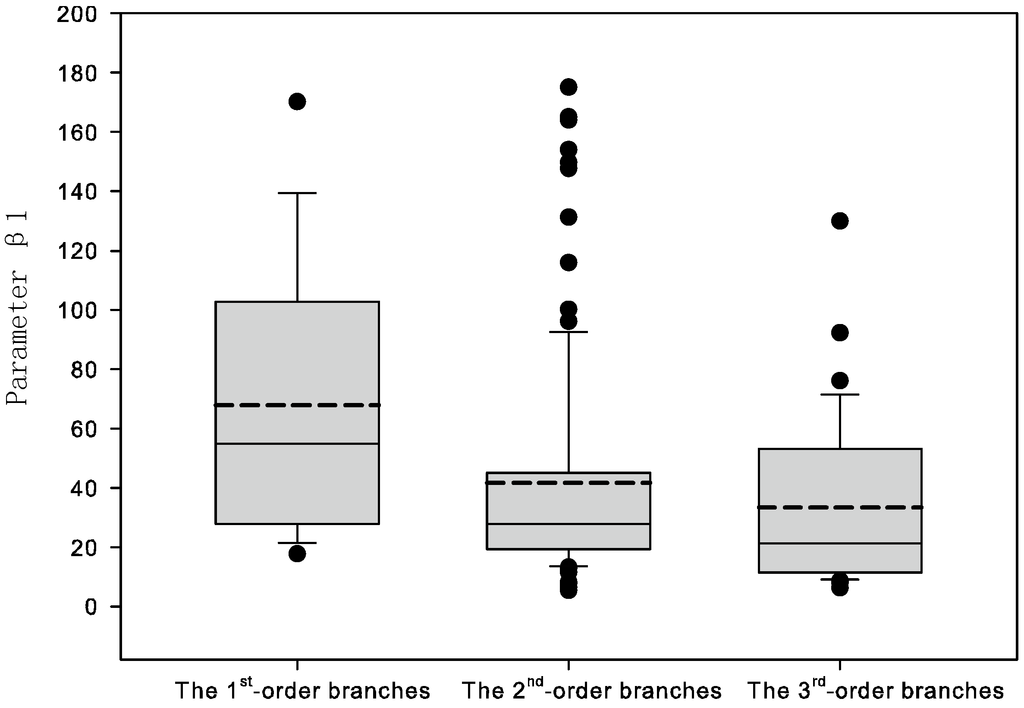
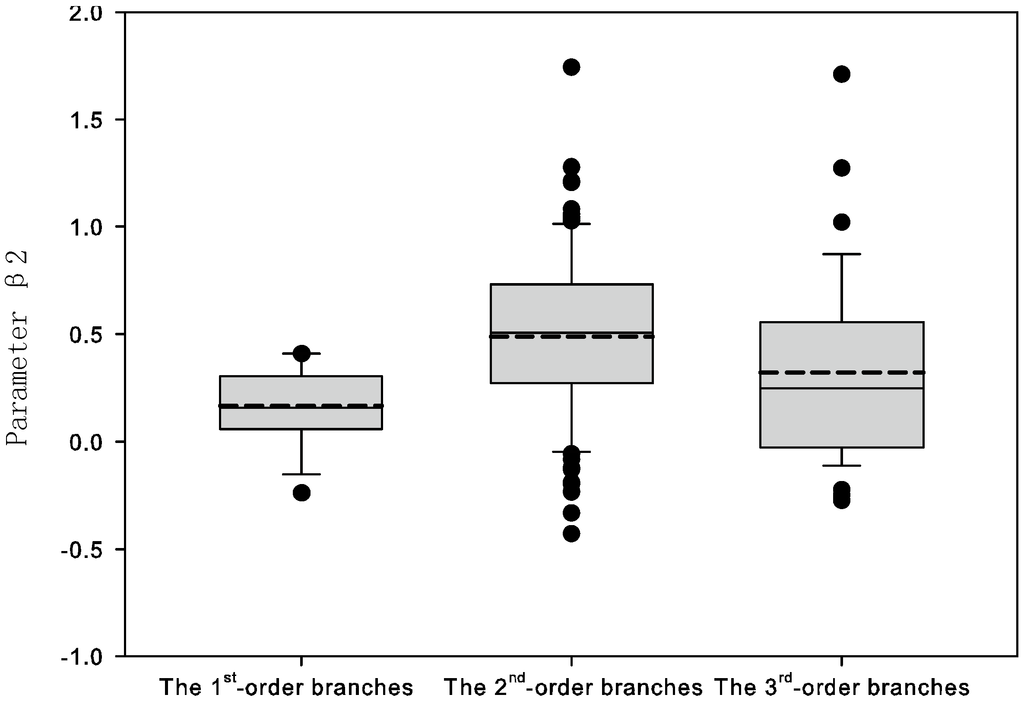
Figure 3. Box-plots of parameters β₁ and β₂ for the first-order branches, the second-order branches, and the third-order branches (dashed line indicates the mean value).

3.2. Model Fitting and Validation

All models with fixed and random parameters were evaluated based on the fit statistics AIC and BIC listed in Table 3, Table 4 and Table 5. The values of AIC and BIC for all mixed-effects models were smaller than those of the base models. We selected the three models with the smallest AIC and BIC for first-, second-, and third-order branches for further calibration.

For the first-order branches, the mixed-effect model 1 with two random effect parameters, b_1,i and b_2,i, was selected (Table 3). Model 1 in Table 4 was selected as the calibrated model for the internodes on the second-order branches, where the random effects of fixed parameters β₁ and β₂ were considered at both the tree and first-order branch levels. For the internodes on the third-order branches, model 20 (Table 5) was selected for further calibration, where the random effect of fixed parameter β₂ at the tree level, the random effects of fixed parameters β₁ and β₂ at the first-order branch level, and the random effects of fixed parameter β₁ at the third-order branch level were considered.

The parameters of the fixed part and the variance and covariance of the random part of each mixed-effect model are listed in Table 6. All random effects were statistically significant with the exception of the tree-level effect on β1 and the second-order branch-level effect on β2 for models of third-order branches, demonstrating significant variability in fixed parameters between and within trees, and within and between branches, and indicating the necessity of including random effects in the allometric model. Random effects accounted for a high proportion of the variance, but the importance of the hierarchal levels differed (Table 6). Parameters β1 and β2 varied much more between trees than between branches, which indicates that the random effects resulting from different trees are stronger than those resulting from different branches. For branches of the same order, the random effects characterized by their variance in allometric models decreased with increasing branch order (Table 6). To examine possible reasons behind the pattern of variability, we used box-plots of random effects for parameters β1 and β2 for the second- and third-order branches among different sites, ages and densities to illustrate the parameter distribution (Figure 4 and Figure 5). Those for the first-order branches were not plotted because of the scarcity of data. They indicated that the distributions of random parameters clearly differ among sites, ages, and densities.

Table 6. Estimates of parameters for mixed models.

Fixed Part	Parameter	First-Order Branches			Second-Order Branches			Third-Order Branches
	β1	94.792 (20.954)			59.992(13.234)			4.043(0.286)
	β2	0.122(0.042)			0.361(0.068)			0.513(0.036)
Random Part		Tree Level	Tree Level	First-Order Branch Level		Tree Level	First-Order Branch Level		Second-Order Branch Level
	${\sigma }_{1,k}^2$	5.478×103	2.153×103	93.700		-	2.651		0.248
	${\sigma }_{2,k}^2$	1.646 × 10−2	4.836 × 10−2	3.323 × 10−2		1.676 × 10−2	3.562 × 10−3		-
	${\sigma }_{12,k}^2$	−0.525	−0.592	0.709		-	0.879		-
	${\delta }^2$	3.514		0.378					0.116

Note: Standard errors are shown in parentheses.

Table 6. Estimates of parameters for mixed models.

Fixed Part	Parameter	First-Order Branches			Second-Order Branches			Third-Order Branches
	β1	94.792 (20.954)			59.992(13.234)			4.043(0.286)
	β2	0.122(0.042)			0.361(0.068)			0.513(0.036)
Random Part		Tree Level	Tree Level	First-Order Branch Level		Tree Level	First-Order Branch Level		Second-Order Branch Level
	${\sigma }_{1,k}^2$	5.478×103	2.153×103	93.700		-	2.651		0.248
	${\sigma }_{2,k}^2$	1.646 × 10−2	4.836 × 10−2	3.323 × 10−2		1.676 × 10−2	3.562 × 10−3		-
	${\sigma }_{12,k}^2$	−0.525	−0.592	0.709		-	0.879		-
	${\delta }^2$	3.514		0.378					0.116

Note: Standard errors are shown in parentheses.

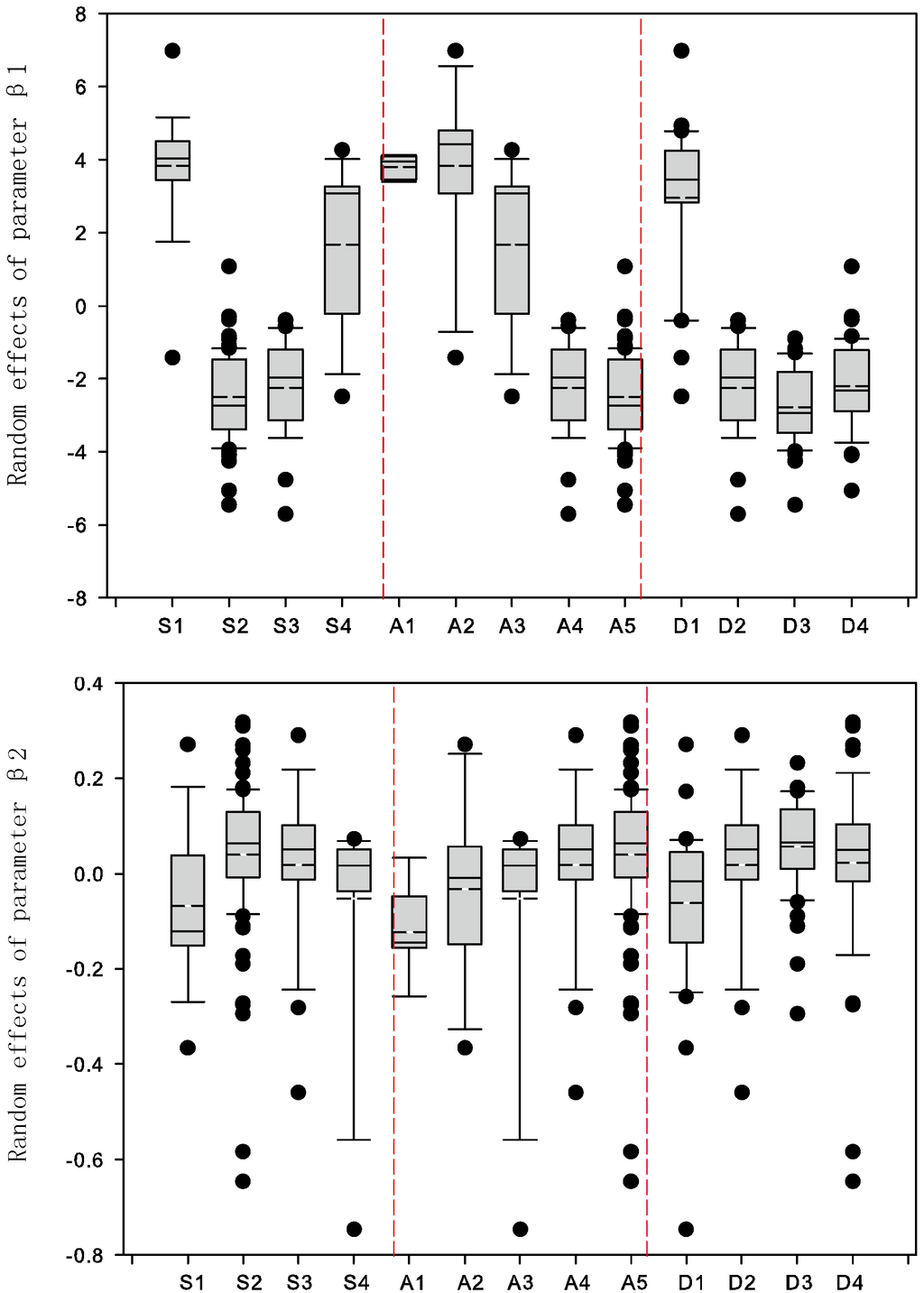
Figure 4. Box-plots of random effects for parameters β₁ and β₂ for the second-order branches by site (S1–S4), age (A1–A5), and density (D1–D4) (dashed line denotes the mean value).

Figure 4. Box-plots of random effects for parameters β₁ and β₂ for the second-order branches by site (S1–S4), age (A1–A5), and density (D1–D4) (dashed line denotes the mean value).

Figure 5. Box-plots of random effects for parameters β₁ and β₂ for the third-order branches by site (S1–S4), age (A1–A5), and density (D1–D4) (dashed line denotes the mean value).

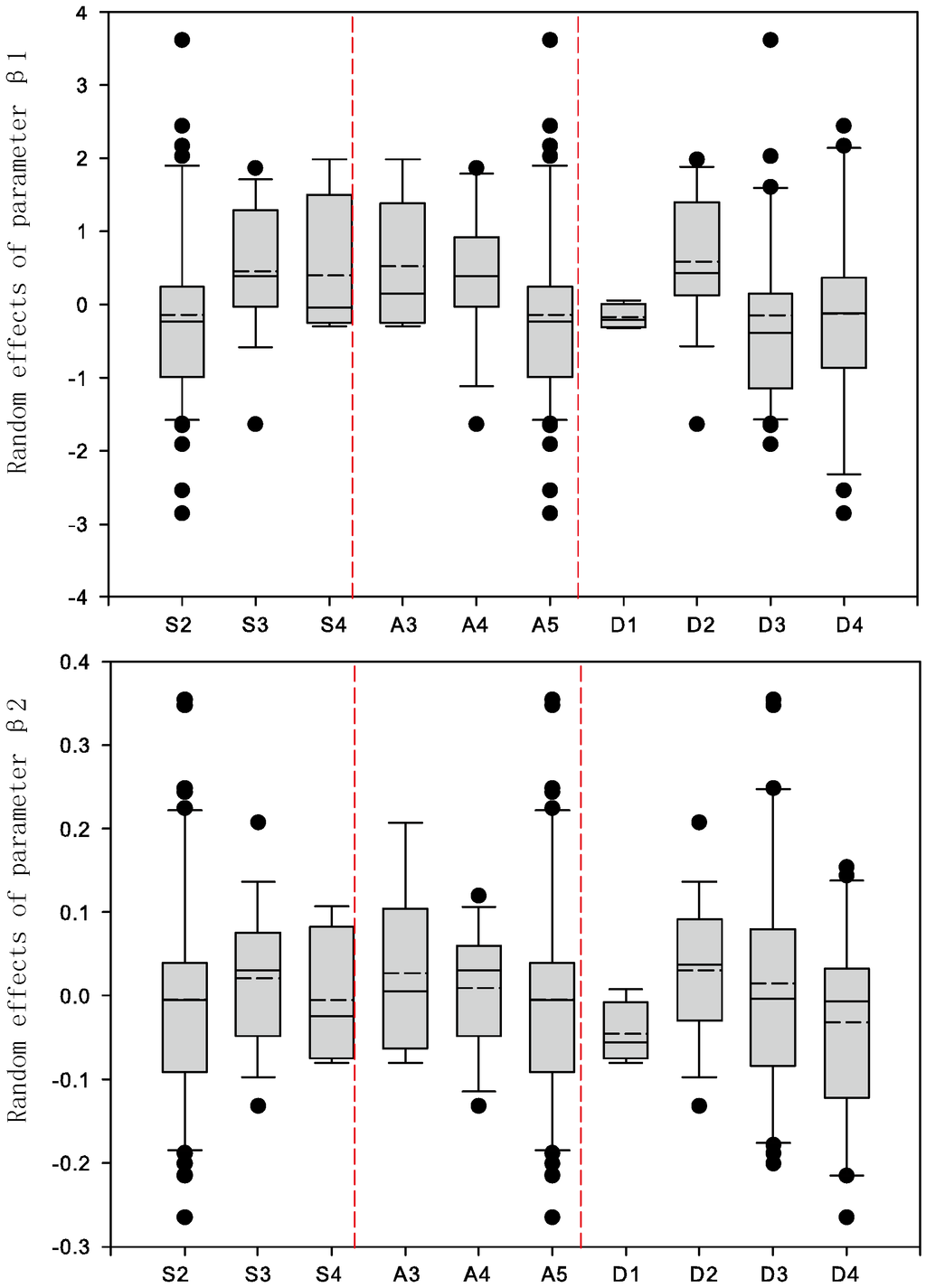
Figure 5. Box-plots of random effects for parameters β₁ and β₂ for the third-order branches by site (S1–S4), age (A1–A5), and density (D1–D4) (dashed line denotes the mean value).

The likelihood ratio test indicated that the model performances were improved by including random effects for all orders of branches. Compared with the base models for the first-, second- and third-order branches, the average relative error (ARE) and root mean squared error (RMSE) decreased by 69.14% and 60.82%, 46.43% and 25.35%, and 40.74% and 55.32%, respectively (Table 7). Residual distribution plots were constructed for the mixed-effect and base models (Figure 6). The inclusion of random effects in the models, which accounts for a large portion of the variability, effectively decreased the residuals and removed the heterogeneous residual variance. A one-sample Kolmogorov—Smirnov test indicated that the residuals of the mixed models are normally distributed (p = 0.383, 0.081, and 0.064 for Equations (2)–(4), respectively).

Table 7. Comparison between the base model and mixed model calibrations.

Branch Order	Models	ARE		ARE Reduction (%)		RMSE	RMSE Reduction (%)
1	Base model		0.071		−25.35	5.745	−69.14
	Mixed model		0.053			1.773
2	Base model		0.027		−40.74	1.460	−60.82
	Mixed model		0.016			0.572
3	Base model		0.047		−55.32	0.560	−46.43
	Mixed model		0.021			0.300

Table 7. Comparison between the base model and mixed model calibrations.

Branch Order	Models	ARE		ARE Reduction (%)		RMSE	RMSE Reduction (%)
1	Base model		0.071		−25.35	5.745	−69.14
	Mixed model		0.053			1.773
2	Base model		0.027		−40.74	1.460	−60.82
	Mixed model		0.016			0.572
3	Base model		0.047		−55.32	0.560	−46.43
	Mixed model		0.021			0.300

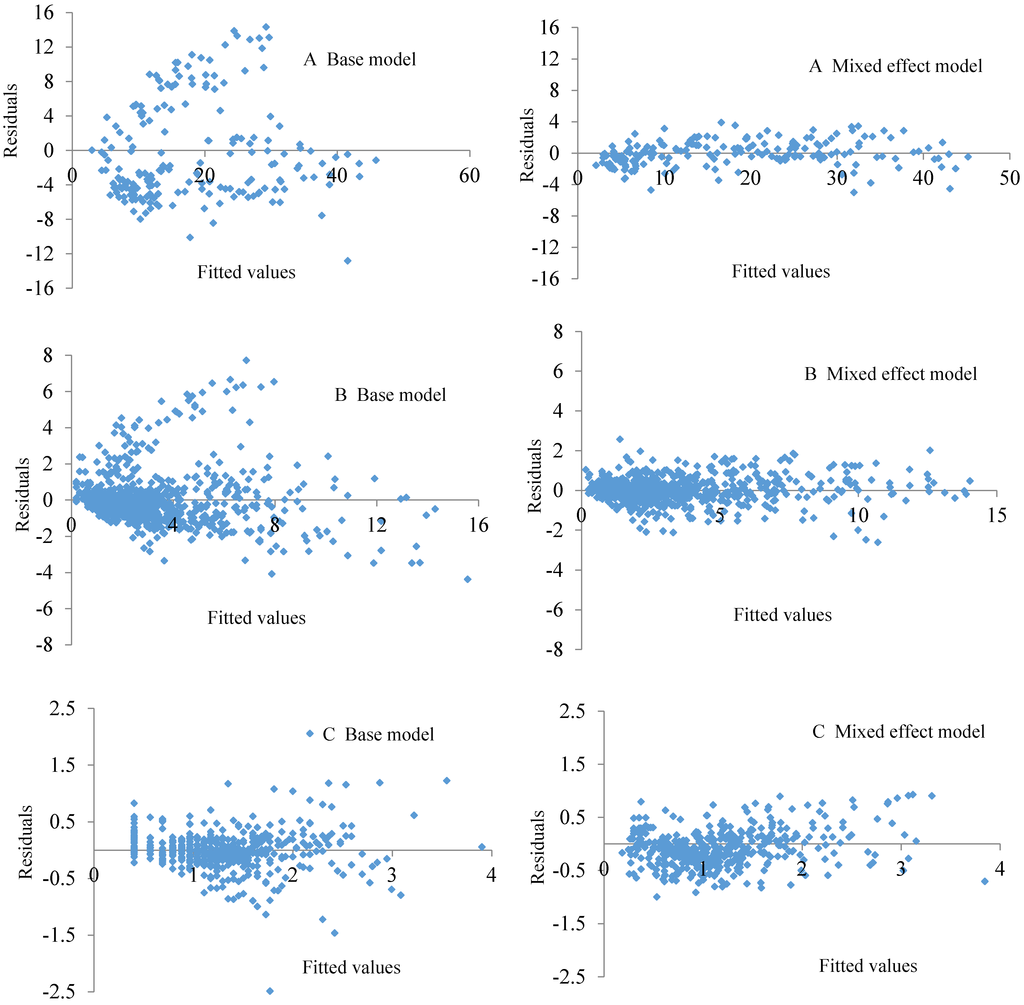
Figure 6. The distributions of residuals for the base models and mixed-effect models (A: First-order branches; B: Second-order branches; C: Third-order branches).

Figure 6. The distributions of residuals for the base models and mixed-effect models (A: First-order branches; B: Second-order branches; C: Third-order branches).

The internode length predicted by the mixed models was compared to the observed values on the basis of bias and precision using the reserved validation data (three trees). The ARE and RMSE were calculated for each branch order for model validation (Table 8). The results indicated that both the ARE and RMSE of the mixed-effect models decreased compared with those of the base models for all branch orders. The ARE and RMSE decreased by 13.97% and 41.67%, 37.68% and 13.63%, and by 85.16% and 56.06% compared with the base models for the first-, second- and third-order branches, respectively.

Table 8. Comparison between base model and mixed model validation.

Branch Order	Models	ARE	ARE Reduction (%)	RMSE	RMSEReduction (%)
1	Base model	0.087	−13.97	4.616	−13.63
	Mixed model	0.075		3.594
2	Base model	0.036	−41.67	1.226	−85.16
	Mixed model	0.021		0.182
3	Base model	0.069	−37.68	0.503	−56.06
	Mixed model	0.043		0.221

Table 8. Comparison between base model and mixed model validation.

Branch Order	Models	ARE	ARE Reduction (%)	RMSE	RMSEReduction (%)
1	Base model	0.087	−13.97	4.616	−13.63
	Mixed model	0.075		3.594
2	Base model	0.036	−41.67	1.226	−85.16
	Mixed model	0.021		0.182
3	Base model	0.069	−37.68	0.503	−56.06
	Mixed model	0.043		0.221

4. Discussion

Allometric relationships in organisms are considered a universal phenomenon; however, the fact that universal scaling exponents cannot be defined for trees has previously been noted [23,52]. Here we have, for the first time, been able to attribute internode allometry to trees and branches of different orders, and showed the variation of internode allometry at different levels using hierarchical nonlinear mixed-effect models. These mixed models provided more accurate parameter estimations. We found significant variability in internode allometry within and between trees and branches, which was quantified as the variances of the random effects of shape and geometric parameters in the model. Of the random variation, the variation in the allometric relationships occurring between trees was much greater than that between branches, and variation between lower-order branches was much greater than between higher-order branches. We also tested Equation (1) after log-transformation of both sides, i.e. Ln(L) and Ln (Q) were treated as dependent and independent variables, respectively. The log-transformed equation, however, did not change our conclusion on the variation of allometry among different scales. Additionally, the values of scaling coefficient increased from the first- to third-level branches but the values of scaling exponent showed the opposite, which implies a complicated biomass allocation pattern. This may be attributed to the nonlinear relationship between biomass and length, characterized as a convex downward curve on the log-log coordinates. It is tempting to consider our findings with regard to the debate surrounding the mechanistic basis of metabolic scaling explained through the West, Brown, and Enquist (WBE) theory [53] or the Dynamic Energy Budget (DEB) theory [54,55,56,57,58,59,60]. Our results on the allometry between internode length and biomass were inconsistent with universal models such as elastic similarity, stress similarity, geometric similarity, and WBE, according to the results of Price [15]. This may further confirm the conclusion that universal scaling exponents cannot be defined for trees [23,52].

Many biotic and abiotic factors, as suggested by previous studies, may potentially affect allometric relationships, including genetics, ontogeny, size, age, structure, site, climate, and their interactions [2,25,26,31,54,61,62,63]. As shown in Figure 4 and Figure 5, parameters of the allometric equations for different sites, age groups, and stand densities were heterogeneous at different scales, which implied that site, age, and stand density are attributed to the variation of internode allometry within and among Chinese pine trees. Trees in different development stages have different growth patterns caused by chronological changes in light conditions, as illustrated by dynamic height-diameter allometry [64]. Site characteristics reflect local climate, soil, and topology, which affect internode (last internode of branches in this study) growth. Trees within a high-density stand always have strong competition from neighbors, which means they may receive limited light intensity, water, and nutrition during primary growth. Such competition-related phenotypic plasticity has been observed [41,65]. Besides the effects of stand age, site, and density, the topological position and the orientation of branches within trees are possible sources of variability, which can lead to a heterogeneous light environment; however, their effects are low compared with the allometric relationships among trees.

A constant allometry rule between the length and biomass of internodes in the GreenLab model (where branches belonging to the same order are identical) has been validated for crops and tree species in the literature [32,44]; however, random processes for growth, death, and branch pattern have also been applied to characterize stochastic structure and functioning in different versions of the GreenLab functional-structural model [66,67], especially stochastic modeling of annual tree shoot dynamics in the recent GL5 version [68]. In this study, single-level, nested two-level and nested three-level nonlinear mixed-effect models were developed for the internode allometry of first-, second-, and third-order branches of Chinese Pine, respectively. The random effects of the mixed models were significant at the tree, first-order, and second-order branch levels. The mixed models address coherence and variation by setting the structure of variance and covariance in the random part, thus improving the prediction accuracy of the model. The results indicated that all errors in the mixed models decrease compared to those of the base models for all branch orders. Ma et al. [69] evaluated the stability of GreenLab parameters in response to maize individuals from a common population, individuals from populations subjected to different environments (seasons), and different development stages of the same individuals by comparing their CVs. They concluded that parameter values were largely independent of developmental stage, but mean allometric mass ratios (the mean of the ratios of leaf blade to above-ground, leaf sheath to above-ground, internode/above-ground, and cob/above-ground), only showed 12.5% and 2.1% variation among seasons, inter- and intra-season, respectively. Unlike crops, trees have a complicated architecture and a more heterogeneous environment. There are some implications for the application of FSPM from our above findings. Tree- or branch-specific allometric models should be developed instead of averaged models to obtain unbiased and accurate internode length predictions. Such models will be useful in determining internode shape and generating stochastic structure as simulated using stochastic models [35,68,70], which will affect light interception, photosynthesis, and tree architecture in functional-structural modeling. Information about the allometric relationships of trees can be used in models to constrain the form and structure of trees to ensure that they conform to natural systems. The variation among trees and branches leads us to suggest that replication of the mid-internode sampling is required for accurate estimates of the internode mean. The study did not prove that estimation of internode allometry could improve the model quality of GreenLab since we neglected the functional part, but the tree- and branch-specific shape parameters and geometric parameters of internodes can be applied and tested in the GreenLab model in the future. Although we quantified the variation in internode allometry within the GreenLab framework, the methodology and conclusion have universal implications for functional-structural tree models.

5. Conclusions

An allometric model of internodes is of great importance for determining the shape of internodes in functional-structural tree modeling. We examined the variability of internode allometry by describing the relationship between internode length and biomass in Pinus tabulaeformis Carr. trees using a multilevel nonlinear mixed-effect model. We found that there was significant variability in allometry at the tree and different-order branch levels, and the variability decreased from trees, first-order branches to second-order branches. Therefore, tree- and branch-specific allometric models are recommended to produce unbiased and accurate internode length estimations with biological significance. The new model can be useful for improved descriptions and understanding of the structure and functioning of trees.