A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Site and Field Measurements
2.2. Unmanned Aerial System Survey
2.2.1. Small UAS Platform and the Sensor Used in the Present Study

2.2.2. UAS Survey
2.3. LiDAR Data
2.4. Photogrammetric Workflow
- Generation of tie points based on the scale-invariant feature transform (SIFT) feature extractor [51].
- Camera calibration and image triangulation: the Apero tool [52] uses both a computer vision approach for the estimation of the initial solution and photogrammetry for a rigorous bundle block adjustment [53] (automatic aerial triangulation). Internal orientation (camera calibration) may be modeled by various polynomials.
2.4.1. Tie Point, Camera Calibration and Relative Orientation
2.4.2. Photo-DSM Georeferencing by Co-Registration with LiDAR-DSM
2.4.3. Dense Matching Strategy
| Parameters | Value for Matching Strategy with Malt |
|---|---|
| Image pyramids | 1:64–1:64–1:32–1:16–1:8–1:4–1:2–1:2 |
| Regularization factor | 0.005 |
| Correlation window size | 3 × 3 |
| Minimum correlation coefficient | 0 |
| Minimal number of images visible in each ground point | 3 |
| Parameters | Value for Matching Strategy with MICMAC |
| Image pyramids | 1:32–1:16-1:16–1:16–1:8–1:4 |
| Altimetric dilatation | 15–15–8–8–8–8 |
| Regularization factor | 0.05–0.05–0.001–0.001–0.001–0.003 |
| Correlation window size | 3 × 3 |
| Minimum correlation coefficient | 0 |
| Minimal number of image visible in each ground point | 3 |
2.5. Investigation of Photo-CHM Quality
- Window level: metrics using 20 m × 20 m windows were computed for both CHMs and correlation coefficients between photo-CHM and LiDAR-CHM metrics were calculated. This comparison technique was first introduced by St-Onge et al. [32]. The technique gives an overall idea of the photo-CHM and LiDAR-CHM correlation stand metrics, but has only a poor ecological meaning. Metrics were correlated only for forested windows: crop fields and meadow areas were therefore discarded. Forested areas were identified by means of the forest stand localization map and a mean height threshold of 3 m.
- Stand level: stand models were constructed based on inventory data (plot inventory) for predicting dominant height. The model residual (residual mean square error) and the model fit coefficient () served as indicators of CHMs quality. For each CHM, two regression models were adjusted, the first with one single explanatory variable and the second with two explanatory variables. The selection of these variables was performed with the best subset regression analysis.
- Tree level: the model for individual tree heights was established. Tree crowns were delineated by hand by a photo interpreter, and metrics were computed on this crown area. The best model, using only one metric, was selected using the best subset regression procedure. Its performance was presented in terms of RMSE (residual mean square error) and model fit coefficient ().
3. Results
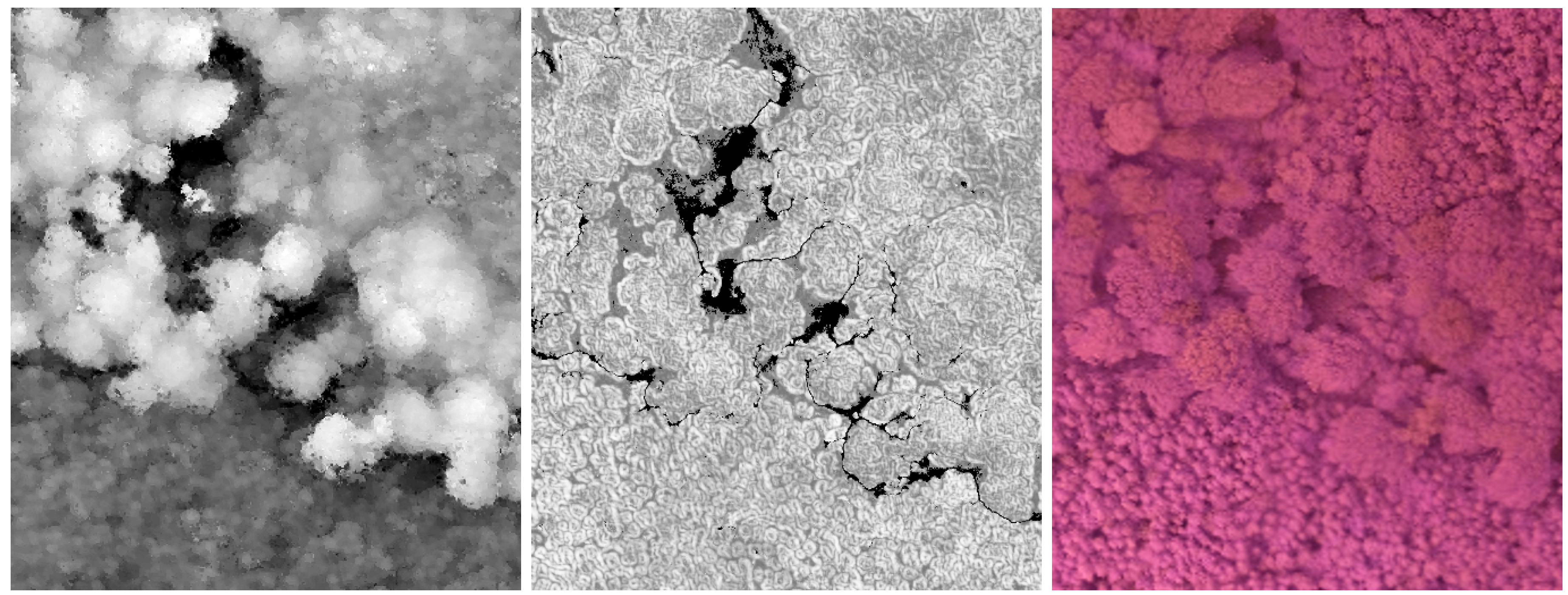
3.1. Photo-DSM Generation


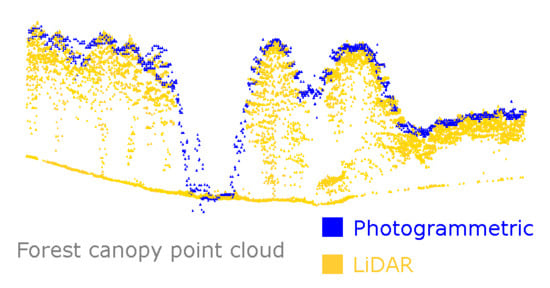
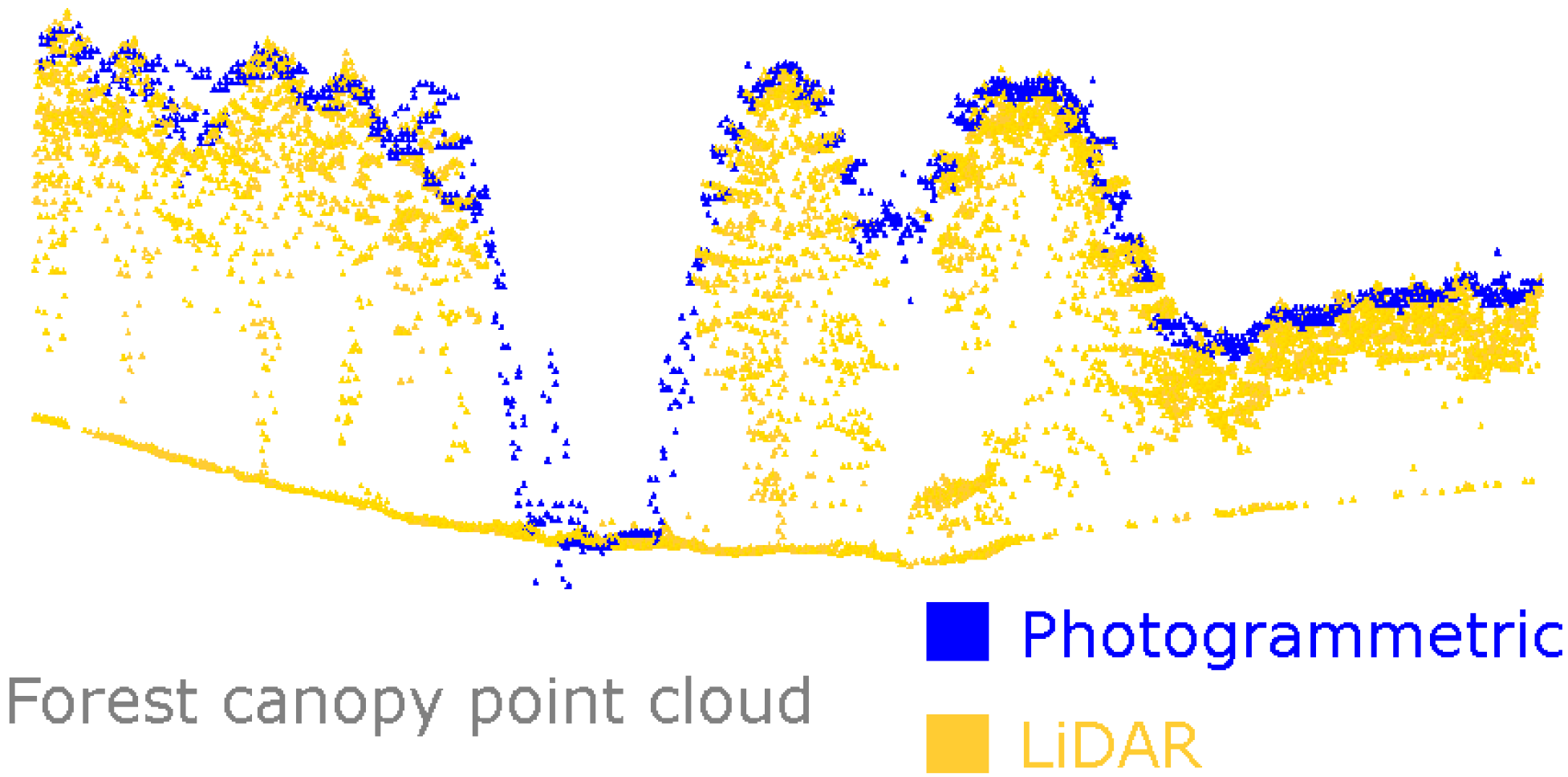
3.2. Investigation of Photo-CHM Quality
3.2.1. Overall Comparison of Photo-CHM and LiDAR-CHM

| Photo-CHM Metrics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | ||||||||||||
| LiDAR-CHM Metrics | Mean | 0.96 | 0.67 | 0.93 | 0.95 | 0.91 | 0.86 | 0.85 | 0.84 | 0.82 | 0.80 | 0.74 |
| p0 | 0.17 | 0.27 | 0.20 | 0.16 | 0.12 | 0.10 | 0.10 | 0.10 | 0.09 | 0.09 | 0.07 | |
| p25 | 0.87 | 0.77 | 0.92 | 0.84 | 0.76 | 0.69 | 0.67 | 0.66 | 0.64 | 0.62 | 0.56 | |
| p50 | 0.96 | 0.62 | 0.93 | 0.96 | 0.90 | 0.84 | 0.82 | 0.81 | 0.78 | 0.76 | 0.72 | |
| p75 | 0.93 | 0.49 | 0.83 | 0.93 | 0.95 | 0.92 | 0.91 | 0.89 | 0.87 | 0.85 | 0.81 | |
| p90 | 0.88 | 0.42 | 0.76 | 0.87 | 0.93 | 0.94 | 0.94 | 0.93 | 0.92 | 0.90 | 0.86 | |
| p925 | 0.87 | 0.41 | 0.75 | 0.86 | 0.92 | 0.94 | 0.93 | 0.93 | 0.92 | 0.90 | 0.86 | |
| p95 | 0.86 | 0.39 | 0.73 | 0.84 | 0.91 | 0.93 | 0.93 | 0.93 | 0.92 | 0.91 | 0.87 | |
| p975 | 0.85 | 0.38 | 0.72 | 0.82 | 0.89 | 0.92 | 0.92 | 0.92 | 0.92 | 0.91 | 0.88 | |
| p99 | 0.83 | 0.37 | 0.71 | 0.81 | 0.88 | 0.91 | 0.91 | 0.92 | 0.92 | 0.91 | 0.88 | |
| p100 | 0.80 | 0.35 | 0.68 | 0.78 | 0.85 | 0.88 | 0.88 | 0.89 | 0.89 | 0.89 | 0.86 | |
3.2.2. Window Level
3.2.3. Stand Level
| Mean | Minimum | Maximum | Standard Deviation | |
|---|---|---|---|---|
| Plot radius (m) | 13.2 | 7.4 | 18 | 3.8 |
| Number of trees (n/ha) | 537.3 | 69 | 1,395 | 336.7 |
| Basal area (m2/ha) | 21.8 | 3.6 | 46.2 | 9.8 |
| Total volume (m3/ha) | 277 | 25.1 | 570.1 | 147.6 |
| Dominant height (m) | 19.7 | 9.6 | 27.3 | 3.9 |
| CHM | ID | Regression Model Form | Explanatory | Adjusted | RMSE (m) | RMSE (%) |
|---|---|---|---|---|---|---|
| Variable(s) | ||||||
| Photo-CHM | 1 | 0.82 | 1.68 | 8.5 | ||
| Photo-CHM | 2 | , | 0.82 | 1.65 | 8.4 | |
| LiDAR-CHM | 3 | 0.86 | 1.45 | 7.4 | ||
| LiDAR-CHM | 4 | , | 0.86 | 1.45 | 7.4 |
3.2.4. Tree Level
| CHM | Explanatory Variable | Adjusted | RMSE (m) | RMSE (%) | |
|---|---|---|---|---|---|
| Photo-CHM | 0.91 | 1.04 | 4.7 | 1.58 | |
| LiDAR-CHM | 0.94 | 0.83 | 3.7 | 1.23 |
4. Conclusions and Perspectives
Acknowledgments
Conflicts of Interest
References
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Watson, C. An automated technique for generating georectified mosaics from ultra-high resolution unmanned aerial vehicle (UAV) imagery, based on structure from motion (SfM) point clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Koh, L.P.; Wich, S.A. Dawn of drone ecology: Low-cost autonomous aerial vehicles for conservation. Trop. Conserv. Sci. 2012, 5, 121–132. [Google Scholar]
- Haala, N. Comeback of digital image matching. Photogram. Week 2009, 9, 289–301. [Google Scholar]
- Pierrot-Deseilligny, M.; Clery, I. Évolutions récentes en photogrammétrie et modélisation 3d par photo des milieux naturels. Collect. EDYTEM 2011, 12, 51–64. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the world from internet photo collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Baltsavias, E.; Gruen, A.; Eisenbeiss, H.; Zhang, L.; Waser, L.T. High-quality image matching and automated generation of 3D tree models. Int. J. Remote Sens. 2008, 29, 1243–1259. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. Remote sensing of vegetation structure using computer vision. Remote Sens. 2010, 2, 1157–1176. [Google Scholar] [CrossRef]
- Corona, P.; Fattorini, L. Area-based lidar-assisted estimation of forest standing volume. Can. J. For. Res. 2008, 38, 2911–2916. [Google Scholar] [CrossRef]
- Steinmann, K.; Mandallaz, D.; Ginzler, C.; Lanz, A. Small area estimations of proportion of forest and timber volume combining lidar data and stereo aerial images with terrestrial data. Scand. J. For. Res. 2013, 28, 373–385. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, A.; Söderman, U. Laser scanning of forest resources: The Nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. J. Photogram. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Zimble, D.A.; Evans, D.L.; Carlson, G.C.; Parker, R.C.; Grado, S.C.; Gerard, P.D. Characterizing vertical forest structure using small-footprint airborne LiDAR. Remote Sens. Environ. 2003, 87, 171–182. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Packalén, P.; Hyyppä, H. Estimation of stem volume using laser scanning-based canopy height metrics. Forestry 2006, 79, 217–229. [Google Scholar] [CrossRef]
- Miura, N.; Jones, S.D. Characterizing forest ecological structure using pulse types and heights of airborne laser scanning. Remote Sens. Environ. 2010, 114, 1069–1076. [Google Scholar] [CrossRef]
- Jaskierniak, D.; Lane, P.N.J.; Robinson, A.; Lucieer, A. Extracting LiDAR indices to characterise multilayered forest structure using mixture distribution functions. Remote Sens. Environ. 2011, 115, 573–585. [Google Scholar] [CrossRef]
- Zhao, K.G.; Popescu, S.; Meng, X.L.; Pang, Y.; Agca, M. Characterizing forest canopy structure with lidar composite metrics and machine learning. Remote Sens. Environ. 2011, 115, 1978–1996. [Google Scholar] [CrossRef]
- Lindberg, E.; Hollaus, M. Comparison of methods for estimation of stem volume, stem number and basal area from airborne laser scanning data in a hemi-boreal forest. Remote Sens. 2012, 4, 1004–1023. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. ISPRS J. Photogram. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Progr. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Véga, C.; St-Onge, B. Mapping site index and age by linking a time series of canopy height models with growth curves. For. Ecol. Manag. 2009, 257, 951–959. [Google Scholar] [CrossRef]
- Véga, C.; St-Onge, B. Height growth reconstruction of a boreal forest canopy over a period of 58 years using a combination of photogrammetric and lidar models. Remote Sens. Environ. 2008, 112, 1784–1794. [Google Scholar] [CrossRef]
- Huang, H.; Gong, P.; Cheng, X.; Clinton, N.; Li, Z. Improving measurement of forest structural parameters by co-registering of high resolution aerial imagery and low density LiDAR data. Sensors 2009, 9, 1541–1558. [Google Scholar] [CrossRef] [PubMed]
- Bohlin, J.; Wallerman, J.; Fransson, J.E.S. Forest variable estimation using photogrammetric matching of digital aerial images in combination with a high-resolution DEM. Scand. J. For. Res. 2012, 27, 692–699. [Google Scholar] [CrossRef]
- Mora, B.; Wulder, M.A.; Hobart, G.W.; White, J.C.; Bater, C.W.; Gougeon, F.A.; Varhola, A.; Coops, N.C. Forest inventory stand height estimates from very high spatial resolution satellite imagery calibrated with lidar plots. Int. J. Remote Sens. 2013, 34, 4406–4424. [Google Scholar] [CrossRef]
- Nurminen, K.; Karjalainen, M.; Yu, X.; Hyyppä, J.; Honkavaara, E. Performance of dense digital surface models based on image matching in the estimation of plot-level forest variables. ISPRS J. Photogram. Remote Sens. 2013, 83, 104–115. [Google Scholar] [CrossRef]
- White, J.; Wulder, M.; Vastaranta, M.; Coops, N.; Pitt, D.; Woods, M. The utility of image-based point clouds for forest inventory: A comparison with airborne laser scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- Eisenbeiss, H. UAV Photogrammetry. Ph.D. Thesis, ETH, Zurich, Switzerland, 2009. [Google Scholar]
- St-Onge, B.; Vega, C.; Fournier, R.A.; Hu, Y. Mapping canopy height using a combination of digital stereo-photogrammetry and lidar. Int. J. Remote Sens. 2008, 29, 3343–3364. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Tao, W.; Lei, Y.; Mooney, P. Dense Point Cloud Extraction from UAV Captured Images in Forest Area. In Proceedings of the 2011 IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services (ICSDM), Fuzhou, China, 29 June–1 July 2011; pp. 389–392.
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR system with application to forest inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Jaakkola, A.; Hyyppä, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomäki, M.; Lin, Y. A low-cost multi-sensoral mobile mapping system and its feasibility for tree measurements. ISPRS J. Photogram. Remote Sens. 2010, 65, 514–522. [Google Scholar] [CrossRef]
- Rondeux, J. La Mesure des Arbres et des Peuplements Forestiers; Presses Agronomiques de Gembloux: Gembloux, Belgium, 1999. [Google Scholar]
- Kitahara, F.; Mizoue, N.; Yoshida, S. Effects of training for inexperienced surveyors on data quality of tree diameter and height measurements. Silv. Fenn. 2010, 44, 657–667. [Google Scholar] [CrossRef]
- Description of the Gatewing X100. Available online: http://uas.trimble.com/X100 (accessed on 4 September 2013).
- Laliberte, A.S.; Winters, C.; Rango, A. UAS remote sensing missions for rangeland applications. Geocarto Int. 2011, 26, 141–156. [Google Scholar] [CrossRef]
- Dunford, R.; Michel, K.; Gagnage, M.; Piegay, H.; Tremelo, M. Potential and constraints of unmanned aerial vehicle technology for the characterization of Mediterranean riparian forest. Int. J. Remote Sens. 2009, 30, 4915–4935. [Google Scholar] [CrossRef]
- Wolf, P.; Dewitt, B. Elements of Photogrammetry: With Applications in GIS, 3rd ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Aber, J.; Marzolff, I.; Ries, J. Small-Format Aerial Photography: Principles, Techniques and Applications; Elsevier Science: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Hodgson, M.E.; Jensen, J.; Raber, G.; Tullis, J.; Davis, B.A.; Thompson, G.; Schuckman, K. An evaluation of lidar-derived elevation and terrain slope in leaf-off conditions. Photogram. Eng. Remote Sens. 2005, 71, 817. [Google Scholar] [CrossRef]
- Suarez, J.; Ontiveros, C.; Smith, S.; Snape, S. Use of airborne LiDAR and aerial photography in the estimation of individual tree heights in forestry. Comput. Geosci. 2005, 31, 253–262. [Google Scholar] [CrossRef]
- Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.E.; Carson, W.W. Accuracy of a high-resolution lidar terrain model under a conifer forest canopy. Can. J. Remote Sens. 2003, 29, 527–535. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Mills, J.P.; Delgado, J.; Aguilar, M.A.; Negreiros, J.G.; Perez, J.L. Modelling vertical error in LiDAR-derived digital elevation models. ISPRS J. Photogram. Remote Sens. 2010, 65, 103–110. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, J.; Hao, L. Photogrammetric processing of low-altitude images acquired by unpiloted aerial vehicles. Photogram. Record 2011, 26, 190–211. [Google Scholar] [CrossRef]
- Läbe, T.; Förstner, W. Geometric Stability of Low-Cost Digital Consumer Cameras. In Proceedings of the 20th ISPRS Congress, Istanbul, Turkey, 12–23 July 2004; pp. 528–535.
- Presentation of the Photogrammetric Suite MICMAC. Available online: http://www.micmac.ign.fr/ (accessed on 4 September 2013).
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Pierrot-Deseilligny, M.; Clery, I. Apero, an Open Source Bundle Adjustment Software for Automatic Calibration and Orientation of Set of Images. In Proceedings of the ISPRS Symposium, 3D-ARCH 2011, Trento, Italy, 24 March 2011.
- Triggs, B.; McLauchlan, P.; Hartley, R.; Fitzgibbon, A. Bundle Adjustment—A Modern Synthesis. In Vision Algorithms: Theory and Practice; Springer-Verlag: Berlin Heidelberg, Germany, 2000; pp. 298–372. [Google Scholar]
- Pierrot-Deseilligny, M.; Paparoditis, N. A multiresolution and optimization-based image matching approach: An application to surface reconstruction from SPOT5-HRS stereo imagery. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2006, 36, 73–77. [Google Scholar]
- Roy, S.; Cox, I.J. A Maximum-Flow Formulation of the n-Camera Stereo Correspondence Problem. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 492–499.
- CloudCompare (Version 2.3) (GPL Software); EDF R&D and Telecom ParisTech: Paris, France, 2011. Available online: http://www.danielgm.net/cc/ (accessed on 4 September 2013).
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Patt. Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Kasser, M.; Egels, Y. Digital Photogrammetry; Taylor & Francis: London, UK, 2002. [Google Scholar]
- Järnstedt, J.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Holopainen, M.; Viitala, R. Forest variable estimation using a high-resolution digital surface model. ISPRS J. Photogram. Remote Sens. 2012, 74, 78–84. [Google Scholar] [CrossRef]
- Kraus, K.; Karel, W.; Briese, C.; Mandlburger, G. Local accuracy measures for digital terrain models. Photogram. Record 2006, 21, 342–354. [Google Scholar] [CrossRef]
- Lin, S.Y.; Muller, J.P.; Mills, J.P.; Miller, P.E. An assessment of surface matching for the automated co-registration of MOLA, HRSC and HiRISE DTMs. Earth Planet. Sci. Lett. 2010, 294, 520–533. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2011. [Google Scholar]
- Gruen, A. Development and status of image matching in photogrammetry. Photogram. Record 2012, 27, 36–57. [Google Scholar] [CrossRef]
- St-Onge, B.; Jumelet, J.; Cobello, M.; Véga, C. Measuring individual tree height using a combination of stereophotogrammetry and lidar. Can. J. For. Res. 2004, 34, 2122–2130. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests 2013, 4, 922-944. https://doi.org/10.3390/f4040922
Lisein J, Pierrot-Deseilligny M, Bonnet S, Lejeune P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests. 2013; 4(4):922-944. https://doi.org/10.3390/f4040922
Chicago/Turabian StyleLisein, Jonathan, Marc Pierrot-Deseilligny, Stéphanie Bonnet, and Philippe Lejeune. 2013. "A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery" Forests 4, no. 4: 922-944. https://doi.org/10.3390/f4040922
APA StyleLisein, J., Pierrot-Deseilligny, M., Bonnet, S., & Lejeune, P. (2013). A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests, 4(4), 922-944. https://doi.org/10.3390/f4040922