Assessment of Potential Crown Fire Danger in Major Forest Types of the Da Xing’anling (Inner Mongolia) Mountains, China
Abstract
1. Introduction
2. Materials and Methods
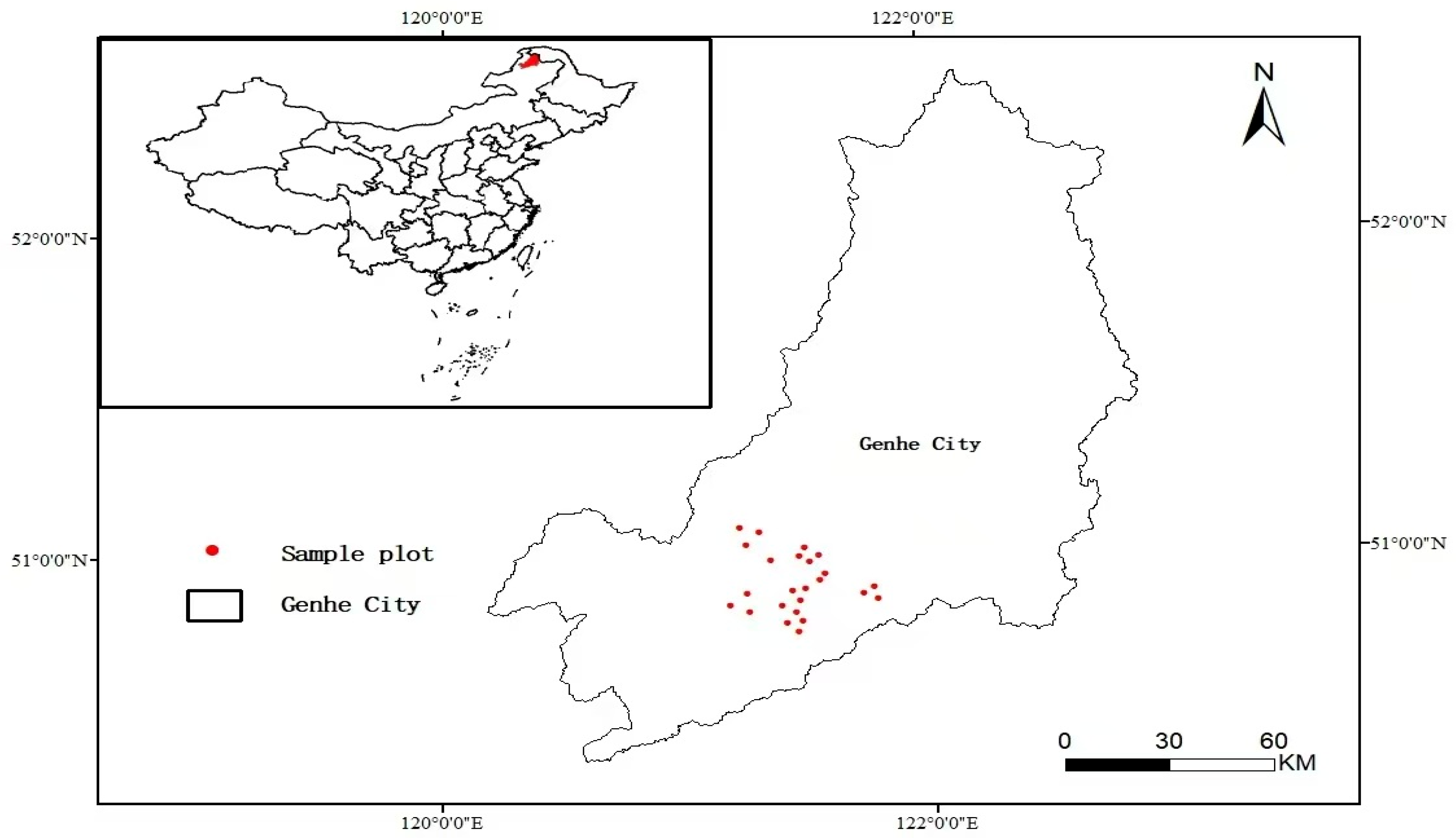
2.1. Overview of the Study Area
2.2. Sample Survey
2.3. Research Methodology
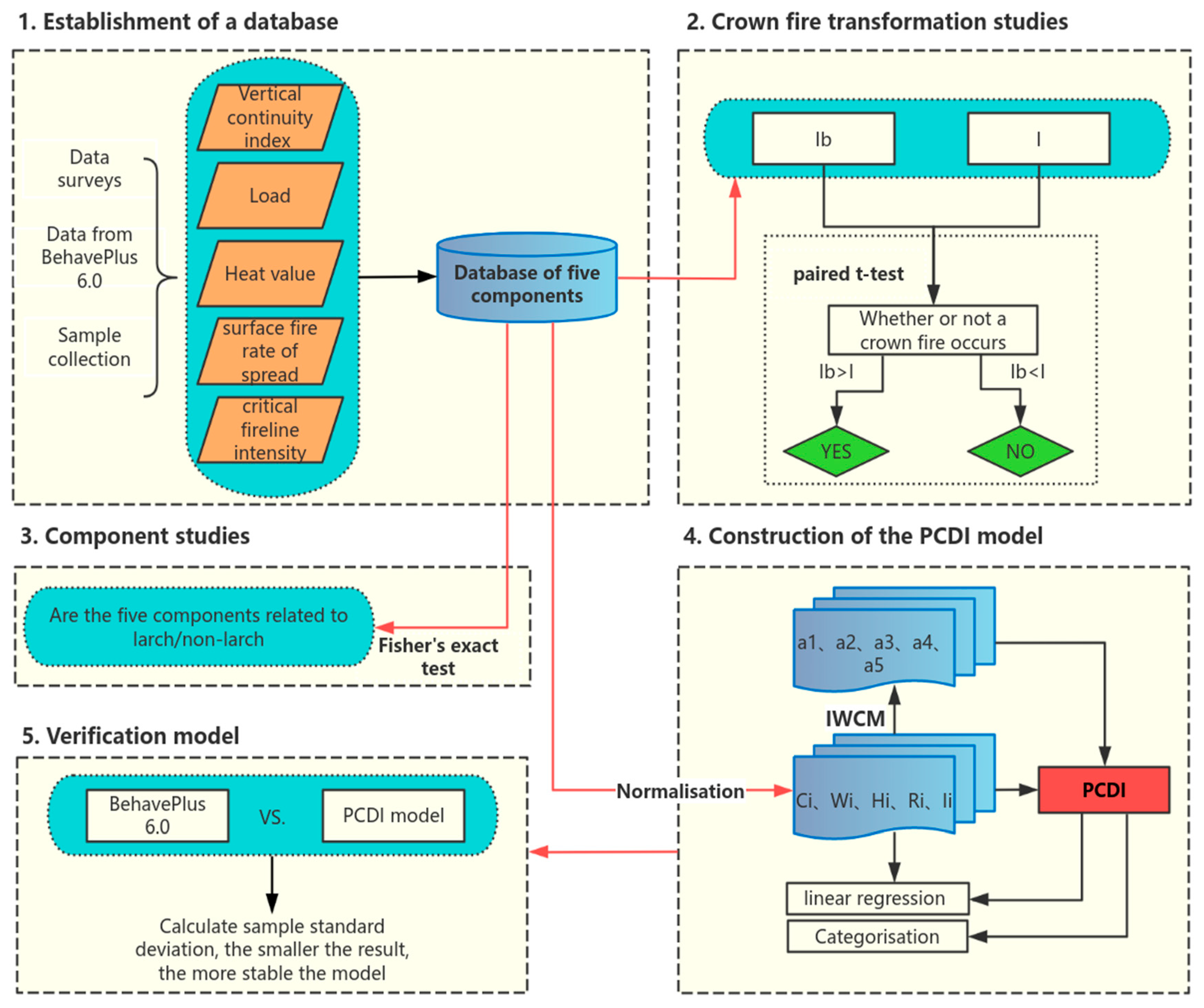
2.3.1. Components
- Vertical continuity index
- b.
- Fuel Load
- c.
- Heat Value
- d.
- Surface Fire Behavior
- e.
- Crown Fire Behavior
2.3.2. PCDI Model
2.3.3. Validation Model
2.3.4. Statistical Analysis
3. Results
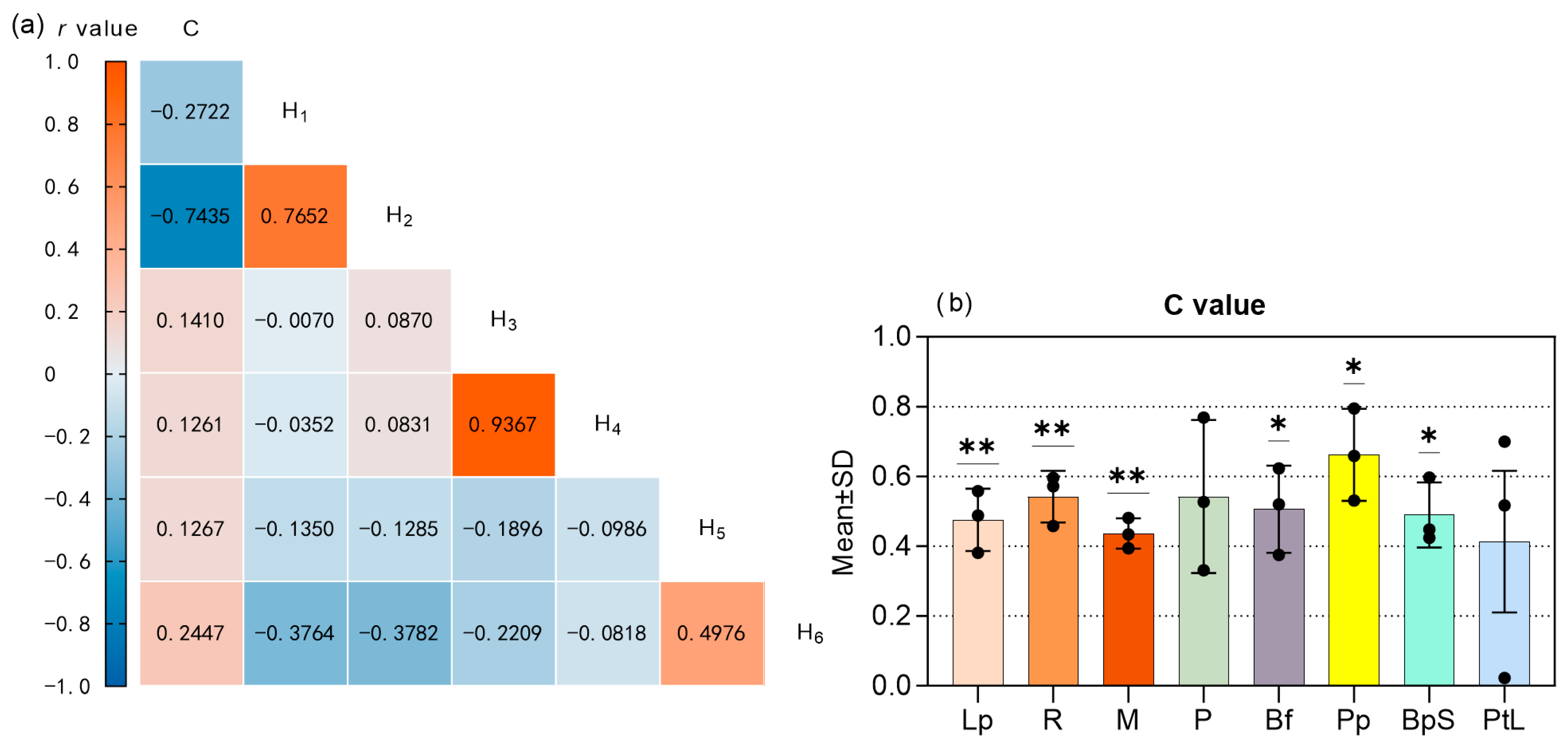
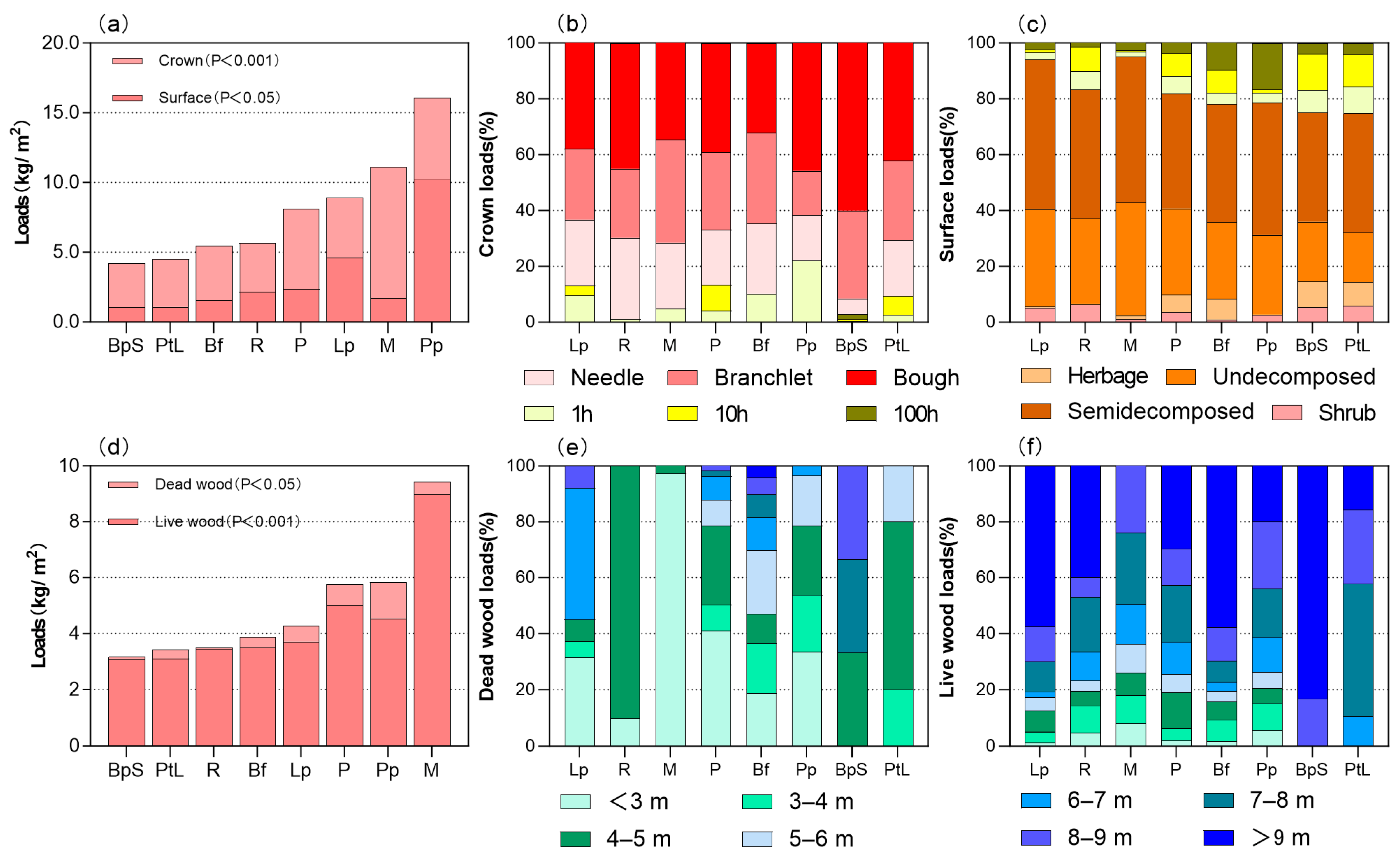
3.1. Component Results
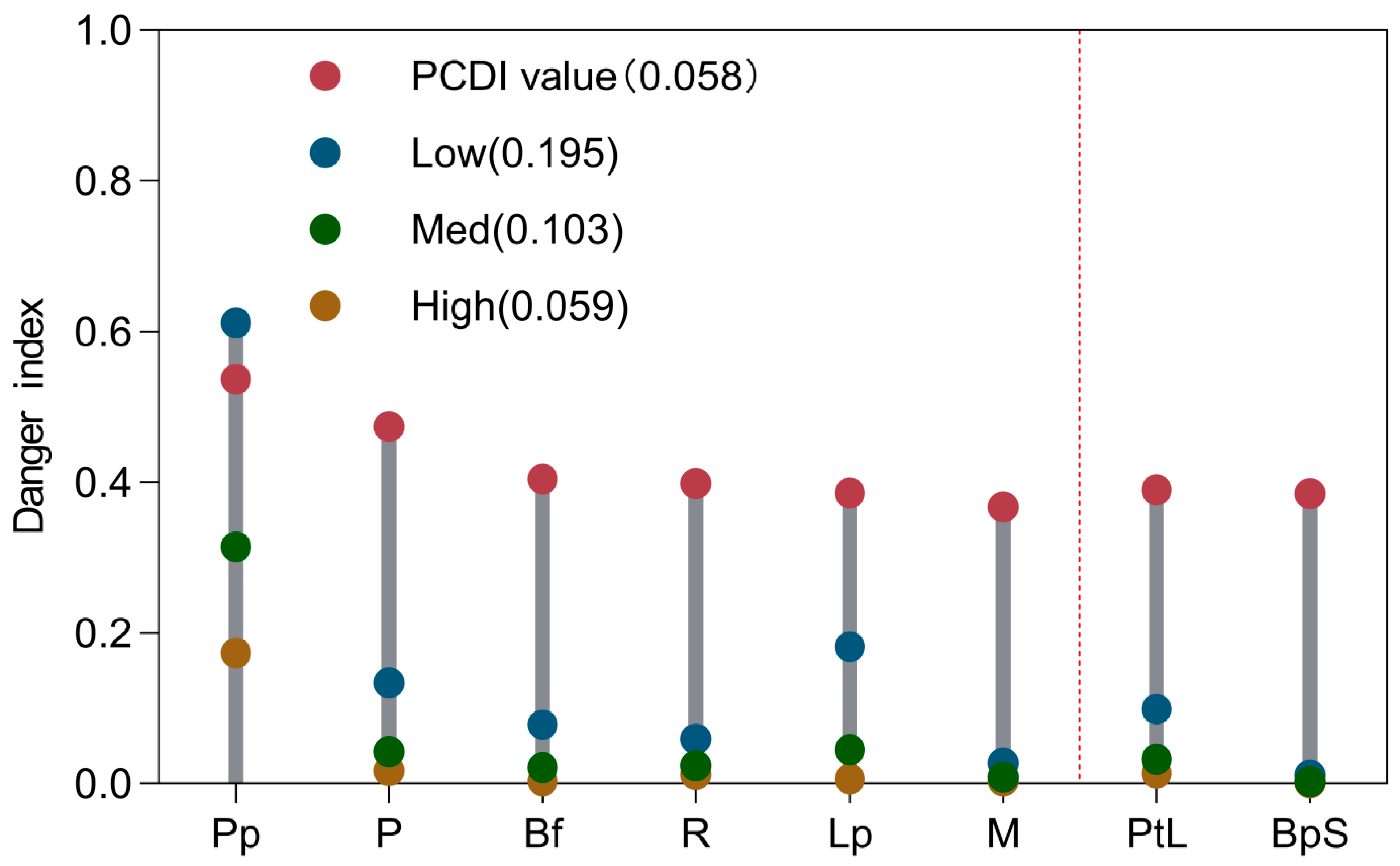
3.2. PCDI
3.3. Model Comparison
4. Discussion
4.1. Danger of Crown Fire
4.2. Modelling Feasibility
4.3. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Magalhes, N.; Evangelista, H.; Gonalves, S.J.; Alencar, A.S.; Santos, E.A.D.; Cataldo, M.; Mcconnell, J.R.; Silveira, R.S.; Mayewski, P.A.; Potocki, M. Seasonal changes in black carbon footprint on the Antarctic Peninsula due to rising shipborne tourism and forest fires. Sci. Adv. 2024, 10, eadp1682. [Google Scholar] [CrossRef]
- Jones, M.W.; Veraverbeke, S.; Andela, N.; Doerr, S.H.; Kolden, C.; Mataveli, G.; Pettinari, M.L.; Le Quéré, C.; Rosan, T.M.; van der Werf, G.R.; et al. Global rise in forest fire emissions linked to climate change in the extratropics. Science 2024, 386, eadl5889. [Google Scholar] [CrossRef] [PubMed]
- Naderpour, M.; Rizeei, H.M.; Ramezani, F. Forest fire risk prediction: A spatial deep neural network-based framework. Remote Sens. 2021, 13, 2513. [Google Scholar] [CrossRef]
- Quan, X.; Wang, W.; Xie, Q.; He, B.; Resco de Dios, V.; Yebra, M.; Jiao, M.; Chen, R. Improving wildfire occurrence modelling by integrating time-series features of weather and fuel moisture content. Environ. Model. Softw. 2023, 170, 105840. [Google Scholar] [CrossRef]
- Mišić, N.; Protić, M.; Cerdà, A.; Raos, M.; Blagojević, M. Transition from surface to crown fires: Effects of moisture content. Fire Technol. 2024, 60, 669–700. [Google Scholar] [CrossRef]
- Grishin, A.M. Mathematical Modeling of Forest Fires and New Methods of Fighting Them; Publishing House of the Tomsk State University: Tomsk, Russia, 1997. [Google Scholar]
- de Groot, W.J.; Hanes, C.C.; Wang, Y. Crown fuel consumption in Canadian boreal forest fires. Int. J. Wildland Fire 2022, 31, 255–276. [Google Scholar] [CrossRef]
- Finney, M.A. FARSITE: Fire Area Simulator—Model Development and Evaluation; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 1998. [CrossRef]
- Tymstra, C.; Bryce, R.W.; Wotton, B.M.; Taylor, S.W.; Armitage, O.B. Development and Structure of Prometheus: The Canadian Wildland Fire Growth Simulation Model. Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre, Edmonton, Alberta. Information Report NOR-X-417. 102p. 2010. Available online: https://ostrnrcan-dostrncan.canada.ca/handle/1845/247413 (accessed on 10 July 2025).
- Wagner, C.E. Conditions for the start and spread of crown fire. Rev. Can. Rech. For. 1977, 7, 23–34. [Google Scholar] [CrossRef]
- Alexandridis, A.; Vakalis, D.; Siettos, C.I.; Bafas, G.V. A Cellular Automata Model for Forest Fire Spread Prediction: The Case of the Wildfire That Swept Through Spetses Island in 1990. Appl. Math. Comput. 2008, 204, 191–201. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland Surface Fire Spread Modelling, 1990–2007. 3: Simulation and Mathematical Analogue Models. Int. J. Wildland Fire 2009, 18, 387–403. [Google Scholar] [CrossRef]
- Chen, R.; He, B.; Li, Y.; Zhang, Y.; Liao, Z.; Fan, C.; Yin, J.; Zhang, H. Incorporating fire spread simulation and machine learning algorithms to estimate crown fire potential for pine forests in Sichuan, China. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104080. [Google Scholar] [CrossRef]
- Gao, M.; Chen, S.; Suo, A.; Chen, F.; Liu, X. Response of fuel characteristics, potential fire behavior, and understory vegetation diversity to thinning in Platycladus orientalis forest in Beijing, China. Forests 2024, 15, 1667. [Google Scholar] [CrossRef]
- Tenny, J.T.; Sankey, T.T.; Munson, S.M.; Meador, A.J.S.; Goetz, S.J. Canopy and Surface Fuels Measurement Using Terrestrial Lidar Single-Scan Approach in the Mogollon Highlands of Arizona. Int. J. Wildland Fire 2025, 34, WF24221. [Google Scholar] [CrossRef]
- Shin, P.; Sankey, T.; Moore, M.M.; Thode, A.E. Evaluating Unmanned Aerial Vehicle Images for Estimating Forest Canopy Fuels in a Ponderosa Pine Stand. Remote Sens. 2018, 10, 1266. [Google Scholar] [CrossRef]
- Guo, H.; Gao, Y.; Ye, Z.; Yang, Z.; Zhang, Y.; Lei, Z.; Sun, A. Experimental Investigation of Fire Behaviours and Heat Transfer in Single Cypress Tree Crown Fires. Int. J. Wildland Fire 2025, 34, WF24030. [Google Scholar] [CrossRef]
- Marino, E.; Hernando, C.; Madrigal, J.; Guijarro, M.; Díez, C. Short-term effect of fuel treatments on fire behaviour in a mixed heathland: A comparative assessment in an outdoor wind tunnel. Int. J. Wildland Fire 2014, 23, 1002–1013. [Google Scholar] [CrossRef]
- Xu, H.; Chen, J.; He, G.; Lin, Z.; Bai, Y.; Ren, M.; Zhang, H.; Yin, H.; Liu, F. Immediate assessment of forest fire using a novel vegetation index and machine learning based on multi-platform, high temporal resolution remote sensing images. Int. J. Appl. Earth Obs. Geoinf. 2024, 134, 104210. [Google Scholar] [CrossRef]
- Szpakowski, D.M.; Jensen, J.R. A Review of the Applications of Remote Sensing in Fire Ecology. Remote Sens. 2019, 11, 2638. [Google Scholar] [CrossRef]
- Filipponi, F. Exploitation of Sentinel-2 Time Series to Map Burned Areas at the National Level: A Case Study on the 2017 Italy Wildfires. Remote Sens. 2019, 11, 622. [Google Scholar] [CrossRef]
- Lyell, C.S.; Nattala, U.; Keeble, T.; Vella, E.M.; Joshi, R.C.; Joukhadar, Z.; Garber, J.; Mutch, S.J.; Gazzard, T.; Duff, T.; et al. Forecasting dead fuel moisture content below forest canopies—A seven-day forecasting system. Agric. For. Meteorol. 2024, 358, 110217. [Google Scholar] [CrossRef]
- Hou, X.; Wu, Z.; Zhu, S.; Li, Z.; Li, S. Comparative analysis of machine learning-based predictive models for fine dead fuel moisture of subtropical forest in China. Forests 2024, 15, 736. [Google Scholar] [CrossRef]
- Xu, H.; Zlatanova, S.; Liang, R.; Canbulat, I. Generative AI as a Pillar for Predicting 2D and 3D Wildfire Spread: Beyond Physics-Based Models and Traditional Deep Learning. Fire 2025, 8, 293. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, H.; Wang, S.; Ma, X. A Multi-Scale Deep Learning Algorithm for Enhanced Forest Fire Danger Prediction Using Remote Sensing Images. Forests 2024, 15, 1581. [Google Scholar] [CrossRef]
- Castle, D.; Mell, W.; Miller, F.J. Examination of the Wildland-Urban Interface Fire Dynamics Simulator in Modeling of Laboratory-Scale Surface-to-Crown Fire Transition. Available online: https://www.academia.edu/download/32039588/Castle_LabCrwnFireIniti_June2013USNatCombMtng070FR-0300.pdf (accessed on 10 July 2025).
- Modarres, M. Experimental and Numerical Analysis of Fire Behaviour in Typical Fuels at the Wildland-Urban Interface. Ph.D. Thesis, University of Coimbra, Coimbra, Portugal, 2025. Available online: https://estudogeral.uc.pt/handle/10316/118566 (accessed on 10 July 2025).
- Da Ponte, E.; Costafreda-Aumedes, S.; Vega-Garcia, C. Lessons learned from arson wildfire incidence in reforestations and natural stands in Spain. Forests 2019, 10, 229. [Google Scholar] [CrossRef]
- Fernandes, P.; Loureiro, C.; Botelho, H. Fire behaviour and severity in a maritime pine stand under differing fuel conditions. Ann. For. Sci. 2004, 61, 537–544. [Google Scholar] [CrossRef]
- Robert, D.F. Department of Applied Physics and Applied Mathematics, Columbia University, NASA Goddard Institute for Space Studies. Evaluation of Global Fire Weather Database Reanalysis and Short-Term Forecast Products. Nat. Hazards Earth Syst. Sci. 2020, 20, 1123–1147. [Google Scholar] [CrossRef]
- Kucuk, O.; Goltas, M.; Demirel, T.; Mitsopoulos, I.; Bilgili, E. Predicting Canopy Fuel Characteristics in Pinus brutia Ten., Pinus nigra Arnold and Pinus pinaster Ait. Forests from Stand Variables in North-Western Turkey. Environ. Eng. Manag. J. 2021, 20, 207–219. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. The 10% Wind Speed Rule of Thumb for Estimating a Wildfire’s Forward Rate of Spread in Forests and Shrublands. Ann. For. Sci. 2019, 76, 44. [Google Scholar] [CrossRef]
- Loboda, E.; Kasymov, D.; Agafontsev, M.; Reyno, V.; Lutsenko, A.; Staroseltseva, A.; Perminov, V.; Martynov, P.; Loboda, Y.; Orlov, K. Crown fire modeling and its effect on atmospheric characteristics. Atmosphere 2022, 13, 1982. [Google Scholar] [CrossRef]
- Morvan, D. Physical phenomena and length scales governing the behaviour of wildfires: A case for physical modelling. Fire Technol. 2011, 47, 437–460. [Google Scholar] [CrossRef]
- Conrad, E.; Jolly, W.M.; Brown, T.; Hillman, S. Branching out: Species-Specific Canopy Architecture Limits Live Crown Fuel Consumption in Intermountain West USA Conifers. Fire Ecol. 2024, 20, 28. [Google Scholar] [CrossRef]
- Cruz, M.G.; Sullivan, A.L.; Gould, J.S.; Sims, N.C.; Bannister, A.J.; Hollis, J.J.; Hurley, R.J. Anatomy of a Catastrophic Wildfire: The Black Saturday Kilmore East Fire in Victoria, Australia. For. Ecol. Manag. 2012, 284, 269–285. [Google Scholar] [CrossRef]
- Salis, M.; Arca, B.; Alcasena, F.; Arianoutsou, M.; Bacciu, V.; Duce, P.; Duguy, B.; Koutsias, N.; Mallinis, G.; Mitsopoulos, I.; et al. Predicting wildfire spread and behaviour in Mediterranean landscapes. Int. J. Wildland Fire 2016, 25, 1015–1032. [Google Scholar] [CrossRef]
- Pierce, A.D.; McDaniel, S.; Wasser, M.; Ainsworth, A.; Litton, C.M.; Giardina, C.P.; Cordell, S. Using a prescribed fire to test custom and standard fuel models for fire behaviour prediction in a non-native, grass-invaded tropical dry shrubland. Appl. Veg. Sci. 2014, 17, 700–710. [Google Scholar] [CrossRef]
- De Luca, G.; Modica, G.; Silva, J.M.N.; Praticò, S.; Pereira, J.M.C. Assessing Tree Crown Fire Damage Integrating Linear Spectral Mixture Analysis and Supervised Machine Learning on Sentinel-2 Imagery. Int. J. Digit. Earth 2023, 16, 3162–3198. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, H.; Wu, Z. Effects of Forest Fire Prevention Policies on Probability and Drivers of Forest Fires in the Boreal Forests of China during Different Periods. Remote Sens. 2022, 14, 5724. [Google Scholar] [CrossRef]
- Porto, M.; Correia, O.; Beja, P. Modelling Fuel Succession in Mediterranean Cork Oak Forests along a 70-Year Chronosequence. Forest Ecol. Manag. 2013, 302, 221–230. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y.; Ryu, J.; Kwon, C.; Seo, K.; Kim, S. Prediction of Wildfire Fuel Load for Pinus densiflora Stands in South Korea Based on the Forest-Growth Model. Forests 2022, 13, 1372. [Google Scholar] [CrossRef]
- Agbeshie, A.A.; Abugre, S.; Atta Darkwa, T.; Awuah, R. A Review of the Effects of Forest Fire on Soil Properties. J. For. Res. 2022, 33, 1419–1441. [Google Scholar] [CrossRef]
- Zhang, G. A Case Study on the Integration of Remote Sensing for Predicting Complicated Forest Fire Spread. Remote Sens. 2024, 16, 3969. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wild Land Fuels; US Department of Agriculture, Intermountain Forest & Range Experiment Station: Ogden, UT, USA, 1972. [Google Scholar]
- Wang, Z.F. Estimation method of initial spread velocity of mountain fire. Mount. Res. 1983, 1, 42–51. [Google Scholar]
- Byram, G.M. Combustion of forest fuels. In Forest Fire: Control and Use; Davis, K.P., Ed.; McGraw-Hill: New York, NY, USA, 1959; pp. 61–89. [Google Scholar]
- Aini, A.; Jolly, W.M.; Brown, T.P.; Hillman, S.C. Modelling Fire Hazard in the Southern Mediterranean Fire Rim (Bejaia Region, Northern Algeria). Environ. Monit. Assess. 2019, 191, 747. [Google Scholar] [CrossRef]
- Zhao, F.-J.; Shu, L.-F.; Wang, Q.-H.; Wang, M.-Y.; Tian, X.-R. Emissions of volatile organic compounds from heated needles and twigs of Pinus pumila. J. For. Res. 2011, 22, 243–248. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, X.; Du, Y.; Zhang, G.; Wang, Q.; Han, D.; Zhang, J. Estimation of Short-Term Vegetation Recovery in Post-Fire Siberian Dwarf Pine (Pinus pumila) Shrublands Based on Sentinel-2 Data. Fire 2025, 8, 47. [Google Scholar] [CrossRef]
- Kharuk, V.I.; Dvinskaya, M.L.; Ranson, K.J. Fire return intervals within the northern boundary of the larch forest in Central Siberia. Int. J. Wildland Fire 2013, 22, 251–257. [Google Scholar] [CrossRef]
- Alexander, H.D.; Natali, S.M.; Loranty, M.M.; Ludwig, S.M.; Spektor, V.V.; Davydov, S.; Zimov, N.; Trujillo, I.; Mack, M.C. Impacts of Increased Soil Burn Severity on Larch Forest Regeneration on Permafrost Soils of Far Northeastern Siberia. Forest Ecol. Manag. 2018, 417, 144–153. [Google Scholar] [CrossRef]
- Kharuk, V.I.; Shvetsov, E.G.; Buryak, L.V.; Golyukov, A.S.; Dvinskaya, M.L.; Petrov, I.A. Wildfires in the Larch Range within Permafrost, Siberia. Fire 2023, 6, 301. [Google Scholar] [CrossRef]
- Kharuk, V.I.; Ponomarev, E.I.; Ivanova, G.A.; Dvinskaya, M.L.; Coogan, S.C.P.; Flannigan, M.D. Wildfires in the Siberian Taiga. Ambio 2021, 50, 1953–1974. [Google Scholar] [CrossRef]
- Ramírez, J.; Mendes, M.; Monedero, S. Enhanced Forest Fire Risk Assessment through the Use of Fire Simulation Models. J. For. Ecol. Manag. 2015, 349, 32–41. [Google Scholar]
- Shi, C.; Zhang, F. A Forest Fire Susceptibility Modeling Approach Based on Integration Machine Learning Algorithm. Forests 2023, 14, 1506. [Google Scholar] [CrossRef]
- Botequim, B.; Fernandes, P.M.; Garcia-Gonzalo, J.; Silva, A.; Borges, J.G. Coupling Fire Behaviour Modelling and Stand Characteristics to Assess and Mitigate Fire Hazard in a Maritime Pine Landscape in Portugal. Eur. J. For. Res. 2017, 136, 527–542. [Google Scholar] [CrossRef]
- Han, H.; Yu, C.; Liu, Z.; Xiong, Z.; Zhao, L. Evaluations on the Consequences of Fire Suppression and the Ecological Effects of Fuel Treatment Scenarios in a Boreal Forest of the Great Xing’an Mountains, China. Forests 2023, 14, 85. [Google Scholar] [CrossRef]
- Changfeng, Y.; Yulong, Z.; Jiahui, W.; Yating, T. Modeling and Evaluation of Causal Factors in Emergency Responses to Fire Accidents Involving Oil Storage Systems. Sci. Rep. 2021, 11, 19018. [Google Scholar] [CrossRef]
- Gupta, S.K.; Kanga, S.; Gowhar, M.; Kumar, P.; Kumar, S. The Impact of Hydro-Meteorological Drivers on Forest Fires in Simlipal, India. Appl. Climatol. 2023, 153, 675–695. [Google Scholar] [CrossRef]
- Jellouli, O.; Bernoussi, A.; Amharref, M.; Ouardouz, M. Modeling of Wind Flow and Its Impact on Forest Fire Spread: Cellular Automata Approach; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 269–279. [Google Scholar] [CrossRef]
- Kolaitis, D.I.; Pallikarakis, C.; Founti, M. Comparative Assessment of Wildland Fire Rate of Spread Models: Effects of Wind Velocity. Fire 2023, 6, 188. [Google Scholar] [CrossRef]
- Dastour, H.; Bhuian, H.; Ahmed, M.R.; Hassan, Q.K. Active Fire Clustering and Spatiotemporal Dynamic Models for Forest Fire Management. Fire 2024, 7, 355. [Google Scholar] [CrossRef]
- Homhuan, S.; Humhong, C. Development of Forest Fire Monitoring and Warning System for Agroforestry Areas in Uttaradit Province, Thailand. Earth Environ. Sci. 2020, 538, 012008. [Google Scholar] [CrossRef]

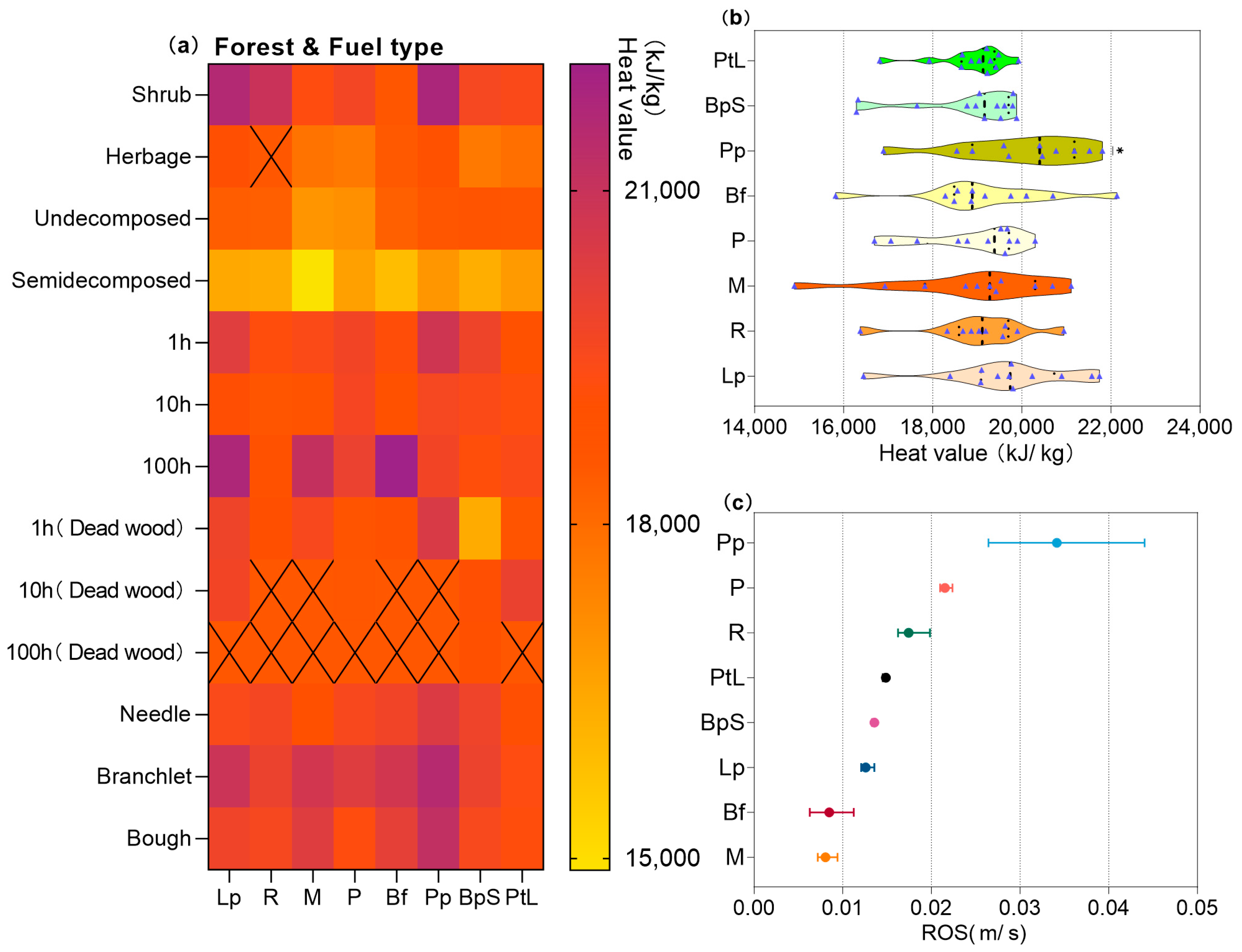
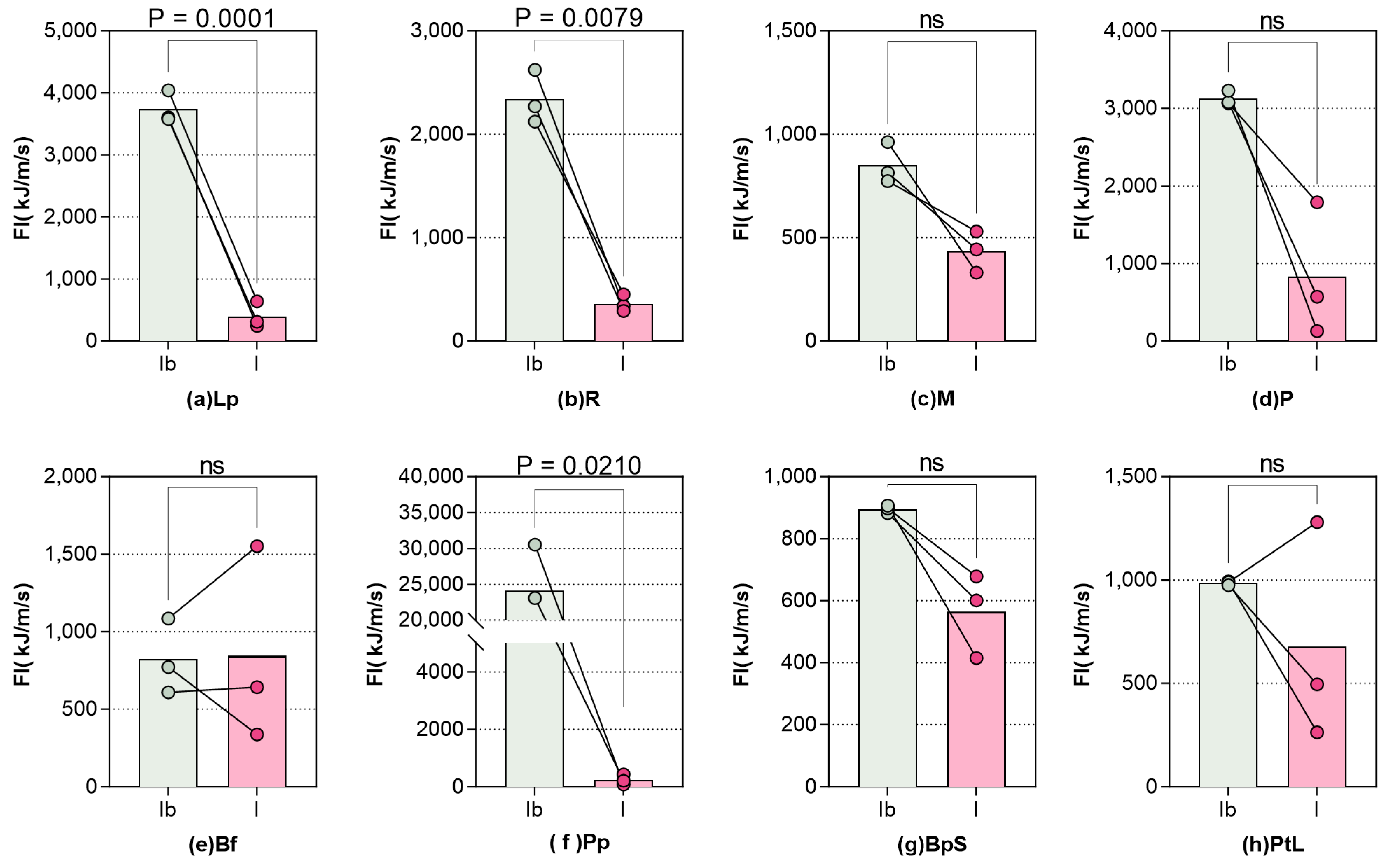
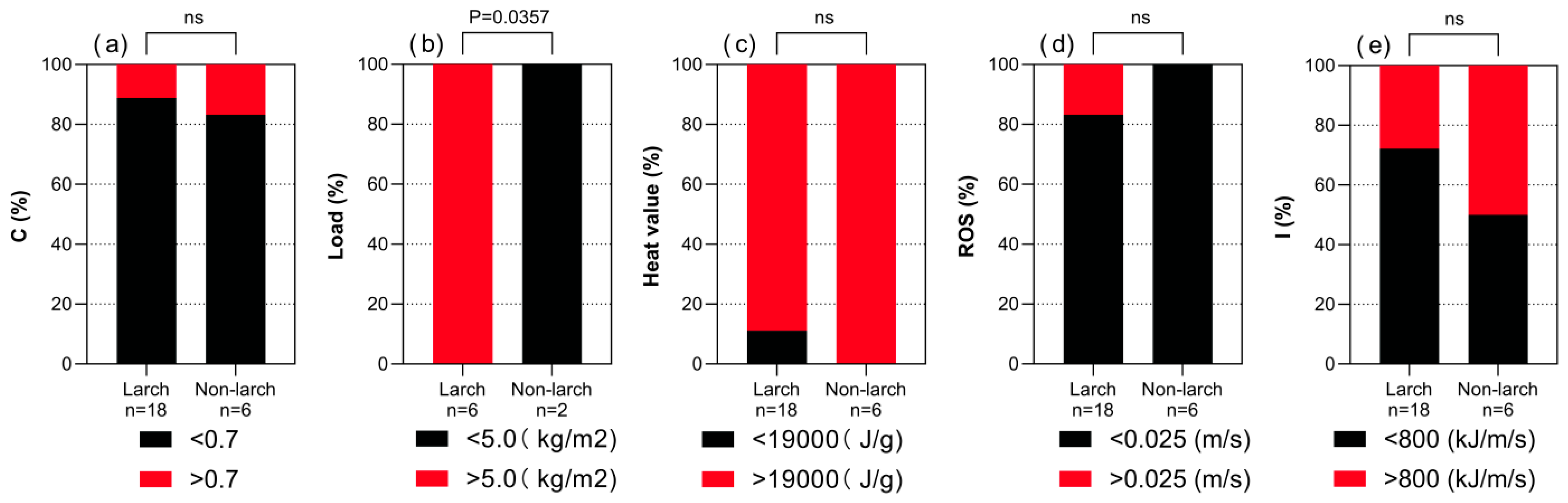
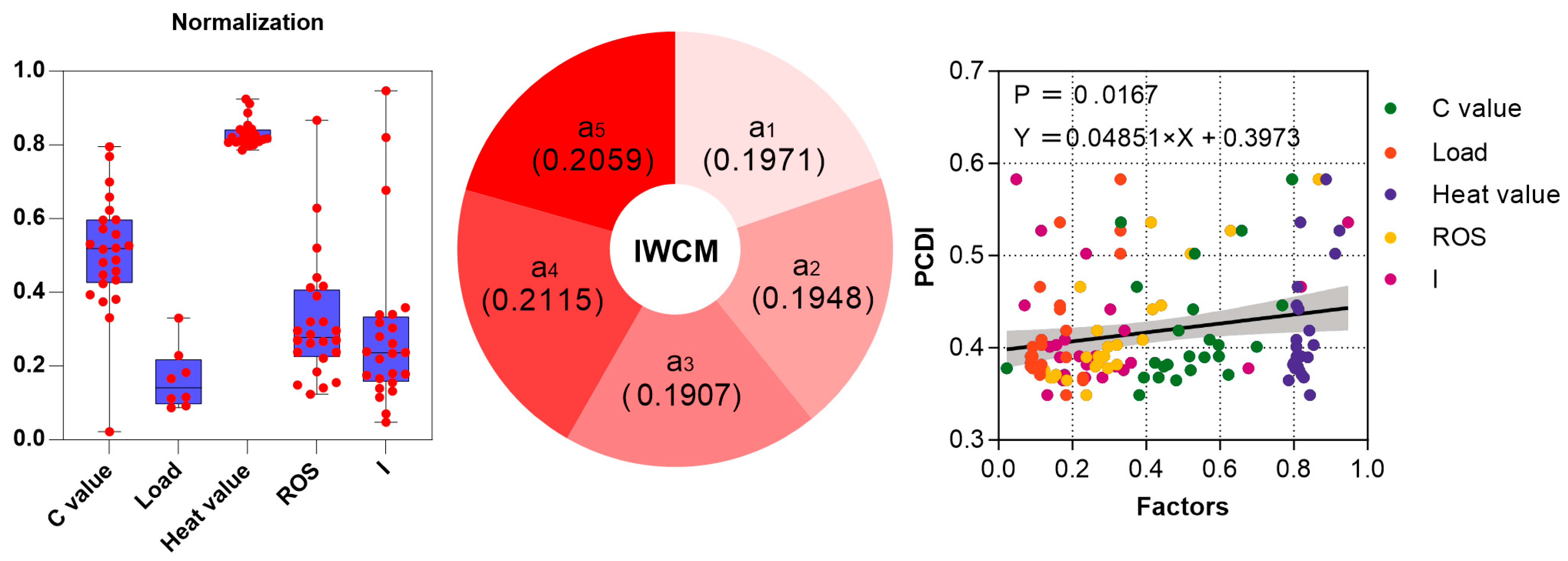
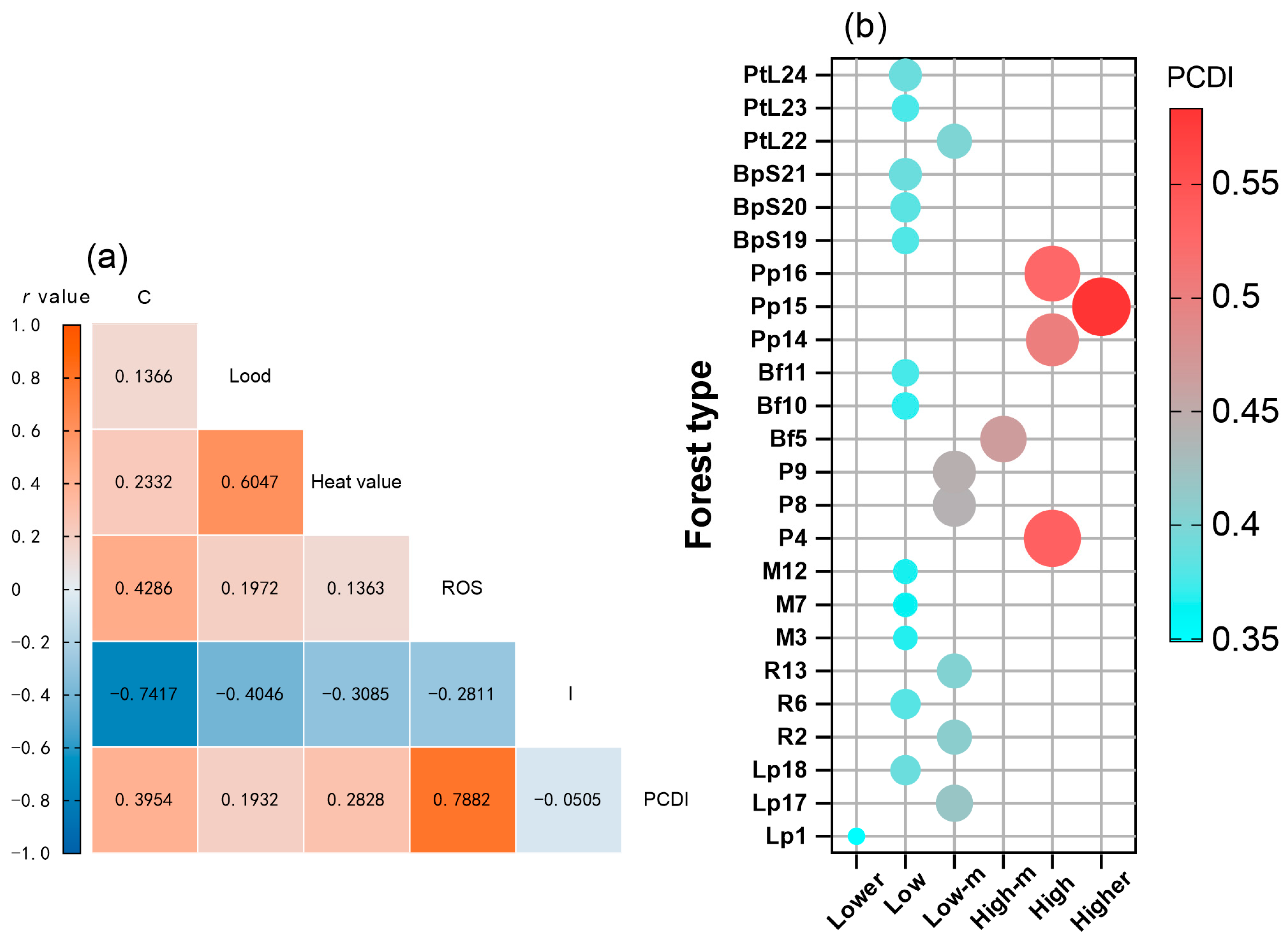
| Forest Type | Sample Number | Crown Length (m) | Diameter at Breast Height (cm) | Tree Height (m) | Crown Width (m) | Dead Wood Height (m) | Live Wood Height (m) | Slope (°) |
|---|---|---|---|---|---|---|---|---|
| Lp | 1/17/18 | 5.93 | 9.06 | 9.90 | 2.22 | 1.56 | 2.31 | 15 |
| R | 2/6/13 | 4.83 | 7.14 | 9.17 | 2.01 | 3.44 | 5.19 | 12 |
| M | 3/7/12 | 3.53 | 7.57 | 8.87 | 1.90 | 2.36 | 3.97 | 18 |
| P | 4/8/9 | 6.33 | 8.83 | 13.87 | 1.78 | 3.43 | 7.71 | 20 |
| Bf | 5/10/11 | 6.83 | 9.23 | 14.82 | 1.77 | 3.00 | 7.37 | 27 |
| Pp | 14/15/16 | 5.33 | 8.06 | 8.91 | 1.66 | 0.90 | 3.47 | 17 |
| BpS | 19/20/21 | ~ | 8.53 | 11.36 | 2.17 | ~ | 6.34 | 10 |
| PtL | 22/23/24 | ~ | 9.97 | 11.26 | 2.66 | 3.83 | 8.76 | 30 |
| BehavePlus Input Parameter Table | 8 Species of Forest Types | |||||||
|---|---|---|---|---|---|---|---|---|
| Lp | R | M | P | Bf | Pp | BpS | PtL | |
| Fuel Parameter Initialization | tu3 | |||||||
| Fuel Model Type | D | |||||||
| 1 h Fuel Load (kg/m2) | 0.108 | 0.139 | 0.033 | 0.147 | 0.060 | 0.356 | 0.086 | 0.102 |
| 10 h Fuel Load (kg/m2) | 0.050 | 0.187 | 0.006 | 0.195 | 0.129 | 0.137 | 0.134 | 0.125 |
| 100 h Fuel Load (kg/m2) | 0.111 | 0.032 | 0.045 | 0.085 | 0.150 | 1.694 | 0.042 | 0.045 |
| Live Herbaceous Fuel Load (kg/m2) | 0.015 | 0.070 | 0.023 | 0.147 | 0.113 | 0.004 | 0.096 | 0.093 |
| Live Woody Fuel Load (kg/m2) | 0.241 | 0.138 | 0.018 | 0.087 | 0.015 | 0.271 | 0.056 | 0.062 |
| 1 h Fuel SA/V (cm2/cm3) | 59.06 | |||||||
| Live Herbaceous Fuel SA/V (cm2/cm3) | 52.49 | |||||||
| Live Woody Fuel SA/V (cm2/cm3) | 45.93 | |||||||
| Fuel Bed Depth (cm) | 13.67 | 11.89 | 13.44 | 14.67 | 11.08 | 18.67 | 8.89 | 9.56 |
| Dead Fuel Moisture of Extinction (%) | 40 | |||||||
| Dead Fuel Heat Content (kJ/kg) | 19,181.13 | 18,285.41 | 18,215.94 | 18,598.36 | 18,859.66 | 19,100.45 | 18,693.59 | 18,594.07 |
| Live Fuel Heat Content (kJ/kg) | 20,325.90 | 20,942.70 | 18,551.66 | 18,661.03 | 18,516.77 | 20,058.45 | 18,628.53 | 18,698.67 |
| Canopy Base Height (m) | 1.56 | 3.44 | 2.36 | 3.43 | 3.00 | 0.90 | 6.34 | 3.83 |
| Foliar Moisture (%) | 100 | |||||||
| 20 ft Wind Speed (m/s) | 0.8 | |||||||
| Wind Adjustment Factor | 0.4 | |||||||
| Slope Steepness (°) | 15 | 12 | 18 | 20 | 27 | 17 | 10 | 30 |
| Fuel Type | Moisture Scenario | ||
|---|---|---|---|
| Low | Mid | High | |
| 1 h Fuel | 3% | 6% | 12% |
| 10 h Fuel | 4% | 7% | 13% |
| 100 h Fuel | 5% | 8% | 14% |
| Surface Live Herbaceous Fuel | 70% | 120% | 170% |
| Surface Live Woody Fuel | 70% | 120% | 170% |
| Index Range | Crown Fire Danger Level |
|---|---|
| <0.35 | Lower |
| 0.35–0.40 | Low |
| 0.40–0.45 | Low–middle |
| 0.45–0.50 | High–middle |
| 0.50–0.55 | High |
| >0.55 | Higher |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, B.; Han, T.; Li, A.; Shi, S.; Li, J.; Yang, S. Assessment of Potential Crown Fire Danger in Major Forest Types of the Da Xing’anling (Inner Mongolia) Mountains, China. Forests 2025, 16, 1449. https://doi.org/10.3390/f16091449
Yi B, Han T, Li A, Shi S, Li J, Yang S. Assessment of Potential Crown Fire Danger in Major Forest Types of the Da Xing’anling (Inner Mongolia) Mountains, China. Forests. 2025; 16(9):1449. https://doi.org/10.3390/f16091449
Chicago/Turabian StyleYi, Bole, Tong Han, Ang Li, Shufeng Shi, Jing Li, and Shuxiang Yang. 2025. "Assessment of Potential Crown Fire Danger in Major Forest Types of the Da Xing’anling (Inner Mongolia) Mountains, China" Forests 16, no. 9: 1449. https://doi.org/10.3390/f16091449
APA StyleYi, B., Han, T., Li, A., Shi, S., Li, J., & Yang, S. (2025). Assessment of Potential Crown Fire Danger in Major Forest Types of the Da Xing’anling (Inner Mongolia) Mountains, China. Forests, 16(9), 1449. https://doi.org/10.3390/f16091449






