Multi-Scale LAI Estimation Integrating LiDAR Penetration Index and Point Cloud Texture Features
Abstract
1. Introduction
1.1. Ecological Importance of LAI
1.2. Limitations of Traditional Optical Methods
1.3. Advantages and Challenges of LiDAR
1.4. Methodological Proposal and Hypothesis
2. Materials and Methods
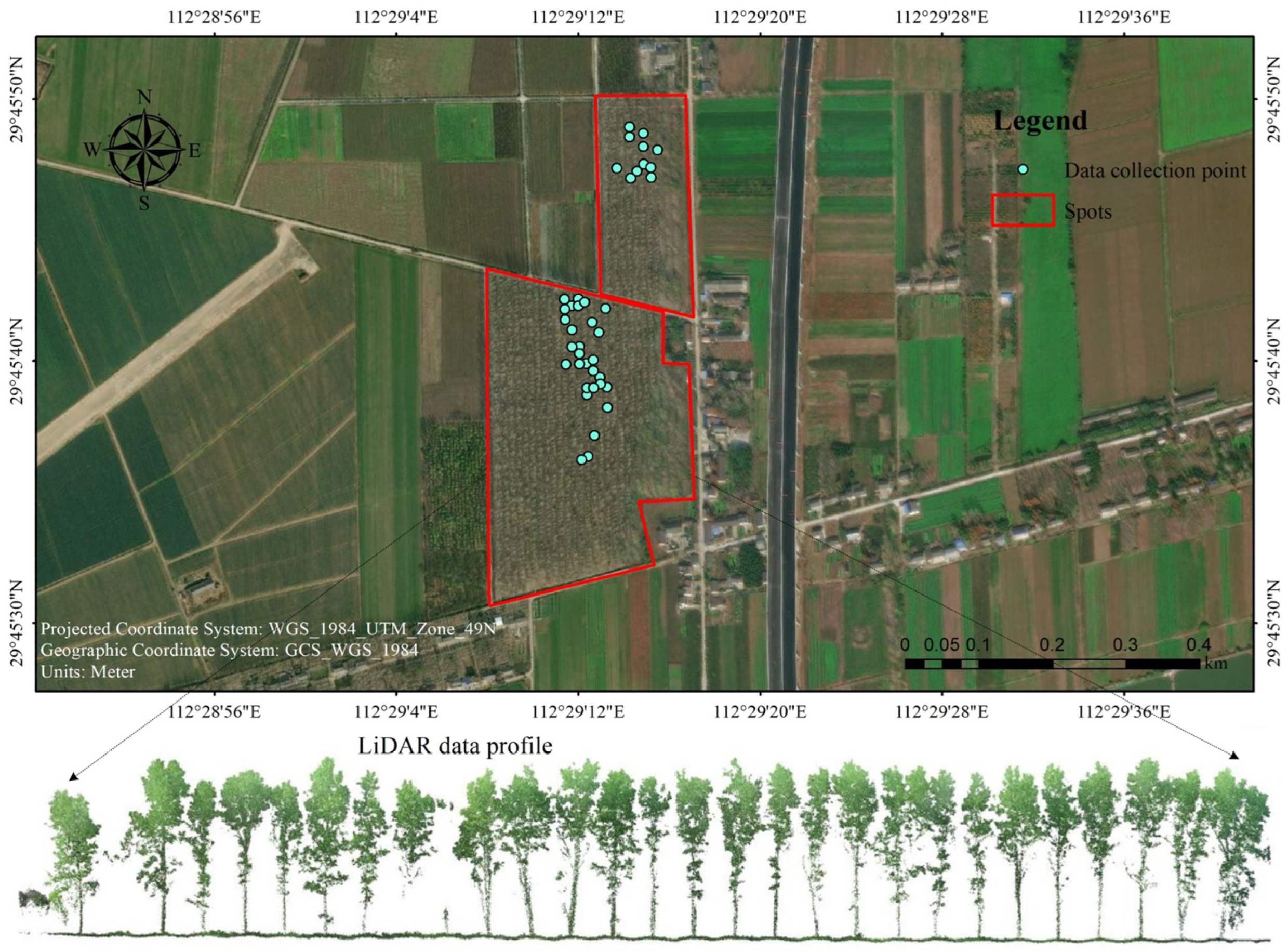
2.1. Study Area
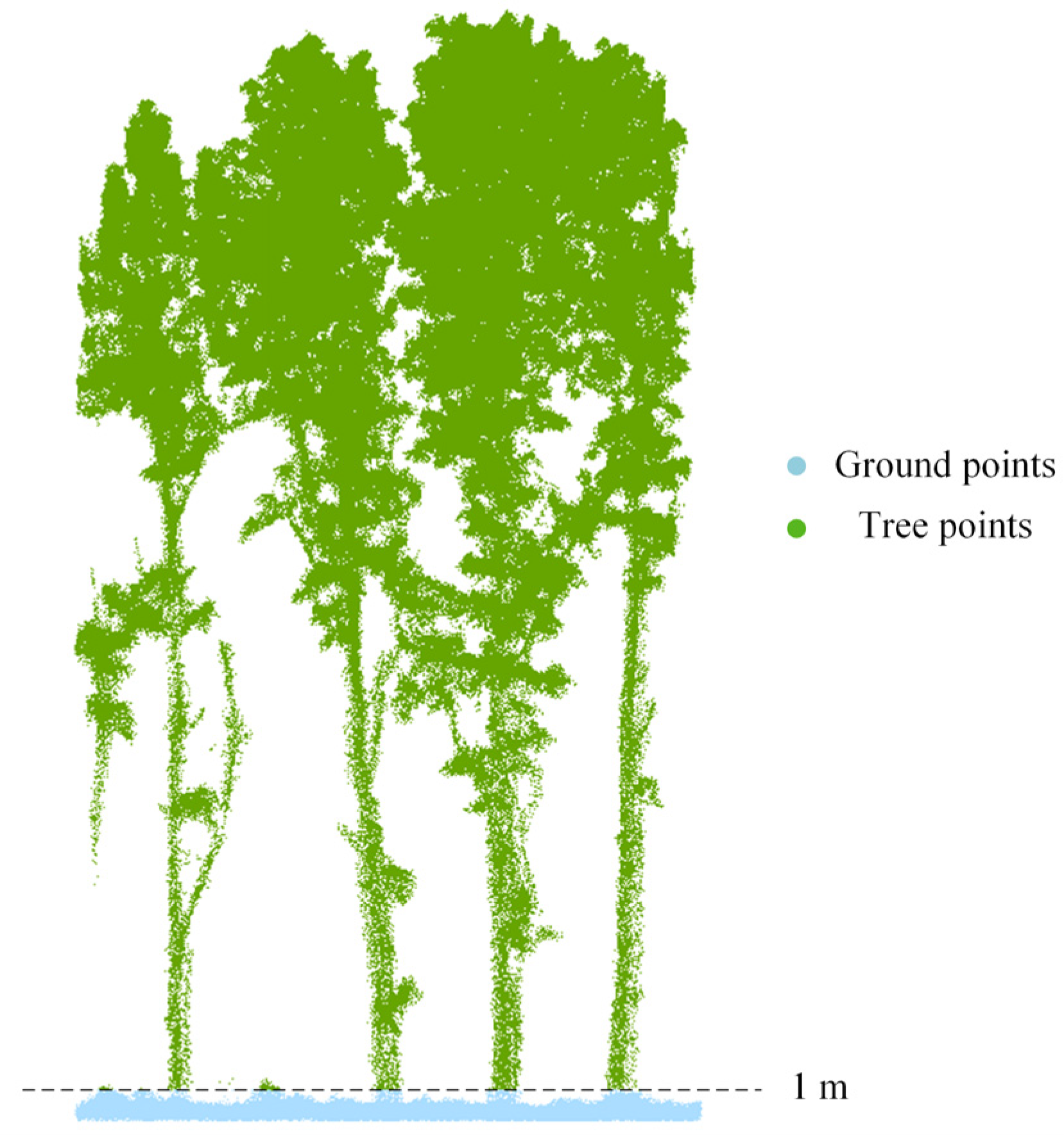
2.2. Data Collection
2.3. Calculation of LiDAR Penetration Index Based on Return Echoes
2.4. Calculation of Point Cloud Texture Features
2.4.1. Roughness
2.4.2. Curvature
2.4.3. Density
2.5. Multivariate Linear Regression Model for LAI Estimation Integrating Texture Features and LPI
3. Results
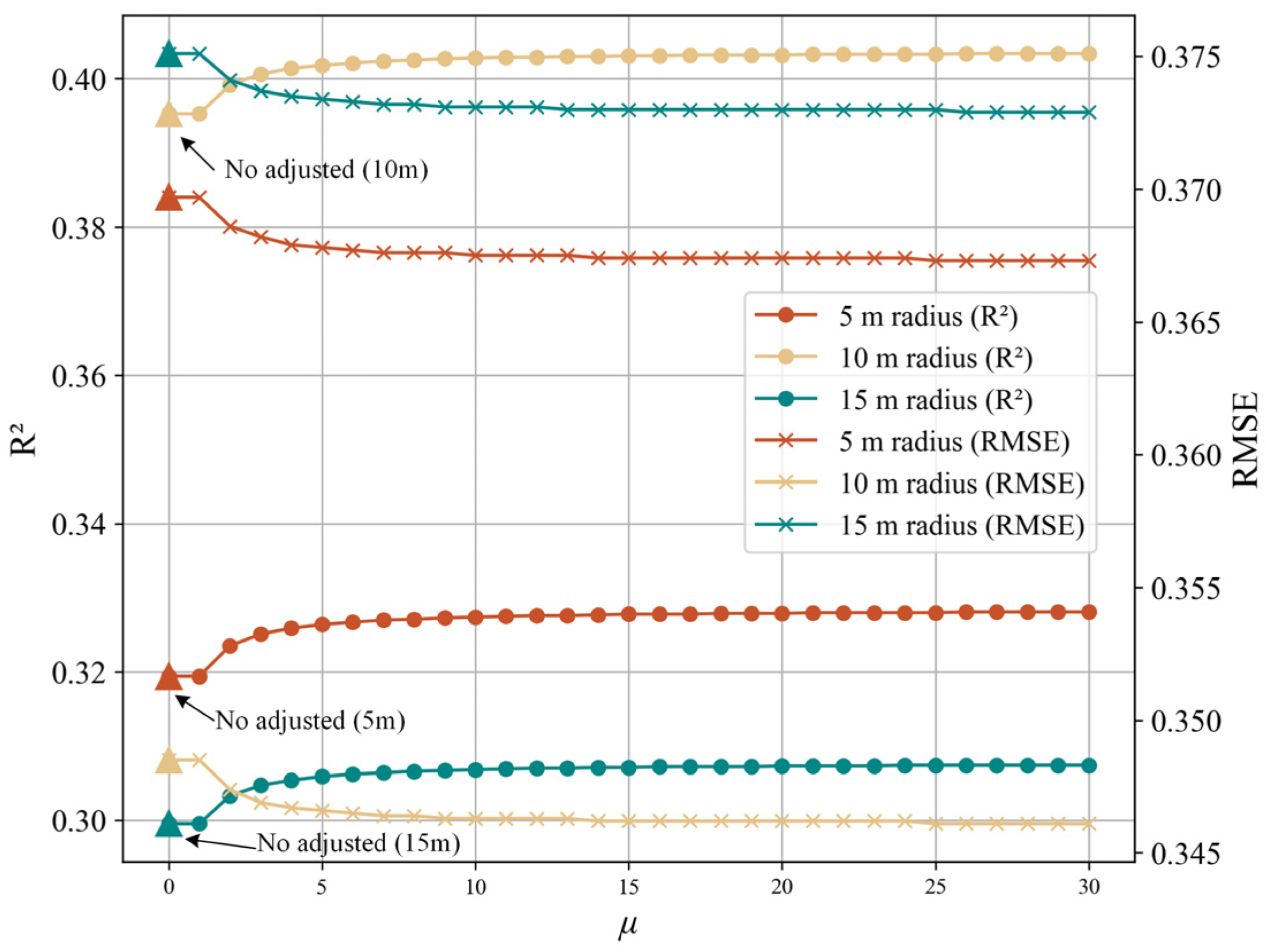
3.1. Optimal Adjustment Coefficient for LPI
3.2. LAI Estimation Accuracy Using LPI at Different Spatial Scales
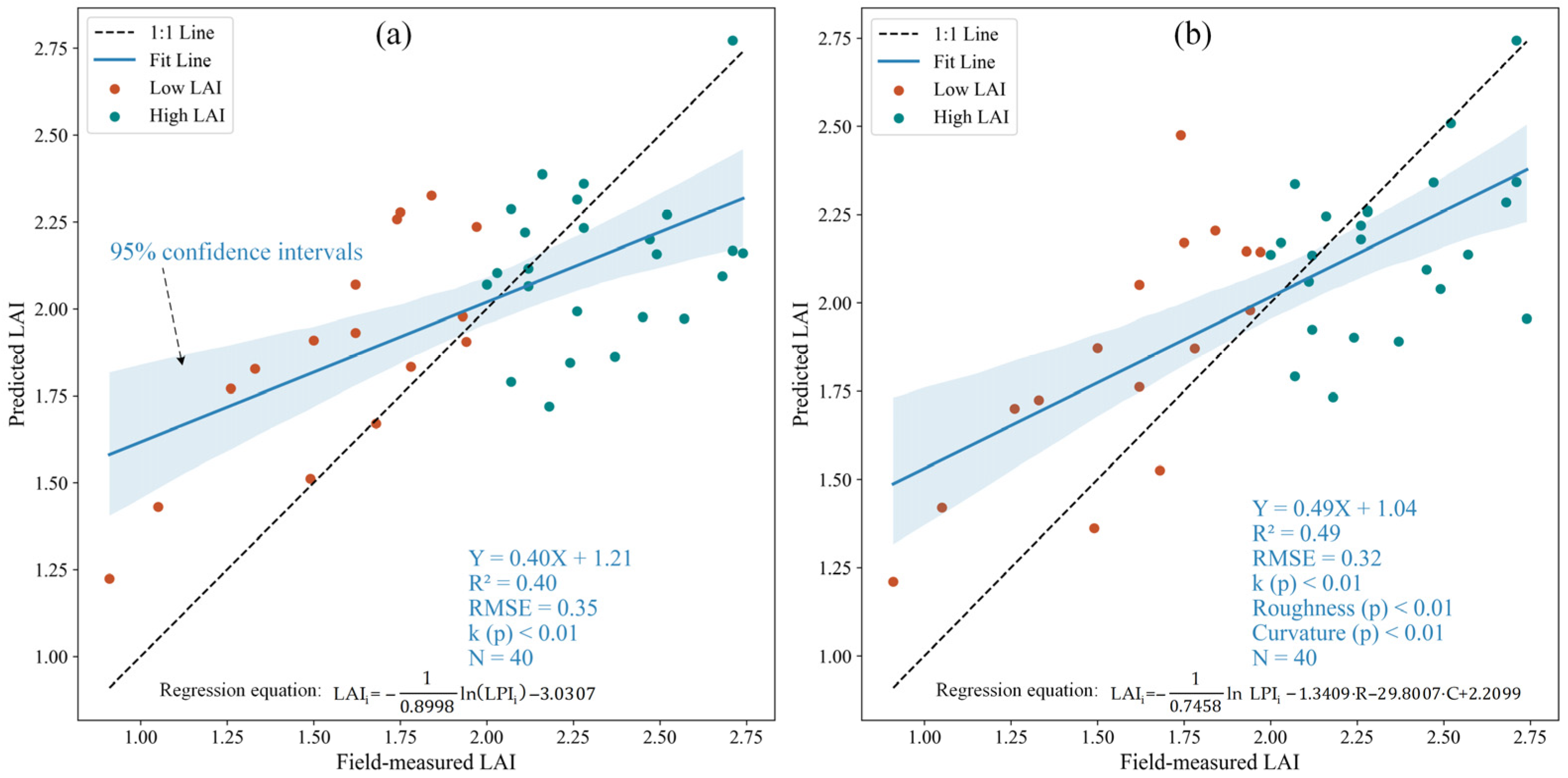
3.3. LAI Estimation Incorporating Texture Features
4. Discussion
4.1. Limitations of LAI Estimation Using LPI
4.2. Scientific Justification for Using Texture Features to Enhance LPI-Based LAI Estimation
4.3. Adaptability Analysis of Multi-Scale Modeling Strategy
4.4. Model Enhancement and Future Research Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lafont, S.; Zhao, Y.; Calvet, J.-C.; Peylin, P.; Ciais, P.; Maignan, F.; Weiss, M. Modelling LAI, Surface Water and Carbon Fluxes at High-Resolution over France: Comparison of ISBA-A-Gs and ORCHIDEE. Biogeosciences 2012, 9, 439–456. [Google Scholar] [CrossRef]
- Chen, J.M.; Ju, W.; Ciais, P.; Viovy, N.; Liu, R.; Liu, Y.; Lu, X. Vegetation Structural Change since 1981 Significantly Enhanced the Terrestrial Carbon Sink. Nat. Commun. 2019, 10, 4259. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Shi, H.; Zhou, L.; Eamus, D.; Huete, A.; Li, L.; Cleverly, J.; Hu, Z.; Harahap, M.; Yu, Q.; et al. Disentangling Climate and LAI Effects on Seasonal Variability in Water Use Efficiency Across Terrestrial Ecosystems in China. J. Geophys. Res. Bio Geosci. 2018, 123, 2429–2443. [Google Scholar] [CrossRef]
- Xu, Y.; Calvet, J.-C.; Bonan, B. The Joint Assimilation of Satellite Observed LAI and Soil Moisture for the Global Root Zone Soil Moisture Production and Its Impact on Land Surface and Ecosystem Variables. Agric. For. Meteorol. 2025, 360, 110299. [Google Scholar] [CrossRef]
- Cordak, A.S.; Kooperman, G.J.; Zarakas, C.M.; Swann, A.L.S.; Koven, C.D. The Role of Leaf Area Changes Within Plant CO2 Physiological Impacts on the Global Hydrological Cycle. Geophys. Res. Lett. 2025, 52, e2024GL110904. [Google Scholar] [CrossRef]
- Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G. A Commentary Review on the Use of Normalized Difference Vegetation Index (NDVI) in the Era of Popular Remote Sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; van Leeuwen, W.; Miura, T.; Glenn, E. MODIS Vegetation Indices. In Land Remote Sensing and Global Environmental Change: NASA’s Earth Observing System and the Science of ASTER and MODIS; Ramachandran, B., Justice, C.O., Abrams, M.J., Eds.; Springer: New York, NY, USA, 2011; pp. 579–602. ISBN 978-1-4419-6749-7. [Google Scholar]
- Chen, J.M.; Cihlar, J. Retrieving Leaf Area Index of Boreal Conifer Forests Using Landsat TM Images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
- Martinez, A.D.L.I.; Labib, S.M. Demystifying Normalized Difference Vegetation Index (NDVI) for Greenness Exposure Assessments and Policy Interventions in Urban Greening. Environ. Res. 2023, 220, 115155. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Grigorov, B. An Investigation of The Forests of Pernik Province (Western Bulgaria) by the Use of The Perpendicular Vegetation Index (PVI). Civ. Environ. Eng. Rep. 2022, 32, 96–104. [Google Scholar] [CrossRef]
- Pamungkas, S. Analysis of Vegetation Index for Ndvi, Evi-2, And Savi For Mangrove Forest Density Using Google Earth Engine In Lembar Bay, Lombok Island. IOP Conf. Ser. Earth Environ. Sci. 2023, 1127, 012034. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar Remote Sensing for Ecosystem Studies: Lidar, an Emerging Remote Sensing Technology That Directly Measures the Three-Dimensional Distribution of Plant Canopies, Can Accurately Estimate Vegetation Structural Attributes and Should Be of Particular Interest to Forest, Landscape, and Global Ecologists. BioScience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H. Estimation of LAI with the LiDAR Technology: A Review. Remote Sens. 2020, 12, 3457. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping Forest Canopy Height Globally with Spaceborne Lidar. J. Geophys. Res. Bio Geosci. 2011, 116. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, J.; Skidmore, A.K.; Premier, J.; Heurich, M. A Voxel Matching Method for Effective Leaf Area Index Estimation in Temperate Deciduous Forests from Leaf-on and Leaf-off Airborne LiDAR Data. Remote Sens. Environ. 2020, 240, 111696. [Google Scholar] [CrossRef]
- Su, W.; Huang, J.; Liu, D.; Zhang, M. Retrieving Corn Canopy Leaf Area Index from Multitemporal Landsat Imagery and Terrestrial LiDAR Data. Remote Sens. 2019, 11, 572. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [PubMed]
- Duan, S.-B.; Li, Z.-L.; Wu, H.; Tang, B.-H.; Ma, L.; Zhao, E.; Li, C. Inversion of the PROSAIL Model to Estimate Leaf Area Index of Maize, Potato, and Sunflower Fields from Unmanned Aerial Vehicle Hyperspectral Data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Luo, S.-Z.; Wang, C.; Zhang, G.-B.; Xi, X.-H.; Li, G.-C. Forest Leaf Area Index (LAI) Estimation Using Airborne Discrete-Return Lidar Data. Chin. J. Geophys. 2013, 56, 233–242. [Google Scholar] [CrossRef]
- Saitoh, T.M.; Nagai, S.; Noda Hibiki, M.; Muraoka, H.; Nasahara, K.N. Examination of the Extinction Coefficient in the Beer–Lambert Law for an Accurate Estimation of the Forest Canopy Leaf Area Index. For. Sci. Technol. 2012, 8, 67–76. [Google Scholar] [CrossRef]
- Tan, K.; Ke, T.; Tao, P.; Liu, K.; Duan, Y.; Zhang, W.; Wu, S. Discriminating Forest Leaf and Wood Components in TLS Point Clouds at Single-Scan Level Using Derived Geometric Quantities. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, Y.; Tang, J.; Guo, B.; Warner, T.A.; Guo, C.; Zheng, H.; Hosoi, F.; Cheng, T.; Zhu, Y.; et al. Quantify Wheat Canopy Leaf Angle Distribution Using Terrestrial Laser Scanning Data. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, X.; Yang, J. Exploring the Performance of Spectral and Textural Information for Leaf Area Index Estimation with Homogeneous and Heterogeneous Surfaces. Photogramm. Rec. 2023, 38, 233–251. [Google Scholar] [CrossRef]
- Wang, C.; Luo, S.; Xi, X.; Nie, S.; Ma, D.; Huang, Y. Influence of Voxel Size on Forest Canopy Height Estimates Using Full-Waveform Airborne LiDAR Data. For. Ecosyst. 2020, 7, 31. [Google Scholar] [CrossRef]
- Lai, X.; Yang, J.; Li, Y.; Wang, M. A Building Extraction Approach Based on the Fusion of LiDAR Point Cloud and Elevation Map Texture Features. Remote Sens. 2019, 11, 1636. [Google Scholar] [CrossRef]
- Brodu, N.; Lague, D. 3D Terrestrial Lidar Data Classification of Complex Natural Scenes Using a Multi-Scale Dimensionality Criterion: Applications in Geomorphology. ISPRS J. Photogramm. Remote Sens. 2012, 68, 121–134. [Google Scholar] [CrossRef]
- Fan, L. Comparisons of Five Indices for Estimating Local Terrain Surface Roughness Using LiDAR Point Clouds. In Proceedings of the 2022 29th International Conference on Geoinformatics, Beijing, China, 15 August 2022; pp. 1–6. [Google Scholar]
- Bischoff, S.; Kobbelt, L. Sub-Voxel Topology Control for Level-Set Surfaces. Comput. Graph. Forum 2003, 22, 273–280. [Google Scholar] [CrossRef]
- Lindberg, E.; Holmgren, J. Individual Tree Crown Methods for 3D Data from Remote Sensing. Curr. For. Rep. 2017, 3, 19–31. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Fast Semantic Segmentation of 3D Point Clouds with Strongly Varying Density. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-3, 177–184. [Google Scholar] [CrossRef]
- Tan, C.-W.; Zhang, P.-P.; Zhou, X.-X.; Wang, Z.-X.; Xu, Z.-Q.; Mao, W.; Li, W.-X.; Huo, Z.-Y.; Guo, W.-S.; Yun, F. Quantitative Monitoring of Leaf Area Index in Wheat of Different Plant Types by Integrating NDVI and Beer-Lambert Law. Sci. Rep. 2020, 10, 929. [Google Scholar] [CrossRef]
- Kukkonen, M.; Lähivaara, T.; Packalen, P. Combination of Lidar Intensity and Texture Features Enable Accurate Prediction of Common Boreal Tree Species with Single Sensor UAS Data. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–8. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Salas, J.; Danson, F.M. Multispectral and LiDAR Data Fusion for Fuel Type Mapping Using Support Vector Machine and Decision Rules. Remote Sens. Environ. 2011, 115, 1369–1379. [Google Scholar] [CrossRef]
- Jakovljevic, G.; Govedarica, M.; Alvarez-Taboada, F. A Deep Learning Model for Automatic Plastic Mapping Using Unmanned Aerial Vehicle (UAV) Data. Remote Sens. 2020, 12, 1515. [Google Scholar] [CrossRef]
- Morsdorf, F.; Kötz, B.; Meier, E.; Itten, K.I.; Allgöwer, B. Estimation of LAI and Fractional Cover from Small Footprint Airborne Laser Scanning Data Based on Gap Fraction. Remote Sens. Environ. 2006, 104, 50–61. [Google Scholar] [CrossRef]
- Qu, Y.; Shaker, A.; Korhonen, L.; Silva, C.A.; Jia, K.; Tian, L.; Song, J. Direct Estimation of Forest Leaf Area Index Based on Spectrally Corrected Airborne LiDAR Pulse Penetration Ratio. Remote Sens. 2020, 12, 217. [Google Scholar] [CrossRef]
- Solberg, S. Mapping Gap Fraction, LAI and Defoliation Using Various ALS Penetration Variables. Int. J. Remote Sens. 2010, 31, 1227–1244. [Google Scholar] [CrossRef]
- Armston, J.; Disney, M.; Lewis, P.; Scarth, P.; Phinn, S.; Lucas, R.; Bunting, P.; Goodwin, N. Direct Retrieval of Canopy Gap Probability Using Airborne Waveform Lidar. Remote Sens. Environ. 2013, 134, 24–38. [Google Scholar] [CrossRef]
- De Almeida, D.R.A.; Stark, S.C.; Shao, G.; Schietti, J.; Nelson, B.W.; Silva, C.A.; Gorgens, E.B.; Valbuena, R.; de Papa, D.A.; Brancalion, P.H.S. Optimizing the Remote Detection of Tropical Rainforest Structure with Airborne Lidar: Leaf Area Profile Sensitivity to Pulse Density and Spatial Sampling. Remote Sens. 2019, 11, 92. [Google Scholar] [CrossRef]
- You, H.; Wang, T.; Skidmore, A.K.; Xing, Y. Quantifying the Effects of Normalisation of Airborne LiDAR Intensity on Coniferous Forest Leaf Area Index Estimations. Remote Sens. 2017, 9, 163. [Google Scholar] [CrossRef]
- Vaccari, S.; van Leeuwen, M.; Calders, K.; Coops, N.C.; Herold, M. Bias in Lidar-Based Canopy Gap Fraction Estimates. Remote Sens. Lett. 2013, 4, 391–399. [Google Scholar] [CrossRef]
- LaRue, E.A.; Fahey, R.; Fuson, T.L.; Foster, J.R.; Matthes, J.H.; Krause, K.; Hardiman, B.S. Evaluating the Sensitivity of Forest Structural Diversity Characterization to LiDAR Point Density. Ecosphere 2022, 13, e4209. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H.; Zhang, Y.; Li, S.; Pang, Y.; Ma, T.; Li, Y. Retrieval and Validation of Vertical LAI Profile Derived from Airborne and Spaceborne LiDAR Data at a Deciduous Needleleaf Forest Site. GIScience Remote Sens. 2023, 60, 2214987. [Google Scholar] [CrossRef]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.-L.; Fournier, R.A.; Verstraete, M.M. On Seeing the Wood from the Leaves and the Role of Voxel Size in Determining Leaf Area Distribution of Forests with Terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling Lidar-Derived Estimates of Forest Attributes over Space and Time: A Review of Approaches and Future Trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Peng, X.; Calders, K.; Terryn, L.; Verbeeck, H. Evaluating Tree Branch Angle Measurements of European Beech Using Terrestrial Laser Scanning. For. Ecosyst. 2025, 12, 100279. [Google Scholar] [CrossRef]
- Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. (Tony) Estimating Canopy Structure of Douglas-Fir Forest Stands from Discrete-Return LiDAR. Trees 2007, 21, 295–310. [Google Scholar] [CrossRef]
- Jakubowski, M.K.; Guo, Q.; Kelly, M. Tradeoffs between Lidar Pulse Density and Forest Measurement Accuracy. Remote Sens. Environ. 2013, 130, 245–253. [Google Scholar] [CrossRef]
- Campbell, M.J.; Dennison, P.E.; Butler, B.W. A LiDAR-Based Analysis of the Effects of Slope, Vegetation Density, and Ground Surface Roughness on Travel Rates for Wildland Firefighter Escape Route Mapping. Int. J. Wildland Fire 2017, 26, 884–895. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, H.; Xiong, J.; Miao, G. Influence of Topography on UAV LiDAR-Based LAI Estimation in Subtropical Mountainous Secondary Broadleaf Forests. Forests 2024, 15, 17. [Google Scholar] [CrossRef]
- Zou, J.; Hou, W.; Chen, L.; Wang, Q.; Zhong, P.; Zuo, Y.; Luo, S.; Leng, P. Evaluating the Impact of Sampling Schemes on Leaf Area Index Measurements from Digital Hemispherical Photography in Larix Principis-Rupprechtii Forest Plots. For. Ecosyst. 2020, 7, 52. [Google Scholar] [CrossRef]
- Liu, L.; Coops, N.C.; Aven, N.W.; Pang, Y. Mapping Urban Tree Species Using Integrated Airborne Hyperspectral and LiDAR Remote Sensing Data. Remote Sens. Environ. 2017, 200, 170–182. [Google Scholar] [CrossRef]
- Leinonen, I.; Jones, H.G. Combining Thermal and Visible Imagery for Estimating Canopy Temperature and Identifying Plant Stress. J. Exp. Bot. 2004, 55, 1423–1431. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]

| Radius | 5 m | 10 m | 15 m |
|---|---|---|---|
| R2 | 0.3194 | 0.3953 | 0.2995 |
| adjusted R2 | 0.3278 | 0.4030 | 0.3070 |
| RMSE | 0.3674 | 0.3463 | 0.3730 |
| Shapiro–Wilk (p) | 0.0135 | 0.0250 | 0.0432 |
| Kruskal–Wallis (p) | 0.0025 | ||
| Breusch–Pagan (p) | 0.1535 | 0.1825 | 0.1256 |
| Variable | VIF (Before Removing Density) | VIF (After Removing Density) |
|---|---|---|
| LPI | 1.33 | 1.18 |
| Roughness | 1.44 | 1.16 |
| Curvature | 28.48 | 1.34 |
| Density | 28.05 | - |
| Coefficient | Value | p-Value | Evaluation Index | Value |
|---|---|---|---|---|
| k | 0.7458 | <0.01 | RMSE | 0.32 |
| c | −1.3409 | <0.01 | R2 | 0.49 |
| d | −29.8007 | <0.01 | MAE | 0.26 |
| b (Intercept) | 2.2099 | / | AIC | 30.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, Z.; Dian, Y.; Cai, S.; Chen, Z. Multi-Scale LAI Estimation Integrating LiDAR Penetration Index and Point Cloud Texture Features. Forests 2025, 16, 1321. https://doi.org/10.3390/f16081321
Li Z, Zhang Z, Dian Y, Cai S, Chen Z. Multi-Scale LAI Estimation Integrating LiDAR Penetration Index and Point Cloud Texture Features. Forests. 2025; 16(8):1321. https://doi.org/10.3390/f16081321
Chicago/Turabian StyleLi, Zhaolong, Ziyan Zhang, Yuanyong Dian, Shangshu Cai, and Zhulin Chen. 2025. "Multi-Scale LAI Estimation Integrating LiDAR Penetration Index and Point Cloud Texture Features" Forests 16, no. 8: 1321. https://doi.org/10.3390/f16081321
APA StyleLi, Z., Zhang, Z., Dian, Y., Cai, S., & Chen, Z. (2025). Multi-Scale LAI Estimation Integrating LiDAR Penetration Index and Point Cloud Texture Features. Forests, 16(8), 1321. https://doi.org/10.3390/f16081321








