Estimating Aboveground Biomass of Mangrove Forests in Indonesia Using Spatial Attention Coupled Bayesian Aggregator
Abstract
1. Introduction
- To develop, evaluate, and compare the performance of four ML models (RF, Cubist, SVR, and XGBoost) for estimating AGB;
- To design a spatial attention mechanism that incorporates slope and LISA clustering to account for spatial heterogeneity in AGB distribution;
- To propose a novel SAC-BA that integrates spatial statistics and model uncertainty into Bayesian model averaging for generating high-resolution AGB maps.
2. Materials and Methods
2.1. Materials
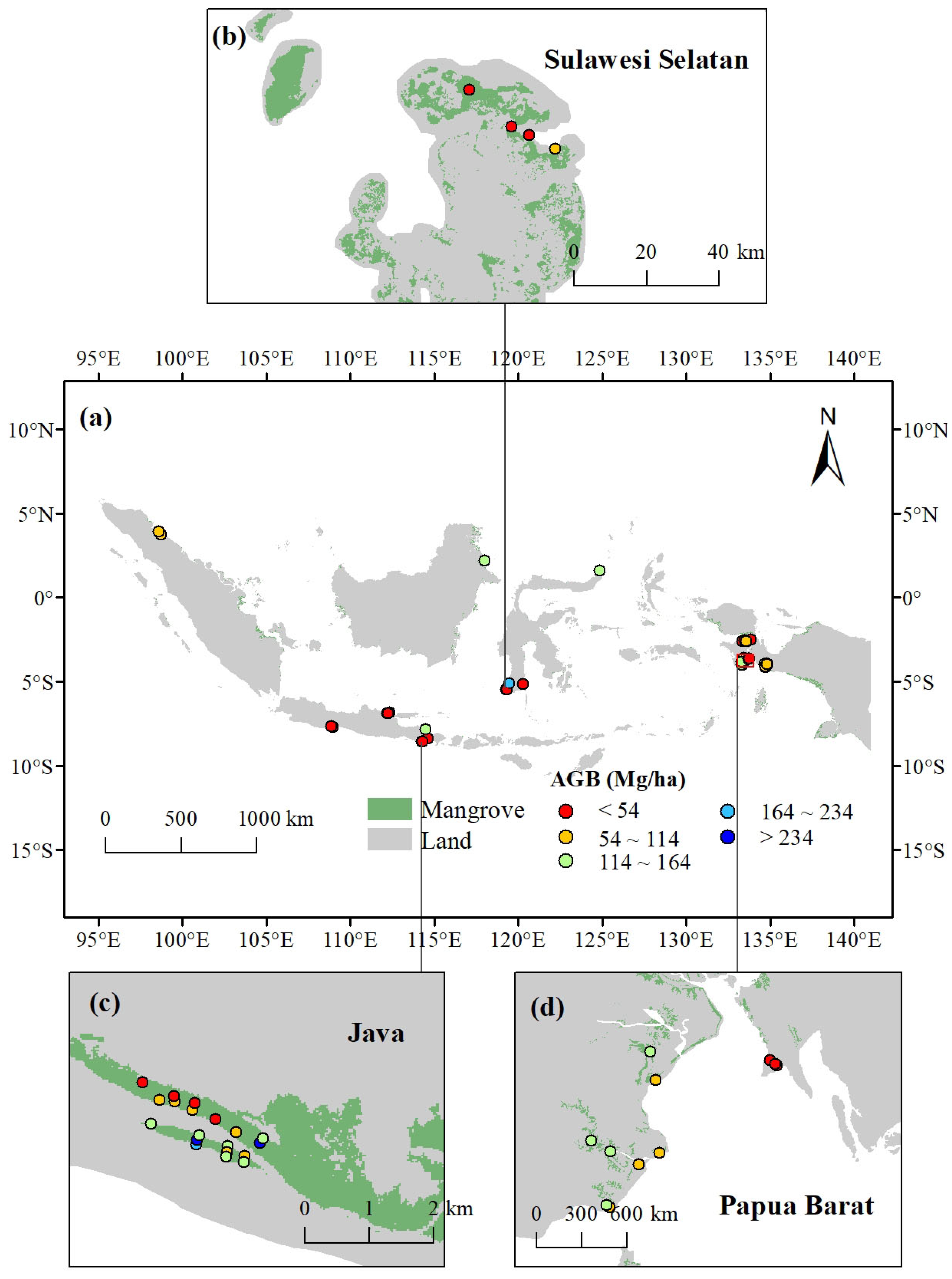
2.1.1. Study Area
2.1.2. The Field Observation Data
2.1.3. Satellite Remote Sensing Data
2.1.4. Explanatory Variables from Additional Data Sources
2.2. Methods
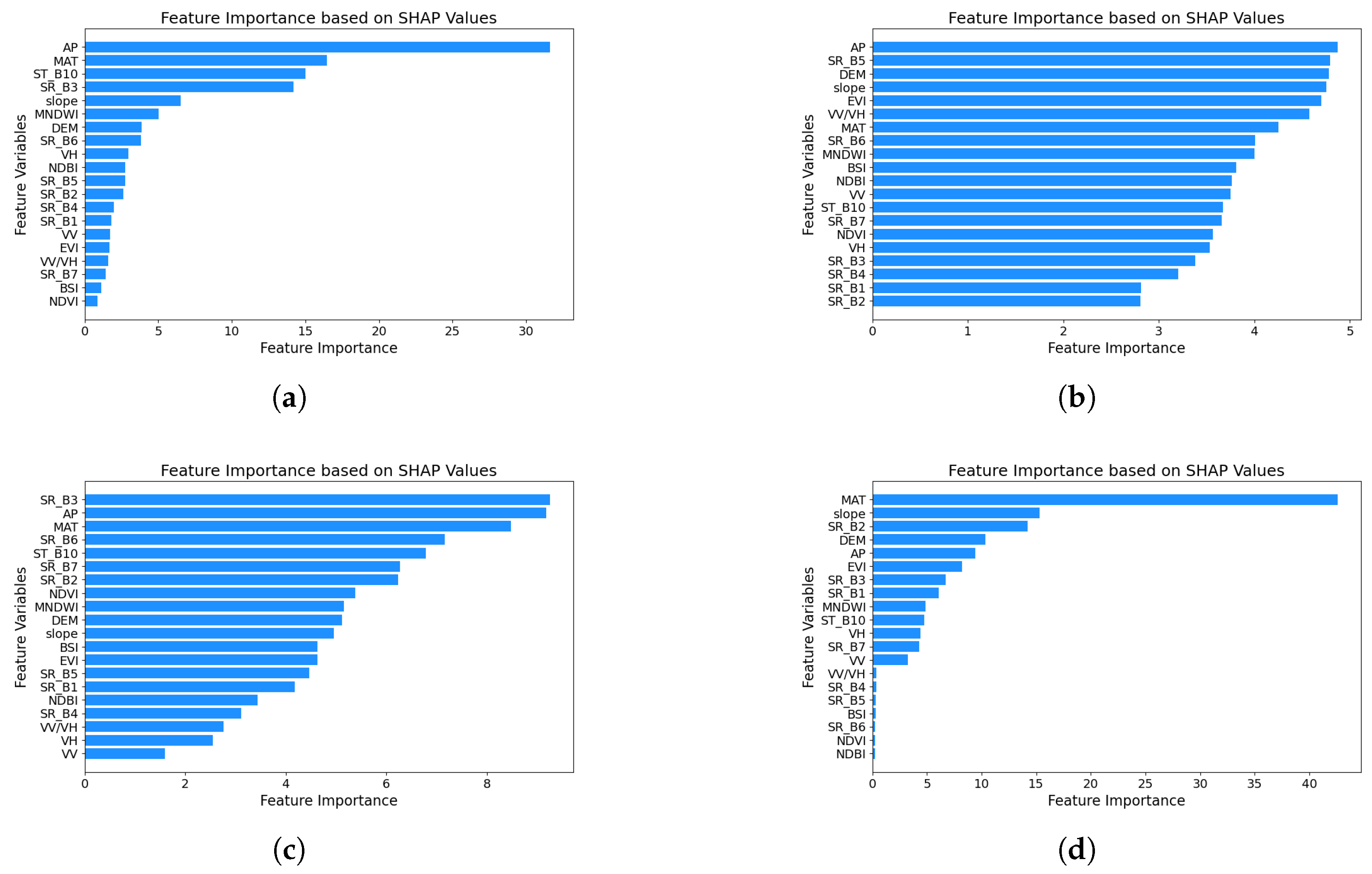
2.2.1. Four Machine Learning (ML) Methods and Feature Selection
2.2.2. Machine Learning with Bayesian Model Averaging (ML-BMA)
2.2.3. Spatial Attention Coupled Bayesian Aggregator (SAC-BA)
- Spatial Autocorrelation Analysis:To characterize the spatial clustering and structural stability of AGB, spatial autocorrelation analysis was employed to construct structural penalty factors in the model fusion process. Global Moran’s I [23], defined in Equation (3), quantifies overall spatial autocorrelation, with values ranging from –1 (dispersion) to 1 (clustering), and values near 0 indicating randomness. To mitigate uncertainty diffusion in spatial transition zones, a local spatial penalty was further introduced based on LISA. Each pixel was classified into five types based on local and neighboring values: high–high (HH) for high-value pixels surrounded by high-value neighbors, low–low (LL) for low-value pixels surrounded by low-value neighbors, high–low (HL) for high-value pixels surrounded by low values, low–high (LH) for low-value pixels surrounded by high values, and Not Significant (NS) where no significant local spatial association was detected.where, and represent the and variable values, and is the mean of all X. represents the spatial weight or relationship between the and variables. represents the sum of all weights, and N represents.
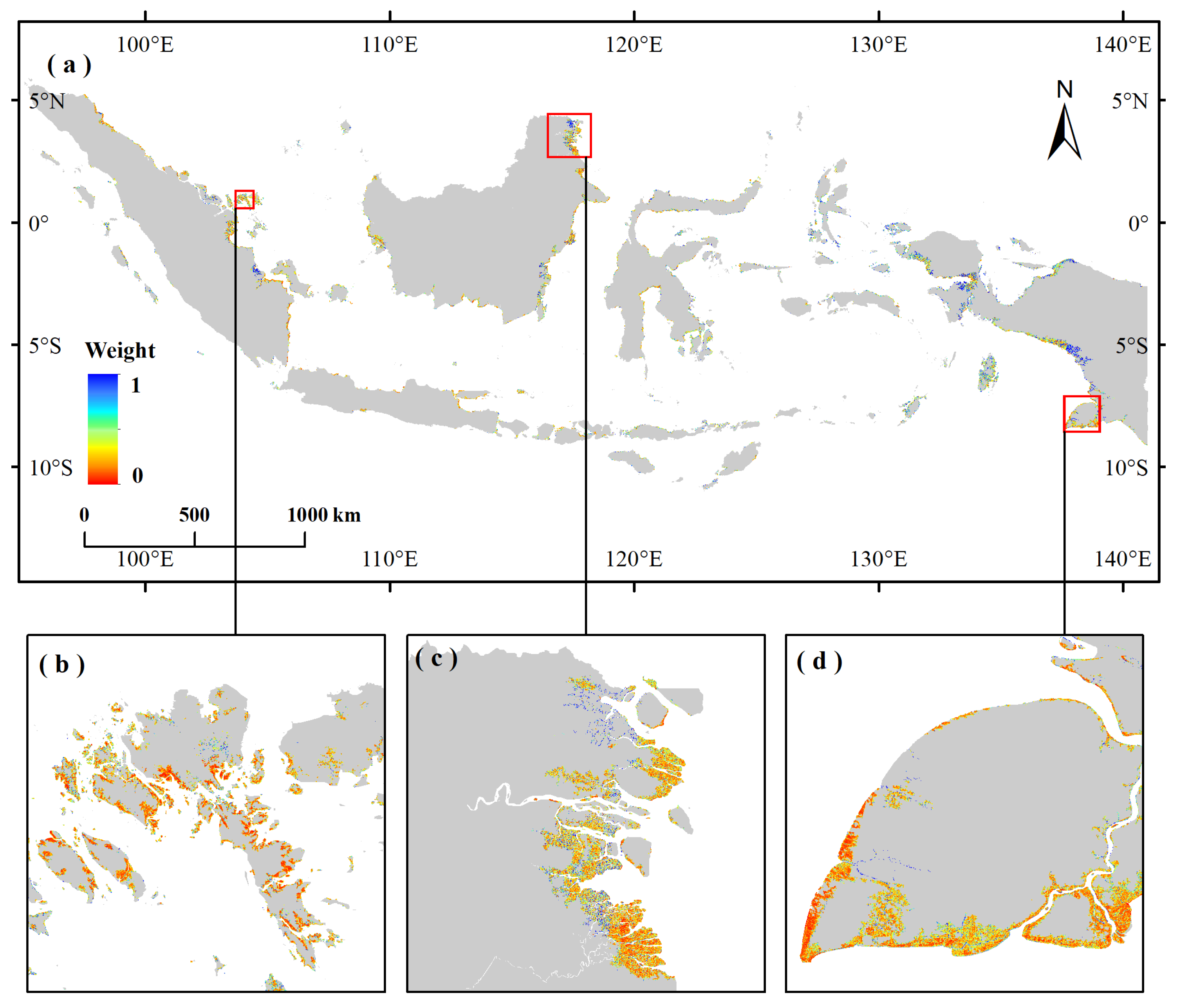
- Spatial Attention Weight Construction:The attention mechanism, originally used in natural language processing and image recognition, is a key component in the efficient allocation of resources during information processing [48]. The attention mechanism assigns sufficient focus to critical information by means of a probability distribution. In spatial modeling, it is used to measure the similarity between the target pixel and its neighboring pixels, and based on this, different weighted contributions are allocated. In this study, we first construct a 3 × 3 sliding window centered on each target pixel and extract the 8 neighboring pixels within its neighborhood. For each neighboring pixel j, we calculate the difference between it and the center pixel c in three aspects: first, the difference between the AGB prediction values; second, whether the LISA clustering categories are consistent; and third, the difference in terrain factors, specifically the slope.The AGB value difference is calculated through the absolute value difference and adjusted by the coefficient , as shown in Equation (4):The LISA classification difference is represented by an indicator function, where if the two classifiers are different, it takes the value 1, otherwise, it is 0. This is adjusted by the coefficient , as shown in Equation (5):The terrain difference is calculated through slope difference and adjusted by the weight coefficient , as shown in Equation (6):The above three items are summed up as an index, used as the unified attention weight for the region around pixel j, as shown in Equation (7):Finally, the attention coefficient for the center pixel i is obtained as in Equation (8):
- Fusion Weight Calculation Method:This study designs a fusion method based on uncertain prediction, where the uncertainty of spatial and terrain heterogeneity is introduced into the modeling process. The method improves the model’s prediction uncertainty and stability. This paper, based on the ML-BMA framework, proposes a SAC-BA model to handle fusion uncertainty. LISA aggregation and spatial attention based on three factors are incorporated.The specific fusion formula is shown in Equation (9):where
- represents the impact weight of uncertainty factors;
- represents the impact weight of structural factors;
- is the predicted uncertainty of model m at pixel i; the uncertainty is treated as a model difference in our study;
- is the LISA cluster type of pixel i, which indicates different spatial distribution of cluster stability. It is set as follows in Equation (10):
The final fused prediction value is expressed as Equation (11):where denotes the fused prediction at pixel i, is the fusion weight of model m at pixel i, and is the prediction result of model m at pixel i.
3. Results
3.1. Variable Characteristics and Contributions to AGB Prediction
3.2. Performance of Different AGB Estimation Models
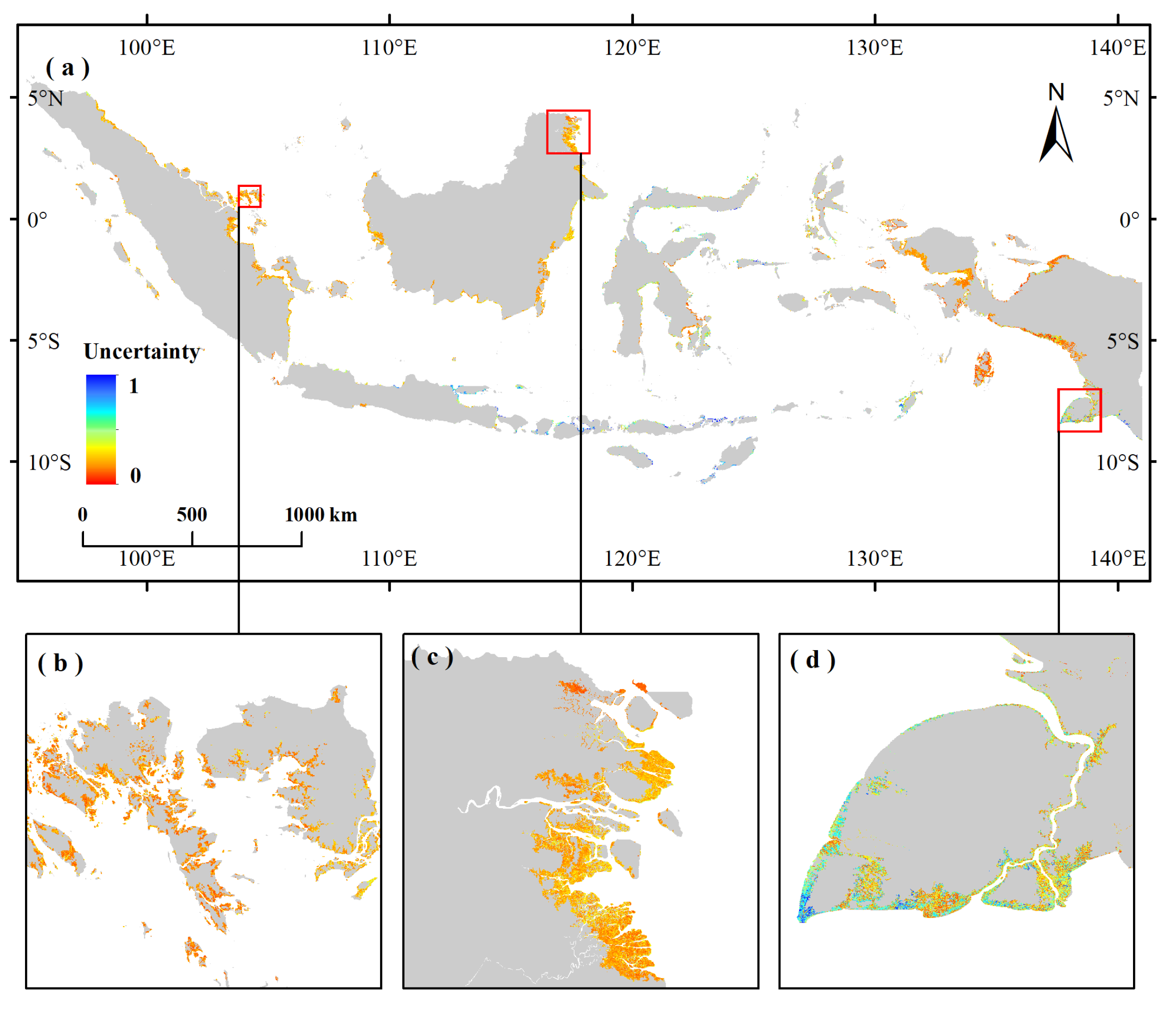
3.3. Spatial Pattern Analysis
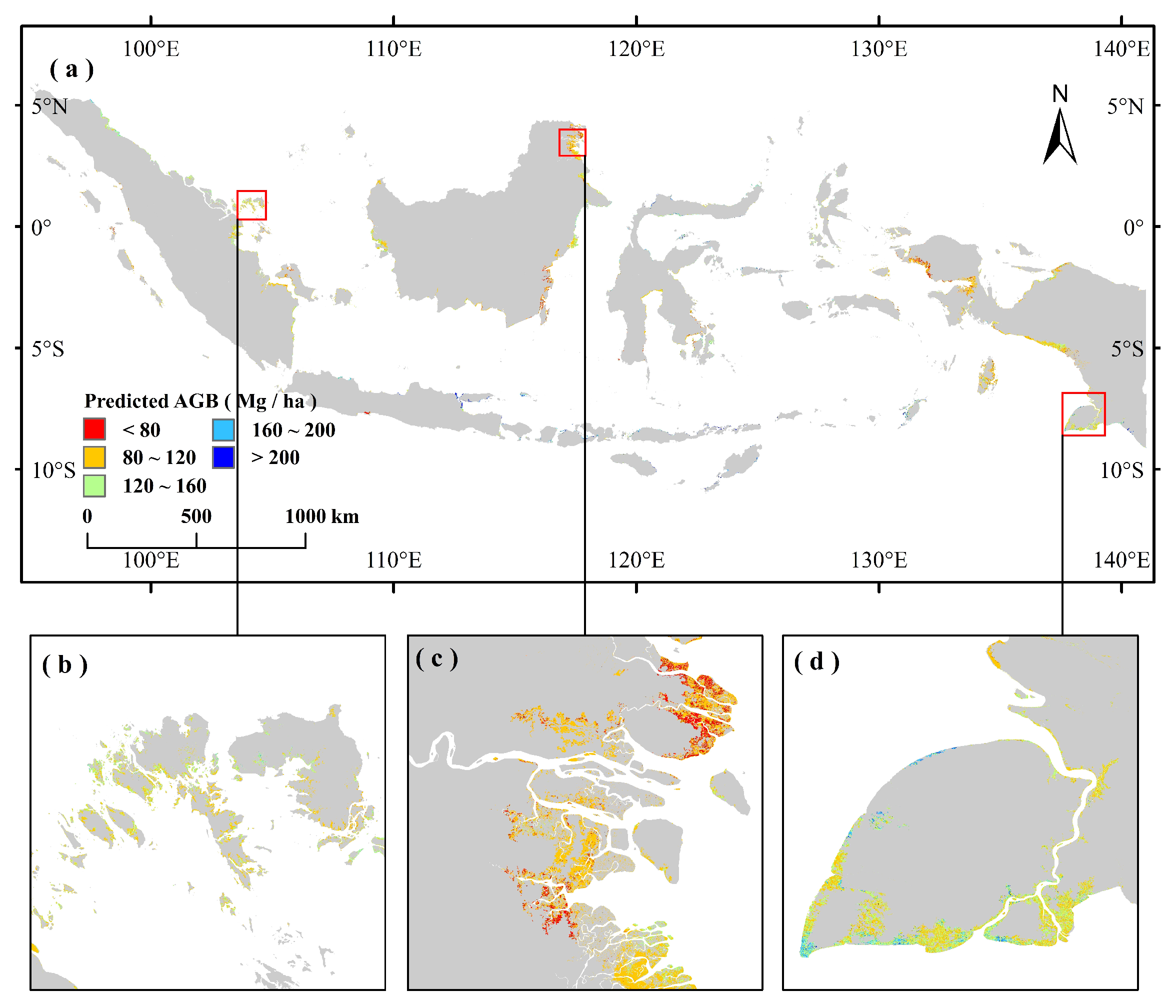
3.4. The Spatial Distribution of AGB
4. Discussion
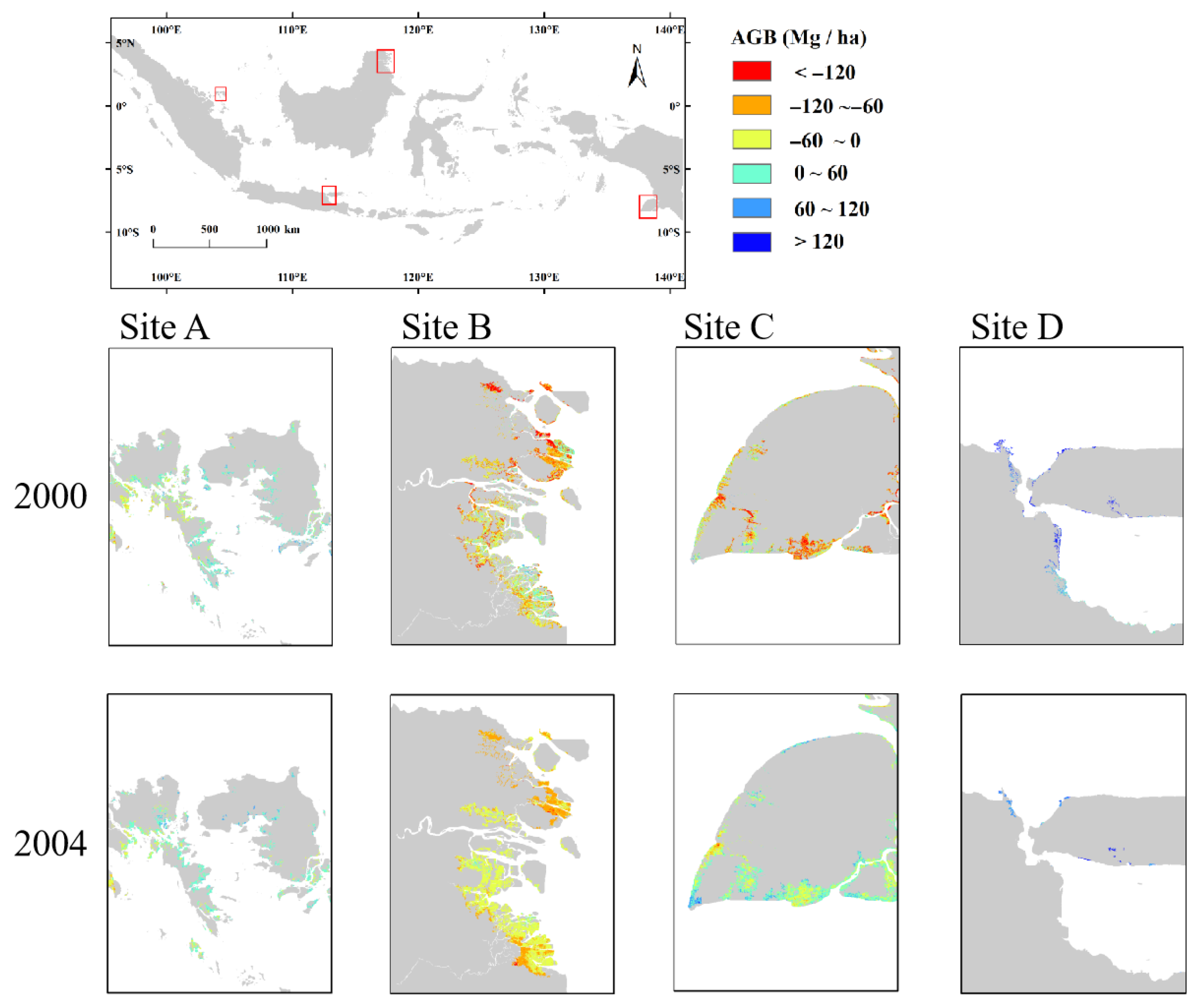
4.1. Comparison with Historical AGB Maps
4.2. Novelty and Advantages of the SAC-BA Method
4.3. Limitations of the Current Study
4.4. Further Improvement of Mangrove AGB Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Data Name | Variable Index | Variable Name | Description | Spatial Resolution |
|---|---|---|---|---|
| Sentinel-1 | 1 | VV | Radar band with vertical | 10 m |
| transmission and vertical reception | ||||
| 2 | VH | Radar band with vertical | ||
| transmission and horizontal reception | ||||
| 3 | VV/VH | Ratio of VV to VH bands | ||
| Landsat 8 | 4 | SR_B1 | Coastal aerosol band | 30 m |
| 5 | SR_B2 | Blue band | ||
| 6 | SR_B3 | Green band | ||
| 7 | SR_B4 | Red band | ||
| 8 | SR_B5 | Near-infrared band | ||
| 9 | SR_B6 | Shortwave infrared band 1 | ||
| 10 | SR_B7 | Shortwave infrared band 2 | ||
| 11 | ST_B10 | Thermal infrared band | ||
| 12 | BSI | (SR_B6 + SR_B4 − SR_B5 − SR_B2)/ | ||
| (SR_B6 + SR_B4 + SR_B5 + SR_B2) | ||||
| 13 | EVI | 2.5 × (SR_B5 − SR_B4)/ | ||
| (SR_B5 + 6 × SR_B4 − 7.5 × SR_B2 + 1) | ||||
| 14 | MNDWI | (SR_B3 − SR_B6) / (SR_B3 + SR_B6) | ||
| 15 | NDBI | (SR_B6 − SR_B5) / (SR_B6 + SR_B5) | ||
| 16 | NDVI | (SR_B5 − SR_B4) / (SR_B5 + SR_B4) | ||
| Copernicus DEM | 17 | DEM | Digital elevation model | 30 m |
| 18 | Slope | The steepness of the terrain | ||
| Climate Research Unit | 19 | MAT | Mean Annual temperature | |
| 20 | AP | Annual precipitation |
| Mean | Maximum | Minimum | Median | SD | CV (%) | Range | |
|---|---|---|---|---|---|---|---|
| AGB | 109.66 | 329.36 | 1.70 | 108.51 | 71.27 | 64.99 | 327.66 |
| AP | 2518.40 | 3937.10 | 1302.00 | 2631.70 | 585.92 | 23.27 | 2635.10 |
| BSI | −0.25 | −0.07 | −0.55 | −0.24 | 0.09 | - | 0.48 |
| EVI | 0.34 | 0.55 | 0.08 | 0.35 | 0.10 | 30.05 | 0.47 |
| MAT | 26.98 | 28.68 | 24.83 | 26.87 | 0.78 | 2.89 | 3.842 |
| MNDWI | −0.10 | 0.20 | −0.47 | −0.11 | 0.16 | - | 0.67 |
| NDBI | −0.41 | −0.19 | −0.60 | −0.42 | 0.08 | - | 0.37 |
| NDVI | 0.47 | 0.87 | 0.11 | 0.43 | 0.21 | 44.27 | 0.76 |
| SR_B1 | 0.07 | 0.27 | 0.00 | 0.04 | 0.07 | 98.32 | 0.27 |
| SR_B2 | 0.08 | 0.27 | 0.01 | 0.05 | 0.07 | 83.96 | 0.26 |
| SR_B3 | 0.12 | 0.30 | 0.04 | 0.01 | 0.06 | 55.42 | 0.26 |
| SR_B4 | 0.10 | 0.30 | 0.01 | 0.09 | 0.07 | 64.47 | 0.28 |
| SR_B5 | 0.31 | 0.45 | 0.12 | 0.32 | 0.07 | 20.88 | 0.33 |
| SR_B6 | 0.13 | 0.21 | 0.06 | 0.13 | 0.03 | 24.48 | 0.15 |
| SR_B7 | 0.10 | 0.19 | 0.04 | 0.09 | 0.04 | 38.51 | 0.15 |
| ST_B10 | 0.87 | 1.08 | 0.28 | 0.94 | 0.18 | 21.08 | 0.80 |
| VH | −16.14 | −13.22 | −22.66 | −15.41 | 2.32 | - | 9.44 |
| VV | −10.20 | −7.23 | −17.27 | −9.44 | 2.45 | - | 10.05 |
| VV/VH | 0.61 | 0.77 | 0.52 | 0.60 | 0.06 | 9.18 | 0.25 |
| DEM | 9.47 | 26.82 | 0.50 | 8.51 | 5.57 | 58.80 | 26.32 |
| slope | 4.39 | 12.19 | 0.75 | 3.73 | 2.65 | 60.35 | 11.45 |
References
- Zhang, Y.; Zhao, M.; Cui, Q.; Fan, W.; Qi, J.; Chen, Y.; Zhang, Y.; Gao, K.; Fan, J.; Wang, G.; et al. Processes of coastal ecosystem carbon sequestration and approaches for increasing carbon sink. Sci. China Earth Sci. 2017, 60, 809–820. [Google Scholar] [CrossRef]
- Alongi, D.M.; Mukhopadhyay, S.K. Contribution of mangroves to coastal carbon cycling in low latitude seas. Agric. For. Meteorol. 2015, 213, 266–272. [Google Scholar] [CrossRef]
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- McLeod, E.; Chmura, G.L.; Bouillon, S.; Salm, R.; Björk, M.; Duarte, C.M.; Lovelock, C.E.; Schlesinger, W.H.; Silliman, B.R. A blueprint for blue carbon: Toward an improved understanding of the role of vegetated coastal habitats in sequestering CO2. Front. Ecol. Environ. 2011, 9, 552–560. [Google Scholar] [CrossRef]
- Pendleton, L.; Donato, D.C.; Murray, B.C.; Crooks, S.; Jenkins, W.A.; Sifleet, S.; Craft, C.; Fourqurean, J.W.; Kauffman, J.B.; Marbà, N.; et al. Estimating global “blue carbon” emissions from conversion and degradation of vegetated coastal ecosystems. PLoS ONE 2012, 7, e43542. [Google Scholar] [CrossRef] [PubMed]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Alongi, D.M. Carbon Cycling and Storage in Mangrove Forests. Annu. Rev. Mar. Sci. 2014, 6, 195–219. [Google Scholar] [CrossRef]
- Valiela, I.; Bowen, J.L.; York, J.K. Mangrove Forests: One of the World’s Threatened Major Tropical Environments: At least 35% of the area of mangrove forests has been lost in the past two decades, losses that exceed those for tropical rain forests and coral reefs, two other well-known threatened environments. Bioscience 2001, 51, 807–815. [Google Scholar] [CrossRef]
- Malik, A.; Jalil, A.; Arifuddin, A.; Syahmuddin, A. Biomass Carbon Stocks in the mangrove rehabilitated area of Sinjai District, South Sulawesi, Indonesia. Geogr. Environ. Sustain. 2020, 13, 32–38. [Google Scholar] [CrossRef]
- Murdiyarso, D.; Purbopuspito, J.; Kauffman, J.B.; Warren, M.W.; Sasmito, S.D.; Donato, D.C.; Manuri, S.; Krisnawati, H.; Taberima, S.; Kurnianto, S. The potential of Indonesian mangrove forests for global climate change mitigation. Nat. Clim. Change 2015, 5, 1089–1092. [Google Scholar] [CrossRef]
- Clough, B.; Scott, K. Allometric relationships for estimating above-ground biomass in six mangrove species. For. Ecol. Manag. 1989, 27, 117–127. [Google Scholar] [CrossRef]
- Amarasinghe, M.; Balasubramaniam, S. Net primary productivity of two mangrove forest stands on the northwestern coast of Sri Lanka. Hydrobiologia 1992, 247, 37–47. [Google Scholar] [CrossRef]
- Wicaksono, P. Mangrove above-ground carbon stock mapping of multi-resolution passive remote-sensing systems. Int. J. Remote Sens. 2017, 38, 1551–1578. [Google Scholar] [CrossRef]
- Mariano Neto, M.; da Silva, J.B.; de Brito, H.C. Carbon Stock Estimation in a Brazilian Mangrove Using Optical Satellite Data. Environ. Monit. Assess. 2023, 196, 9. [Google Scholar] [CrossRef]
- Hamdan, O.; Aziz, H.K.; Hasmadi, I.M. L-band ALOS PALSAR for biomass estimation of Matang Mangroves, Malaysia. Remote Sens. Environ. 2014, 155, 69–78. [Google Scholar] [CrossRef]
- Dashtbozorgi, F.; Hedayatiaghmashhadi, A.; Dashtbozorgi, A.; Ruiz-Agudelo, C.A.; Fürst, C.; Cirella, G.T.; Naderi, M. Ecosystem services valuation using InVEST modeling: Case from southern Iranian mangrove forests. Reg. Stud. Mar. Sci. 2023, 60, 102813. [Google Scholar] [CrossRef]
- Dai, Z.; Trettin, C.C.; Burton, A.J.; Tang, W.; Mangora, M.M. Estimated mangrove carbon stocks and fluxes to inform MRV for REDD+ using a process-based model. Estuar. Coast. Shelf Sci. 2023, 294, 108512. [Google Scholar] [CrossRef]
- Li, Z.; Zan, Q.; Yang, Q.; Zhu, D.; Chen, Y.; Yu, S. Remote estimation of mangrove aboveground carbon stock at the species level using a low-cost unmanned aerial vehicle system. Remote Sens. 2019, 11, 1018. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, H.; Zhou, G.; Zhang, Q.; Tao, J.; Zhang, Y.; Lin, J. Aboveground mangrove biomass estimation in Beibu Gulf using machine learning and UAV remote sensing. Sci. Total Environ. 2021, 781, 146816. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Purwanto, A.D.; Wikantika, K.; Deliar, A.; Darmawan, S. Decision tree and random forest classification algorithms for mangrove forest mapping in Sembilang National Park, Indonesia. Remote Sens. 2022, 15, 16. [Google Scholar] [CrossRef]
- Darmawan, S.; Takeuchi, W.; Vetrita, Y.; Winarso, G.; Wikantika, K.; Sari, D. Characterization of mangrove forest types based on ALOS-PALSAR in overall Indonesian archipelago. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 7th IGRSM International Remote Sensing & GIS Conference and Exhibition; Kuala Lumpur, Malaysia, 22–23 April 2014, IOP Publishing: Bristol, UK, 2014; Volume 20, p. 012051. [Google Scholar] [CrossRef]
- Bunting, P.; Rosenqvist, A.; Lucas, R.M.; Rebelo, L.M.; Hilarides, L.; Thomas, N.; Hardy, A.; Itoh, T.; Shimada, M.; Finlayson, C.M. The global mangrove watch—A new 2010 global baseline of mangrove extent. Remote Sensing 2018, 10, 1669. [Google Scholar] [CrossRef]
- Suwignyo, R.A.; Ulqodry, T.Z.; Sarno, S.; Miyakawa, H.; Tatang, T. Mangrove plant condition in the Greenbelt area of Banyuasin Peninsula, Sembilang National Park, South Sumatra, Indonesia and its restoration plan. Chiang Mai Univ. J. Nat. Sci. 2012, 11, 123–134. [Google Scholar]
- Arifanti, V.B.; Kauffman, J.B.; Subarno; Ilman, M.; Tosiani, A.; Novita, N. Contributions of mangrove conservation and restoration to climate change mitigation in Indonesia. Glob. Change Biol. 2022, 28, 4523–4538. [Google Scholar] [CrossRef]
- Hutchison, J.; Manica, A.; Swetnam, R.; Balmford, A.; Spalding, M. Predicting global patterns in mangrove forest biomass. Conserv. Lett. 2014, 7, 233–240. [Google Scholar] [CrossRef]
- Fatoyinbo, T.E.; Simard, M. Height and biomass of mangroves in Africa from ICESat/GLAS and SRTM. Int. J. Remote Sens. 2013, 34, 668–681. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, Y.; Su, Y.; Zheng, Y.; Lin, G.; Guo, Q. Mapping the global mangrove forest aboveground biomass using multisource remote sensing data. Remote Sens. 2020, 12, 1690. [Google Scholar] [CrossRef]
- Goïta, K.; Mouloungou, J.; Bénié, G.B. Estimation of aboveground biomass and carbon in a tropical rain forest in Gabon using remote sensing and GPS data. Geocarto Int. 2019, 34, 243–259. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ghosh, S.; Behera, M.; Jagadish, B.; Das, A.; Mishra, D. A novel approach for estimation of aboveground biomass of a carbon-rich mangrove site in India. J. Environ. Manag. 2021, 292, 112816. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Rijal, S.S.; Pham, T.D.; Noer’Aulia, S.; Putera, M.I.; Saintilan, N. Mapping mangrove above-ground carbon using multi-source remote sensing data and machine learning approach in Loh Buaya, Komodo National Park, Indonesia. Forests 2023, 14, 94. [Google Scholar] [CrossRef]
- Roy, A.D.; Arachchige, P.S.P.; Watt, M.S.; Kale, A.; Davies, M.; Heng, J.E.; Daneil, R.; Galgamuwa, G.P.; Moussa, L.G.; Timsina, K.; et al. Remote sensing-based mangrove blue carbon assessment in the Asia-Pacific: A systematic review. Sci. Total Environ. 2024, 938, 173270. [Google Scholar] [CrossRef]
- Kimeldorf, G.S.; Wahba, G. A correspondence between Bayesian estimation on stochastic processes and smoothing by splines. Ann. Math. Stat. 1970, 41, 495–502. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Le, N.N.; Bui, D.T. Estimating aboveground biomass of a mangrove plantation on the Northern coast of Vietnam using machine learning techniques with an integration of ALOS-2 PALSAR-2 and Sentinel-2A data. Int. J. Remote Sens. 2018, 39, 7761–7788. [Google Scholar] [CrossRef]
- Prakash, A.J.; Behera, M.D.; Ghosh, S.M.; Das, A.; Mishra, D. A new synergistic approach for Sentinel-1 and PALSAR-2 in a machine learning framework to predict aboveground biomass of a dense mangrove forest. Ecol. Inform. 2022, 72, 101900. [Google Scholar] [CrossRef]
- Wang, K.; Franklin, S.E.; Guo, X.; Cattet, M. Remote sensing of ecology, biodiversity and conservation: A review from the perspective of remote sensing specialists. Sensors 2010, 10, 9647–9667. [Google Scholar] [CrossRef]
- Quinlan, J.R. (1992) Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Australia, 16–18 November 1992; World Scientific: Singapore, 1992; Volume 92, pp. 343–348. [CrossRef]
- Huang, C.; Townshend, J. A stepwise regression tree for nonlinear approximation: Applications to estimating subpixel land cover. Int. J. Remote Sens. 2003, 24, 75–90. [Google Scholar] [CrossRef]
- Arruda, D.L.d.; Ker, J.C.; Veloso, G.V.; Henriques, R.J.; Fernandes-Filho, E.I.; Camêlo, D.d.L.; Gomes, L.d.C.; Schaefer, C.E.G.R. Soil carbon prediction in Marajó island wetlands. Rev. Bras. CiÊNcia Solo 2024, 48, e0230162. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, X.; Ouyang, Z.; Avitabile, V.; Qi, J.; Chen, J.; Giannico, V. Estimating aboveground biomass in subtropical forests of China by integrating multisource remote sensing and ground data. Remote Sens. Environ. 2019, 232, 111341. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Tenneson, K.; Patterson, M.S.; Mellin, T.; Nigrelli, M.; Joria, P.; Mitchell, B. Development of a regional lidar-derived above-ground biomass model with Bayesian model averaging for use in ponderosa pine and mixed conifer forests in Arizona and New Mexico, USA. Remote Sens. 2018, 10, 442. [Google Scholar] [CrossRef]
- Chaudhari, S.; Mithal, V.; Polatkan, G.; Ramanath, R. An attentive survey of attention models. ACM Trans. Intell. Syst. Technol. (TIST) 2021, 12, 1–32. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G.o.; Wang, S.; Liu, K.; Liu, X. Estimating mangrove wetland biomass using radar remote sensing. J. Remote Sens. Beijing 2006, 10, 387. [Google Scholar]
- Bai, J.; Meng, Y.; Gou, R.; Lyu, J.; Dai, Z.; Diao, X.; Zhang, H.; Luo, Y.; Zhu, X.; Lin, G. Mangrove diversity enhances plant biomass production and carbon storage in Hainan island, China. Funct. Ecol. 2021, 35, 774–786. [Google Scholar] [CrossRef]
- Purwanto, A.D.; Wikantika, K.; Deliar, A.; Darmawan, S.; Harto, A.B.; Khomarudin, M.R.; Ardli, E.R. Improving the accuracy of mangrove forest mapping using sentinel image and developed classification algorithm based on machine learning. J. Spat. Sci. 2024, 69, 1019–1045. [Google Scholar] [CrossRef]
- Maxwell, T.L.; Hengl, T.; Parente, L.L.; Minarik, R.; Worthington, T.A.; Bunting, P.; Smart, L.S.; Spalding, M.D.; Landis, E. Global mangrove soil organic carbon stocks dataset at 30 m resolution for the year 2020 based on spatiotemporal predictive machine learning. Data Brief 2023, 50, 109621. [Google Scholar] [CrossRef]
- Simard, M.; Fatoyinbo, L.; Smetanka, C.; Rivera-Monroy, V.H.; Castañeda-Moya, E.; Thomas, N.; Van der Stocken, T. Mangrove canopy height globally related to precipitation, temperature and cyclone frequency. Nat. Geosci. 2019, 12, 40–45. [Google Scholar] [CrossRef]
- Mitchard, E.T.; Saatchi, S.S.; Baccini, A.; Asner, G.P.; Goetz, S.J.; Harris, N.L.; Brown, S. Uncertainty in the spatial distribution of tropical forest biomass: A comparison of pan-tropical maps. Carbon Balance Manag. 2013, 8, 10. [Google Scholar] [CrossRef] [PubMed]
- Baccini, A.; Goetz, S.J.; Walker, W.; Laporte, N.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.; Dubayah, R.; Friedl, M.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Change 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Avitabile, V.; Herold, M.; Heuvelink, G.B.; Lewis, S.L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Ashton, P.S.; Banin, L.; Bayol, N.; et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Change Biol. 2016, 22, 1406–1420. [Google Scholar] [CrossRef]
- Bouvet, A.; Mermoz, S.; Le Toan, T.; Villard, L.; Mathieu, R.; Naidoo, L.; Asner, G.P. An above-ground biomass map of African savannahs and woodlands at 25 m resolution derived from ALOS PALSAR. Remote Sens. Environ. 2018, 206, 156–173. [Google Scholar] [CrossRef]
- Zeng, N.; Ren, X.; He, H.; Zhang, L.; Li, P.; Niu, Z. Estimating the grassland aboveground biomass in the Three-River Headwater Region of China using machine learning and Bayesian model averaging. Environ. Res. Lett. 2021, 16, 114020. [Google Scholar] [CrossRef]
- Pham, T.D.; Le, N.N.; Ha, N.T.; Nguyen, L.V.; Xia, J.; Yokoya, N.; To, T.T.; Trinh, H.X.; Kieu, L.Q.; Takeuchi, W. Estimating mangrove above-ground biomass using extreme gradient boosting decision trees algorithm with fused sentinel-2 and ALOS-2 PALSAR-2 data in can Gio biosphere reserve, Vietnam. Remote Sens. 2020, 12, 777. [Google Scholar] [CrossRef]
- Basyuni, M.; Mubaraq, A.; Amelia, R.; Wirasatriya, A.; Iryanthony, S.B.; Slamet, B.; Al Mustaniroh, S.S.; Pradisty, N.A.; Sidik, F.; Hanintyo, R.; et al. Mangrove aboveground biomass estimation using UAV imagery and a constructed height model in Budeng–Perancak, Bali, Indonesia. Ecol. Inform. 2025, 86, 103037. [Google Scholar] [CrossRef]
- Twomey, A.; Lovelock, C. Global spatial dataset of mangrove genus distribution in seaward and riverine margins. Sci. Data 2024, 11, 306. [Google Scholar] [CrossRef] [PubMed]

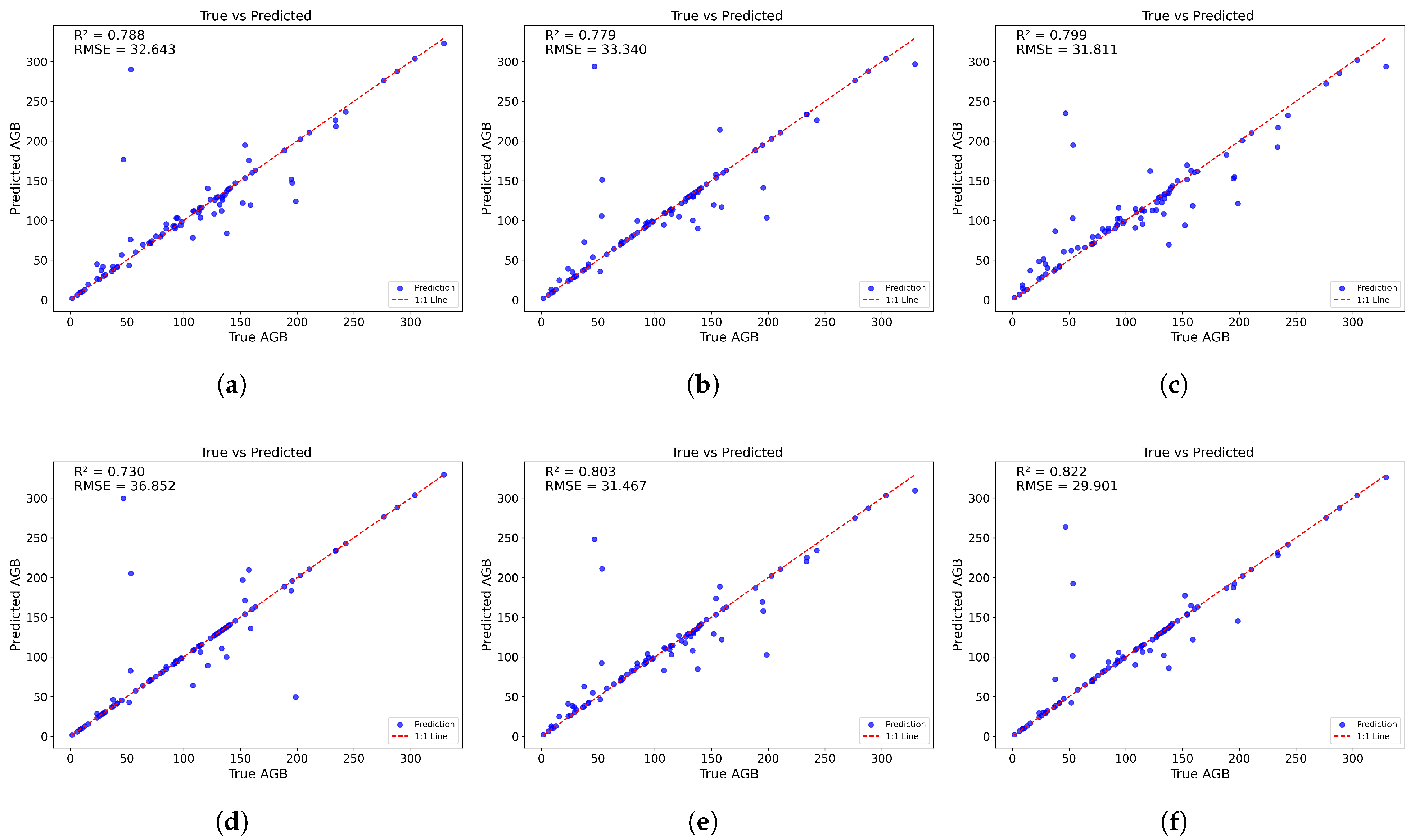



| Model | Input Variables | Training | Validation | AIC | ||
|---|---|---|---|---|---|---|
| RMSE | RMSE | |||||
| RF | All features | 0.88 | 28.61 | 0.79 | 33.13 | 129.27 |
| Optimized features | 0.89 | 27.86 | 0.79 | 32.64 | 129.02 | |
| Cubist | All features | 0.89 | 26.07 | 0.73 | 36.86 | 124.67 |
| Optimized features | 0.90 | 25.06 | 0.73 | 36.85 | 123.01 | |
| SVR | All features | 0.86 | 23.03 | 0.78 | 33.34 | 126.66 |
| Optimized features | – | – | – | – | – | |
| XGBoost | All features | 0.87 | 21.52 | 0.78 | 33.08 | 132.77 |
| Optimized features | 0.88 | 26.07 | 0.80 | 31.81 | 132.22 | |
| ML-BMA | – | 0.89 | 25.38 | 0.80 | 31.47 | – |
| SAC-BA | – | 0.90 | 21.08 | 0.82 | 29.90 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Xue, Z.; Qian, S.; Sun, C. Estimating Aboveground Biomass of Mangrove Forests in Indonesia Using Spatial Attention Coupled Bayesian Aggregator. Forests 2025, 16, 1296. https://doi.org/10.3390/f16081296
Zhu X, Xue Z, Qian S, Sun C. Estimating Aboveground Biomass of Mangrove Forests in Indonesia Using Spatial Attention Coupled Bayesian Aggregator. Forests. 2025; 16(8):1296. https://doi.org/10.3390/f16081296
Chicago/Turabian StyleZhu, Xinyue, Zhaohui Xue, Siyu Qian, and Chenrun Sun. 2025. "Estimating Aboveground Biomass of Mangrove Forests in Indonesia Using Spatial Attention Coupled Bayesian Aggregator" Forests 16, no. 8: 1296. https://doi.org/10.3390/f16081296
APA StyleZhu, X., Xue, Z., Qian, S., & Sun, C. (2025). Estimating Aboveground Biomass of Mangrove Forests in Indonesia Using Spatial Attention Coupled Bayesian Aggregator. Forests, 16(8), 1296. https://doi.org/10.3390/f16081296





