Evaluating Forest Canopy Structures and Leaf Area Index Using a Five-Band Depth Image Sensor
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Field Measurement
2.2. Depth Image Sensor Data Processing and LAI Calculation
3. Results
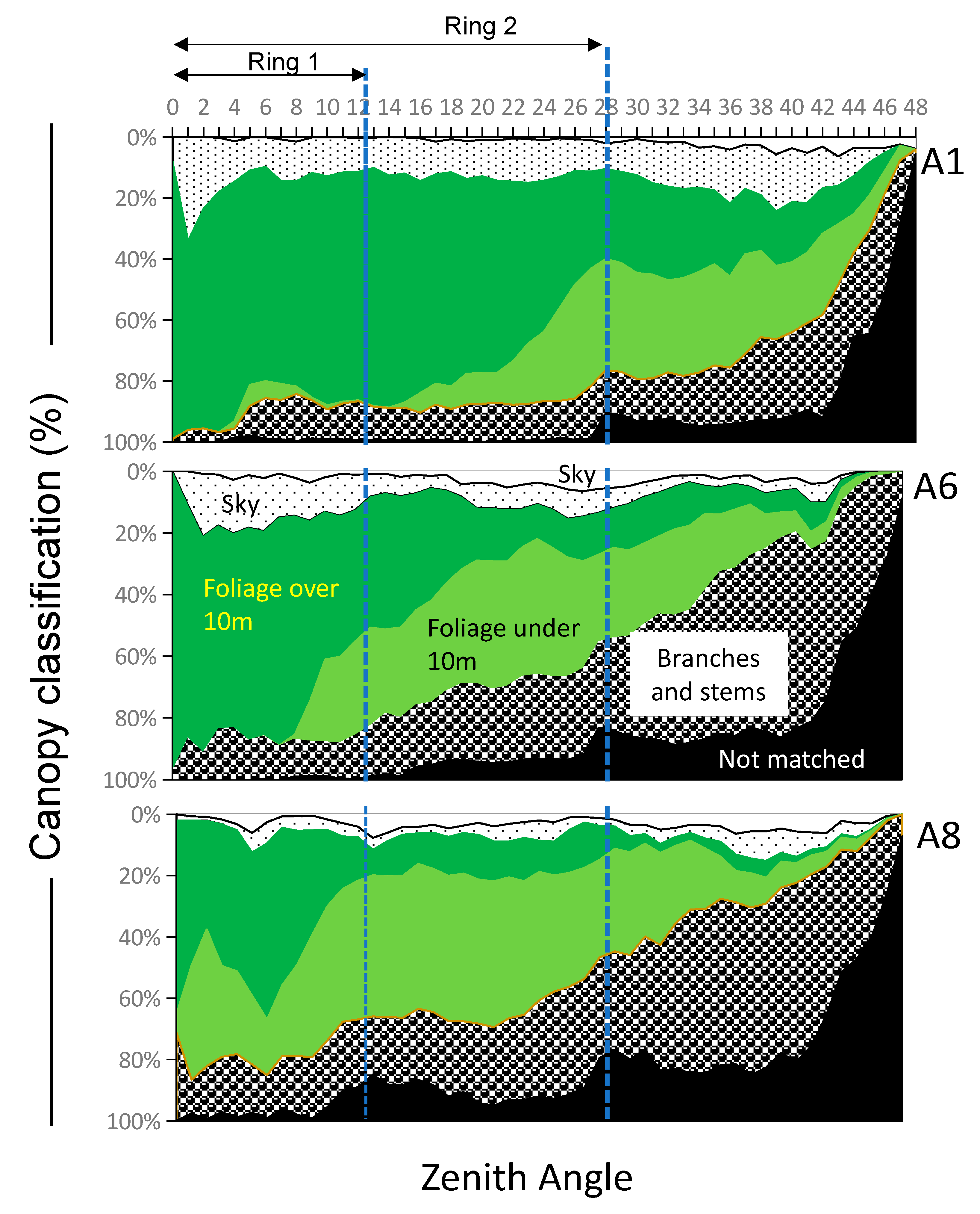
3.1. Image Information Using Depth Image Sensor
3.2. Estimated LAI and PAI
3.3. Classification of Canopy Structures
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LAI | Leaf Area Index |
| PAI | Plant Area Index |
| WAI | Woody Area Index |
| DBH | Diameter at Breast Height |
| FOV | Field of View |
| RGB | Red, Green, Blue |
| IR | Near-Infrared |
| SD | Standard Deviation |
| GLA | Gap Light Analyzer |
References
- Lowman, M.D.; Rinker, H.B. Forest Canopies, 2nd ed.; Academic Press: San Diego, CA, USA, 2004. [Google Scholar]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Öquist, G.; Huner, N.P.A. Photosynthesis of overwintering evergreen plants. Annu. Rev. Plant Biol. 2003, 54, 329–355. [Google Scholar] [CrossRef]
- Reich, P.B.; Walters, M.B.; Kloeppel, B.D.; Ellsworth, D.S. Different photosynthesis-nitrogen relations in deciduous hardwood and evergreen coniferous tree species. Oecologia 1995, 104, 24–30. [Google Scholar] [CrossRef]
- von Arx, G.; Dobbertin, M.; Rebetez, M. Spatio-temporal effects of forest canopy on understory microclimate in a long-term experiment in Switzerland. Agric. For. Meteorol. 2012, 166–167, 144–155. [Google Scholar] [CrossRef]
- Davies-Colley, R.J.; Payne, G.W.; van Elswijk, M. Microclimate Gradients across a Forest Edge. N. Z. J. Ecol. 2000, 24, 111–121. [Google Scholar]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Monsi, M.; Saeki, T. On the factor light in plant communities and its importance for matter production. Ann. Bot. 2005, 95, 549–567. [Google Scholar] [CrossRef]
- Holst, T.; Hauser, S.; Kirchgäßner, A.; Matzarakis, A.; Mayer, H.; Schindler, D. Measuring and modelling plant area index in beech stands. Int. J. Biometeorol. 2004, 48, 192–201. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Ma, C.; Luo, Y.; Shao, M.; Jia, X. Estimation and testing of linkages between forest structure and rainfall interception characteristics of a Robinia pseudoacacia plantation on China’s Loess Plateau. J. For. Res. 2022, 33, 529–542. [Google Scholar] [CrossRef]
- Fathizadeh, O.; Hosseini, S.M.; Zimmermann, A.; Keim, R.F.; Darvishi Boloorani, A. Estimating linkages between forest structural variables and rainfall interception parameters in semi-arid deciduous oak forest stands. Sci. Total Environ. 2017, 601–602, 1824–1837. [Google Scholar] [CrossRef]
- Bréda, N.; Granier, A. Intra- and interannual variations of transpiration, leaf area index and radial growth of a sessile oak stand (Quercus petraea). Ann. For. Sci. 1996, 53, 521–536. [Google Scholar] [CrossRef]
- Wang, Y.R.; Wang, Y.H.; Yu, P.T.; Xiong, W.; Du, A.P.; Li, Z.H.; Liu, Z.B.; Ren, L.; Xu, L.H.; Zuo, H.J. Simulated responses of evapotranspiration and runoff to changes in the leaf area index of a Larix principis-rupprechtii plantation. Acta Ecol. Sin. 2016, 36, 6928–6938. [Google Scholar]
- Bonan, G.B. Importance of leaf area index and forest type when estimating photosynthesis in boreal forests. Remote Sens. Environ. 1993, 43, 303–314. [Google Scholar] [CrossRef]
- Norman, J.M.; Campbell, G.S. Canopy structure. In Plant Physiological Ecology; Pearcy, R.W., Ehleringer, J.R., Mooney, H.A., Rundel, P.W., Eds.; Springer: Dordrecht, The Netherlands, 1989; pp. 301–325. [Google Scholar] [CrossRef]
- Soudani, K.; Trautmann, J.; Walter, J.M. Comparison of optical methods for estimating canopy openness and leaf area index in broad-leaved forests. Comptes Rendus Biol. 2001, 324, 381–392. [Google Scholar] [CrossRef]
- Gower, S.T.; Norman, J.M. Rapid estimation of leaf area index in conifer and broad-leaf plantations. Ecology 1991, 72, 1896–1900. [Google Scholar] [CrossRef]
- Liu, F.; Wang, C.; Wang, X. Sampling protocols of specific leaf area for improving accuracy of the estimation of forest leaf area index. Agric. For. Meteorol. 2021, 298–299, 108286. [Google Scholar] [CrossRef]
- Chen, J.M.; Govind, A.; Sonnentag, O.; Zhang, Y.; Barr, A.; Amiro, B. Leaf area index measurements at Fluxnet-Canada forest sites. Agric. For. Meteorol. 2006, 140, 257–268. [Google Scholar] [CrossRef]
- Cutini, A.; Matteucci, G.; Mugnozza, G.S. Estimation of leaf area index with the Li-Cor LAI 2000 in deciduous forests. For. Ecol. Manag. 1998, 105, 55–65. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, W.; Hu, R.; Qi, J.; Shao, J.; Li, D.; Wan, P.; Qiao, C.; Shen, A.; Yan, G. Estimation of forest leaf area index using terrestrial laser scanning data and path length distribution model in open-canopy forests. Agric. For. Meteorol. 2018, 263, 323–333. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Gilardelli, C.; Orlando, F.; Movedi, E.; Confalonieri, R. Quantifying the accuracy of digital hemispherical photography for leaf area index estimates on broad-leaved tree species. Sensors 2018, 18, 1028. [Google Scholar] [CrossRef] [PubMed]
- Penner, M.; White, J.C.; Woods, M.E. Automated characterization of forest canopy vertical layering for predicting forest inventory attributes by layer using airborne LiDAR data. Forestry 2024, 97, 59–75. [Google Scholar] [CrossRef]
- Brockerhoff, E.G.; Jactel, H.; Parrotta, J.A.; Quine, C.P.; Sayer, J. Plantation forests and biodiversity: Oxymoron or opportunity? Biodivers. Conserv. 2008, 17, 925–951. [Google Scholar] [CrossRef]
- Uttarakhand Open University. Forest Ecology (MSCBOT-607); Uttarakhand Open University: Haldwani, India, 2023; Available online: https://uou.ac.in/sites/default/files/slm/MSCBOT-607.pdf (accessed on 5 July 2025).
- Song, Y.; Ryu, Y. Seasonal changes in vertical canopy structure in a temperate broadleaved forest in Korea. Ecol. Res. 2015, 30, 821–831. [Google Scholar] [CrossRef]
- Olivas, P.C.; Oberbauer, S.F.; Clark, D.B.; Clark, D.A.; Ryan, M.G.; O’Brien, J.J.; Ordoñez, H. Comparison of direct and indirect methods for assessing leaf area index across a tropical rain forest landscape. Agric. For. Meteorol. 2013, 177, 110–116. [Google Scholar] [CrossRef]
- Japan Meteorological Agency. Available online: https://www.jma.go.jp/jma/indexe.html (accessed on 8 April 2024).
- Biodiversity Center of Japan. Available online: https://www.biodic.go.jp/index_e.html (accessed on 12 May 2024).
- Liu, Z.; Wang, X.; Chen, J.M.; Wang, C.; Jin, G. On improving the accuracy of digital hemispherical photography measurements of seasonal leaf area index variation in deciduous broadleaf forests. Can. J. For. Res. 2015, 45, 721–731. [Google Scholar] [CrossRef]
- Chianucci, F.; Bajocco, S.; Ferrara, C. Continuous observations of forest canopy structure using low-cost digital camera traps. Agric. For. Meteorol. 2021, 307, 108516. [Google Scholar] [CrossRef]
- Bater, C.W.; Coops, N.C.; Wulder, M.A.; Hilker, T.; Nielsen, S.E.; McDermid, G.; Stenhouse, G.B. Using digital time-lapse cameras to monitor species-specific understorey and overstorey phenology in support of wildlife habitat assessment. Environ. Monit. Assess. 2011, 180, 1–13. [Google Scholar] [CrossRef]
- Intel Corporation. Intel RealSense D400 Series Datasheet. Available online: https://www.intelrealsense.com/wp-content/uploads/2022/03/Intel-RealSense-D400-Series-Datasheet-March-2022.pdf (accessed on 18 June 2024).
- LI-COR Biosciences. LAI-2200C Instruction Manuals. Available online: https://www.licor.com/support/MicroContent/Resources/MicroContent/manuals/lai-2200c-instruction-manuals.html (accessed on 24 June 2024).
- Danner, M.; Locherer, M.; Hank, T.; Richter, K. Measuring Leaf Area Index (LAI) with the LI-Cor LAI 2200C or LAI-2200 (+2200Clear Kit)—Theory, Measurement, Problems, Interpretation; EnMAP Field Guide Technical Report; GFZ Data Services: Potsdam, Germany, 2015. [Google Scholar] [CrossRef]
- ter Steege, H. Hemiphot. R: Free R Scripts to Analyse Hemispherical Photographs for Canopy Openness, Leaf Area Index and Photosynthetic Active Radiation Under Forest Canopies; Unpublished Report; Naturalis Biodiversity Center: Leiden, The Netherlands, 2018. [Google Scholar]
- Frazer, G.W.; Canham, C.D.; Lertzman, K.P. Gap Light Analyzer (GLA), Version 2.0: Imaging Software to Extract Canopy Structure and Gap Light Transmission Indices from True-Colour Fisheye Photographs, User’s Manual and Program Documentation; Simon Fraser University: Burnaby, BC, Canada; Institute of Ecosystem Studies: Millbrook, NY, USA, 1999. [Google Scholar]
- Intel Corporation. C/C++ Code Samples for Intel RealSense SDK 2.0. Intel® RealSense™ Developer Documentation. Available online: https://dev.intelrealsense.com/docs/code-samples (accessed on 24 July 2024).
- Maphanga, T. The use of modified and unmodified digital cameras to monitor small-scale savannah rangeland vegetation. J. Rangel. Sci. 2025, 15, 1–8. [Google Scholar] [CrossRef]
- Kirk, K.; Andersen, H.J.; Thomsen, A.G.; Jørgensen, J.R.; Jørgensen, R.N. Estimation of leaf area index in cereal crops using red–green images. Biosyst. Eng. 2009, 104, 308–317. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving leaf area index (LAI) using remote sensing: Theories, methods and sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [PubMed]
- Campbell, G.S.; Norman, J.M. The description and measurement of plant canopy structure. In Plant Canopies: Their Growth, Form and Function; Marshall, B., Russell, G., Jarvis, P.G., Eds.; Cambridge University Press: Cambridge, UK, 1989; pp. 1–20. [Google Scholar] [CrossRef]
- de Castro, F.; Fetcher, N. Three dimensional model of the interception of light by a canopy. Agric. For. Meteorol. 1998, 90, 215–233. [Google Scholar] [CrossRef]
- Barclay, H.J.; Trofymow, J.A.; Leach, R.I. Assessing bias from boles in calculating leaf area index in immature Douglas-fir with the LI-COR canopy analyzer. Agric. For. Meteorol. 2000, 100, 255–260. [Google Scholar] [CrossRef]
- Sasaki, T.; Imanishi, J.; Ioki, K.; Morimoto, Y.; Kitada, K. Estimation of leaf area index and canopy openness in broad-leaved forest using an airborne laser scanner in comparison with high-resolution near-infrared digital photography. Landsc. Ecol. Eng. 2008, 4, 47–55. [Google Scholar] [CrossRef]
- Luo, T.; Neilson, R.P.; Tian, H.; Vörösmarty, C.J.; Zhu, H.; Liu, S. A model for seasonality and distribution of leaf area index of forests and its application to China. J. Veg. Sci. 2002, 13, 817–830. [Google Scholar] [CrossRef]
- Tang, H.; Dubayah, R.; Brolly, M.; Ganguly, S.; Zhang, G. Large-Scale Retrieval of Leaf Area Index and Vertical Foliage Profile from the Spaceborne Waveform Lidar (GLAS/ICESat). Remote Sens. Environ. 2014, 154, 8–18. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Disney, M.; Nightingale, J.; Woodgate, W.; Armston, J.; Lewis, P. Variability and Bias in Active and Passive Ground-Based Measurements of Effective Plant, Wood and Leaf Area Index. Agric. For. Meteorol. 2018, 252, 231–240. [Google Scholar] [CrossRef]
- Zhu, X.; Skidmore, A.K.; Wang, T.; Liu, J.; Darvishzadeh, R.; Shi, Y.; Premier, J.; Heurich, M. Improving Leaf Area Index (LAI) Estimation by Correcting for Clumping and Woody Effects Using Terrestrial Laser Scanning. Agric. For. Meteorol. 2018, 263, 276–286. [Google Scholar] [CrossRef]
- Ryu, Y.; Sonnentag, O.; Nilson, T.; Vargas, R.; Kobayashi, H.; Wenk, R.; Baldocchi, D.D. How to Quantify Tree Leaf Area Index in an Open Savanna Ecosystem: A Multi-Instrument and Multi-Model Approach. Agric. For. Meteorol. 2010, 150, 63–76. [Google Scholar] [CrossRef]
- Coops, N.C.; Smith, M.L.; Jacobsen, K.L.; Martin, M.; Ollinger, S. Estimation of Plant and Leaf Area Index Using Three Techniques in a Mature Native Eucalypt Canopy. Austral Ecol. 2004, 29, 332–341. [Google Scholar] [CrossRef]
- Ren, H.; Peng, S.-L. Comparison of methods for estimating leaf area index in Dinghushan forests. Acta Ecol. Sin. 1997, 17, 220–223. (In Chinese) [Google Scholar]
- Rao, J.; Yang, T.; Tian, X.; Liu, W.; Wang, X.; Qian, H.; Shen, Z. Vertical Structural Characteristics of a Semi-Humid Evergreen Broad-Leaved Forest and Common Tree Species Based on a Portable Backpack LiDAR. Biodivers. Sci. 2023, 31, 23216. [Google Scholar] [CrossRef]
- Zawawi, A.A.; Shiba, M.; Jemali, N.J.N. Accuracy of LiDAR-Based Tree Height Estimation and Crown Recognition in a Subtropical Evergreen Broad-Leaved Forest in Okinawa, Japan. For. Syst. 2015, 24, e002. [Google Scholar] [CrossRef]
- Fotis, A.T.; Morin, T.H.; Fahey, R.T.; Hardiman, B.S.; Bohrer, G.; Curtis, P.S. Forest structure in space and time: Biotic and abiotic determinants of canopy complexity and their effects on net primary productivity. Agric. For. Meteorol. 2018, 250, 181–191. [Google Scholar] [CrossRef]
- de Conto, T.; Armston, J.; Dubayah, R. Characterizing the structural complexity of the Earth’s forests with spaceborne lidar. Nat. Commun. 2024, 15, 8116. [Google Scholar] [CrossRef] [PubMed]
- Dufrêne, E.; Bréda, N. Estimation of deciduous forest leaf area index using direct and indirect methods. Oecologia 1995, 104, 156–162. [Google Scholar] [CrossRef]


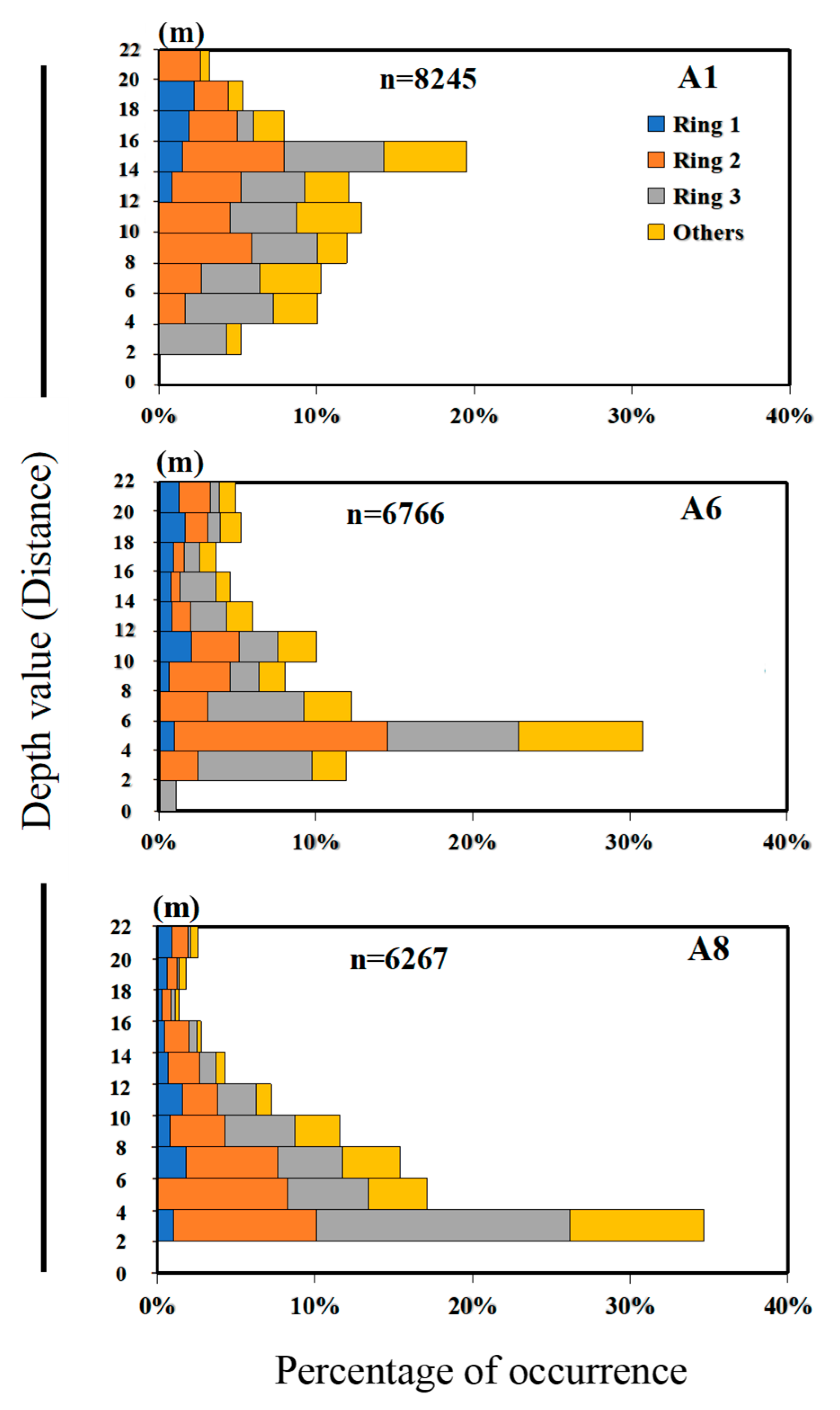


| 30 March 2022 | 21 April 2022 | 27 April 2022 | ||||
|---|---|---|---|---|---|---|
| Location | Canopy Openness (%) | Transmitted Total (%) | Canopy Openness (%) | Transmitted Total (%) | Canopy Openness (%) | Transmitted Total (%) |
| A1 | 13.00 | 12.96 | 13.02 | 14.25 | 12.66 | 13.23 |
| A2 | 11.76 | 9.64 | 13.99 | 12.30 | 14.60 | 13.93 |
| A3 | 14.43 | 10.44 | 15.09 | 12.26 | 17.35 | 13.13 |
| A4 | 13.63 | 10.26 | 15.88 | 14.73 | 20.00 | 16.80 |
| A5 | 11.05 | 7.92 | 12.53 | 10.36 | 13.74 | 9.51 |
| A6 | 15.00 | 13.78 | 12.13 | 11.16 | 14.43 | 11.45 |
| A7 | 12.89 | 16.48 | 11.02 | 15.41 | 12.82 | 16.91 |
| A8 | 11.68 | 14.38 | 12.70 | 14.69 | 13.10 | 13.54 |
| A9 | 14.34 | 12.29 | 16.44 | 15.04 | 17.92 | 16.44 |
| Mean | 13.09 | 12.02 | 13.64 | 13.36 | 15.18 | 13.88 |
| Depth Image Sensor | LAI-2200 | Fish-Eye Camera | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Location | P | L | L (Upper Canopy) | P (Ring 1) | L (Ring 1) | P (Ring 1 + 2) | L (Ring 1 + 2) | P | P (Ring 1) | P (Ring 1 + 2) | P | P (Ring 1) | P (Ring 1 + 2) | |
| 30 March 2022 | A1 | 2.23 | 1.82 | 1.24 | 2.38 | 2.35 | 3.86 | 2.27 | 3.55 | 4.49 | 5.58 | 3.68 | 3.57 | 4.76 |
| A2 | 2.86 | 1.59 | 0.78 | 2.37 | 2.27 | 3.78 | 2.64 | 4.34 | 3.56 | 5.46 | 3.88 | 3.29 | 4.30 | |
| A3 | 2.53 | 2.09 | 1.28 | 3.11 | 2.41 | 3.70 | 2.36 | 3.93 | 4.69 | 5.40 | 3.44 | 3.29 | 4.26 | |
| A4 | 2.61 | 2.47 | 1.13 | 3.15 | 3.12 | 3.55 | 2.76 | 3.22 | 5.18 | 5.19 | 3.61 | 4.68 | 4.25 | |
| A5 | 2.94 | 1.73 | 0.52 | 2.66 | 2.17 | 3.47 | 2.19 | 4.76 | 5.42 | 5.16 | 3.82 | 4.06 | 4.19 | |
| A6 | 3.01 | 2.40 | 0.77 | 2.65 | 2.51 | 3.46 | 2.43 | 4.56 | 4.49 | 5.16 | 3.48 | 3.90 | 4.17 | |
| A7 | 3.65 | 2.67 | 0.48 | 3.87 | 3.28 | 3.45 | 3.40 | 4.79 | 5.77 | 5.01 | 3.77 | 4.84 | 4.14 | |
| A8 | 3.31 | 2.49 | 0.61 | 3.80 | 3.36 | 3.44 | 3.19 | 5.08 | 5.84 | 4.95 | 3.89 | 4.73 | 4.11 | |
| A9 | 2.56 | 1.88 | 0.89 | 2.84 | 2.57 | 3.36 | 2.38 | 3.74 | 4.55 | 4.92 | 3.52 | 4.05 | 4.07 | |
| Mean (SD) | 2.85 (0.41) | 2.13 (0.37) | 0.85 (0.29) | 2.98 (0.52) | 2.67 (0.43) | 3.56 (0.16) | 2.62 (0.40) | 4.22 (0.60) | 4.89 (0.69) | 5.20 (0.22) | 3.68 (0.16) | 4.05 (0.57) | 4.25 (0.19) | |
| 21 April 2022 | A1 | 2.79 | 2.29 | 1.26 | 2.55 | 2.52 | 3.34 | 2.62 | 3.93 | 3.41 | 4.85 | 3.64 | 3.10 | 4.07 |
| A2 | 3.29 | 2.15 | 0.75 | 2.70 | 2.65 | 3.20 | 3.19 | 4.22 | 2.92 | 4.84 | 3.75 | 2.82 | 4.03 | |
| A3 | 2.65 | 2.15 | 1.05 | 2.98 | 2.41 | 3.09 | 2.27 | 4.01 | 3.84 | 4.79 | 3.48 | 3.27 | 3.99 | |
| A4 | 2.49 | 2.28 | 1.25 | 2.58 | 2.56 | 3.03 | 2.29 | 3.76 | 3.86 | 4.66 | 3.27 | 4.03 | 3.92 | |
| A5 | 3.45 | 2.54 | 0.42 | 3.04 | 3.04 | 2.92 | 3.34 | 4.92 | 5.03 | 4.49 | 3.64 | 3.95 | 3.92 | |
| A6 | 3.68 | 3.04 | 0.98 | 2.82 | 2.61 | 2.89 | 2.82 | 4.14 | 2.66 | 4.46 | 3.93 | 3.54 | 3.88 | |
| A7 | 3.30 | 2.22 | 0.53 | 3.44 | 2.75 | 2.87 | 2.84 | 4.57 | 4.86 | 4.43 | 3.92 | 4.60 | 3.85 | |
| A8 | 3.41 | 2.18 | 0.59 | 3.01 | 2.49 | 2.86 | 2.69 | 5.03 | 4.77 | 4.39 | 3.79 | 3.86 | 3.81 | |
| A9 | 2.93 | 2.18 | 0.76 | 2.76 | 2.53 | 2.84 | 2.39 | 4.12 | 3.68 | 4.35 | 3.40 | 3.29 | 3.79 | |
| Mean (SD) | 3.11 (0.38) | 2.33 (0.27) | 0.84 (0.29) | 2.88 (0.26) | 2.62 (0.18) | 3.00 (0.17) | 2.72 (0.36) | 4.30 (0.42) | 3.89 (0.80) | 4.58 (0.19) | 3.65 (0.22) | 3.60 (0.52) | 3.92 (0.09) | |
| 27 April 2022 | A1 | 2.82 | 2.36 | 1.27 | 2.52 | 2.5 | 2.74 | 2.61 | 3.71 | 3.72 | 4.16 | 3.71 | 3.15 | 3.78 |
| A2 | 3.11 | 2.05 | 0.71 | 2.27 | 2.23 | 2.74 | 2.94 | 4.14 | 2.99 | 4.05 | 3.91 | 2.65 | 3.73 | |
| A3 | 2.64 | 2.25 | 0.99 | 2.87 | 2.3 | 2.69 | 2.28 | 4.03 | 4.06 | 3.98 | 3.42 | 3.11 | 3.58 | |
| A4 | 2.48 | 2.21 | 1.16 | 2.56 | 2.55 | 2.62 | 2.30 | 3.71 | 3.94 | 3.94 | 3.06 | 3.48 | 3.57 | |
| A5 | 3.13 | 2.05 | 0.39 | 2.69 | 2.01 | 2.62 | 2.33 | 4.92 | 5.08 | 3.88 | 3.67 | 4.26 | 3.53 | |
| A6 | 3.20 | 2.35 | 0.65 | 2.37 | 2.16 | 2.61 | 2.48 | 4.60 | 3.71 | 3.86 | 3.55 | 3.25 | 3.52 | |
| A7 | 3.13 | 2.19 | 0.47 | 3.46 | 2.67 | 2.49 | 2.82 | 4.22 | 4.88 | 3.84 | 3.90 | 4.99 | 3.44 | |
| A8 | 3.34 | 2.39 | 0.59 | 3.12 | 2.59 | 2.46 | 2.71 | 5.00 | 5.04 | 3.81 | 3.75 | 3.73 | 3.41 | |
| A9 | 2.76 | 2.14 | 0.88 | 2.65 | 2.41 | 2.46 | 2.27 | 3.96 | 3.69 | 3.68 | 3.32 | 3.39 | 3.29 | |
| Mean (SD) | 2.96 (0.27) | 2.22 (0.12) | 0.79 (0.29) | 2.72 (0.35) | 2.38 (0.21) | 2.60 (0.11) | 2.52 (0.24) | 4.25 (0.45) | 4.12 (0.68) | 3.19 (0.13) | 3.59 (0.26) | 3.56 (0.66) | 3.54 (0.14) | |
| Total mean (SD) | 2.97 (0.38) | 2.23 (0.29) | 0.83 (0.29) | 2.86 (0.41) | 2.56 (0.32) | 3.06 (0.42) | 2.62 (0.35) | 4.26 (0.50) | 4.30 (0.84) | 4.57 (0.56) | 3.64 (0.22) | 3.74 (0.62) | 3.90 (0.33) | |
| Location | Foliage Over 10 m (%) | Foliage Below 10 m (%) | Branch and Stem (%) | |
|---|---|---|---|---|
| 30 March 2022 | A1 | 48% | 29% | 24% |
| A2 | 26% | 41% | 32% | |
| A3 | 42% | 29% | 30% | |
| A4 | 38% | 12% | 50% | |
| A5 | 12% | 55% | 33% | |
| A6 | 22% | 31% | 48% | |
| A7 | 11% | 31% | 58% | |
| A8 | 12% | 36% | 52% | |
| A9 | 31% | 31% | 38% | |
| 21 April 2022 | A1 | 38% | 32% | 30% |
| A2 | 21% | 31% | 48% | |
| A3 | 36% | 25% | 39% | |
| A4 | 46% | 15% | 39% | |
| A5 | 9% | 35% | 56% | |
| A6 | 20% | 44% | 37% | |
| A7 | 13% | 38% | 49% | |
| A8 | 13% | 44% | 43% | |
| A9 | 25% | 26% | 48% | |
| 27 April 2022 | A1 | 38% | 33% | 29% |
| A2 | 21% | 32% | 47% | |
| A3 | 33% | 21% | 45% | |
| A4 | 45% | 13% | 42% | |
| A5 | 10% | 40% | 51% | |
| A6 | 18% | 36% | 47% | |
| A7 | 11% | 38% | 50% | |
| A8 | 12% | 41% | 47% | |
| A9 | 30% | 28% | 43% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geilebagan; Tanaka, T.; Gomi, T.; Kotani, A.; Nakaoki, G.; Wang, X.; Inokoshi, S. Evaluating Forest Canopy Structures and Leaf Area Index Using a Five-Band Depth Image Sensor. Forests 2025, 16, 1294. https://doi.org/10.3390/f16081294
Geilebagan, Tanaka T, Gomi T, Kotani A, Nakaoki G, Wang X, Inokoshi S. Evaluating Forest Canopy Structures and Leaf Area Index Using a Five-Band Depth Image Sensor. Forests. 2025; 16(8):1294. https://doi.org/10.3390/f16081294
Chicago/Turabian StyleGeilebagan, Takafumi Tanaka, Takashi Gomi, Ayumi Kotani, Genya Nakaoki, Xinwei Wang, and Shodai Inokoshi. 2025. "Evaluating Forest Canopy Structures and Leaf Area Index Using a Five-Band Depth Image Sensor" Forests 16, no. 8: 1294. https://doi.org/10.3390/f16081294
APA StyleGeilebagan, Tanaka, T., Gomi, T., Kotani, A., Nakaoki, G., Wang, X., & Inokoshi, S. (2025). Evaluating Forest Canopy Structures and Leaf Area Index Using a Five-Band Depth Image Sensor. Forests, 16(8), 1294. https://doi.org/10.3390/f16081294






