A Site Index-Based Approach for Arid Lands: A Multivariate Ecological Assessment for Shrubby Species

Abstract

Development of site index models for shrubby species in arid ecosystems remains a challenge, due to the absence of dominant height–age relationships and the complexity of ecological drivers in these environments. In this study, a multivariate approach to classify site quality for Agave lechuguilla Torr, a wild non-timber species of ecological and economic importance in northern Mexico, was performed. Data were collected from 112 sampling plots where the abundance, height, basal diameter, and crown diameter for the A. lechuguilla plants were measured. Sites were grouped into three site index categories (low, medium, and high) using the Importance Value Index (IVI). Afterward a classical discriminant analysis (CDA) was applied to derive linear functions capable of classifying new sites into these predefined categories. Statistical assumptions of multivariate normality, homogeneity of covariance matrices, and low multicollinearity were met. The discriminant functions showed high classification accuracy (95.54%), with full correct classification of low and high site index categories. Additional validation through MANOVA and principal component analysis (PCA) confirmed the separation of groups and the ecological coherence of the selected variables. This approach provides a simple, practical, and replicable model for assessing shrubland site quality using field measurable features. It also offers a tool for sustainable harvesting and conservation of A. lechuguilla.

1. Introduction

The site index (SI) is widely used to evaluate the productive quality of forest stands [1]. It plays a crucial role in defining harvest intensities and informing forest ecosystem management strategies [2]. While the SI is commonly applied in temperate and tropical forests, its use in arid ecosystems, particularly for shrub species, remains largely underdeveloped [3].

Methods for generating SI models can generally be classified into two categories: geocentric and phytocentric [4]. Geocentric methods rely on environmental factors such as soil quality, topography, and other physical variables, whereas phytocentric methods are based on plant growth as an indicator of site productivity [5]. In forest ecosystems, the most commonly used phytocentric method involves adjusting age–height regression models for dominant trees [6]. This theory assumes that the height of dominant trees reflects site productivity, as height growth is less influenced by light competition [7,8]. Height is also strongly correlated with timber volume accumulation [6]. However, in arid ecosystems, shrub species are often harvested for leaves, stems, roots, or other parts [9]. Therefore, variables such as the basal area, crown diameter, and plant height are commonly used to estimate biomass and productivity in these cases [10,11,12].

Aside from that, in the traditional silviculture, the SI is typically based on dominant height growth models as in long-living forest species with vertical growth patterns, height is a reliable indicator of site productivity over time [13]. However, for shrubby species such as A. lechuguilla, other attributes such as abundance or variables related to plant size may serve as more appropriate indicators of site quality. This is due to their xerophytic habitat, life cycle adapted to water stress, and the absence of vertical dominance typically found in coniferous or broadleaf forests. In this context, various studies have shown that in grassland and shrubland ecosystems, variables such as vegetation cover, species frequency, aboveground biomass, and floristic composition are commonly used as indicators of site condition or quality [14,15,16]. Similarly, in the management of non-timber forest products, multivariate approaches based on ecological attributes have been employed to classify stands, assess their suitability for harvesting, and promote sustainable use [17,18].

In this respect, environmental, climatic, and ecological factors are known to strongly influence plant morphology, vigor, and population structure in arid and semi-arid ecosystems [19,20,21]. Variables such as the soil texture, organic matter, moisture availability, and nutrient content affect plant growth and productivity, while climatic drivers, particularly temperature and precipitation gradients, regulate the biomass accumulation and structural development of plant communities [19,22,23]. Topographic attributes such as the elevation, slope, and aspect further shape microclimatic conditions, influencing vegetation distribution and site productivity [20,21]. Furthermore, biotic factors including intra- and interspecific competition, grazing pressure, and species-specific functional traits contribute to spatial variation in plant performance [24,25]. These complex interactions might provide a robust ecological foundation for the use of morphological and abundance-related variables as indicators of site productivity in arid landscapes.

Currently, SI modeling in arid shrubland ecosystems is limited. For instance, Loera-Gallegos et al. developed SI models using the age and dominant height for Agave durangensis Gentry in Durango, Mexico [3]. While their models provide a useful reference, they did not describe how the plant age was estimated, nor did they examine the relationship between height and the commercial plant structure (bulb or stem), which is used in mezcal production. Other studies in arid zones have focused on species distribution, population structure, and non-timber product estimation [24,26,27], as well as the potential impacts of climate change [22,23,25,28] and biomass prediction [29,30,31].

This study proposes an alternative approach for evaluating site quality in arid shrublands using a multivariate analysis focused on classical discriminant analysis (CDA). We selected A. lechuguilla as the focal species for the analysis, a species of high economic and ecological relevance in northern Mexico [30,32]. This species, which is dominant in rosetophyllous scrub communities, plays a key role in ecosystem functioning and is widely harvested for fiber and other products [29,32,33]. Although many shrub species are commercially exploited in northern Mexico, A. lechuguilla is among the species most widely utilized by rural communities in arid and semi-arid regions due to its economic and cultural relevance [9,24,33]. In addition to its social importance, A. lechuguilla is one of the dominant species in the Chihuahuan Desert’s rosetophyllous scrub communities, playing a key ecological role in these ecosystems [34,35,36]. Given its dual significance, both ecological and economic, A. lechuguilla was selected as the focal species for this study, with the aim of developing a method to assess site quality in their natural populations.

CDA is a robust statistical tool used to identify variables that maximize differentiation among predefined groups and classify new observations into those groups [37]. One of its main advantages is its ability to combine multiple variables into linear functions that optimize separation between categories, offering an objective and quantitative approach to classification issues [38]. In ecological studies and natural resource management, CDA has proven useful for distinguishing vegetation types [39] and supporting management decisions grounded in measurable ecological attributes [17].

To define SI categories, we employed the Importance Value Index (IVI), which integrates the relative measures of abundance, dominance, and frequency [40,41,42,43,44]. Based on the IVI values, sites were classified into low-, medium-, and high-quality groups. Then, a CDA, principal component analysis (PCA), and multivariate analysis of variance (MANOVA) were applied to identify the most informative variables and derive linear classification functions. These functions aim to consistently and meaningfully assign new observations to predefined site quality categories. In this context, the study aimed to evaluate whether morphoetrical and abundance attributes of arid shrub species can effectively distinguish site quality groups, with the goal of exploring their potential use as SI indicators for shrub-dominated stands in arid environments. As an initial case study, we focused on A. lechuguilla, a representative and economically important species in northern Mexico. Specifically, we sought to develop a site quality classification model for A. lechuguilla populations using multivariate analysis of structural and ecological variables, thereby providing a foundation for future applications in the sustainable management of arid shrublands.

This study contributes to the evaluation of site quality in arid and semiarid shrublands, where conventional forestry metrics are not always applicable. It provides a novel, field-based framework for assessing stand productivity in shrub-dominated ecosystems, particularly for non-timber species that are commercially and ecologically important. For the scientific community, the proposed method enhances understanding of site productivity patterns and offers a replicable multivariate approach for classification. For land managers and rural communities, it can serve as a decision support tool to guide sustainable harvesting, restoration planning, and conservation prioritization based on site potential.

2. Materials and Methods

2.1. Study Area

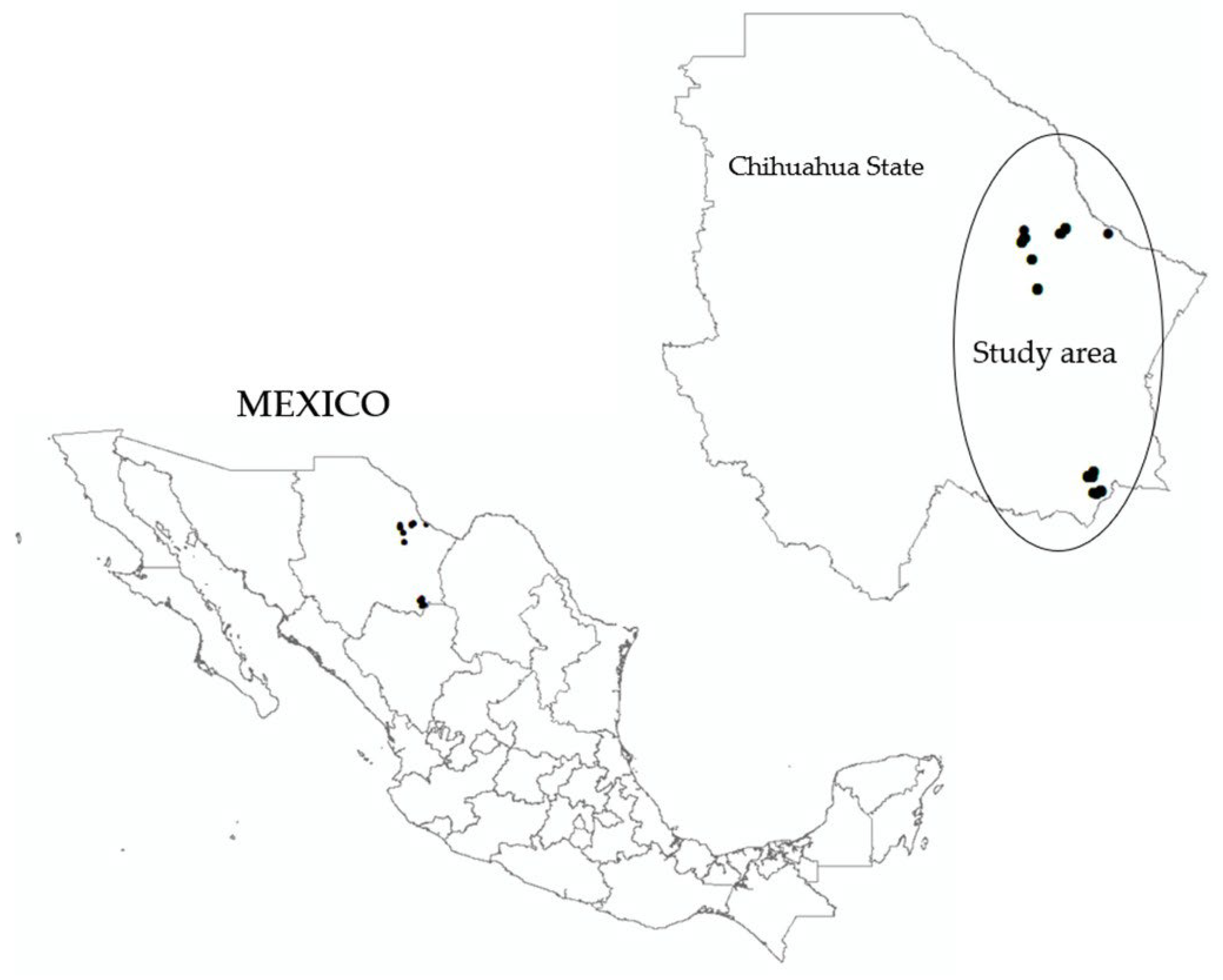
The study was conducted in desert scrubland ecosystems characterized by rosette-forming vegetation, particularly the presence of A. lechuguilla, located in the arid and semi-arid regions of the state of Chihuahua, México (Figure 1). The predominant vegetation includes shrub species such as Euphorbia antisyphilitica Zucc, A. lechuguilla, Lippia graveolens HBK, Larrea tridentata (DC) Coville, and members of the genera Dasylirion and Opuntia [24,45]. The elevation ranges from 700 to 1850 m above sea level, with an average annual precipitation of 250 mm and temperatures ranging from −5 °C in winter to 40 °C in summer [46].

2.2. Field Sampling

A targeted sampling strategy was implemented in communities containing A. lechuguilla. Eleven sampling clusters were established in the state of Chihuahua, Mexico. Each cluster consisted of 16 circular plots, each measuring 250 m² and arranged in 4 rows and 4 columns, with 100 m between the rows and 200 m between the columns. Therefore, each cluster covered an approximate sampling area of 20 hectares. In total, 176 plots were sampled across all clusters. Each plot was subdivided into four sampling quadrants. Within each quadrant, the number of A. lechuguilla individuals was recorded, and a mode plant was selected, defined as a plant whose size was representative of the majority of individuals in the quadrant. The following variables were measured for the mode plant: height (m), largest crown diameter (m), smallest crown diameter (m), and base diameter (cm) [21]. For the analysis, plots where no individuals of A. lechuguilla were recorded were excluded. Only the 112 plots in which the species was present were included in the dataset.

2.3. Procedure for Site Index

Considering that the plant size and abundance variables are indicative of the productive status of a stand, sites with larger plants and higher population densities may correspond to more productive land conditions, and vice versa. To construct the SI, an Importance Value Index (IVI) was first calculated for the dataset of A. lechuguilla. Three plant size variables—the basal diameter (BD), mean crown diameter (CD), and plant height (H)—along with one abundance variable (ABU), the number of individuals per site, were used to construct the IVI.

In ecological studies, the IVI is typically used to evaluate community structure, with the importance value applied across multiple species within a community [40]. However, in this study, the equation was adapted to estimate an IVI using data from a single species, A. lechuguilla, across 112 sampling sites. Thus, the IVI was calculated based on the abundance and size attributes of the A. lechuguilla individuals at each site.

The procedure for calculating the IVI is described below:

ABU is the number of A. lechuguilla plants per 250 m² site.

BD is the diameter of the base of the plants at each site, measured 10 cm above the ground.

CD is the average of the largest and smallest crown diameters of the plants at each site, measured at the crown of the plants.

H is the average height of the plants for each site, measured from the ground to the apex of the plants.

The relative values of each variable were obtained by dividing the value of each variable per site by the sum of the values of variable Xi at all sites. The following equation shows an example of this calculation with the ABU:

$$\mathrm{A}\mathrm{B}\mathrm{U}\mathrm{R}\mathrm{E}\mathrm{L}={\displaystyle \frac{\mathrm{A}\mathrm{B}\mathrm{U}i}{{\sum }_{i=1}^n\mathrm{A}\mathrm{B}\mathrm{U}}}$$

(1)

where ABU REL is the relative abundance value, ABUi is the number of A. lechuguilla plants sampled for site i, and ${\sum }_{i=1}^n\mathrm{A}\mathrm{B}\mathrm{U}$ is the sum of the abundances of all sites.

Once the relative values of each variable were calculated for all sampling sites, the Importance Value Index was generated using the following equation [40]:

$$\mathrm{I}\mathrm{V}\mathrm{I}=\mathrm{ABU}\mathrm{REL}+\mathrm{BD}\mathrm{REL}+\mathrm{CD}\mathrm{REL}+\mathrm{H}\mathrm{REL}$$

(2)

where IVI is the Importance Value Index, ABU REL is the relative abundance, BD REL is the relative basal diameter, CD REL is the relative crown diameter, and H REL is the relative plant height.

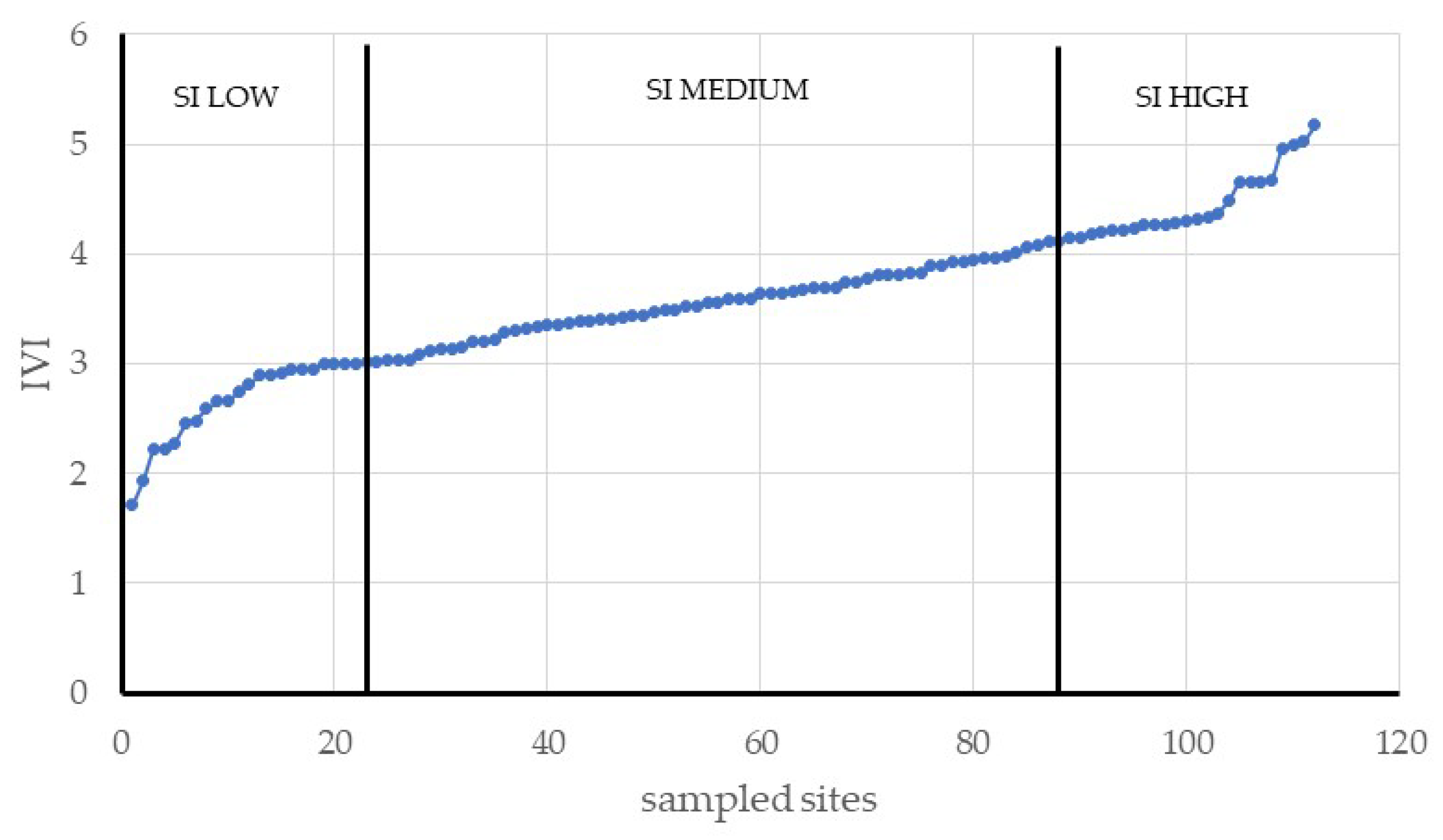
Subsequently, the IVI values were exclusively used to establish three SI categories or groups (low, medium, and high).

To assign sites to these SI categories, the IVI values were ordered from highest to lowest, and three SIs were defined based on the distribution pattern of the IVI value curve. The classification thresholds were as follows:

Low SI: bottom 20% of IVI values;

Medium SI: middle 60% of IVI values;

High SI: top 20% of IVI values.

As a result, 23 sites were classified as low SI, 65 sites were classified as medium SI, and 24 sites were classified as high SI (Figure 2). Although two of the SI categories (low and high) included fewer than 30 observations, the number of cases per group relative to the number of predictor variables (n > 5p) satisfied the commonly accepted criteria for multivariate analysis [38]. In this context, n refers to the number of observations per group, and p represents the number of predictor variables included in the multivariate analysis. Following this criterion, a minimum of 5 observations is recommended for each variable, meaning that with four variables used in this study, each group should have at least 20 observations to ensure the stability and validity of the discriminant model.

To define the SI categories, the IVI values were ranked and grouped into three classes using a 20–60–20% distribution. This criterion was selected based on the sigmoidal shape of the IVI distribution curve, which showed a steep slope at the extremes and a flatter slope in the middle range. This pattern reflects greater ecological contrast at the ends of the gradient, where stands exhibit either low or high structural development and abundance of A. lechuguilla. Grouping the top and bottom 20% as “extreme” categories improved the discriminatory power of the classification model and reduced the misclassification error, compared with alternative groupings such as natural breaks. Based on our experience, thresholds that assign between 20% and 30% of the data to the extreme classes tend to offer sufficient ecological contrast to discriminate among groups effectively while maintaining low classification error. Furthermore, this stratification aligns with the ecological patterns observed in arid ecosystems, where high-quality sites support larger and more abundant individuals, while low-quality sites exhibit limited plant growth and density.

Once the three SI categories were established, multivariate analyses were applied to verify the correct separation among categories and generate equations for assigning site quality to new data. These equations could be used in A. lechuguilla inventories to assess the quality of the stands.

2.4. Data Analysis

Data analysis was conducted using SAS software, version 9.4 [47]. To ensure that the assumptions required for conducting multivariate analyses were satisfied, three preliminary tests were performed. In the first step, a multivariate normality analysis was assessed by the skewness and kurtosis measures using Mardia’s test [48], applied using the SI through the appropriate procedure in SAS. Then, the homogeneity of the covariance matrices among the site quality categories was evaluated using Box’s M test [49], which was implemented throughout the DISCRIM procedure. Finally, the multicollinearity among the predictor variables was assessed through the variance inflation factors (VIFs), tolerance values, and condition indices, following the approach of Belsley, Kuh, and Welsch [50], using the REG procedure.

Afterward, a stepwise discriminant analysis was performed to identify the most relevant variables for group discrimination [51]. This method selects variables based on their discriminatory power, where the R² criterion reflects the contribution of each variable to group separation and Wilks’s lambda statistic indicates the statistical significance of each variable (p < 0.05).

Subsequently, a CDA was conducted to derive the final linear discriminant functions used to classify new observations into the previously established SI categories [37].

The general form of the linear discriminant functions generated is as follows:

$$Dg\left(x\right)=a_{g_1}{x}_1+a_{g_2}{x}_2+a_{g_3}{x}_3+a_{g_4}{x}_4+C_g$$

(3)

where Dg(X) is the discriminant score for group g, a_gj is the coefficients that maximize the separation between groups, and Cg is the constant (intercept) for group g.

After the application of these functions to new values, a new observation is assigned to the group with the highest Dg(x) result or the lowest generalized squared distance (Mahalanobis).

The generalized squared distance (Mahalanobis) is estimated according to the following function:

$$D_g^2\left(x\right)={\left(x-{\mu }_g\right)}^T{S}_p^{-1}\left(x-{\mu }_g\right)$$

(4)

where Dg²(x) is the generalized squared distance or Mahalanobis distance, X is the vector of values of the predictor variables for the observation, μg is the vector of means of group g, Sp is the common covariance matrix (grouped), which is assumed to be the same for all groups, S_p⁻¹ is the inverse of that covariance matrix, and T is the transpose of the matrix.

CDA was selected in this study for its ability to identify linear combinations of variables that maximize separation among predefined groups (in this case, the levels of site quality).

Additionally, the following complementary analyses were performed to support the discriminant model and validate the separation among site quality groups. A MANOVA was conducted to evaluate the effect of SI categories on the set of dependent variables (ABU, BD, CD, and H). Subsequently, a PCA was applied as an exploratory tool to visualize the distribution of sites in a reduced multivariate space. Furthermore, a biplot was constructed using the R environment to illustrate the effect of the linear discriminant functions on the spatial distribution of sites [52], highlighting the grouping patterns and the internal consistency of each category.

3. Results

Based on Mardia’s multivariate normality test, no significant deviations from normality were detected in any of the site quality groups. The multivariate kurtosis values (b2p) were close to the expected values, and the associated p values (SI_1: p = 0.85; SI_2: p = 0.061; SI_3: p = 0.17) were not statistically significant. These results indicate that the assumption of multivariate normality was met, thus fulfilling one of the key requirements for conducting multivariate analysis (

Table 1. Results of Mardia’s test for multivariate normality across sites.

Group	n	P	b1p	b2p	Expected b2p	z Kurtosis	p Value (b2p)
Low	23	4	8.9721	24.5439	24	0.1882	0.8507
Medium	65	4	2.0498	20.7858	24	−1.8702	0.0615
High	24	4	5.3523	20.1234	24	−1.3706	0.1705

Note: n = number of observations per group; P = number of variables; b1p = Mardia’s multivariate skewness measure; b2p = Mardia’s multivariate kurtosis measure; Expected b2p = expected value under multivariate normality; z kurtosis = test statistic for b2p; p value (b2p) = p value associated with the multivariate kurtosis test.

).

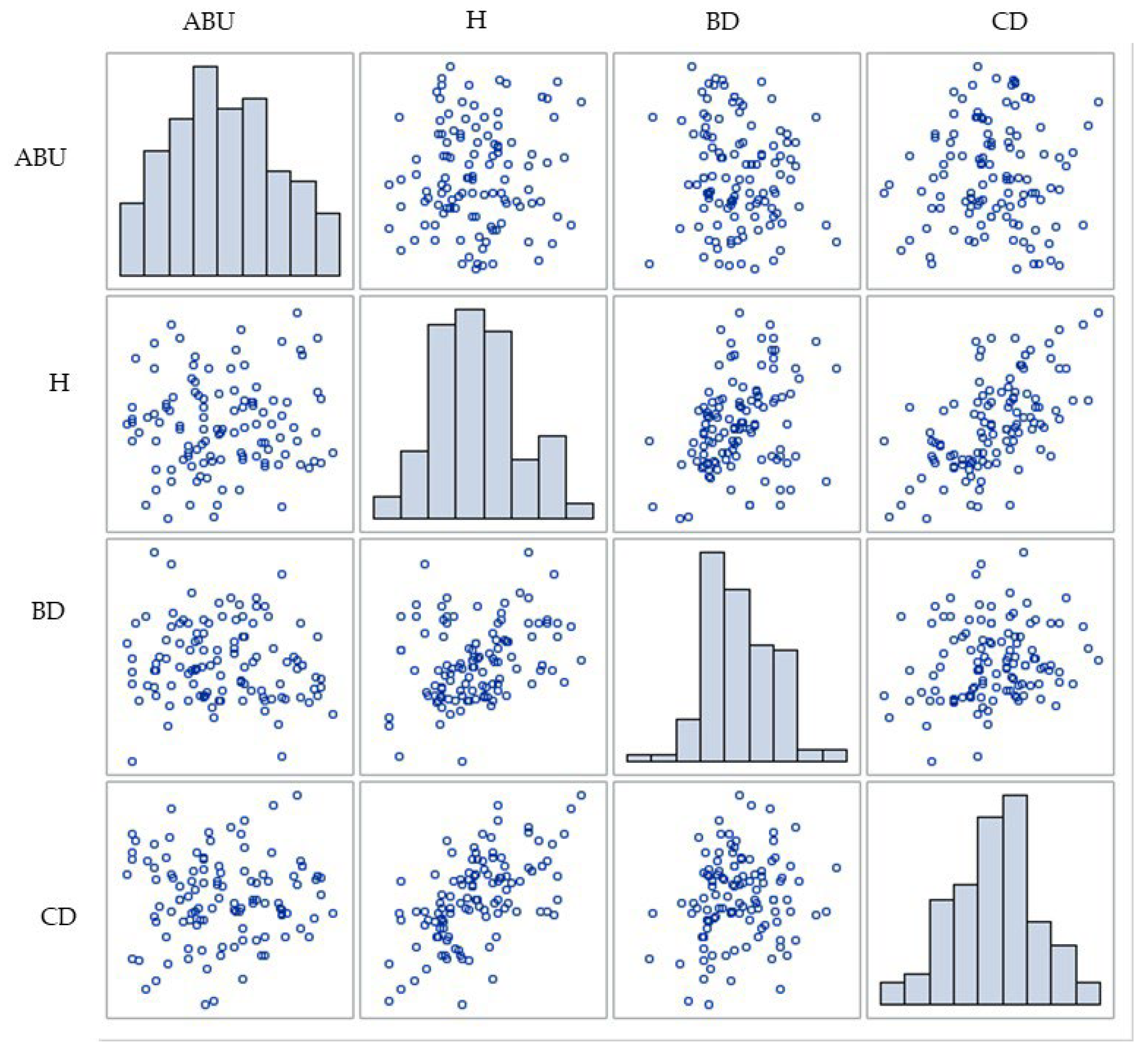
To visually explore the bivariate relationships among the quantitative variables included in the discriminant analysis, a scatterplot matrix was constructed (Figure 3). Visual inspection revealed no evidence of patterns suggesting violations of the assumptions of linearity or marginal normality. Therefore, the graphical matrix supports the joint use of these variables within a multivariate analytical framework.

Meanwhile, the homogeneity of covariance matrices among the three site quality levels was evaluated using the DISCRIM procedure in SAS. The likelihood ratio test indicated no significant differences among the matrices (χ² = 17.39; p = 0.6275). Therefore, the assumption of homogeneity required for linear discriminant analysis was satisfied. Furthermore, the results of the multicollinearity analysis indicated that all variance inflation factor (VIF) values were below two (range: 1.006–1.626), and the tolerance values were above 0.6, suggesting low collinearity among predictors. In addition, the condition indices remained below 16 (maximum = 15.46), which is well under the commonly accepted threshold of 30 that signals severe multicollinearity. These results confirm the absence of significant multicollinearity, thereby supporting the joint use of the variables in multivariate models (

Table 2. Multicollinearity diagnostics for predictor variables used in the CDA.

Model (Dependent Variable)	Variable	Tolerance	VIF (Variance Inflation Factor)	Max Condition Index
ABU	H	0.615	1.626	15.46
	BD	0.909	1.100
	CD	0.656	1.524
H	ABU	0.983	1.018	12.91
	BD	0.954	1.048
	CD	0.966	1.035
BD	ABU	0.994	1.006	15.18
	H	0.653	1.531
	CD	0.656	1.524
CD	ABU	0.973	1.028	14.19
	H	0.896	1.116
	BD	0.889	1.125

ABU = abundance; H = plant height; BD = basal diameter; CD = crown diameter.

).

According to the results of the stepwise discriminant analysis, the most relevant variables for discriminating among the SI levels established a priori for A. lechuguilla are presented in

Table 3. Summary of stepwise discriminant analysis for variable.

Variable	Partial R2	F Value	Pr > F	Wilks’s Lambda	Pr < Lambda
H	0.3650	31.32	<0.0001	0.6350	<0.0001
ABU	0.4232	39.62	<0.0001	0.3663	<0.0001
BD	0.3444	28.10	<0.0001	0.2401	<0.0001
CD	0.0871	5.06	0.0080	0.2192	<0.0001

ABU = abundance; H = plant height; BD = basal diameter; CD = crown diameter.

. According to Wilks’s lambda test, all variables demonstrated significant discriminatory power with respect to the categorical SI variable (p < 0.0001). Additionally, all variables met the criteria for both entry and retention in the stepwise discriminant analysis (p < 0.05). Therefore, among the four variables, the CD contributed the least to group discrimination (partial R² = 0.0871), while abundance and height showed the highest discriminatory power, with partial R² values of 0.4232 and 0.3650, respectively.

Moreover, the generalized Mahalanobis distance was used to evaluate the degree of separation between the predefined SI groups. In this context, smaller values indicate greater similarity between groups, while larger values reflect greater separation. As shown in

Table 4. Generalized Mahalanobis distances among SI categories.

A. lechuguilla Site Index
	Low	Medium	High
Low	0.00	7.94	32.45
Medium	7.94	0.00	8.40
High	32.45	8.40	0.00

, the greatest separation was observed between the high-SI and low-SI groups, as expected. In contrast, the distances between the intermediate-SI group and each of the extreme groups (high and low) were smaller. However, in all cases, the Mahalanobis distances were substantially greater than zero, indicating that meaningful separation existed among all three SI groups, thereby contributing to the overall discriminatory accuracy of the model.

The linear discriminant functions generated in this study (

Table 5. Coefficients of linear discriminant functions for classifying A. lechuguilla SIs.

Variable	Site Index of A. lechuguilla
	Low	Medium	High
Constant	−39.945	−67.717	−105.267
ABU	0.586	0.816	1.040
BD	86.433	108.001	135.680
CD	134.137	181.702	225.765
H	43.524	55.365	66.506

ABU = abundance; H = plant height; BD = basal diameter; CD = crown diameter.

) are proposed as a tool for assigning SI values (high, medium, or low) to areas where A. lechuguilla is distributed in the study area. Each discriminant function operates as a multiple linear equation, where the assignment of a site to an SI group is determined by the highest score obtained among the three functions. The intercepts and coefficients corresponding to each discriminant variable are provided in Table 5.

To estimate the classification error, a resubstitution procedure was performed, in which the original site data were reclassified using the derived linear discriminant functions. This allowed for a direct comparison between the initial group assignments (based on IVI classification) and the predicted assignments from the discriminant model.

As shown in

Table 6. Classification results from resubstitution using discriminant functions.

Classification of Observations (%) by A. lechuguilla Site Index Category
From SI	Low	Medium	High	Total
Low	23	0	0	23
	100	0	0	100
Medium	6	56	3	65
	9.23	86.15	4.62	100
High	0	0	24	24
	0	0	100	100
Total	29	56	27	112
	25.89	50	24.11	100
Priors	0.33	0.33	0.33

Note: “Priors” refers to the prior probabilities assigned to each SI category in the classification analysis, assuming equal probabilities for the three groups (1/3 for each class), with no dominance of one class over the others.

, all 23 low-SI sites and all 24 high-SI sites were correctly reclassified into their respective categories, with no misclassifications observed in either group. In contrast, within the medium SI group, six sites were reassigned to the low-SI category, and three sites were reassigned to the high-SI category.

The resubstitution analysis yielded a classification error of 13.9% for the medium-SI group and a total error rate of 4.60%, indicating a high level of reliability in the discriminant analysis (

Table 7. Classification error rates by SI category based on discriminant analysis.

	Low	Medium	High	Total
Rate	0.000	0.139	0.000	0.046
Priors	0.333	0.333	0.333

). Based on these results, the use of linear discriminant functions might be recommended for assessing the productive quality of A. lechuguilla stands that are managed and harvested in Chihuahua, Mexico.

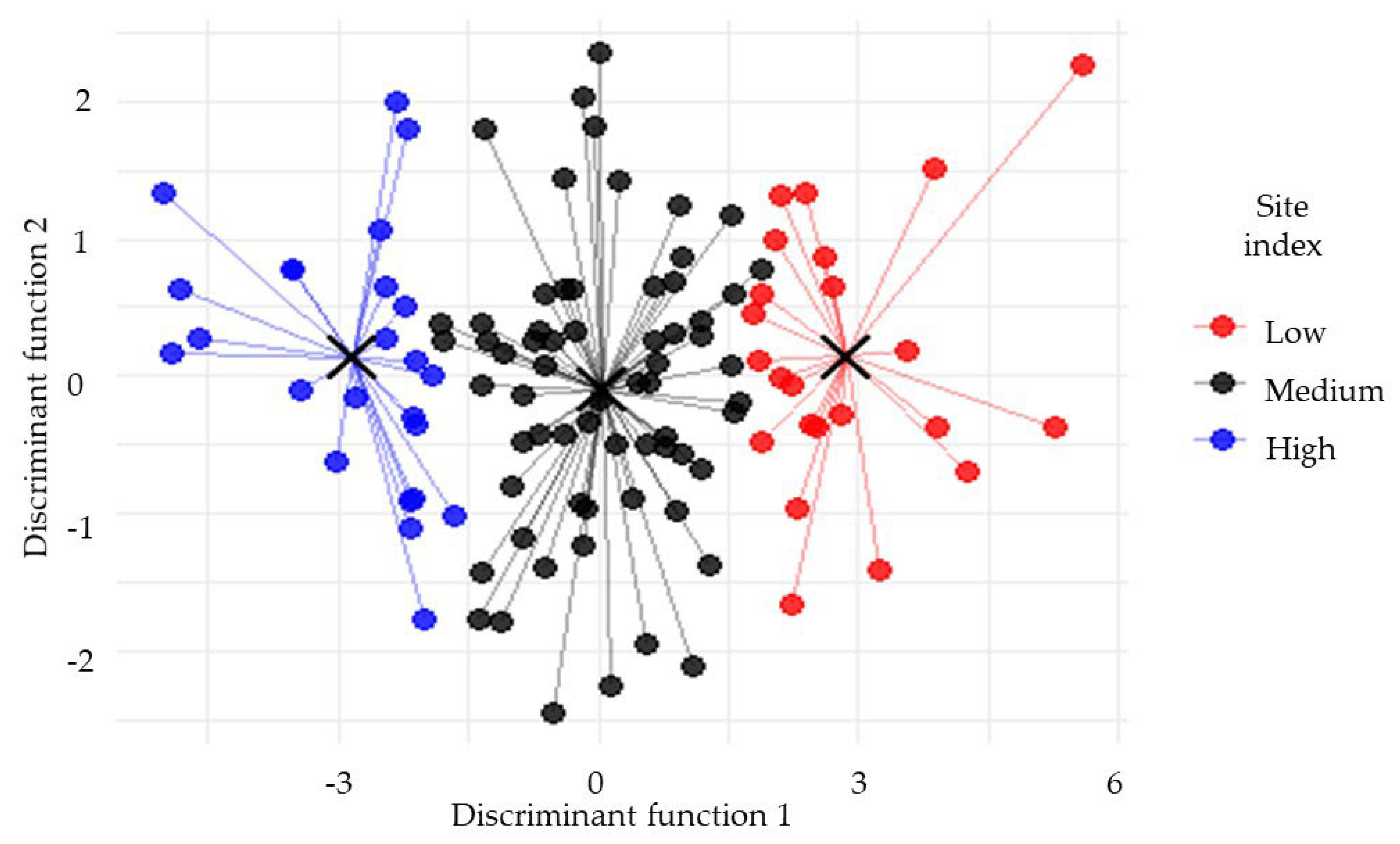
The linear discriminant analysis (LDA) revealed a clear multivariate separation of sites according to the SI level proposed using the IVI. The resulting biplot displays the distribution of sites in the space defined by the first two discriminant functions, which were constructed to maximize between group variance (Figure 4). Lines drawn from each observation to its corresponding group centroid emphasize the internal consistency within groups and highlight the degree of clustering. This graphical representation provides strong visual support for the model’s discriminative power in classifying sites based on structural and abundance-related variables.

Furthermore, the results of the MANOVA support the discriminant analysis by confirming that the site quality level (SI) had a statistically significant effect on the set of structural and abundance variables. Wilks’s lambda was 0.2192 with high significance (p < 0.0001), indicating that the multivariate means of the groups differed substantially.

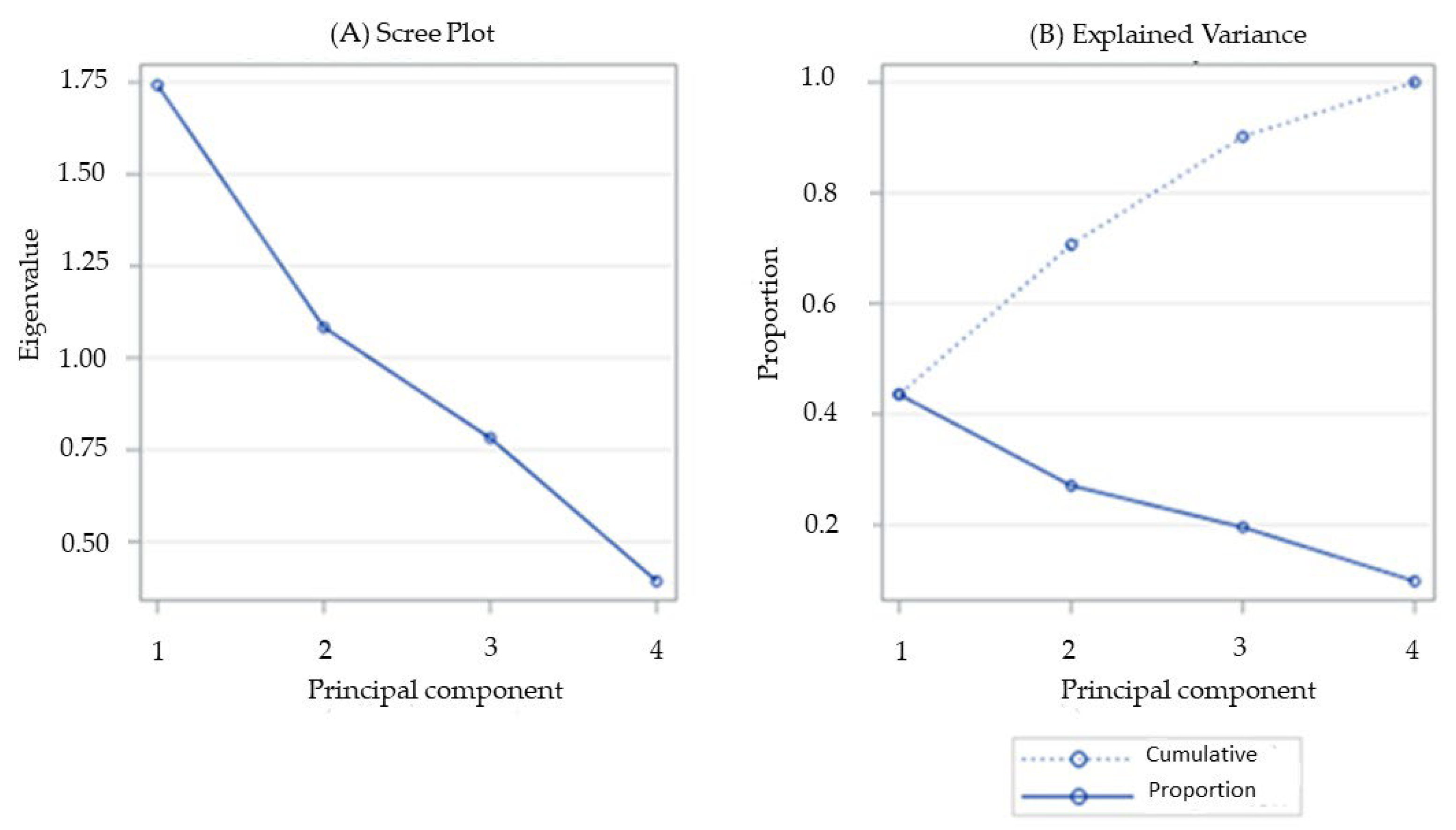
In addition, the PCA results are illustrated in the scree plot and the explained variance plot (Figure 5). This plot shows a sharp decline in the eigenvalues from the first to the second principal component (A), followed by a more gradual decrease, suggesting that the first two components captured most of the variation in the data. The explained variance plot (B) confirms this, indicating that PC1 and PC2 together accounted for approximately 70.63% of the total variance. This supports the selection of the first two components for visualizing multivariate patterns and interpreting the main ecological gradients represented in the dataset.

PCA showed that the first principal component (PC1) was strongly associated with the morphological variables H and CD, while the second component (PC2) primarily reflected the variability in ABU (

Table 8. Eigenvectors of A. lechuguilla’s morphological and abundance variables for the first four principal components from PCA.

Variable	PC1	PC2	PC3	PC4
ABU	0.0315	0.8552	0.5095	0.0895
H	0.6637	0.1127	–0.1015	–0.7325
BD	0.4122	–0.4815	0.7483	0.1957
CD	0.6234	0.1552	–0.4125	0.6459

ABU = abundance; H = plant height; BD = basal diameter; CD = crown diameter.

). These same variables were also identified as important in the discriminant functions obtained through the CDA, which revealed a clear separation among SI levels. This concordance suggests that the natural axes of variation in the data (as identified by PCA) are aligned with the factors that discriminate between the defined groups, thereby reinforcing the robustness of the discriminant model.

4. Discussion

SI equations are traditionally generated by modeling the relationship between the age and height of dominant trees [6,13]. However, there are rather few long-term monitoring studies focused on the growth dynamics of shrub species, unlike temperate forest coniferous trees, where age can be reliably estimated through growth rings [53]. No standardized or reliable methods currently exist for determining the age of individual shrubs based on their structural features. This lack of age markers limits the ability to establish growth trajectories or site productivity curves for many non-timber species in arid ecosystems.

The SI is a widely used tool in forest science for evaluating stand productivity and guiding silvicultural decisions, typically based on dominant height–age models [13,54]. However, in arid and semi-arid ecosystems, particularly for shrubby species, the application of SIs remains largely unexplored. This is due in part to the difficulty of applying age-based growth models in species adapted to xeric conditions, with irregular growth patterns and limited long-term data [55]. The procedure proposed in this study using linear discriminant functions derived from structural and abundance variables offers a viable alternative for rating site quality in A. lechuguilla stands, especially under field conditions where such variables are routinely measured. Statistical assumption testing and multivariate analyses confirmed the distinctiveness of the predefined SI categories, reinforcing the validity of the classification approach. While previous studies on arid lands have addressed aspects of plant productivity or environmental influences [26,27,56], few have established a method for categorically classifying stand quality.

Several studies on non-timber species focused on biomass prediction and the influence of certain biophysical variables on species growth but not on-site productivity classification [11,21,23,30,32]. Early research established environmental productivity indices (EPIs) that linked abiotic factors such as temperature, soil moisture, and solar radiation to plant structure and biomass accumulation [36], and further modeling efforts predicted dry matter productivity using physiological and site-based parameters [57]. These contributions underscore the importance of structural plant variables such as height, crown diameter, and density for assessing site potential. On the other hand, at a broader scale, recent work has combined spatial distribution models with environmental GIS layers to estimate biomass productivity and habitat suitability for A. lechuguilla across arid and semi-arid regions [29]. While these approaches focus on biomass prediction and spatial habitat potential, this study offers a complementary method focused on classifying site quality at the stand level using field-based morphological and abundance data.

From a biological and ecological perspective, the use of SIs provides an indirect yet integrative assessment of stand quality, often reflecting environmental conditions that influence species performance [5]. Even in forest ecosystems where the SI is widely applied, the method is fundamentally phytocentric, as it evaluates site productivity based on plant derived attributes, typically the dominant height [5,6,8]. In the present study, a similar phytocentric approach was adapted for A. lechuguilla. This approach is biologically meaningful given that the measured variables, such as the plant size and crown dimensions, are closely linked to the harvested portions of the species [30], namely the leaves used for fiber extraction. Thus, evaluating stand quality through these variables is both ecologically valid and directly relevant to resource use. Alternatively, geocentric approaches based on environmental variables such as soil characteristics, topography, and climate have also been employed in site classification studies [19,20,58], providing a complementary perspective grounded in abiotic factors. However, for A. lechuguilla, there are no existing reports on ecological indicators associated with the SI for assessing stand quality. Nevertheless, incorporating ecological data could enhance the understanding of the species productivity from a geocentric perspective and further support the robustness of the method developed in this study.

With respect to the use of abiotic variables, studies have demonstrated that the soil texture, organic matter, moisture availability, and nutrient content significantly affect plant vigor, morphological traits, and population density in arid and semi-arid ecosystems [9,59]. Meanwhile, climatic drivers, particularly temperature and precipitation gradients, have also been shown to regulate the biomass and structural development of life forms [19,22,23]. Likewise, topographic attributes such as the elevation, slope, and aspect are known to influence microclimatic conditions and shape plant distribution and productivity patterns [19,20]. On the other hand, biotic factors like intra- and interspecific competition, grazing pressure, and plant functional traits can modulate plant responses to environmental gradients [24,25,60,61]. These findings highlight the strong ecological basis for using morphological and abundance-related variables, such as those considered in this study. Nevertheless, it is also feasible to consider that periodic measurements of the growth of the species could be incorporated to evaluate the seasonal, topographic, or climatic influence on the productivity of the sites.

A. lechuguilla is widely harvested across Mexico [31,62], yet there are currently no models available for assessing the productive quality of its stands. Therefore, the generalized linear discriminant equations developed in this study could provide a practical method for rating the SI in A. lechuguilla stands under management. Furthermore, this approach may be extended to other commercially harvested species in arid ecosystems, such as Euphorbia antisyphilitica, Lippia graveolens, Dasylirion spp., Agave spp., or Prosopis spp. [9]. For more of these species, Mexican regulations require forest inventories for shrub communities in arid regions [63,64], where the key variables monitored include the height, crown diameter, basal diameter, and plant density [21,65]. These same variables were incorporated into the linear discriminant functions presented in this study. Although phytocentric approaches may be considered empirical, they provide a practical framework to link the ecological condition with sustainable harvesting practices. In theory, sites with lower SI values are less productive and may support only limited extraction, whereas high-index sites offer greater resource availability.

The multivariate analysis process employed in this study confirmed statistically significant separation among the predefined groups based on the IVI. As previously discussed, the linear discriminant functions generated might represent a tool for assessing stand quality, offering a practical and replicable method for classifying A. lechuguilla habitats. Additionally, complementary multivariate techniques such as MANOVA and PCA provided supporting evidence that reinforced the discriminant analysis results. Together, these analyses contribute to the robustness of the proposed methodology and highlight its potential for application in ecological assessment and sustainable resource management [38].

Regarding sample size considerations, although two of the SI categories included fewer than 30 observations, the number of cases per group relative to the number of predictor variables (n > 5p) satisfied the commonly accepted criteria for multivariate analysis [38]. Furthermore, all statistical assumptions for the CDA were met, including multivariate normality, homogeneity of covariance matrices, and absence of multicollinearity. The discriminant functions yielded high classification accuracy, particularly for the extreme SI levels (100%), highlighting the robustness and internal consistency of the model. This distribution pattern reflects the natural variability and frequency of A. lechuguilla populations along the ecological productivity gradient, where medium-quality sites are more prevalent. Therefore, the sample structure should not be interpreted as a design limitation but as a representation of the ecological patterns. However, although the current model demonstrates strong discriminatory capacity, future studies incorporating a larger number of plots, particularly at the low and high ends of the productivity spectrum, could enhance its generalizability and allow for broader application across arid shrubland ecosystems.

Regardless of the lack of a direct comparison between the procedure developed in this study and traditional approaches, the site index model developed in this study differs from traditional forestry approaches that rely on dominant height–age curves [2,8,13], which currently are not feasible for arid land shrubs mainly due to the lack of reliable age estimates and long-term data. While classical models for timber species use tree height as a proxy for productivity [2,7], our phytocentric, multivariate method based on the structural and abundance variables of A. lechuguilla provides a practical alternative for site classification. Although not directly comparable in terms of structure, both approaches aim to assess site quality through plant variables that reflect ecological performance. In this context, our model developed using multivariate discriminant analysis achieved classification accuracy levels (total error rate of 4.60%) comparable to those reported in site index studies of forest species [5,6,7], despite the constraints inherent to arid shrublands. This highlights its potential value for non-timber species where conventional models are not applicable.

Additionally, the SI developed in this study is based on a multivariate discriminant approach rather than depending on any single variable. Therefore, the model accounts for the combined discriminatory power of these variables. Moreover, the classification functions weigh each variable differently according to its discriminatory power (partial R²), and thus their influence is not equal. While it is theoretically possible for two plots with contrasting structural variables to fall within the same SI category, this is uncommon, as higher SI values are generally associated with larger plants and greater density across variables, and vice versa. This integrative interpretation makes the index robust for differentiating stand conditions, rather than relying on isolated variables. On the other hand, although modal plants (one per quadrant, four per site) were used to estimate site value averages, this method offered a practical compromise for sampling dense shrublands [21], with normality tests confirming the adequacy of the data for multivariate analysis. Nonetheless, this method offers a practical trade-off between efficiency and representativeness, especially in arid shrublands, where the plant density is high and full sampling would be logistically and economically prohibitive. Nonetheless, it is acknowledged that this strategy may not capture the full structural variability of the stand. Based on this, future studies may consider comparing this approach with exhaustive sampling to quantify potential deviations and optimize effort versus accuracy in site classification.

The SI model also has broader applications in restoration, conservation, and land management. By categorizing stands into distinct productivity levels, the tool can support the identification of areas requiring protective measures, such as low-quality sites vulnerable to degradation, or zones with high productivity potential suitable for sustainable use. Remote sensing technologies such as LiDAR, vegetation indices, or hemispherical photography could complement or scale this approach by estimating variables over large spatial extents. Biomass estimation models may also provide useful complementary information, particularly at regional scales, although they generally focus on dry matter accumulation without directly addressing site quality classification. Overall, the SI framework presented here offers a field-based, ecologically grounded tool for supporting site-level decision making in arid and semiarid shrublands.

Finally, to apply the discriminant functions developed in this study, it is necessary to calculate the values of the resulting linear equations for each new stand or sampling site using field-collected variables (abundance, height, basal diameter, and canopy cover). Each observation is evaluated across the functions corresponding to the predefined groups (low, medium, and high) and is assigned to the group whose discriminant function yields the highest value. This approach enables an objective and replicable classification of new stands, facilitating its integration into existing inventory and management systems. Moreover, its use can enhance sustainable decision making by more accurately identifying sites with ecological conditions suitable for the responsible harvesting of A. lechuguilla.

5. Conclusions

The combination of multivariate analyses and classical discriminant analysis statistically validates the site quality classification initially performed using the IVI. The CDA achieved an overall classification accuracy of 95.54%, with 100% correct classification for both low and high site quality categories, confirming a high degree of internal consistency and model robustness.

The MANOVA results (Wilks’s lambda = 0.2192, p < 0.0001) confirmed significant multivariate differences among the SI levels, while PCA revealed that the first two principal components accounted for 70.63% of the total variance, aligning with the discriminant structure. These findings reinforce the ecological and statistical coherence of the IVI-based classification and support the practical application of this simplified IVI approach to assigning site quality.

In contrast to traditional site index models based on height–age relationships, which require long term data and reliable age estimation (often unavailable for arid land shrubs), our approach achieved a classification accuracy with 4.6% error using structural and abundance variables. Although not directly comparable to classical height–age models, this level of predictive performance is consistent with the accuracy typically reported for such models in forestry. While our method does not currently allow for dynamic site monitoring over time, it offers a practical and ecologically meaningful alternative for assessing site quality in non-timber ecosystems, particularly for species like A. lechuguilla, under field conditions where age-related data are lacking.

The proposed SI model provides an approach to assessing stand quality in arid shrublands based on morphological and abundance variables. This methodological alignment might offer a replicable tool for site-level decision making. To reinforce these findings, future studies are encouraged to integrate geocentric methods for land evaluation, remote sensing technologies, and long-term monitoring strategies to improve the spatial and temporal resolution of site productivity assessments.