Abstract
Redwood (Sequoia sempervirens (Lamb. ex D. Don) Endl.) is a fast-growing, long-lived conifer native to a narrow coastal zone along the western seaboard of the United States. Redwood can accumulate very high amounts of carbon in plantation settings and continuous cover forestry (CCF) represents a highly profitable option, particularly for small-scale forest growers in the North Island of New Zealand. We evaluated the profitability of conceptual CCF regimes using two case study forests: Blue Mountain (109 ha, Taranaki Region, New Zealand) and Spring Creek (467 ha, Manawatu-Whanganui Region, New Zealand). We ran a strategic harvest scheduling model for both properties and used its results to guide a tactical-spatially explicit model harvesting small 0.7 ha units over a period that spanned 35 to 95 years after planting. The internal rates of return (IRRs) were 9.16 and 10.40% for Blue Mountain and Spring Creek, respectively, exceeding those considered robust for other forest species in New Zealand. The study showed that small owners could benefit from carbon revenue during the first 35 years after planting and then switch to a steady annual income from timber, maintaining a relatively constant carbon stock under a continuous cover forestry regime. Implementing adjacency constraints with a minimum green-up period of five years proved feasible. Although small coupes posed operational problems, which were linked to roading and harvesting, these issues were not insurmountable and could be managed with appropriate operational planning.
1. Introduction
Redwood (Sequoia sempervirens (Lamb. ex D. Don) Endl.) is a coniferous species indigenous to the western coast of the United States. This species exhibits shade tolerance and, within its native habitat, can develop stands of varying ages, with trees attaining heights of 115 m and ages surpassing 2200 years [1,2,3]. Redwood forests store exceptionally high quantities of biomass and carbon within the decay-resistant heartwood of old-growth stands, and growth rates have been found to be highest in plantation forests [1]. Generally, redwood stands are healthy [4], being resistant against damage from wind [3,5] and fire [6,7,8]. Consequently, the significant carbon reserves accumulated in these forests are relatively well-protected from threats such as pests, pathogens, and environmental stressors.
Redwood trees yield high-quality timber, which is primarily utilized for aesthetic purposes given its red-brown heartwood and pale sapwood, workability and dimensional stability [5]. This timber is recognized for its lack of odor, attractive grain, and importantly, its naturally durable heartwood [9]. The exceptional timber quality of mature redwood trees has led to rapid depletion of old-growth forests within their native range. Over the past 170 years, the area covered by these forests has decreased from 8900 km2 to 457 km2, with only seven remaining locations exceeding 4 km2 in the United States [10]. The timber demand has been partly met by plantations established within the native range, and there is potential for sourcing timber from plantations established outside the United States [5].
Redwood can thrive under a wide array of environmental conditions, but optimal growth occurs in temperate climates characterized by mild temperatures and moderate to high rainfall. Successful plantations have been established in numerous countries with such climates, including France [11], Germany [12], and Chile [13]. Redwood has proven to be particularly well-suited to New Zealand, where 8000 hectares were established between 2000 and 2018 [5]. Afforestation rates saw a sharp increase after 2019, with approximately 2000 hectares established in 2023 alone [14]. Redwood is currently the second most widely planted species in New Zealand, following radiata pine (Pinus radiata D. Don) [14]. Most of these plantations are in the North Island, where the climate is particularly favorable for this species [5]. As a result, growth rates in these areas, which reach maximum periodic annual increments (PAI) of 87–90 m3/ha/yr, surpass those in native-range plantations, where maximum PAI of 75.6 m3/ha/yr have been observed [15].
Data collected from a network of permanent sample plots (PSPs), along with predictive models and spatial data, have demonstrated the substantial potential of redwood in New Zealand for both timber volume and carbon sequestration [15]. Within New Zealand redwood is a low-risk species to establish as it is very resistant to pests, diseases [4,16], wind [17] and fire [6,7,8]. Additionally, redwood has a very low risk of wilding spread [18]. The species reproduces both vegetatively and through seedlings [19], but cone production is irregular and seeds are characterized by very low viability.
Growth models that can predict carbon accumulation have been used to undertake a financial comparison of the net present value of redwood and radiata pine of New Zealand forests for which the only derived income was from carbon accumulation [20]. This research showed that by age 100 years, the total carbon stored in redwood forests exceeded that of radiata pine in eight out of nine regions in New Zealand. Mean regional carbon for redwood exceeded that of radiata pine in the five North Island regions by on average 74%, with regional differences reaching up to 85% (5203 vs. 2808 t CO2/ha at 100 years of age). The net present value of redwood was found to be closely comparable to that of radiata pine across a spectrum of carbon prices in four out of five regions in the North Island [20].
Carbon now represents a major source of revenue for forest growers [21]. Globally, compliance carbon markets play a central role in climate mitigation, with Emissions Trading Systems (ETSs) serving as key policy instruments. As of 2024, 36 ETSs are active worldwide, covering roughly 18% of global greenhouse gas emissions and generating a record USD 74 billion in revenue in 2023 [22]. An additional 22 ETSs are currently in development or under consideration in countries such as Japan, Canada, Brazil, India, and Türkiye, highlighting growing international momentum toward carbon pricing as a climate strategy [22].
The New Zealand Emissions Trading Scheme (ETS) stands out globally for its inclusion of the forestry sector [22]. First introduced in 2008 under the Climate Change Response Act, the ETS remains one of the government’s primary tools for supporting both domestic and international efforts to reduce greenhouse gas (GHG) emissions. Under the scheme, registered forest growers earn one New Zealand Unit (NZU) for every tonne of CO2 sequestered. Over time, the total number of NZUs is gradually reduced, placing a cap on allowable emissions and creating a financial incentive for businesses to adopt lower-emission practices. The ETS serves as a key policy tool for meeting New Zealand’s international obligations under the Paris Agreement, as well as its 2050 net-zero target and emissions budgets outlined in the Climate Change Response Act 2002 [23].
Managing redwood under a continuous cover forestry (CCF) regime is likely to be highly profitable, particularly in the North Island of New Zealand. Initial carbon revenue can be leveraged to support the transition to a steady-state forest that generates a continuous stream of valuable timber with a very high rate of return [24]. However, several challenges, important to forest practitioners, remain regarding CCF implementation–particularly around coupe size, green-up requirements and operational costs. Therefore, the aim of this study was to develop CCF tactical plans for two forest estates with dissected terrain, exploring the potential of CCF to produce high-quality timber while maintaining a constant carbon stock over time. Specifically, we aimed to test the hypothesis that harvesting small coupes while leaving all adjacent coupes unharvested for a defined green-up period is operationally and economically viable. We predict that some of the alleged drawbacks of continuous cover forestry are not insurmountable.
2. Materials and Methods
2.1. Forest Estates Under Study
The case study simulates the management of two forest estates: Blue Mountain, Taranaki (109 ha) and Spring Creek, Manawatu-Whanganui (467 ha) both of which are located in the North Island of New Zealand (Figure 1). For modeling purposes, both estates were assumed to be fully planted with redwood on bare land at the beginning of the planning horizon (year 0). The strategic planning horizon was 300 years while the tactical horizon was 60 years (1/5 of the strategic horizon). Time was aggregated into 5-year periods.
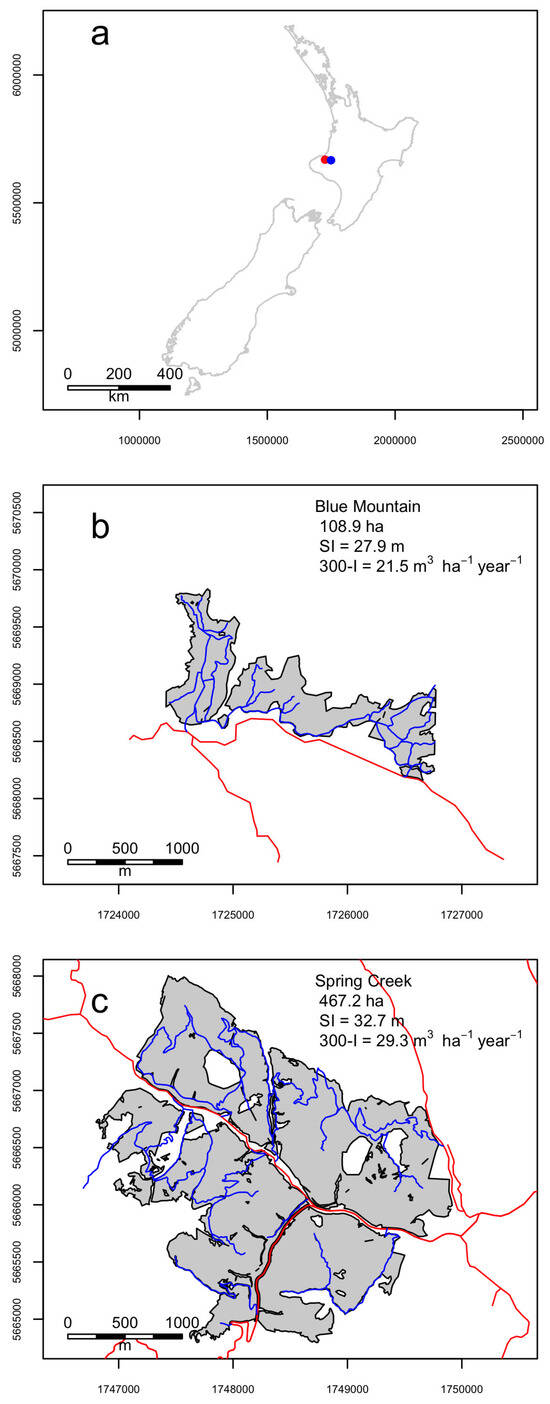
Figure 1.
Blue Mountain and Spring Creek forest estates which were assumed to be fully planted with redwood on bare land at the start of the planning horizon. The red dot in (a) represents the location of Blue Mountain while the blue dot shows Spring Creek. The properties in (b,c) include the area (ha), 300 Index (300-I, m3 ha−1 year−1) and site index (SI, m). In (b,c) red lines are highways and blue lines internal roads. CRS: NZGD2000/New Zealand Transverse Mercator 2000.
Continuous cover forestry was defined within this study as the retention of at least 30% of each hectare in forest with an age ≥ 5 years. In practice this was achieved by dividing both forest estates into 0.7 ha hexagonal units, with the condition that once a unit is harvested the neighboring units could not be harvested for a period of at least 5 years.
The methods used for this theoretical study were developed in conjunction with four senior forest managers who had an advanced understanding of harvesting and redwood management and silviculture. An initial draft of the manuscript was circulated to managers and then modified to incorporate their feedback. This process was repeated two more times until the managers were satisfied that the developed methods could be practically implemented.
Terrain across the two properties differed substantially. Blue Mountain had a gentler landscape, with an average slope of 25%, while Spring Creek was more rugged, averaging 42%. Slopes between 30% and 40% are generally considered the upper operational limit for ground-based harvesting systems, whereas cable systems can be used on steeper terrain [25,26,27]. At Blue Mountain, 65% of the area had slopes below 30%, and 77% below 40% (Table 1), suggesting that ground-based harvesting systems are likely to be feasible across most of the estate. In contrast, 77% of Spring Creek exceeded a 30% slope, indicating that cable-based harvesting systems would be required—an assumption supported by the highly dissected terrain (Appendix A).

Table 1.
Variation in the percentage area within both properties by slope category (%).
The silvicultural regime consists of planting 625 stems/ha, prune 450 stems/ha at ages 6 (8.2–9.9 cm dbh, 4.1–4.9 m height), 8 (10.6–14 cm, 6.1–7.4 m) and 10 (20.8–23.5 cm, 8.2–9.8 m) to a height of 6.5 m, and thin at age 11 (24.5–27.6 cm, 8.2–11.1 m), to 450 stems/ha. This silvicultural regime was selected to maximize the yield of high-value clear heartwood, which commands a substantial market premium over grades containing sapwood or unpruned “tight knot” timber—both of which are still more valuable than timber with bark-encased knots [28]. Harvesting will be undertaken on stands aged 35 years and older, and natural regeneration (coppice) will be established after felling the first rotation. The coppice will be thinned at ages 2 to three–five dominant shoots/stump, and at age 5 to a single dominant shoot/stump, maintaining the same pruning regime, outlined above, at ages 6, 8 and 10 years old. Assumptions are that yield tables will not be changed by plant source (seedling vs. coppice) or by re-establishing trees in 0.7 ha coupes surrounded by well-established stands.
2.2. Overall Modeling Framework
The modeling framework comprised the six stages depicted in Figure 2. The first stage consisted of predicting carbon and timber yield over ages 0–100 years for both properties. We consider 100 years to be the maximum harvesting age based on piece size. The second stage consisted of estimating realistic carbon and timber prices achievable for the region where both properties are located. During the third stage we estimated likely silvicultural, management, harvesting and transport costs. The fourth stage consisted of planning potential roads to access all 0.7 ha units to estimate the total fixed roading cost. Once all data needed was collected, we ran a strategic harvest scheduling model based on linear programming in order to derive a general strategy for the management of redwood for both properties. The sixth and last stage, which is the focal point of this study, was to run a tactical spatially explicit harvest scheduling model, based on integer (binary) programming, analyzing the feasibility of implementing a continuous cover forestry regime for redwood. The tactical level uses the outputs produced at the strategic level, such as timber flow, applying them over shorter periods of time that are typically less than a rotation [29]. All these stages are described in greater detail in the following sections.
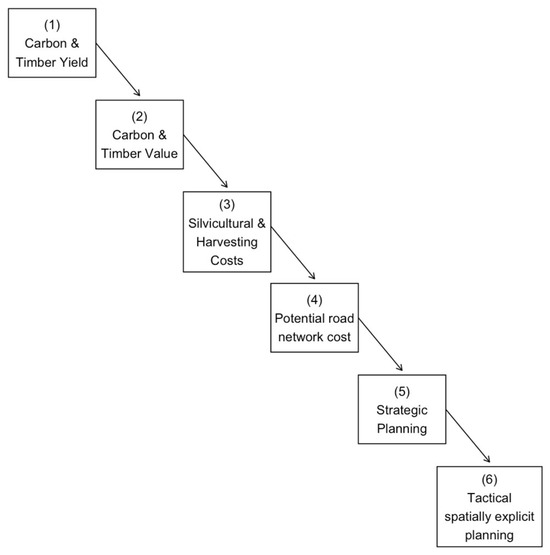
Figure 2.
Conceptual diagram outlining the methodological framework.
2.3. Estimates of Carbon and Total Recoverable Stem Volume
Regional estimates of volume and carbon were based on a redwood growth model which is fully described in [30,31]. In brief, the redwood growth model, which was based on the 300 Index methodology, was developed using a comprehensive set of plot data distributed throughout New Zealand. The 300 Index approach incorporates both site index and the volume-based 300 Index as key inputs for the growth model. Using these inputs, the model estimates annual changes in stem volume, carbon accumulation, and log out-turn through an integrated framework of growth equations, allometric relationships, and functions for carbon partitioning and basic wood density. The redwood growth model is implemented in the freely available multi-species carbon calculator (Version 1.2) available at: https://fgr.nz/tools/multi-species%20carbon-calculator/ (accessed on the 20 February 2025).
Estimation of the two key productivity metrics (site index and 300 Index) forms the foundation of volume and carbon predictions. For redwood, site index is defined as the mean height of the 100 largest-diameter trees (mean top height, MTH) at a reference age of 30 years. The 300 Index, a normalized volume measure developed to address the limitations of site index, represents the mean annual stem volume increment of a stand stocked at 300 stems per hectare at age 30. These two productivity indices, which are used as input to the growth model, can be extracted from plot data. Alternatively, if no plot data are available these two productivity indices can be extracted from national spatial predictions, described in detail in [31], which are freely available at: https://koordinates.com/ (accessed on the 14 January 2025).
The spatial predictions of productivity indices were used to determine 300 Index and site index shown in Figure 1 for Blue Mountain while existing redwood plot data was used in the Multi Species Carbon Calculator to estimate both productivity metrics for Spring Creek. Once the 300 Index and site index were defined, the Multispecies Carbon Calculator was used to predict redwood volume, carbon and log grade out-turn. Compared to Spring Creek, Blue Mountain exhibited lower values of both 300-Index (21.5 vs. 29.3 m3 ha−1 yr−1) and site index (27.9 vs. 32.7 m). Consequently, timber and carbon yield were lower in Blue Mountain than Spring Creek (Figure 3).
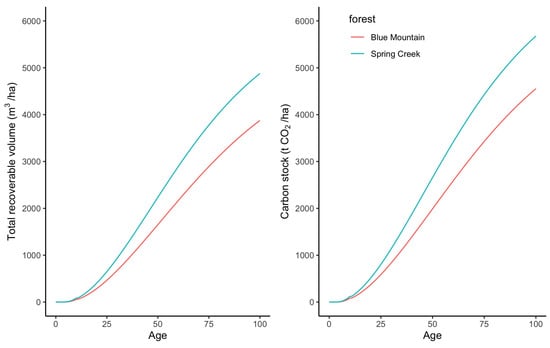
Figure 3.
Changes in (left) total recoverable volume and (right) carbon stock with age for Blue Mountain and Spring Creek provided that no harvesting is performed.
For strategic and tactical harvest scheduling purposes, we used a fitted model to interpolate the data presented in Figure 3: Blue Mountain: TRV = 5844 (1−1/e (0.01945 age)) 2.6563; CAR = 6841 (1−1/e (0.01916 age)) 2.5488; Spring Creek: TRV = 6663 (1−1/e (0.02241 age)) 2.7591; CAR = 7726 (1−1/e (0.022186 age)) 2.65939, where TRV is total recoverable volume (m3/ha), CAR is carbon stock (t CO2/ha) and age is expressed in years since planting.
2.4. Timber and Carbon Value
Redwood log values were estimated using two complementary approaches that included a comparative price analysis and lumber recovery, or ‘millback’, analysis [32]. These at mill gate (AMG) values, by log diameter and pruned status, are shown in Table A2. These values were integrated with predicted timber grade recoveries generated by the Excel-based redwood growth model, which estimates under-bark stem volume by pruned butt logs and unpruned upper logs across small-end diameter (SED) classes. The resulting mean AMG log values per cubic meter by stand age are shown in Table 2 for both Blue Mountain and Spring Creek. These AMG values increased markedly with harvest age by 38.2% from ages 35 to 100 years (Table 2).

Table 2.
Variation in mean at mill gate (AMG) redwood log values for the Waikato region for selected harvest ages ranging from 35 to 100 years.
A base carbon price value of NZD 80/t CO2 was assumed for this study, according to current projections by the New Zealand Ministry for the Environment [23]. A sensitivity analysis was conducted using selected carbon price points to represent different scenarios that included: a timber-only regime (NZD 0/t CO2), the current minimum auction price under the ETS (NZD 35/t CO2), and an upper bound of NZD 160/t CO2, reflecting the Climate Change Commission’s projected carbon price for 2035 [33].
For strategic and tactical harvest scheduling purposes, we used a fitted model to interpolate the data presented in Table 2: y = 213.39775910 + 3.23221289 x − 0.01023076 x2, where y is price AMG (NZD/m3) and x is age (years).
2.5. Establishment, Silviculture, Harvesting, Roading and Management Costs
All costs related to establishment, silviculture, roading, and management were estimated based on a combination of industry consultation and published sources (see Table 3). Initial establishment expenses in year 0 were NZD 3159/ha and covered activities such as land preparation, planting, release spraying, and mapping. Since redwood regenerates via coppicing after harvest, these upfront costs were not incurred in subsequent rotations. During the first rotation, pruning was carried out to a height of 6.5 m in years 6, 8, and 10, with each lift costing NZD 2329/ha. Thinning was performed at age 11 to reduce stocking to 450 stems/ha at a cost of NZD 900/ha. For second and later rotations, the same cost for the three pruning operations from the first rotation were used. However, there was a higher total cost for thinning the coppicing redwood sprouts (NZD 2000/ha) at age 2 (selecting 3–5 dominant shoots per stump), and age 5 (selecting a single dominant stem per stump).

Table 3.
Summary of costs and the year in which they occurred from the start of the simulation for the continuous cover forestry regime. All costs are given in New Zealand dollars (NZD). Costs followed by the asterisk * only occur in the year shown.
Periodic costs included carbon-related administration, upkeep of infrastructure such as roads, tracks, and fencing, as well as animal pest control. Participation in the ETS was assumed to incur a cost of NZD 71/ha, with assessments scheduled every five years which is the minimum interval allowed under current regulations [32]. These periodic expenses were incurred up to 35–40 years after establishment. Annual operating costs covered forest management, local rates, insurance, and general administration. A forest management cost of NZD 60/ha/year was applied to reflect the greater complexity involved in managing continuous-cover forestry (see Table 3).
Ground-based harvesting was estimated at a cost of 60 NZD/m3 through consultation with industry experts. As usual in NZ forestry, we referred to felling by a feller-buncher and extraction of the stems by a grapple skidder. Cable based harvesting (90 NZD/m3) was estimated to cost 50% more than ground-based harvesting based on figures by [34]. Considering an extraction distance in the range of 300–400 m, we selected a guyless excavator-based yarder (shovel yarder) equipped with a grapple carriage. For the felling operation, a tethered feller-buncher was chosen. This machinery enables significantly faster relocation times, between 1 and 1.5 h to establish a new line, compared to conventional tower or swing yarders [35].
It is useful to define the theoretical layout of the cable harvesting lines that we have tentatively considered for tactical planning. This also helps assess whether there is sufficient harvestable material to justify the use of this extraction system. The proposed layout involves placing the shovel yarder at the edge of the patch, from which approximately three lines radiate to cover the area. Three lines are sufficient, given the use of a feller-buncher, which produces stacks accessible by the grapple carriage, and considering that the coupes are about 94 m wide at their broadest point.
To determine whether cable harvesting is justified, we can refer to a common rule of thumb in forest engineering: at least one cubic meter of harvestable timber is needed per meter of cable line. Given a 7000 m2 hexagon, the maximum width is approximately 94 m. Assuming an average extraction distance of 350 m and three lines required to extract timber from the entire patch, the total line length amounts to 1050 m, which implies a need for 1050 m3 of timber. This number will be reached and far surpassed once trees are 40 and 50 years old in Spring Creek and Blue Mountain, respectively. Furthermore, the rule of thumb was established for conventional tower yarders. Through using shovel yarders the relocation costs are lower, and this will further reduce the amount of harvestable volume required for making a given cable line profitable.
Transport costs to a mill were estimated at 19 NZD/m3, assuming a cart distance of 100 km and transport carried out by a log truck [36]. Other costs included road maintenance (3.75 NZD/m3), post-harvest ancillary costs (1.88 NZD/m3), a harvest management fee (5.63 NZD/ha) and the forest growers levy (0.33 NZD/m3). These values totaled NZD 91/m3 for ground-based and 121 NZD/m3 for cable-based harvesting. These total costs were within or marginally above the range provided by [37] (total cost range 42.2–119.0 NZD/m3, average 68.6 NZD/m3, corrected by CPI Q4 2017–Q4 2024) for small-scale owners of the Canterbury, Otago, and Southland regions. Harvesting and transport costs were subtracted from the AMG values in Table 2 estimates to calculate net harvest returns. These net figures were then multiplied by the associated total recoverable volumes to estimate the value of timber extracted. Based on slopes (Table 1), we assumed that harvesting will be ground-based in Blue Mountain and cable-based in Spring Creek. Although this is an oversimplification this could be readily refined during operational planning.
Using historical road construction costs (pers. comm. Robin Webster, 7 February 2025) corrected for inflation we arrived at a value of 137,091 NZD/km for primary roads, which ranged across forests from NZD 105,600 to NZD 166,320. The preceding was equivalent to a unitary cost per cubic meter of harvested timber ranging from 7.71 to 12.80 NZD/m3 (average 9.01 NZD/m3). A similar range was estimated by [37] (7.7–19.2 NZD/m3, average 12.4 NZD/m3, corrected by CPI Q4 2017–Q4 2024) for small-scale owners in Canterbury, Otago and Southland. It was assumed that all existing roads in Blue Mountain and Spring Creek are primary roads while all new roads that need to be constructed to access coupes will be spur roads (single lane). Secondary roads construction costs were assumed to be half the cost of primary roads at 68,546 NZD/km. These values are similar to values reported by [38] for spur roads (NZD 72,000/km) and higher standard secondary roads (NZD 90,000/km) in New Zealand.
2.6. Current and Potential Road Network
The current road network comprises 10.517 km and 20.446 km, which equates to a road density of 96.6 m/ha and 43.8 m/ha, for Blue Mountain and Spring Creek, respectively.
The tactical planning required an estimation of the size of the current and potential road network. The current road network is assumed to be primary roads, but secondary roads and skid tracks need to be planned. This is necessary because harvesting small, dispersed 0.7 ha hexagons across the landscape presents both logistical and cost-related challenges. To estimate an efficient access network, we applied the minimum spanning tree algorithm [39], which identifies the shortest path that connects all nodes in a network. In the simplest case the weights or penalties are the distances between the nodes (the centroid within each coupe) although using construction cost as penalties are more common. The algorithm searches for the route connecting all nodes with the minimum sum of weights or penalties.
In this study, each arc connecting two nodes was assigned a penalty. Lower penalties were applied to arcs within a 25 m buffer of internal roads and ridgelines (for Spring Creek only), while penalties increased with slope for all other arcs. While this is a simplified approximation, and more detailed operational planning is needed to determine harvesting systems, landing locations, and spur road construction, the primary objective of this analysis was to estimate the potential road network length for calculating fixed costs.
The total road network corresponds to estimated fixed costs of NZD 2,109,494 for Blue Mountain—comprising NZD 1,441,791 for primary roads and NZD 667,704 for secondary roads—and NZD 6,372,969 for Spring Creek, including NZD 2,802,971 for primary and NZD 3,569,998 for secondary roads (Appendix A). Although primary roads exist in reality, we conservatively assumed that this incurred cost should be included in our financial analysis.
2.7. Strategic Planning Model
Strategic planning in this study was based on a simplified version of Model III. This model, implemented through FOLPI (Forestry-Oriented Linear Programming Interpreter), was originally designed to optimize the timing and spatial distribution of harvesting activities across extensive forested landscapes [40]. By solving this problem, we define the management strategy that should be adopted to guide the forest from its current condition to its ideal condition. Although strategic planning is not spatially explicit, this process provides key information (i.e., allowable cut, harvesting strategy, steady-state condition, rotation length) for the tactical planning which will be spatially explicit. Strategic planning is typically undertaken over relatively long periods of time that comprise several rotations.
In our particular case, the model identifies the optimal harvest schedule that maximizes net present value (NPV), subject to a series of management and financial constraints. The strategic planning horizon runs from year 0 to 300, and is split as a period of transition (0–150 years) and a steady-state period (150–300 years). Time was aggregated into 5-years periods. Trees are eligible for harvest at ages 35 and older, and from year 40 onward, at least 50% of the forest estate must consist of stands older than 20 years. Additionally, a non-declining carbon stock constraint is imposed to ensure that carbon income remains zero or positive throughout the planning horizon—thereby avoiding scenarios where carbon credits would need to be repaid. There are no restrictions on how many times a given hectare can be harvested over the planning horizon, aside from the constraints specified earlier. This modeling framework was applied to Blue Mountain and Spring Creek under the CCF regime.
The strategic model is described by four components: decision variables, parameters (or known values), an objective function and constraints which are described in more detail, below.
2.7.1. Decision Variables at the Strategic Level
As this is a strategic model, decision variables are not spatially explicit and represent the area being harvested from each age class in each period.
where t is an index of time periods and j is an index of age classes.
ytj = area (ha) harvested in period t from age class j
2.7.2. Parameters Used at the Strategic Level
The parameters of the strategic model refer to specific values that characterize the forest and its management over the long run. They comprise area by age class, carbon stock and recoverable volume along the planning horizon, costs and prices, among others. A list of these parameters is given below:
| T | total number of periods; |
| Pj | Net price per cubic meter (NZD/m3) of timber harvested from age class j; |
| ϕ | Net price per tonne of CO2 stored (NZD/t CO2); |
| Vj | Realizable (merchantable) yield per hectare (m3/ha) in age class j; |
| Sj | Carbon stock (t CO2/ha) in age class j; |
| r | Discount rate (as decimal number); |
| aj | area (ha) of age class j at the beginning of the planning horizon; |
| E | variable cost of establishing and tending 1 ha that was harvested. |
2.7.3. Auxiliary Variables at the Strategic Level
Auxiliary variables do not influence the optimization outcome but are included to aid in interpretation of the results. These variables include the following:
where ztj is the area remaining in age class j at period t, Ht is the total merchantable volume (m3) harvested in period t, and Kt is the total carbon stock (t CO2) in period t.
2.7.4. Objective Function at the Strategic Level
The objective function, which is given below, consists of maximizing the net present value over a 300-year planning horizon. The base discount rate was set to 6% p.a. The revenues were derived from two sources: harvesting and carbon sequestration.
2.7.5. Constraints at the Strategic Level
- (a)
- Area constraintsThree groups of constraints were implemented in order to ensure the conservation of area:
- (i)
- The area harvested must be immediately replanted (Rt).
- (ii)
- The area planted in any period (Rt) must be subsequently harvested.
- (iii)
- The area at the beginning of the planning horizon in each age class must be subsequently cut.
But (i) and (ii) can be equal as Rt is the same for both constraints, thus, - (b)
- Minimum and maximum harvest ages: harvesting is permitted for trees aged between 35 and 100 years, i.e.,where j− and j+ are the age classes below and above which trees cannot be harvested.
- (c)
- Minimum canopy cover. Ensure that 50% of the forest estate should be age 20 years or older after year 35 along the planning horizon. That is,where fa is the fraction of the forest estate that should be over a given age (fa = 0.5, j· = 5 [20–25 years]) and A is the total area of the forest estate.
- (d)
- Non-declining carbon stock. This constraint ensures that carbon stock does not decline so that revenue from carbon is received but does not have to be returned.
- (e)
- Timber flow constraints. These are expressed as relationships between consecutive time periods, specifying the allowable maximum increase (α) or decrease (β) in harvest volume. Both α and β are defined as proportions, ensuring that the volume harvested in any period does not deviate beyond these limits relative to the previous period.Timber flow constraints were introduced beginning in period 8 (years 35–40), reflecting the assumed minimum harvest age of 35 years. The parameters α and β were both set at 0.1, limiting harvest volume fluctuations between periods to a maximum of ±10%.
2.8. Tactical Planning Model
At the tactical level, numerous management models exist, with those incorporating spatial and adjacency restrictions gaining prominence [41,42]. These models schedule harvests in a way that ensures adjacent units are not harvested simultaneously, maintaining compliance with clearcut size regulations and policy limits [29].
From a modeling perspective, representing spatial constraints can be challenging. There are two potential models that can be applied in tactical forest management planning. The Unit Restriction Model (URM) evaluates harvest units so that they do not exceed a maximum permitted area. A mathematical model is then applied to ensure that adjacent units are not simultaneously harvested. In other words, the URM harvests previously defined spatial units of a size less than the area restriction, so that simultaneously harvesting two adjacent units would violate the spatial constraint [43]. In contrast, the Area Restriction Model (ARM) allows adjacent smaller units to be harvested simultaneously, provided the combined contiguous area remains within the upper limit [43].
In this study, spatial restrictions were imposed using the URM. A grid of 0.7 ha hexagons was overlaid across both Blue Mountain and Spring Creek. This unit size was selected to ensure that, under adjacency constraints, at least 30% of any given hectare retained forest cover at all times. A key consideration when applying adjacency rules is the minimum interval before any other neighboring unit can be harvested. Based on practices in Californian redwood forests, where common time lags for harvesting adjacent clear cuts are around four years [29], a five-year interval was adopted in our analysis. Under these conditions several questions arise about coupe size, green-up, and the operational costs of CCF. For example, managers may question whether using a coupe size of 0.7 ha is feasible or whether it is viable to maintain unharvested stands of a minimum age around a harvested stand for a designated green-up period. Under current legislation, a conservative minimum age for green-up would be at least five years.
The proposed tactical spatially explicit model aims to determine a harvest schedule for a set of stands that maximizes profit while adhering to adjacency constraints and maintains a relatively even flow of timber harvested and carbon stock. This model was applied to both Blue Mountain and Spring Creek forest estates.
The tactical model is described by four components: decision variables, parameters (or known values), an objective function and constraints which are described in more detail, below.
2.8.1. Decision Variables at the Tactical Level
The decision variable selected is a integer binary variable, which means that could take either a value of 0 or 1 but not a fractional value. There are as many variables as stands and periods.
| xit | A binary variable that indicates whether stand i is harvested in period t (1) or not (0) |
- where
- i ∈ A (stand, A is the set of stands);
- t: 1, 2, ……, m (time period).
2.8.2. Auxiliary Variables at the Tactical Level
Auxiliary variables are a combination of decision variables and parameters. They do not influence the final solution but document and keep track of management quantities relevant for decision making. For the purposes of the exercise there are two auxiliary variables:
| Ht | An auxiliary variable to account for the total volume harvested in period t; |
| Ct | An auxiliary variable to account for total carbon stock in period t. |
2.8.3. Parameters at the Tactical Level
The parameters of the model refer to specific values that characterize the forest and its management at the tactical level. Parameters describing the forest estate include the stand areas, recoverable volume and carbon stock along the planning horizon, among others. A list of these parameters is given below:
| A | Set or list of all stands that are within a forest estate. |
| Bi | Set or list of stands adjacent to a particular stand i. For each stand in list A there is a list of stands which are neighbors of stand i, e.g., B[1] = {2,4,6,7,9}, meaning that the neighbors of stand 1 are stands 2,4,6,7 and 9. |
| m | Number of periods, e.g., for 12 periods of 5 years each, m = 12. |
| ai | Area of stand i (ha). |
| vit | Total recoverable volume (m3/ha) that could be harvested from stand i in period t (period t goes from 1 to m). |
| npvit | Net present value (NZD/ha) from harvesting stand i in period t. |
| Hmin | Minimum volume to be harvested per period (it comes from the results of the strategic planning). |
| Hmax | Maximum volume to be harvested per period (it comes from the results of the strategic planning). |
The npvit is an auxiliary parameter derived from harvesting 1 ha of spatial unit i in period t. Therefore,
where pit is the net price per cubic meter (at mill gate price from Table 2 minus the harvesting cost, i.e., 91 NZD/m3 for ground-based and 121 NZD/m3 for cable-based harvesting) harvested from unit i in period t, Cs is the discounted silvicultural cost of pruning and thinning after harvesting, and r is the interest rate.
2.8.4. Objective Function at the Tactical Level
The objective function aims to maximize the net present value from harvesting the stands over the planning horizon. This is represented by:
2.8.5. Constraints at the Tactical Level
- (a)
- Area Constraints: Each stand can only be harvested once along the tactical planning horizon (60 years) or left unharvested:
- (b)
- Adjacency Constraints: Two adjacent stands cannot be harvested in the same period:
- (c)
- Total volume harvested per period: The total volume harvested in each period is calculated as:
- (d)
- Total volume harvested per period within a range: The total harvest volume in each period should stay relatively constant within a range given by the results of the strategic planning (Hmin, Hmax):
2.9. Optimization Algorithm
The strategic model was developed in Microsoft Excel (version 16.54, 2021) and solved using the OpenSolver add-in [44]. OpenSolver is an open-source extension for Excel that enables the formulation and solution of linear and integer programming problems. Optimization was performed using the COIN-OR CBC solver, which is integrated within the OpenSolver platform.
The tactical problem was programmed using the Operation Research’s language MATHPROG (a subset of AMPL) and solved using packages Rglpk (version 0.6-5.1) and Rsymphony (version 0.1-33) in the R system for statistical computing [45]. Both R packages provide a high-level interface to R for solving large-scale linear programming (LP) and mixed integer linear programming (MILP) problems based on GLPK and COIN-OR SYMPHONY solvers.
2.10. Sensitivity Analyses
Sensitivity analyses were carried out for each forest estate by changing interest rates (4, 6, 8% p.a.), yields (±50%, ±20% base condition), timber prices (±20% base condition), carbon prices (NZD 0, 35, 80, 160/t CO2), harvesting costs (1× and 2× those in Table 3), roading costs (1× and 2× those in Table 3) and whether primary roads were constructed just before planting or when harvesting starts. We also considered delaying harvesting by 5 years from year 35 to 40. During the sensitivity analysis everything else was kept constant (ceteris paribus), changing one value at the time and recording the effect on the optimization run.
3. Results
3.1. Strategic Planning
We applied the strategic model described in Section 2.7 to Blue Mountain and Spring Creek using a guiding rate of return of 6% p.a. The model was run for 300 years with timesteps of 5-year periods (60 periods). The model maximized the net present value (NPV), subject to non-declining carbon stock, timber yield not changing by more than 10% from one period to the next, minimum harvest age of 35 years and forest cover greater than 50% for stands with age ≥ 20 years after year 35 along the planning horizon.
We found that under transition (years 0–150) and steady-state conditions (years 150–300), both Blue Mountain and Spring Creek represent excellent investment opportunities (Table 4). The forest cover for areas over 20 years old were on average 71% and 72%, respectively, for the transition and steady-state of both properties, although during transition for some periods, forest cover was lower but always >50%. At the forest estate level, carbon stocks after year 40 were on average 1265 and 1683 t CO2/ha for Blue Mountain and Spring Creek, respectively, and remained relatively constant thereafter. Wood flow was relatively even (provided that it could vary ± 10% from one period to the next) but less variable during steady state conditions. The internal rate of return was very competitive for the forestry sector, being 8.5% and 9.9% under transition, for Blue Mountain and Spring Creek, respectively. The IRRs were extremely high under the steady-state (39.5%, 43.4%) for both properties, which highlights that once a sustainable yield is achieved, owners could regularly cut a constant amount of high-value timber rendering the operation highly profitable.

Table 4.
Net present value (NPV), area cover ≥ 20 years-old after year 35 along the planning horizon, carbon stock, wood flow, and internal rate of return (IRR) under transition (years 0–150) and steady state (years 150–300) conditions for both Blue Mountain and Spring Creek redwood forest estates. Values in parentheses for area cover represent the range observed in values.
Carbon accumulated over the first 35 years during which time there was no harvesting for both properties. Harvesting started at year 35 along the planning horizon, and during the next 60 years all areas planted were harvested and naturally re-established using a second-rotation coppice (Table 5). Over the period 35–95 years along the planning horizon, the harvested area per period declined, yet timber flow remained relatively stable while carbon stocks stayed mostly constant (Table 5).

Table 5.
Area harvested, timber flow and carbon stock during the 60 years following year 35 along the planning horizon when harvesting started at for both properties: Blue Mountain (108.9 ha) and Spring Creek (467.2 ha). The steady-state (years 150–300) values for these three variables are also shown.
The steady-state area being harvested for each 5-year period was about 7.6 and 32.8 ha, or about 7% of the total forest area per period for both Blue Mountain and Spring Creek, respectively (Table 5). We can deduce from these figures that the optimal rotation was about 71 years for both properties. The steady-state timber flow was ca. six-fold higher for Spring Creek than Blue Mountain, as the former property had a higher productivity and was ca. four-fold larger than the latter. Carbon stock steadily increased to approximately even out after year 45 (period 9) for both properties, although timber flow progressively varied less to even out after year 150. The steady-state carbon stock was 5.7 times greater in Spring Creek (786,340 t CO2) than Blue Mountain (137,755 t CO2). An expanded view of timber flow and carbon stock over 300 years can be seen in Figure 4.
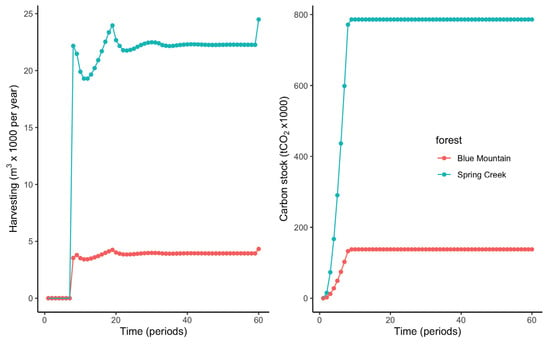
Figure 4.
Timber flow and carbon stock over the strategic planning horizon for Blue Mountain and Spring Creek redwood forest estates. Time was aggregated into periods of 5-years with the 60 periods covering 300 years.
The timber flow was permitted to vary by ±10% between periods. From period 59 to 60, there is a sharp 10% increase in timber flow for both properties, which remains within the model’s constraints (Figure 4). This peak arises because the model is not bound by harvest volume requirements in period 61, as the planning horizon concludes at period 60. As a result, the model maximizes harvest in the final period. This increase in volume is also reflected in higher net income for that period (Figure 5). However, the impact on overall profitability is negligible, as discounting income 300 years into the future at a 6% rate renders it virtually insignificant.
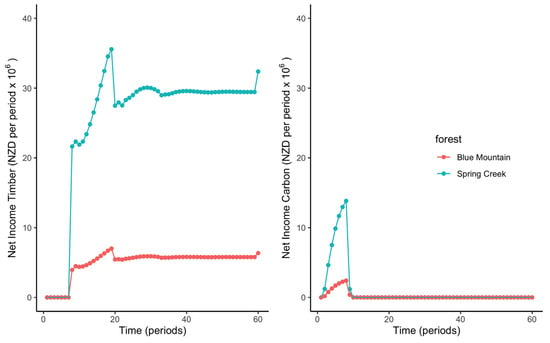
Figure 5.
Net income per period derived from timber harvesting (left) and carbon credits (right). Time was aggregated into periods of 5-years with the 60 periods covering 300 years.
The net income for timber over time followed a similar pattern to the timber flow for both properties, stabilizing at around 5.79 and 29.45 million NZD per period (5 years) after year 150 (period 30) for Blue Mountain and Spring Creek, respectively (Figure 5, left). Net income from carbon credits steadily increased until year 35–40 (period 8) and then dropped to zero beyond year 45 (period 9). Revenue from carbon peaked at period 8, at 2.42 and 13.84 million NZD for that period, respectively, for Blue Mountain and Spring Creek (Figure 5, right). Hence carbon was the only source of income during the first 35 years after planting while timber was the only source of income following year 40. During period 35–40, carbon income peaked and timber income started.
Our results demonstrate the economic viability of managing redwood under a continuous cover forestry (CCF) regime and show how early carbon income can help fund the transition to a steady-state forest, generating a sustained supply of high-value timber with a very high return on investment.
3.2. Tactical Planning
3.2.1. Profit, Timber and Carbon Flows
Final NPVs were 23,573 and 35,180 NZD/ha while IRRs were 9.16% and 10.40%, for Blue Mountain and Spring Creek, respectively (Figure 6). These values were very similar to the results obtained for the strategic transition-state NPVs (Table 4) which were 21,625 and 34,144 for Blue Mountain and Spring Creek, respectively. Similarly, the allowable cut for the tactical level were in the range for the transition-state at the strategic level, i.e., 3673 ± 142 m3 yr−1 was in the range [3419–4329 m3 yr−1] for Blue Mountain and 20,763 ± 546 m3 yr−1 was in the range [19,294–24,490 m3 yr−1] for Spring Creek. Carbon stock at the tactical level remained relatively constant at 119,830 ± 5253 t CO2 and 701,307 ± 28,463 t CO2 for Blue Mountain and Spring Creek, respectively; being very similar to the carbon stock accumulated up to year 35, i.e., 120,552 and 701,267 t CO2 (Figure 6).
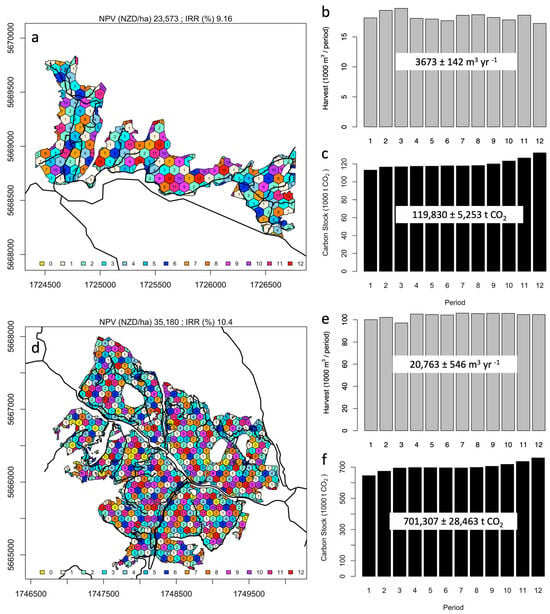
Figure 6.
Tactical spatially explicit harvest scheduling for Blue Mountain (above) and Spring Creek (below). Shown in (a,d) is the spatial distribution of harvested coupes, which were felled over the planning horizon while (b,e) shows variation in wood flows and (c,f) carbon stock. The planning horizon comprises 12 periods (60 years) from period 1 (0–5 years) when the plantation was 35–40 years old to period 12 (55–60 years) when the oldest plantations were 90–95 years old. In (a,d) different colors and numbers within hexagons represent different harvesting periods from 1 to 12. Units in yellow and “0” within the unit means that the unit was not harvested along the planning horizon. CRS: NZGD2000/New Zealand Transverse Mercator 2000.
3.2.2. Adjacency Constraints
We divided both forest estates into a grid of 0.7 ha hexagons with a total of 229 units for Blue Mountain and 849 units for Spring Creek. Some units were less than 0.7 ha as they were cut by the boundary of the properties. Each 0.7 ha unit can be either harvested along the tactical planning horizon or left unharvested. The tactical model maximizes the net present value (NPV) based on timber production subject to even flow constraints with upper and lower boundaries extracted from the strategic planning (Table 4). The carbon stock was kept relatively constant as a consequence of limiting the timber flow (Figure 6). We also imposed adjacency constraints which prevents two adjacent units being harvested during the same period, which only marginally reduced profitability by <0.4% of the NPV compared to the run without adjacency constraints. This marginal reduction in profitability is likely due to the uniform age and productivity of all units, which provided sufficient flexibility to meet green-up constraints.
3.2.3. Age Difference Between Adjacent Units
Since most units will be harvested within the planning horizon, we assessed the extent to which harvesting one unit may delay the harvesting of its neighboring units—specifically for at least five years, which was the time required for coppice to reach a height of 5 m. To do this we calculated the difference in harvesting periods between adjacent units. For instance, if a particular unit is scheduled to be harvested in period 6, while its neighbors are scheduled in periods 1, 2, 3, 4, 7 and 9, the respective differences in harvest timing are 5, 4, 3, 2, 1 and 3 periods. Given that each period spans 5 years, in this example there are at least 5 years that have passed between the harvest of a unit and that of any adjacent unit.
The histograms of age differences between pairs of adjacent units for both properties (Figure 7) show that the minimum time between adjacent harvestings is 5 years while the maximum is 60 years, with an average of 20.7 years for Blue Mountain and 21.7 years for Spring Creek. It is worth noting that this strategy ensures that in any given hectare, a maximum of 0.7 ha will be clear felled while the remaining 0.3 ha will be at least 5 years of age, which easily meets the current New Zealand definition of a permanent carbon forest.
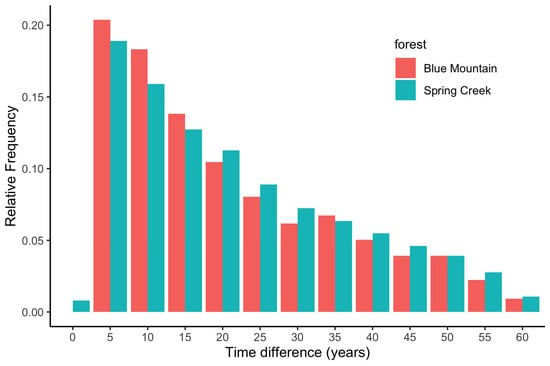
Figure 7.
Histograms of age differences between all coupes and their neighbors for Blue Mountain and Spring Creek.
3.2.4. Roads First Policy
Redwood managers raised the question whether it was feasible to harvest units close to roads first, leaving units that will be harvested many years into the future with road construction pending, which we called a “roads-first-policy”. To this end, we applied a buffer around roads—100 m for highways and 50 m for internal roads—which we intersected with the centroids of all 0.7 ha units. We then arbitrarily prioritized the intersecting units by doubling the values of NPV per ha in the objective function. However, once the optimization problem was solved we recalculated the global NPV using the original (non-doubled) NPVs for units near roads to ensure consistency with the prior condition. The resulting difference in global NPV was marginal, being less than 1.6%. The approach was considered reasonable by managers outperforming the alternative without a ‘roads-first policy’, leading to its adoption. This can be observed from the harvest scheduling presented in Figure 6, where the blue palette comprises the first six periods (0–30 years) while the red palette comprises the second half of the tactical planning periods (30–60 years). From this figure it can be seen that units in the blue range are generally clustered around roads while units in the red are more distant from roads.
3.2.5. Unharvested Coupes
The tactical model does not require all units to be harvested within the planning horizon, as doing so could render the problem infeasible. In the case of Blue Mountain (Figure 6a), all units were harvested. In contrast, for Spring Creek (Figure 6d), 28 out of 849 units—covering 14.6 hectares or 3.1% of the area—remained unharvested (shown in yellow and labeled “0” in Figure 6). These stands will be 90–95 years old at the end of the tactical horizon and are likely to be prime candidates for harvest in the subsequent planning period.
3.2.6. Coupe Shape
Hexagon-shaped 0.7 ha units were adopted for all the previous analyses, although there are some other possibilities such as square (83.7 m each side) and rectangular units (35 × 200 m). We found results using squares and rectangles were nearly identical to those obtained with hexagons, with NPV differing by no more than 1.4%. Based on discussions with redwood managers, we concluded that hexagonal units are preferable to squares or rectangles, although we acknowledge that this choice remains open to further discussion.
3.2.7. Sensitivity Analysis
The sensitivity analysis (Table 6) showed that even under the most pessimistic conditions managing redwood was highly profitable (NPVs > 283 NZD/ha, IRRs > 6.0%). As expected, profitability of the higher productivity Spring Creek was greater than that observed for the lower productivity Blue Mountain under all scenarios. The guiding interest rates (4%, 6%, 8%), which are commonly used to assess forestry projects (4.0%–9.2%, average 7%) [46], strongly influenced profitability although NPVs were always positive.

Table 6.
Sensitivity analysis showing variation in NPV and IRR for Blue Mountain and Spring Creek as a function of changes in key variables.
Carbon price was the most influential factor on profitability. At a base carbon price of NZD 80/t CO2, NPVs were 23,573 and 35,180 NZD/ha while IRRs were 9.16% and 10.40% for Blue Mountain and Spring Creek, respectively. The timber-only regimes (NZD 0/t CO2) exhibited the lowest NPV (283 NZD/ha) and IRR (6.04%). The minimum value for auctioned carbon scenario (NZD 35/t CO2), exhibited NPVs about half those for the base condition, while those NPVs for the upper carbon value (NZD 160/t CO2) were about twice those of the base condition. The highest IRRs (12.06% for Blue Mountain and 13.83% for Spring Creek) among all factors studied in Table 6 were found under this upper carbon value (NZD 160/t CO2).
Timber yield was the second most influential factor on profitability. As expected, moderate (+20%) to high (+50%) increases in productivity, substantially improved profitability, with IRRs increasing from the base condition to a 50% productivity increase by about 2%. From a risk analysis perspective, however, reductions in volume are more relevant. Moderate (−20%) decreases in productivity resulted in NPVs greater than 15,114 NZD/ha (IRRs > 8.22%). Even when timber yield was reduced by 50% profitability was still relatively high (NPVs > 2424 NZD/ha, IRR > 6.43%) (Table 6). It is worth noting that timber and carbon yield are coupled and therefore the sensitivity analysis for this factor considers both, which accounts for the strong impact of this factor. Timber price exhibited a smaller influence on profitability than timber yield, although this factor was still quite influential (Table 6). The greater importance of carbon price compared to timber price is strongly influenced by the fact that carbon revenue accrues earlier in the rotation (years 0–35) than timber revenue (years 35 onwards) and therefore has more influence on discounted cash flows.
The harvesting and roading cost had relatively little impact on profitability. Even when harvesting cost was doubled from 91 to 182 NZD/m3 (ground-based harvesting, Blue Mountain) and from 121 to 242 NZD/m3 (cable-based harvesting, Spring Creek) the effect on NPVs and IRRs were relatively small (Table 6). The impact of increasing road cost had even less impact. In the base condition, all roads were assumed to be constructed at year 35, and when the cost was doubled the effect on NPV and IRR was relatively marginal. However, profitability dropped drastically from the base condition in which all roads were constructed at year 35, to the condition when primary roads were paid up front (year 0) and secondary roads at year 35, although the impact on Spring Creek was less evident (Table 6).
Delaying the start of harvesting by 5 years from ages 35 to 40 years old had very little impact on profitability (Table 6). However, it is worth noting that a higher level of carbon stock could be achieved by this action, i.e., 119,830 vs. 133,234 t CO2 (11.2%) for Blue Mountain and 701,307 vs. 762,614 t CO2 (8.7%) for Spring Creek. Given the potential condition that carbon price increases, small owners could decide when the plantation is 35 years old whether to start harvesting or to postpone by 5 years to store that extra carbon, before harvesting starts.
4. Discussion
The management of redwood plantations under continuous-cover forestry (CCF) has been shown to be highly profitable particularly in the North Island of New Zealand [24]. Our research hypothesis about the operational feasibility of managing redwood forests by harvesting 0.7 ha coupes under a CCF regime was confirmed. The IRRs were 9.16 and 10.40% p.a. for Blue Mountain and Spring Creek, respectively, which exceed those considered to be robust IRRs for radiata pine and other forest species (Douglas-fir, eucalypts and blackwood) in New Zealand [47]. The same authors reported an average IRR of 9.3% for redwood plantations managed under clearcut regimes in New Zealand.
A key advantage of managing redwood plantations under a CCF regime is the ability for small-scale owners to generate substantial and continuous annual income by harvesting small 0.7 ha coupes starting from age 35. This contrasts with species such as radiata pine, which typically require the harvesting of larger stands at longer intervals. For instance, at Blue Mountain about 3673 m3 will be harvested annually, over ages 35–95 years, according to the tactical modeling. Considering a net price of about NZD 299/m3 (price 390 NZD/m3 at age 70, minus a variable cost of 91 NZD/m3) that would amount to about 1,098,227 NZD/year from only 108.9 ha. For Spring Creek, about 20,763 m3 will be harvested per year, over ages 35–95 years, which at a net price of NZD 269/m3 (price 390 NZD/m3 at age 70, minus variable cost of 121 NZD/m3) would amount for 5,585,247 NZD/year from only 467.2 ha. These figures highlight the strong financial returns achievable through the steady harvesting of small, high-value coupes under a redwood CCF system.
An interesting finding of this study was that the optimal rotation length exceeded that typically used in New Zealand for redwood managed under clearcutting regimes. Previous research [47] proposed a silvicultural regime for redwood involving an initial planting density of 800 stems/ha, followed by up to three pruning lifts and one thinning to a final stand density of 350 stems/ha, with a rotation length of 35 years. However, strategic and tactical modeling, accounting for both timber and carbon income, indicated an optimal rotation length of approximately 71 years. Adopting a shorter rotation (i.e., 35 years) would result in a lower steady-state carbon stock and potentially trigger the repayment of carbon credits. Consistent with our findings, [48] suggest that the optimal rotation for second-growth redwood stands lies between 60 and 80 years, and these older ages are associated with superior wood quality, with higher heartwood content [49].
The coupe size used in our study was generally consistent with those previously reported for redwood. Silvicultural systems for redwood in California are grouped into even-aged (clearcuts) and uneven-aged (selection cuts) with both producing heterogeneous landscape patterns, where the group selection system consists of small clearcuts of 0.04–1.2 ha [48]. Similarly, our proposed system for redwood plantations in New Zealand consists of harvesting small 0.7 ha coupes which are spread across relatively small properties (100–500 ha). A previous study [50] argues that smaller coupes of less than 0.25 ha should be used under continuous cover forestry, but when redwood experts were consulted, they suggested that such small coupes would not be operationally feasible for New Zealand. Additionally, although redwood trees continue to grow and develop rapidly even after crown closure [48], the species grows most rapidly under large openings [51], that have at least 50% of the above canopy light [19], with this threshold easily achieved using a coupe size of 0.7 ha [52].
The coupe shape did not show any influence on profitability, timber and carbon flows. For tactical planning, group clearcuts were defined using hexagonal units, which can be operationally approximated by harvesting a cluster of adjacent trees covering approximately 0.7 ha in a roughly circular shape. Following thinning at age 11, stand density is reduced to 450 trees/ha, resulting in an expected density of around 315–325 trees/ha by the end of the rotation (~71 years). At this density, a 0.7 ha unit would contain approximately 224 trees. Thus, knowing the UTM coordinates of the centroids of each 0.7 ha unit, should be sufficient to locate that point in the field and from that point draw a circle with an imaginary radius of 47.2 m from which 224 trees will be harvested. The trees harvested per coupe would have a recoverable volume of 630–869 m3 if harvested at age 35 and 1862–2450 m3 if harvested at age 70. The tactical model was also run using square (83.7 m sides) and rectangular (35 × 200 m) coupes, yielding results that were nearly identical to those obtained with hexagons. This indicates that alternative shapes—such as ridge-to-gully rectangular coupes—could be readily integrated into operational planning at no extra cost.
Adjacency constraints prevent contiguous units being harvested at the same time so that the maximum size of clearcuts does not exceed statutory or policy limits [29]. These constraints are now being routinely used in harvest scheduling planning for erosion control, biodiversity conservation and reducing the negative impacts of storms on forests, among others [29,41,42,53]. We found that imposing green-up constraints on the continuous-cover management of redwood had a marginal effect on profitability (<0.4% in NPV). Similarly, Ref. [54] using a 5-year exclusion period for a 500 ha forest in Japan, resulted in a small reduction in NPV (0.96%) compared to a no exclusion period. Consistent with our study, Ref. [29] suggested that common time lags for harvesting adjacent clear cuts of redwood forests in California are 4 years. In our case we set the lag to 5 years, which is the time considered necessary for coppice to reach a height of 5 m, which conservatively aligns with New Zealand ETS legislation.
Harvesting small 0.7 ha coupes spread over the landscape might impose operational constraints dictated by the terrain. Slopes up to 30–40% are generally considered as feasible for ground-based systems while cable-based systems are able to work at greater slopes [25,26,27]. However, ground-based systems have also been employed on steeper country while operating from off contour roads spaced up to 100 m apart [50]. At Blue Mountain, 66% of the area had slopes below 30%, and 78% below 40%, suggesting that ground-based harvesting systems are likely to be feasible across most of the estate. In contrast, 77% of Spring Creek exceeded a 30% slope, indicating that cable-based harvesting systems would be required. Given the hexagonal shape of the coupes, ground-based harvesting methods typically involve dragging logs through the stand to the nearest road. In cases where ridges and spurs can be tracked, ground-based systems may be extended to steeper areas; otherwise, cable-based systems will be required [50]. Skylines set at ridges are routinely used to harvest small coupes under CCF in broken terrain in Europe, although this method is generally limited to distances of 300–500 m [55]. These ridge-to-ridge distances are well within reach for both Blue Mountain and, in particular, the more dissected terrain of Spring Creek. The above suggests that detailed operational planning would be needed to harvest small 0.7 ha coupes particularly in broken terrain although difficulties are not unsurmountable.
The large piece size resulting from the extended rotation age under the CCF regime may pose operational challenges. The tactical planning shows that all first rotation crop will be harvested within 60 years (ages 35–95), with regeneration by coppice. The mean diameter at breast height (dbh) size range over these ages ranges from 62 to 118 cm in Blue Mountain and 68–133 cm in Spring Creek. Experts argue that up to age 50 the piece sizes are easily manageable (77–84 cm in dbh) but that after that harvesting and logging would be more difficult although still feasible. Difficulties can arise specifically in the mechanized felling of trees. Fully mechanized tree harvesting is generally limited to trees with a dbh of 60–80 cm, depending on the machine type. Feller bunchers typically handle trees up to 60–65 cm dbh, with productivity and safety declining near the upper limit. Cut-to-length harvesters, particularly larger models used for final felling of conifers, can process trees up to 75–80 cm dbh, though performance and efficiency decrease at these extremes. Trees exceeding these thresholds often require manual felling or specialized equipment. However, in the short term, a sensitivity analysis of costs indicates that shifting to motor-manual felling is feasible. While this method is more expensive, it allows larger trees to be harvested. The analysis clearly shows that, despite higher harvesting costs, the economic viability of redwood plantations managed under a CCF regime remains unaffected.
Continuous cover forestry would generally require a higher road density than forests under rotational clearfell regimes [50]. The road density in our case study was in the range 155–186 m/ha. As expected, these values are much higher than the average of 25.2 m/ha (range 0 to 52.8 m/ha) for small-scale clearfelled radiata pine plantation forests (woodlots) in New Zealand [56]. However, in the alpine region of Europe, where CCF is more widely practiced, higher road densities of 38–51 m/ha are required to reduce extraction distances and minimize cable logging costs [57,58]. Despite the high density of our roading system the sensitivity analysis shows that the effect of a doubling of the roading cost was marginal on the profitability of redwood CCF. This insensitivity was attributable to the high timber value, high timber volume and the fact that the roading cost was discounted 35 years.
In tactical planning, prioritizing harvesting areas near existing roads is a common strategy to minimize road construction, transportation and streamline harvest operations [59]. In our study we implemented a “roads-first-policy” by doubling the selection priority for units located within a 50 m buffer of primary roads, with additional emphasis placed on units scheduled for earlier harvest. As a result, most units harvested during the initial periods were clustered near existing roads, while those scheduled for later harvest were generally located farther away. The implementation of this policy incurred a marginal cost of less than 1.6% of the net present value (NPV) compared to the condition without it, which was deemed to be acceptable by redwood managers.
Several potential limitations of this study warrant further investigation. Firstly, although redwood is shade-tolerant [7], there is uncertainty regarding whether coppice shoots will suffer from shading by surrounding mature trees. This could potentially reduce carbon accumulation and hinder regeneration across significant portions of the coupe, particularly the most shaded areas along the coupe edge. Nevertheless, past research generally supports our assumption that 0.7 ha coupes will not be unduly impacted by shade [19,52,60], and future studies should examine the resprouting success of redwood coppices, and growth rate of young trees, within coupes bordered by trees with a range of heights. Second, tactical planning on steep terrain may require modifications to coupe size and shape to ensure cost-effective operation of cable-based harvesting systems. While the high timber volume of redwood suggests that even small 0.7 ha coupes could yield enough to justify cable-based extraction, this assumption should be validated in operational settings. Thirdly, the generation of a potential road network based on extensions from existing primary roads likely overestimates the required length and cost of secondary and spur roads. Our model assumed a road density which exceeds those used in clearfell regimes in New Zealand [56] and even within European studies where CCF is more widely practiced [57,58]. However, higher road density may be justifiable under CCF systems [50]. Importantly, sensitivity analysis showed that even doubling the roading cost had a limited effect on overall profitability, reducing the internal rate of return (IRR) only slightly—from 9.16% to 8.92%. Finally, all the simulations were made under the current climate, which we are aware is an oversimplification.
Land use change from agriculture to forestry is currently a topic of active debate in New Zealand, particularly due to its potential implications for emerging carbon market needs under the New Zealand Emissions Trading Scheme (ETS) [61]. Estimates suggest there are approximately 1.2 million hectares of marginal or unproductive agricultural land suitable for afforestation [62]. Future afforestation is expected to occur primarily on former sheep and beef farming land, especially in areas with low grass productivity or terrain too steep for dairy farming [63]. Exotic forests are commonly established on Land Use Capability (LUC) classes 6 and 7—land also traditionally used for sheep and beef farming. However, afforestation must comply with the National Environmental Standards (NES) (https://www.environmentguide.org.nz/rma/planning-documents-and-processes/national-environmental-standards/, accessed on 28 June 2025) and the Resource Management Act (1991) (https://www.legislation.govt.nz/act/public/1991/0069/latest/DLM230265.html, accessed on 28 June 2025), which together form the core framework for sustainable land use planning in New Zealand. These regulations may constrain afforestation in certain areas to ensure the sustainable management of natural and physical resources [64]. While sheep and beef farming may at times compete with forestry, robust institutional frameworks and legislation help balance competing land uses to achieve New Zealand’s broader social, environmental, and economic sustainability goals.
Our model, while currently theoretical and not yet field-tested, suggests that the proposed management approach is financially attractive for high-productivity, high-value timber species like redwood. We predict that harvesting small coupes (approximately 0.7 hectares), with a minimum five-year green-up period, would likely be more ecologically and socially acceptable than large clearcuts. This is supported by evidence that smaller harvest patch sizes enhance wildlife habitat, biodiversity, and landscape aesthetics [65]. In addition, we anticipate this approach would be perceived as superior to other alternatives by a relevant segment of society [66].
5. Conclusions
The results from the tactical spatially explicit planning were consistent with the results from the strategic planning. The profitability of redwood plantations under continuous-cover forestry for both properties under study was highly competitive, with IRRs of 9.16 and 10.40% p.a. for Blue Mountain and Spring Creek, respectively. The study showed that small owners could benefit from carbon revenue during the first 35 years after planting and then switch to a steady annual income from timber maintaining a relatively constant carbon stock. Analyses showed the steady-state rotation length to be 71 years.
Among all factors, carbon price had the greatest influence on profitability under CCF. IRRs increased progressively with rising carbon prices, from 6.04% at NZD0/t CO2, to 7.35%, 9.16%, and 12.06% at NZD35, NZD80, and NZD160/t CO2, respectively. Imposing green-up constraints, a “roads-first-policy”, and different coupe shapes (hexagons, squares and rectangles) only marginally impacted profitability, timber flow or carbon stock compared to the base situation without these conditions. While harvesting and roading costs have historically been cited as key barriers to CCF, our sensitivity analysis shows that for high-productivity high-value species such as redwood, these costs, though influential, are less prohibitive than previously assumed.
Author Contributions
Conceptualization, M.S.W. and H.E.B.; methodology, H.E.B. and M.S.W.; software, H.E.B. and M.S.W.; validation, H.E.B. and M.S.W.; formal analysis, H.E.B. and M.S.W.; investigation, H.E.B. and M.S.W.; resources, M.S.W. and H.E.B.; data curation, M.S.W. and H.E.B.; writing—original draft preparation, M.S.W., H.E.B., F.L. and R.P.; writing—review and editing, M.S.W., H.E.B., F.L. and R.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was mainly supported by the Scion Strategic Science Investment Fund (SSIF). This work was also supported by the statutory research fund of Institute of Dendrology, Polish Academy of Sciences and by the Italian Ministry for Education, University and Research (MIUR) for financial support (Law 232/2016, Italian University Departments of Excellence 2023\u20132027) project\u201C Digitali, Intelligenti, Verdi e Sostenibili (D.I.Ver.So)\u2014UNITUSDAFNE WP3\u201D).
Data Availability Statement
The growth measurements used to develop the model are proprietary data owned by forestry companies and are not publicly available. However, the growth model itself, along with its outputs, can be provided upon request to interested parties.
Acknowledgments
The authors gratefully acknowledge the expert advice of Rien Visser, Rob Webster, Paul Silcock, and Mark Dean, whose insights were invaluable in aligning the tactical planning for Blue Mountain and Spring Creek with practical, on-the-ground realities.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Methods for Selecting Potential Roads and Skid Tracks
The optimal roading network to access stands to be harvested can be approached based on the minimum spanning tree algorithm [39]. This algorithm looks for the shortest route within a network, as the one formed connecting all coupes (0.7 ha) within the Blue Mountain and Spring Creek forest estates. The centroid within each coupe is called a node while the link between two adjacent nodes is called an arc. Weights or penalties could be assigned to each arc, e.g., distances or costs. Then, the algorithm searches for the route connecting all nodes with the minimum sum of weights or penalties. In our case we used road maintenance or construction costs.
The optimal route builds on the current road network (Figure A1) so that existing roads should be maintained and new roads constructed. We started by drawing highways and primary (internal) roads within or close to Blue Mountain and Spring Creek, composing a buffer around highways (50 m) and primary roads (25 m). Then we intersected the centroids of each 0.7 ha coupe against the road buffer. For the arcs (connection between two nodes) fully contained within the buffer we assume a very low penalty (100 penalty units), which would be a surrogate for a road maintenance cost.
For arcs outside the buffer we assumed a penalty (or construction cost) equal to: distance × (15 + 90 |slope|), where slope is equal to the tangent of the inclination angle, being a value generally between 0 and 1 (e.g., 14% is 0.14 to be used in the formula). Therefore, if the arc was located in flat terrain the construction cost would be 15 penalty units/m while for 14% slope it would be 27.6 penalty units/m. For instance, for a 50 m arc within flat terrain the penalty would be 750 penalty units while for the same distance with a 14% slope the penalty would be 1380 penalty units. For arcs with one node within the buffer and the other node outside the buffer we assume a lower construction cost equal to the one when the arcs are outside the buffer divided by two, i.e., [distance × (15 + 90 |slope|)/2]. Also for the steeper terrain Spring Creek compared to Blue Mountain, we set a 25 m buffer around ridges, and for the arcs fully contained within those ridges we also used a penalty equivalent to: [distance × (15 + 90 |slope|)/2]. Such a strategy ensured that the optimal route would: (1) use existing roads, (2) give preference to road construction on ridges in Spring Creek and (3) choose arcs outside roads and ridges with lower slopes.
Through using the minimum spanning tree algorithm with cost penalties, new potential roads and skid tracks were projected to access all 0.7 ha units. Once the optimal network was selected, we used the historical cost of roading to make all calculations (137,091 NZD/km for primary roads and half that value for secondary roads and skid tracks) as presented in Table A1. For Blue Mountain, the network increased from the current 10,517 m to 20,258 m at a total cost (including cost of current road network) of 2,109,494 NZD, equivalent to 19,371 NZD/ha and 8.88 NZD/m3. For Spring Creek, the network increased from the current 20,446 m to 72,528 m at a cost of 6,372,969 NZD, equivalent to 13,641 NZD/ha and 4.85 NZD/m3 (Table A1). Figure A2 shows the potential road network for Blue Mountain and Spring Creek.
Figure A1.
Digital elevation model (DEM), contours, highway (red lines), internal roads (blue lines) and boundaries (white lines) for Blue Mountain (above) and Spring Creek (below). CRS: NZGD2000/New Zealand Transverse Mercator 2000. UTM coordinates and contour lines in meters.
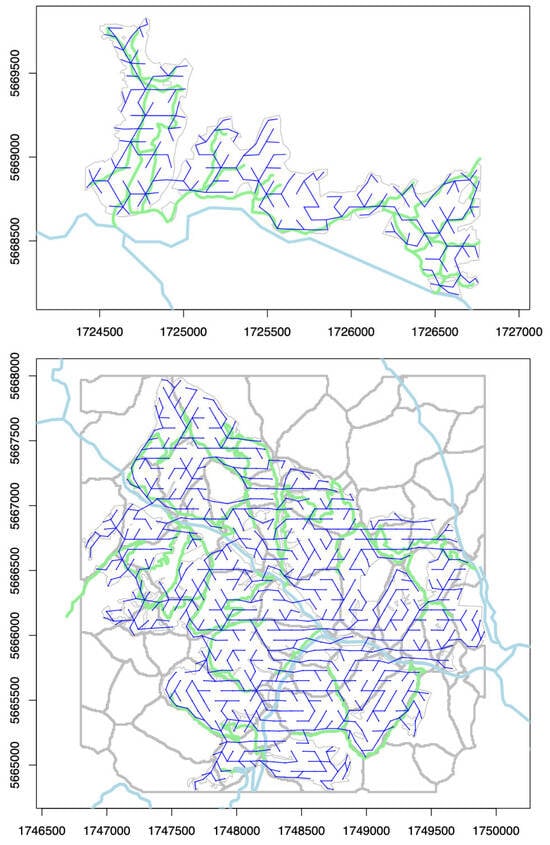
Figure A2.
Current and potential road and skid network for (top) Blue Mountain (108.9 ha) and (bottom) Spring Creek (467.2 ha). The current road network comprises the highway (light blue) and internal roads (light green). The potential road and skid network are shown as straight lines (dark blue) joining the centroids of all 0.7 ha units. Gray lines show ridges for Spring Creek.

Table A1.
Primary and secondary road metrics for Blue Mountain and Spring Creek.
Table A1.
Primary and secondary road metrics for Blue Mountain and Spring Creek.
| Metric | Units | Blue Mountain | Spring Creek |
|---|---|---|---|
| Area | (ha) | 108.9 | 467.2 |
| Primary Roads | (km) | 10.517 | 20.446 |
| (NZD) | $1,441,791 | $2,802,971 | |
| Secondary Roads | (km) | 9.741 | 52.082 |
| (NZD) | $667,704 | $3,569,998 | |
| All roads | (km) | 20.258 | 72.528 |
| (NZD) | $2,109,494 | $6,372,969 | |
| (NZD/ha) | $19,371 | $13,641 | |
| Timber harvested over 60 yrs | (m3) | 237,537 | 1,313,896 |
| (NZD/m3) | 8.88 | 4.85 |

Table A2.
Variation in at mill gate (AMG) redwood log values by log type (pruned, unpruned) and small end diameter (SED) class.
Table A2.
Variation in at mill gate (AMG) redwood log values by log type (pruned, unpruned) and small end diameter (SED) class.
| SED | Log Values (NZD/m3) | |
|---|---|---|
| Class (cm) | Pruned | Unpruned |
| 10 | - | 51 |
| 20 | - | 153 |
| 30 | 295 | 167 |
| 40 | 428 | 242 |
| 50 | 460 | 274 |
| 60 | 515 | 330 |
| 70 | 609 | 423 |
| 80 | 611 | 425 |
| 90 | 614 | 428 |
| 100 | 614 | 428 |
References
- Sillett, S.C.; Van Pelt, R.; Carroll, A.L.; Campbell-Spickler, J.; Antoine, M.E. Aboveground Biomass Dynamics and Growth Efficiency of Sequoia Sempervirens Forests. For. Ecol. Manag. 2020, 458, 117740. [Google Scholar] [CrossRef]
- Earle, C.J. Sequoia sempervirens. The Gymnosperm Database. Available online: https://www.conifers.org/cu/Sequoia.php (accessed on 17 April 2025).
- Brown, J.E. Monarchs of the Mist: The Story of Redwood National Park and the Coast Redwoods; Redwood Natural History Association: Pyrmont, Australia, 1982. [Google Scholar]
- Bain, J.; Nicholas, I. Health. In Best Practice with Farm Forestry Timber Species; Nicholas, I., Ed.; NZFFA Electronic Handbook Series No. 3; New Zealand Farm Forestry Association: Wellington, New Zealand, 2008. [Google Scholar]
- Rapley, S. Redwood in New Zealand. N. Z. J. For. 2018, 63, 29–33. [Google Scholar]
- Jacobs, D.F.; Cole, D.W.; McBride, J.R. Fire History and Perpetuation of Natural Coast Redwood Ecosystems. J. For. 1985, 83, 494–497. [Google Scholar] [CrossRef]
- Olson, D.F.; Roy, D.F.; Walters, G.A. Sequoia sempervirens (D. Don) Endl. Silv. N. Am. 1990, 1, 541–551. [Google Scholar]
- Stuart, J.D. Fire History of an Old-Growth Forest of Sequoia sempervirens (Taxodiaceae) Forest in Humboldt Redwoods State Park, California. Madrono 1987, 34, 128–141. [Google Scholar]
- Knowles, F.B.; Miller, J.T. Introduced Forest Trees in New Zealand: Recognition, Role, and Seed Source; FRI Bulletin N°124, Part 13: Rotorua, New Zealand, 1993. [Google Scholar]
- Burns, E.; Campbell, R.; Cowan, P.D. State of Redwoods Conservation Report; Save The Redwoods League: San Francisco, CA, USA, 2018. [Google Scholar]
- Arnaud, Y.; Franclet, A.; Tranvan, H.; Jacques, M. Micropropagation and Rejuvenation of Sequoia sempervirens (Lamb) Endl: A Review. Ann. Des. Sci. For. 1993, 50, 273–295. [Google Scholar] [CrossRef][Green Version]
- Breidenbach, N.; Gailing, O.; Krutovsky, K.V. Genetic Structure of Coast Redwood (Sequoia sempervirens [D. Don] Endl.) Populations in and Outside of the Natural Distribution Range Based on Nuclear and Chloroplast Microsatellite Markers. PLoS ONE 2020, 15, e0243556. [Google Scholar] [CrossRef]
- Toral, M.; Caru, M.; Herrera, M.A.; Gonzalez, L.; Martin, L.M.; Miranda, J.; Navarro-Cerrillo, R.M. Clones Identification of Sequoia sempervirens (D. Don) Endl. in Chile by Using PCR-RAPDs Technique. J. Zhejiang Univ. B 2009, 10, 112–119. [Google Scholar] [CrossRef]
- Forest Growers Research. The Specialty Wood Products Research Partnership: Final Report 2015–2023; Forest Growers Research: Rotorua, New Zealand, 2023. [Google Scholar]
- Watt, M.S.; Kimberley, M.O. Spatial Comparisons of Carbon Sequestration for Redwood and Radiata Pine Within New Zealand. For. Ecol. Manag. 2022, 513, 120190. [Google Scholar] [CrossRef]
- Peters, T.; Hardaker, A.; Dauksta, D.; Newman, G.; Lellig, C.; Healey, J. Top Five Alternative Conifer Tree Species in Great Britain; GSR Report C160/2020/2021; Welsh Government: Cardiff, Wales, 2021.
- Brown, I.; Low, C.; McConnochie, R.; Nicholas, I.; Webster, R. Chapter 3: Site Selection. In Best Practice with Farm Forestry Timber Species: N° 3 Redwoods; Nicholas, I., Ed.; NZFFA Electronic Handbook Series No. 3; New Zealand Farm Forestry Association: Wellington, New Zealand, 2008. [Google Scholar]
- Watt, M.S.; Kimberley, M.O.; Rapley, S.; Webster, R. A Spatial Comparison of Redwood and Radiata Pine Productivity Throughout New Zealand. N. Z. J. For. 2021, 66, 33–41. [Google Scholar]
- O’Hara, K.L.; Stancioiu, P.T.; Spencer, M.A. Understory Stump Sprout Development Under Variable Canopy Density and Leaf Area in Coast Redwood. For. Ecol. Manag. 2007, 244, 76–85. [Google Scholar] [CrossRef]
- Watt, M.S.; Kimberley, M.O.; Steer, B.S.C.; Neumann, A. Financial Comparison of Afforestation Using Redwood and Radiata Pine Under Carbon Regimes Within New Zealand. Trees For. People 2023, 13, 100422. [Google Scholar] [CrossRef]
- Manley, B. Impact of Carbon Price on the Relative Profitability of Production Forestry and Permanent Forestry for New Zealand Plantations. For. Policy Econ. 2023, 156, 103057. [Google Scholar] [CrossRef]
- Doda, B.; Wildgrube, T.; Borghesi, S.; Ferrari, A.; Heinrich, L. State-of-Play in International Carbon Markets in 2024. In EUI, RSC, Policy Brief, 2024/15; LIFE COASE—Collaborative Observatory for Assessment of the EU ETS; Florence School of Regulation: Florence, Italy, 2024. [Google Scholar]
- Ministry for the Environment. About the New Zealand Emissions Trading Scheme. Available online: https://environment.govt.nz/what-government-is-doing/areas-of-work/climate-change/ets/about-nz-ets/#about-the-nz-ets (accessed on 10 March 2025).
- Bown, H.E.; Watt, M.S. Financial Comparison of Continuous-Cover Forestry, Rotational Forest Management and Permanent Carbon Forest Regimes for Redwood within New Zealand. Forests 2024, 15, 344. [Google Scholar] [CrossRef]
- Mologni, O.; Grigolato, S.; Cavalli, R. Harvesting Systems for Steep Terrain in the Italian Alps: State of the Art and Future Prospects. Contemp. Eng. Sci. 2016, 9, 1229–1242. [Google Scholar] [CrossRef]
- Erber, G.; Visser, R.; Leitner, S.; Harrill, H.; Spinelli, R.; Picchio, R.; Varch, T.; Stampfer, K. Advances in Cable Yarding: A Review of Recent Developments in Carriers for Mobile Skyline Cable Yarding. Curr. For. Rep. 2025, 11, 14. [Google Scholar] [CrossRef]
- Leitner, S.; Spinelli, R.; Bont, L.G.; Vidoni, R.; Renzi, M.; Schweier, J. Technical, Safety and Environmental Challenges in the Electrification of Cable Yarding Equipment. Curr. For. Rep. 2023, 9, 263–275. [Google Scholar] [CrossRef]
- Watt, M.; Kimberley, M.; Steer, B. Evaluating the Potential for a Default Carbon Table for Redwoods and an Updated Default Table for the Exotic Softwoods Forest Type for Use in the ETS; New Zealand Government: Wellington, New Zealand, 2024.
- O’Hara, A.; Faaland, B.; Bare, B. Spatially Constrained Timber Harvest Scheduling. Can. J. For. Res. 1989, 19, 715–724. [Google Scholar] [CrossRef]
- Kimberley, M.O.; Watt, M.S. A Novel Approach to Modelling Stand-Level Growth of an Even-Aged Forest Using a Volume Productivity Index with Application to New Zealand-Grown Coast Redwood. Forests 2021, 12, 1155. [Google Scholar] [CrossRef]
- Watt, M.; Kimberley, M.; Steer, B.; Scholer, M. Carbon Sequestration Estimates for Minor Exotic Softwood Species for Use in New Zealand’s Emissions Trading Scheme. Forests 2025, 16, 598. [Google Scholar] [CrossRef]
- Watt, M.S.; Kimberley, M.O. Financial Comparison of Afforestation Using Redwood and Radiata Pine within New Zealand for Regimes That Derive Value from Timber and Carbon. Forests 2023, 14, 2262. [Google Scholar] [CrossRef]
- Ministry for Primary Industries. Managing Permanent Exotic Afforestation Incentives: Regulatory Impact Statement. Available online: http://www.mpi.govt.nz/news-and-resources/publications/ (accessed on 20 January 2025).
- Visser, R.; Obi, F. Benchmarking 2019 Data and Longer-Term Productivity and Cost Analyses; Report N° H045, Harvesting and Logistics Programme; University of Canterbury: Christchurch, New Zealand, 2020; pp. 1–22. [Google Scholar]
- Visser, R.; Abeyratne, H.; Spinelli, R. Productivity Benchmarks for Unguyed Excavator-Based Tower Yarders. Int. J. For. Eng. 2024, 35, 421–427. [Google Scholar] [CrossRef]
- Manley, B. Afforestation Economic Modelling. Final Report Prepared for Ministry for Primary Industries; New Zealand Government: Christchurch, New Zealand, 2021.
- Manley, B.; Morgenroth, J.; Visser, R. Quantifying the Small-Scale Owners’ Estate in Canterbury, Otago and Southland. N. Z. J. For. 2017, 62, 24–32. [Google Scholar]
- Brown, K.; Visser, R. Adoption of Emergent Technology for Forest Road Management in New Zealand. N. Z. J. For. 2018, 63, 23–29. [Google Scholar]
- Prim, R.C. Shortest Connection Networks and Some Generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- García, O. FOLPI, A Forestry-Oriented Linear Programming Interpreter. In Proceedings IUFRO Symposium on Forest Management Planning and Managerial Economics; Nagumo, H., Ed.; University of Tokyo: Tokyo, Japan, 1984. [Google Scholar]
- Boston, K.; Sessions, J. Development of a Spatial Harvest Scheduling System to Promote the Conservation Between Indigenous and Exotic Forests. Int. For. Rev. 2006, 8, 297–306. [Google Scholar] [CrossRef]
- Boston, K.; Bettinger, P. Combining Tabu Search and Genetic Algorithm Heuristic Techniques to Solve Spatial Harvest Scheduling Problems. For. Sci. 2002, 48, 35–46. [Google Scholar] [CrossRef]
- Murray, A.T. Spatial Restrictions in Harvest Scheduling. For. Sci. 1999, 45, 45–52. [Google Scholar] [CrossRef]
- Mason, A.J. OpenSolver—An Open Source Add-in to Solve Linear and Integer Programmes in Excel. In Proceedings of the Operations Research Proceedings 2011, Zurich, Switzerland, 30 August–2 September 2011; Springer: Berlin/Heidelberg, Germany, 2012; pp. 401–406. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2024. [Google Scholar]
- Manley, B. Discount Rates Used for Forest Valuation—Results of 2017 Survey. N. Z. J. For. 2018, 63, 35–43. [Google Scholar]
- Nicholas, I.; Silcock, P.; Webster, R. Chapter 9: Economic Analyses. In Best Practice with Farm Forestry Timber Species: N° 3 Redwoods; Nicholas, I., Ed.; NZFFA Electronic Handbook Series No. 3; New Zealand Farm Forestry Association: Wellington, New Zealand, 2008. [Google Scholar]
- Thornburgh, D.; Noss, R.; Angelides, D.; Olson, C.; Euphrat, F.; Welsh, H. Managing Redwoods. In The Redwood Forest: History, Ecology, and Conservation of the Coast Redwoods; Noss, R.F., Ed.; Island Press: Covelo, CA, USA, 2000; pp. 229–261. [Google Scholar]
- Cown, D.; Marshall, H.; Silcock, P.; Meason, D. Sawn Timber Grade Recovery from a Planted Coast Redwood Stand Growing in New Zealand. N. Z. J. For. Sci. 2013, 43, 8. [Google Scholar] [CrossRef]
- Barton, I. Continuous Cover Forestry: A Handbook for the Management of New Zealand Forests; Tane’s Tree Trust: Pukekohe, New Zealand, 2008; ISBN 978-0-473-13134-0. [Google Scholar]
- Boldenow, R.; Mcbride, J. Redwood Seedling Responses to Light Patterns and Intensities. In Proceedings of the Coast Redwood Science Symposium, Eureka, CA, USA, 13–16 September 2016. [Google Scholar]
- Hossain, K.L.; Comeau, P.G. Characterizing Light across a Strip Shelterwood in a Mixed Conifer Forest. For. Ecol. Manag. 2019, 445, 134–145. [Google Scholar] [CrossRef]
- Loehle, C. Optimal Control of Spatially Distributed Process Models. Ecol. Model. 2000, 131, 79–95. [Google Scholar] [CrossRef]
- Yoshimoto, A. Potential Use of a Spatially Constrained Harvest Scheduling Model for Biodiversity Concerns: Exclusion Periods to Create Heterogeneity in Forest Structure. J. For. Res. 2001, 6, 21–30. [Google Scholar] [CrossRef]
- Spinelli, R.; Magagnotti, N.; Cosola, G.; Grigolato, S.; Marchi, L.; Proto, A.R.; Labelle, E.R.; Visser, R.; Erber, G. Skyline Tension and Dynamic Loading for Cable Yarding Comparing Conventional Single-Hitch Versus Horizontal Double-Hitch Suspension Carriages. Int. J. For. Eng. 2021, 32, 31–41. [Google Scholar] [CrossRef]
- Allum, J.; Harvey, C.; Visser, R.; Hoffmann, S. Infrastructure Requirements for Clear-Fell Harvesting of Small-Scale Plantation Forests in New Zealand. Croat. J. For. Eng. 2024, 45, 115–123. [Google Scholar] [CrossRef]
- Ghaffariyan, M.R.; Stampfer, K.; Sessions, J. Optimal Road Spacing of Cable Yarding Using a Tower Yarder in Southern Austria. Eur. J. For. Res. 2010, 129, 409–416. [Google Scholar] [CrossRef]
- Toscani, P.; Sekot, W.; Holzleitner, F. Forest Roads from the Perspective of Managerial Accounting-Empirical Evidence from Austria. Forests 2020, 11, 378. [Google Scholar] [CrossRef]
- Wells, C. Forest Harvesting Roads: Meeting Operational, Social and Environmental Needs with efficiency and Economy. In Proceedings of the Applying Reduced Impact Logging to Advance Sustainable Forest Management: International Conference Proceedings, Kuching, Malaysia, 26 February–1 March 2001; Enters, T., Durst, P., Applegate, G., Kho, P., Man, G., Eds.; FAO: Rome, Italy, 2002; p. 311. ISBN 9747946238. [Google Scholar]
- Beaudet, M.; Harvey, B.D.; Messier, C.; Coates, K.D.; Poulin, J.; Kneeshaw, D.D.; Brais, S.; Bergeron, Y. Managing Understory Light Conditions in Boreal Mixedwoods through Variation in the Intensity and Spatial Pattern of Harvest: A Modelling Approach. For. Ecol. Manag. 2011, 261, 84–94. [Google Scholar] [CrossRef]
- Parliamentary Commissioner for the Environment. Alt-F Reset: Examining the Drivers of Forestry in New Zealand; Parliamentary Commissioner for the Environment: Wellington, New Zealand, 2025.
- Kaine, G.; Edwards, P.; Polyakov, M.; Stahlmann-Brown, P. Who Knew Afforestation Was Such a Challenge? Motivations and Impediments to Afforestation Policy in New Zealand. For. Policy Econ. 2023, 154, 103031. [Google Scholar] [CrossRef]
- West, T.A.P.; Monge, J.J.; Dowling, L.J.; Wakelin, S.J.; Gibbs, H.K. Promotion of Afforestation in New Zealand’s Marginal Agricultural Lands Through Payments for Environmental Services. Ecosyst. Serv. 2020, 46, 101212. [Google Scholar] [CrossRef]
- Ministry for Primary Industries. National Direction for Plantation and Exotic Carbon Afforestation; MPI Discussion Paper No: 2022/10; Ministry for Primary Industries: Wellington, New Zealand, 2022.
- Bettinger, P.; Boston, K.; Siry, J.; Grebner, D. Forest Management and Planning; Academic Press: San Diego, CA, USA, 2009; ISBN 978-0-12-374304-6. [Google Scholar]
- Franklin, J.; Johnson, K.; Johnson, D. Ecological Forest Management; Waveland Press: Long Grove, IL, USA, 2018; ISBN 978-1-4786-3350-1. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).