Mechanical Property Prediction of Wood Using a Backpropagation Neural Network Optimized by Adaptive Fractional-Order Particle Swarm Algorithm
Abstract
1. Introduction
- (1)
- A BP neural network model optimized using the adaptive fractional-order particle swarm optimization algorithm (AFPSO) is proposed, which significantly improves parameter optimization. This method enhances prediction accuracy, accelerates convergence, and avoids local optima—common limitations of traditional BP models.
- (2)
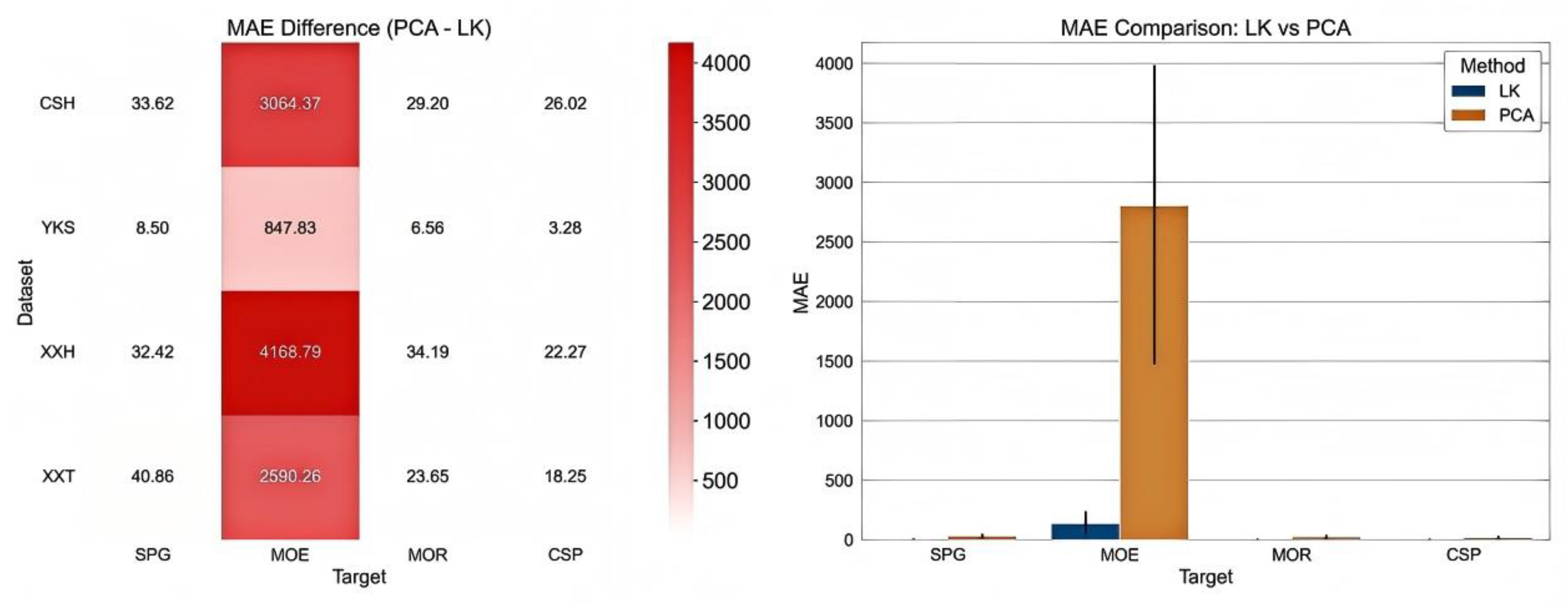
- The LK information flow theory is innovatively applied to wood property prediction, enabling feature importance ranking based on causal influence. And it is proved that its influence on the prediction accuracy of the model is far better than principal component analysis (PCA).
- (3)
- A unified evaluation framework is established for different wood types (YKS, CSH, XXH, and XXT), and multiple intelligent optimization algorithms (AFPSO, PSO, GWO, WOA, FA, and DE) are systematically compared within the BP framework. The results confirm that the proposed LK-BP-AFPSO model outperforms alternatives in both accuracy and stability across datasets, showing strong generalizability.
2. Related Works
- (1)
- From a model optimization perspective, we innovatively incorporate an adaptive fractional-order particle swarm optimization (AFPSO) algorithm to optimize the weights and thresholds of BP neural networks. This approach, leveraging a fractional-order update mechanism and dynamic inertia adjustment strategy, enhances the network’s global search capability and robustness.
- (2)
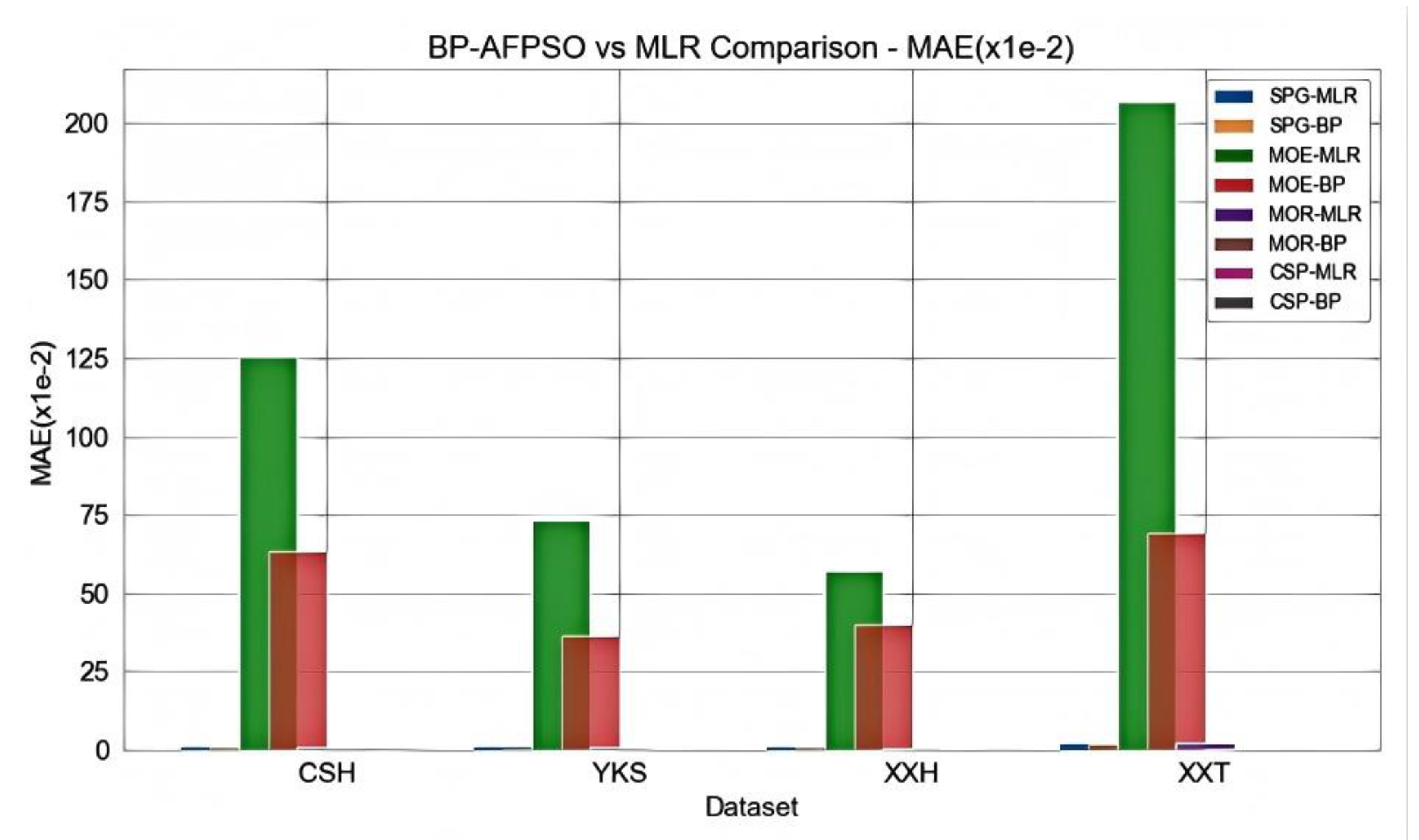
- To comprehensively validate model performance, we construct both a LK-BP-AFPSO model and a multiple linear regression (MLR) baseline model, allowing comparison across nonlinear and linear paradigms.
- (3)
- On the data front, we gather thermally treated Chinese fir samples (CSH2, YKS2, XXH2, and XXT2) from various regions and treatment conditions, significantly improving the model’s generalizability and practical applicability.
- (4)
- Lastly, the proposed hybrid framework integrates LK information flow with the AFPSO algorithm, enabling interpretable modeling by quantifying the causal strength between wood physical attributes and mechanical performance. The causally relevant features are then used to guide AFPSO in optimizing neural network parameters, culminating in a high-efficiency predictive model with strong interpretability and robustness.
3. Related Theories
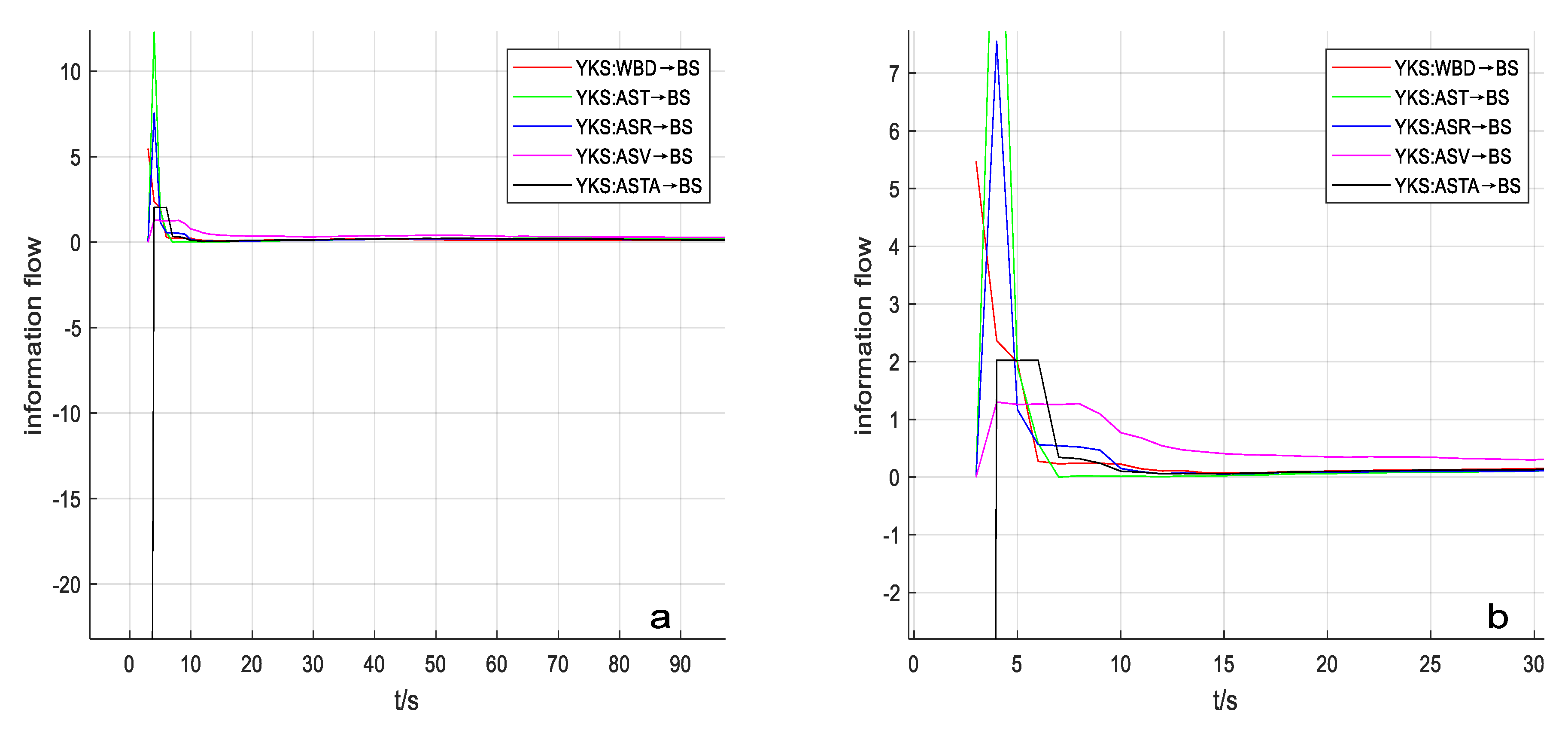
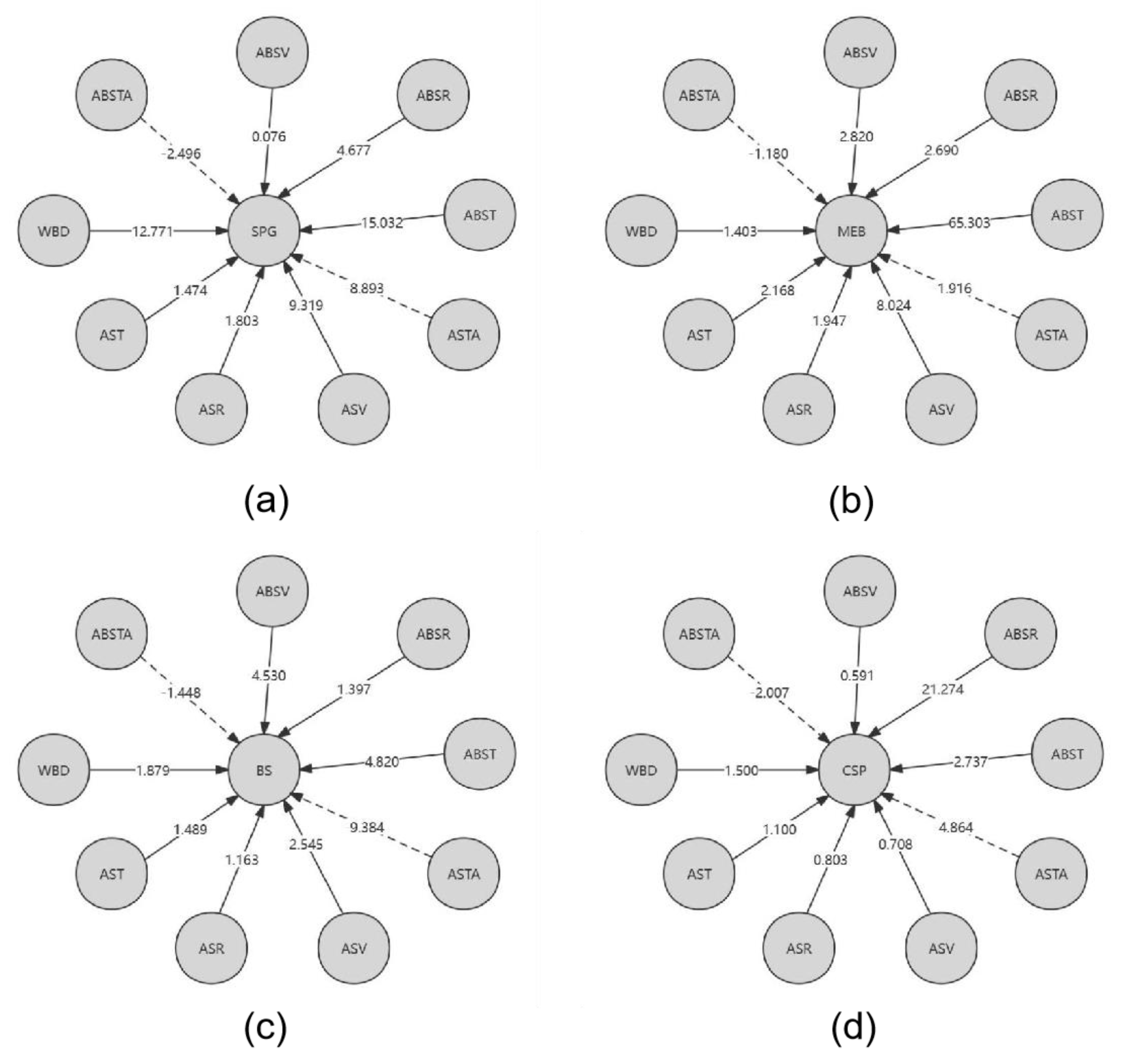
3.1. Liang–Kleeman Information Flow and Causal Directed Graph
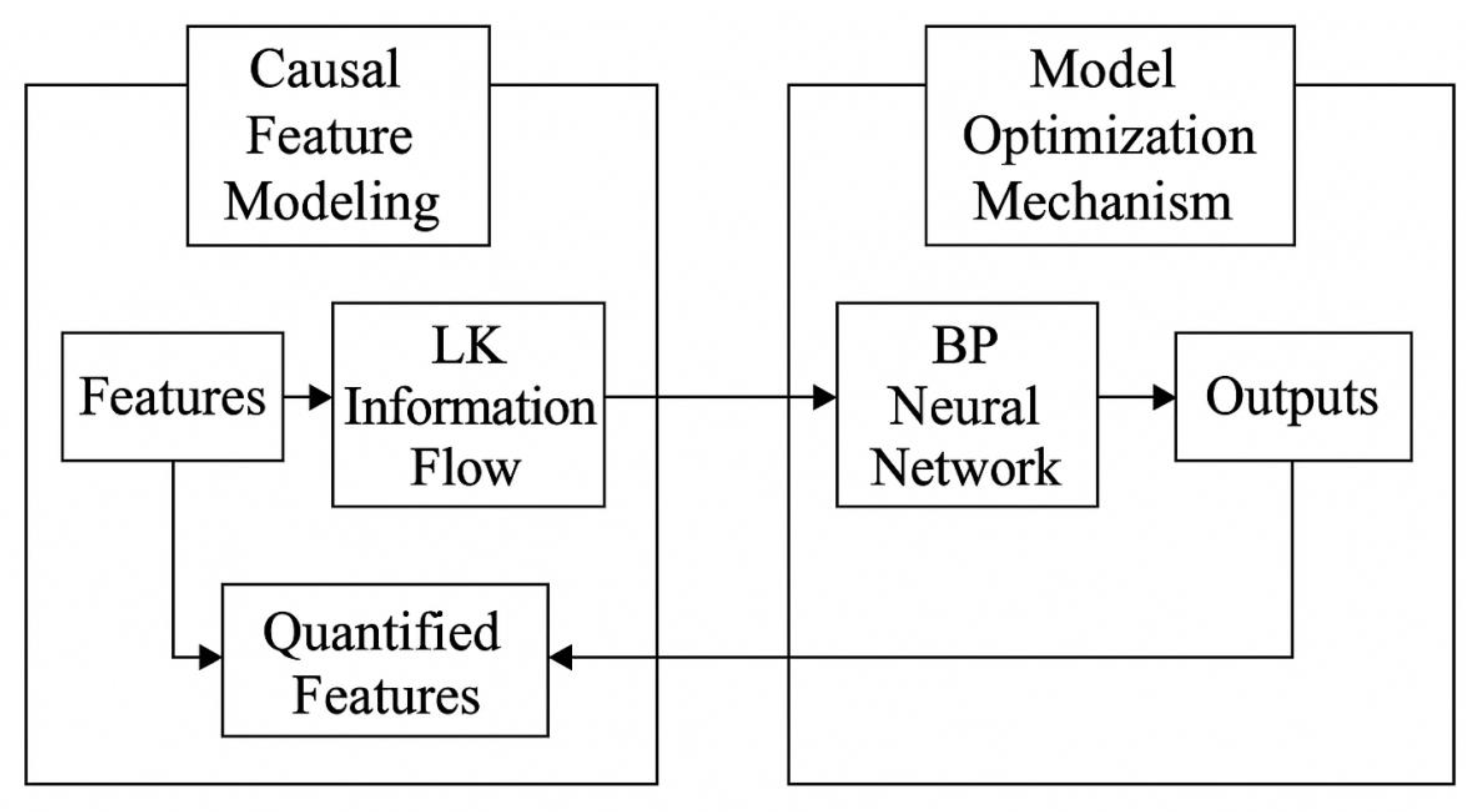
3.2. LK-LK-BP-AFPSO Model
3.2.1. A. Backpropagation Neural Network (BP)
3.2.2. B. Adaptive Fractional-Order Particle Swarm Optimization (AFPSO)
3.2.3. C. Hybrid Model Structure and Advantages
3.2.4. D. Model Performance Evaluation
- (1)
- Causality-Driven Feature Selection**: By leveraging the LK information flow, the model emphasizes physically interpretable and causally relevant features, leading to more meaningful and robust predictions.
- (2)
- Enhanced Global Optimization**: The AFPSO algorithm overcomes the limitations of traditional training methods by preventing entrapment in local minima and adapting to dynamic optimization landscapes.
- (3)
- Improved Accuracy and Convergence**: The synergy between AFPSO and BP enables faster convergence and higher prediction precision.
- (4)
- High Generalizability**: The modular structure of the model supports easy adaptation to other tasks involving nonlinear system modeling and prediction.
4. Experiment
4.1. Materials and Sample Preparation
4.2. Wood Properties and Grain Direction Characteristics
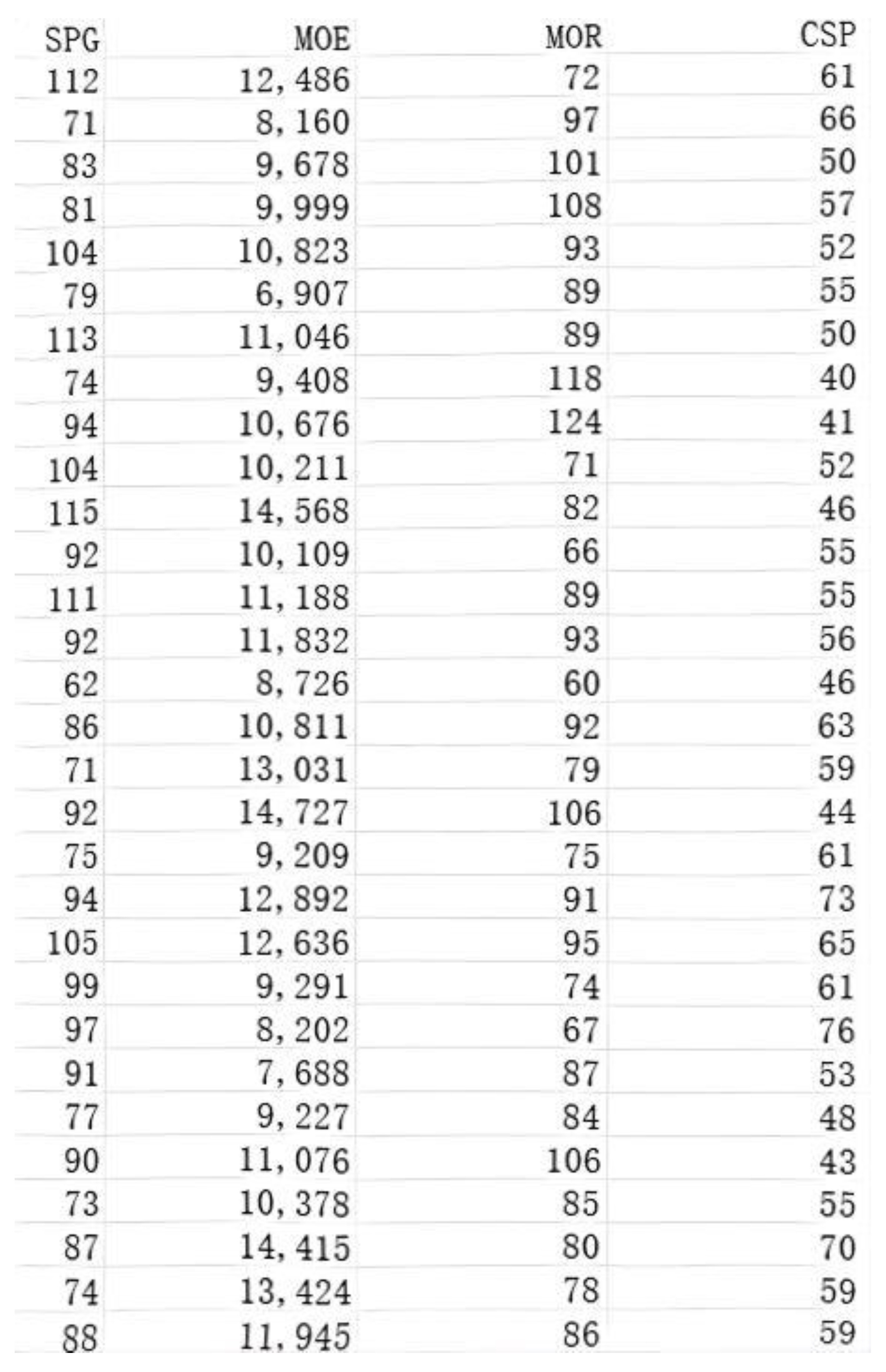
4.3. Data Acquisition and Processing
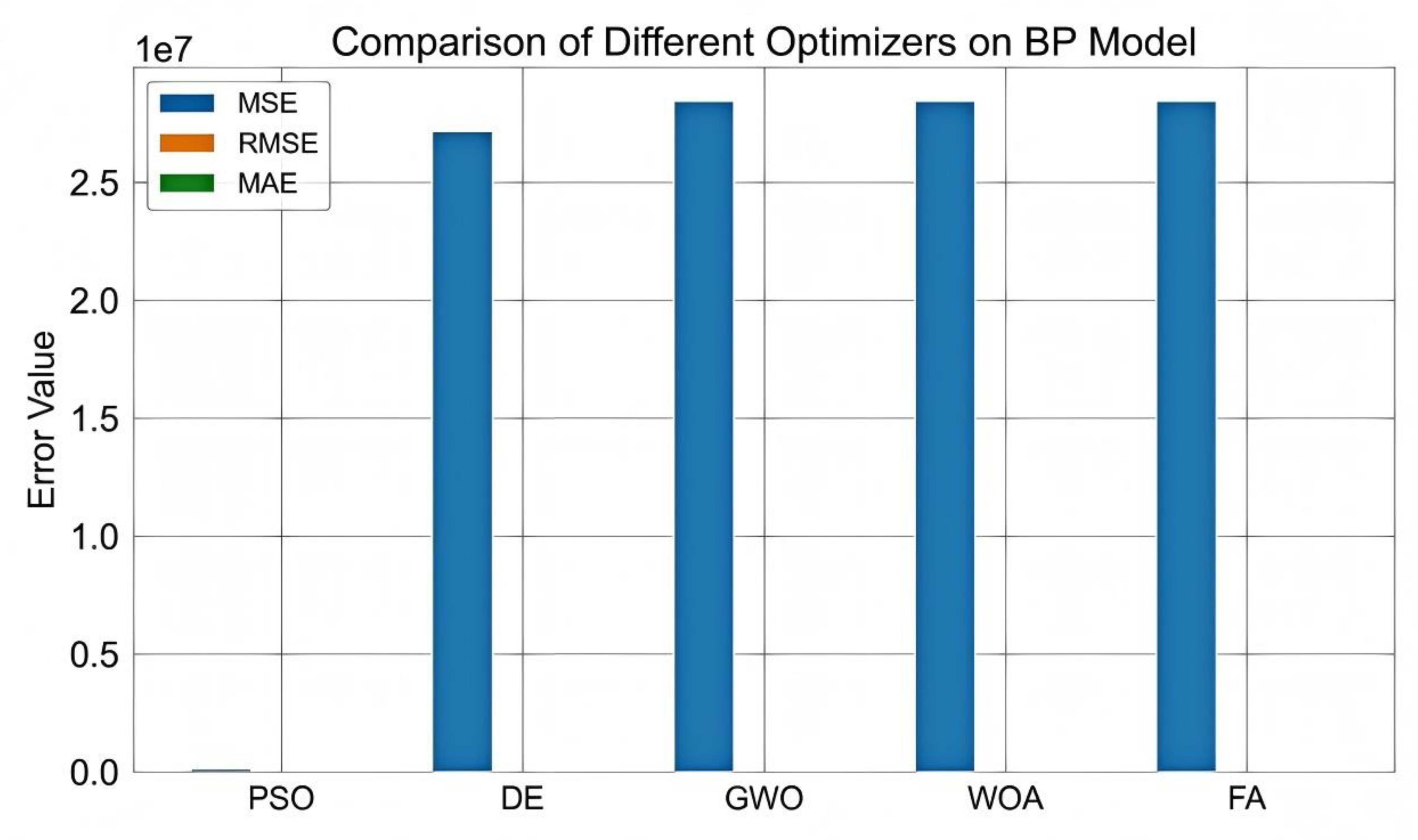
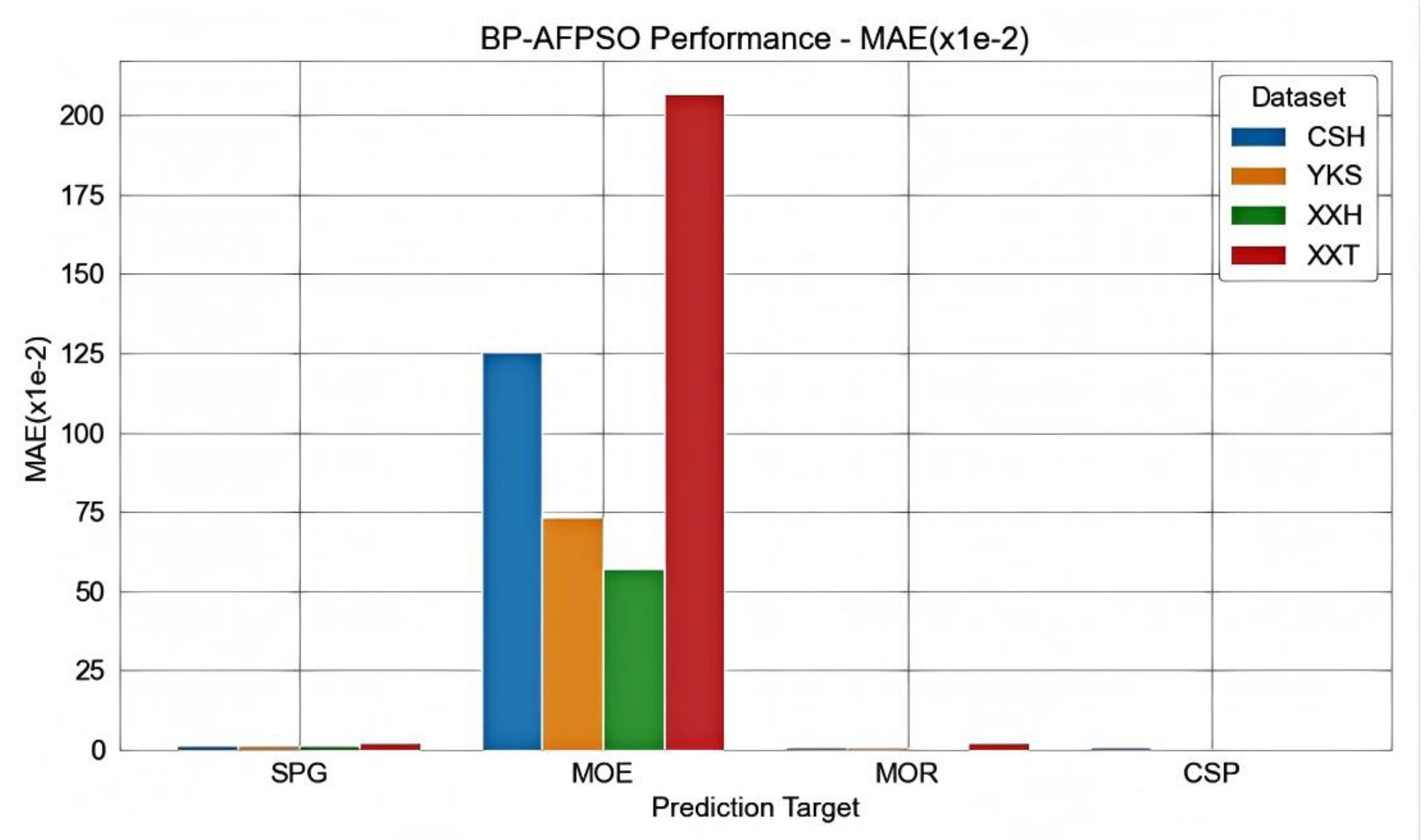
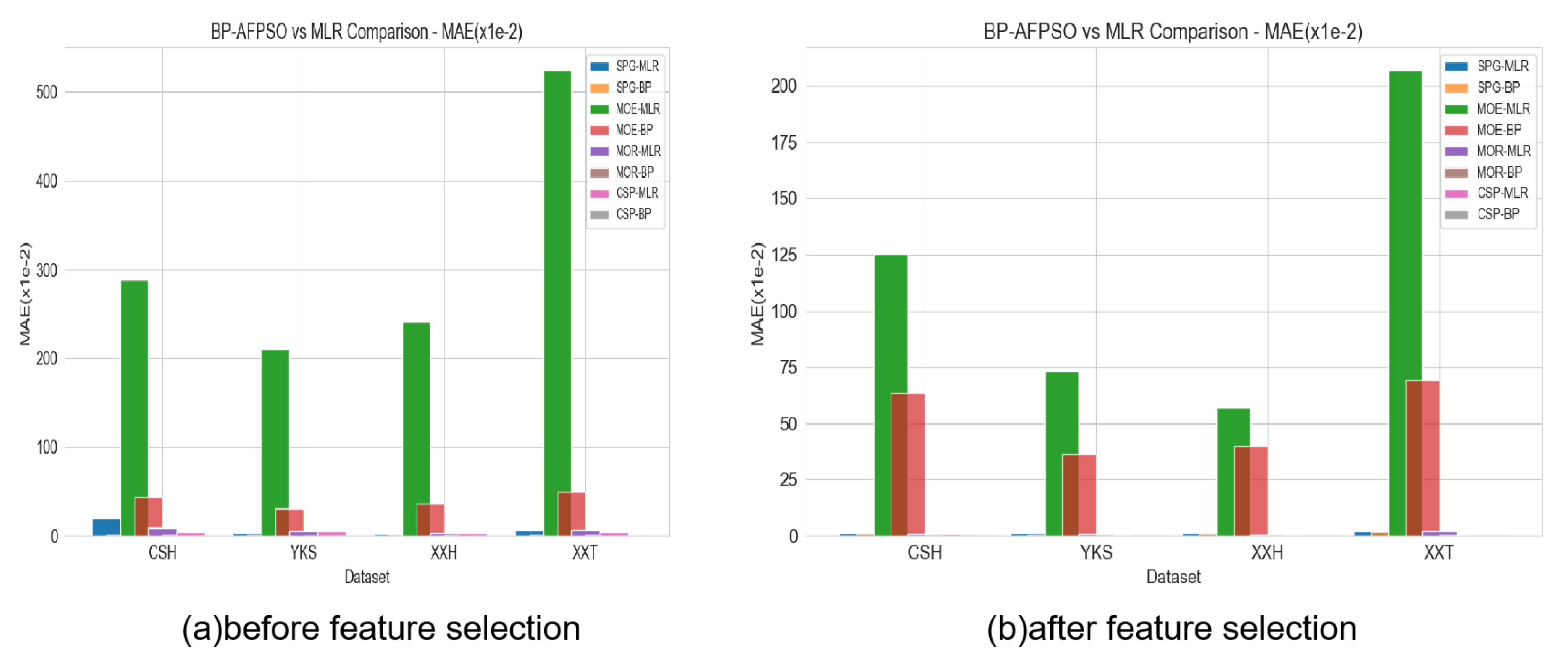
4.4. Results and Analysis
4.5. Validation and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Yang, Z.; Wang, X. Recent Advances in the Functionalization of Wood Research. For. Eng. J. 2019, 4, 9. [Google Scholar]
- Qing, Y.; Liao, Y.; Liu, J. Recent Advances in Wood-based Energy Storage Materials. For. Eng. J. 2021, 6, 1–13. [Google Scholar] [CrossRef]
- Chen, C. AI in materials science: Charting the course to Nobel-worthy breakthroughs. Matter 2024, 7, 4123–4125. [Google Scholar] [CrossRef]
- Zhang, R.; Zhu, Y. Predicting the Mechanical Properties of Heat-treated Woods Using Optimization-Algorithm-Based BPNN. Forests 2023, 14, 935. [Google Scholar] [CrossRef]
- Zhang, P.; Shang, X.; Wu, Z. Comparison of Physical and Mechanical Properties of Eucalyptus Wood. J. Northwest For. Univ. 2020. [Google Scholar] [CrossRef]
- Liang, X.S. Information flow and causality as rigorous notions ab initio. Am. Phys. Soc. 2016. [Google Scholar] [CrossRef]
- Shang, X.; Zhang, P.; Luo, J. Study on the Physical and Mechanical Properties of Young Eucalyptus Wood. J. Northwest AF Univ. (Nat. Sci. Ed.) 2019, 47, 32–41. [Google Scholar] [CrossRef]
- Chen, K.; Liu, H.; Wang, Z. Study on the Differences in Physical and Mechanical Properties Between Clonal and Seedling Chinese Fir. J. Southwest For. Univ. 2023, 43, 1–7. [Google Scholar]
- Liu, X.; Xu, F.; Sun, Y.; Zhang, H.; Chen, Z. Convolutional Recurrent Neural Networks for Observation-Centered Plant Identification. J. Electr. Comput. Eng. 2018, 2018, 9373210. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Han, Y.; Ma, Y.; Zhao, H.; Nowak, A.; Li, J. Deep Learning for Ultra-fast and High Precision Screening of Energy Materials. Energy Storage Mater. 2021, 39, 45–53. [Google Scholar] [CrossRef]
- Liu, J.; Kuang, Z.; Deng, L. GCNPCA: MiRNA-Disease Associations Prediction Algorithm Based on Graph Convolutional Neural Networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 20, 1041–1052. [Google Scholar] [CrossRef] [PubMed]
- Yang, X. Research on Classification and Recognition Algorithms Based on the Microscopic Structure of Rosewood. Ph.D. Thesis, Shandong Jianzhu University, Shenyang, China, 2022. [Google Scholar] [CrossRef]
- Yang, C. Research on the Construction of a Data-driven Performance Prediction Model for Particleboard. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2021. [Google Scholar] [CrossRef]
- Li, N.; Wang, W. Prediction of Mechanical Properties of Thermally Modified Wood Based on TSSA-BP Model. Forests 2022, 13, 160. [Google Scholar] [CrossRef]
- Ma, W.; Wang, W.; Cao, Y. Mechanical Properties of Wood Prediction Based on the NAGGWO-BP Neural Network. Forests 2022, 13, 1870. [Google Scholar] [CrossRef]
- Chen, S.; Wang, J.; Liu, Y.; Chen, Z.; Lei, Y.; Yan, L. The Relationship Between Color and Mechanical Properties of Heat-treated Wood Predicted Based on Support Vector Machines Model. Holzforschung 2022, 76, 994–1002. [Google Scholar] [CrossRef]
- Osuna-Sequera, C.; Arriaga, F.; Llana, D.F.; Íñiguez-González, G. Predicting the Mechanical Properties of Timber from Existing Structures by the Longitudinal Vibration Method, Visual Grading, and Definition of the Nominal Cross-section. Wood Mater. Sci. Eng. 2024, 19, 366–374. [Google Scholar] [CrossRef]
- Huang, J.; Kuang, Z.; Ma, J.; Fang, Y. Performance Prediction Method Based on Liang-Kleeman Information Flow and Wood Tracheid Morphology. Mater. Today Commun. 2024, 39, 108620. [Google Scholar] [CrossRef]
- Fathi, H.; Nasir, V.; Kazemirad, S. Prediction of the Mechanical Properties of Wood Using Guided Wave Propagation and Machine Learning. Constr. Build. Mater. 2020, 262, 120848. [Google Scholar] [CrossRef]
- Chen, S.; Shiina, R.; Nakai, K.; Awano, T.; Yoshinaga, A.; Sugiyama, J. Potential of Machine Learning Approaches for Predicting Mechanical Properties of Spruce Wood in the Transverse Direction. J. Wood Sci. 2023, 69, 22. [Google Scholar] [CrossRef]
- Yin, T.; He, L.; Huang, Q.; Gong, Y.; Wang, Z.; Gong, M. Effect of Lamination Grade on Bending and Shear Properties of CLT Made from Fast-Growing Chinese Fir. Ind. Crops Prod. 2024, 207, 117741. [Google Scholar] [CrossRef]
- Elrhayam, Y.; El Bachiri, A. Study of the effect of heat temperature on the chemical changes and hygroscopicity of eucalyptus wood by FT-IR and prediction of mechanical properties by the MLR regression method. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2024, 321, 124576. [Google Scholar] [CrossRef] [PubMed]
- Bardak, S.; Tiryaki, S.; Bardak, T.; Aydin, A.Y.T.A. Predictive Performance of Artificial Neural Network and Multiple Linear Regression Models in Predicting Adhesive Bonding Strength of Wood. Strength Mater. 2016, 48, 811–824. [Google Scholar] [CrossRef]


| Area | Type | Code | Average Age/a | Average DBH/cm |
|---|---|---|---|---|
| Yangkou | Fast-growing Chinese fir | YKS | 53 | 47.5 |
| Chenshan | Red-heart Chinese fir | CSH | 51 | 29.5 |
| XXH | 50 | 30.8 | ||
| Xiaoxi | Iron-heart Chinese fir | XXT | 53 | 28.6 |
| Number | Name | Abbreviations |
|---|---|---|
| 1 | Wood basic density | WBD |
| 2 | Tangential air-dry shrinkage | AST |
| 3 | Radial air-dry shrinkage | ASR |
| 4 | Volumetric air-dry shrinkage | ASV |
| 5 | Tangential-to-radial air-dry shrinkage | ASTA |
| 6 | Absolute tangential dry shrinkage | ABST |
| 7 | Absolute radial dry shrinkage | ABSR |
| 8 | Absolute volumetric dry shrinkage | ABSV |
| 9 | Absolute tangential-to-radial dry shrinkage | ABSTA |
| Number | Name | Abbreviations |
|---|---|---|
| 1 | Tensile Strength parallel to grain | SPG |
| 2 | Modulus of elasticity | MOE |
| 3 | Bending strength | MOR |
| 4 | Compression strength parallel to grain | CSP |
| Event | Mean (YKS) | Mean (CSH) | Mean (XXH) | Mean (XXT) |
|---|---|---|---|---|
| ) | 0.023 f | 0.034 f | 0.035 f | 0.025 f |
| AST/% | 0.559 e | 0.413 c | 0.607 b | 0.842 a |
| ASR/% | 0.225 d | 0.399 b | 0.428 a | 0.521 a |
| ASV/% | 0.762 d | 0.729 c | 0.957 b | 1.264 a |
| ASTA/% | 2.773 b | 1.05 b | 0.574 b | 0.656 b |
| ABST/% | .047 bc | d | 0.518 b | 1.389 bc |
| ABSR/% | 0.498 c | 0.618 c | 0.454 ab | 0.959 ab |
| ABSV/% | 1.11 cd | 0.993 e | 0.819 b | 2.019 bc |
| ABSTA/% | 0.655 a | 0.479 cd | 0.284 cd | 0.453 d |
| SPG/MPa | 15.676 c | 4.636 b | 22.953 a | 38.980 a |
| MOE/MPa | 1151.049 d | 1646.908 b | 1069.154 b | 1212.171 ab |
| MOR/MPa | 7.409 f | 16.747 d | 15.557 b | 13.123 ab |
| CSP/MPa | 4.022 d | 8.604 a | 5.128 b | 4.927 a |
| WBD | AST | ASR | ASV | ASTA | SPG | MOE | MOR | CSP | |
|---|---|---|---|---|---|---|---|---|---|
| WBD | 1.00 | ||||||||
| AST | 0.89 | 1.00 | |||||||
| ASR | 0.93 | 0.99 | 1.00 | ||||||
| ASV | 0.90 | 1.00 | 0.99 | 1.00 | |||||
| ASTA | −0.84 | −0.87 | −0.91 | −0.90 | 1.00 | ||||
| SPG | 0.92 | 0.95 | 0.96 | 0.95 | −0.80 | 1.00 | |||
| MOE | 0.67 | 0.89 | 0.86 | 0.88 | −0.78 | 0.78 | 1.00 | ||
| MOR | 0.89 | 0.95 | 0.97 | 0.95 | −0.86 | 0.96 | 0.83 | 1.00 | |
| CSP | 0.91 | 0.88 | 0.89 | 0.89 | −0.81 | 0.83 | 0.81 | 0.80 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Kuang, Z. Mechanical Property Prediction of Wood Using a Backpropagation Neural Network Optimized by Adaptive Fractional-Order Particle Swarm Algorithm. Forests 2025, 16, 1223. https://doi.org/10.3390/f16081223
Huang J, Kuang Z. Mechanical Property Prediction of Wood Using a Backpropagation Neural Network Optimized by Adaptive Fractional-Order Particle Swarm Algorithm. Forests. 2025; 16(8):1223. https://doi.org/10.3390/f16081223
Chicago/Turabian StyleHuang, Jiahui, and Zhufang Kuang. 2025. "Mechanical Property Prediction of Wood Using a Backpropagation Neural Network Optimized by Adaptive Fractional-Order Particle Swarm Algorithm" Forests 16, no. 8: 1223. https://doi.org/10.3390/f16081223
APA StyleHuang, J., & Kuang, Z. (2025). Mechanical Property Prediction of Wood Using a Backpropagation Neural Network Optimized by Adaptive Fractional-Order Particle Swarm Algorithm. Forests, 16(8), 1223. https://doi.org/10.3390/f16081223




