Determining the Structural Characteristics of Farmland Shelterbelts in a Desert Oasis Using LiDAR
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Methods
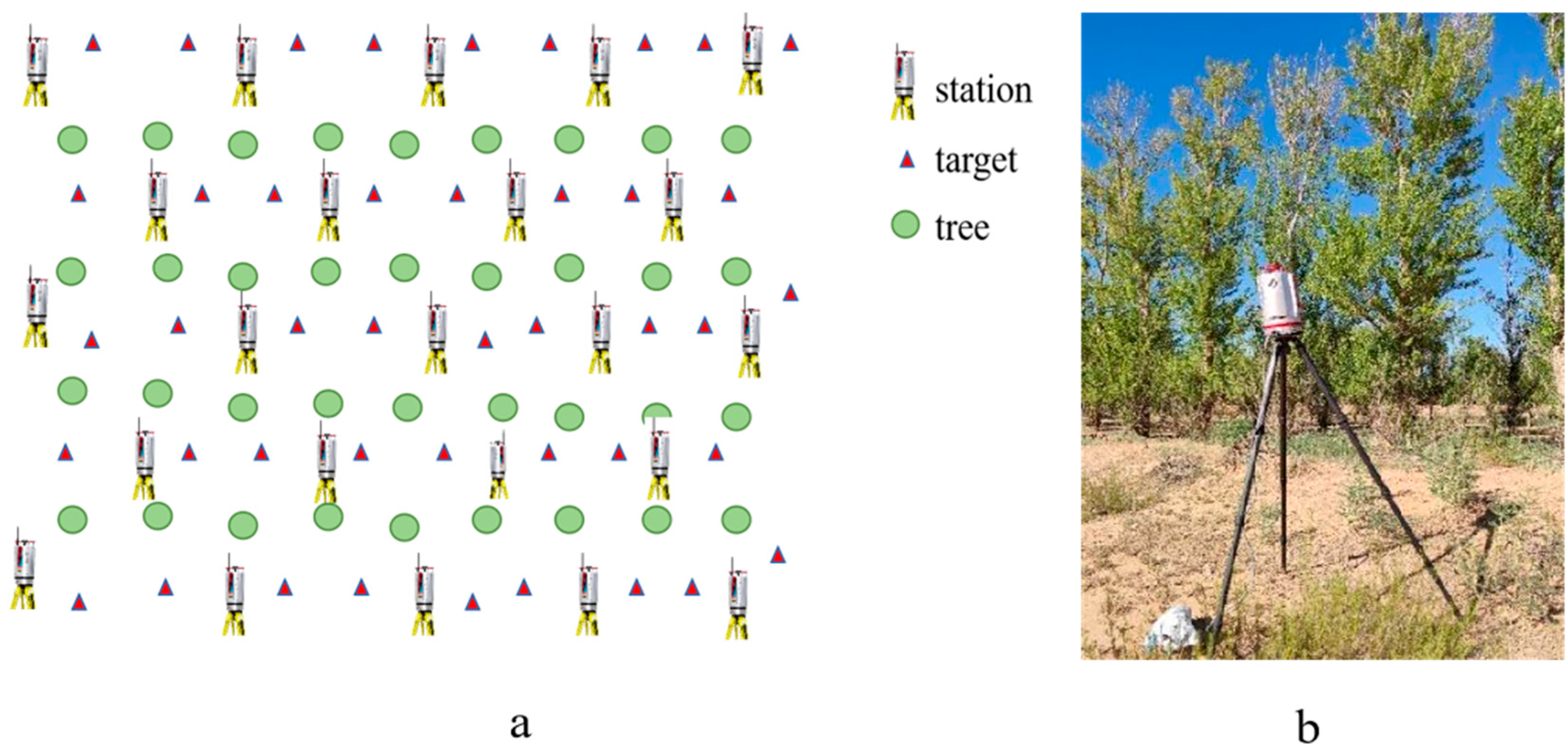
2.2.1. Field Survey
2.2.2. LiDAR Data Acquisition
2.2.3. Measurement of Structural Parameters
2.3. Data Processing
2.3.1. Shelterbelt Point Cloud Data Pretreatment
2.3.2. Single Tree Segmentation and Parameter Extraction
2.3.3. Algorithm Optimization
2.3.4. Tree Branching Feature and Leaf Parameters Acquisition
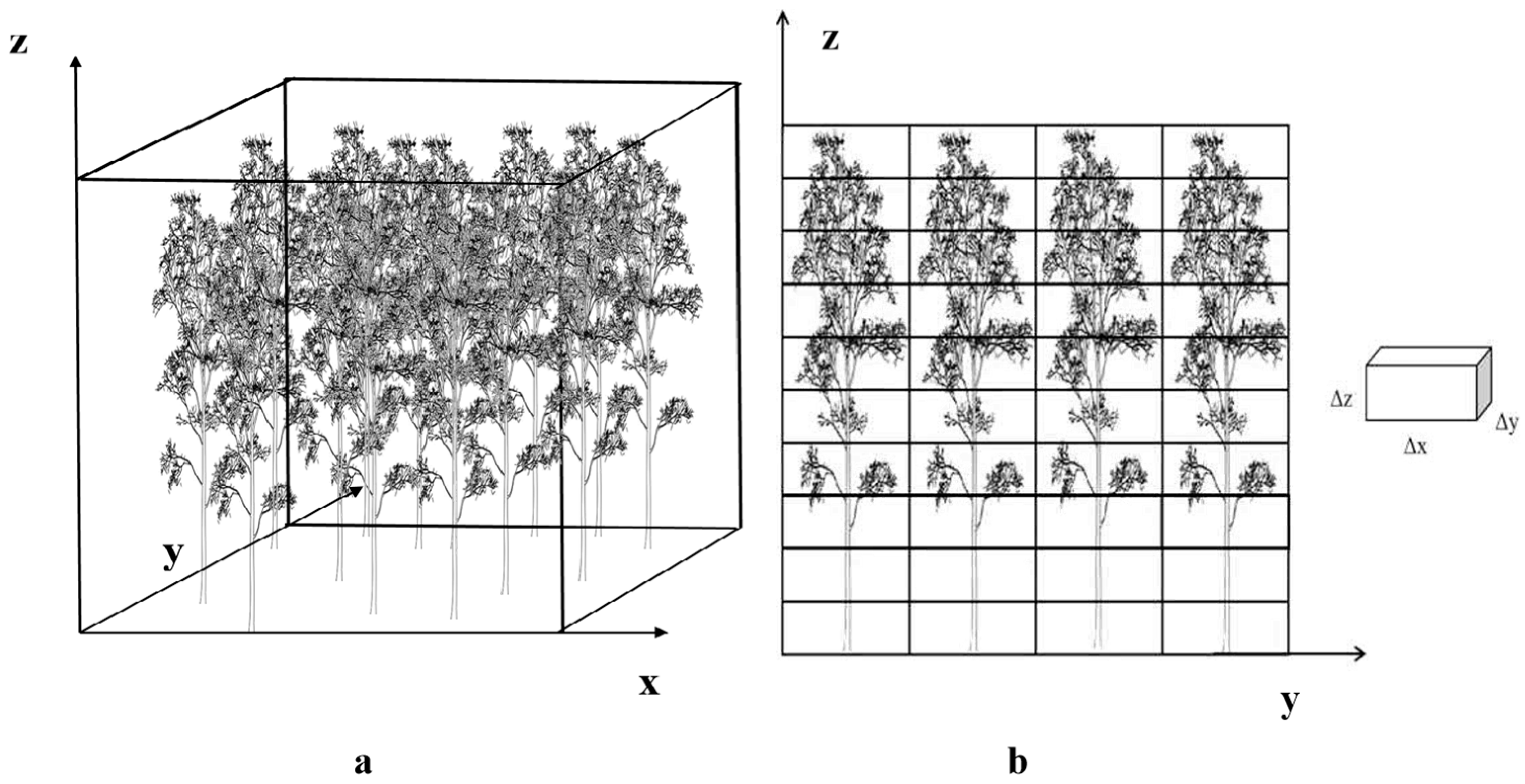
2.3.5. Shelterbelt Parameter Calculation
2.3.6. Accuracy Evaluation
3. Results
3.1. Single Tree Structure
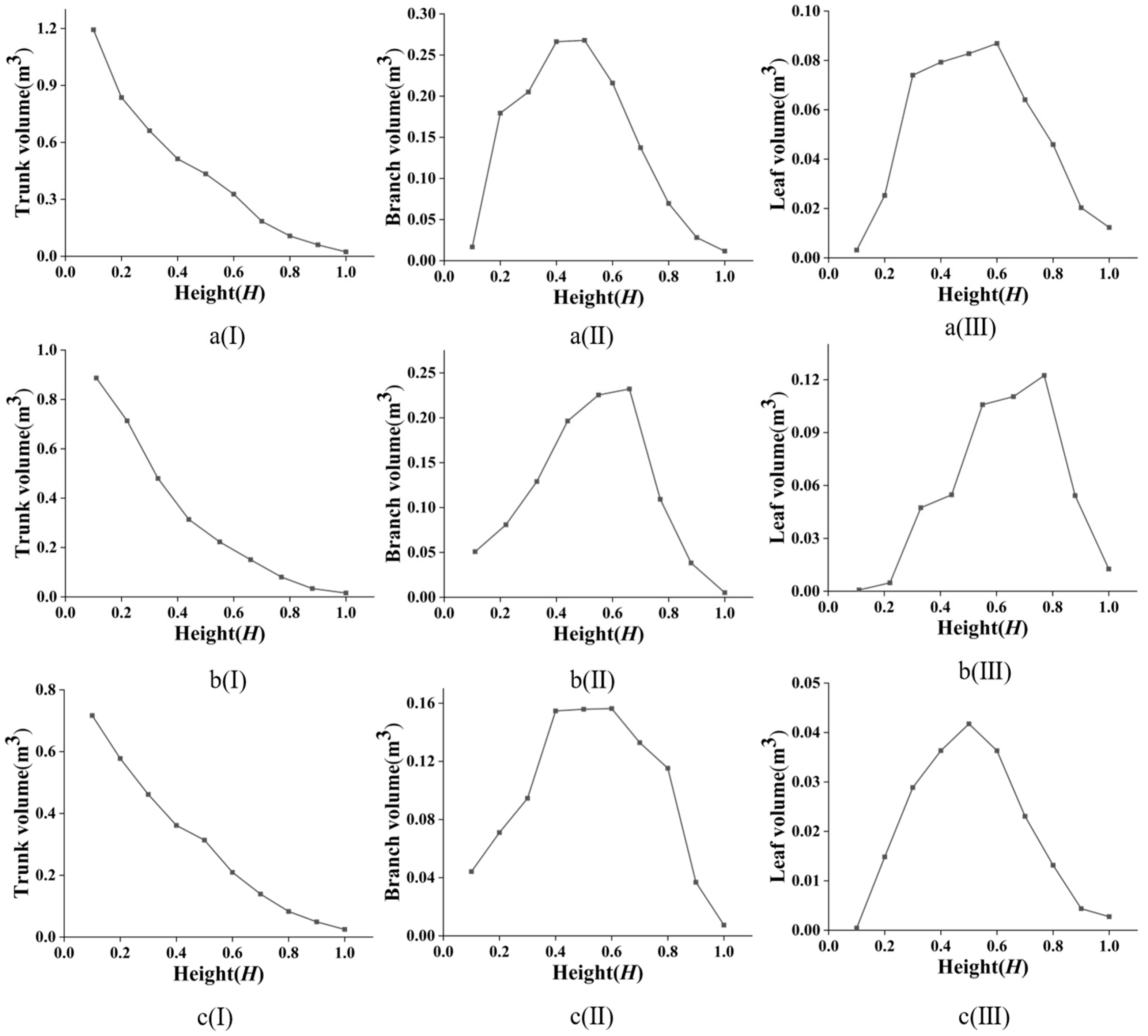
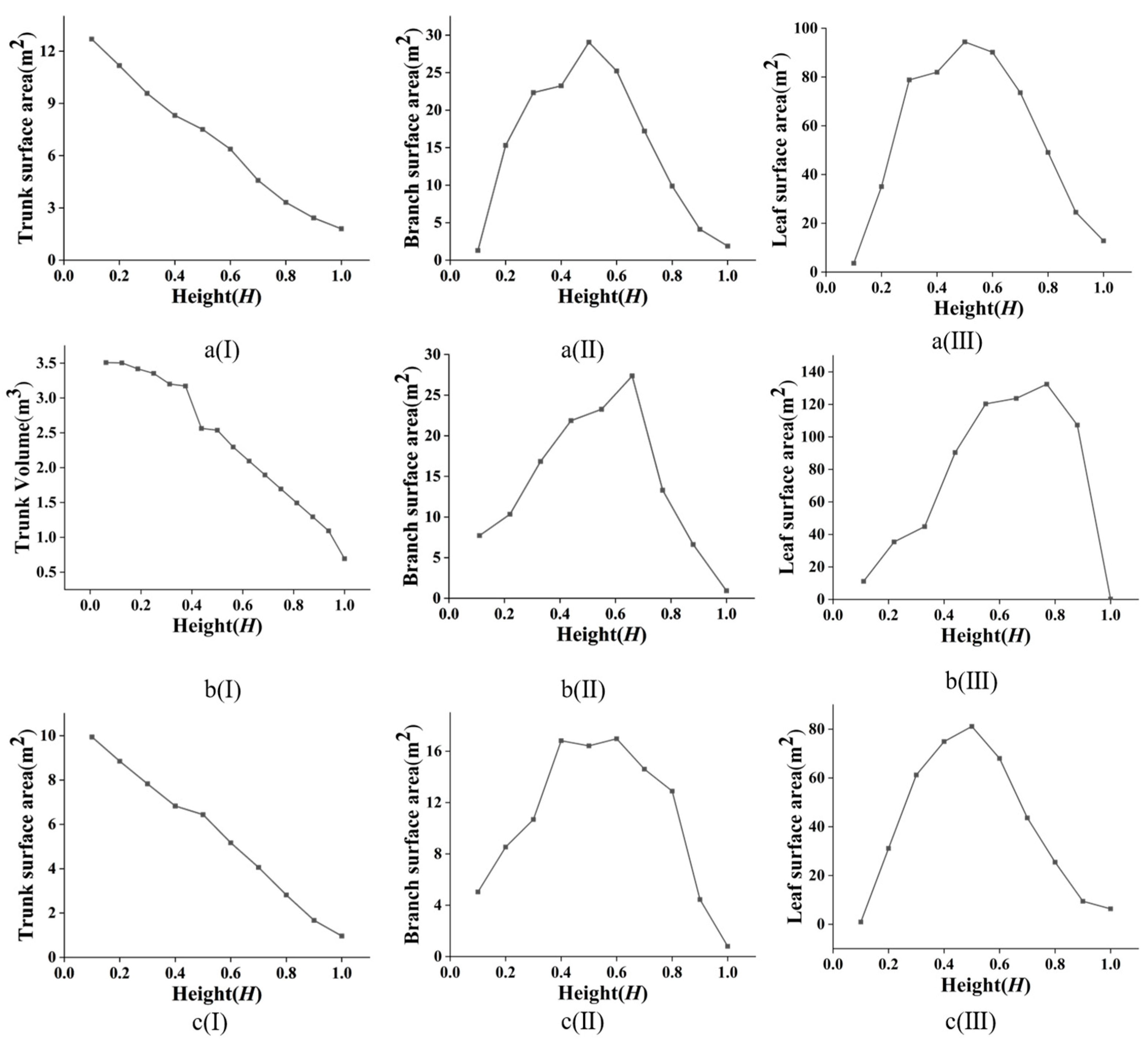
3.1.1. Integral Structure of Single Tree
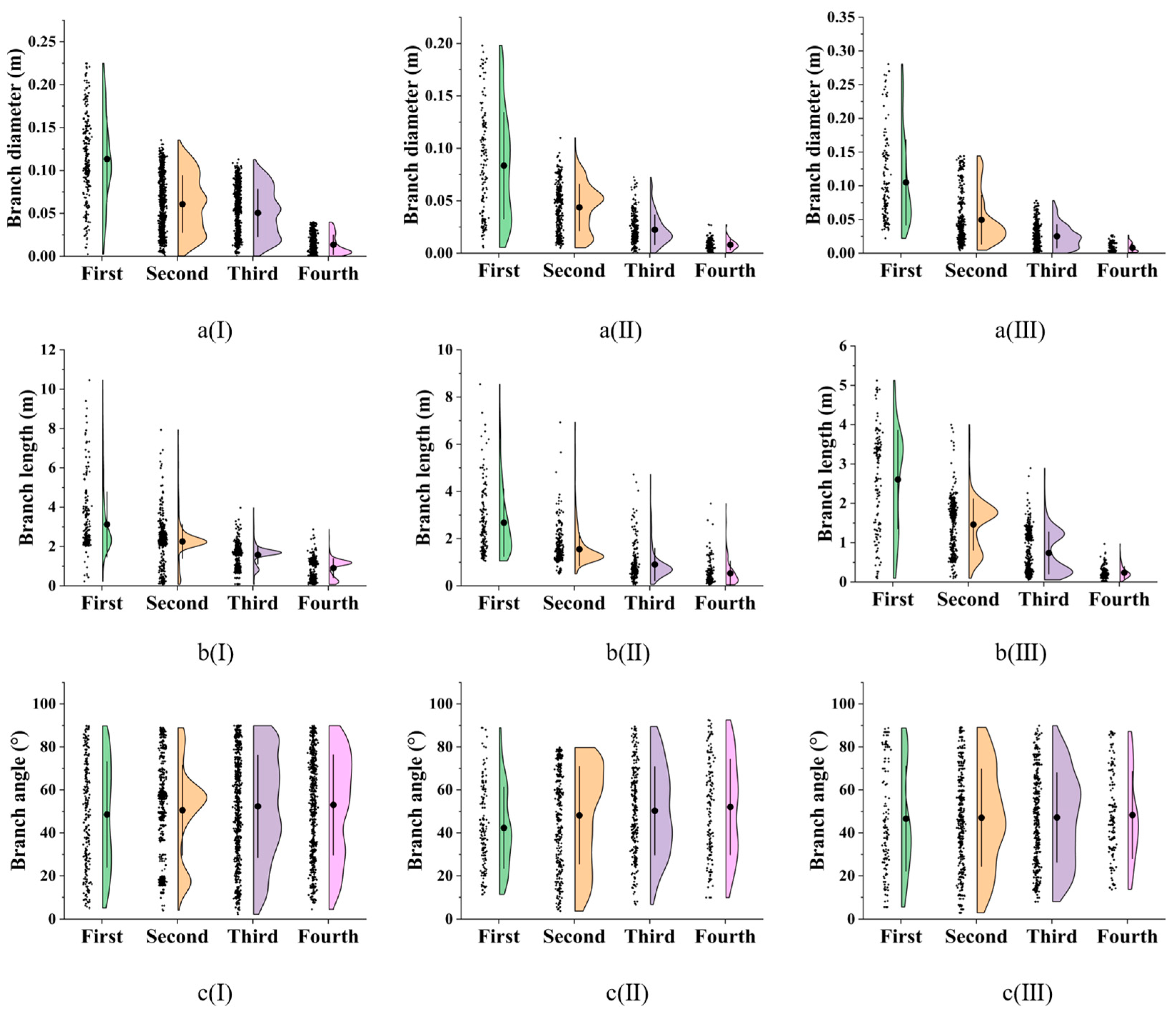
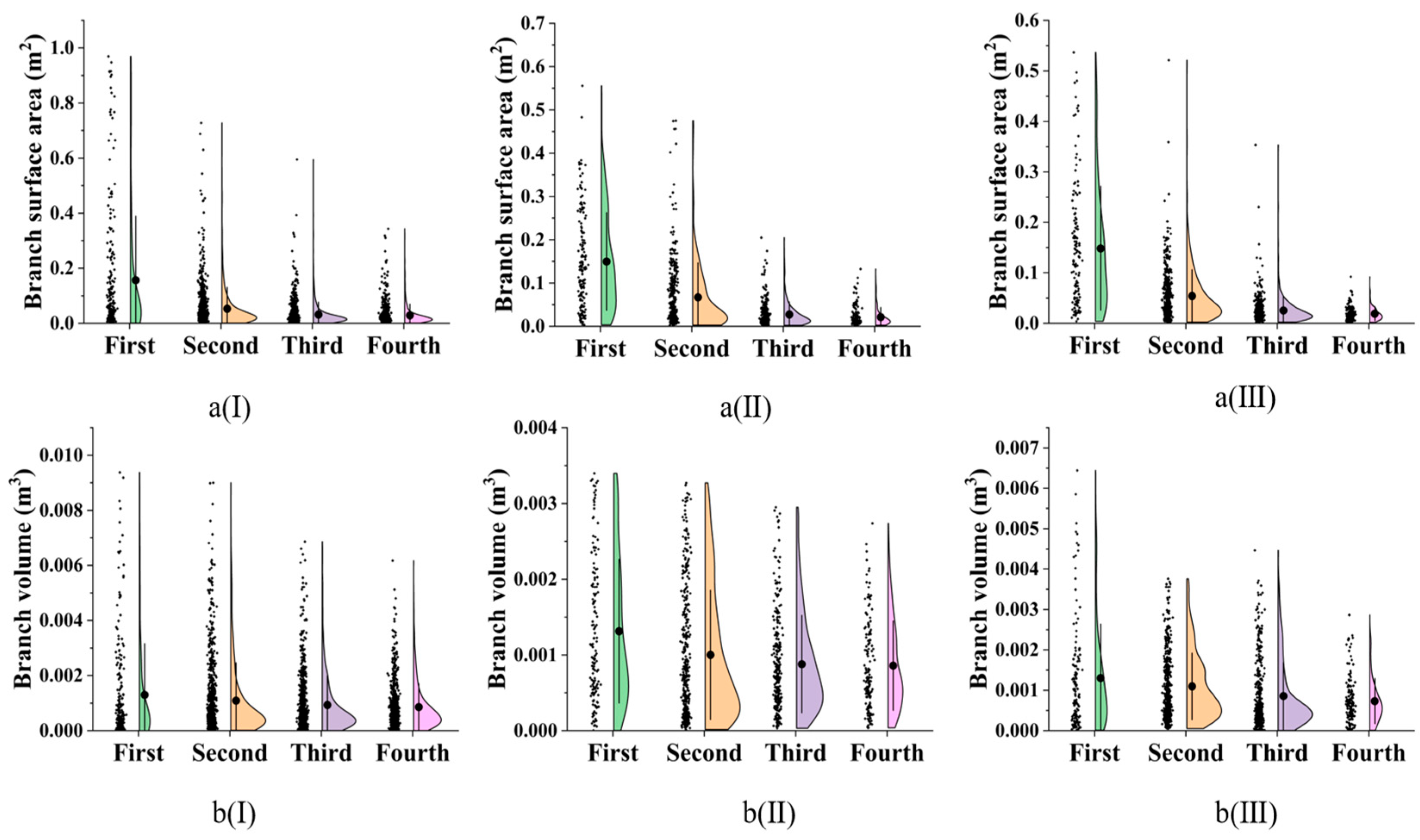
3.1.2. Tree Branch Structure
3.1.3. Tree Leaf Structure
3.2. Shelterbelt Structure
3.2.1. Integral Structure of Shelterbelt
3.2.2. Spatial Distributions of Trunk, Branch, and Leaf in the Shelterbelts
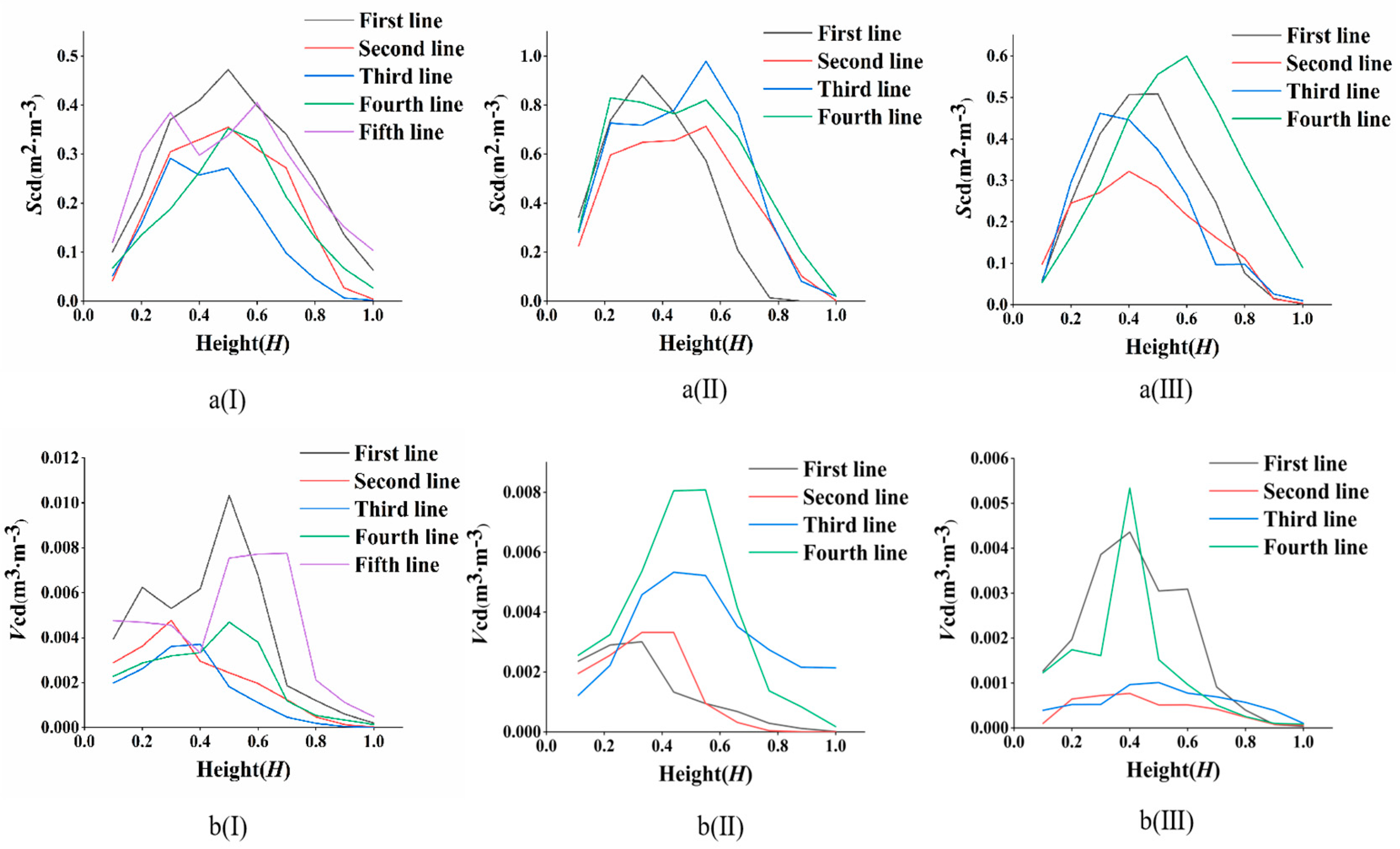
3.2.3. Spatial Distributions of Scd and Vcd in the Shelterbelts
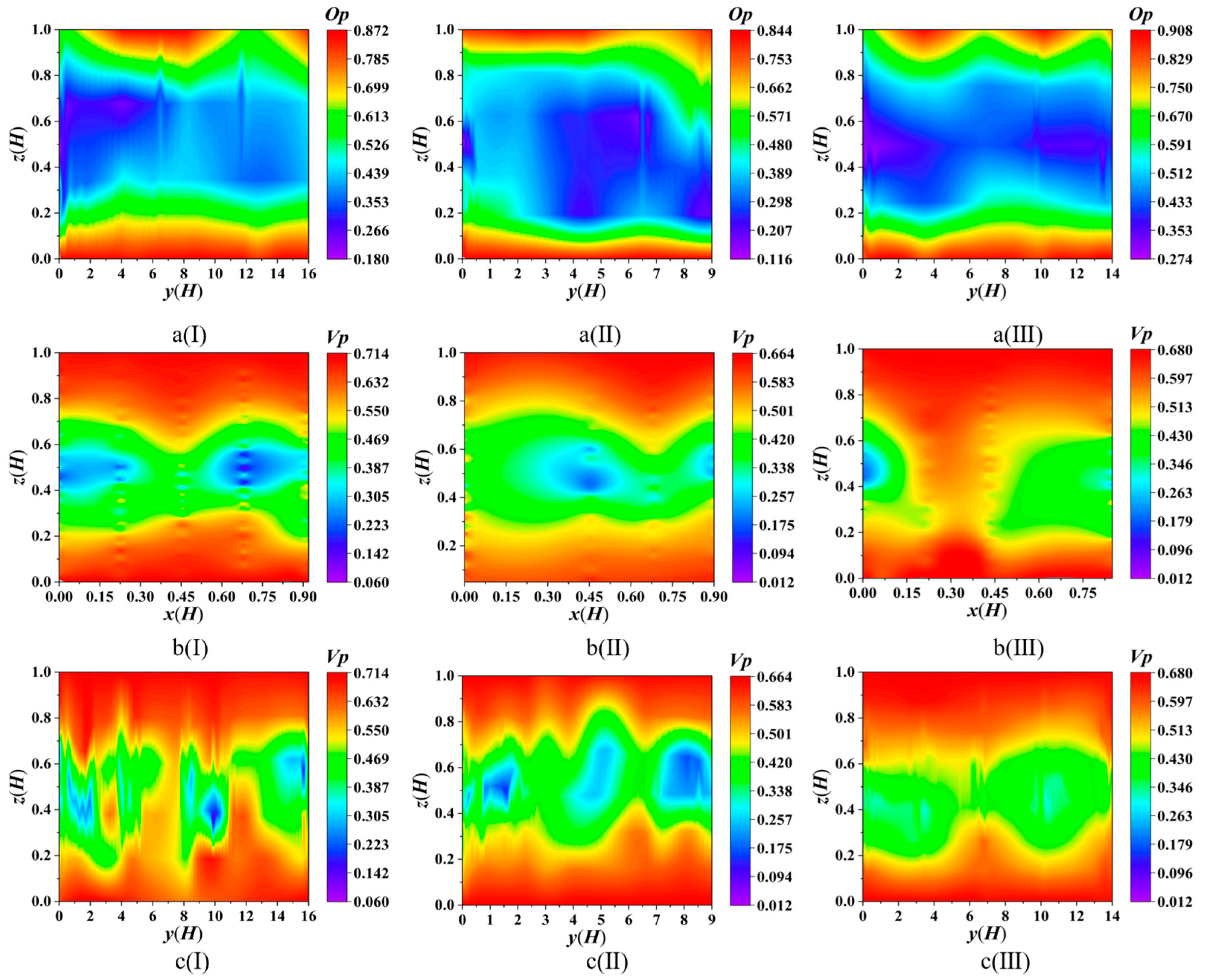
3.2.4. Spatial Distributions of Op and Vp in the Shelterbelts
4. Discussion
4.1. Feasibility Analysis of the Methodology
4.2. The Significance of Stratified Porosity
4.3. Shelterbelt Planning and Management Guidelines
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brandle, J.R.; Hodges, L.; Zhou, X.H. Windbreaks in North American agricultural systems. Agrofor. Syst. 2004, 61, 65–78. [Google Scholar] [CrossRef]
- Campi, P.; Palumbo, A.D.; Mastrorilli, M. Effects of tree windbreak on microclimate and wheat productivity in a Mediterranean environment. Eur. J. Agron. 2009, 30, 220–227. [Google Scholar] [CrossRef]
- Shi, X.; Li, Y.; Deng, R. A method for spatial heterogeneity evaluation on landscape pattern of farmland shelterbelt networks: A case study in midwest of Jilin Province, China. Chin. Geogr. Sci. 2011, 21, 48–56. [Google Scholar] [CrossRef]
- Stadnik, A.P. The role of the structure of field shelterbelts in the forming of the agricultural landscape. Lesn. Khoz Yaistvo 1989, 8, 54–56. [Google Scholar]
- Heisler, G.M.; Dewalle, D.R. Effects of windbreak structure on wind flow. Agric. Ecosyst. Environ. 1988, 22, 41–69. [Google Scholar] [CrossRef]
- Cornelis, W.; Gabriëls, D. 25 years of assessment of erosion-Preface. Catena 2005, 64, 139–141. [Google Scholar] [CrossRef]
- Torita, H.; Satou, H. Relationship between shelterbelt structure and mean wind reduction. Agric. For. Meteorol. 2007, 145, 186–194. [Google Scholar] [CrossRef]
- Cao, X.S. Shelterbelt for Farmland; China Forestry Publishing House: Beijing, China, 1983. (In Chinese) [Google Scholar]
- Loeffler, A.E.; Gordon, A.M.; Gillespie, T.J. Optical porosity and windspeed reduction by coniferous windbreaks in Southern Ontario. Agrofor. Syst. 1992, 17, 119–133. [Google Scholar] [CrossRef]
- Zhu, J.J.; Matsuzaki, T.; Gonda, Y. Optical stratification porosity as a measure of vertical canopy structure in a Japanese coastal forest. For. Ecol. Manag. 2003, 173, 89–104. [Google Scholar] [CrossRef]
- You, K.P.; Kim, Y.M. Wind Velocity Decreasing Effects of Windbreak Fence for Snowfall Measurement. Adv. Meteorol. 2014, 1, 791256. [Google Scholar] [CrossRef]
- Hong, S.W.; Lee, I.B.; Seo, I.H. Modelling and predicting wind velocity patterns for windbreak fence design. J. Wind Eng. Ind. Aerodyn. 2015, 142, 53–64. [Google Scholar] [CrossRef]
- Moskal, L.M.; Zheng, G. Retrieving Forest Inventory Variables with Terrestrial Laser Scanning (TLS) in Urban Heterogeneous Forest. Remote Sens. 2012, 4, 1–20. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M.; Kim, S.H. Retrieval of Effective Leaf Area Index in Heterogeneous Forests with Terrestrial Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 777–786. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing forest metrics with a ground-based scanning lidar. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef]
- Palace, M.; Sullivan, F.B.; Ducey, M.; Herrick, C. Estimating tropical forest structure using a terrestrial lidar. PLoS ONE 2016, 11, e0154115. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez de Tanago, J.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Calders, K. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 2018, 9, 223–234. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Li, C.P.; Guan, W.B.; Fan, Z.P.; Su, F.X.; Wang, X.L. Advances in studies on the structure of farmland shelterbelt ecosystem. Chin. J. Appl. Ecol. 2003, 11, 2037–2043. (In Chinese) [Google Scholar]
- Tao, S.L.; Guo, Q.H.; Xu, S.W.; Su, Y.J.; Li, Y.M.; Wu, F.F. A Geometric Method for Wood-Leaf Separation Using Terrestrial and Simulated Lidar Data. Photogramm. Eng. Remote Sens. 2015, 81, 767–776. [Google Scholar] [CrossRef]
- Wang, M.L.; Wong, M.S. A novel geometric feature-based wood-leaf separation method for large and crown-heavy tropical trees using handheld laser scanning point cloud. Int. J. Remote Sens. 2023, 44, 3227–3258. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and wood classification framework for terrestrial LiDAR point clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
- Wang, D.; Takoudjou, S.M.; Casella, E. LeWoS: A universal leaf-wood classification method to facilitate the 3D modelling of large tropical trees using terrestrial LiDAR. Methods Ecol. Evol. 2020, 11, 376–389. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Luo, F.; Xin, Z.; Gao, J.; Ma, Y.; Li, X.; Liu, H. Ecological Effects of Oasis Shelterbelts in Ulan Buh Desert. In Deserts and Desertification; IntechOpen: London, UK, 2021. [Google Scholar]
- Feng, T.J.; Wang, D.; Wang, R.; Wang, Y.; Xin, Z.; Luo, F.; Ma, Y.; Li, X.; Xiao, H.; Andres, C.C.; et al. Spatial-temporal heterogeneity of environmental factors and ecosystem functions in farmland shelterbelt systems in desert oasis ecotones. Agric. Water Manag. 2022, 271, 107790. [Google Scholar] [CrossRef]
- Cao, B.; Xu, X. Effects of Mixed Forest of Ailanthus altissima and Populus bolleana on Host Choice of Anoplophora glabripennis. Sci. Silvae Sin. 2006, 42, 56–60. (In Chinese) [Google Scholar]
- Zhang, Y.; Liu, F.; Genge, B.; Ma, B.; Huang, Y.; Ba, Y. Evaluation of Growth Adaptability of 20 Poplar Species in Oasis Region of Ulan Buh Sandy Land. Bull. Soil Water Conserv. 2015, 35, 117–121. (In Chinese) [Google Scholar]
- Zhang, W.M.; Qi, J.B.; Wan, P.; Wang, H.T.; Xie, D.H.; Wang, X.Y.; Yan, G.J. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Schraik, D.; Wang, D.; Hovi, A.; Rautiainen, M. Quantifying stand-level clumping of boreal, hemiboreal and temperate European forest stands using terrestrial laser scanning. Agric. For. Meteorol. 2023, 339, 109564. [Google Scholar] [CrossRef]
- Lau, A.; Calders, K.; Bartholomeus, H.; Martius, C.; Raumonen, P.; Herold, M.; Vicari, M.; Sukhdeo, H.; Singh, J.; Goodman, R.C. Tree Biomass Equations from Terrestrial LiDAR: A Case Study in Guyana. Forests 2019, 10, 527. [Google Scholar] [CrossRef]
- Lim, S.P.; Haron, H. Surface reconstruction techniques: A review. Artif. Intell. Rev. 2014, 42, 59–78. [Google Scholar] [CrossRef]
- Arias-Castro, E.; Rodríguez-Casal, A. On estimating the perimeter using the alpha-shape. Ann. De L Inst. Henri Poincare-Probab. Stat. 2017, 53, 1051–1068. [Google Scholar] [CrossRef]
- Cao, J.X.; Tamura, Y.; Yoshida, A. Wind tunnel study on aerodynamic characteristics of shrubby Specimens of three tree species. Urban For. Urban Green. 2012, 11, 465–476. [Google Scholar] [CrossRef]
- Zhang, L.B.; Liang, T.; Wei, X.X.; Wang, H. An improved indicator standardization method for multi-indicator composite evaluation: A case study in the evaluation of ecological civilization construction in China. Environ. Impact Assess. Rev. 2024, 108, 107600. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Li, Y.; Yuan, J.; Song, L.; Li, H.; Wu, M. Estimation model of canopy stratification porosity based on morphological characteristics: A case study of cotton. Biosyst. Eng. 2020, 193, 174–186. [Google Scholar] [CrossRef]
- Fan, Z.P.; Gao, J.G.; Zeng, D.H.; Zhou, X.H.; Sun, X.K. Three-dimensional (3D) structure model and its parameters for poplar shelterbelts. Sci. China-Earth Sci. 2010, 53, 1513–1526. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, W.; Cai, S.; Shao, J.; Cheng, S.; Xie, D.; Yan, G. Stem and branch volume estimation using terrestrial laser scanning data. Natl. Remote Sens. Bull. 2023, 27, 1653–1666. (In Chinese) [Google Scholar] [CrossRef]
- Hildebrandt, R.; Iost, A. From points to numbers: A database-driven approach to convert terrestrial LiDAR point clouds to tree volumes. Eur. J. For. Res. 2012, 131, 1857–1867. [Google Scholar] [CrossRef]
- Lau, A.; Bentley, L.P.; Martius, C.; Shenkin, A.; Bartholomeus, H.; Raumonen, P.; Malhi, Y.; Jackson, T.; Herold, M. Quantifying branch architecture of tropical trees using terrestrial LiDAR and 3D modelling. Trees 2018, 32, 1219–1231. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.-L.; Fournier, R.A.; Côté, J.-F.; Verstraete, M.M. Estimating leaf area distribution in savanna trees from terrestrial LiDAR measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Wang, H.; Takle, E.S. On three-dimensionality of shelterbelt structure and its influences on shelter effects. Bound. Layer Meteorol. 1996, 79, 83–105. [Google Scholar] [CrossRef]
- Poh, H.; Chan, W.; Wise, D.; Lim, C.; Khoo, B.; Gobeawan, L.; Ge, Z.; Eng, Y.; Peng, J.; Raghavan, V.; et al. Wind load prediction on single tree with integrated approach of L-system fractal model, wind tunnel, and tree aerodynamic simulation. AIP Adv. 2020, 10, 075202. [Google Scholar] [CrossRef]
- Mochida, A.; Tabata, Y.; Iwata, T.; Yoshino, H. Examining tree canopy models for CFD prediction of wind environment at pedestrian level. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1667–1677. [Google Scholar] [CrossRef]
- Wuyts, K.; Verheyen, K.; De Schrijver, A.; Cornelis, W.M.; Gabriels, D. The impact of forest edge structure on longitudinal patterns of deposition, wind speed, and turbulence. Atmos. Environ. 2008, 42, 8651–8660. [Google Scholar] [CrossRef]
- Lalic, B.; Mihailovic, D.T.; Rajkovic, B.; Arsenic, I.D.; Radlovic, D. Wind profile within the forest canopy and in the transition layer above it. Environ. Model. Softw. 2003, 18, 943–950. [Google Scholar] [CrossRef]
- Ma, R.; Wang, J.; Qu, J.; Liu, H. Effectiveness of shelterbelt with a non-uniform density distribution. J. Wind Eng. Ind. Aerodyn. 2010, 98, 767–771. [Google Scholar] [CrossRef]
- Yuan, W.; Zhu, N.; Zhang, L.; Tong, R.; Miao, Y.; Zhou, F.; Wang, G.G.; Wu, T. Three-dimensional aerodynamic structure estimation and wind field simulation for wide tree shelterbelts. For. Ecol. Manag. 2024, 559, 121813. [Google Scholar] [CrossRef]
- Gijzen, H.; Goudriaan, J. A flexible and explanatory model of light distribution and photosynthesis in row crops. Agric. For. Meteorol. 1989, 48, 1–20. [Google Scholar] [CrossRef]
- Ding, S.; Su, P. Effects of tree shading on maize crop within a Poplar-maize compound system in Hexi Corridor oasis, northwestern China. Agrofor. Syst. 2010, 80, 117–129. [Google Scholar] [CrossRef]
- Palmer, J.W.; Snelgar, W.P.; Manson, P.J. Shade cast by shelterbelts around kiwifruit orchards; validation of a computer model. Agric. For. Meteorol. 1993, 66, 21–30. [Google Scholar] [CrossRef]
- Holzwarth, F.; Kahl, A.; Bauhus, J.; Wirth, C. Many ways to die–partitioning tree mortality dynamics in a near-natural mixed deciduous forest. J. Ecol. 2013, 101, 220–230. [Google Scholar] [CrossRef]
- Buettel, J.C.; Ondei, S.; Brook, B.W. Look down to see what’s up: A systematic overview of treefall dynamics in forests. Forests 2017, 8, 123. [Google Scholar] [CrossRef]
- Kong, T.; Liu, B.; Henderson, M.; Zhou, W.; Su, Y.; Wang, S.; Wang, G. Effects of shelterbelt transformation on soil aggregates characterization and erodibility in China black soil farmland. Agriculture 2022, 12, 1917. [Google Scholar] [CrossRef]
- Gupta, J.P.; Rao, G.G.S.N.; Gupta, G.N.; Rao, B.R. Soil drying and wind erosion as affected by different types of shelterbelts planted in the desert region of Western Rajasthan, India. J. Arid Environ. 1983, 6, 53–58. [Google Scholar] [CrossRef]
- Luo, W.; Dong, Z.; Qian, G.; Lu, J. Near-wake flow patterns in the lee of adjacent obstacles and their implications for the formation of sand drifts: A wind tunnel simulation of the effects of gap spacing. Geomorphology 2014, 213, 190–200. [Google Scholar] [CrossRef]

| Species | Row | Age (a) | Spacing (m) | Quadrate (m) |
|---|---|---|---|---|
| Populus alba var. pyramidalis Bunge | 5 | 28 | 4.5 × 5 | 20 × 25 |
| Populus popular’s Zhonghua | 4 | 35 | 4 × 5 | 20 × 20 |
| Populus nigra var. thevestina (Dode) Bean | 4 | 33 | 5 × 5 | 20 × 20 |
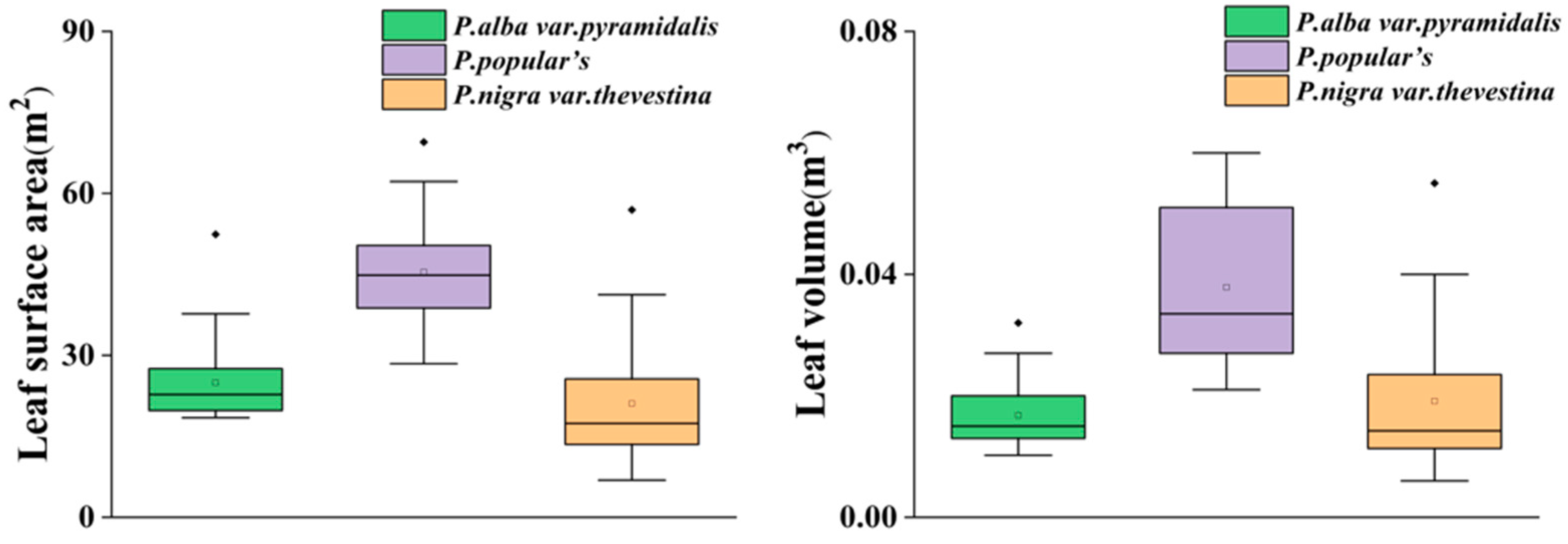
| Species | Height (m) | DBH (m) | Crown Width (m) | Under-Branch Height (m) | Surface Area (m2) | Volume (m3) |
|---|---|---|---|---|---|---|
| P. alba var. pyramidalis | 20.113 | 0.331 | 3.232 | 2.171 | 113.991 | 1.411 |
| P. popular’s | 16.365 | 0.242 | 4.673 | 0.912 | 88.014 | 1.049 |
| P. nigra var. thevestina | 20.241 | 0.290 | 2.911 | 1.384 | 87.219 | 1.068 |
| Species | Height (m) | Width (m) | Length (m) | Op |
|---|---|---|---|---|
| P. alba var. pyramidalis | 20.113 | 25.120 | 450.340 | 0.449 |
| P. popular’s | 16.365 | 20.041 | 196.511 | 0.424 |
| P. nigra var. thevestina | 20.241 | 18.114 | 390.328 | 0.492 |
| Species | Surface Area (m2) | Volume (m3) | Scd (m2·m−3) | Vcd (m3·m−3) | Vp |
|---|---|---|---|---|---|
| P. alba var. pyramidalis | 44,225.921 | 445.254 | 0.205 | 0.002 | 0.532 |
| P. popular’s | 15,789.813 | 154.843 | 0.252 | 0.003 | 0.490 |
| P. nigra var. thevestina | 33,068.122 | 314.342 | 0.235 | 0.002 | 0.528 |
| Structural Parameters | Species | Evaluation Indicators | |||
|---|---|---|---|---|---|
| Bias (m) | rBias (%) | RMSE (m) | rRMSE (%) | ||
| Tree Height | P. alba var. pyramidalis | −1.177 | −5.874 | 1.498 | 7.471 |
| DBH | −0.011 | −3.401 | 0.014 | 4.360 | |
| Crown width | −0.077 | −2.544 | 0.222 | 7.314 | |
| Under-branch height | 0.053 | 2.621 | 0.098 | 4.880 | |
| Tree volume | 0.005 | 1.172 | 0.078 | 16.517 | |
| Tree surface area | −0.796 | 8.190 | 1.052 | 10.830 | |
| Tree Height | P. popular’s | −0.455 | −3.041 | 0.775 | 5.183 |
| DBH | −0.021 | −7.978 | 0.030 | 11.494 | |
| Crown width | −0.239 | −4.946 | 0.4005 | 8.306 | |
| Under-branch height | −0.007 | −0.732 | 0.057 | 5.416 | |
| Tree volume | 0.002 | 0.697 | 0.004 | 1.802 | |
| Tree surface area | −0.078 | 1.393 | 0.127 | 2.278 | |
| Tree Height | P. nigra var. thevestina | −0.755 | −3.669 | 1.005 | 4.883 |
| DBH | −0.007 | −2.260 | 0.222 | 7.019 | |
| Crown width | −0.051 | −1.628 | 0.136 | 4.327 | |
| Under-branch height | 0.140 | 8.779 | 0.183 | 11.483 | |
| Tree volume | 0.009 | 2.750 | 0.015 | 4.676 | |
| Tree surface area | −0.009 | 0.152 | 0.088 | 1.484 | |
| Structural Parameters | Species | Evaluation Indicators | |||
|---|---|---|---|---|---|
| Bias (m) | rBias (%) | RMSE (m) | rRMSE (%) | ||
| Branch length | P. alba var. pyramidalis | 0.140 | 5.812 | 0.206 | 8.550 |
| Branch diameter | 0.002 | 2.614 | 0.001 | 1.832 | |
| Branch angle | −1.815 | −4.003 | 2.687 | 5.906 | |
| Branch volume | 0.006 | 4.122 | 0.008 | 5.554 | |
| Branch surface area | 0.199 | 1.084 | 1.153 | 6.272 | |
| Leaf volume | 0.001 | 2.862 | 0.002 | 15.246 | |
| Leaf surface area | 0.820 | 2.941 | 2.967 | 10.642 | |
| Branch length | P. popular’s | 0.057 | 4.316 | 0.102 | 7.575 |
| Branch diameter | 0.001 | 1.843 | 0.002 | 2.087 | |
| Branch angle | −0.656 | −1.500 | 2.114 | 4.707 | |
| Branch volume | 0.005 | 4.165 | 0.008 | 7.150 | |
| Branch surface area | 0.035 | 0.225 | 0.692 | 4.442 | |
| Leaf volume | −0.001 | −4.692 | 0.005 | 26.325 | |
| Leaf surface area | 1.597 | 2.989 | 3.917 | 9.016 | |
| Branch length | P. nigra var. thevestina | 0.148 | 9.226 | 0.225 | 15.457 |
| Branch diameter | 0.003 | 2.059 | 0.006 | 4.814 | |
| Branch angle | 1.067 | 2.612 | 1.926 | 4.715 | |
| Branch volume | 0.003 | 2.513 | 0.007 | 6.080 | |
| Branch surface area | −0.393 | −2.765 | 1.038 | 7.294 | |
| Leaf volume | −0.001 | −0.946 | 0.001 | 10.911 | |
| Leaf surface area | −2.629 | −23.133 | 3.306 | 29.087 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Xiao, H.; Xin, Z.; Li, J.; Fan, G. Determining the Structural Characteristics of Farmland Shelterbelts in a Desert Oasis Using LiDAR. Forests 2025, 16, 1221. https://doi.org/10.3390/f16081221
Jia X, Xiao H, Xin Z, Li J, Fan G. Determining the Structural Characteristics of Farmland Shelterbelts in a Desert Oasis Using LiDAR. Forests. 2025; 16(8):1221. https://doi.org/10.3390/f16081221
Chicago/Turabian StyleJia, Xiaoxiao, Huijie Xiao, Zhiming Xin, Junran Li, and Guangpeng Fan. 2025. "Determining the Structural Characteristics of Farmland Shelterbelts in a Desert Oasis Using LiDAR" Forests 16, no. 8: 1221. https://doi.org/10.3390/f16081221
APA StyleJia, X., Xiao, H., Xin, Z., Li, J., & Fan, G. (2025). Determining the Structural Characteristics of Farmland Shelterbelts in a Desert Oasis Using LiDAR. Forests, 16(8), 1221. https://doi.org/10.3390/f16081221




