Abstract
Accurate estimation of stem profiles is critical for forest management, timber yield prediction, and ecological modeling. However, traditional taper equations often fail to capture species-specific growth variability and exhibit significant biases, particularly in the upper stem regions. Machine learning regression models were applied to estimate Quercus mongolica stem profiles across South Korea, and performance was compared with that of a traditional taper equation. A total of 2503 sample trees were used to train and validate Random Forest (RF), XGBoost (XGB), Artificial Neural Network (ANN), and Support Vector Regression (SVR) models. Predictive performance was evaluated using root mean square error, mean absolute error, and coefficient of determination metrics, and performance differences were validated statistically. The ANN model exhibited the highest predictive accuracy and stability across all diameter classes, maintaining smooth and consistent stem profiles even in the upper stem regions where the traditional taper model exhibited significant errors. RF and XGB models had moderate performance but exhibited localized fluctuations, whereas the Kozak taper equation tended to overestimate basal diameters and underestimate crown-top diameters. Machine learning models, particularly ANN, offer a robust alternative to fixed-form taper equations, contributing substantially to forest resource inventory, carbon stock assessment, and climate-adaptive forest management planning.
1. Introduction
In response to climate change and the pursuit of sustainable forest management, the role of forests has become increasingly critical. Forests function as vital carbon sinks, absorbing and storing atmospheric carbon dioxide, while also providing essential ecosystem services [,]. Accurate estimation of tree volume is fundamental for the effective management and utilization of forest resources, serving as a basis for forest inventory, timber production planning, biomass estimation, and carbon stock assessment [,,].
Taper equations mathematically model diameter variation along the stem based on measurements such as diameter at breast height (DBH) and total tree height (TH), and they are essential tools for reconstructing tree form and estimating stem volume []. Segmented models proposed by Max and Burkhart [] and variable-exponent models developed by Kozak [,,] have been applied extensively to various tree species. In South Korea, taper equations based on Kozak’s model have been used to develop volume tables and stand yield tables for forest management [].
However, fixed-form taper equations have been criticized for their limited ability to capture species-specific growth characteristics and site-dependent growth variations [,,,,,,,,,,]. Particularly in the upper stem regions (relative height [RH] > 0.7), data collection challenges and increased morphological variability among individual trees often lead to decreased prediction accuracy. Such limitations undermine the reliability of forest resource surveys and negatively impact long-term forest management planning and carbon stock assessments [,,,].
Recent advances in machine learning techniques have opened new possibilities for improving stem profile estimation. Machine learning regression models, such as Random Forest (RF), XGBoost (XGB), Artificial Neural Networks (ANN), and Support Vector Regression (SVR), are capable of learning complex, non-linear relationships among multidimensional input variables without assuming fixed functional forms [,,,,]. RF and XGB effectively capture interactions between variables, whereas ANN excels at modeling high-dimensional, non-linear patterns, making these methods particularly suitable for predicting stem diameters in species with high morphological variability and significant site effects [,,,,,,,,,,].
Despite such advancements, the application of machine learning for stem profile estimation in South Korea remains limited [], particularly for major broadleaved species such as Quercus mongolica. The species, widely distributed across South Korea, exhibits a decurrent growth form and high morphological variability, posing challenges for accurate modeling with traditional fixed-form taper equations [].
The present study applied machine learning regression models (Random Forest, XGBoost, ANN, SVR) to estimate the stem profiles of Q. mongolica across South Korea and to compare their predictive performance with that of the traditional Kozak [] taper equation [,]. This study aimed to demonstrate the feasibility of high-accuracy stem profile estimation, even for morphologically variable broadleaved species, which could facilitate the development of precise forest resource information systems for applications such as digital forest inventory, timber yield prediction, and carbon stock assessment.
2. Materials and Methods
2.1. Study Materials
The present study was based on stem profile data collected from Q. mongolica trees across South Korea. The dataset included measurements of TH, DBH, stem height (SH), and tree age. The dataset consisted of 2503 individual Quercus mongolica trees sampled from 51 forest stands located within state-owned forests managed by the Korea Forest Service. The data were collected across 27 National Forest Management Offices, with efforts made to ensure that the number of trees sampled per site was as evenly distributed as possible. Tree height and DBH were measured following standard forest inventory protocols. For each tree, cross-sectional diameters were obtained every 2 m along the stem from 0.2 m above ground up to the top. When the remaining distance to the apex was less than 2 m, additional measurements were taken at 1 m intervals. After felling and branch removal, vertical height from the ground to the crown apex was measured using a tape. DBH was measured at 1.2 m above ground level. Stem diameter data were collected at consistent relative heights, based on the proportion of stem height to total height. To improve data quality, outliers were removed and missing values addressed. Additionally, an RH variable was established to account for the irregular stem form characteristic of Q. mongolica. In total, 2503 individual trees were analyzed, with a mean DBH of 18.35 cm, a mean TH of 12.56 m, and a mean age of 35.91 years. DBH was 6–46 cm, TH was 4–21 m, and age was 13–62 years (Table 1; Figure 1 and Figure 2).

Table 1.
Summary statistics of the diameter at breast height (DBH), tree height (TH), and age for the Quercus mongolica trees sampled in the present study.
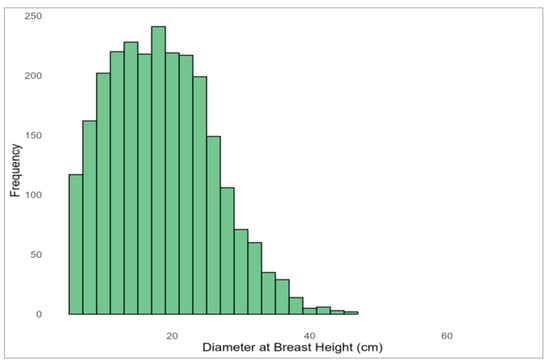
Figure 1.
Histogram of the diameter at breast height (DBH) distribution for sampled Quercus mongolica trees.
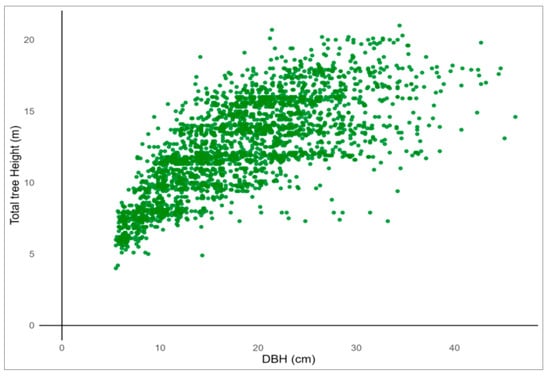
Figure 2.
Scatter plot of the diameter at breast height (DBH) versus total tree height (TH) for sampled Quercus mongolica trees.
2.2. Variable Exponent-Based Model
Stem profile-based volume estimation provides a non-destructive method for accurately assessing individual tree growth, and it has been applied widely in forest management planning and productivity assessments in countries such as the United States and Canada. In South Korea, stem profile models have been developed for major species []. In the present study, a variable-exponent taper model structure was adopted to capture the continuity and flexibility of stem form simultaneously. Specifically, the model proposed by Kozak was employed [] (Table 2).

Table 2.
Kozak (1988) [] stem taper equation used for model comparison in this study.
Unlike segmented approaches such as the method proposed by Max & Burkhart [], the Kozak model expresses the entire stem profile as a continuous function, enabling smooth diameter transitions. Its flexibility in controlling both basal and crown forms makes it highly practical for estimating merchantable volume [].
In the present study, data were collected based on the diameter outside bark (DOB). Although the original Kozak [] model was developed for diameter inside bark (DIB), previous studies have confirmed a strong linear relationship between DOB and DIB, justifying the application of the model to DOB data [,]. The variable-exponent structure allows the model to continuously represent transitions from neiloid to paraboloid to conical shapes along the stem, outperforming simple and segmented taper equations in terms of both shape reconstruction and prediction accuracy [].
However, the statistical complexity of the model and the high numerical stability required during diameter prediction have been cited as practical limitations.
Model parameters were estimated using non-linear least squares (NLS) via the nls() function in R. Initial values were selected based on preliminary data analysis and previous studies. Optimization was conducted to minimize prediction error. Model goodness-of-fit and predictive performance were evaluated using root mean square error (RMSE) and the coefficient of determination (R2).
2.3. Development of Machine Learning Regression Models
To improve the accuracy of stem profile estimation for Q. mongolica, the present study applied four representative machine learning regression models: Random Forest (RF), XGBoost (XGB), Artificial Neural Network (ANN), and Support Vector Regression (SVR). The models were selected based on their ability to effectively capture the non-linear and complex structure of stem profile data.
Random Forest is an ensemble method that builds multiple decision trees using bootstrap sampling and random feature selection, aggregating their predictions to produce the final output. It offers high predictive stability and resistance to overfitting, making it particularly suitable for modeling complex non-linear patterns. In the present study, RF was employed to robustly capture intricate variations in stem shape [].
XGBoost is a gradient boosting framework that incrementally minimizes residual errors through iterative model updates. It offers advantages such as high computational efficiency, built-in regularization to prevent overfitting, and flexible hyperparameter tuning. Considering the strong non-linearity and multi-scale variability of stem profile data, XGB was applied to effectively model the complexities [].
Artificial Neural Networks consist of an input layer, one or more hidden layers, and an output layer, with neurons connected through weighted links. ANN models are well-suited for learning complex and high-dimensional nonlinear patterns. In the present study, both single-hidden-layer and double-hidden-layer structures were tested, adjusting the number of neurons per layer and activation functions to optimize model complexity [].
Support Vector Regression is a model that seeks a function within a specified margin of tolerance, penalizing samples outside the margin. By employing a radial basis function (RBF) kernel, SVR maps input features into a higher-dimensional space to effectively capture non-linear relationships. SVR was selected for its robustness in handling small or irregular datasets, making it suitable for the varied patterns in stem profile data [,].
2.4. Model Training and Validation
The dataset was divided into training, validation, and test subsets at a 70:15:15 ratio, based on individual trees. To minimize the risk of spatial autocorrelation, trees from the same location were assigned to the same subset, ensuring no overlap across groups.
All models were trained to predict external stem diameter (DOB) based on three input variables, namely, diameter at breast height (DBH), total tree height (TH), and relative height (RH). For ANN and SVR models, input variables were standardized using the mean and standard deviation of the training dataset to account for scale sensitivity.
Model training involved fitting each algorithm to the training data, while hyperparameter optimization was performed using the validation set to prevent overfitting. Final model evaluation was conducted on the independent test set (Table 3).

Table 3.
Formulas for calculating root mean square error (RMSE), mean absolute error (MAE), and coefficient of determination (R2) for model performance evaluation.
RMSE (Root Mean Square Error) measures the magnitude of prediction errors, with lower values indicating higher accuracy. MAE (Mean Absolute Error) quantifies the average absolute difference between predicted and observed values, providing a measure that is less sensitive to outliers. R2 represents the proportion of variance in the observed data explained by the model, with values closer to 1 indicating better explanatory power.
During model development, the following optimization strategies were employed:
- Random Forest and XGBoost: Key hyperparameters (e.g., tree depth, number of trees, learning rate) were optimized through grid search combined with five-fold cross-validation.
- Artificial Neural Network: The number of hidden layers (one or two) and neurons per layer (32 or 64) were adjusted, using the ReLU activation function and the Adam optimizer (learning rate = 0.001).
- Support Vector Regression: An RBF kernel was employed, and hyperparameters were optimized through grid search over the ranges C ∈ {0.1,1,10,100} and ϵ ∈ {0.01,0.1,0.5}
Final predictive performance was evaluated using the test dataset, and model comparisons were statistically validated to assess significant differences in predictive accuracy. The following R packages were used for modeling and evaluation: randomForest (RF), xgboost (XGB), nnet (ANN), e1071 (SVR), caret (model training and validation workflows), and ggplot2 (visualization).
2.5. Comparison of Model Performance and Statistical Significance in the Methodology
To quantitatively compare the predictive performance of the machine learning models, statistical significance tests were conducted based on the evaluation metrics (RMSE, R2, and MAE) computed from the test dataset. Performance comparisons were made between each pair of models using predictions derived from the same set of test samples.
To assess the statistical significance of performance differences, both paired t-tests and Wilcoxon signed-rank tests were applied. When differences in prediction errors (RMSE, MAE) were assumed to follow a normal distribution, a paired t-test was employed. The normality assumption was evaluated using the Shapiro–Wilk test, and if the null hypothesis could not be rejected at a significance level of p = 0.05, the paired t-test was applied [,,].
In cases where the normality assumption was violated or the distribution characteristics were ambiguous, the non-parametric Wilcoxon signed-rank test was employed. This test does not require any distributional assumptions and yields reliable results even with small sample sizes.
All statistical analyses were performed using R software (version 4.3.2; R Foundation for Statistical Computing, Vienna, Austria). The paired t-tests were conducted using the t.test() function, and Wilcoxon signed-rank tests were conducted using the wilcox.test() function. Results were interpreted based on p-values, with a significance threshold set at p = 0.05.
3. Results and Discussion
3.1. Prediction Results Using the Variable-Exponent Model
The variable-exponent taper model proposed by Kozak [] was applied to estimate Q. mongolica stem profiles. The model uses RH as the independent variable to describe diameter variation along the stem and was calibrated using NLS estimation.
Model performance was evaluated on the test dataset. The results showed an RMSE of 0.919 cm and an R2 value of 0.987, indicating a high level of accuracy in predicting diameter along the stem (Table 4).

Table 4.
Estimated parameters and model fit statistics (coefficient of variation [R2], root mean square error [RMSE]) for the Kozak taper equation.
The scatter plot of observed versus predicted values (Figure 3) demonstrated a strong clustering around the 1:1 line, confirming the model’s overall consistency. Residual analysis revealed that residuals were relatively evenly distributed between RH 0.2 and 0.8, whereas larger fluctuations were observed near the stem base (RH close to 0) and top (RH close to 1). These edge-region deviations suggest a limitation in the model’s capacity to fully account for structural irregularities, such as crown taper or basal swelling, when using a single continuous function to describe the entire stem. Similar patterns have been reported in previous studies, including Kozak [,] and Sharma & Zhang [], where structural features such as abrupt diameter decreases near the crown or bark thickening at the base were identified as major contributors to increased model error. As this study used outside-bark diameter (DOB) for modeling, small discrepancies may also result from variation in bark thickness.
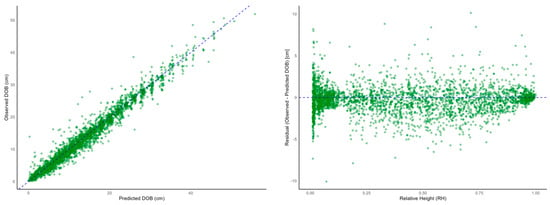
Figure 3.
Scatter plot (left) and residual plot (right) for observed versus predicted values using the Kozak taper model.
Nevertheless, the RMSE and R2 values obtained in this study indicate superior predictive performance compared to previous studies. These findings support the practical applicability of the Kozak model in accurately representing the average stem form of Quercus mongolica [].
3.2. Prediction Results and Performance Comparison of Machine Learning Models
In the present study, four machine learning models—RF, XGB, ANN, and SVR—were trained to predict Q. mongolica stem profiles. The models utilized DBH, TH, and RH as input variables, and their predictive performance was evaluated using the test dataset.
The performance metrics for each model are summarized in Table 5. The ANN model achieved the highest predictive accuracy, with an RMSE of 1.654 cm, an R2 of 0.968, and an MAE of 1.138 cm. The SVR model followed, achieving an RMSE of 1.710 cm, an R2 of 0.966, and an MAE of 1.170 cm. In contrast, the RF and XGB models exhibited slightly higher errors, with RMSE values of 1.829 cm and 1.834 cm, respectively, and R2 values of 0.963 and 0.960, respectively.

Table 5.
Prediction performance of machine learning regression models (Random Forest [RF], XGBoost [XGB], Artificial Neural Network [ANN], Support Vector Regression [SVR]) for stem diameter estimation.
The superior performance of the ANN model is attributed to its ability to learn complex, high-dimensional nonlinear patterns inherent in the stem profile data. Similarly, the SVR model demonstrated robust predictive performance, maintaining stability even across regions of high data variability. Conversely, the RF and XGB models, while effective at capturing localized patterns, showed limitations in modeling the continuous variation across the entire stem profile.
Visualization of observed versus predicted values (Figure 4, left column) revealed that all models produced reasonable distributions around the 1:1 reference line, with ANN and SVR models particularly excelling in maintaining prediction stability for outlier cases. Analysis of residuals against RH (Figure 4, right column) showed that ANN and SVR achieved relatively uniform residual distributions across the stem, whereas RF and XGB exhibited increased errors in the upper crown region (RH > 0.7).
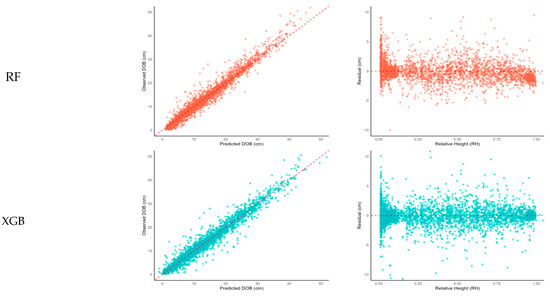
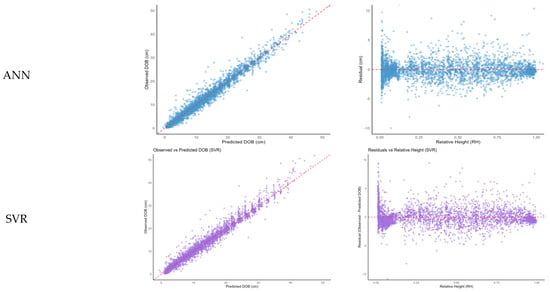
Figure 4.
Scatter plots (left) and residual plots (right) for observed versus predicted values by machine learning models (Random Forest [RF], XGBoost [XGB], Artificial Neural Network [ANN], Support Vector Regression [SVR]). DOB: diameter outside bark.
Specifically, the RF and XGB models showed a tendency for error magnification above RH 0.7, likely due to their structural limitations in approximating the rapid diameter decrease in the upper stem. RF, an ensemble model aggregating multiple decision trees based on bootstrap sampling and random feature selection [], is well-suited for capturing localized variations but may struggle to model continuous trends such as stem profiles []. The inherent design of tree-based models, which optimizes local splits, can lead to difficulty in maintaining the smooth, continuous changes observed along the entire stem, particularly near the crown.
In contrast, the ANN model maintained stable predictions across the entire range of RH, including the crown region, highlighting its strength in modeling high-dimensional non-linear patterns. The SVR model also exhibited generally stable residual distributions but exhibited slightly increased variability below RH 0.2, suggesting potential difficulties in modeling structural irregularities near the tree base [].
The results indicate that ANN and SVR models, due to their ability to effectively capture high-dimensional and non-linear growth patterns, are more suitable for predicting stem profiles of broadleaved species like Q. mongolica, where structural irregularities and abrupt diameter changes are common.
3.3. Model Performance Comparison and Statistical Significance Testing
To statistically validate the differences in predictive performance among the models, absolute errors (AEs) between the predicted and observed diameters over bark (DOB) were calculated for each model across the test dataset.
Pairwise model comparisons were conducted for ANN vs RF, ANN vs XGBoost, ANN vs SVR, and ANN vs the traditional Kozak taper equation. For each model pair, the difference in absolute errors (ΔError) was computed. The Shapiro–Wilk test was first applied to assess the normality of the error differences. Since most comparisons showed non-normal distributions (p < 0.05), the non-parametric Wilcoxon signed-rank test was used to evaluate statistical significance. All analyses were conducted using R v4.3.2 with the wilcox.test () function, adopting a significance level of α = 0.05.
The results are summarized in Table 6. The ANN model showed significantly lower prediction errors than RF, SVR, and the traditional Kozak taper model (p < 0.01 for all cases), indicating superior performance in terms of accuracy. However, there was no statistically significant difference between ANN and XGBoost (p = 0.6588), suggesting that their predictive performances were comparable [].

Table 6.
Statistical comparison results (Wilcoxon signed-rank test p-values) of prediction performance among all models, including the traditional Kozak taper equation.
These findings support the robustness of ANN in modeling stem profiles, especially in species like Quercus mongolica with high morphological variability. While the Kozak taper model has been widely used in Korean forest inventory systems due to its simplicity and empirical basis, the ANN model significantly outperformed it in terms of prediction accuracy. This was particularly evident in the upper stem regions and in small-diameter trees, as visualized in Figure 5
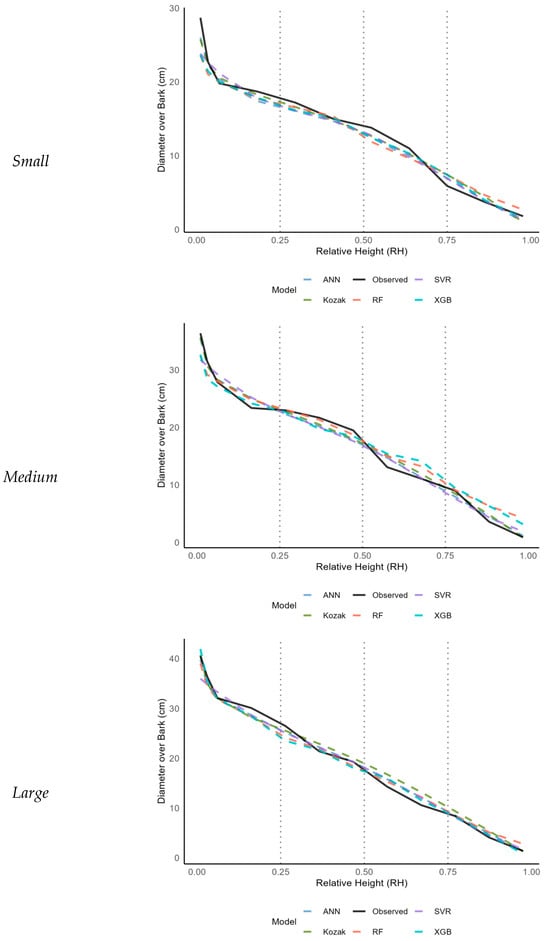
Figure 5.
Comparison of stem profiles for representative trees based on the diameter at breast height (DBH) class (small, medium, large) predicted by the Kozak and machine learning models.
The superior performance of ANN is likely attributable to its multilayer perceptron architecture, which effectively captures complex, non-linear relationships throughout the stem. In contrast, RF and SVR exhibited greater residual variability in the crown regions, while XGBoost performed comparably to ANN, potentially due to its boosting structure that improves local predictions [].
Overall, these results highlight the practical viability of machine learning models—particularly ANNs—as alternative taper modeling tools under Korea’s current forest inventory framework.
3.4. Visualization and Interpretation of Representative Tree Stem Profiles
To further evaluate the predictive characteristics of each model, representative trees from small, medium, and large diameter classes were selected, and their stem diameter (DOB) variations were visualized (Figure 5). The DBH-based diameter classes were defined as follows: small (<20 cm), medium (20–30 cm), and large (>30 cm). The models compared were the Kozak taper equation, RF, ANN, XGB, and SVR, with performance assessed based on their agreement with observed data.
For large-diameter trees, both the ANN and XGB models produced stem profiles aligned closely with the observed measurements across the full stem height, maintaining smooth and continuous patterns even in the upper crown region (RH > 0.7). The SVR model exhibited slight overestimation in the upper stem, whereas the RF model showed greater fluctuations in the middle stem section. The Kozak taper model tended to overestimate diameters near the base and underestimate them near the crown.
In medium-diameter trees, differences between models became more pronounced. The ANN model maintained high agreement across the entire stem, whereas the XGB model performed well up to the middle section but tended to underestimate diameters in the upper crown. The RF model displayed increased variability in the middle region, and the SVR model exhibited slight underestimation in the upper stem. The Kozak taper model exhibited larger prediction deviations at both the base and crown.
In small-diameter trees, prediction differences among models became even more apparent toward the crown. Whereas the ANN model maintained stable predictions closely matching the observed values even at higher RHs, the RF and XGB models exhibited increased oscillations, leading to reduced reliability. The SVR model performed adequately through the middle sections but exhibited underestimation near the crown. The Kozak taper model displayed significant overprediction errors in the highly variable upper portions of the stem.
These visualization results align with findings from previous studies. Pokhrel et al. [] reported that fixed-form taper equations, such as the Kozak model, exhibited biases at both the stem base and crown, whereas variable-exponent models provided more stable predictions. Similarly, Sandoval & Acuña [] demonstrated that ANN models outperformed traditional taper functions in predicting diameters and volumes of Nothofagus species, maintaining consistent accuracy even in upper stem regions. Consistent with the findings, the present study confirmed that the ANN model maintained robust predictive performance across the entire stem of Q. mongolica, even under high morphological variability.
Furthermore, Gómez-García et al. [] emphasized that traditional taper functions were insufficient to fully describe the stem profiles of decurrent-form species such as Quercus rubra, advocating for the development of whole-tree volume equations. The present study’s results corroborate this view, demonstrating that ANN-based models can effectively overcome the limitations of fixed-form taper functions in modeling the complex, irregular stem profile characteristics of broadleaved species like Q. mongolica.
4. Conclusions
This study evaluated the performance of four machine learning models, RF, XGB, ANN, and SVR, in predicting stem profiles of Quercus mongolica, a representative native broadleaf species in Korea. Among the models, ANN exhibited superior performance, particularly in the crown and basal stem sections, where traditional taper equations often show substantial prediction errors. While RF and XGB demonstrated robust and interpretable results, SVR was advantageous in scenarios with limited training data. A key strength of machine learning-based stem profile models lies in their ability to flexibly capture complex and irregular stem shapes without assuming a predetermined functional form. This is particularly beneficial for broadleaf species with irregular tapering patterns caused by crown lifting, asymmetric growth, or large branches. By utilizing fine-scale predictors such as RH and DOB, the models achieved consistent accuracy across the full stem length.
In Korea, standardized stem volume tables based on the Kozak taper equation are widely used in forest practice. However, these tables rely on fixed function structures that may not adequately reflect variability in stem shape across different species or site conditions. In contrast, machine learning approaches can adapt to diverse patterns found in the data, offering higher flexibility and better field applicability. As such, the proposed models have both academic and practical significance in overcoming the structural limitations of conventional taper functions.
Importantly, the models employed only readily measurable variables, DBH, TH, RH, and DOB, enabling immediate application in forest inventory and log-grade estimation without the need for additional measurements. This makes the models suitable for a range of operational uses, including precise stem volume estimation, log quality classification, and carbon stock assessment. Furthermore, these models can be integrated with remote sensing technologies such as UAV or TLS to establish next-generation digital forest monitoring systems.
Future studies should aim to incorporate environmental and ecological variables—including climate factors (e.g., temperature, precipitation), site conditions (e.g., slope, aspect, elevation), and stand dynamics (e.g., competition index, dominance)—to better capture the biological mechanisms influencing stem form development. Integrating such ecological knowledge into data-driven models may enhance their explanatory power and facilitate climate-adaptive forest management and sustainable resource planning.
Author Contributions
Conceptualization, C.K. and C.L.; methodology, C.K. and M.L.; software, C.K. and C.L.; validation, C.K. and J.K.; formal analysis, C.K.; investigation, C.K.; resources, C.K. and D.K.; data curation, C.K. and M.L.; writing—original draft preparation, C.K.; writing—review and editing, C.K. and D.K.; visualization, C.K.; supervision, J.K.; project administration, C.K.; funding acquisition, C.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Institute of Forest Science, grant number FM0300-2024-01-2025.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AE | Absolute Error |
| ANN | Artificial Neural Network |
| DBH | Diameter at Breast Height |
| DOB | Diameter Outside Bark |
| DIB | Diameter Inside Bark |
| MAE | Mean Absolute Error |
| NLS | Non-linear Least Squares |
| RMSE | Root Mean Square Error |
| R2 | Coefficient of Determination |
| RBF | Radial Basis Function |
| SVR | Support Vector Regression |
| SH | Stem Height |
| TH | Tree Height |
References
- Shin, J.-H.; Han, H.; Ko, C.; Kang, J.T.; Kim, Y.-H. Applying nonlinear mixed-effects models to taper equations: A case study of Pinus densiflora in Gangwon Province, Republic of Korea. J. Korean Soc. For. Sci. 2022, 111, 136–149. [Google Scholar] [CrossRef]
- Lee, M.W.; Lee, S.; You, J.W.; Kang, J.T.; Lee, Y.J.; Ko, C. Estimating greenhouse gas (GHG) removal by Cryptomeria japonica and Chamaecyparis obtusa Stands using new stem volume tables. J. Korean Soc. For. Sci. 2023, 112, 515–522. [Google Scholar] [CrossRef]
- Abegg, M.; Bösch, R.; Kükenbrink, D.; Morsdorf, F. Tree volume estimation with terrestrial laser scanning—Testing for bias in a 3D virtual environment. Agric. For. Meteorol. 2023, 331, 109348. [Google Scholar] [CrossRef]
- Bae, E.J.; Joo, J.W.; Jeong, J.Y.; Choi, S.-Y.; Roh, H.; Park, J.-H.; Son, Y.-M. Estimation of annual carbon absorption and derivation of stem taper form for Quercus glauca. J. Agric. Life Sci. 2023, 57, 23–30. [Google Scholar] [CrossRef]
- You, L.; Chang, X.; Sun, Y.; Pang, Y.; Feng, Y.; Song, X. Volume Estimation of Stem Segments Based on a Tetrahedron Model Using Terrestrial Laser Scanning Data. Remote Sens. 2023, 15, 5060. [Google Scholar] [CrossRef]
- Tewari, V.P.; Kumar, V.S.K. Construction and validation of tree volume functions for Dalbergia sissoo grown under irrigated conditions in the hot desert of India. J. Trop. For. Sci. 2001, 13, 503–511. [Google Scholar]
- Max, T.A.; Burkhart, H.E. Segmented polynomial regression applied to taper equations. For. Sci. 1976, 22, 283–289. [Google Scholar]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1363–1368. [Google Scholar] [CrossRef]
- Kozak, A. Effects of multicollinearity and autocorrelation on the variable-exponent taper functions. Can. J. For. Res. 1997, 27, 619–629. [Google Scholar] [CrossRef]
- Kozak, A. My last words on taper equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef]
- National Institute of Forest Science (NIFoS). Stem Volume and Biomass, Yield Table; NIFoS: Seoul, Republic of Korea, 2023. [Google Scholar]
- Kublin, E.; Breidenbach, J.; Kändler, G. A flexible stem taper and volume prediction method based on mixed-effects B-spline regression. Eur. J. For. Res. 2013, 132, 983–997. [Google Scholar] [CrossRef]
- Lee, W.K. Stem and stand taper model using spline function and linear equation. J. Korean Soc. For. Sci. 1994, 83, 63–74. [Google Scholar]
- Fonweban, J.; Gardiner, B.; Macdonald, E.; Auty, D. Taper functions for Scots pine (Pinus sylvestris L.) and Sitka Spruce (Picea sitchensis (Bong.) Carr.) in Northern Britain. Forestry 2011, 84, 49–60. [Google Scholar] [CrossRef]
- Li, R.; Weiskittel, A.R. Comparison of model forms for estimating stem taper and volume in the primary conifer species of the North American Acadian region (Comparaison de formules modèles pour estimer la décroissance de la tige et le volume des principales espèces de conifères dan). Ann. For. Sci. 2010, 67, 302. [Google Scholar] [CrossRef]
- Arias-Rodil, M.; Castedo-Dorado, F.; Cámara-Obregón, A.; Diéguez-Aranda, U. Fitting and Calibrating a Multilevel Mixed-Effects Stem Taper Model for Maritime Pine in NW Spain. PLoS ONE 2015, 10, e0143521. [Google Scholar] [CrossRef]
- Kang, J.T.; Ko, C.U. The development of a stem taper equation and a stem table for standing trees of Chamaecyparis obtusa on Jeju island and in the southern regions of South Korea. J. Korean Isl. (TJOKI) 2020, 32, 221–233. [Google Scholar] [CrossRef]
- Ko, C.; Lee, S.H.; Lee, S.J.; Kim, D.G.; Kang, J.T. Development of a stem taper equation and a stem table for Cryptomeria japonica Stands in South Korea. J. Korean Soc. For. Sci. 2020, 109, 461–467. [Google Scholar]
- Hjelm, B. Taper and Volume Equations for Poplar Trees Growing on Farmland in Sweden. Licentiate Thesis, Department of Energy and Technology, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2011. [Google Scholar]
- Ko, C.; Moon, G.H.; Yim, J.S.; Lee, S.; Kim, D.G.; Kang, J.T. Estimation and comparison of stem volume for Larix kaempferi in South Korea using the stem volume model. J. Korean Soc. For. Sci. 2019, 108, 592–599. [Google Scholar] [CrossRef]
- Son, Y.M.; Jeon, J.H.; Pyo, J.K.; Kim, K.N.; Kim, S.W.; Lee, K.H. Development of stem volume table for Robinia pseudoacacia using Kozak’s stem profile model. J. Agric. Life Sci. 2012, 46, 43–49. [Google Scholar]
- Son, Y.M.; Kim, S.W.; Lee, S.J.; Kim, J.S. Estimation of stand yield and carbon stock for Robinia pseudoacacia Stands in Korea. J. Korean Soc. For. Sci. 2014, 103, 264–269. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Vapnik, V.; Smola, A.J. Support Vector regression machines. In Advances in Neural Information Processing Systems; Touretzky, D.S., Mozer, M.C., Hasselmo, M.E., Eds.; MIT Press: Cambridge, MA, USA, 1996; Volume 9, pp. 155–161. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support Vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Scrinzi, G.; Marzullo, L.; Galvagni, D. Development of a neural network model to update forest distribution data for managed alpine stands. Ecol. Model. 2007, 206, 331–346. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G.; Learning, D. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Nunes, M.H.; Görgens, E.B. Artificial intelligence procedures for tree taper estimation within a complex vegetation mosaic in brazil. PLoS ONE 2016, 11, e0154738. [Google Scholar] [CrossRef]
- Mauro, F.; Frank, B.; Monleon, V.J.; Temesgen, H.; Ford, K.R. Prediction of diameter distributions and tree-lists in Southwestern Oregon using LiDAR and stand-level auxiliary information. Can. J. For. Res. 2019, 49, 775–787. [Google Scholar] [CrossRef]
- Socha, J.; Netzel, P.; Cywicka, D. Stem taper approximation by artificial neural network and a regression set models. Forests 2020, 11, 79. [Google Scholar] [CrossRef]
- Yang, S.I.; Burkhart, H.E. Robustness of parametric and nonparametric fitting procedures of tree-stem taper with alternative definitions for validation data. J. For. 2020, 118, 576–583. [Google Scholar] [CrossRef]
- Salekin, S.; Catalán, C.H.; Boczniewicz, D.; Phiri, D.; Morgenroth, J.; Meason, D.F.; Mason, E.G. Global tree taper modelling: A review of applications, methods, functions, and their parameters. Forests 2021, 12, 913. [Google Scholar] [CrossRef]
- Sandoval, S.; Acuña, E. Stem taper estimation using artificial neural networks for Nothofagus Trees in natural forest. Forests 2022, 13, 2143. [Google Scholar] [CrossRef]
- Yang, S.I.; Burkhart, H.E.; Seki, M. Evaluating semi- and nonparametric regression algorithms in quantifying stem taper and volume with alternative test data selection strategies. Forestry 2023, 96, 465–480. [Google Scholar] [CrossRef]
- Pokhrel, N.R.; Subedi, M.R.; Malego, B. Fitting and evaluating taper functions to predict upper stem diameter of planted teak (Tectona grandis L.f.) in eastern and central regions of Nepal. Forests 2025, 16, 77. [Google Scholar] [CrossRef]
- Lee, S.H.; Ko, C.U.; Shin, J.H.; Kang, J.T. Estimation of Stem Taper for Quercus acutissima Using Machine Learning Techniques. J. Agirc Life Sci. 2020, 54, 29–37. [Google Scholar] [CrossRef]
- Ko, C.; Kang, J.T.; Son, Y.M.; Kim, D.-G. Estimating stem volume using stem taper equation for Quercus mongolica in South Korea. For. Sci. Technol. 2019, 15, 58–62. [Google Scholar] [CrossRef]
- Czaplewski, R.L.; Brown, A.S.; Guenther, D.G. Estimating Merchantable Tree Volume in Oregon and Washington Using Stem Profile Models; res [Note], PNW-RN; USDA Forest Service: Fort Collins, CO, USA, 1989; Volume 459, pp. 1–15. [Google Scholar]
- Li, R.; Weiskittel, A.; Dick, A.R.; Kershaw, J.A., Jr.; Seymour, R.S. Regional stem taper equations for eleven conifer species in the Acadian region of North America: Development and assessment. North J. Appl. For. 2012, 29, 5–14. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of Shapiro–Wilk, Kolmogorov–Smirnov, Lilliefors and Anderson–darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann Publishers: Waltham, MA, USA, 2011; pp. 394–395. [Google Scholar]
- Sharma, M.; Zhang, S.Y. Variable-exponent taper equations for jack pine, black Spruce, and balsam fir in Eastern Canada. For. Ecol. Manag. 2004, 198, 39–53. [Google Scholar] [CrossRef]
- Özçelik, R.; Diamantopoulou, M.J.; Trincado, G. Evaluation of potential modeling approaches for Scots pine stem diameter prediction in north-eastern Turkey. Comput. Electron. Agric. 2019, 162, 773–782. [Google Scholar] [CrossRef]
- de la Torre, F.; Kanade, T. Smooth and consistent probabilistic regression trees. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 8289–8299. [Google Scholar]
- Moeinaddini, M.; Zhang, S.Y.; Auty, D. Nonlinear modeling of tree stem profiles using deep learning algorithms: A comparison with classical taper equations. Eur. J. For. Res. 2023, 142, 311–327. [Google Scholar]
- Sakici, O.E.; Ozdemir, G. Stem taper estimations with artificial neural networks for mixed oriental beech and Kazdağı fir stands in Turkey. CERNE 2018, 24, 439–451. [Google Scholar] [CrossRef]
- Gómez-García, E.; Alonso Ponce, R.; Pérez-Rodríguez, F.; Molina Terrén, C. A preliminary system of equations for predicting merchantable whole-tree volume for the decurrent non-native Quercus rubra L. Grown in Navarra (Northern Spain). Forests 2024, 15, 1698. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).