Vibration Control of Forestry Storage Ventilation Fans Through Structural Parameter Optimization Considering Substructure Uncertainty

Abstract

The operational stability and vibration performance of large-scale ventilation fans used in forestry storage facilities are critical for ensuring the safety and environmental control of timber and wood-based materials. To effectively reduce vibration levels and mitigate resonance risks, this study proposes a structural parameter optimization method that explicitly considers substructure uncertainty. By establishing an interval uncertainty optimization model, critical substructures and key structural parameters affecting natural frequencies were systematically identified. Structural parameters were optimized using response surface methodology to maximize the separation between the fan’s natural frequencies and its operating frequency, thereby reducing the likelihood of resonance. Experimental results validated a substantial reduction in vibration levels, confirming the method’s effectiveness in enhancing operational stability and prolonging the service life of these large-scale ventilation systems. This approach provides valuable insights and practical guidance for vibration control and reliability improvement of mechanical equipment in forestry storage and environmental control systems

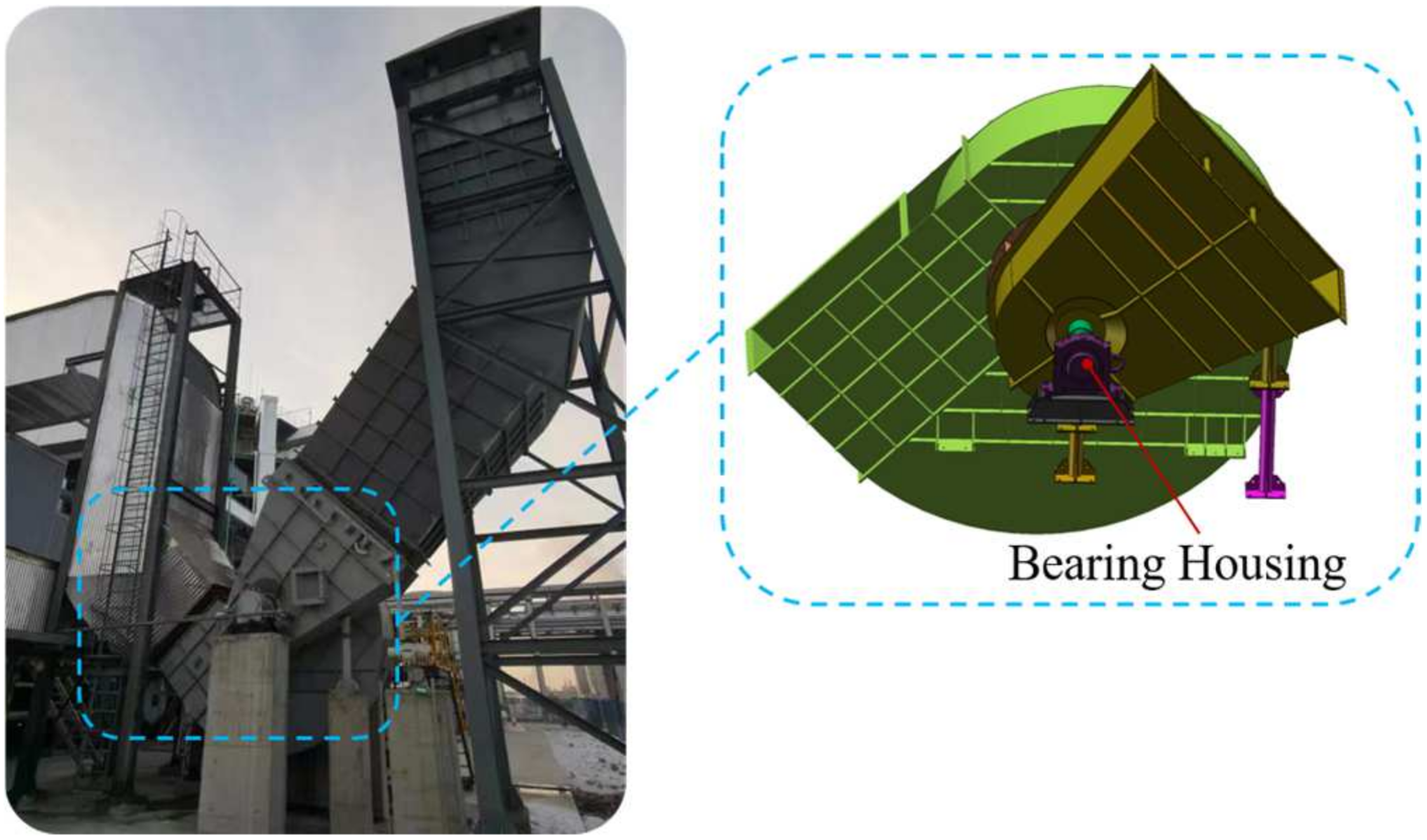
1. Introduction

In the forest product supply chain, the safe storage of timber and wood-based materials is crucial for ensuring material quality and minimizing resource loss [1,2]. Currently, forestry storage methods are predominantly open-air or semi-enclosed, relying on natural ventilation to regulate humidity and temperature. However, with the increasing demand for high-value wood products, as well as the need to enhance storage quality and duration, closed storage systems combined with mechanical ventilation have gradually become a viable development direction. These systems provide more stable environmental control, especially under complex climatic conditions, but also introduce new challenges regarding operational stability and equipment reliability.

Large-scale ventilation fans, as core components that maintain environmental stability in forestry storage warehouses, play a crucial role. These systems directly impact the moisture content, preservation time, and overall quality of stored timber, while also significantly affecting energy consumption and storage costs [3,4,5]. However, uncertainties in the fan structure—such as material fluctuations, manufacturing errors, and assembly deviations—often lead to operational issues, including excessive vibrations and resonance risks. These problems not only affect the effectiveness of environmental control but also reduce the reliability and lifespan of the equipment.

With the rapid advancement of engineering technologies, modern optimization techniques such as genetic algorithms and particle swarm optimization, combined with finite element analysis, have provided effective methods for achieving vibration suppression [6,7]. Some of these methods have been applied to the design of industrial fans and ventilation systems. For example, Zhou et al. [8] performed modal and harmonic response analysis of a volute-less centrifugal fan structure, significantly improving its dynamic performance. Fakhari [9] optimized the blade structure of axial-flow ventilation fans, achieving a balance between aerodynamic and acoustic performance. Despite these advancements, most existing research on fan systems has not systematically considered the impact of uncertainties in the structure on the system’s dynamic behavior. Furthermore, most studies have concentrated on general industrial scenarios, with few addressing the specific needs of fans used in forestry closed storage systems. The fan structures in forestry ventilation systems are complex, and each component introduces varying degrees of uncertainty due to material differences, manufacturing tolerances, and assembly deviations, thereby increasing the difficulty of optimization [10,11]. Additionally, due to the large size and complex operating environments of these fans, the optimization process must simultaneously balance structural stability, vibration control, and airflow efficiency, making precise optimization more challenging [12,13,14]. In large-scale finite element modeling and uncertainty analysis, high computational costs make it difficult to balance both accuracy and efficiency using traditional optimization methods [15,16].

In recent years, some uncertainty optimization methods, such as interval finite element methods, Bayesian calibration, and surrogate modeling techniques, have provided new approaches for enhancing the robustness of system design [17,18,19]. Particularly in large and complex structural systems, traditional global modeling faces computational bottlenecks when dealing with high-dimensional uncertainty parameters, and substructuring methods have gradually become a research focus to address this issue. These methods divide the structure into multiple physical or functional substructures, with each substructure being modeled and optimized separately. This approach effectively handles uncertainty sources locally while reducing the system’s dimensionality and computational complexity [20,21]. Therefore, when considering the uncertainty modeling and optimization of fan systems, which are composed of multiple coupled components, employing substructure-level model decomposition strategies will better meet engineering demands and hold significant theoretical and practical value.

In summary, despite significant progress in modern optimization techniques and computational methods for vibration control and structural optimization of critical mechanical equipment, many challenges still remain regarding the structural complexity, inherent uncertainties, and high computational costs associated with large-scale ventilation systems used in forestry storage. To address these challenges, this study proposes a structural parameter optimization strategy that incorporates substructure uncertainty, aimed at improving the vibration control and operational stability of forestry ventilation systems.

2. Fault Diagnosis of the Induced Draft Fan

2.1. Overview of the Induced Draft Fan

The single-suction, double-support centrifugal ventilation fan evaluated in this study is a large-scale system designed specifically for environmental control in forestry timber storage warehouses. Its structural design accounts for the unique airflow distribution needs of such facilities, where maintaining stable temperature and humidity is essential for preventing wood degradation and fungal growth. In actual operation, the fan (Nantong Datong Baofu Fan Co., Ltd., Nantong, China) rotates at 895 r/min, providing a test block (TB) airflow capacity of 583,000 m³/h and a pressure head of 10,230 Pa. These performance characteristics ensure that sufficient ventilation is achieved to support the long-term preservation of bulk-stored timber. Figure 1 illustrates the overall structure of the fan. Ambient air is drawn through the inlet, accelerated by the high-speed impeller, and then discharged uniformly into the storage space. This process actively regulates environmental conditions within the warehouse. However, abnormal noise was detected at the bearing housing during operation, indicating potential mechanical faults. This not only affects the working conditions for facility personnel but also points to underlying issues that warrant detailed vibration analysis and corrective engineering measures.

2.2. Vibration Measurement

Unusual noises in operating equipment are often caused by excessive vibration. Therefore, vibration amplitudes were first measured at various support points along the fan shaft. A Scout140-EX vibration analyzer (GE Bently Nevada, Minden, NV, USA) was used to measure three-directional vibration velocities at the free end fan bearing, drive end fan bearing, and drive motor (positions A, B, and C in Figure 2). The axial direction of the motor output shaft was defined as the y-axis, the perpendicular horizontal direction as the x-axis, and the vertical direction as the z-axis.

As shown in Figure 2, the axial vibration velocities at the two fan bearings exceeded normal values, reaching 9 mm/s and 7.1 mm/s, respectively, while the axial vibration velocity at the drive motor was only 1.5 mm/s. This indicates that there is no significant misalignment in the coupling between the motor and the fan. Additionally, the circumferential (x-direction) and vertical (z-direction) vibration velocities at both fan bearings remained low, suggesting that the abnormal simulated vibration was not caused by excessive rotor imbalance.

Further vibration measurements were taken at fan speeds of 800 r/min and 1000 r/min. At 800 r/min, the axial vibration velocities at positions A and B were 4.6 mm/s and 3.8 mm/s, respectively. At 1000 r/min, the corresponding values were 7.2 mm/s and 4.6 mm/s. Compared to the operating speed of 895 r/min, the vibration velocities at these alternative speeds were significantly lower. Theoretically, with constant vibration displacement, axial vibration velocity should increase with rotational speed. However, the measured axial vibration acceleration at 1000 r/min was lower than that at 895 r/min, indicating a strong likelihood of resonance occurring at the operational speed.

2.3. Modal Analysis

To reduce the computational burden of finite element analysis, modal analysis was performed on components associated with impeller rotation, including the bearing housings, main shaft, impeller, and wheel disc, as shown in Figure 3. In the modal analysis, all components were assumed to be made of structural steel, with displacement and rotational constraints applied to the base surfaces of the bearing housings.

The modal analysis results in Figure 3 indicate that the first-order natural frequency of the structure is 7.78 Hz, characterized by an impeller oscillation mode. The second-order natural frequency is nearly identical to the first, with the impeller oscillating perpendicular to the first-order mode due to the circumferential symmetry of the fan structure. The third-order natural frequency is 15.37 Hz, corresponding to axial vibration of the impeller. Given that the operating speed of 895 r/min corresponds to a frequency of 14.9 Hz, which is only 0.47 Hz away from the third-order natural frequency, and that the axial vibration of the bearing housings aligns with the third-order mode shape, resonance is highly likely.

Additionally, the fourth-order mode shape exhibits torsional motion of the impeller, while the fifth and sixth modes primarily show bending of the main shaft. From the perspective of natural frequency values, the fourth-order natural frequency is 7.33 Hz higher than the operating frequency, while the fifth and sixth natural frequencies are significantly above the working frequency, making resonance unlikely for these modes.

3. Parameter Uncertainty Modeling and Optimization

3.1. Simplified Uncertainty Parameter Model

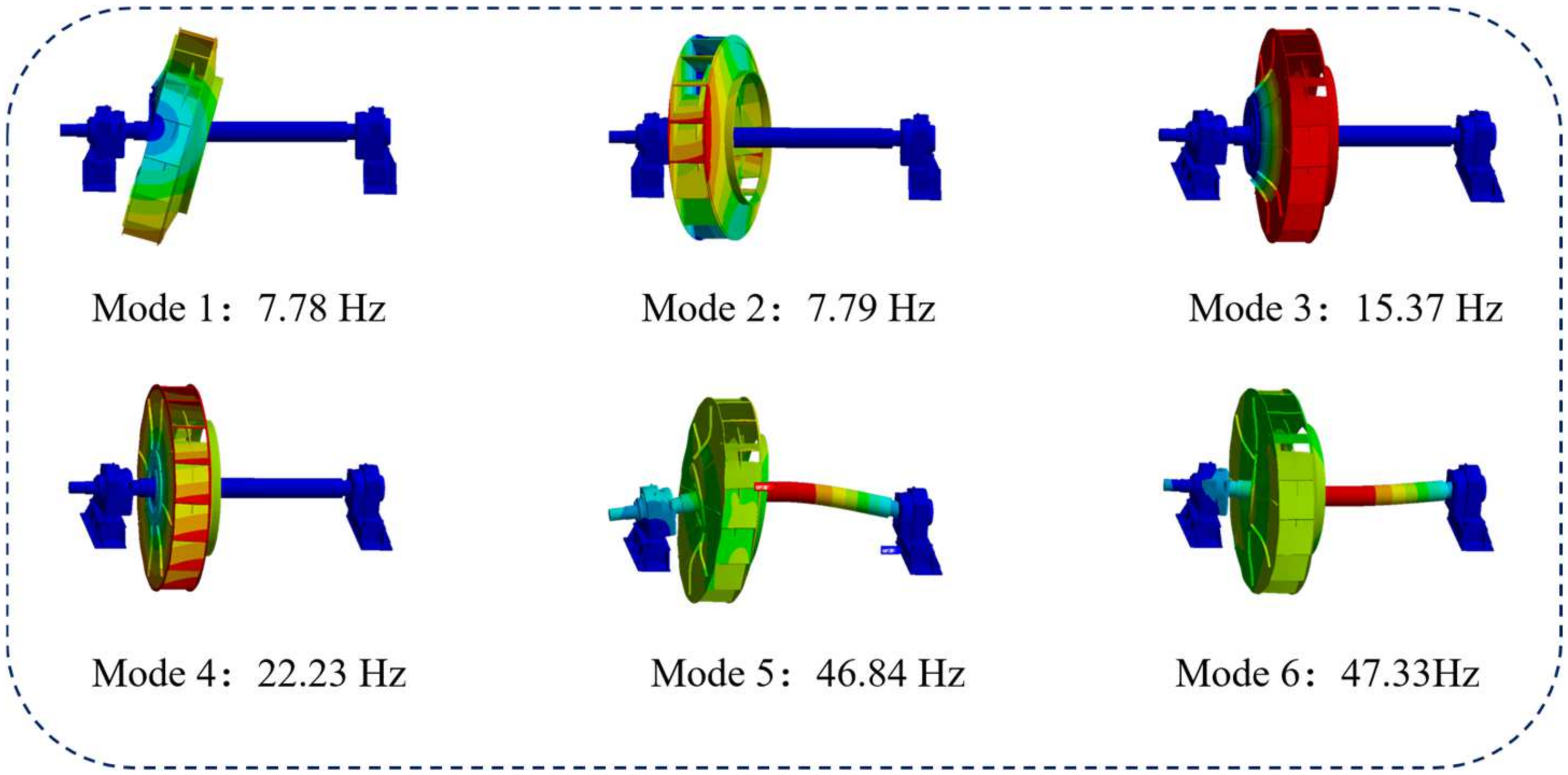
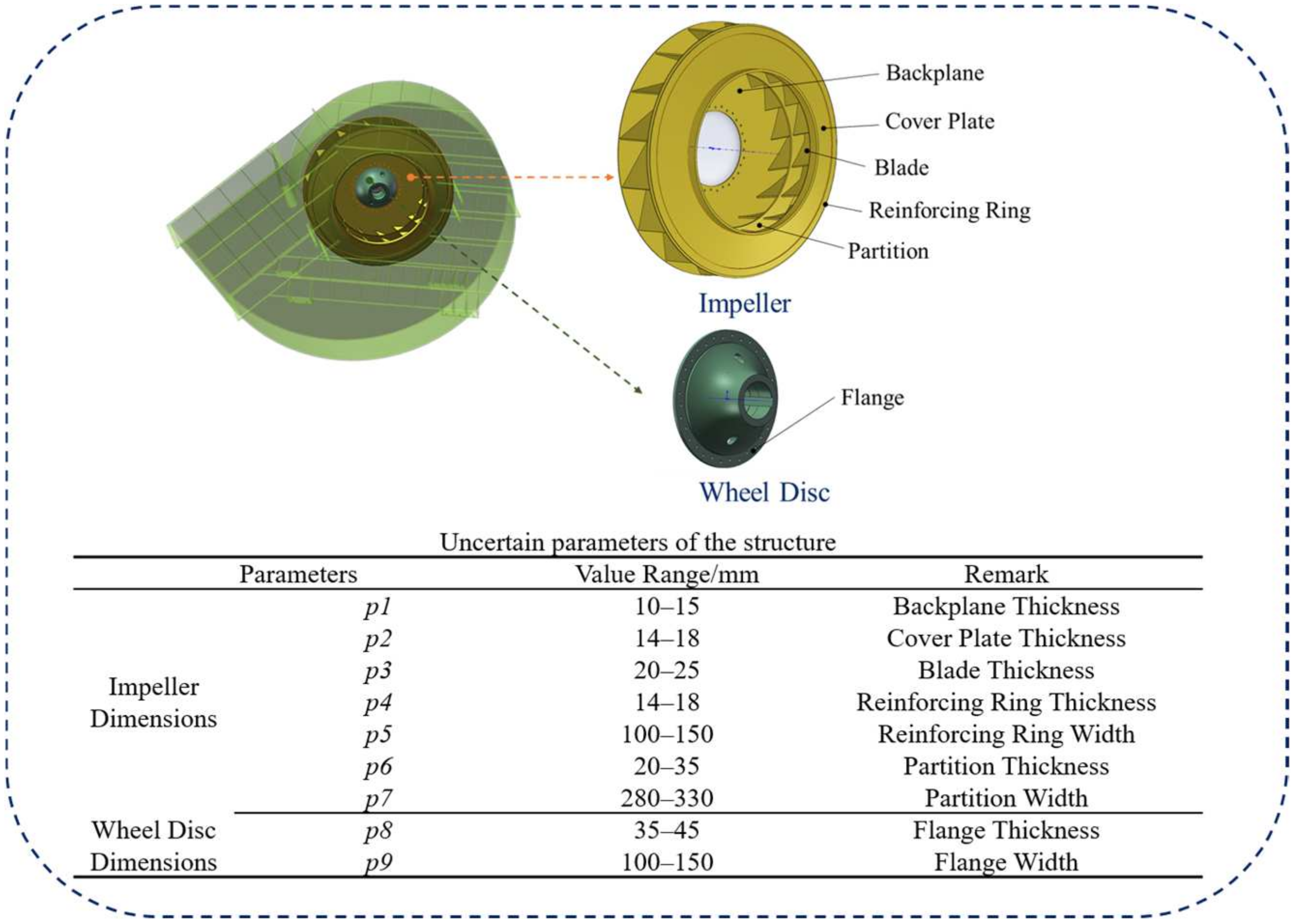
To ensure the normal operation of the induced draft fan, structural optimization is required to prevent resonance frequencies from coinciding with the operating frequency. From a cost-saving perspective, modifications to the fan’s structural components should be minimized. According to the modal analysis results in Figure 3, the resonance of the induced draft fan primarily occurs in the impeller and the wheel disc, which connects the impeller to the main shaft. Therefore, when optimizing the fan structure, only the structural parameters of the impeller and wheel disc, as shown in Figure 4, need to be considered. Nine key geometric parameters of the impeller and wheel disc were selected as optimization variables. These parameters were treated as uncertain parameters to construct an uncertainty parameter model for subsequent optimization. An interval model was employed to describe these uncertain parameters, with their upper and lower bounds listed in Figure 4. While optimizing the natural frequency of the fan, structural strength and performance must also be ensured. The lower bound of each uncertain parameter was set to its initial value, while the upper bound was determined based on the maximum empirical value.

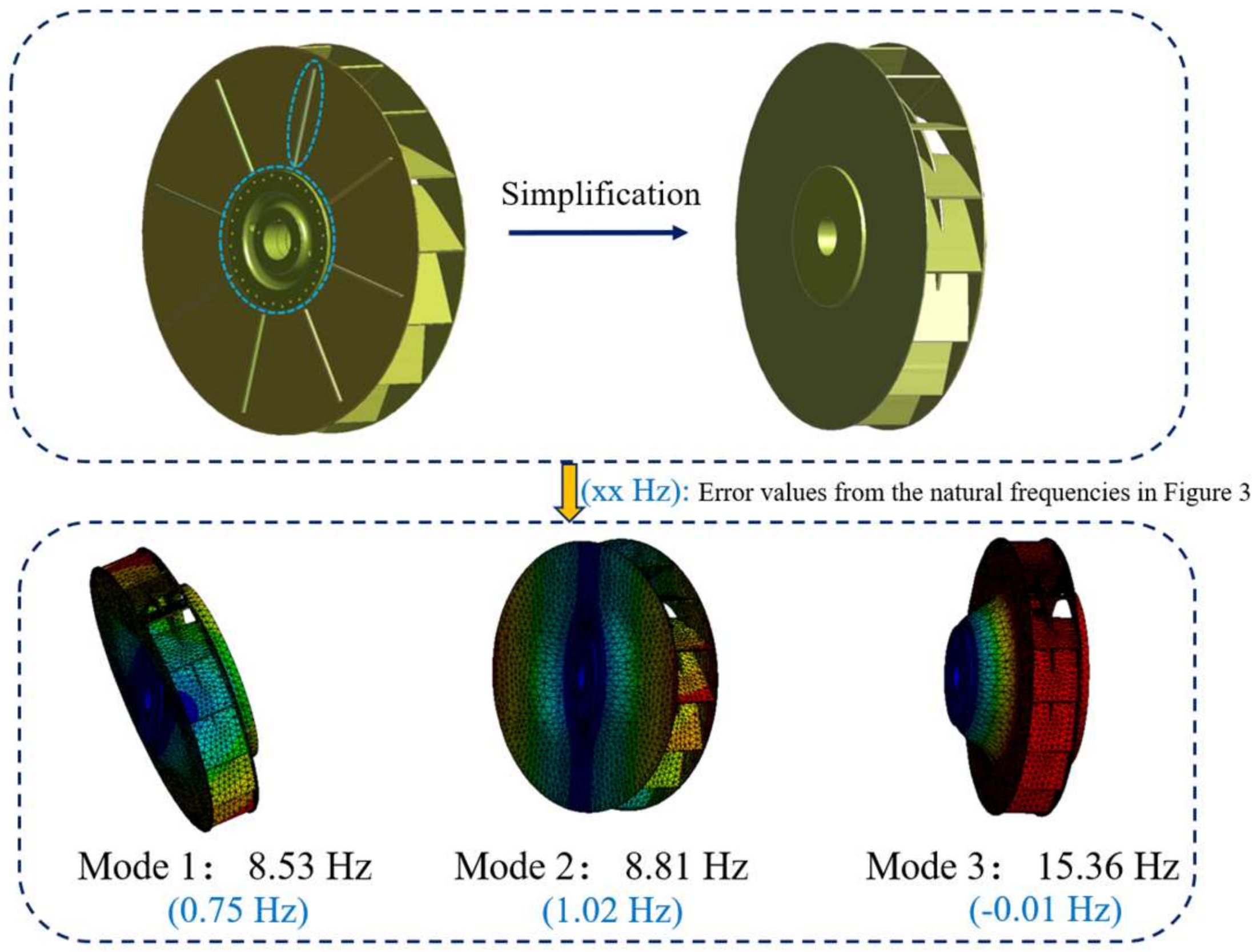
Based on the modal analysis results of the rotating components in Figure 3 and the operating speed of the fan, the first three modal frequencies of the rotating components were identified as the key modes to focus on during structural optimization. Since the mode shapes of these three modes primarily involve deformations of the impeller and wheel disc, computational costs during parameter optimization can be reduced by simplifying the model. In this simplification process, only the impeller and wheel disc were retained, while further geometric refinements were performed, such as removing threaded holes, grooves, and other small features. Additionally, the displacement and rotational degrees of freedom of the inner hole surface of the wheel disc were constrained, resulting in a simplified model, as shown in Figure 5. Figure 5 also presents the modal analysis results of the simplified model when all structural parameters are set to their initial values. Compared to the modal analysis results of the original rotating components in Figure 3, the first two natural frequencies increased by 0.75 Hz and 1.02 Hz, respectively, while the third natural frequency decreased by only 0.01 Hz. This discrepancy was caused by the geometric simplifications applied to the model. Since the optimization primarily focuses on the third mode, such minor errors are considered acceptable. Therefore, the substructure method was employed to construct an interval uncertainty finite element model based on the simplified model, which was then used for subsequent optimization.

3.2. Optimization Process

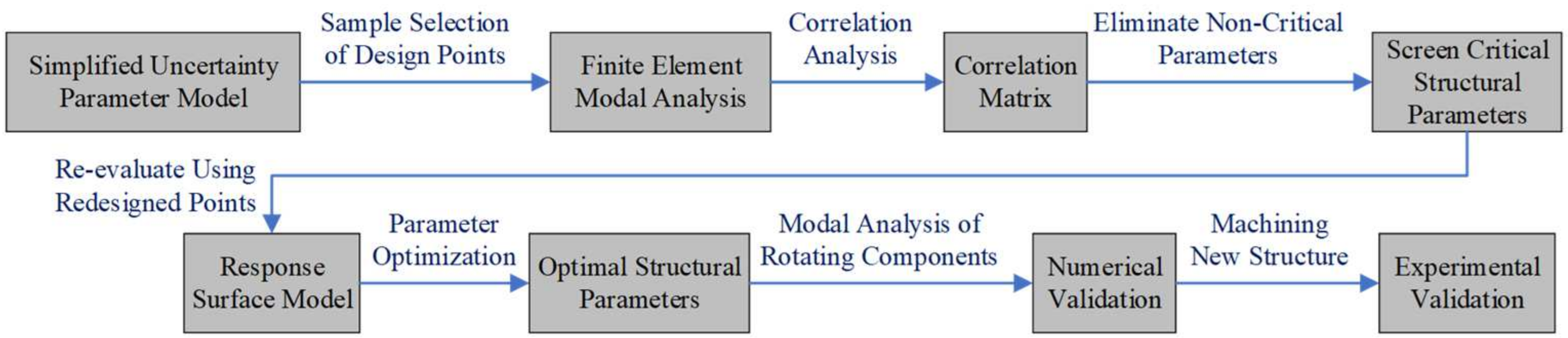
For the structural optimization of the induced draft fan, a simplified uncertainty parameter model was established in the previous section, and nine structural parameters that potentially affect the natural frequencies were selected. The range of values for each parameter was defined as an interval, reflecting the inherent uncertainty. This step provides a comprehensive uncertainty framework for optimization analysis. The overall optimization process is illustrated in Figure 6.

First, the Latin Hypercube Sampling (LHS) method was employed to divide the range of each parameter into 100 equal subintervals, where each subinterval represents a possible value range for that parameter. A random value was selected within each subinterval for each parameter. This ensured that every subinterval of each parameter was covered by at least one sample point, achieving uniform sampling across the entire parameter space. For each sample point, the values extracted from the subintervals were combined to form a multi-dimensional design point, ultimately generating 100 sample points. This approach ensures that the design points are evenly distributed across the multi-dimensional parameter space, avoiding bias toward any specific region, thereby serving as input for subsequent finite element analysis [22,23].

For each generated design point, a finite element modal analysis was conducted to compute the first three natural frequencies of the structure. By calculating the correlation coefficients between each uncertain parameter and the first three natural frequencies, the influence of each parameter on the natural frequencies was evaluated. Key parameters with a significant impact on the natural frequencies were identified, while parameters with negligible effects were eliminated. This refinement process was conducted to streamline the response surface optimization.

During the response surface analysis, the identified key structural parameters were treated as input variables, while the first three natural frequencies served as response variables. To more precisely investigate the effects of these key structural parameters on the response variables and improve the accuracy and reliability of the response surface model, new design points were selected based on the key structural parameters. The eliminated non-key structural parameters were held at their initial values during finite element analysis.

Subsequently, parameter optimization was performed based on the response surface model [24,25]. The primary optimization goal was to maximize the difference between the third natural frequency and the operating frequency to ensure that the third natural frequency is significantly higher than the operating frequency of 14.9 Hz. The secondary optimization goal was to avoid new resonance points, ensuring that the first two natural frequencies do not become too close to the operating frequency. Common constraints in structural optimization include structural parameter constraints and performance constraints related to strength and stiffness, which were already incorporated through the upper and lower bounds of the uncertain structural parameters.

After determining the optimal structural parameters, a new finite element modal analysis was conducted on the rotating components of the fan to verify the results. Since the response surface optimization was performed using the simplified model, which only included the impeller and wheel disc, performing a new finite element analysis on the entire rotating assembly ensured that the optimization considered a more complex and complete system behavior. Additionally, this verification step allowed for the detection of new or previously unpredicted resonance frequencies. Once the optimal structural parameters were numerically validated, these parameters were applied to fabricate a new structure, followed by real-world operating tests and experimental validation to confirm the effectiveness of the optimization.

4. Numerical Computation and Validation

4.1. Parameter Correlation

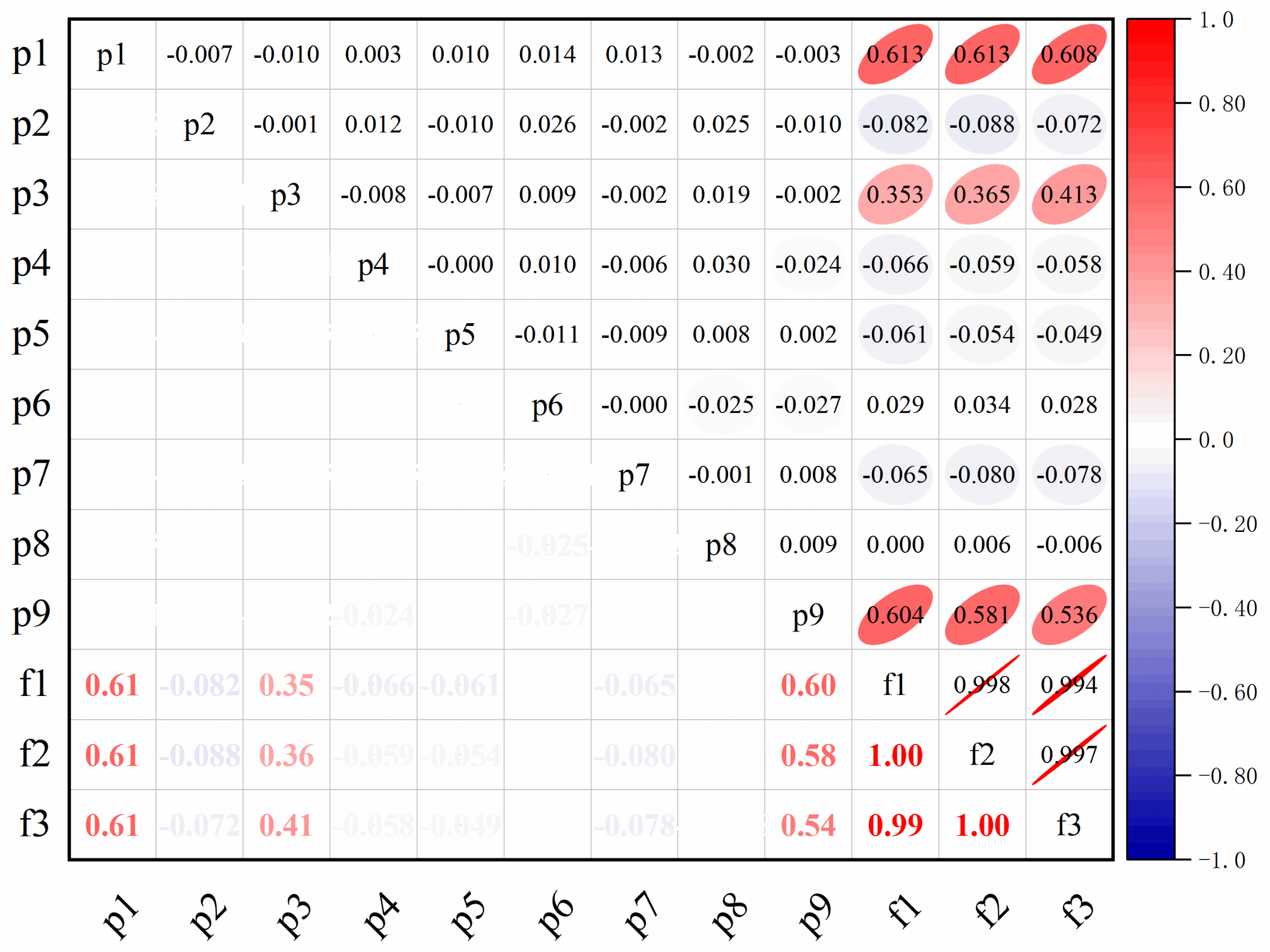
After completing the modal analysis for each set of parameter design points using the simplified model, correlation analysis was conducted using the built-in sensitivity analysis tool in ANSYS Workbench 2022 R1, which automatically calculates the correlation coefficients between design parameters and the corresponding natural frequencies. The resulting correlation matrix is shown in Figure 7. As observed, among the nine structural parameters, parameter p₁, which represents the backplate thickness of the impeller, exhibited the highest correlation with the first three natural frequencies of the structure, with correlation coefficients of 0.80 for all three modes. This indicates that variations in p₁ significantly impact the natural frequencies of the structure. Similarly, parameter p₉, which corresponds to the flange width of the wheel disc, also demonstrated a strong correlation with the structural natural frequencies, with correlation coefficients of 0.60, 0.58, and 0.54, respectively. In addition to p₁ and p₉, parameter p₃, representing the blade thickness of the impeller, exhibited a moderate correlation with the natural frequencies, with correlation coefficients of 0.35, 0.36, and 0.41. A common characteristic among these three parameters (p₁, p₃, and p₉) is that they all exhibit positive correlations with the structural natural frequencies, which is advantageous for structural parameter optimization. A positive correlation implies that when these parameters vary within their given ranges, the natural frequencies of the structure always increase compared to the initial values. As the values of these parameters increase, the natural frequencies also increase, thereby widening the gap between the structural natural frequency and the operating frequency, which effectively reduces the likelihood of resonance.

Moreover, the remaining parameters exhibited generally low correlation with the natural frequencies, with some parameters having correlation coefficients close to zero, indicating that their influence on the structural natural frequencies is negligible. Therefore, in the subsequent parameter optimization process, only parameters p₁, p₃, and p₉ will be considered, while the remaining uncertain structural parameters will be excluded from further optimization.

4.2. Response Surface Optimization

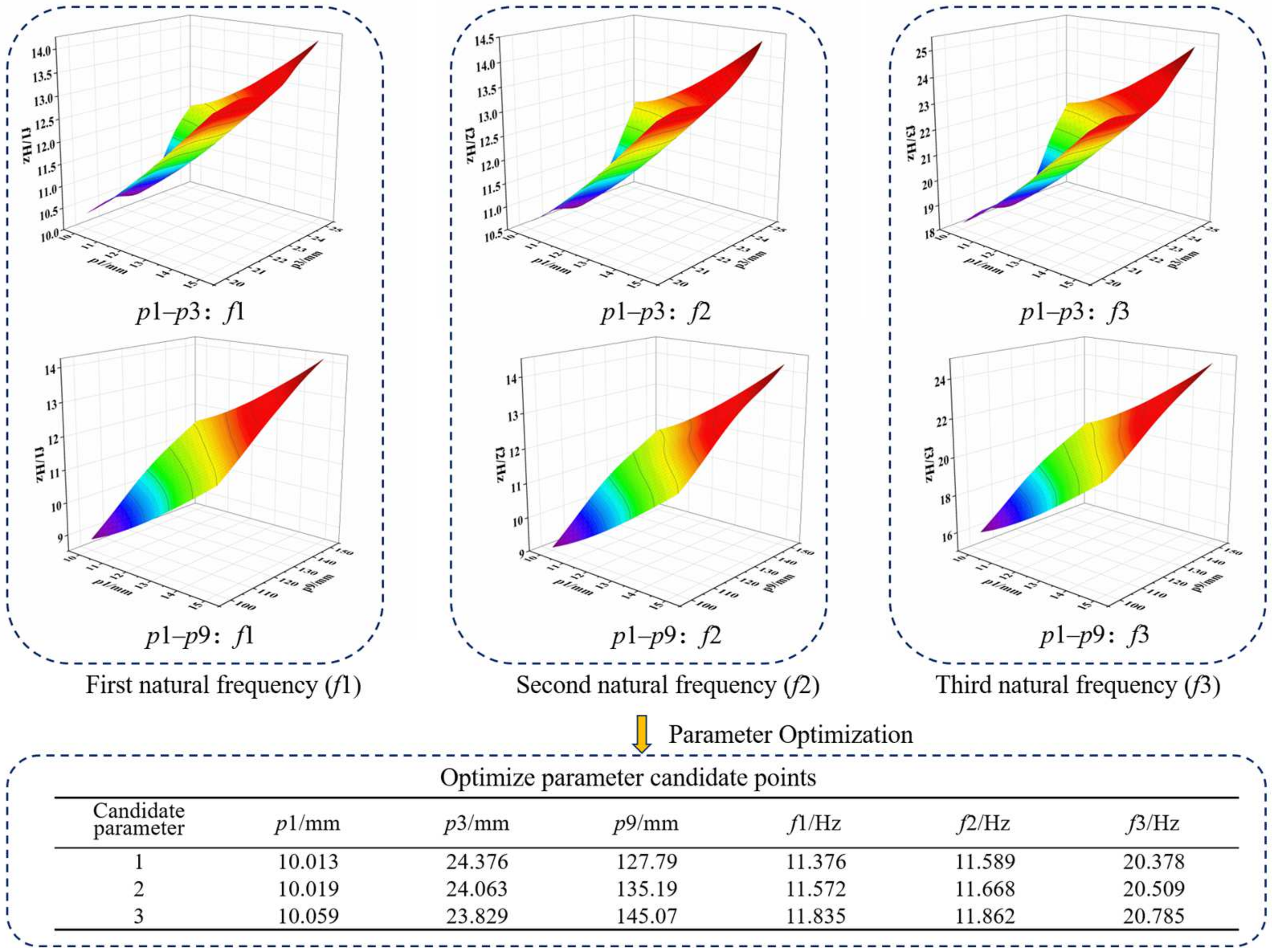
After identifying the three key uncertain parameters that significantly influence the natural frequencies of the structure, response surface analysis was conducted to determine the relationship between the first three natural frequencies and parameters p₁, p₃, and p₉ in the simplified model. Based on the response surface results, three sets of candidate optimized parameter points were obtained, as shown in Figure 8. By comparing these three sets of candidate parameters, it was observed that the structural natural frequencies remained consistent across all three cases. The first two natural frequencies were in the range of 11–12 Hz, while the third natural frequency was in the range of 20–21 Hz. In terms of natural frequency values, all three sets of parameters successfully ensured that the first two natural frequencies remained low while simultaneously increasing the third natural frequency, moving it further away from the operating frequency. Examining the numerical values of the three sets of optimized parameters, p₁ and p₃ were found to be nearly identical across all three sets, while p₉ exhibited some variation. After comprehensive consideration of the candidate parameter sets, taking manufacturing feasibility and structural lightweight design into account, the final optimized reference values for p₁, p₃, and p₉ were determined to be 10 mm, 24 mm, and 130 mm, respectively. The corresponding first three natural frequencies of the structure were 11.24 Hz, 11.36 Hz, and 20.47 Hz, respectively.

It is important to note that the natural frequencies calculated using the optimized reference values were obtained based on a simplified model that only included the impeller and wheel disc. Therefore, the feasibility of these optimized reference values must be validated through a full modal analysis of the entire rotating assembly of the fan after modification. If validated, the corresponding fan components will be reprocessed accordingly.

4.3. Numerical and Experimental Validation

To ensure that the optimization results are effective not only for the simplified model but also for the entire rotating assembly of the fan, a new modal analysis was conducted on the modified rotating components. Since only parameters p₃ and p₉ were altered, while the overall structural configuration remained unchanged, the mode shapes of the optimized induced draft fan remained consistent with those before optimization. The first six natural frequencies of the optimized system are presented in

Table 1. First six natural frequencies (Hz) of the optimized rotating components of the fan.

Order	1	2	3	4	5	6
Optimized value	11.2	11.42	20.78	22.34	54.78	54.90
Difference from Pre-optimization Value	3.42	3.63	5.41	0.11	7.94	7.57

. It was observed that the first three natural frequencies of the optimized rotating assembly closely matched those obtained from the simplified model, verifying the feasibility of using the simplified model during the optimization process. Furthermore, comparing the natural frequencies of the rotating assembly before and after optimization, it was found that while the fourth natural frequency remained largely unchanged, the other natural frequencies increased significantly. For the critical third natural frequency, the optimized value was 5.41 Hz higher than before, representing a 39.4% increase relative to the operating frequency. In common engineering practice, it is generally recommended that the difference between the operating frequency and the natural frequency should be 10%–20% to avoid resonance as a rough guideline [26,27,28]. In this case, the frequency separation after optimization far exceeds the typical recommended range, significantly reducing the risk of resonance. However, determining what constitutes a “sufficiently large” frequency gap depends on specific application requirements and vibration sensitivity, necessitating experimental validation.

It is also important to note that after optimization, the first two natural frequencies increased, bringing them closer to the operating frequency. However, the frequency gaps between the first two natural frequencies and the operating frequency remained at 24.8% and 23.3%, which are still above the recommended values in engineering practice. Moreover, the occurrence of structural resonance is influenced not only by the proximity between the operating frequency and natural frequencies but also by the mode shape characteristics. Since the first two mode shapes of the rotating assembly primarily involve impeller oscillations, which are unlikely to be excited under actual operating conditions, the risk of resonance in these modes remains low. However, this assumption still requires experimental verification.

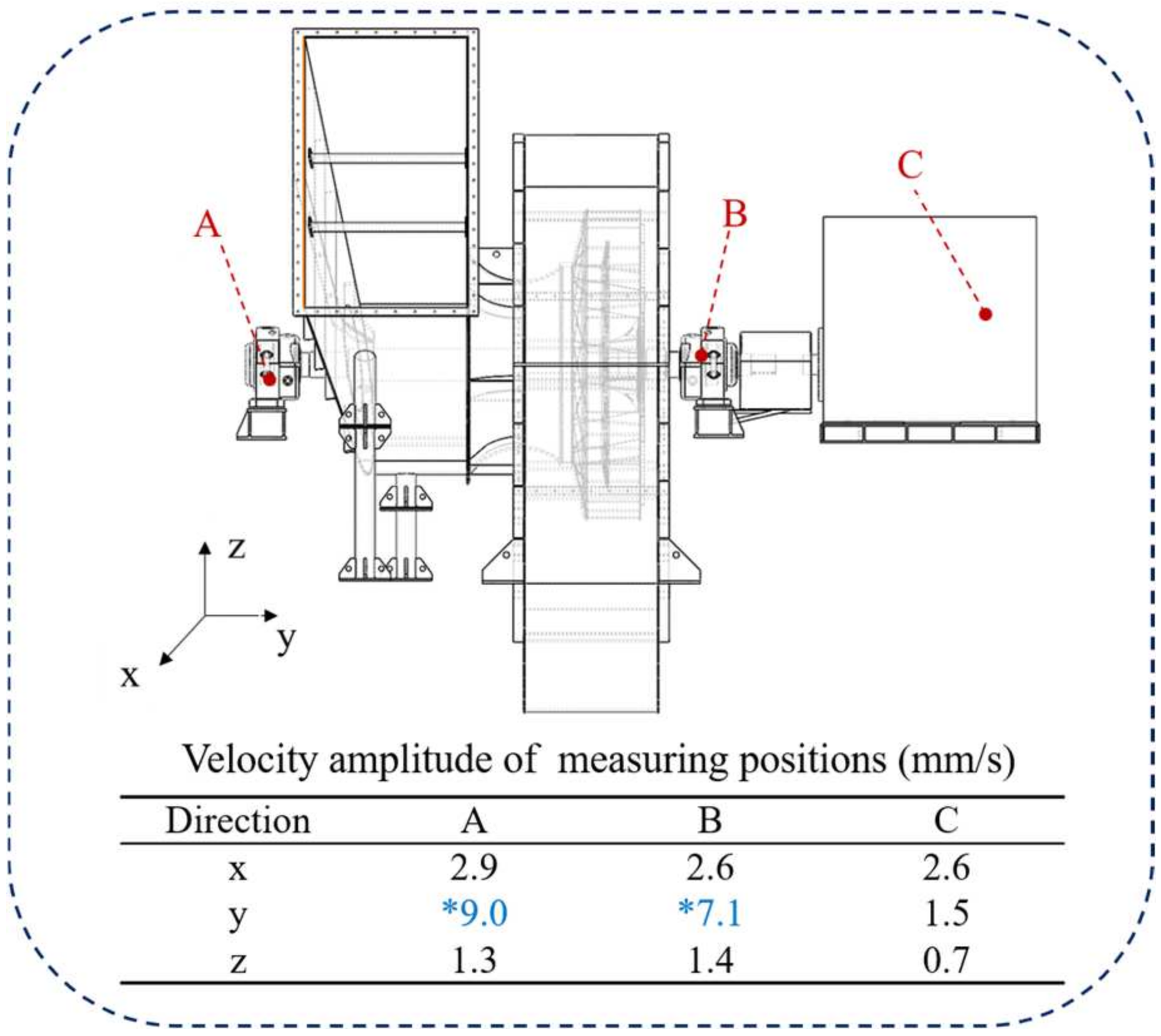
The actual structural modifications required for the optimized induced draft fan involved only parameters p₃ and p₉, which correspond to the blade thickness of the impeller and the flange width of the wheel disc, respectively. Therefore, only the impeller and wheel disc components needed to be re-machined and replaced. Figure 9 presents the measured axial vibration velocity of the bearing housings under the improved operating conditions. It can be observed that the axial vibration velocity of both bearing housings significantly decreased compared to the pre-optimization state. The vibration acceleration amplitude was reduced to below 2 mm/s, meeting the requirements for normal operation, while also enhancing the operational stability and service life of the equipment. These results validate the effectiveness of the optimization strategy and methods proposed in this study. By minimizing structural modifications, the performance of the induced draft fan was significantly improved at the lowest possible cost.

5. Conclusions

This study presents a structural optimization approach for large-scale ventilation fans used in forestry storage facilities, with a specific focus on addressing vibration control under substructure-level uncertainty. By constructing a simplified interval uncertainty model and conducting stochastic finite element and correlation analyses, nine candidate structural parameters were evaluated, and three key parameters significantly affecting the system’s natural frequencies were identified.

The optimized design significantly increased the separation between the third natural frequency and the operating frequency, while effectively avoiding resonance in the first two modes. Specifically, the third natural frequency was raised by 5.41 Hz (a 39.4% increase relative to the operating frequency), surpassing standard engineering recommendations for frequency separation. Experimental validation further confirmed a marked reduction in axial vibration levels to below 2 mm/s, indicating enhanced vibration control and improved operational stability.

The substructure-oriented uncertainty modeling approach not only improves vibration control but also reduces computational costs, offering a scalable framework for robust design in large-scale ventilation and rotating machinery systems.