Next Article in Journal
Why Are Seed Dispersal Models Rarely Used? Limitations of Scalability and Improvement Measures
Previous Article in Journal
Toward Safer Resin Tapping: Assessing Alternative Chemical Stimulants for Pinus pinaster
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 5
10.3390/f16050850
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Multi-Dimensional Patterns of Variation in First-Order Shoot Traits of Larix principis-rupprechtii in Northern China

by
Yang Yu
1,
Huayong Zhang
1,2,*,
Zhongyu Wang
1 and
Zhao Liu
2
1
Research Center for Engineering Ecology and Nonlinear Science, North China Electric Power University, Beijing 102206, China
2
Theoretical Ecology and Engineering Ecology Research Group, School of Life Sciences, Shandong University, Qingdao 250100, China
*
Author to whom correspondence should be addressed.
Forests 2025, 16(5), 850; https://doi.org/10.3390/f16050850
Submission received: 1 April 2025 / Revised: 22 April 2025 / Accepted: 15 May 2025 / Published: 20 May 2025
(This article belongs to the Section Forest Inventory, Modeling and Remote Sensing)
Browse Figures
Versions Notes

Abstract

As the most active fundamental unit in the aboveground branching system of woody plants, it remains unclear the relative importance of acclimation at the level of allocation and morphology in shoots. Additionally, the main dimensions of trait variation in shoots and whether their trait relationships conform to the common assumptions of the root economics spectrum (RES) have not yet been established. By collecting 1551 larch shoots, we measured and estimated five functional traits, including shoot diameter (SD), length (SL), dry matter content (SDM), specific stem length (SSL), and stem tissue density (STD). Furthermore, we assessed the relationships between bivariate and multivariate traits through a Pearson correlation analysis and principal component analysis (PCA), including standardized major axis (SMA) regression analysis. We found that SDM exhibited the greatest degree of variation. Meanwhile, SL and SDM were significantly and strongly positively correlated with SD. In contrast, SSL and STD were significantly negatively correlated with SD, and SSL and STD showed a weak positive correlation. In addition, these five functional traits were distributed across two nearly orthogonal (independent) principal component analysis (PCA) axes. These results revealed that shoots generally exhibit greater flexibility in altering their biomass allocation compared to their morphology. Meanwhile, the variation in shoot traits is associated with two main dimensions: a diameter-related dimension potentially integrating shoot construction, maintenance, and persistence, and the other dimension consisting of SSL and STD traits representing shoot plastic responses to the environment. And the relationship between SD and STD does not support the predictions of the root economics spectrum (RES). Our study may offer a promising pathway for better understanding the functions and ecological strategies of shoots.

1. Introduction

A tree is composed of numerous modular units, such as shoots, which grow independently according to their microenvironment [1]. Shoots are defined as the terminal portions of the aboveground branching system in woody plants, generally consisting of stems and leaves [2]. As the fundamental units of growth and reproduction in woody plants, shoot structures serve multiple functions and evolve under various selective pressures [3]. In other words, shoots are essential for positioning leaves to receive light and perform efficient photosynthesis [3,4], and their development is shaped by trade-offs among shoots, which are crucial for efficient photosynthesis, growth, and survival at both the shoot and whole-tree levels.
Shoot traits may play a crucial role in determining how individual plants and species respond to environmental gradients [5]. Shoot length (SL) is considered a key trait for resource acquisition, especially when plants compete for aboveground resources [6]. Shoot dry matter content (SDM) reflects the investment of photosynthetic products in shoot elongation. Specific stem length (SSL), regarded as the aboveground counterpart of specific root length, is a core trait in shoot economics, as it indicates the potential leaf deployment (photosynthetic capacity) per unit biomass investment [7]. Stem tissue density (STD) is a key functional trait of woody plants, as it is closely related to mechanical stability, hydraulic conductivity, and major ecological characteristics such as life history strategies [8,9,10,11]. It has been proposed as an integrator of wood economics and a central axis of plant functional strategies [12].
Functional trait variation is the result of interactions between vegetation and the environment during evolution, playing a crucial role in understanding the mechanisms underlying plant responses to environmental gradients. This topic remains a core issue in contemporary ecological research [4,13]. Plant trait variation can be classified into interspecific variation and intraspecific variation [14]. While many ecological theories have been developed based on interspecific trait comparisons using species mean values [13,15], intraspecific trait variation (ITV) is equally important [13,16,17]. ITV refers to trait differences among individuals or organs within the same species and represents a key mechanism by which plant species respond to local spatial resource heterogeneity [14,18]. It is also closely related to environmental gradients within a species’ range. For species with broad geographic distributions [19,20], greater ITV suggests a stronger ability to adapt to environmental changes [14,16,19,21]. Therefore, determining the extent and patterns of intraspecific trait variation is essential for understanding key physiological and ecological processes across different environments. However, most research has focused on ITV in root and leaf traits, while studies on trait variation in the aboveground branching systems of woody plants remain scarce.
The variation in plant functional traits is a response to the continuous changes in the surrounding environment, aimed at meeting the requirements for normal growth and reproduction [22]. Generally, woody plants can adapt to environmental changes through three different aspects: they can alter the relative allocation of biomass among the roots, stems, and leaves; change the morphological and structural characteristics of each organ; or modify the physiological properties within these tissues. Importantly, they may adjust all three aspects simultaneously [23]. Therefore, comparing the relative importance of these three adjustment levels would be a highly meaningful task. In this study, we quantify allocation as the dry mass content in the shoots (SDM), morphology is represented by shoot diameter (SD) and length (SL), and structure is characterized by specific stem length (SSL) and stem tissue density (STD).
The emergence of the economics spectrum is considered the result of the long-term evolutionary adaptation of plants to their environment, reflecting the trade-off between resource acquisition efficiency and lifespan, and holds significant ecological theoretical value [24,25,26]. Currently, the leaf economics spectrum and root economics spectrum have been confirmed [27,28]. Under the predictions of the root economics spectrum (RES), root diameter and root tissue density are positively correlated. However, as an aboveground branching system similar to underground root systems, it is unclear whether the variation and coordination patterns of shoot traits follow the trait trade-offs predicted by the root economics spectrum, that is, whether shoot diameter and stem tissue density are positively correlated.
As the most active basic structural unit of the above-ground parts in woody plants, shoots play important roles in mechanical support and the transport of water and nutrients. Unlike previous studies that mainly focused on the patterns of functional trait variation in fine roots and leaves, we aim to emphasize whether shoots exhibit an economic spectrum similar to that of roots and leaves. To this end, this study aims to explore the patterns of functional trait variation in shoots at the branch level. Specifically, our research objectives were to (i) compare the relative importance of adaptations at the allocation and morphological levels; (ii) identify the main dimensions of variation in shoot traits; and (iii) determine whether the relationships among shoot functional traits support the predictions and assumptions of the root economics spectrum (RES). To achieve these goals, we quantified the degree of variation in shoot traits, determined the correlations among traits, and extracted the dimensions of trait variation (if present).

2. Materials and Methods

2.1. Study Species

As a dominant tree species in cold-temperature coniferous forests, Larix principis-rupprechtii is mainly distributed in north-central China at medium and high altitudes (1800–2800 m) [29], and it is usually used for afforestation in northern China due to its high timber value and cold tolerance. Therefore, studying the growth and development of shoots in Larix principis-rupprechtii plantation forests is of great value in improving forest structure, increasing forest productivity, and exerting multiple ecological and social benefits.

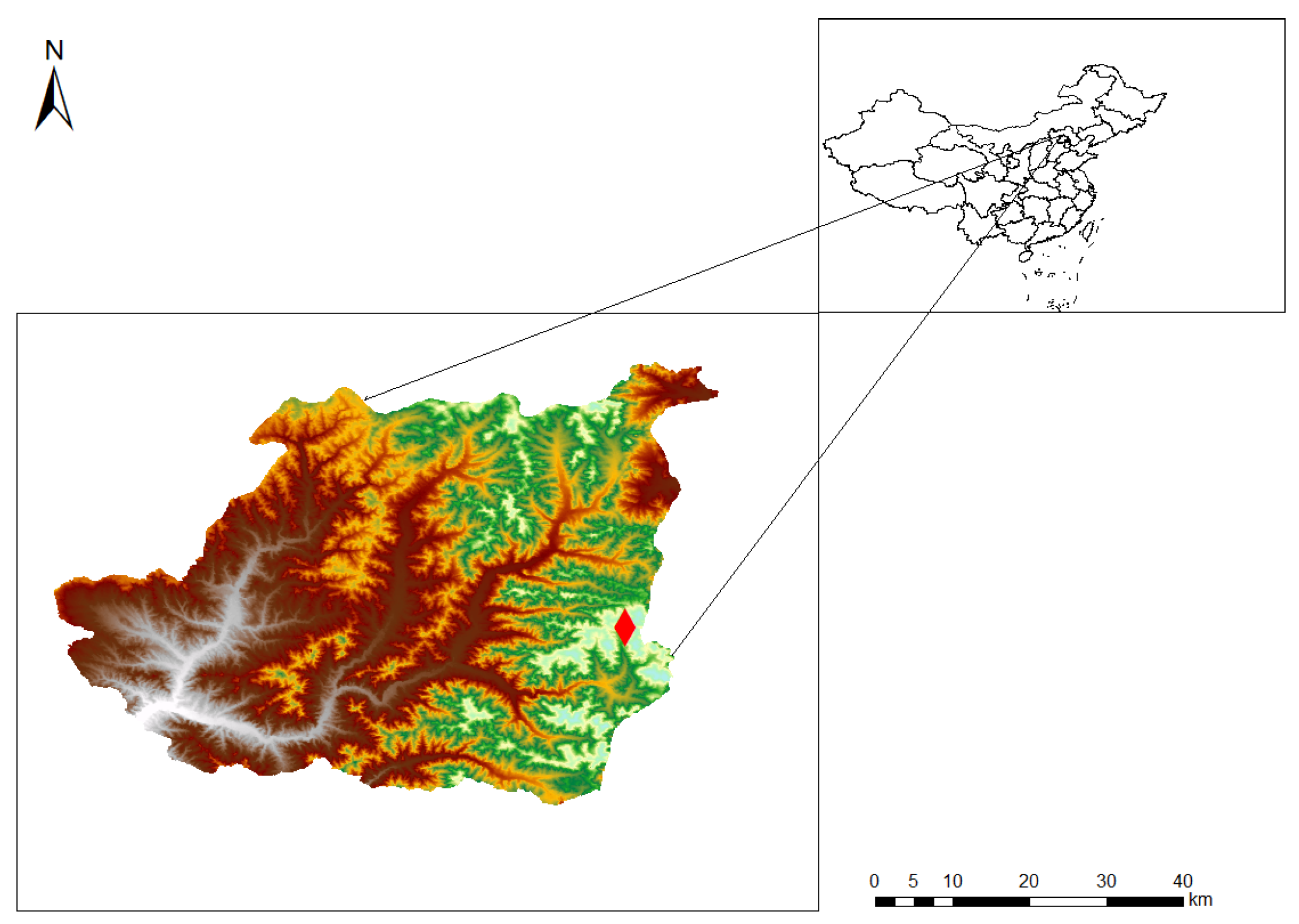
2.2. Study Site

The study was conducted in a plantation forest dominated by Larix principis-rupprechtii at the 2022 Winter Olympic core zone (40°57′ to 40°59′ N, 115°26′ to 115°27′ E), approx. 24 km northeast of the Chongli District, Zhangjiakou City, Hebei Province, North China. This study area is a typical mountainous area. The total forested area in the region is 1.761 million mu, with a forest coverage rate of 50.22%, making it one of the largest areas of natural secondary forest in Hebei Province. It has a warm temperate continental monsoon climate with an average annual temperature of 3.3 °C. Due to its unique geographical location, good ecological vegetation, and distinctive mountainous terrain, the average annual snowfall is higher than that of the surrounding areas. Snowfall begins in mid- to late October and lasts until early April of the following year, with an average annual snow depth of over one meter (Figure 1).

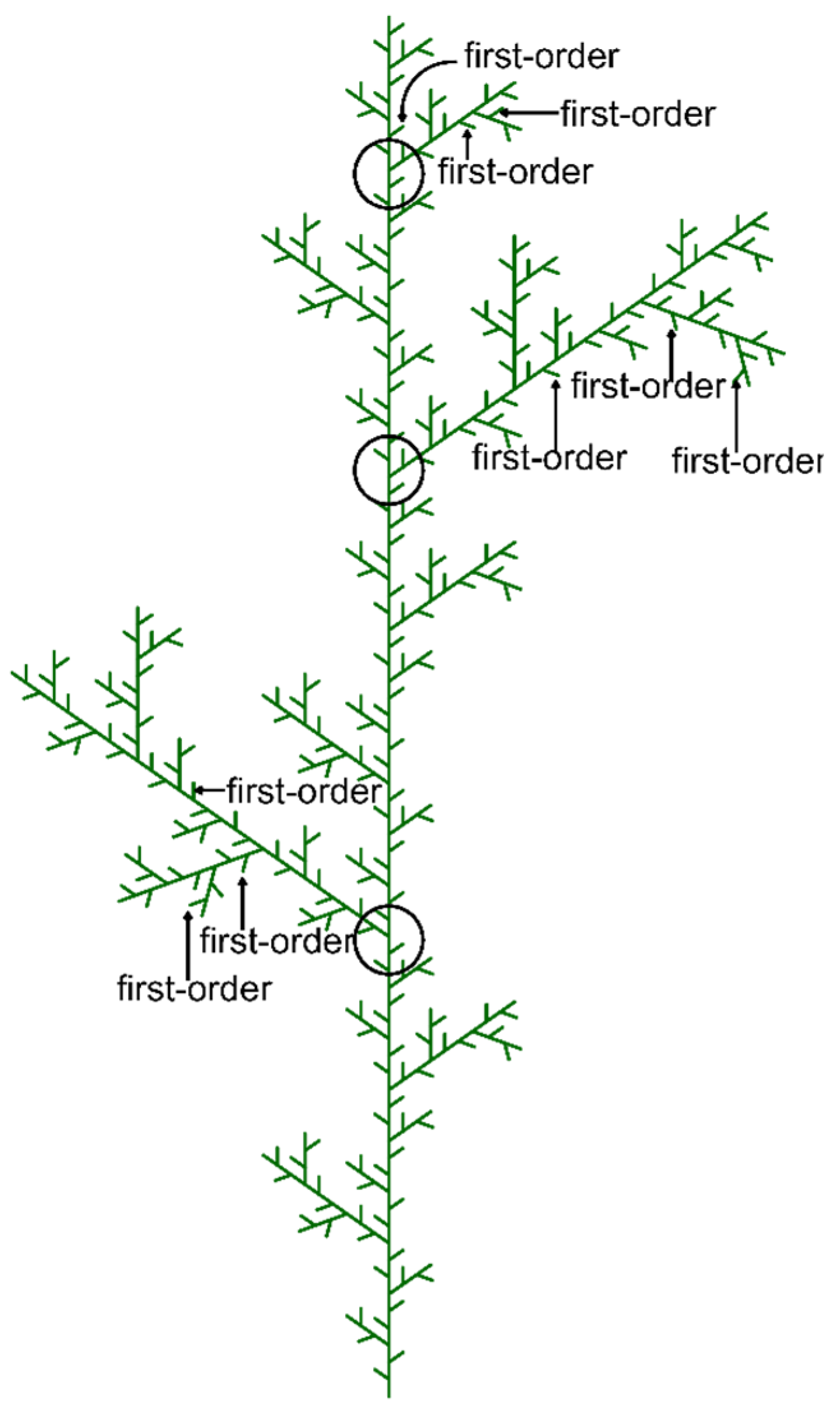
2.3. Sampling Procedures

A 20 × 20 m plot was established within a larch plantation. In early August 2019, the height and diameter at breast height (DBH) of every tree within the plot were recorded. Three larch saplings, each between 5.5 and 6.0 m tall, were randomly selected. At the beginning of the study, branch systems from the upper crown of each tree were chosen to minimize differences in branch size. A total of 29 branch systems were selected (10, 10, and 9 branch systems from each tree, respectively). The branching structure of each sampled branch system was described by drawing two-dimensional diagrams. Since larch trees grow horizontally oriented branches along the vertical stem (with coniferous trees arranged in a planar fashion), all shoots within a branch system were almost in the same horizontal plane. In this study, terminal branches are defined as each unbranched segment at the end of a branch, corresponding to first-order branches in a centripetal ranking system, similar to the Strahler system [30] (Figure 2).

2.4. Shoot Trait Measurements

We collected more than 20 intact shoots for morphometric measurements. Here, we mainly measured the most distal shoots, i.e., first-order shoots [31]. The diameter of first-order shoots was measured with a vernier caliper. For shoot length, relatively short sections were measured using a vernier caliper, and relatively long sections were measured using a tape measure. All thin slices and shoot segments were dried at 60 °C for 72 h and then weighed (±0.01 g). Stem tissue density (STD) was estimated as the ratio of the shoot dry mass to its volume [23,32], assuming a cylindrical cross-section of the shoots. Specific stem length (SSL) was calculated by dividing the shoot length by its dry mass [23,32] (Table 1).

2.5. Data Analysis

For each functional trait of the shoots, we calculated the mean, median, minimum, maximum, and coefficient of variation (CV). Pearson correlation coefficients were used to assess pairwise relationships between traits. In addition, a standardized major axis (SMA) regression analysis was used to quantify the allometric relationships among stem diameter (SD), stem length (SL), and stem dry mass (SDM) [27]. We chose SMA regression for two main reasons: first, unlike a simple linear regression, SMA regression does not assume a unidirectional effect of one parameter on another, nor is it intended to predict one trait from another; second, SMA fits a line along the longest axis of the data cloud by minimizing the sum of squares in both the X and Y dimensions simultaneously. Thus, SMA regression provides the slope of the first principal component computed from the correlation matrix. Principal component analysis (PCA) was used to determine the major dimensions of functional trait variation. All statistical analyses were conducted using R version 4.1.3 (R Core Team, 2022, New York, NY, USA).

3. Results

3.1. Magnitude of Variation for First-Order Shoot Traits

Considering all 1151 first-order shoots combined, the magnitude of the coefficient of variation was from 35.3% % to 92.6% (Table 2). Specifically, SDM showed the largest variation (CV = 92.6%), ranging from 0.01 to 1.49 g, but SD had the smallest variation (CV = 35.3%), varying from 0.54 to 4.25 mm (Table 2). The coefficient of shoot trait variation among all shoots was ranked as SDM > SL > STD > SSL > SD (Table 2).

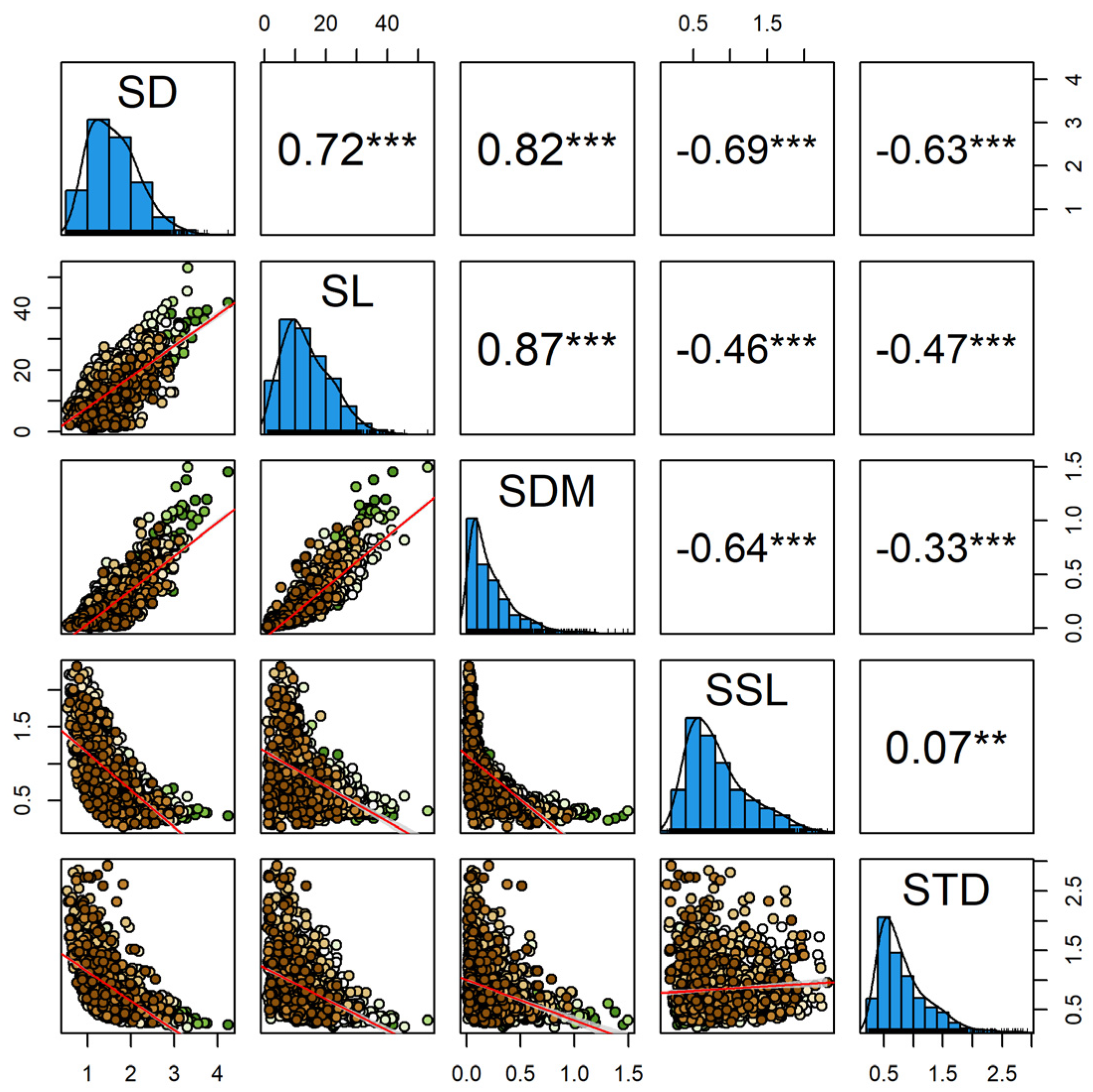
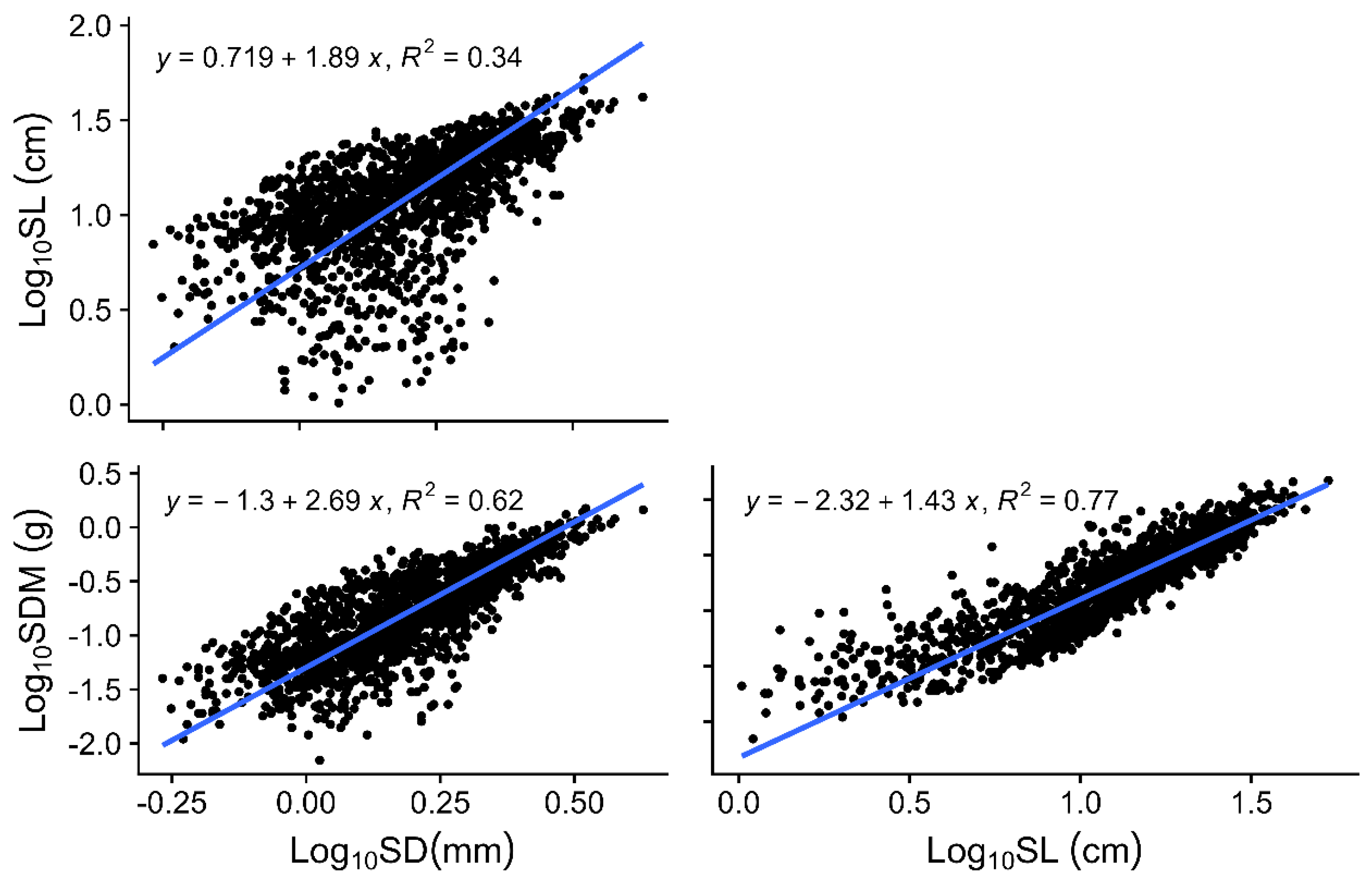
3.2. Trait Correlations in the First-Order Shoot

Here, we summarized the covariation patterns of all first-order shoots of Larix principles-rupprechtii. When considered in pairs, almost all shoot traits showed significant correlations (Figure 3). Specifically, SL and SDM were both positively correlated with SD (r = 0.72 and r = 0.82, respectively, with p-values < 0.001; Figure 3), while SSL and STD were both negatively correlated with SD (r = −0.69 and r = −0.63, respectively, with p-values < 0.001; Figure 3). The relationship between SSL and STD was weak (r = 0.07, p-value < 0.001; Figure 3). Moreover, the allometric relationships among shoots functional traits in larch had not been reported previously. The slope, or “scaling exponent”, on the logarithmic axes represents the proportional relationship between paired traits. The slopes of all three standardized major axis regression lines were significantly greater than 1 (Figure 4). In other words, the three simple functional traits exhibited allometric growth relationships, rather than proportional (“isometric”) relationships.

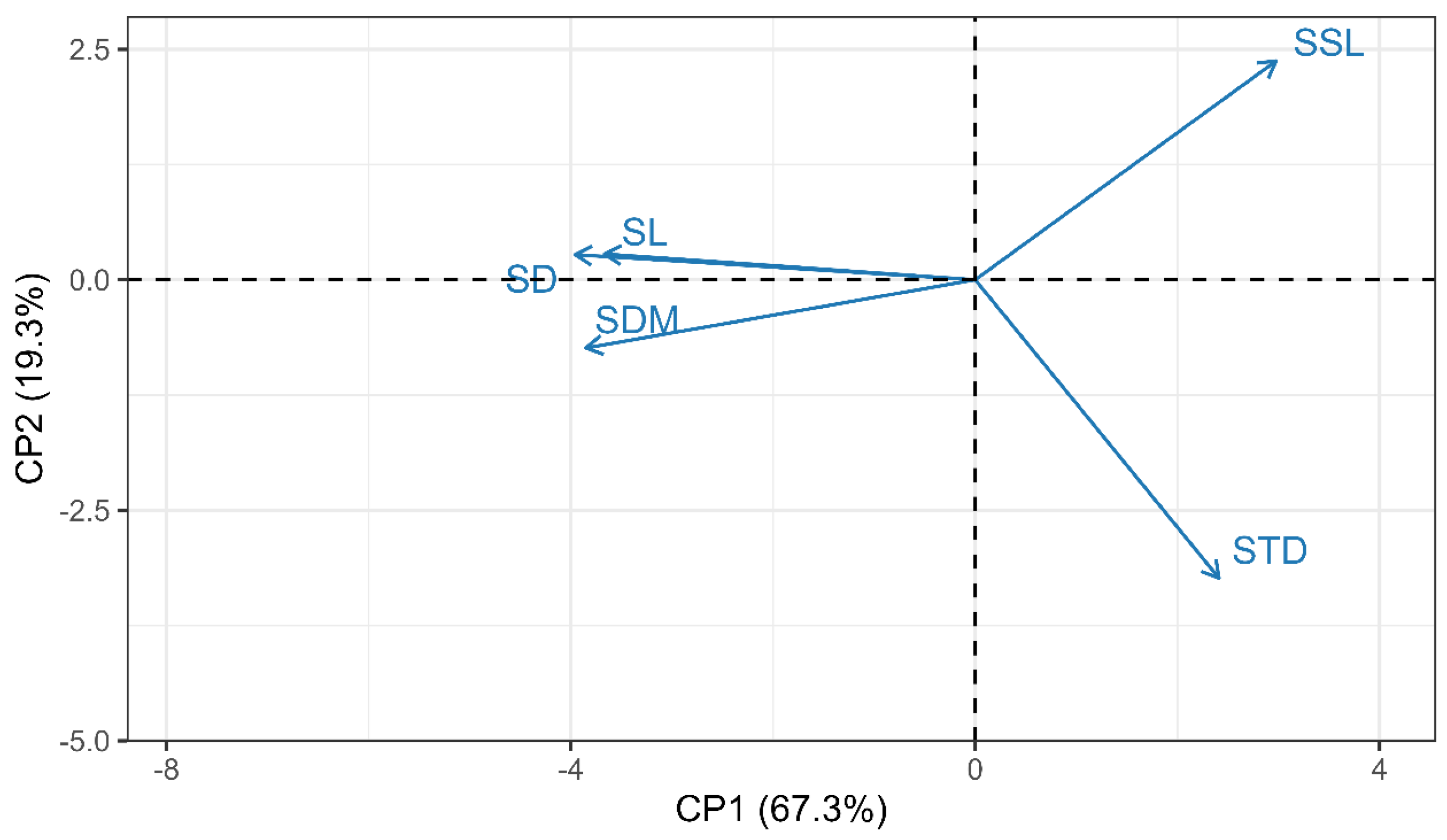
3.3. Multivariate Coordination

A multivariate analysis of all 1551 first-order samples revealed two important dimensions of five coexisting traits (adjusted eigenvalues: PC1 = 3.36; PC2 = 0.96). The first principal component (PC1) explained 67.3% of the total variation among the five traits and was negatively correlated with SD, SL, and SDM. In contrast, SSL and STD were positively correlated with PC1, though their strength was lower than that of SD, SL, and SDM (Figure 5 and Supplementary Table S1). In other words, twigs with relatively high PC1 scores were thinner, shorter, and lighter but had particularly high SSL and STD. PC2 explained an additional 19.3% of the total trait variation, mainly associated with variations in SSL and STD. Therefore, twigs with high PC2 scores had higher SSL but lower STD (Figure 5 and Supplementary Table S1).

4. Discussion

4.1. Variation in First-Order Shoot Traits

Our results show that the coefficient of variation (CV) for shoot biomass (SDM) is the highest among all functional traits. This finding suggests that, in response to environmental changes, plants exhibit greater flexibility and a preference for adjusting biomass allocation rather than modifying organ morphology and structure. In other words, allocation adjustments play a more significant role than morphological and structural adjustments. However, this result contrasts sharply with previous studies, which suggest that plants generally have a greater capacity to modify organ morphology than to adjust biomass allocation [32]. This discrepancy arises because earlier studies focused on the whole-plant scale, whereas our study examines a much finer organ scale (e.g., shoots). Moreover, to maximize light capture and competitive advantage, terminal branching systems prioritize resource investment in increasing the number of young shoots rather than altering their morphological traits [23]. Therefore, the high plasticity of biomass allocation within the branching system is reasonable. A major challenge for future research will be quantifying the contribution of each level of adjustment to overall trait variation and understanding how these trait modifications coordinate with one another.
In our study, we observed an interesting phenomenon: at the overall level, specific stem length (SSL) showed minimal response to changes in nutrient availability. This can be attributed to two main factors. First, although low nutrient availability positively affects SSL, it also reduces the number of shoots and limits branch elongation, which in turn negatively impacts SSL [33]. As a result, the overall variation in SSL remains small under low-nutrient conditions. Similarly, under high-nutrient conditions, SSL exhibits a comparable pattern. Therefore, the overall effect of nutrient availability on SSL is relatively mild. Second, as the terminal components of the aboveground branching system, shoots are responsible not only for nutrient and water absorption but also for structural support and transport. This requires a certain proportion of supportive and conductive tissues, making the woody plant’s branching system a continuously expanding structural organ. To maintain transport efficiency and mechanical stability, shoots inevitably expand in biomass more rapidly than in length, exhibiting an allometric growth relationship between biomass and shoot length [23]. Since SSL is defined as the ratio of shoot length to biomass, the continuous expansion of the branching system leads to a gradual decrease in SSL. This explains why SSL responds so weakly to changes in nutrient supply. Therefore, in this study, it is essential to describe the overall distribution of SSL within the entire shoot system rather than focusing solely on the average SSL of the branch system.

4.2. Bivariate Relationships Among the First-Order Shoot Traits

The tight linkage among SD, SL, and SDM was currently found at the level of small-scale shoots (Figure 3), which should be particularly useful for predicting how the SL and SDM would vary with SD across other shoot individuals. Variation in SSL is a result of variation in two-component traits: shoot diameter, which determines the length of the shoot produced per unit shoot volume, and STD, which determines the shoot volume produced per unit dry mass. SSL can be mathematically represented by these two traits, as stated by Ostonen et al. [33], where
SSL = 4 / ( π × D 2 × S T D )
This equation implies that SSL increases with decreasing D and/or STD. The negative relationship between SSL and STD can be explained mathematically, as a high stem tissue density implies more stem mass per unit stem volume and generally decreases the stem mass per unit stem length. The association of SSL and growth among these shoots could imply that differences in SSL among woody plants are associated with differences in growth strategies if thin shoots with high SSL ultimately have shorter lengths for nutrient acquisition or are otherwise less dependent on allocation.
The negative correlation between STD and the three simple traits, including SD, SL, and SDM, suggests that the growth of first-order shoots decreases with increasing stem tissue density. There may be three possible reasons for this. First, by definition, denser shoots produce less shoot volume per unit biomass [12]. Second, the proportion of vascular tissue in denser shoots may be lower, potentially leading to reduced transpiration, photosynthesis, and biomass growth. Some studies have reported a significant negative correlation between stem tissue density and the average diameter of woody plants [34,35]. Comparisons across different plots have found that diameter growth is associated with high stem tissue density, such as in the Amazon rainforest [36] and Malaysia [37]. Finally, this may also be due to the influence of multiple growth-related factors, as well as differences in growth measurement methods. Notably, in some cases, high stem tissue density may result in greater annual shoot growth [38].
Most pairwise traits showed allometric relationships rather than scaling in direct proportion with one another, which verified that the shoots had higher flexibility and importance of variation in allocation than in critical morphological and structural traits. In particular, the slope of the SDM–SL allometric relationship was 1.43, meaning that a tenfold longer SL coincided with a 50-fold greater dry mass invested, indicating that shoots generally have more variability in the SDM than in the SL. Because the aboveground branching system of woody plants is a continuously expanding organ, branches inevitably expand more in mass than in length while maintaining transport capacity and stability [23]. The result explained why SSL shows so little response to changes in nutrient availability.

4.3. Leading Dimensions of Shoot Trait Variation

Our results indicate that the five measured shoot traits exhibit varying degrees of variation and correlation, allowing them to be classified into two major trait dimensions. The first dimension is primarily characterized by three simple traits: SD, SL, and SDM (Figure 5). The second dimension is largely independent of the first (i.e., forming an orthogonal axis with the first dimension; Figure 5) and is dominated by two composite traits, SSL and STD.
The coordinated variation pattern of traits along the first principal component axis (PC1) may represent different strategies for shoot construction, maintenance, and persistence. Thicker first-order shoots invest more carbon and nutrients per unit length. These shoots appear to be less efficient in producing a specific stem length. However, the loss of specific stem length caused by this thick-shoot strategy can be compensated by an increase in soluble nutrients and biomass allocation (Figure 5). Therefore, compared to thinner first-order shoots, the total length per unit mass of thicker first-order shoots may not be significantly lower. This trade-off strategy among traits makes it similar to the belowground collaboration axis in the root economics spectrum (RES), which reflects the trade-off between species with thick, highly mycorrhizal roots and species with high specific root length (SRL) that rely less on mycorrhizal fungi for resource absorption [28].
The coordinated variation in traits along the second principal component axis (PC2) may represent the trade-off between nutrient acquisition and mechanical support. Specific stem length (SSL) is a key trait that determines the plastic response of shoots to nutrient stress, while stem tissue density is an important functional trait for mechanical support and tissue protection. Many studies have shown that low nutrient availability can, to some extent, increase SSL. This enhancement in nutrient acquisition capability may be crucial for environmental adaptation and gaining a competitive advantage. Although we did not measure nitrogen concentration in the shoots, we observed that PC2 was closely related to stem tissue density. Therefore, the PC2 axis is highly similar to the independent conservation axis in the root economics spectrum (RES), which reflects the trade-off between root tissue density (associated with extending root lifespan) and root nitrogen concentration (assumed to be related to nutrient acquisition [28]. Further research is needed to clarify the aboveground traits that reflect shoot resource conservatism.
This study found some relationships that were inconsistent with the predictions of the root economics spectrum (RES). According to RES predictions, shoot diameter and stem tissue density should be positively correlated. However, the study results showed a significant negative correlation between them, which contradicts the root economics spectrum (RES) hypothesis. One possible reason for this contradiction is that the two anatomical traits of twigs—stele tissue and cortex tissue—exhibit an allometric growth relationship [39], with the cortex growing at a faster rate than the stele. As a result, as the radius increases, the proportion of the cortex becomes larger than that of the stele. Since the tissue density of the cortex is lower than that of the stele, the allometric growth relationship leads to an inverse relationship between stem tissue density and diameter. Therefore, the observed relationship between branch diameter and stem tissue density does not support the predictions of the root economics spectrum (RES). Another possible explanation is that our study was limited to a relatively small scale or a restricted geographic range, which constrained the range of trait variation and may have masked broader trends [39]. Therefore, it is important for future research to use larger, global datasets to further examine these trait relationships.

5. Conclusions

In this study, we found that the stem dry mass (SDM) had the highest coefficient of variation (CV = 92.6%), indicating that biomass allocation is more important than morphological variation in the process of environmental adaptation. This is also supported by the allometric relationships between dry mass (SDM) and diameter (SD) and length (SL). Additionally, principal component analysis (PCA) revealed that the variation in shoot functional traits is associated with two main dimensions, and the relationship between stem tissue density (STD) and diameter (SD) does not support the common assumptions and predictions of the root economics spectrum (RES). Our work provides a new approach to understanding branch function and ecological strategies. Future studies should focus on quantitatively assessing the functional contributions of each level of adjustment and their interactions, and the extent to which various environmental factors influence the patterns of variation in shoot functional traits.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f16050850/s1, Table S1: Results of principal component analysis on the five traits from 1551 first-order shoots, including the proportion of variation explained (top section) and loading scores of traits on each component (bottom section).

Author Contributions

H.Z. designed the experiments, determined the article framework and research methods, and wrote the paper. Y.Y. completed the experiment sampling, performed the data analysis, and wrote the paper. Z.W. and Z.L. contributed to the research and writing of the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Major Science and Technology Program for Water Pollution Control and Treatment (No. 2017ZX07101-002) and the Discipline Construction Program of Huayong Zhang, at the School of Life Sciences, Shandong University (61200082363001).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author or the first author upon reasonable request.

Acknowledgments

The authors would like to acknowledge with great gratitude the support of the National Major Science and Technology Program for Water Pollution Control and Treatment and the Discipline Construction Program of Huayong Zhang, Shandong University, School of Life Sciences.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Sprugel, D.G.; Hinckley, T.M.; Schaap, W. The Theory and Practice of Branch Autonomy. Annu. Rev. Ecol. Evol. Syst. 1991, 22, 309–334. [Google Scholar] [CrossRef]
  2. Minden, V.; Kleyer, M. Internal and External Regulation of Plant Organ Stoichiometry. Plant Biol. 2014, 16, 897–907. [Google Scholar] [CrossRef]
  3. Valladares, F.; Pearcy, R.W. The Functional Ecology of Shoot Architecture in Sun and Shade Plants of Heteromeles Arbutifolia M. Roem., a Californian Chaparral Shrub. Oecologia 1998, 114, 1–10. [Google Scholar] [CrossRef]
  4. Westoby, M.; Wright, I.J. The Leaf Size—Twig Size Spectrum and Its Relationship to Other Important Spectra of Variation among Species. Oecologia 2003, 135, 621–628. [Google Scholar] [CrossRef] [PubMed]
  5. Violle, C.; Navas, M.-L.; Vile, D.; Kazakou, E.; Fortunel, C.; Hummel, I.; Garnier, E. Let the Concept of Trait Be Functional! Oikos 2007, 116, 882–892. [Google Scholar] [CrossRef]
  6. Freschet, G.T.; Pagès, L.; Iversen, C.M.; Comas, L.H.; Rewald, B.; Roumet, C.; Klimešová, J.; Zadworny, M.; Poorter, H.; Postma, J.A.; et al. A Starting Guide to Root Ecology: Strengthening Ecological Concepts and Standardising Root Classification, Sampling, Processing and Trait Measurements. New Phytol. 2021, 232, 973–1122. [Google Scholar] [CrossRef]
  7. Liu, R.; Yang, X.; Gao, R.; Huang, Z.; Cornelissen, J.H.C. Coordination of Economics Spectra in Leaf, Stem and Root within the Genus Artemisia along a Large Environmental Gradient in China. Glob. Ecol. Biogeogr. 2023, 32, 324–338. [Google Scholar] [CrossRef]
  8. Bucci, S.J.; Goldstein, G.; Meinzer, F.C.; Scholz, F.G.; Franco, A.C.; Bustamante, M. Functional Convergence in Hydraulic Architecture and Water Relations of Tropical Savanna Trees: From Leaf to Whole Plant. Tree Physiol. 2004, 24, 891–899. [Google Scholar] [CrossRef] [PubMed]
  9. McCulloh, K.A.; Meinzer, F.C.; Sperry, J.S.; Lachenbruch, B.; Voelker, S.L.; Woodruff, D.R.; Domec, J.-C. Comparative Hydraulic Architecture of Tropical Tree Species Representing a Range of Successional Stages and Wood Density. Oecologia 2011, 167, 27–37. [Google Scholar] [CrossRef]
  10. Poorter, L.; McDonald, I.; Alarcón, A.; Fichtler, E.; Licona, J.-C.; Peña-Claros, M.; Sterck, F.; Villegas, Z.; Sass-Klaassen, U. The Importance of Wood Traits and Hydraulic Conductance for the Performance and Life History Strategies of 42 Rainforest Tree Species. New Phytol. 2010, 185, 481–492. [Google Scholar] [CrossRef]
  11. Van Gelder, H.A.; Poorter, L.; Sterck, F.J. Wood Mechanics, Allometry, and Life-History Variation in a Tropical Rain Forest Tree Community. New Phytol. 2006, 171, 367–378. [Google Scholar] [CrossRef]
  12. Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a Worldwide Wood Economics Spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef]
  13. Garnier, E.; Laurent, G.; Bellmann, A.; Debain, S.; Berthelier, P.; Ducout, B.; Roumet, C.; Navas, M.-L. Consistency of Species Ranking Based on Functional Leaf Traits. New Phytol. 2001, 152, 69–83. [Google Scholar] [CrossRef] [PubMed]
  14. Violle, C.; Enquist, B.J.; McGill, B.J.; Jiang, L.; Albert, C.H.; Hulshof, C.; Jung, V.; Messier, J. The Return of the Variance: Intraspecific Variability in Community Ecology. Trends Ecol. Evol. 2012, 27, 244–252. [Google Scholar] [CrossRef]
  15. Westoby, M.; Falster, D.S.; Moles, A.T.; Vesk, P.A.; Wright, I.J. Plant Ecological Strategies: Some Leading Dimensions of Variation Between Species. Annu. Rev. Ecol. Evol. Syst. 2002, 33, 125–159. [Google Scholar] [CrossRef]
  16. Albert, C.H.; Thuiller, W.; Yoccoz, N.G.; Soudant, A.; Boucher, F.; Saccone, P.; Lavorel, S. Intraspecific Functional Variability: Extent, Structure and Sources of Variation. J. Ecol. 2010, 98, 604–613. [Google Scholar] [CrossRef]
  17. Le Bagousse-Pinguet, Y.; de Bello, F.; Vandewalle, M.; Leps, J.; Sykes, M.T. Species Richness of Limestone Grasslands Increases with Trait Overlap: Evidence from within- and between-Species Functional Diversity Partitioning. J. Ecol. 2014, 102, 466–474. [Google Scholar] [CrossRef]
  18. Shipley, B.; De Bello, F.; Cornelissen, J.H.C.; Laliberté, E.; Laughlin, D.C.; Reich, P.B. Reinforcing Loose Foundation Stones in Trait-Based Plant Ecology. Oecologia 2016, 180, 923–931. [Google Scholar] [CrossRef] [PubMed]
  19. Sides, C.B.; Enquist, B.J.; Ebersole, J.J.; Smith, M.N.; Henderson, A.N.; Sloat, L.L. Revisiting Darwin’s Hypothesis: Does Greater Intraspecific Variability Increase Species’ Ecological Breadth? Am. J. Bot 2014, 101, 56–62. [Google Scholar] [CrossRef]
  20. Fajardo, A.; Piper, F.I. Intraspecific Trait Variation and Covariation in a Widespread Tree Species (Nothofagus Pumilio) in Southern Chile. New Phytol. 2011, 189, 259–271. [Google Scholar] [CrossRef]
  21. Vasseur, F.; Exposito-Alonso, M.; Ayala-Garay, O.J.; Wang, G.; Enquist, B.J.; Vile, D.; Violle, C.; Weigel, D. Adaptive Diversification of Growth Allometry in the Plant Arabidopsis Thaliana. Proc. Natl. Acad. Sci. USA 2018, 115, 3416–3421. [Google Scholar] [CrossRef] [PubMed]
  22. Lusk, C.H.; Reich, P.B.; Montgomery, R.A.; Ackerly, D.D.; Cavender-Bares, J. Why Are Evergreen Leaves so Contrary about Shade? Trends Ecol. Evol. 2008, 23, 299–303. [Google Scholar] [CrossRef]
  23. Poorter, H.; Ryser, P. The Limits to Leaf and Root Plasticity: What Is so Special about Specific Root Length? New Phytol. 2015, 206, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
  24. Diaz, S.; Hodgson, J.G.; Thompson, K.; Cabido, M.; Cornelissen, J.h.c.; Jalili, A.; Montserrat-Martí, G.; Grime, J.p.; Zarrinkamar, F.; Asri, Y.; et al. The Plant Traits That Drive Ecosystems: Evidence from Three Continents. J. Veg. Sci. 2004, 15, 295–304. [Google Scholar] [CrossRef]
  25. Grime, J.P.; Thompson, K.; Hunt, R.; Hodgson, J.G.; Cornelissen, J.H.C.; Rorison, I.H.; Hendry, G.A.F.; Ashenden, T.W.; Askew, A.P.; Band, S.R.; et al. Integrated Screening Validates Primary Axes of Specialisation in Plants. Oikos 1997, 79, 259–281. [Google Scholar] [CrossRef]
  26. Laughlin, D.C. The Intrinsic Dimensionality of Plant Traits and Its Relevance to Community Assembly. J. Ecol. 2014, 102, 186–193. [Google Scholar] [CrossRef]
  27. Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.C.; Diemer, M.; et al. The Worldwide Leaf Economics Spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
  28. Bergmann, J.; Weigelt, A.; van der Plas, F.; Laughlin, D.C.; Kuyper, T.W.; Guerrero-Ramirez, N.; Valverde-Barrantes, O.J.; Bruelheide, H.; Freschet, G.T.; Iversen, C.M.; et al. The Fungal Collaboration Gradient Dominates the Root Economics Space in Plants. Sci. Adv. 2020, 6, eaba3756. [Google Scholar] [CrossRef] [PubMed]
  29. Zhang, X.; Li, X.; Ji, X.; Zhang, Z.; Zhang, H.; Zha, T.; Jiang, L. Elevation and Total Nitrogen Are the Critical Factors That Control the Spatial Distribution of Soil Organic Carbon Content in the Shrubland on the Bashang Plateau, China. Catena 2021, 204, 105415. [Google Scholar] [CrossRef]
  30. Borchert, R.; Slade, N.A. Bifurcation Ratios and the Adaptive Geometry of Trees. Bot. Gaz. 1981, 142, 394–401. [Google Scholar] [CrossRef]
  31. Pregitzer, K.S. Fine Roots of Trees—A New Perspective. New Phytol. 2002, 154, 267–270. [Google Scholar] [CrossRef] [PubMed]
  32. Poorter, H.; Niklas, K.J.; Reich, P.B.; Oleksyn, J.; Poot, P.; Mommer, L. Biomass Allocation to Leaves, Stems and Roots: Meta-Analyses of Interspecific Variation and Environmental Control. New Phytol. 2012, 193, 30–50. [Google Scholar] [CrossRef] [PubMed]
  33. Ostonen, I.; Püttsepp, Ü.; Biel, C.; Alberton, O.; Bakker, M.R.; Lõhmus, K.; Majdi, H.; Metcalfe, D.; Olsthoorn, A.F.M.; Pronk, A.; et al. Specific Root Length as an Indicator of Environmental Change. Plant Biosyst. 2007, 141, 426–442. [Google Scholar] [CrossRef]
  34. Muller-Landau, H.C. Interspecific and Inter-Site Variation in Wood Specific Gravity of Tropical Trees. Biotropica 2004, 36, 20–32. [Google Scholar] [CrossRef]
  35. Nascimento, H.E.M.; Laurance, W.F.; Condit, R.; Laurance, S.G.; D’Angelo, S.; Andrade, A.C. Demographic and Life-history Correlates for Amazonian Trees. J. Vegetation Sci. 2005, 16, 625–634. [Google Scholar] [CrossRef]
  36. Chao, K.-J.; Phillips, O.L.; Gloor, E.; Monteagudo, A.; Torres-Lezama, A.; Martínez, R.V. Growth and Wood Density Predict Tree Mortality in Amazon Forests. J. Ecol. 2008, 96, 281–292. [Google Scholar] [CrossRef]
  37. King, D.A.; Davies, S.J.; Tan, S.; Noor, N.S.M. The Role of Wood Density and Stem Support Costs in the Growth and Mortality of Tropical Trees. J. Ecol. 2006, 94, 670–680. [Google Scholar] [CrossRef]
  38. Hacke, U.G.; Sperry, J.S.; Pockman, W.T.; Davis, S.D.; McCulloh, K.A. Trends in Wood Density and Structure Are Linked to Prevention of Xylem Implosion by Negative Pressure. Oecologia 2001, 126, 457–461. [Google Scholar] [CrossRef]
  39. Kong, D.; Wang, J.; Wu, H.; Valverde-Barrantes, O.J.; Wang, R.; Zeng, H.; Kardol, P.; Zhang, H.; Feng, Y. Nonlinearity of Root Trait Relationships and the Root Economics Spectrum. Nat. Commun. 2019, 10, 2203. [Google Scholar] [CrossRef]
Forests 16 00850 g001
Figure 1. Location of the study area and sample site (red diamond-shaped markers).
Figure 1. Location of the study area and sample site (red diamond-shaped markers).
Forests 16 00850 g001
Forests 16 00850 g002
Figure 2. Diagrams of the branching structure of Larix principis-rupprechtii and branch ordering in this study.
Figure 2. Diagrams of the branching structure of Larix principis-rupprechtii and branch ordering in this study.
Forests 16 00850 g002
Forests 16 00850 g003
Figure 3. Pairwise correlations among five functional traits of all shoots of Larix principis-rupprechtii. Bivariate relationships of branch traits for all shoots (n = 1551) were analyzed using general linear regression. In the scatterplots (lower triangle), significant correlations are indicated by red regression lines (general linear regression). Correlation coefficients are shown in black in the upper triangle based on the linear regression analysis. **, p = 0.01; ***, p = 0.001.
Figure 3. Pairwise correlations among five functional traits of all shoots of Larix principis-rupprechtii. Bivariate relationships of branch traits for all shoots (n = 1551) were analyzed using general linear regression. In the scatterplots (lower triangle), significant correlations are indicated by red regression lines (general linear regression). Correlation coefficients are shown in black in the upper triangle based on the linear regression analysis. **, p = 0.01; ***, p = 0.001.
Forests 16 00850 g003
Forests 16 00850 g004
Figure 4. Standardized major axis (SMA) regressions among simple functional traits (SD, SL, and SDM). The coefficient of determination (R2) is provided, and the SMA regression line is plotted when the relationship is significant.
Figure 4. Standardized major axis (SMA) regressions among simple functional traits (SD, SL, and SDM). The coefficient of determination (R2) is provided, and the SMA regression line is plotted when the relationship is significant.
Forests 16 00850 g004
Forests 16 00850 g005
Figure 5. Shoot trait loadings biplots of principal component analysis (PCA) using original trait data.
Figure 5. Shoot trait loadings biplots of principal component analysis (PCA) using original trait data.
Forests 16 00850 g005
Table 1. Shoot traits included in the current analyses.
Table 1. Shoot traits included in the current analyses.
AbbreviationFull NameDefinitionUnits
SDStem diameter mm
SLStem length cm
SDMStem dry massDry mass of the shootg
SSLSpecific stem lengthShoot length/shoot dry massm·g−1
STDSpecific stem densityShoot dry mass/shoot volumeg·cm−3
Table 2. Summary of the five traits in first-order shoots.
Table 2. Summary of the five traits in first-order shoots.
TraitsMeanMedianMinMaxCV%
SD1.611.540.544.2535.3
SL13.9512.491.0253.2057.2
SDM0.240.160.011.4992.6
SSL0.840.740.152.3149.5
STD0.840.720.212.9353.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Yu, Y.; Zhang, H.; Wang, Z.; Liu, Z. Multi-Dimensional Patterns of Variation in First-Order Shoot Traits of Larix principis-rupprechtii in Northern China. Forests 2025, 16, 850. https://doi.org/10.3390/f16050850

AMA Style

Yu Y, Zhang H, Wang Z, Liu Z. Multi-Dimensional Patterns of Variation in First-Order Shoot Traits of Larix principis-rupprechtii in Northern China. Forests. 2025; 16(5):850. https://doi.org/10.3390/f16050850

Chicago/Turabian Style

Yu, Yang, Huayong Zhang, Zhongyu Wang, and Zhao Liu. 2025. "Multi-Dimensional Patterns of Variation in First-Order Shoot Traits of Larix principis-rupprechtii in Northern China" Forests 16, no. 5: 850. https://doi.org/10.3390/f16050850

APA Style

Yu, Y., Zhang, H., Wang, Z., & Liu, Z. (2025). Multi-Dimensional Patterns of Variation in First-Order Shoot Traits of Larix principis-rupprechtii in Northern China. Forests, 16(5), 850. https://doi.org/10.3390/f16050850

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop