Comparison of Field Sampling- and Airborne Laser Scanning-Derived Stand-Level Inventories in a Mixed Conifer Forest and Volume Validation Using Log Scaling Data
Abstract
1. Introduction
- (1)
- An area-based approach that used gridded summaries of the ALS point cloud and an ensemble learning algorithm to model each stand attribute at 20 m spatial resolution (hereafter referred to as ‘ABA’).
- (2)
- An individual tree approach that used a variable-radius local maximum filter to detect trees and then applied field-derived allometric models to estimate tree diameter at breast height (DBH) and volume (hereafter referred to as ‘ITD-VW’).
- (3)
- ForestView®, a commercial ‘gray box’ method for detecting and estimating individual tree attributes (hereafter referred to as ‘ITD-FV’).
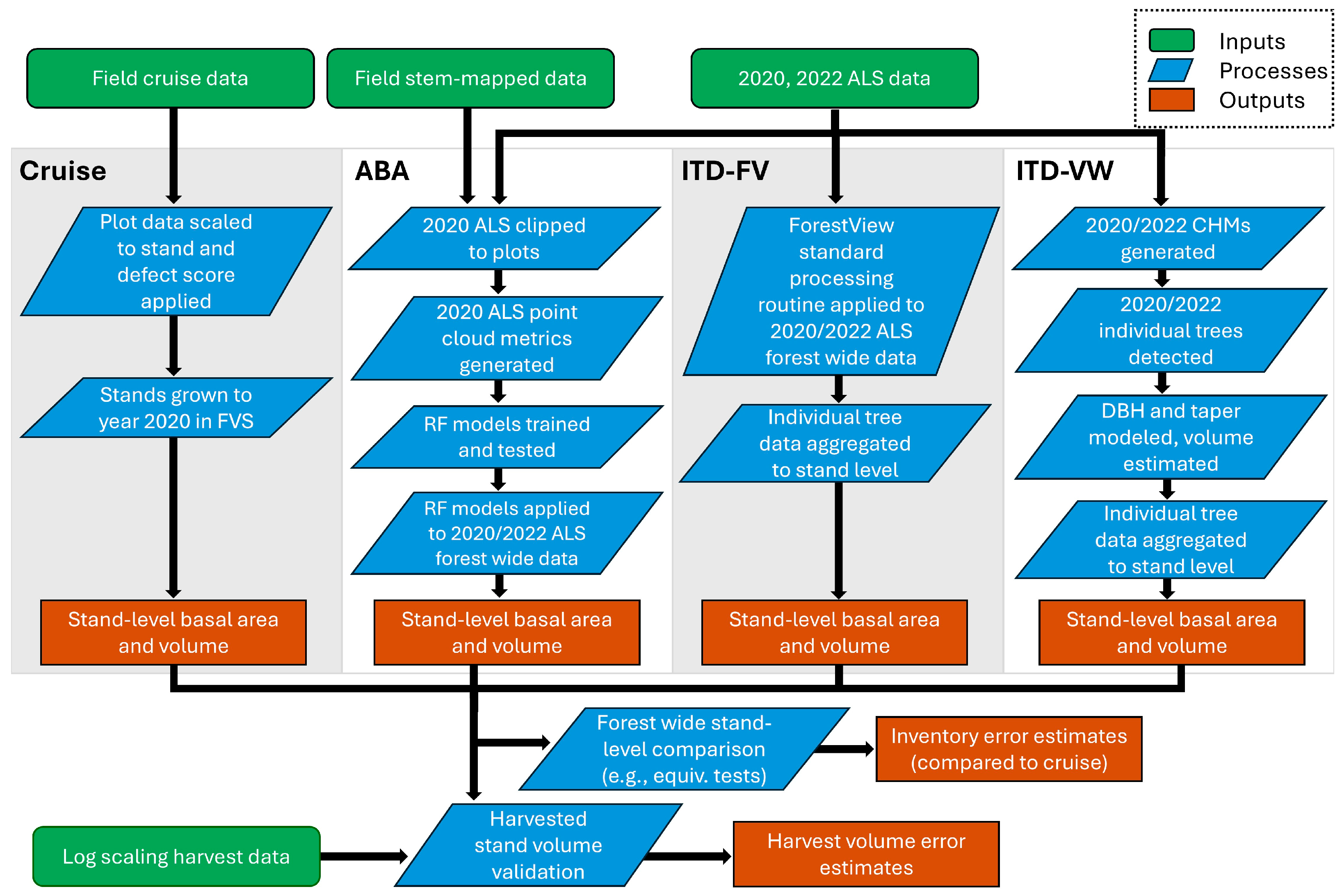
2. Materials and Methods
2.1. Study Area and Data
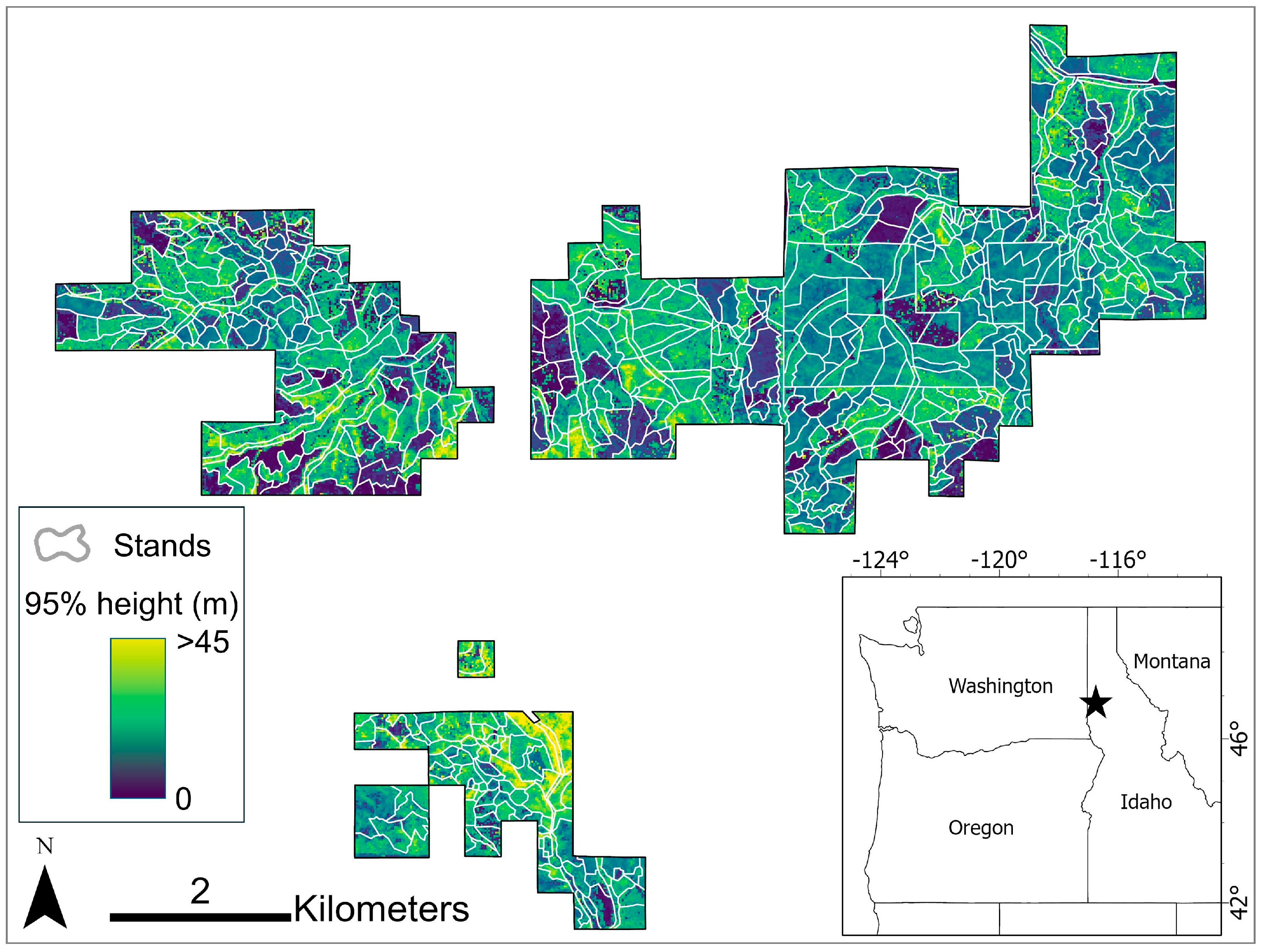
2.1.1. Study Area
2.1.2. Field Inventory Data: Stand-Based ‘Cruise’ Inventory
2.1.3. Field Inventory Data: Independent Stem-Mapped Plots
2.1.4. Airborne Laser Scanning Data and Preprocessing
2.2. Methods
2.2.1. Area-Based Approach Inventory
2.2.2. Local Max Filter Individual Tree Inventory (ITD-VW)
2.2.3. ForestView® Individual Tree Inventory (ITD-FV)
2.2.4. Validation of Inventory Volume Using Log Scaling Data
2.2.5. Comparison of Stand Inventory Methods
3. Results
3.1. Area-Based Approach Prediction Accuracy
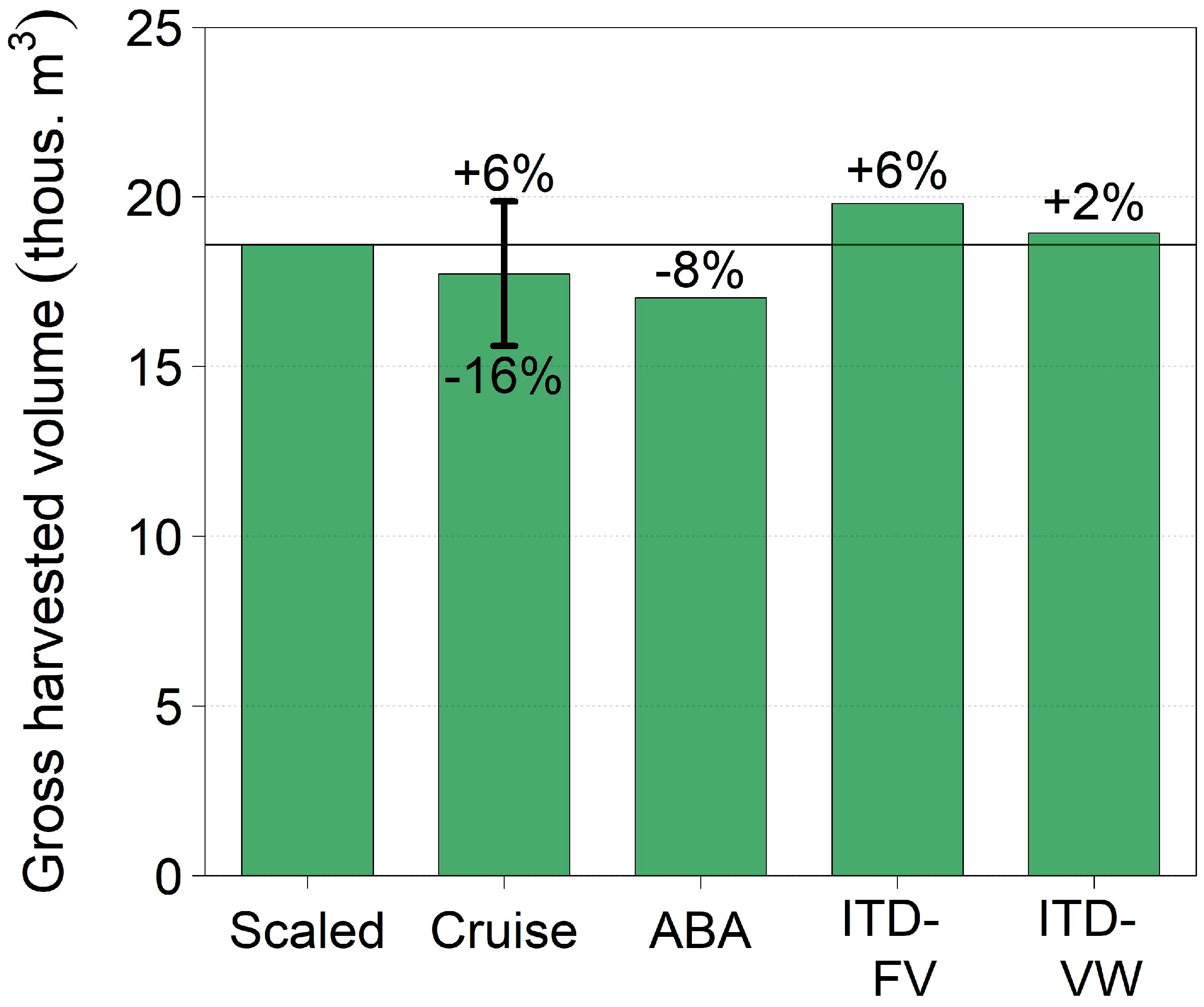
3.2. Validation of Harvested Volume
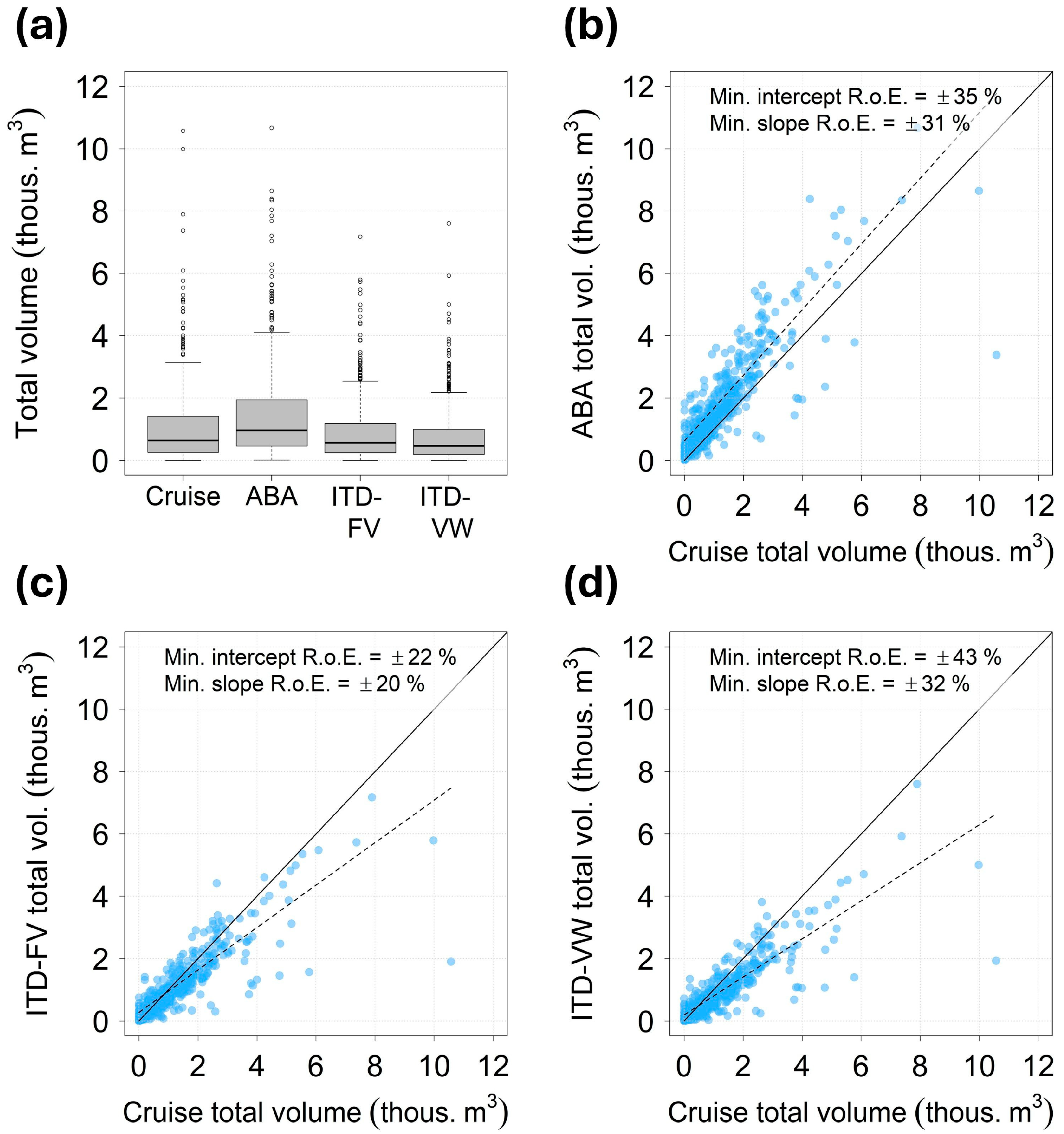
3.3. Comparison of Forest-Wide Inventories
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tinkham, W.T.; Mahoney, P.R.; Hudak, A.T.; Domke, G.M.; Falkowski, M.J.; Woodall, C.W.; Smith, A.M.S. Applications of the United States Forest Inventory and Analysis dataset: A review and future directions. Can. J. For. Res. 2018, 48, 1251–1268. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalen, P.; Kangas, A. From comprehensive field inventories to remotely sensed wall-to-wall stand attribute data—A brief history of management inventories in the Nordic countries. Can. J. For. Res. 2021, 51, 257–266. [Google Scholar] [CrossRef]
- Frayer, W.E.; Furnival, G.M. History of Forest Survey Sampling Designs in the United States. In Integrated Tools for Natural Resources Inventories in the 21st Century; Hansen, M., Burk, T., Eds.; Gen. Tech. Rep. NC-212; USDA Forest Service, North Central Forest Experiment Station: St. Paul, MN, USA, 2000; pp. 42–49. [Google Scholar]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Hemingway, H.; Opalach, D. Integrating Lidar Canopy Height Models with Satellite-Assisted Inventory Methods: A Comparison of Inventory Estimates. For. Sci. 2024, 70, 2–13. [Google Scholar] [CrossRef]
- Woods, M.; Pitt, D.; Penner, M.; Lim, K.; Nesbitt, D.; Etheridge, D.; Treitz, P. Operational implementation of a LiDAR inventory in Boreal Ontario. For. Chron. 2011, 87, 512–528. [Google Scholar] [CrossRef]
- Keefe, R.F.; Zimbelman, E.G.; Picchi, G. Use of individual tree and product level data to improve operational forestry. Curr. For. Rep. 2022, 8, 148–165. [Google Scholar] [CrossRef]
- Meddens, A.J.; Steen-Adams, M.M.; Hudak, A.T.; Mauro, F.; Byassee, P.M.; Strunk, J. Specifying geospatial data product characteristics for forest and fuel management applications. Environ. Res. Lett. 2022, 17, 045025. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Mager, C.; Waser, L.T.; Kanjir, U.; Schäfer, J.; Buhvald, A.P.; Shafeian, E.; Schiefer, F.; Stančič, L.; Immitzer, M.; et al. Forest practitioners’ requirements for remote sensing-based canopy height, wood-volume, tree species, and disturbance products. For. Int. J. For. Res. 2024, 98, 233–252. [Google Scholar] [CrossRef]
- Hummel, S.; Hudak, A.T.; Uebler, E.H.; Falkowski, M.J.; Megown, K.A. A comparison of accuracy and cost of LiDAR versus stand exam data for landscape management on the Malheur National Forest. J. For. 2011, 109, 267–273. [Google Scholar] [CrossRef]
- Hayashi, R.; Weiskittel, A.; Kershaw, J.A., Jr. Influence of prediction cell size on LiDAR-derived area-based estimates of total volume in mixed-species and multicohort forests in northeastern North America. Can. J. Remote Sens. 2016, 42, 473–488. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Klauberg, C.; Vierling, L.A.; Gonzalez-Benecke, C.; de Padua Chaves Carvalho, S.; Rodriguez, L.C.E.; Cardil, A. Combined effect of pulse density and grid cell size on predicting and mapping aboveground carbon in fast-growing Eucalyptus forest plantation using airborne LiDAR data. Carbon Bal. Manag. 2017, 12, 13. [Google Scholar] [CrossRef] [PubMed]
- Falkowski, M.J.; Smith, A.M.S.; Gessler, P.E.; Hudak, A.T.; Vierling, L.A.; Evans, J.S. The influence of conifer forest canopy cover on the accuracy of two individual tree measurement algorithms using lidar data. Can. J. Remote Sens. 2008, 34, S338–S350. [Google Scholar] [CrossRef]
- Sparks, A.M.; Corrao, M.V.; Smith, A.M.S. Cross-comparison of individual tree detection methods using low and high pulse density airborne laser scanning data. Remote Sens. 2022, 14, 3480. [Google Scholar] [CrossRef]
- Vastaranta, M.; Holopainen, M.; Yu, X.; Hyyppä, J.; Mäkinen, A.; Rasinmäki, J.; Melkas, T.; Kaartinen, H.; Hyyppä, H. Effects of individual tree detection error sources on forest management planning calculations. Remote Sens. 2011, 3, 1614–1626. [Google Scholar] [CrossRef]
- Soininen, V.; Kukko, A.; Yu, X.; Kaartinen, H.; Luoma, V.; Saikkonen, O.; Holopainen, M.; Matikainen, L.; Lehtomäki, M.; Hyyppä, J. Predicting growth of individual trees directly and indirectly using 20-year bitemporal airborne laser scanning point cloud data. Forests 2022, 13, 2040. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; White, J.C.; Wulder, M.A.; Næsset, E. Remote sensing in forestry: Current challenges, considerations and directions. For. Int. J. For. Res. 2024, 97, 11–37. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Mehtätalo, L.; Maltamo, M. Comparing individual tree detection and the area-based statistical approach for the retrieval of forest stand characteristics using airborne laser scanning in Scots pine stands. Can. J. For. Res. 2011, 41, 583–598. [Google Scholar] [CrossRef]
- Frank, B.; Mauro, F.; Temesgen, H. Model-based estimation of forest inventory attributes using lidar: A comparison of the area-based and semi-individual tree crown approaches. Remote Sens. 2020, 12, 2525. [Google Scholar] [CrossRef]
- Vieira Leite, R.; Hummel do Amaral, C.; De Paula Pires, R.; Silva, C.A.; Boechat Soares, C.P.; Paulo Macedo, R.; Araújo Lopes Da Silva, A.; North Broadbent, E.; Mohan, M.; Garcia Leite, H. Estimating Stem Volume in Eucalyptus Plantations Using Airborne LiDAR: A Comparison of Area-and Individual Tree-Based Approaches. Remote Sens. 2020, 12, 1513. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Comparison of area-based and individual tree-based methods for predicting plot-level forest attributes. Remote Sens. 2010, 2, 1481–1495. [Google Scholar] [CrossRef]
- Lara-Gómez, M.Á.; Navarro-Cerrillo, R.M.; Clavero Rumbao, I.; Palacios-Rodríguez, G. Comparison of errors produced by ABA and ITC methods for the estimation of forest inventory attributes at stand and tree level in Pinus radiata plantations in Chile. Remote Sens. 2023, 15, 1544. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Maltamo, M.; Malinen, J.; Pitkänen, J.; Packalén, P. Preharvest measurement of marked stands using airborne laser scanning. For. Sci. 2007, 53, 653–661. [Google Scholar] [CrossRef]
- Korhonen, L.; Peuhkurinen, J.; Malinen, J.; Suvanto, A.; Maltamo, M.; Packalen, P.; Kangas, J. The use of airborne laser scanning to estimate sawlog volumes. Forestry 2008, 81, 499–510. [Google Scholar]
- Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. For. Res. 2010, 129, 1131–1142. [Google Scholar] [CrossRef]
- Persson, H.J.; Olofsson, K.; Holmgren, J. Two-phase forest inventory using very-high-resolution laser scanning. Remote Sens. Environ. 2022, 271, 112909. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Buckmaster, G. Validating estimates of merchantable volume from airborne laser scanning (ALS) data using weight scale data. For. Chron. 2014, 90, 378–385. [Google Scholar] [CrossRef]
- Sparks, A.M.; Corrao, M.V.; Keefe, R.F.; Armstrong, R.; Smith, A.M.S. An Accuracy Assessment of Field and Airborne Laser Scanning–Derived Individual Tree Inventories using Felled Tree Measurements and Log Scaling Data in a Mixed Conifer Forest. For. Sci. 2024, 70, 228–241. [Google Scholar] [CrossRef]
- NOAA. NOAA’s US Climate Normals (1991–2020). NOAA National Centers for Environmental Information; 2022. Available online: https://www.ncei.noaa.gov/products/land-based-station/us-climate-normals (accessed on 11 December 2024).
- Dixon, G.E. Essential FVS: A User’s Guide to the Forest Vegetation Simulator; USDA Forest Service, Forest Management Service Center: Fort Collins, CO, USA, 2002.
- Sparks, A.M.; Smith, A.M.S. Accuracy of a lidar-based individual tree detection and attribute measurement algorithm developed to inform forest products supply chain and resource management. Forests 2021, 13, 3. [Google Scholar] [CrossRef]
- ASPRS. ASPRS LAS Format Standard 1.4. 2019. Available online: https://www.asprs.org/wp-content/uploads/2019/07/LAS_1_4_r15.pdf (accessed on 9 December 2024).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards Jr, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; USDA Forest Service, Pacific Northwest Research Station: Seattle, WA, USA, 2024. Available online: http://forsys.cfr.washington.edu/fusion/fusion_overview.html (accessed on 29 November 2024).
- Tinkham, W.T.; Smith, A.M.S.; Hoffman, C.; Hudak, A.T.; Falkowski, M.J.; Swanson, M.E.; Gessler, P.E. Investigating the influence of LiDAR ground surface errors on the utility of derived forest inventories. Can. J. For. Res. 2012, 42, 413–422. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Collins, L.; McCarthy, G.; Mellor, A.; Newell, G.; Smith, L. Training data requirements for fire severity mapping using Landsat imagery and random forest. Remote Sens. Environ. 2020, 245, 111839. [Google Scholar] [CrossRef]
- Lyons, M.B.; Keith, D.A.; Phinn, S.R.; Mason, T.J.; Elith, J. A comparison of resampling methods for remote sensing classification and accuracy assessment. Remote Sens. Environ. 2018, 208, 145–153. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating pit-free canopy height models from airborne lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Plowright, A.; Roussel, J. ForestTools: Tools for Analyzing Remote Sensing Forest Data. R Package Version 1.0.2. 2023. Available online: https://github.com/andrew-plowright/ForestTools (accessed on 20 October 2024).
- Kozak, A. My last words on taper equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef]
- Pancoast, A.D. Evaluation of Taper and Volume Estimation Techniques for Ponderosa Pine in Eastern Oregon and Eastern Washington. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 2018. [Google Scholar]
- Poudel, K.P.; Temesgen, H.; Gray, A.N. Estimating upper stem diameters and volume of Douglas-fir and Western hemlock trees in the Pacific northwest. For. Ecosyst. 2018, 5, 16. [Google Scholar] [CrossRef]
- Corrao, M.V.; Sparks, A.M.; Smith, A.M.S. A Conventional Cruise and Felled-Tree Validation of Individual Tree Diameter, Height and Volume Derived from Airborne Laser Scanning Data of a Loblolly Pine (P. taeda) Stand in Eastern Texas. Remote Sens. 2022, 14, 2567. [Google Scholar] [CrossRef]
- Idaho Board of Scaling Practices. Basic Information About Cubic Scaling. 2018. Available online: https://ibsp.idaho.gov/wp-content/uploads/2018/06/BASIC-INFORMATION-ABOUT-CUBIC-SCALING.pdf (accessed on 7 March 2024).
- Spelter, H. Converting among log scaling methods: Scribner, International, and Doyle versus cubic. J. For. 2004, 102, 33–39. [Google Scholar] [CrossRef]
- Robinson, A.P.; Duursma, R.A.; Marshall, J.D. A regression-based equivalence test for model validation: Shifting the burden of proof. Tree Phys. 2005, 25, 903–913. [Google Scholar] [CrossRef] [PubMed]
- Hyyppa, H.J.; Hyyppa, J.M. Effects of stand size on the accuracy of remote sensing-based forest inventory. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2613–2621. [Google Scholar] [CrossRef]
- Robinson, A. Equivalence: Provides Tests and Graphics for Assessing Tests of Equivalence, Version 0.7.2. Available online: https://cran.r-project.org/web/packages/equivalence/ (accessed on 23 January 2024).
- Wang, Y.; Hyyppä, J.; Liang, X.; Kaartinen, H.; Yu, X.; Lindberg, E.; Holmgren, J.; Qin, Y.; Mallet, C.; Ferraz, A.; et al. International benchmarking of the individual tree detection methods for modeling 3-D canopy structure for silviculture and forest ecology using airborne laser scanning. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5011–5027. [Google Scholar] [CrossRef]
- Wielgosz, M.; Puliti, S.; Xiang, B.; Schindler, K.; Astrup, R. SegmentAnyTree: A sensor and platform agnostic deep learning model for tree segmentation using laser scanning data. Remote Sens. Environ. 2024, 313, 114367. [Google Scholar] [CrossRef]
- Herbert, C.; Fried, J.S.; Butsic, V. Validation of Forest vegetation simulator model finds overprediction of carbon growth in California. Forests 2023, 14, 604. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; White, J.C.; Goodbody, T.R.; Hennigar, C.R.; Wulder, M.A.; Socha, J.; Woods, M.E. Estimating changes in forest attributes and enhancing growth projections: A review of existing approaches and future directions using airborne 3D point cloud data. Curr. For. Rep. 2021, 7, 1–24. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Hall, R.J. The uncertainty in conifer plantation growth prediction from multi-temporal lidar datasets. Remote Sens. Environ. 2008, 112, 1168–1180. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Achim, A.; Mulverhill, C. Framework for near real-time forest inventory using multi source remote sensing data. Forestry 2023, 96, 1–19. [Google Scholar] [CrossRef]
- Strunk, J.; Packalen, P.; Gould, P.; Gatziolis, D.; Maki, C.; Andersen, H.E.; McGaughey, R.J. Large area forest yield estimation with pushbroom digital aerial photogrammetry. Forests 2019, 10, 397. [Google Scholar] [CrossRef]
- Ritz, A.L.; Thomas, V.A.; Wynne, R.H.; Green, P.C.; Schroeder, T.A.; Albaugh, T.J.; Burkhart, H.E.; Carter, D.R.; Cook, R.L.; Campoe, O.C.; et al. Assessing the utility of NAIP digital aerial photogrammetric point clouds for estimating canopy height of managed loblolly pine plantations in the southeastern United States. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 103012. [Google Scholar] [CrossRef]


| Metric | Description |
|---|---|
| HMEAN | Height mean |
| HMAX | Height max |
| HSD | Height standard deviation |
| HCV | Height coefficient of variation |
| HSKEW | Height skewness |
| HKURT | Height kurtosis |
| H01ST | 1st percentile height value |
| H05TH | 5th percentile height value |
| H10TH | 10th percentile height value |
| H20TH | 20th percentile height value |
| H25TH | 25th percentile height value |
| H30TH | 30th percentile height value |
| H40TH | 40th percentile height value |
| H50TH | 50th percentile height value |
| H60TH | 60th percentile height value |
| H70TH | 70th percentile height value |
| H75TH | 75th percentile height value |
| H80TH | 80th percentile height value |
| H90TH | 90th percentile height value |
| H95TH | 95th percentile height value |
| H99TH | 99th percentile height value |
| COV1ST | Fraction of first returns > 2 m to the total number of returns |
| COVALL | Fraction of all returns > 2 m to the total number of returns |
| COV1STMEAN | Fraction of first returns > HMEAN to the total number of returns |
| COVALLMEAN | Fraction of all returns > HMEAN to the total number of returns |
| DNS 0.15–0.5 | Fraction of all returns 0.15–0.5 m to the total number of returns |
| DNS 0.5–1 | Fraction of all returns 0.5–1 m to the total number of returns |
| DNS 1–2 | Fraction of all returns 1–2 m to the total number of returns |
| DNS 2–4 | Fraction of all returns 2–4 m to the total number of returns |
| DNS 4–8 | Fraction of all returns 4–8 m to the total number of returns |
| DNS 8–16 | Fraction of all returns 8–16 m to the total number of returns |
| DNS 16–32 | Fraction of all returns 16–32 m to the total number of returns |
| DNS 32–48 | Fraction of all returns 32–48 m to the total number of returns |
| Metric | r2 | p | RMSE (%) | Bias (%) | ||
|---|---|---|---|---|---|---|
| Basal area (m2 ha−1) | 29.7 | 30.9 (±0.7) | 0.73 (±0.02) | 0.002 (±0.004) | 36.3 (±1.7) | 6.1 (±2.4) |
| Merch. volume (m3 ha−1) | 222.3 | 218.7 (±7.9) | 0.75 (±0.03) | 0.009 (±0.01) | 46.2 (±3.4) | −5.6 (±2.7) |
| Total volume (m3 ha−1) | 242.1 | 239.9 (±8.4) | 0.76 (±0.03) | 0.008 (±0.01) | 42.6 (±3.4) | 5.8 (±2.7) |
| Metric | Inventory | r2 | p | RMSE (%) | Bias (%) |
|---|---|---|---|---|---|
| Basal area | ABA | 0.32 | <0.001 | 76.6 | 12.5 |
| ITD-FV | 0.31 | <0.001 | 78.7 | −16.9 | |
| ITD-VW | 0.31 | <0.001 | 84.2 | −33.4 | |
| Merchantable volume | ABA | 0.85 | <0.001 | 115.2 | 82.8 |
| ITD-FV | 0.85 | <0.001 | 37.9 | −3.0 | |
| ITD-VW | 0.84 | <0.001 | 39.7 | −4.5 | |
| Total volume | ABA | 0.77 | <0.001 | 74.8 | 45.3 |
| ITD-FV | 0.78 | <0.001 | 51.9 | −14.3 | |
| ITD-VW | 0.77 | <0.001 | 59.3 | −26.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sparks, A.M.; Corrao, M.V.; Keefe, R.F.; Armstrong, R.; Smith, A.M.S. Comparison of Field Sampling- and Airborne Laser Scanning-Derived Stand-Level Inventories in a Mixed Conifer Forest and Volume Validation Using Log Scaling Data. Forests 2025, 16, 784. https://doi.org/10.3390/f16050784
Sparks AM, Corrao MV, Keefe RF, Armstrong R, Smith AMS. Comparison of Field Sampling- and Airborne Laser Scanning-Derived Stand-Level Inventories in a Mixed Conifer Forest and Volume Validation Using Log Scaling Data. Forests. 2025; 16(5):784. https://doi.org/10.3390/f16050784
Chicago/Turabian StyleSparks, Aaron M., Mark V. Corrao, Robert F. Keefe, Ryan Armstrong, and Alistair M. S. Smith. 2025. "Comparison of Field Sampling- and Airborne Laser Scanning-Derived Stand-Level Inventories in a Mixed Conifer Forest and Volume Validation Using Log Scaling Data" Forests 16, no. 5: 784. https://doi.org/10.3390/f16050784
APA StyleSparks, A. M., Corrao, M. V., Keefe, R. F., Armstrong, R., & Smith, A. M. S. (2025). Comparison of Field Sampling- and Airborne Laser Scanning-Derived Stand-Level Inventories in a Mixed Conifer Forest and Volume Validation Using Log Scaling Data. Forests, 16(5), 784. https://doi.org/10.3390/f16050784








