Forest Fire Analysis Prediction and Digital Twin Verification: A Trinity Framework and Application
Abstract
1. Introduction
- Decoupling analysis phase: To address the challenge of distinguishing the characteristics of various influencing factors, this study engages in a multi-factor decoupling analysis. By integrating PCA and SHAP, this study develops a framework termed “factor screening-importance ranking-interpretation analysis.” This framework is designed to elucidate the impact of different factors on forest fire occurrence more clearly.
- Model prediction phase: The research introduces a pioneering approach to spatiotemporal decoupling in model prediction. This involves resolving the issue of spatial coupling of multiple factors through PCA and addressing the time-delay effects using the ALSTM time-series prediction model. By decoupling the spatial and temporal data sources, this method enhances the accuracy of forest fire predictions.
- Scenario validation phase: Employing digital twin technology, this paper constructs a three-dimensional model that dynamically analyzes the physical mechanisms and quantitative relationships of key meteorological and combustible indices affecting forest fire behavior. This model addresses the limitations of traditional one-dimensional and two-dimensional static simulations and the challenges faced by conventional machine learning models in field testing.
2. Related Research
2.1. Research on Influencing Factors
2.2. Current Status of Forest Fire Prediction
2.3. Three-Dimensional Fire Modeling
3. Overview
4. Materials and Methods
4.1. Data Preparation
4.2. Multi-Factor Decoupling Analysis
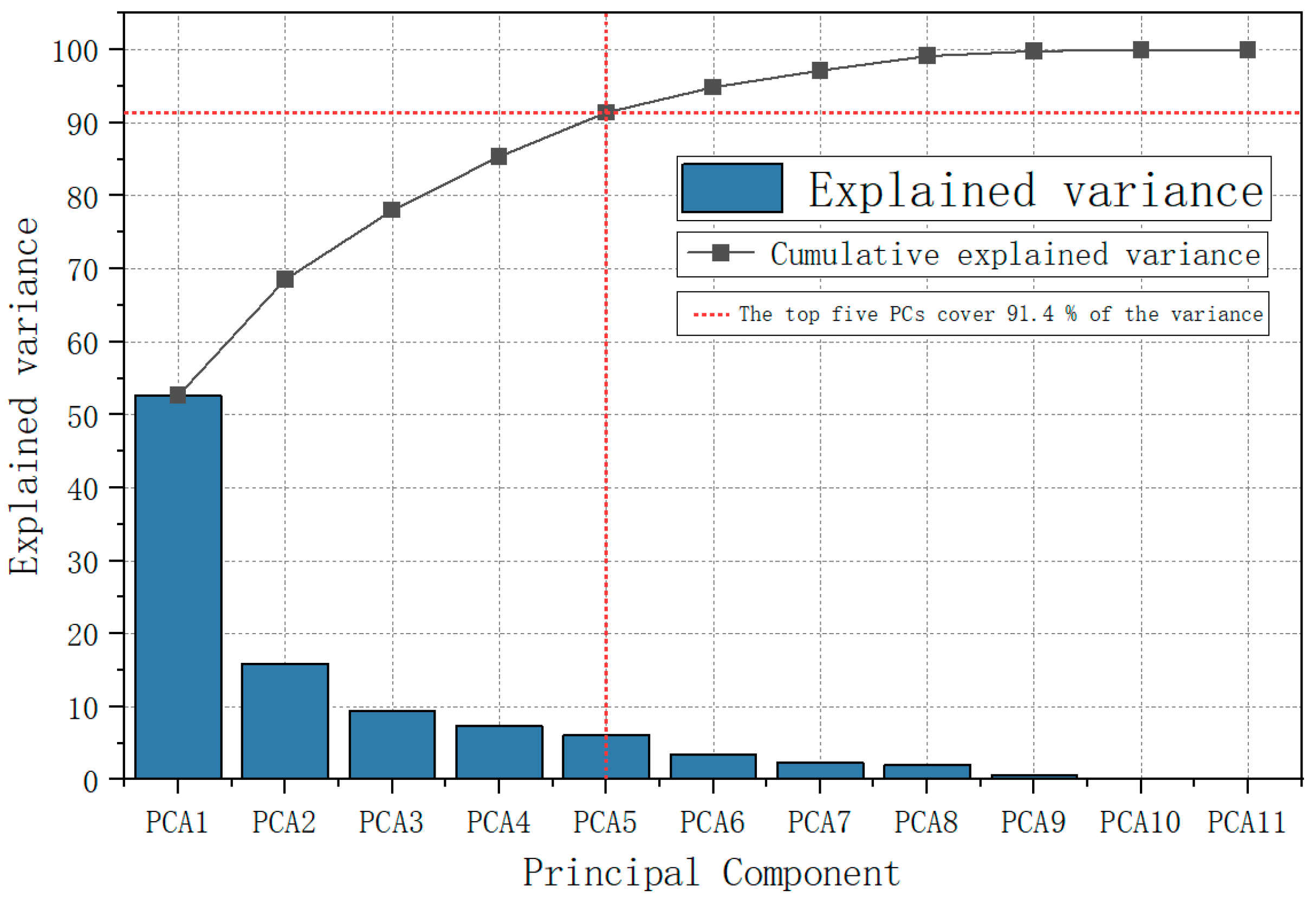
4.2.1. Principal Component Analysis
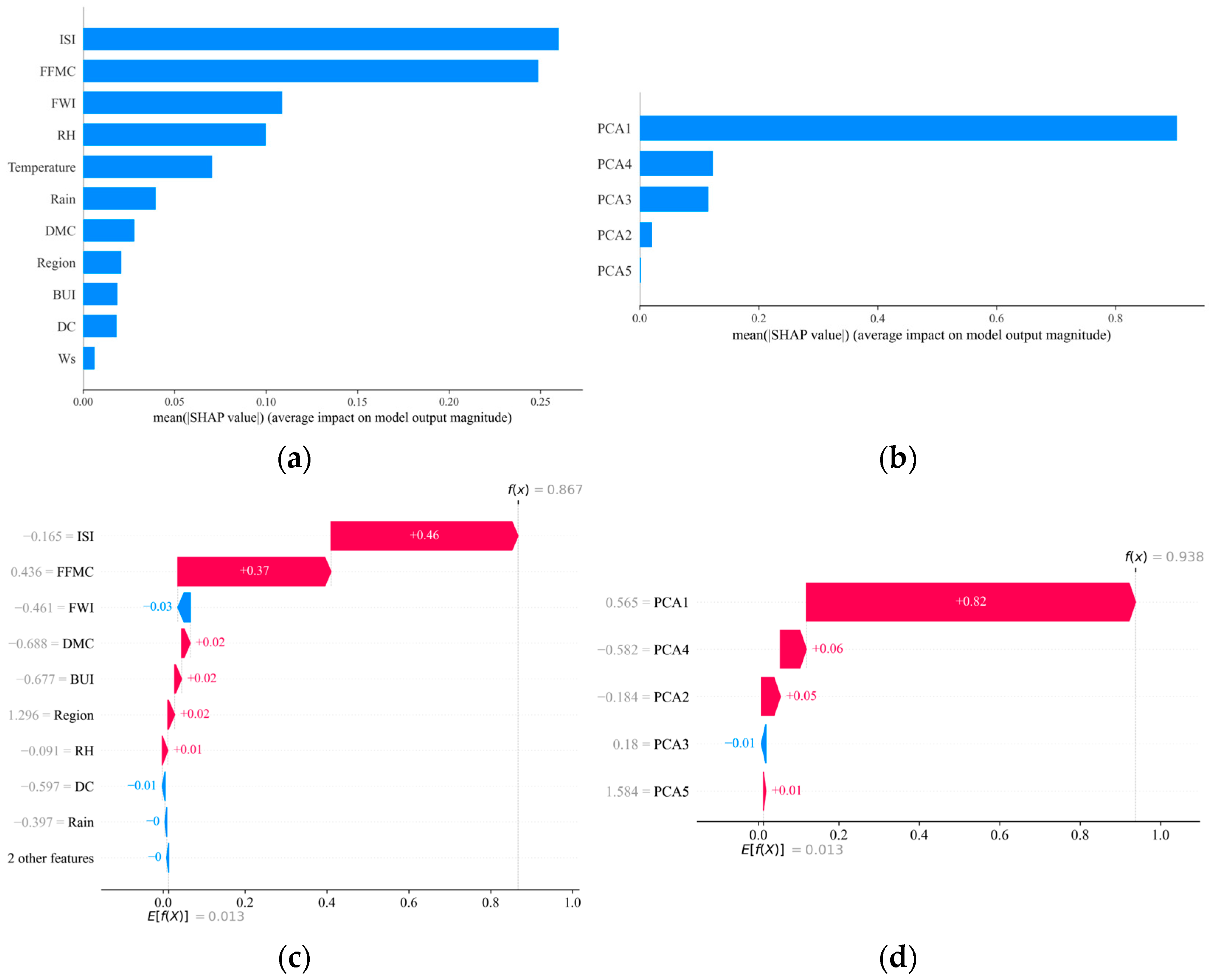
4.2.2. Interpretability Analyses
4.3. Forest Fire Prediction Model
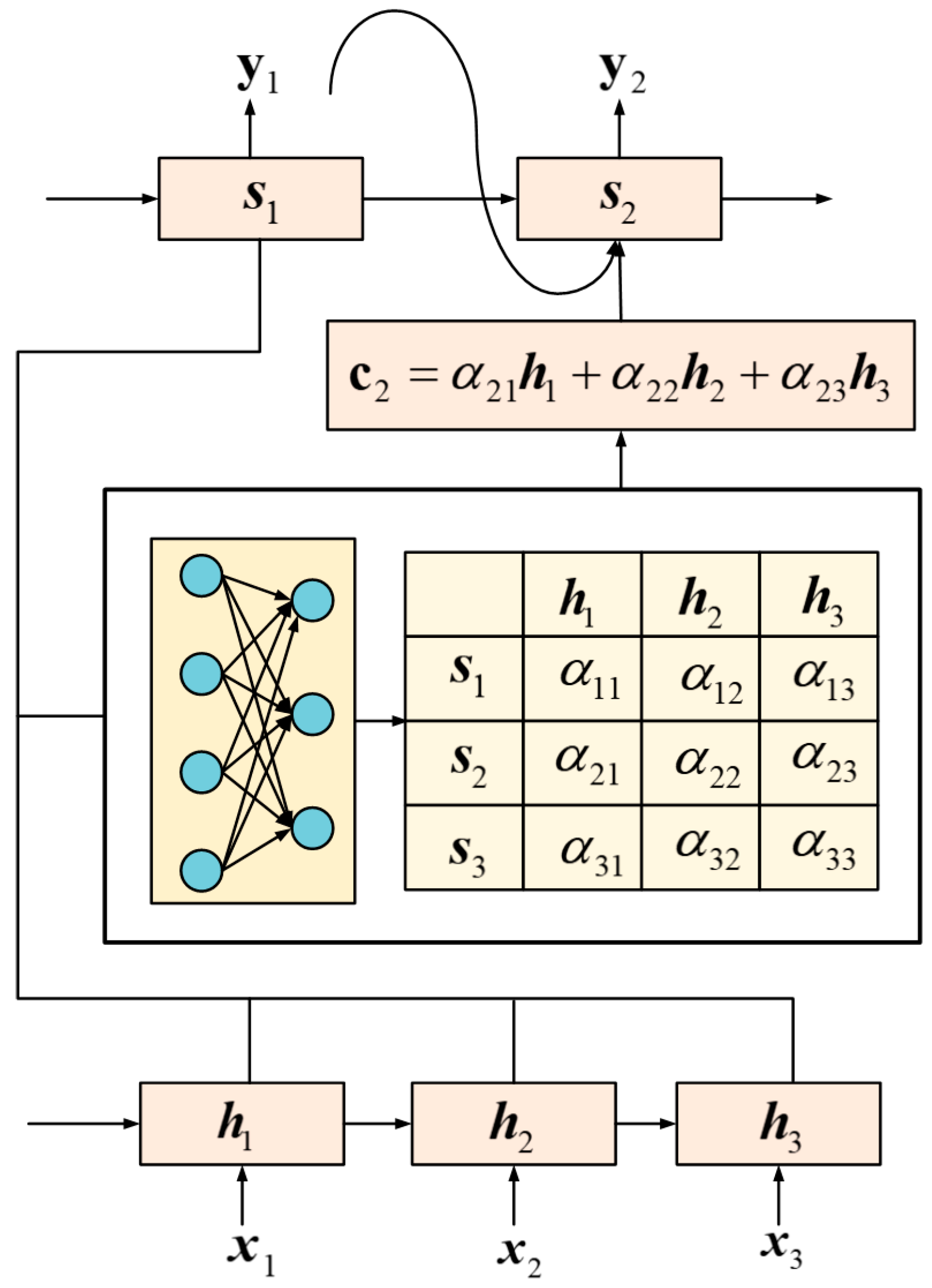
4.3.1. Model Architecture Design
- (1)
- Core time-series feature extraction: This study employs an LSTM layer to capture the long-term dependencies within the sequence data. The layer’s gating mechanisms—comprising a forget gate, an input gate, and an output gate—effectively model the temporal dynamics associated with fire-related factors.
- (2)
- Attention fusion: A Multiply layer is introduced to achieve a weighted fusion between attention weights and LSTM hidden states, thereby emphasizing key factors driving forest fires.
- (3)
- Efficiency and generalization: To reduce the dimensionality and, consequently, the number of parameters and computational overhead, this study utilizes a GlobalAveragePooling1D layer. Additionally, a Dropout layer with a 0.3 inactivation rate is incorporated to effectively mitigate the risk of overfitting, thus enhancing the model’s ability to generalize across diverse and variable forest environments.
- (4)
- Probabilistic output: The model concludes with a layer utilizing a Sigmoid activation function, which outputs the probability of a forest fire occurrence within a range of [0, 1].
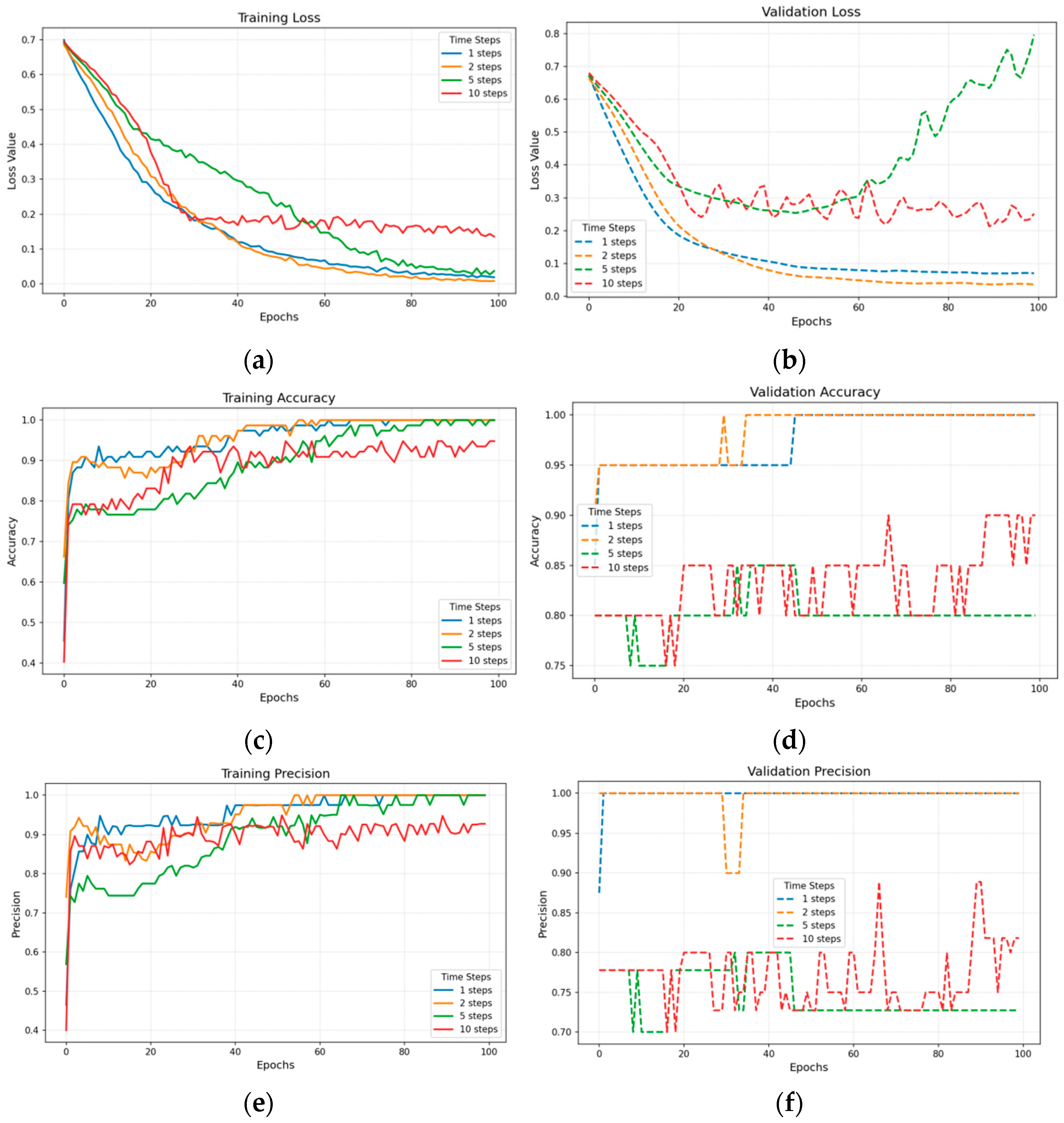
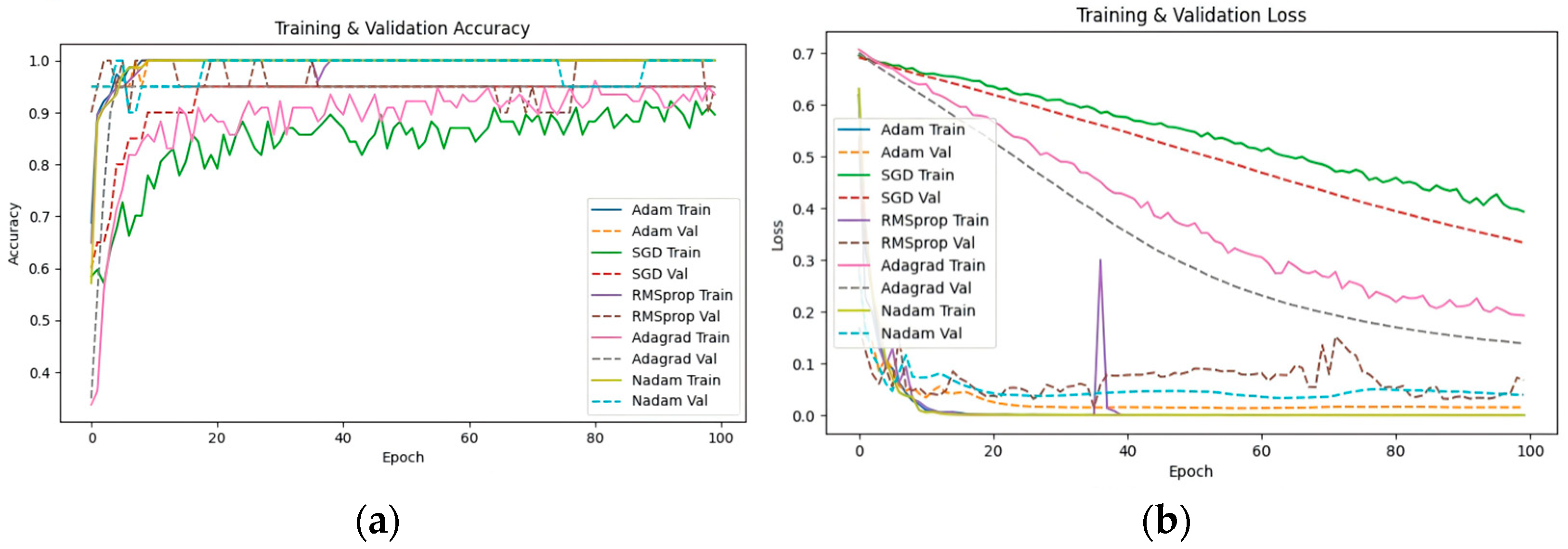
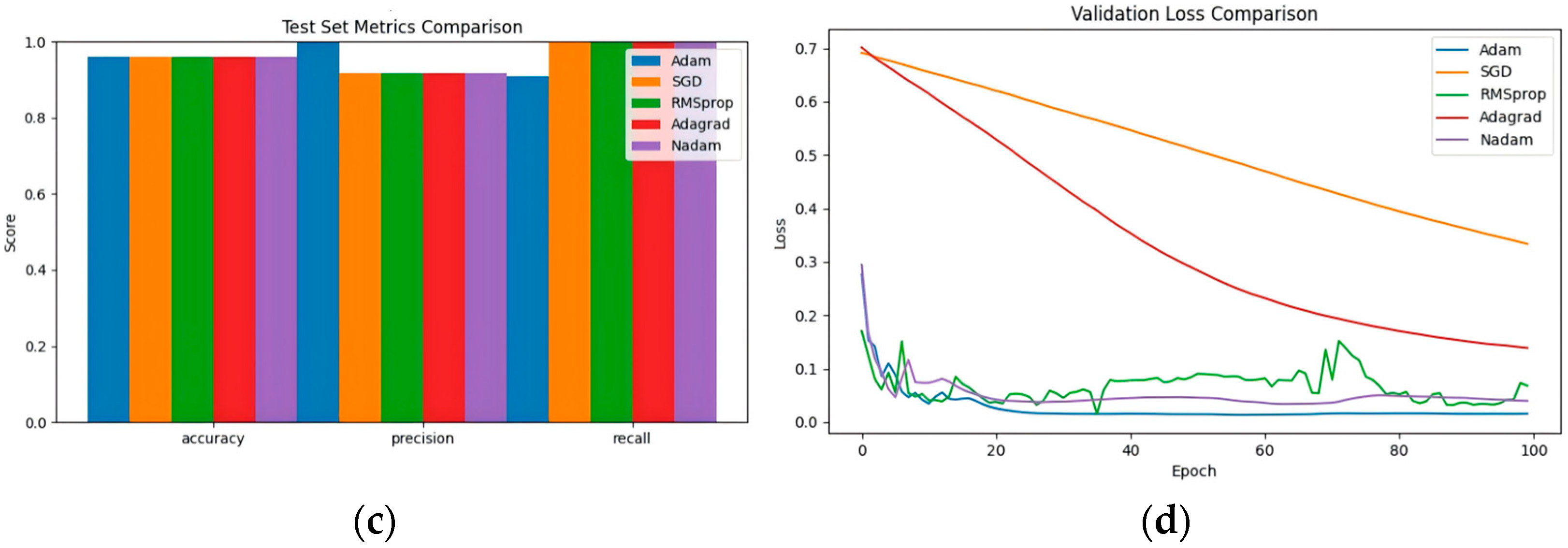
4.3.2. Key Parameter Optimization Experiments
- Time Step Optimization
- 2.
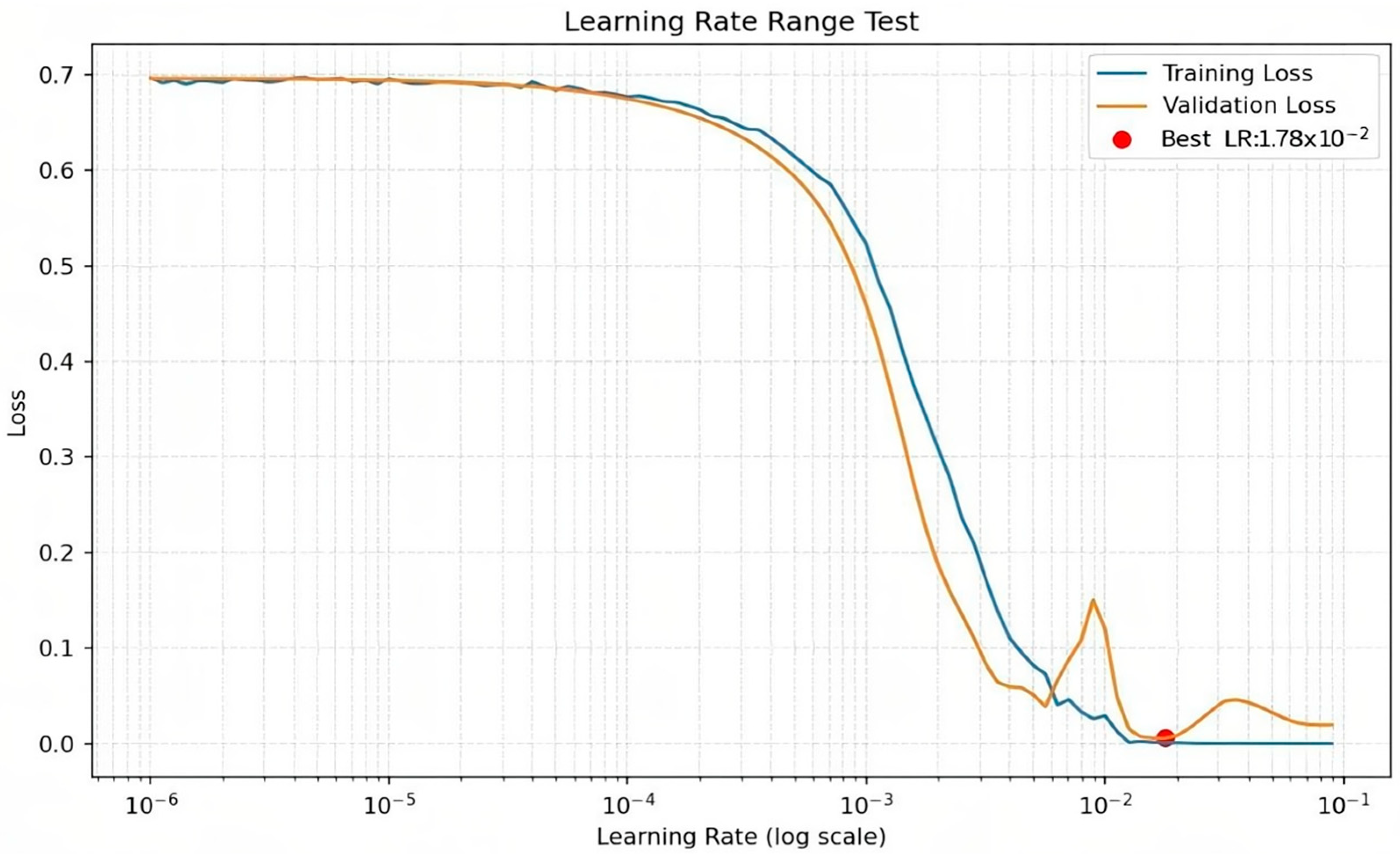
- Learning Rate Optimization
- 3.
- Optimizer Selection
4.4. Mountain Fire Scenario Evolution Model
4.4.1. Physical Driving Equations
4.4.2. Data Preparation for Twin Model Construction
5. Results and Analyses
5.1. Results of Decoupling Analyses
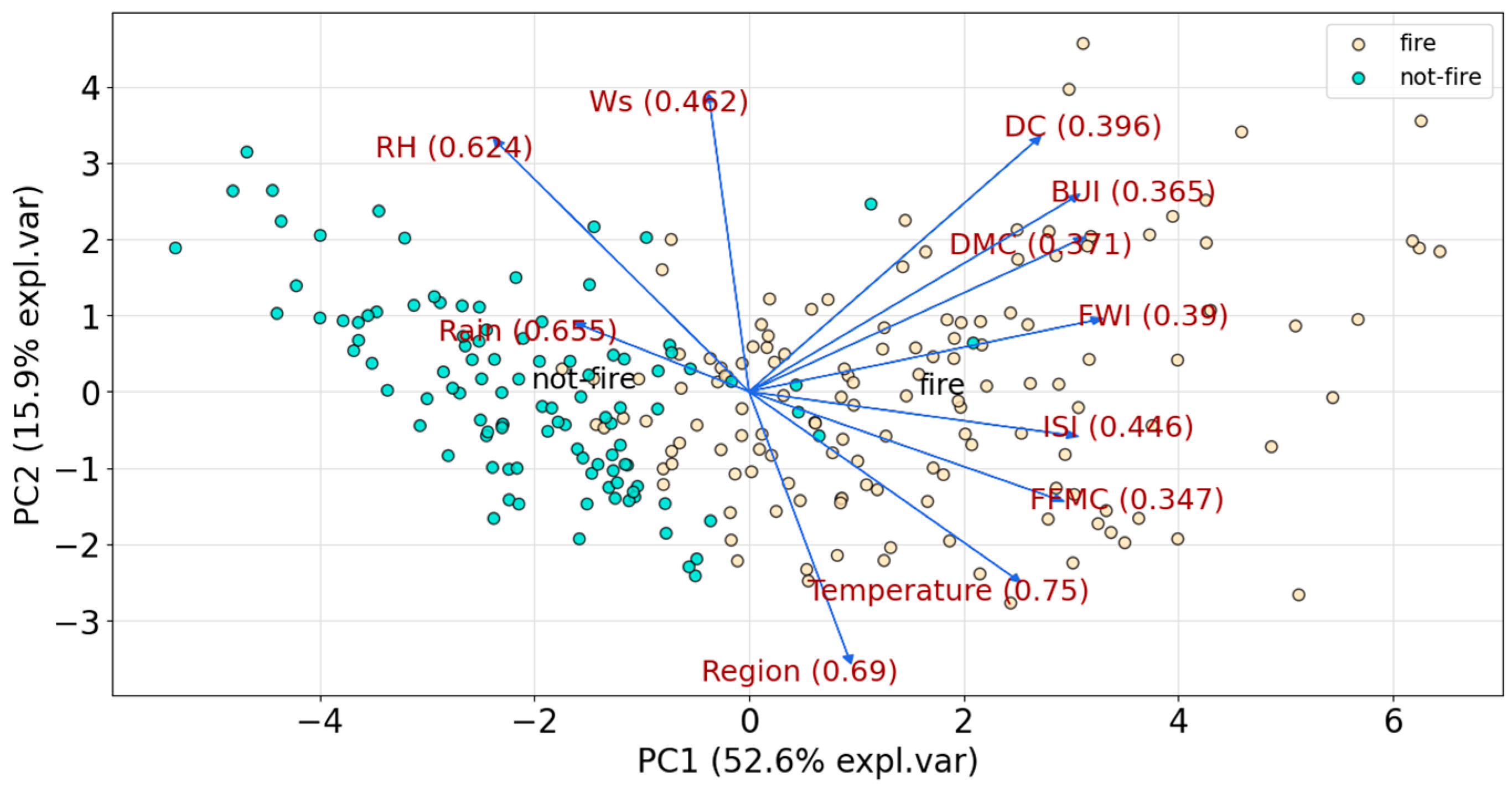
5.1.1. Principal Component Analysis Results
5.1.2. Analysis of Variable Contributions
5.2. Model Prediction Results
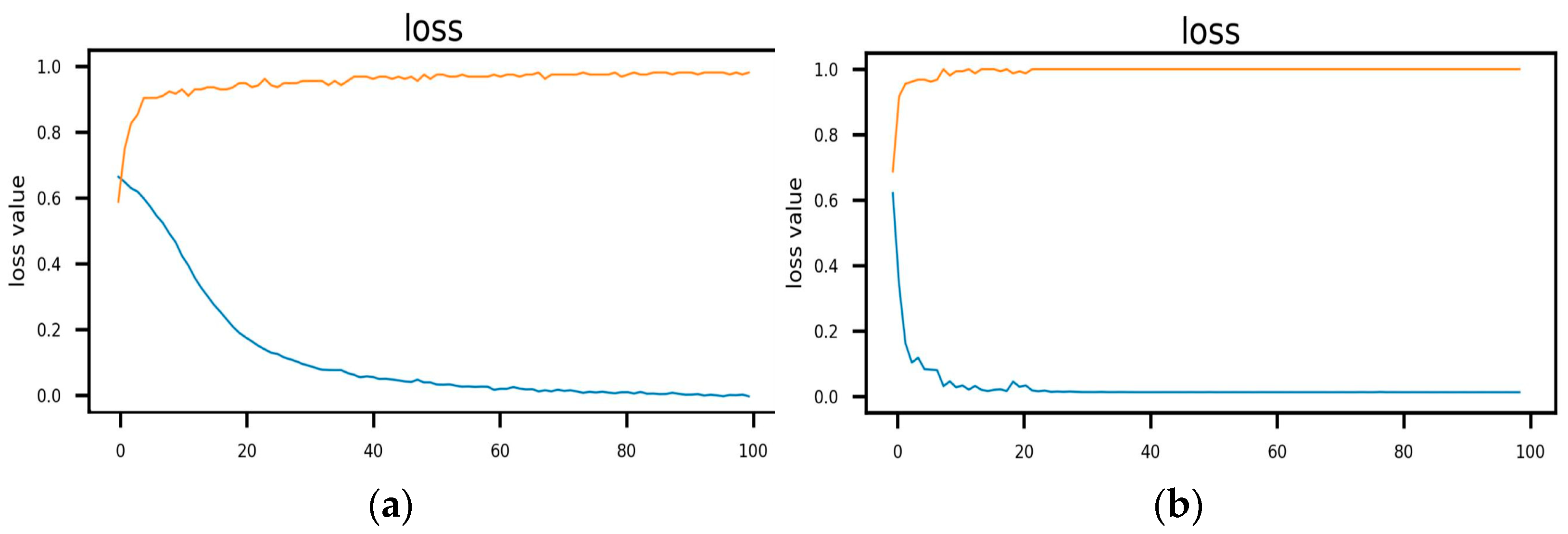
5.2.1. Improvement of Training Effect by Feature Decoupling
5.2.2. Comprehensive Model Accuracy Assessment
5.3. Verification of Simulation Results
6. Conclusions
- (1)
- The model training depends on data from specific climatic zones in Algeria, exhibiting strong regional specificity. Its generalizability to broader forested areas remains to be verified.
- (2)
- The physical-spatial processes under the coupled interactions of the influencing factors are highly complex. The study constructs a mountain fire scenario evolution model based on a simplified hypothetical dynamics module, which restricts the precision of quantitative fire behavior simulations and limits the capacity to fully capture the impacts of extreme weather events.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bargali, H.; Pandey, A.; Bhatt, D.; Sundriyal, R.C.; Uniyal, V.P. Forest fire management, funding dynamics, and research in the burning frontier: A comprehensive review. Trees For. People 2024, 16, 100526. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J.; Durrant, T.; Boca, R.; Libertà, G.; Branco, A.; de Rigo, D.; Ferrari, D.; Maianti, P.; Artés Vivancos, T.; Costa, H.; et al. Advance EFFIS Report on Forest Fires in Europe, Middle East and North Africa 2017; European Commission: Luxembourg, Luxembourg, 2020; pp. 31–32. ISBN 978-92-79-92776-8. [Google Scholar] [CrossRef]
- Abid, F.; Izeboudjen, N. Predicting Forest Fire in Algeria Using Data Mining Techniques: Case Study of the Decision Tree Algorithm. In Proceedings of the Advanced Intelligent Systems for Sustainable Development (AI2SD’2019), Marrakech, Morocco, 8–11 July 2019; pp. 363–370. [Google Scholar] [CrossRef]
- Mishra, M.; Guria, R.; Baraj, B.; Nanda, A.P.; Santos, C.A.G.; da Silva, R.M.; Laksono, F.X.A.T. Spatial analysis and machine learning prediction of forest fire susceptibility: A comprehensive approach for effective management and mitigation. Sci. Total Environ. 2024, 926, 171713. [Google Scholar] [CrossRef] [PubMed]
- Abatzoglou, J.T.; Kolden, C.A.; Cullen, A.C.; Sadegh, M.; Williams, E.L.; Turco, M.; Jones, M.W. Climate change has increased the odds of extreme regional forest fire years globally. Nat. Commun. 2025, 16, 6390. [Google Scholar] [CrossRef]
- El Garroussi, S.; Di Giuseppe, F.; Barnard, C.; Wetterhall, F. Europe faces up to tenfold increase in extreme fires in a warming climate. npj Clim. Atmos. Sci. 2024, 7, 30. [Google Scholar] [CrossRef]
- Turco, M.; Llasat, M.C.; von Hardenberg, J.; Provenzale, A. Impact of climate variability on summer fires in a Mediterranean environment (northeastern Iberian Peninsula). Clim. Change 2013, 116, 665–678. [Google Scholar] [CrossRef]
- Zumbrunnen, T.; Pezzatti, G.B.; Menéndez, P.; Bugmann, H.; Bürgi, M.; Conedera, M. Weather and human impacts on forest fires: 100 years of fire history in two climatic regions of Switzerland. For. Ecol. Manag. 2011, 261, 2188–2199. [Google Scholar] [CrossRef]
- Mollicone, D.; Eva, H.D.; Achard, F. Human role in Russian wild fires. Nature 2006, 440, 436–437. [Google Scholar] [CrossRef]
- Naderpour, M.; Rizeei, H.M.; Ramezani, F. Forest fire risk prediction: A spatial deep neural network-based framework. Remote Sens. 2021, 13, 2513. [Google Scholar] [CrossRef]
- Wu, Z.; Li, M.; Wang, B.; Quan, Y.; Liu, J. Using artificial intelligence to estimate the probability of forest fires in Heilongjiang, northeast China. Remote Sens. 2021, 13, 1813. [Google Scholar] [CrossRef]
- Algerian Forest Fires—UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/dataset/547/algerian+forest+fires+dataset (accessed on 24 October 2024).
- Moritz, M.A.; Batllori, E.; Bradstock, R.A.; Gill, A.M.; Handmer, J.; Hessburg, P.F.; Leonard, J.; McCaffrey, S.; Odion, D.C.; Schoennagel, T.; et al. Learning to coexist with wildfire. Nature 2014, 515, 58–66. [Google Scholar] [CrossRef]
- Black, F.; Schulze, P.; Unger, B. Efficient Wildland Fire Simulation via Nonlinear Model Order Reduction. Fluids 2021, 6, 280. [Google Scholar] [CrossRef]
- Abram, N.J.; Henley, B.J.; Sen Gupta, A.; Lippmann, T.J.R.; Clarke, H.; Dowdy, A.J.; Sharples, J.J.; Nolan, R.H.; Zhang, T.; Wooster, M.J.; et al. Connections of climate change and variability to large and extreme forest fires in southeast Australia. Commun. Earth Environ. 2021, 2, 8. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Ermitão, T.; Páscoa, P.; Trigo, I.; Alonso, C.; Gouveia, C. Mapping the Most Susceptible Regions to Fire in Portugal. Fire 2023, 6, 254. [Google Scholar] [CrossRef]
- Wang, Q.; Hao, Y. ALSTM: An attention-based long short-term memory framework for knowledge base reasoning. Neurocomputing 2020, 399, 342–351. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Huang, J.; Su, C.; Yang, B.; Qi, C. An improved bar-shaped sliding window CNN tailored to industrial process historical data with applications in chemical operational optimizations. Ind. Eng. Chem. Res. 2019, 58, 21219–21232. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, L.; Ji, D.; Xia, Z.; Nan, P.; Zhang, J.; Li, K.; Qi, B.; Du, R.; Sun, Y.; et al. Explainable ensemble machine learning revealing the effect of meteorology and sources on ozone formation in megacity Hangzhou, China. Sci. Total Environ. 2024, 922, 171295. [Google Scholar] [CrossRef] [PubMed]
- Iban, M.C.; Sekertekin, A. Machine learning based wildfire susceptibility mapping using remotely sensed fire data and GIS: A case study of Adana and Mersin provinces, Turkey. Ecol. Inform. 2022, 69, 101647. [Google Scholar] [CrossRef]
- García, M.V.; Aznarte, J.L. Shapley additive explanations for NO2 forecasting. Ecol. Inform. 2020, 56, 101039. [Google Scholar] [CrossRef]
- Yue, W.; Ren, C.; Liang, Y.; Liang, J.; Lin, X.; Yin, A.; Wei, Z. Assessment of wildfire susceptibility and wildfire threats to ecological environment and urban development based on GIS and multi-source data: A case study of Guilin, China. Remote Sens. 2023, 15, 2659. [Google Scholar] [CrossRef]
- Encinas, L.H.; White, S.H.; Del Rey, A.M.; Sánchez, G.R. Modelling forest fire spread using hexagonal cellular automata. Appl. Math. Model. 2007, 31, 1213–1227. [Google Scholar] [CrossRef]
- Koo, E.; Pagni, P.; Woycheese, J.; Stephens, S.; Weise, D.; Huff, J. A simple physical model for forest fire spread rate. Fire Saf. Sci. 2005, 8, 851–862. [Google Scholar] [CrossRef]
- Yassemi, S.; Dragićević, S.; Schmidt, M. Design and implementation of an integrated GIS-based cellular automata model to characterize forest fire behaviour. Ecol. Model. 2008, 210, 71–84. [Google Scholar] [CrossRef]
- Sun, L.; Xu, C.; He, Y.; Zhao, Y.; Xu, Y.; Rui, X.; Xu, H. Adaptive forest fire spread simulation algorithm based on cellular automata. Forests 2021, 12, 1431. [Google Scholar] [CrossRef]
- Li, L.; Sali, A.; Noordin, N.K.; Ismail, A.; Hashim, F. Prediction of peatlands forest fires in Malaysia using machine learning. Forests 2023, 14, 1472. [Google Scholar] [CrossRef]
- Meng, Q.; Lu, H.; Huai, Y.; Xu, H.; Yang, S. Forest fire spread simulation and fire extinguishing visualization research. Forests 2023, 14, 1371. [Google Scholar] [CrossRef]
- Farguell, A.; Cortés, A.; Margalef, T.; Miró, J.R.; Mercader, J. Scalability of a multi-physics system for forest fire spread prediction in multi-core platforms. J. Supercomput. 2019, 75, 1163–1174. [Google Scholar] [CrossRef]
- Sun, X.; Li, N.; Chen, D.; Chen, G.; Sun, C.; Shi, M.; Gao, X.; Wang, K.; Hezam, I.M. A Forest Fire Prediction Model Based on Cellular Automata and Machine Learning. IEEE Access 2024, 12, 55389–55403. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M.; Zhang, S.; Liu, J.; Sun, S.; Hu, T.; Sun, L. Simulating Forest Fire Spread with Cellular Automation Driven by a LSTM Based Speed Model. Fire 2022, 5, 13. [Google Scholar] [CrossRef]
- Xu, Y.; Li, D.; Ma, H.; Lin, R.; Zhang, F. Modeling Forest Fire Spread Using Machine Learning-Based Cellular Automata in a GIS Environment. Forests 2022, 13, 1974. [Google Scholar] [CrossRef]
- Tengteng, L.; Jiyan, Y.; Zhaorong, O.; Qiang, Y.; Yong, L.; Qiuhua, W. Comprehensive assessment and spatial pattern study on forest fire risk in Yunnan Province. China Saf. Sci. J. 2021, 31, 167. [Google Scholar] [CrossRef]
- Wei, S.; Luo, S.; Luo, B.; Li, X.; Wang, Z.; Wu, Z.; Zhou, Y.; Zhong, Y.; Li, Q. Occurrence regularity of forest fire under the background of climate change. For. Environ. Sci. 2020, 36, 133–143. [Google Scholar]
- Tian, C.; Su, Z.; Yang, X.; Guo, F. Investigations on spatial distribution and driving factors of forest fire in western Fujian. For. Environ. 2017, 37, 88–94. [Google Scholar]
- Xiao, Y.; Ji, P. Predicting forest fire occurrence based on zero-inflated negative binomial model using Bayesian method. J. Cent. South Univ. For. Technol. 2021, 41, 49–56. [Google Scholar] [CrossRef]
- Gao, B.; Chen, X.; Shan, Z.H.; Han, X.Y.; Shan, Y.L.; Yin, S.N.; Yu, B. Prediction of forest fire probability in Daxing’an Mountains area based on Logistic regression model. J. Saf. Sci. Technol. 2022, 18, 163–168. [Google Scholar]
- Preisler, H.K.; Westerling, A.L. Statistical Model for Forecasting Monthly Large Wildfire Events in Western United States. J. Appl. Meteorol. Climatol. 2007, 46, 1020–1030. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, L.; Yang, X.; Liang, L.; Yuan, X.; Ren, L.; Zhang, H. Study on the Impact of Atmospheric and Topographical Environments on Wildfire Spread: A Case Study of a Forest Fire in Shanxi Province. Disaster Sci. 2023, 38, 118–125. [Google Scholar]
- Singh, K.R.; Neethu, K.; Madhurekaa, K.; Harita, A.; Mohan, P. Parallel SVM model for forest fire prediction. Soft Comput. Lett. 2021, 3, 100014. [Google Scholar] [CrossRef]
- Majid, S.; Alenezi, F.; Masood, S.; Ahmad, M.; Gündüz, E.S.; Polat, K. Attention based CNN model for fire detection and localization in real-world images. Expert Syst. Appl. 2022, 189, 116114. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable spatio-temporal attention LSTM model for flood forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Yu, Y.; Kim, Y.-J. Attention-LSTM-attention model for speech emotion recognition and analysis of IEMOCAP database. Electronics 2020, 9, 713. [Google Scholar] [CrossRef]
- Lin, X.; Li, Z.; Chen, W.; Sun, X.; Gao, D. Forest fire prediction based on long-and short-term time-series network. Forests 2023, 14, 778. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, X.; Cheng, P.; Wang, M.; Huang, Y. Unveiling spatiotemporal patterns of wildfire risk: A transformer-based earth system analysis. Clim. Dyn. 2025, 63, 21. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M.; Liang, Q. A problem-agnostic approach to feature selection and analysis using shap. J. Big Data 2025, 12, 12. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pradhan, B. Explainable artificial intelligence (XAI) for interpreting the contributing factors feed into the wildfire susceptibility prediction model. Sci. Total Environ. 2023, 879, 163004. [Google Scholar] [CrossRef]
- Sanchez-Guzman, G.; Velasquez, W.; Alvarez-Alvarado, M.S. Modeling a simulated forest to get burning times of tree species using a digital twin. In Proceedings of the 2022 IEEE 12th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 26–29 January 2022; pp. 639–643. [Google Scholar]
- Huang, Y.; Li, J.; Zheng, H. Modeling of Wildfire Digital Twin: Research Progress in Detection, Simulation, and Prediction Techniques. Fire 2024, 7, 412. [Google Scholar] [CrossRef]
- Zhong, C.; Cheng, S.; Kasoar, M.; Arcucci, R. Reduced-order digital twin and latent data assimilation for global wildfire prediction. Nat. Hazards Earth Syst. Sci. 2023, 23, 1755–1768. [Google Scholar] [CrossRef]
- Dourvas, N.I.; Papagianni, A.; Koulalis, I.; Ioannidis, K.; Vrochidis, S.; Kompatsiaris, I. An early-warning system for fire spreading by monitoring simple climate conditions and combining Cellular Automata with Digital Twins. In Proceedings of the 2022 IEEE International Workshop on Metrology for Living Environment (MetroLivEn), Cosenza, Italy, 25–27 May 2022; pp. 252–257. [Google Scholar] [CrossRef]
- Ghodrat, M.; Shakeriaski, F.; Fanaee, S.A.; Simeoni, A. Software-Based Simulations of Wildfire Spread and Wind-Fire Interaction. Fire 2023, 6, 12. [Google Scholar] [CrossRef]
- Eghdami, M.; Juliano, T.W.; Jiménez, P.A.; Kosovic, B.; Castellnou, M.; Kumar, R.; Vila-Guerau de Arellano, J. Characterizing the Role of Moisture and Smoke on the 2021 Santa Coloma de Queralt Pyroconvective Event Using WRF-Fire. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003288. [Google Scholar] [CrossRef]
- Huang, J.; Lucash, M.S.; Scheller, R.M.; Klippel, A. Walking through the forests of the future: Using data-driven virtual reality to visualize forests under climate change. Int. J. Geogr. Inf. Sci. 2021, 35, 1155–1178. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, J.; Wang, S.; Gu, W. Educational application of cognitive digital twins: Connotation, Dilemma and countermeasures. Mod. Distance Educ. 2021, 01, 13–23. [Google Scholar] [CrossRef]
- Tao, F.; Xiao, B.; Qi, Q.; Cheng, J.; Ji, P. Digital twin modeling. J. Manuf. Syst. 2022, 64, 372–389. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q. Make more digital twins. Nature 2019, 573, 490–491. [Google Scholar] [CrossRef]
- Li, H.; Tao, F.; Wang, H.; Song, W.; Zhang, Z.; Fan, B.B.; Wu, C.; Li, Y.; Li, L.L.; Wen, X.Y.; et al. Integration Framework and Key Technologies of Complex Product Design-Manufacturing Based on Digital Twin. Comput. Integr. Manuf. Syst. 2019, 25, 1320–1336. [Google Scholar]
- Cimino, C.; Negri, E.; Fumagalli, L. Review of digital twin applications in manufacturing. Comput. Ind. 2019, 113, 103130. [Google Scholar] [CrossRef]
- Yeh, A.G. From urban modelling, GIS, the digital, intelligent, and the smart city to the digital twin city with AI. Environ. Plan. B Urban Anal. City Sci. 2024, 51, 1085–1088. [Google Scholar] [CrossRef]
- Ferré-Bigorra, J.; Casals, M.; Gangolells, M. The adoption of urban digital twins. Cities 2022, 131, 103905. [Google Scholar] [CrossRef]
- Elayan, H.; Aloqaily, M.; Guizani, M. Digital twin for intelligent context-aware IoT healthcare systems. IEEE Internet Things J. 2021, 8, 16749–16757. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Yang, Y.; Zhou, L.; Ren, L.; Wang, F.; Liu, R.; Pang, Z.; Deen, M.J. A novel cloud-based framework for the elderly healthcare services using digital twin. IEEE Access 2019, 7, 49088–49101. [Google Scholar] [CrossRef]
- Sun, T.; He, X.; Song, X.; Shu, L.; Li, Z. The digital twin in medicine: A key to the future of healthcare? Front. Med. 2022, 9, 907066. [Google Scholar] [CrossRef]
- Aydemir, H.; Zengin, U.; Durak, U. The digital twin paradigm for aircraft review and outlook. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 553. [Google Scholar] [CrossRef]
- Kairat, K.; Ildar, P.; Karygash, A.; Saule, B.; Indira, K.; Markhaba, K.; Aizhan, B. Digital Twins Technology in the Educational Process of the Aviation Equipment Repair. Indones. J. Electr. Eng. Comput. Sci 2023, 32, 752–762. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, H.; Lei, K.; Zhang, H.; Hu, X. Forest digital twin: A new tool for forest management practices based on Spatio-Temporal Data, 3D simulation Engine, and intelligent interactive environment. Comput. Electron. Agric. 2023, 215, 108416. [Google Scholar] [CrossRef]
- Cirulis, A.; Taube, L.; Erics, Z. Automated generation of digital twin in virtual reality for interaction with specific nature ecosystem. In Proceedings of the International Conference on Human-Computer Interaction, Virtual, 26 June–1 July 2022; pp. 187–202. [Google Scholar] [CrossRef]
- The Canadian Forest Fire Weather Index (FWI) System. Available online: https://cwfis.cfs.nrcan.gc.ca/background/summary/fwi (accessed on 23 April 2025).
- Xin, X.-Y.; Jiang, H.; Zhou, G.-M.; Yu, S.-Q.; Wang, Y.-H. The principle and application of the Canadian Forest Fire Hazard Climate Index (FWI) system. J. Zhejiang Agric. For. Univ. 2011, 28, 314–318. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Souane, A.A.; Khurram, A.; Huang, H.; Shu, Z.; Feng, S.; Belgherbi, B.; Wu, Z. Utilizing Machine Learning and Geospatial Techniques to Evaluate Post-Fire Vegetation Recovery in Mediterranean Forest Ecosystem: Tenira, Algeria. Forests 2025, 16, 53. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, 3rd ed.; 2025; Available online: https://christophm.github.io/interpretable-ml-book (accessed on 24 May 2025).
- Heidari, A.; Khovalyg, D. Short-term energy use prediction of solar-assisted water heating system: Application case of combined attention-based LSTM and time-series decomposition. Sol. Energy 2020, 207, 626–639. [Google Scholar] [CrossRef]
- Huang, J.Q.; Qin, L.X. Study on the correlation prediction of temperature and rainfall using alstm model. J. Guangxi Univ. (Nat. Sci. Ed.) 2021, 46, 1024–1035. [Google Scholar] [CrossRef]
- Wenfeng, S. In-Depth Understanding of Natural Language Processing: From Deep Learning to Large Model Applications, 1st ed.; Tsinghua University Press: Beijing, China, 2025. [Google Scholar]
- Zohdi, T. A machine-learning framework for rapid adaptive digital-twin based fire-propagation simulation in complex environments. Comput. Methods Appl. Mech. Eng. 2020, 363, 112907. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, B.; Li, M.; Tian, Y.; Quan, Y.; Liu, J. Simulation of forest fire spread based on artificial intelligence. Ecol. Indic. 2022, 136, 108653. [Google Scholar] [CrossRef]
- Rui, X.; Hui, S.; Yu, X.; Zhang, G.; Wu, B. Forest fire spread simulation algorithm based on cellular automata. Nat. Hazards 2018, 91, 309–319. [Google Scholar] [CrossRef]
- Wang, Z. Current forest fire danger rating system. J. Nat. Disasters 1992, 1, 39–44. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P. Research on improvement of wang zhengfei’s forest fire spread model. J. Shandong For. Sci. Technol. 2020, 50, 1–6. [Google Scholar]
- Gabriel, K.R. The biplot graphic display of matrices with application to principal component analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Xiang, Q.; Wang, X.; Song, Y.; Lei, L. ISONet: Reforming 1DCNN for aero-engine system inter-shaft bearing fault diagnosis via input spatial over-parameterization. Expert Syst. Appl. 2025, 277, 127248. [Google Scholar] [CrossRef]


| Considerations | Meteorological Factor | Combustibility Factor | Topographic Factor | Anthropogenic Factors | Vegetation Factor | Derivatives Index (FWI System) |
|---|---|---|---|---|---|---|
| Impact factor | Temperature | Fine Fuel Moisture Code (FFMC) | Slope | Ignition Sources | Normalized Differential Vegetation Index (NDVI) | Initial Spread Index (ISI) |
| Relative Humidity (RH) | Duff Moisture Code (DMC) | Slope direction | Fire Management | vegetation type | Buildup Index (BUI) | |
| Wind Speed (WS) | Drought Code (DC) | Elevation | Population Density | vegetation cover | Fire Weather Index (FWI) | |
| Rainfall (Rain) | Type of combustible | Topography Complexity | Distance from the river | vegetative diversity | ||
| Atmospheric Pressure | Fuel Load | terrain roughness | Distance from road | vegetation |
| Layer Name | Typology | Parameters/Settings | Output Shape Extrapolation | Function |
|---|---|---|---|---|
| input_layer | input layer | - | (None, 1, 7) | Receives preprocessed time-series data after PCA dimensionality reduction |
| LSTM | LSTM layer | Units = 64, return_sequences = True, Activation = tanh | (None, 1, 64) | Captures sequential dependencies and extracts temporal features via gating mechanisms |
| Dense_1 | full connectivity layer | Units = 1, Activation = tanh | (None, 1, 1) | Computes raw attention weight scores |
| Activation | activation layer | Activation = softmax | (None, 1, 1) | Normalizes attention weights into a probability distribution |
| Multiply | element-by-element multiplication | - | (None, 1, 64) | Applies attention weights to LSTM outputs, emphasizing key features |
| GlobalAveragePooling1D | Global average pooling | - | (None,64) | Reduces temporal dimension while preserving feature information |
| Dense_2 | full connectivity layer | Units = 64, Activation = relu | (None,64) | Performs nonlinear transformation and advanced feature mapping |
| Dropout | stochastic inactivation | Rate = 0.3 | (None,64) | Randomly deactivates 30% of neurons to prevent overfitting |
| Dense_3 | input layer | Units = 1, Activation = sigmoid | (None, 1) | Produces binary classification probability for fire occurrence |
| Optimiser | Accuracy | Precision | Recall |
|---|---|---|---|
| Adam | 96.72% | 0.9983 | 0.9691 |
| SGD | 96.10% | 0.9167 | 0.9856 |
| RMSprop | 96.56% | 0.9248 | 0.9741 |
| Adagrad | 96.45% | 0.9156 | 0.9826 |
| Nadam | 96.06% | 0.9211 | 0.9778 |
| State of Affairs | Trigger Condition | Interaction Events and Scene Effects |
|---|---|---|
| Unburned state | Environmental parameters do not satisfy combustion conditions and topographic “block” impedes combustion equation | Vegetation retains its normal textures and colors; no flame particles are generated, resulting in no smoke effect in the scene; the three-dimensiona model is displayed as a static natural environment. |
| Open flame state | Environmental parameters satisfy combustion conditions, and no topographic “block” impedes combustion equation | Activation of the flame particle system occurs, the flame model expands as temperature rises, and smoke particles are generated concurrently; the vegetation model dynamically transitions to a burning texture, enhanced by particle effects such as sparks and splashes. |
| extinguished state | Environmental parameters no longer satisfy combustion conditions or topographic “block” impedes combustion equation | Flame particles gradually decay and vanish, and smoke concentration diminishes; the vegetation model updates to a “burnt” texture, retaining indications of possible rekindling if combustible material remains unburnt. |
| Ingredient | Explanation of Variance (%) | Cumulative Variance (%) | Main Environmental Impacts |
|---|---|---|---|
| PCA1 | 52.61 | 52.61 | FWI, FFMC, DMC, ISI, BUI |
| PCA2 | 15.93 | 68.54 | Ws, DC |
| PCA3 | 9.47 | 78.01 | Rain, RH |
| PCA4 | 7.35 | 85.36 | Ws, Temperature |
| PCA5 | 6.04 | 91.40 | Region |
| Model | Precision | Accuracy | Recall | F1 | PR-AUC |
|---|---|---|---|---|---|
| ALSTM | 0.9782 (±0.0237) | 0.9571 (±0.0213) | 0.9461 (±0.0373) | 0.9612 (±0.0196) | 0.9945 (±0.0048) |
| LSTM | 0.9634 (±0.0434) | 0.9449 (±0.0205) | 0.9398 (±0.0402) | 0.9499 (±0.0164) | 0.9926 (±0.0068) |
| LR | 0.9865 (±0.0208) | 0.9224 (±0.0238) | 0.8710 (±0.0396) | 0.9246 (±0.0243) | 0.9893 (±0.0087) |
| Metric | Comparison | Mean Difference | 95% CI Lower | 95% CI Upper | p-Value |
|---|---|---|---|---|---|
| Accuracy | ALSTM vs. LSTM | 0.012244898 | 0.001859192 | 0.026348988 | 0.001126189 * |
| Accuracy | ALSTM vs. LR | 0.034693878 | 0.017766171 | 0.051621584 | 0.001225564 * |
| Precision | ALSTM vs. LSTM | 0.014776261 | 0.009789991 | 0.039342513 | 0.002718957 * |
| Precision | ALSTM vs. LR | −0.008263151 | 0.006996895 | 0.010470593 | 0.004445289 * |
| Recall | ALSTM vs. LSTM | 0.006283075 | −0.011413825 | 0.023979976 | 0.442580109 |
| Recall | ALSTM vs. LR | 0.07508576 | 0.045020052 | 0.105151469 | 0.000313807 * |
| F1 Score | ALSTM vs. LSTM | 0.011346472 | 0.00163506 | 0.024328005 | 0.00941261 * |
| F1 Score | ALSTM vs. LR | 0.036625092 | 0.01861564 | 0.054634543 | 0.001289685 * |
| PR-AUC | ALSTM vs. LSTM | 0.001909956 | 0.000994991 | 0.004814904 | 0.001099468 * |
| PR-AUC | ALSTM vs. LR | 0.005237726 | 0.000113348 | 0.010362104 | 0.046070699 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zai, W.; Fan, W.; Tang, Y. Forest Fire Analysis Prediction and Digital Twin Verification: A Trinity Framework and Application. Forests 2025, 16, 1546. https://doi.org/10.3390/f16101546
Li W, Zai W, Fan W, Tang Y. Forest Fire Analysis Prediction and Digital Twin Verification: A Trinity Framework and Application. Forests. 2025; 16(10):1546. https://doi.org/10.3390/f16101546
Chicago/Turabian StyleLi, Wenyan, Wenjiao Zai, Wenping Fan, and Yao Tang. 2025. "Forest Fire Analysis Prediction and Digital Twin Verification: A Trinity Framework and Application" Forests 16, no. 10: 1546. https://doi.org/10.3390/f16101546
APA StyleLi, W., Zai, W., Fan, W., & Tang, Y. (2025). Forest Fire Analysis Prediction and Digital Twin Verification: A Trinity Framework and Application. Forests, 16(10), 1546. https://doi.org/10.3390/f16101546







