The Influence of the Root Diameter of Cunninghamia lanceolata (Chinese Fir) on the Strength and Deformation Behavior of Sand
Abstract
1. Introduction
2. Materials and Methods
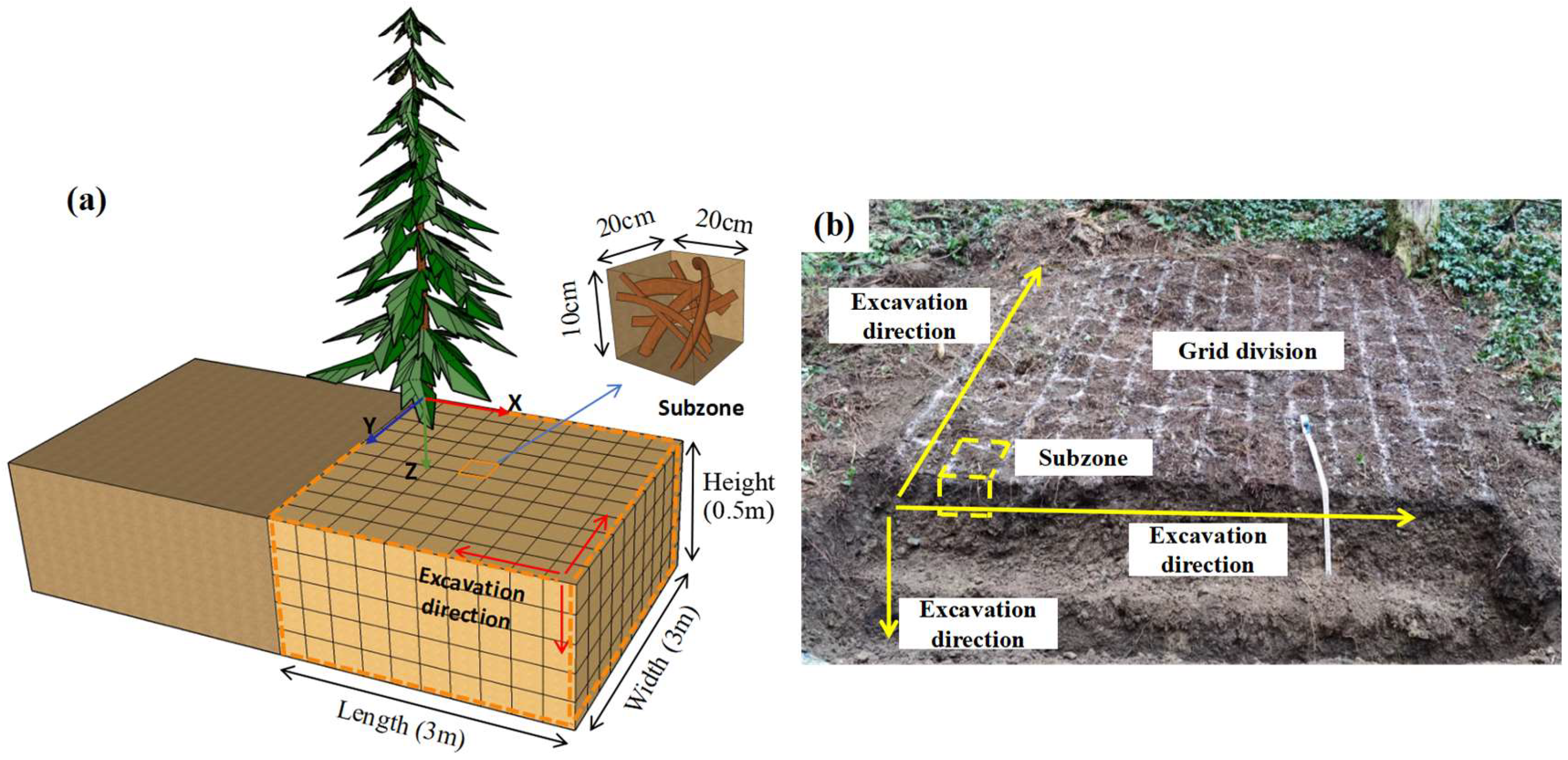
2.1. Study Area and Field Investigations
2.1.1. Study Area
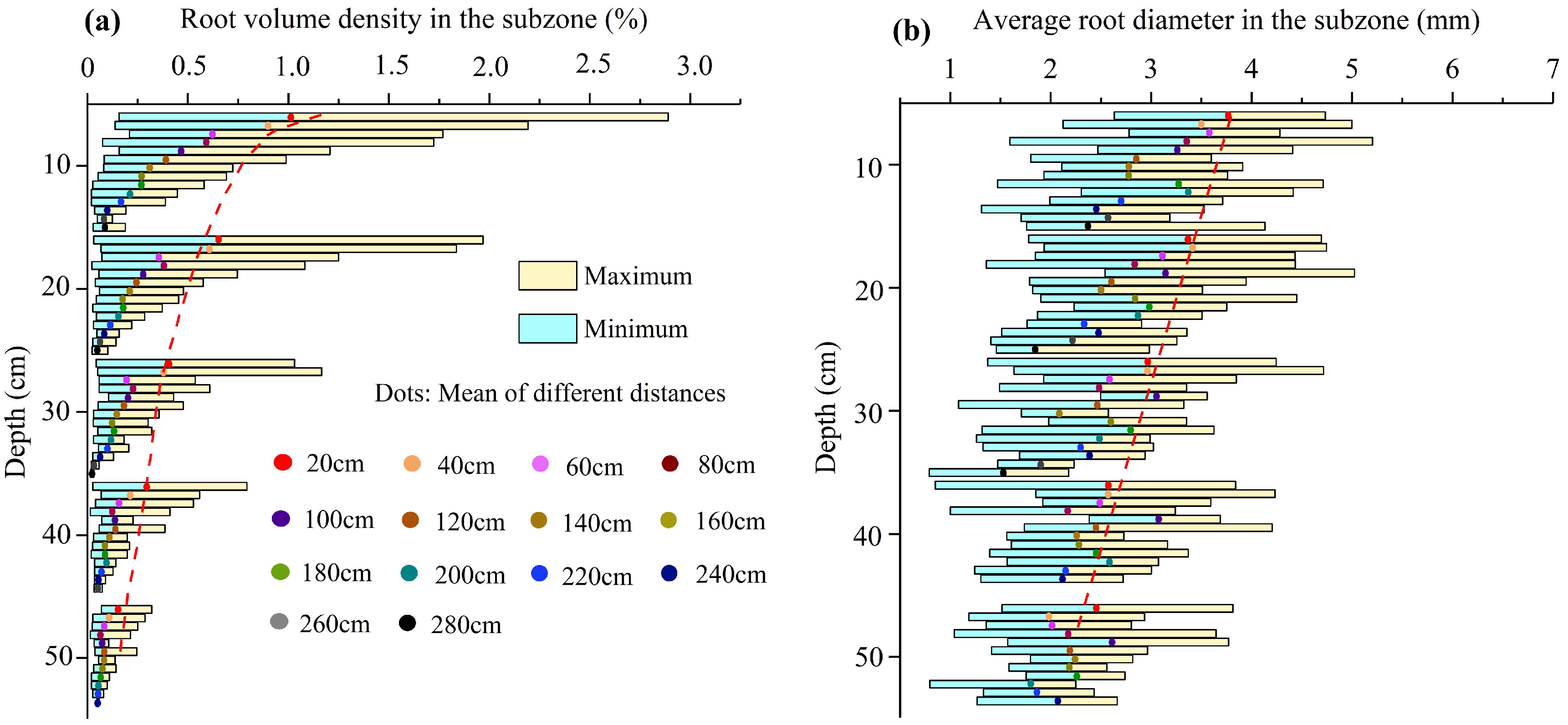
2.1.2. Root Field Investigation
2.2. Soil and Root Properties
2.2.1. Soil
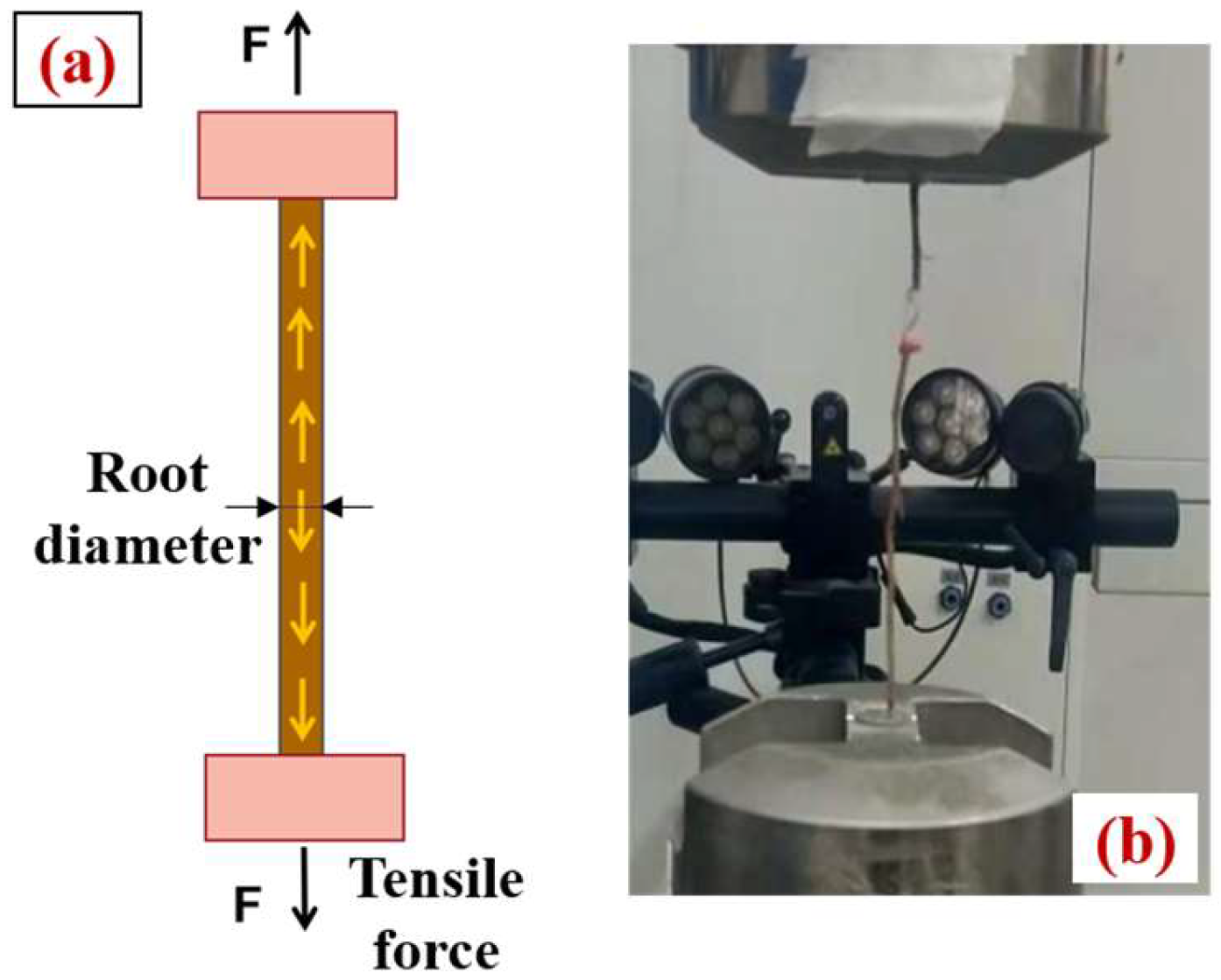
2.2.2. Roots
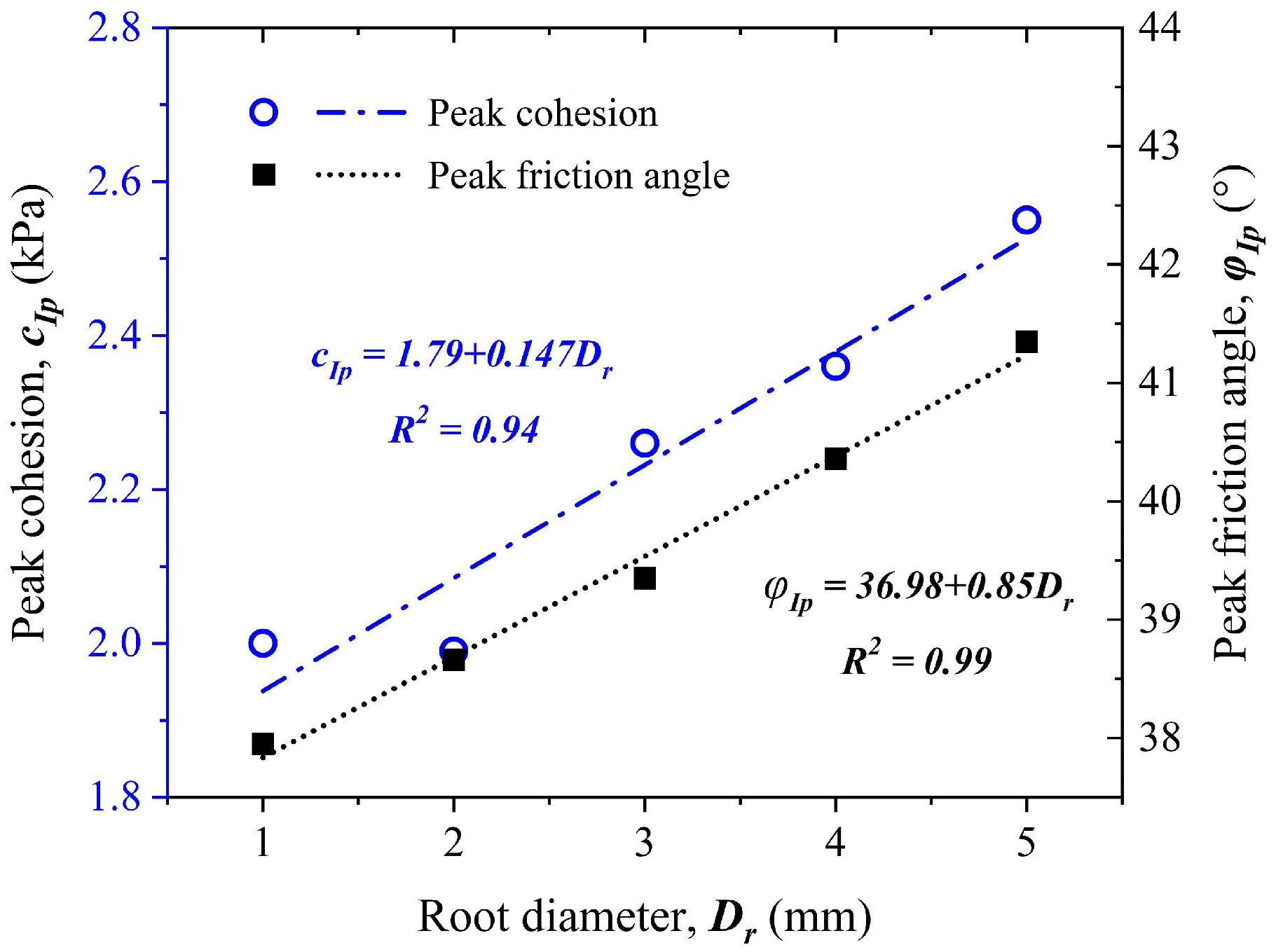
2.2.3. Root–Soil Interface Friction Strength
2.3. Preparation of Triaxial Specimens
2.4. Apparatus and Testing Procedure
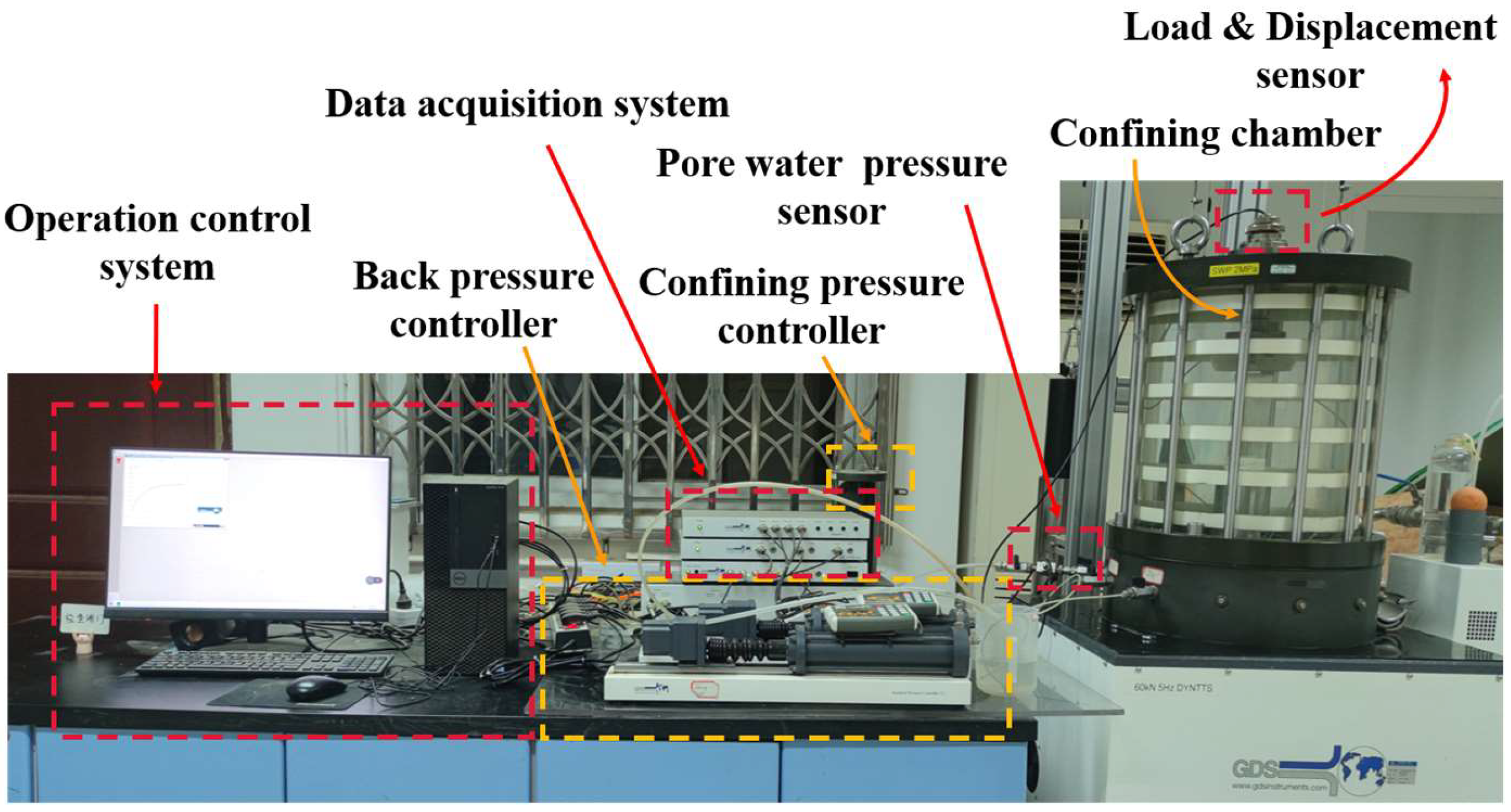
2.4.1. Test Apparatus
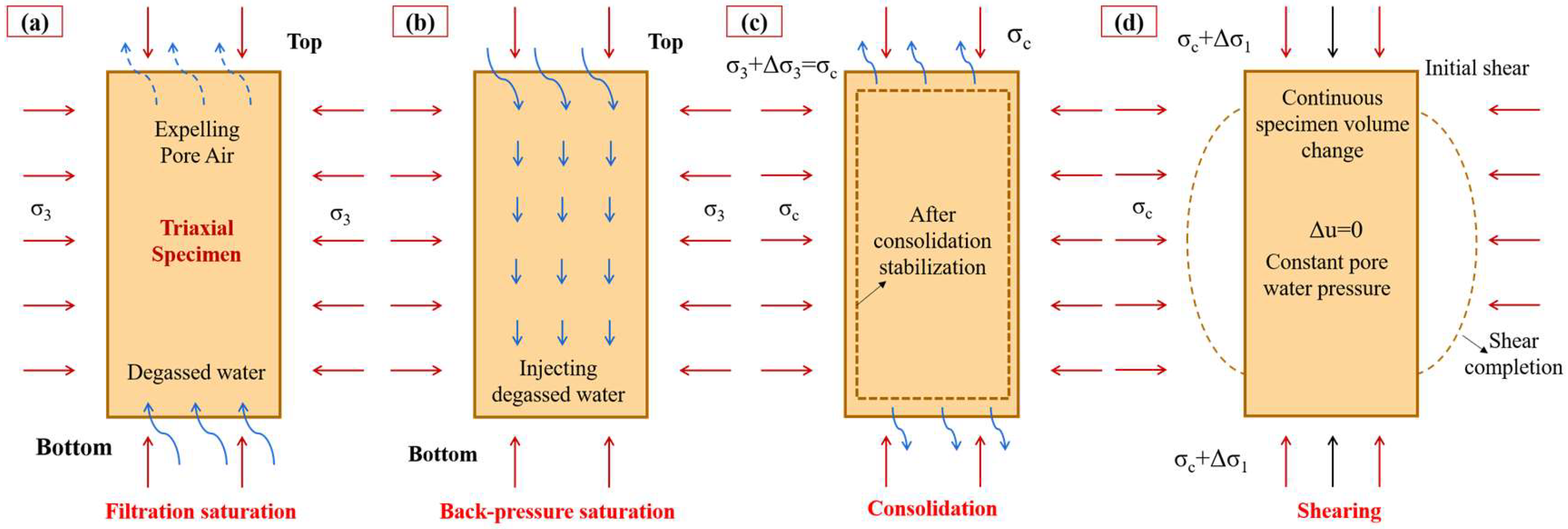
2.4.2. Testing Procedure
3. Results
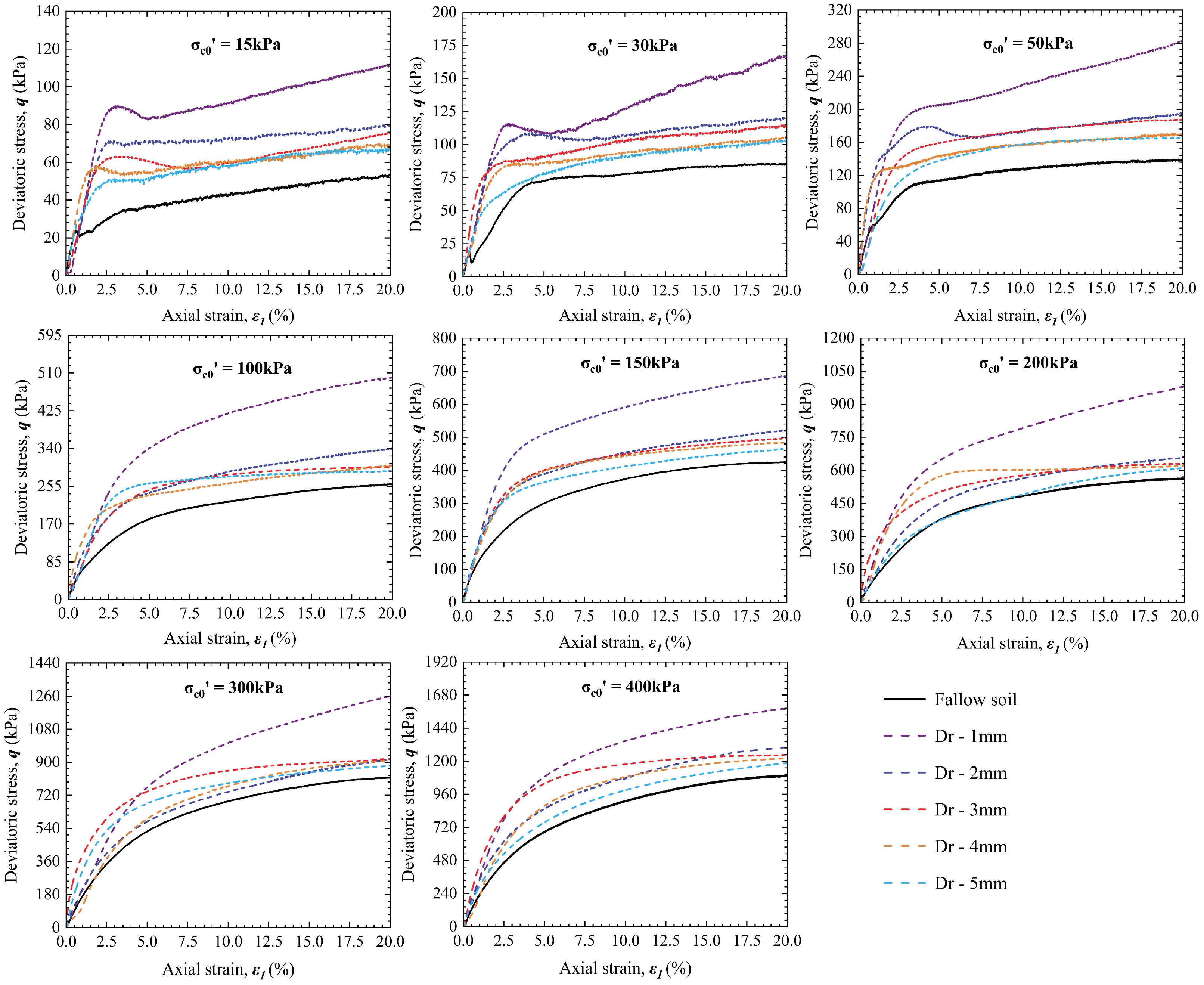
3.1. Stress–Strain Behavior
3.2. Strength Characteristics
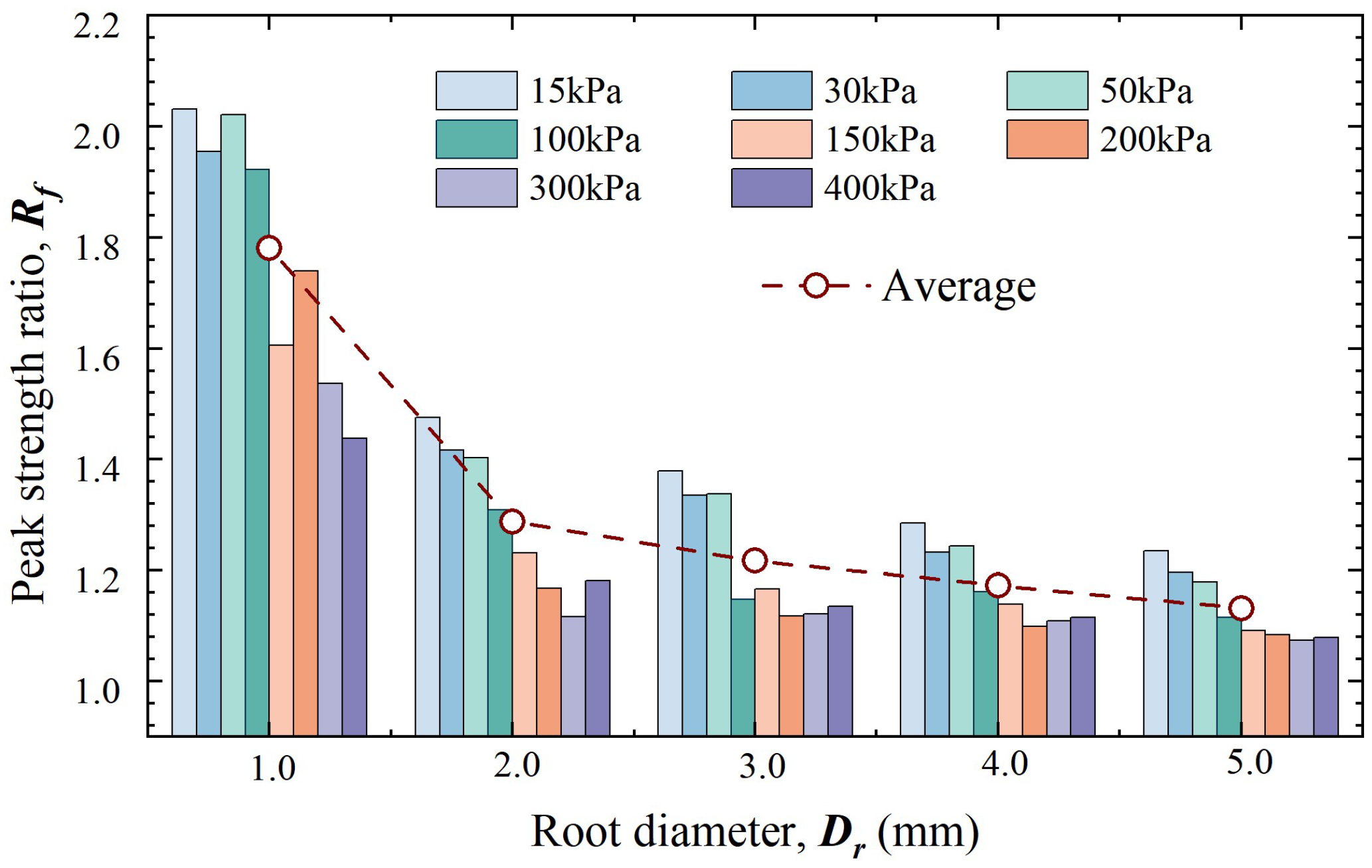
3.2.1. Characteristic Strength Ratio
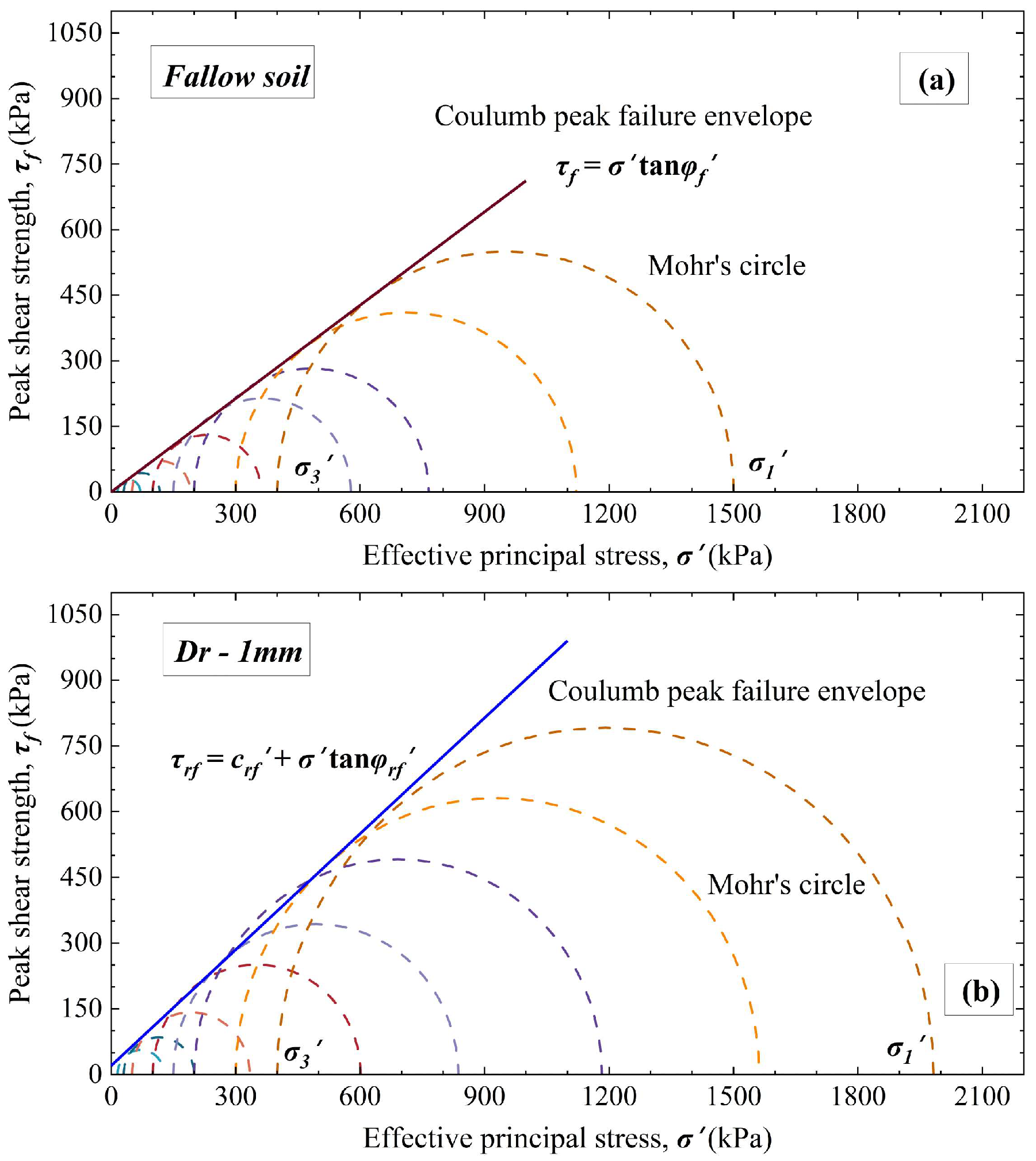
3.2.2. Shear Strength Parameters
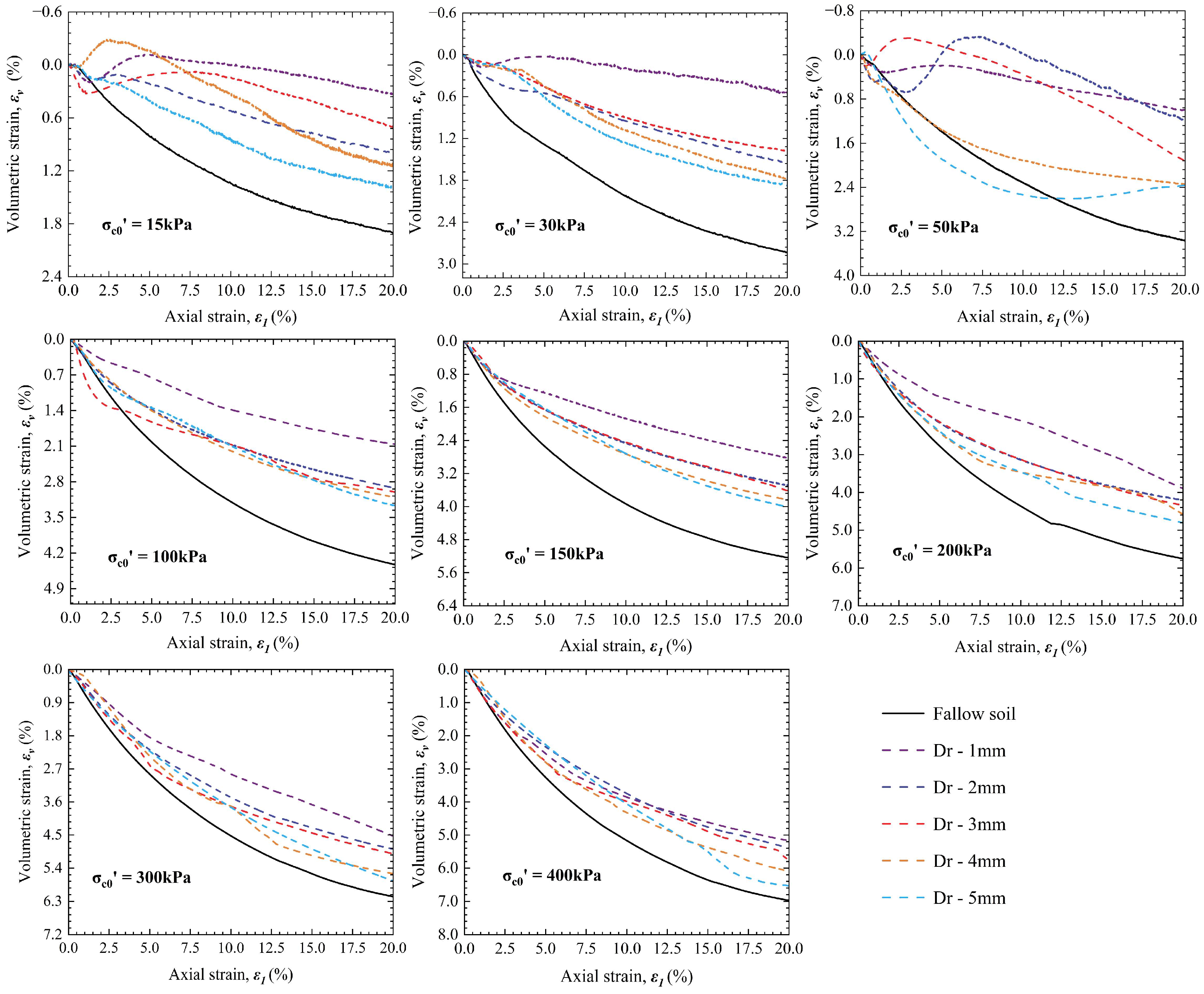
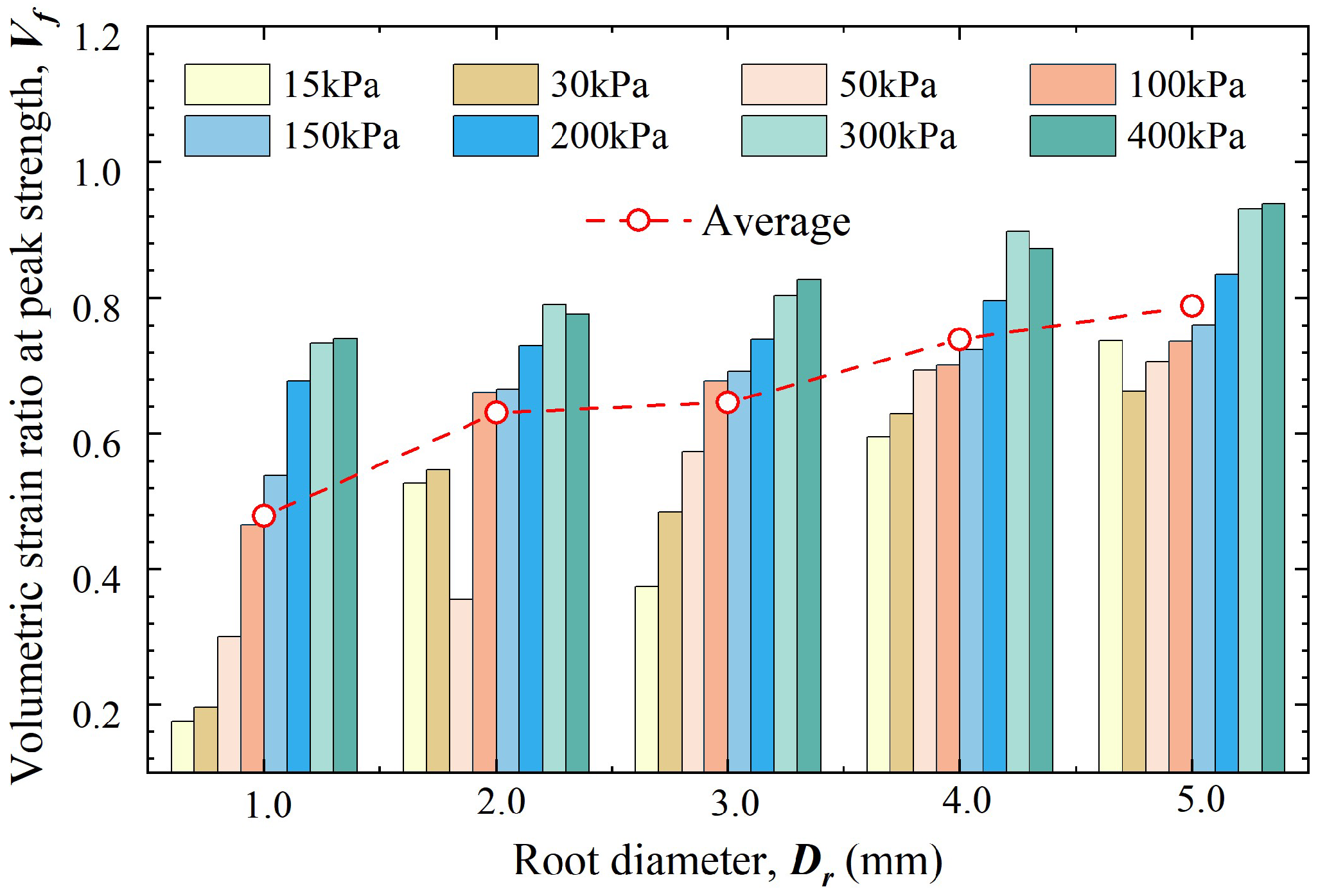
3.3. Volumetric Deformation Behaviour
4. Discussion
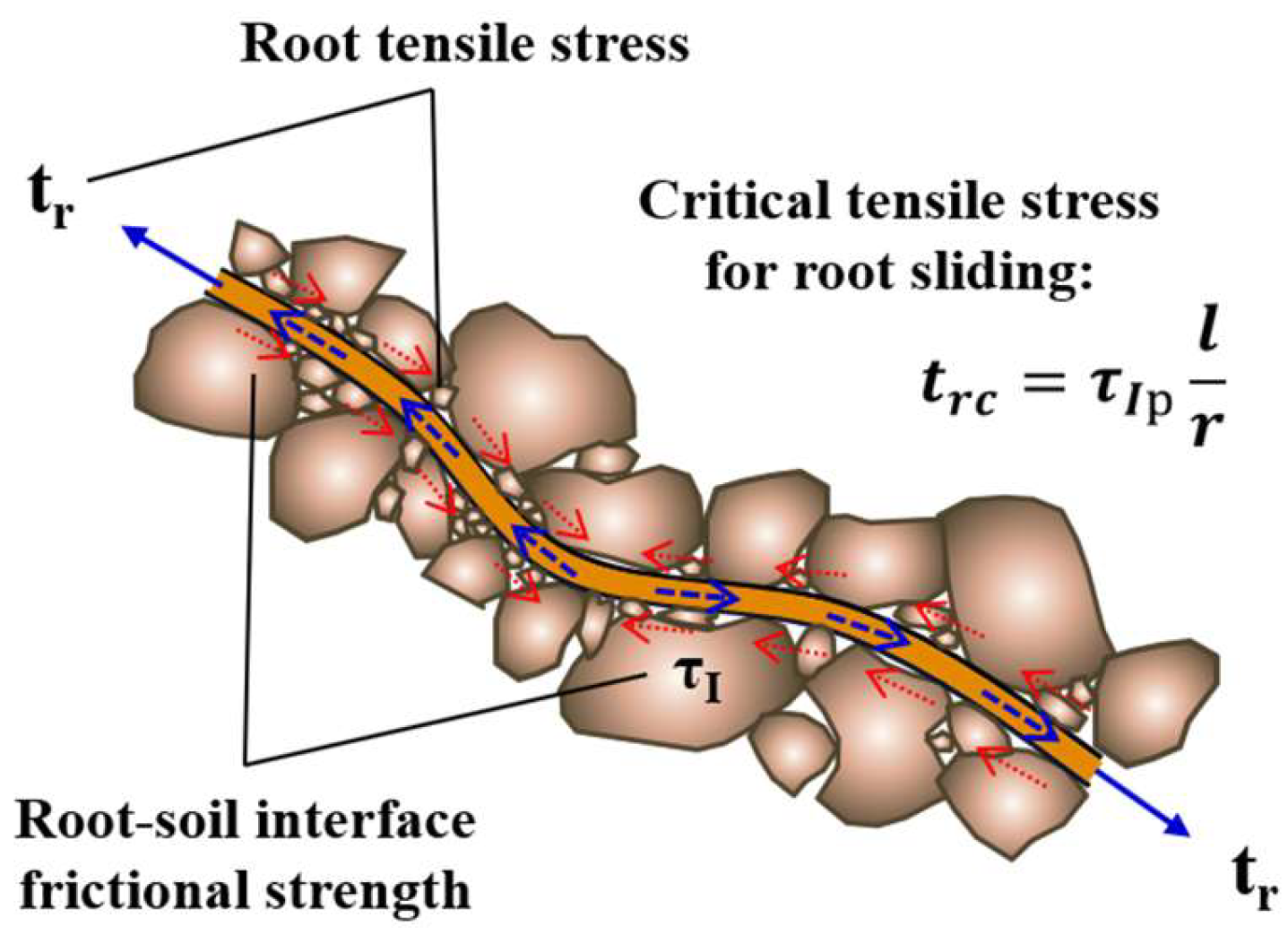
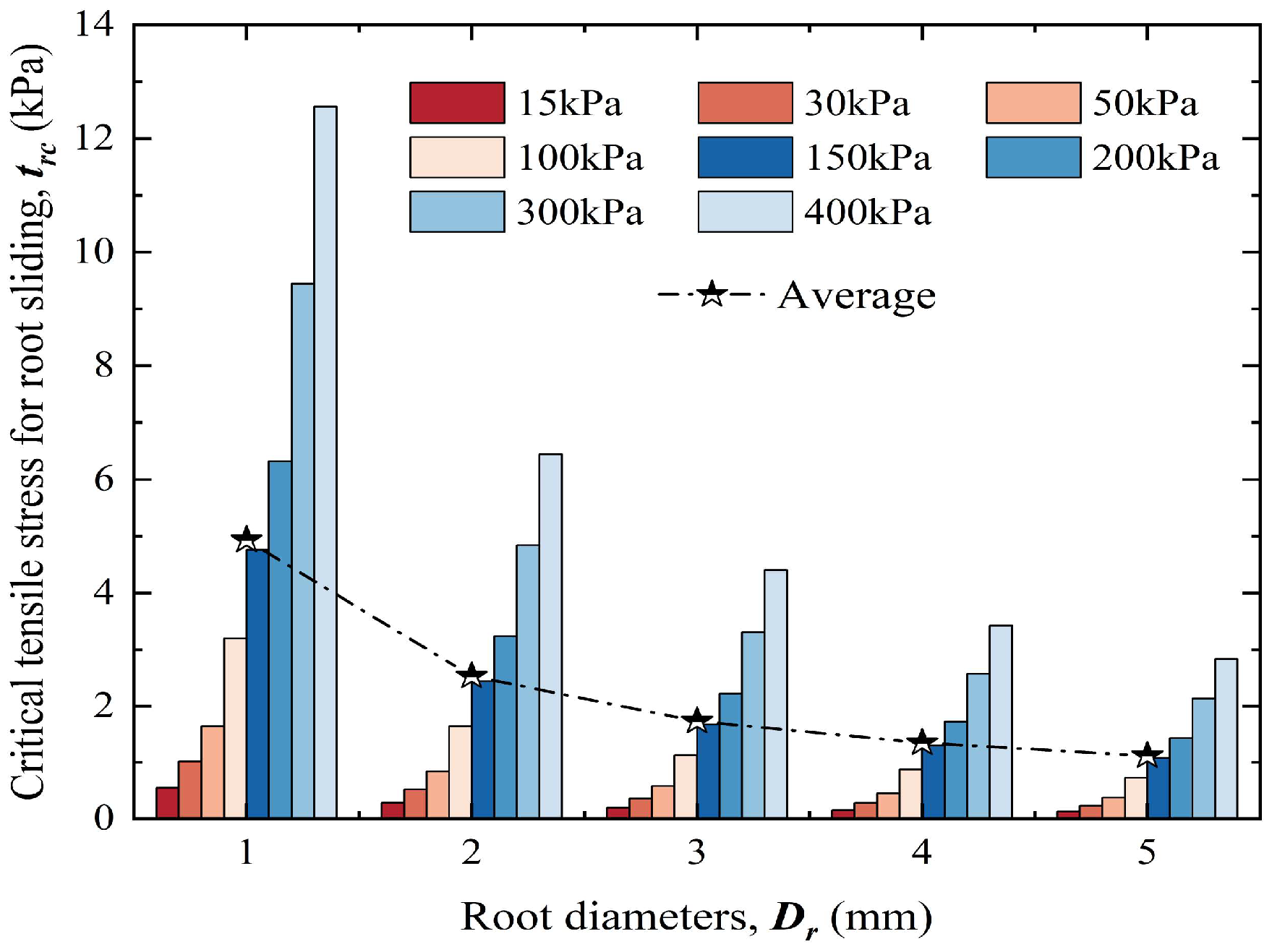
4.1. The Root–Soil Interaction for Different Root Diameters
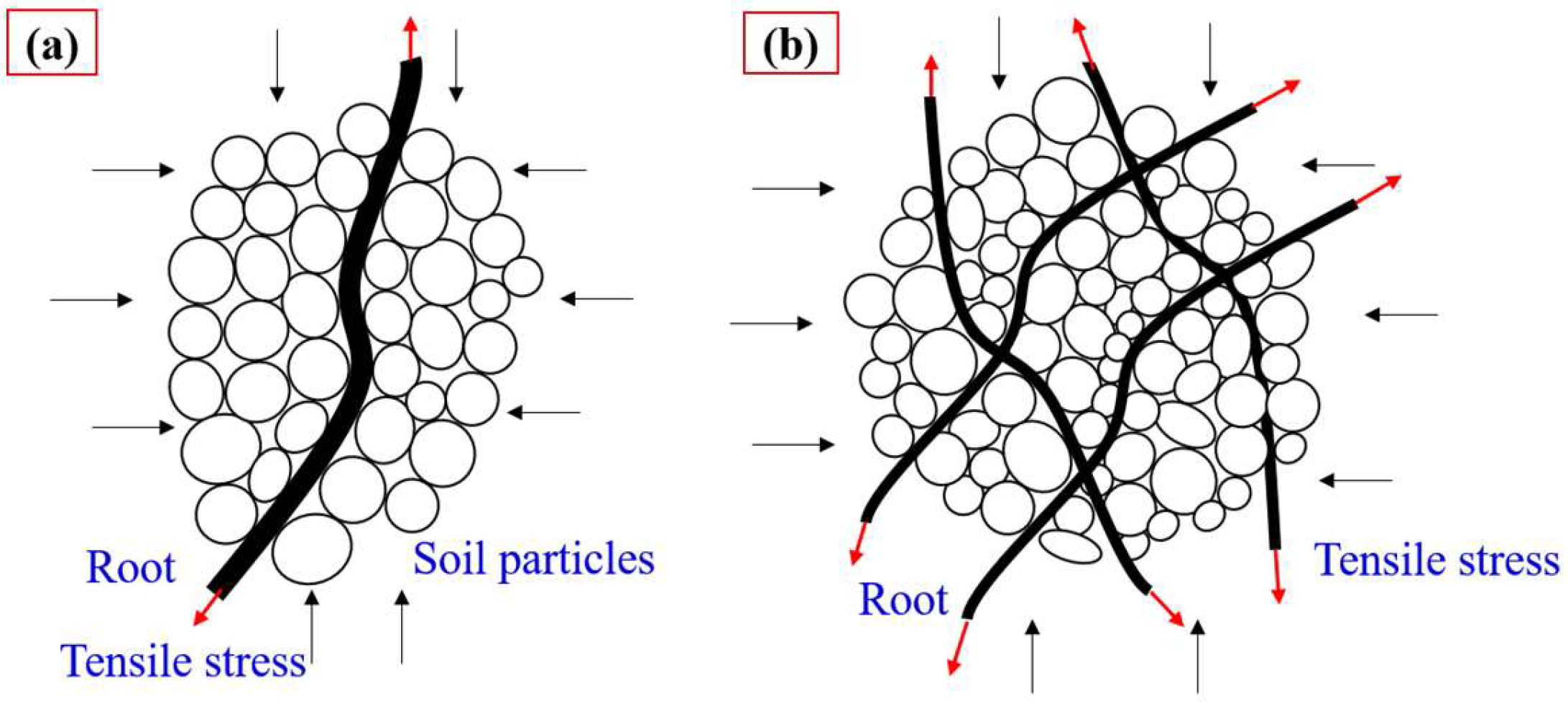
4.2. The Mechanism of Root Diameter’s Influence on Sand Strength
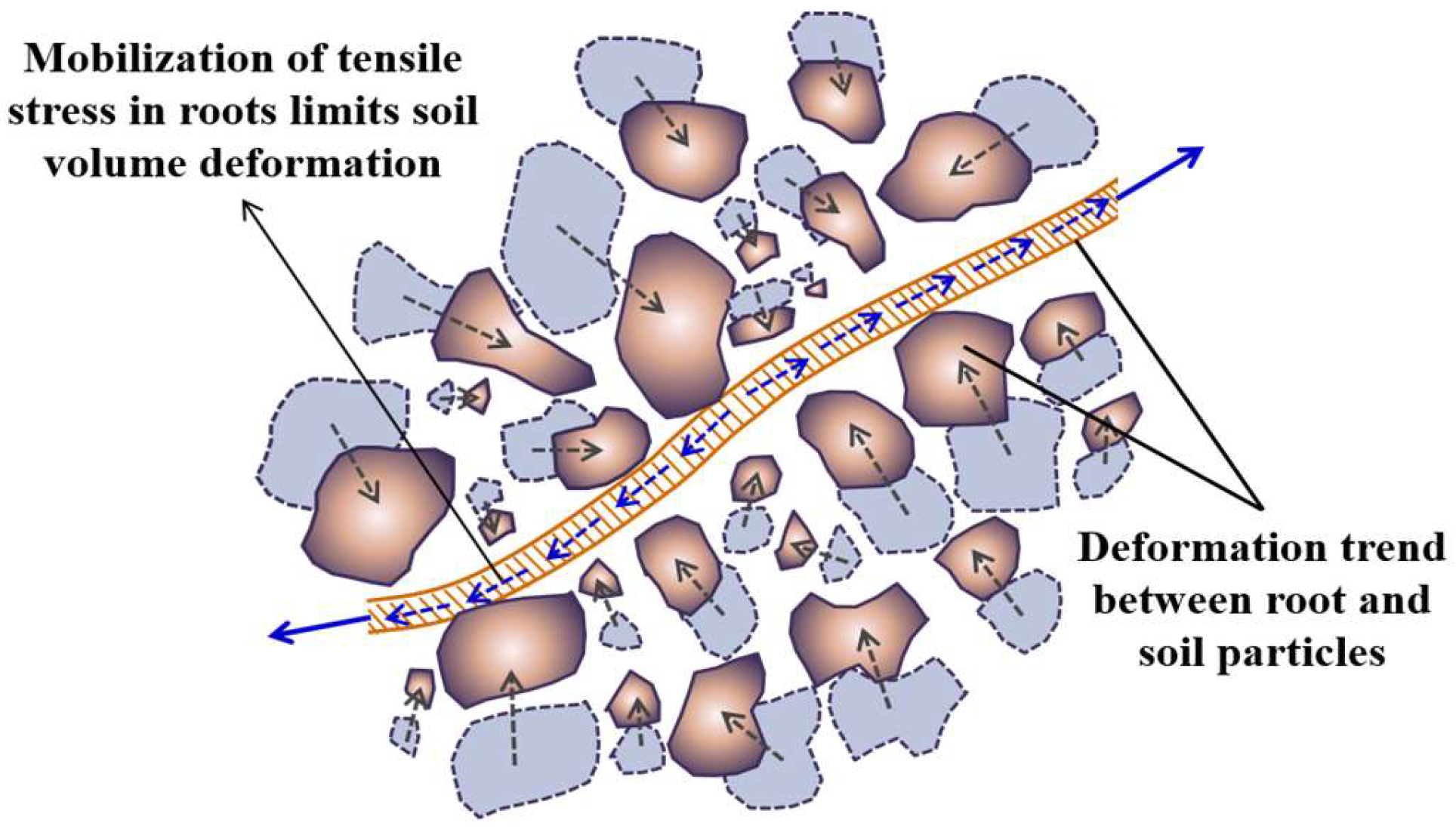
4.3. The Influence of Root Diameter on the Volumetric Deformation of Sand
5. Conclusions
- (1)
- Root addition significantly increased the strength of sand, with an average increase of 31.8% observed for roots with diameters ranging from 1 mm to 5 mm. Smaller root diameters had a more pronounced strengthening effect on sand, as the increase in strength increased from 13.2% to 78.1% as the root diameter decreased from 5 mm to 1 mm;
- (2)
- Roots provide significant additional cohesion to the sand and increase its internal friction angle, thereby raising and reversing the failure envelope of the sand. The cohesion and internal friction angle of the root–soil composite decrease as the root diameter increases. As the root diameter increased from 1 mm to 5 mm, both the additional cohesion provided by the roots and the internal friction angle decreased by 76.8% and 12.1%, respectively;
- (3)
- The addition of roots significantly reduced the volumetric deformation of sand, with the average volumetric strain of the root–soil composites being only 0.66 times that of bare soil. A positive correlation was observed between root diameter and the volumetric strain of the root–soil composites. As the root diameter increased from 1 mm to 5 mm, the volumetric strain ratio increased from 0.48 to 0.79. This suggests that smaller root diameters more effectively limit volumetric deformation, thereby significantly enhancing the sand’s resistance to deformation;
- (4)
- Smaller root diameters more effectively enhance the mechanical properties of sand. They form a denser network, enabling more roots to resist external loads, which strengthens the composite and improves its deformation resistance. Additionally, smaller roots have a higher elastic modulus, resulting in greater tensile stress. Their higher tensile strength and sliding resistance make them less prone to failure, further enhancing the composite’s overall strength and resistance to deformation. Therefore, selecting plants with smaller and denser roots is an effective strategy for vegetative slope protection.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ning, P.; Xia, X.; Jiang, Y. An Estimation Model of the Ultimate Shear Strength of Root-Permeated Soil, Fully Considering Interface Bonding. Forests 2023, 14, 919. [Google Scholar] [CrossRef]
- Huang, J.; Hartemink, A.E. Soil and environmental issues in sandy soils. Earth-Sci. Rev. 2020, 208, 103295. [Google Scholar] [CrossRef]
- Kim, M.S.; Onda, Y.; Uchida, T.; Kim, J.K.; Song, Y.S. Effect of seepage on shallow landslides in consideration of changes in topography: Case study including an experimental sandy slope with artificial rainfall. Catena 2018, 161, 50–62. [Google Scholar] [CrossRef]
- Yang, H.; Yang, T.; Zhang, S.; Zhao, F.; Hu, K.; Jiang, Y. Rainfall-induced landslides and debris flows in Mengdong Town, Yunnan Province, China. Landslides 2020, 17, 931–941. [Google Scholar] [CrossRef]
- Qingmin, S.; Yonggang, G.; Pan, C.; Xinyue, L.; Yuchen, D. Evaluation of Factors Affecting the Shear Strength of Root-Soil Composite of Typical Plants in Wenchuan County. J. Soil Water Conserv. 2022, 36, 58–65. [Google Scholar]
- Dahal, R.K.; Hasegawa, S.; Nonomura, A.; Yamanaka, M.; Masuda, T.; Nishino, K. Failure characteristics of rainfall-induced shallow landslides in granitic terrains of Shikoku Island of Japan. Environ. Geol. 2009, 56, 1295–1310. [Google Scholar] [CrossRef]
- Alam, M. Experimental Study of Soil-Roots Coupled Constitutive Behaviour; University of Chinese Academy of Sciences: Beijing, China, 2021. [Google Scholar]
- Xu, R.; Li, X.; Yang, W.; Jiang, C.; Rabiei, M. Use of local plants for ecological restoration and slope stability: A possible application in Yan’an, Loess Plateau, China. Geomat. Nat. Hazards Risk 2019, 10, 2106–2128. [Google Scholar] [CrossRef]
- Song, G.; He, S.; Song, X.; Duan, Z.; Zhang, Y.; Kong, D.; Huang, M. The use of geocell as soil stabilization and soil erosion countermeasures. Geomat. Nat. Hazards Risk 2021, 12, 2155–2169. [Google Scholar] [CrossRef]
- Liu, J.; Tang, Y.; Jiang, Y.; Luo, S.; Wu, K.; Peng, X.; Pan, Y. Experimental Study on the Effect of Root Content on the Shear Strength of Root–Soil Composite with Thick and Fine Roots of Cryptomeria japonica (Thunb. ex L.f.) D.Don. Forests 2024, 15, 1306. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Leung, A.; Ni, J. Plant-Soil Slope Interaction; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Lin, Y.; Jian, W.; Zhu, Z.; Wu, Y.; Wang, H.; Fan, X. Study on the Mechanical Properties of Roots and Friction Characteristics of the Root–Soil Interface of Two Tree Species in the Coastal Region of Southeastern China. Forests 2024, 15, 1285. [Google Scholar] [CrossRef]
- Tang, L.; Mao, L.; Wang, Z.; Ye, S.; Wang, S. Mixed with broadleaf tree species improved soil aggregate stability in Chinese Fir (Cunninghamia lanceolata) plantations: Based on the Le Bissonnais method. J. Soil Sci. Plant Nutr. 2023, 23, 2110–2121. [Google Scholar] [CrossRef]
- Xing, S.; Zhang, G.; Zhu, P.; Wang, L.; Wang, Z.; Wang, C. Shear strength of soil-root system under different vegetation restoration modes on the Loess Plateau of China. Soil Tillage Res. 2023, 228, 105648. [Google Scholar] [CrossRef]
- Liu, Y.-F.; Meng, L.-C.; Huang, Z.; Shi, Z.-H.; Wu, G.-L. Contribution of fine roots mechanical property of Poaceae grasses to soil erosion resistance on the Loess Plateau. Geoderma 2022, 426, 116122. [Google Scholar] [CrossRef]
- Shuai, F.; Huang, M.; Zhan, Y.; Zhu, Q.; Li, X.; Zhang, Y.; Lin, J.; Huang, Y.; Jiang, F. Effects of Herbaceous Plant Roots on the Soil Shear Strength of the Collapsing Walls of Benggang in Southeast China. Forests 2022, 13, 1843. [Google Scholar] [CrossRef]
- Nilaweera, N. Effects of Tree Roots on Slope Stability—The Case of Khao Lunag Mountain Area, Southern Thiland; Asian Institute of Technology: Bangkok, Thiland, 1994. [Google Scholar]
- Wu, T.H.; Watson, A. In situ shear tests of soil blocks with roots. Can. Geotech. J. 1998, 35, 579–590. [Google Scholar] [CrossRef]
- Operstein, V.; Frydman, S. The influence of vegetation on soil strength. Proc. Inst. Civ. Eng. Ground Improv. 2000, 4, 81–89. [Google Scholar] [CrossRef]
- Comino, E.; Druetta, A. The effect of Poaceae roots on the shear strength of soils in the Italian alpine environment. Soil Tillage Res. 2010, 106, 194–201. [Google Scholar] [CrossRef]
- Yildiz, A.; Graf, F.; Rickli, C.; Springman, S.M. Determination of the shearing behaviour of root-permeated soils with a large-scale direct shear apparatus. Catena 2018, 166, 98–113. [Google Scholar] [CrossRef]
- Forster, M.; Ugarte, C.; Lamandé, M.; Faucon, M.-P.J.G. Root traits of crop species contributing to soil shear strength. Geoderma 2022, 409, 115642. [Google Scholar] [CrossRef]
- Waldron, L.J. Shear Resistance of Root-Permeated Homogeneous and Stratified Soil. Soil Sci. Soc. Am. J. 1977, 41, 843–849. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. 2010, 115, F04035. [Google Scholar] [CrossRef]
- Wu, T.H. Root reinforcement of soil: Review of analytical models, test results, and applications to design. Can. Geotech. J. 2013, 50, 259–274. [Google Scholar] [CrossRef]
- Huang, J.; Wu, P.; Zhao, X. Effects of rainfall intensity, underlying surface and slope gradient on soil infiltration under simulated rainfall experiments. Catena 2013, 104, 93–102. [Google Scholar] [CrossRef]
- Stokes, A.; Atger, C.; Bengough, A.G.; Fourcaud, T.; Sidle, R.C. Desirable plant root traits for protecting natural and engineered slopes against landslides. Plant Soil 2009, 324, 1–30. [Google Scholar] [CrossRef]
- Huang, C.-C.; Lo, C.-L.; Jang, J.-S.; Hwu, L.-K. Internal soil moisture response to rainfall-induced slope failures and debris discharge. Eng. Geol. 2008, 101, 134–145. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Guo, H.; Ni, J.; Chen, R.; Xue, Q.; Zhang, Y.; Feng, Y.; Chen, Z.; Feng, S.; Zhang, Q. Long-term field performance of non-vegetated and vegetated three-layer landfill cover systems using construction waste without geomembrane. Géotechnique 2022, 74, 155–173. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A.; Collison, A. Advances in assessing the mechanical and hydrologic effects of riparian vegetation on streambank stability. Riparian Veg. Fluv. Geomorphol. 2004, 8, 125–139. [Google Scholar]
- Feng, S.; Liu, H.; Ng, C.; Wai, W. Analytical analysis of the mechanical and hydrological effects of vegetation on shallow slope stability. Comput. Geotech. 2020, 118, 103335. [Google Scholar] [CrossRef]
- Lian, B.; Peng, J.; Zhan, H.; Wang, X. Mechanical response of root-reinforced loess with various water contents. Soil Tillage Res. 2019, 193, 85–94. [Google Scholar] [CrossRef]
- Foresta, V.; Capobianco, V.; Cascini, L. Influence of grass roots on shear strength of pyroclastic soils. Can. Geotech. J. 2020, 57, 1320–1334. [Google Scholar] [CrossRef]
- Jiang, Y.-j.; Alam, M.; Su, L.-J.; Umar, M.; Sadiq, S.; Li, J.-J.; Rahman, M. Effect of root orientation on the strength characteristics of loess in drained and undrained triaxial tests. Eng. Geol. 2022, 296, 106459. [Google Scholar] [CrossRef]
- Alam, M.; Jiang, Y.-J.; Umar, M.; Su, L.-j.; Rahman, M.; Ullah, F. Influence of drainage and root biomass on soil mechanical behavior in triaxial tests. Acta Geotech. 2022, 17, 2875–2893. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, L.; Jiang, J. Vertical root distribution and root cohesion of typical tree species on the Loess Plateau, China. J. Arid Land 2014, 6, 601–611. [Google Scholar] [CrossRef]
- Gonzalez-Ollauri, A.; Hudek, C.; Mickovski, S.B.; Viglietti, D.; Ceretto, N.; Freppaz, M. Describing the vertical root distribution of alpine plants with simple climate, soil, and plant attributes. Catena 2021, 203, 105305. [Google Scholar] [CrossRef]
- Burak, E.; Dodd, I.C.; Quinton, J.N. Do root hairs of barley and maize roots reinforce soil under shear stress? Geoderma 2021, 383, 114740. [Google Scholar] [CrossRef]
- Schmid, I.; Kazda, M. Root distribution of Norway spruce in monospecific and mixed stands on different soils. For. Ecol. Manag. 2002, 159, 37–47. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, X.; Jiang, J.; Wei, Y.; Ma, J.; Hallett, P.D. Root moisture content influence on root tensile tests of herbaceous plants. Catena 2019, 172, 140–147. [Google Scholar] [CrossRef]
- Genet, M.; Kokutse, N.; Stokes, A.; Fourcaud, T.; Cai, X.; Ji, J.; Mickovski, S. Root reinforcement in plantations of Cryptomeria japonica D. Don: Effect of tree age and stand structure on slope stability. For. Ecol. Manag. 2008, 256, 1517–1526. [Google Scholar] [CrossRef]
- Wu, Z.; Leung, A.K.; Boldrin, D.; Ganesan, S.P. Variability in root biomechanics of Chrysopogon zizanioides for soil eco-engineering solutions. Sci. Total Environ. 2021, 776, 145943. [Google Scholar] [CrossRef]
- Pollen, N. Temporal and spatial variability in root reinforcement of streambanks: Accounting for soil shear strength and moisture. Catena 2007, 69, 197–205. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, Z.; Xu, W.; Hai, X.; Liu, D.; Liu, L.; Zhao, B. A study on pullout test of root subjected to axial load. Nat. Environ. Pollut. Technol. 2020, 19, 441–452. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour. Res. 2005, 41, W07025. [Google Scholar] [CrossRef]
- Schwarz, M.; Lehmann, P.; Or, D. Quantifying lateral root reinforcement in steep slopes-from a bundle of roots to tree stands. Earth Surf. Process. Landf. 2010, 35, 354–367. [Google Scholar] [CrossRef]
- Chang, M.; Tang, C.; Zhang, D.-D.; Ma, G.-C. Debris flow susceptibility assessment using a probabilistic approach: A case study in the Longchi area, Sichuan province, China. J. Mt. Sci. 2014, 11, 1001–1014. [Google Scholar] [CrossRef]
- Mehtab, A.; Jiang, Y.-J.; Su, L.-J.; Shamsher, S.; Li, J.-J.; Mahfuzur, R. Scaling the Roots Mechanical Reinforcement in Plantation of Cunninghamia R. Br in Southwest China. Forests 2020, 12, 33. [Google Scholar] [CrossRef]
- Meng, S.; Zhao, G.; Yang, Y. Impact of Plant Root Morphology on Rooted-Soil Shear Resistance Using Triaxial Testing. Adv. Civ. Eng. 2020, 2020, 8825828. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. MOHURD: Beijing, China, 2019.
- Boldrin, D.; Leung, A.K.; Bengough, A.G. Effects of root dehydration on biomechanical properties of woody roots of Ulex europaeus. Plant Soil 2018, 431, 347–369. [Google Scholar] [CrossRef]
- Mao, Z.; Saint-André, L.; Genet, M.; Mine, F.-X.; Jourdan, C.; Rey, H.; Courbaud, B.; Stokes, A. Engineering ecological protection against landslides in diverse mountain forests: Choosing cohesion models. Ecol. Eng. 2012, 45, 55–69. [Google Scholar] [CrossRef]
- Lei, M.; Li, Z.; Jiang, Y.; Qin, M.; Li, J. A Measuring Device for the Friction Coefficient Between Tree Roots and Soil. CN Patent CN214584810U, 2 November 2021. [Google Scholar]
- Mickovski, S.; Bransby, M.; Bengough, A.; Davies, M.; Hallett, P. Resistance of simple plant root systems to uplift loads. Can. Geotech. J. 2010, 47, 78–95. [Google Scholar] [CrossRef]
- Estabragh, A.; Bordbar, A.; Javadi, A. A study on the mechanical behavior of a fiber-clay composite with natural fiber. Geotech. Geol. Eng. 2013, 31, 501–510. [Google Scholar] [CrossRef]
- Zhang, M.; Javadi, A.; Min, X. Triaxial tests of sand reinforced with 3D inclusions. Geotext. Geomembr. 2006, 24, 201–209. [Google Scholar] [CrossRef]
- Guangxin, L.; Bingyin, Z.; Yuzhen, Y. Soil Mechanics; Tsinghua University Press: Beijing, China, 2022. [Google Scholar]
- Abernethy, B.; Rutherfurd, I. The Distribution and Strength of Riparian Tree Roots in Relation to Riverbank Reinforcement. Hydrol. Process. 2001, 15, 63–79. [Google Scholar] [CrossRef]
- Schmidt, K.M.; Roering, J.J.; Stock, J.D.; Dietrich, W.E.; Montgomery, D.R.; Schaub, T. The variability of root cohesion as an influence on shallow landslide susceptibility in the Oregon Coast Range. Can. Geotech. J. 2001, 38, 995–1024. [Google Scholar] [CrossRef]
- Michalowski, R.L.; Zhao, A. Failure of fiber-reinforced granular soils. J. Geotech. Eng. 1996, 122, 226–234. [Google Scholar] [CrossRef]
- Lian, B.; Peng, J.; Zhan, H.; Cui, X. Effect of randomly distributed fibre on triaxial shear behavior of loess. Bull. Eng. Geol. Environ. 2020, 79, 1555–1563. [Google Scholar] [CrossRef]
- Kannan, G.; Sujatha, E.R. Effect of nano additive on mechanical properties of natural fiber reinforced soil. J. Nat. Fibers 2023, 20, 2143980. [Google Scholar] [CrossRef]
- Jiang, H.; Cai, Y.; Liu, J. Engineering properties of soils reinforced by short discrete polypropylene fiber. J. Mater. Civ. Eng. 2010, 22, 1315–1322. [Google Scholar] [CrossRef]
- Tang, C.-S.; Shi, B.; Zhao, L.-Z. Interfacial shear strength of fiber reinforced soil. Geotext. Geomembr. 2010, 28, 54–62. [Google Scholar] [CrossRef]
- Mirzababaei, M.; Arulrajah, A.; Haque, A.; Nimbalkar, S.; Mohajerani, A. Effect of fiber reinforcement on shear strength and void ratio of soft clay. Geosynth. Int. 2018, 25, 471–480. [Google Scholar] [CrossRef]
- Michalowski, R.L.; Čermák, J. Triaxial compression of sand reinforced with fibers. J. Geotech. Geoenviron. Eng. 2003, 129, 125–136. [Google Scholar] [CrossRef]

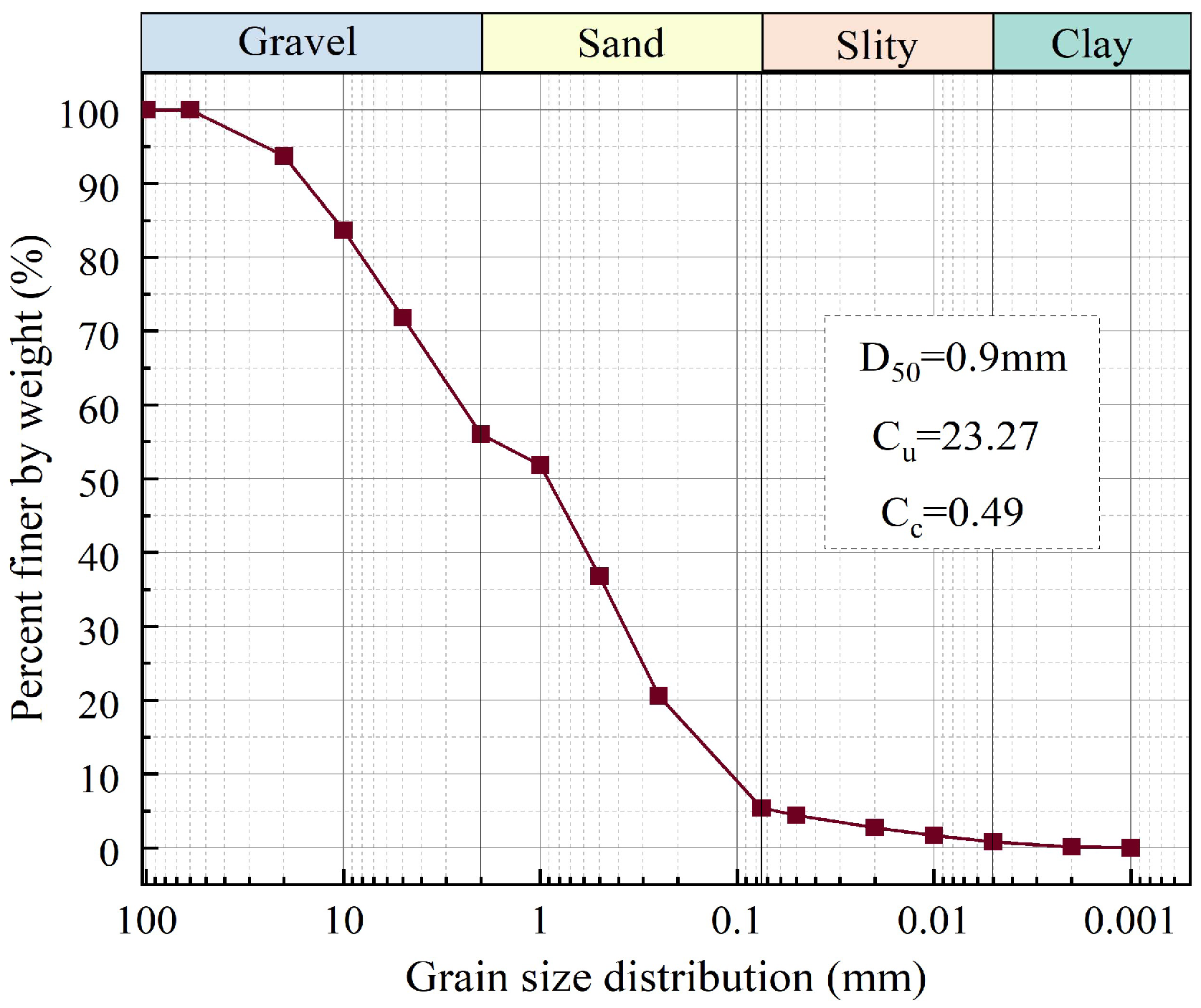



| Maximum Dry Density (g·cm−3) | Minimum Dry Density (g·cm−3) | Unit Weight (g·cm−3) | Field Dry Density (g·cm−3) | Soil Water Content (%) | Plastic Limit (%) | Liquid Limit (%) |
|---|---|---|---|---|---|---|
| 2.10 | 1.41 | 2.65 | 1.62 | 10 | 13.6 | 21.23 |
| Mechanical Parameters | Fitted Curve | R2 |
|---|---|---|
| Maximum tensile force | 0.96 | |
| Tensile strength | ― | |
| Elastic modulus | 0.99 |
| Root Diameter | Peak Frictional Strength Parameters | ||
|---|---|---|---|
| cIp | φIp | R2 | |
| 1 mm | 2.00 | 37.95 | 0.93 |
| 2 mm | 1.99 | 38.66 | 0.90 |
| 3 mm | 2.26 | 39.35 | 0.93 |
| 4 mm | 2.36 | 40.36 | 0.94 |
| 5 mm | 2.55 | 41.35 | 0.95 |
| Confining Pressure (kPa) | Bare Soil | Soil + 1 mm Roots | Soil + 2 mm Roots | Soil + 3 mm Roots | Soil + 4 mm Roots | Soil + 5 mm Roots |
|---|---|---|---|---|---|---|
| 15 | 55.39 | 112.53 | 81.75 | 76.39 | 71.20 | 68.40 |
| 30 | 86.94 | 169.93 | 123.14 | 116.07 | 107.18 | 104.07 |
| 50 | 140.59 | 284.13 | 197.25 | 188.08 | 174.98 | 165.76 |
| 100 | 260.95 | 501.60 | 341.50 | 299.49 | 302.96 | 291.14 |
| 150 | 427.65 | 686.75 | 526.86 | 498.83 | 487.18 | 466.80 |
| 200 | 565.15 | 982.95 | 659.62 | 631.37 | 621.33 | 612.40 |
| 300 | 821.11 | 1261.81 | 916.78 | 921.02 | 911.08 | 882.26 |
| 400 | 1100.53 | 1582.34 | 1300.73 | 1249.05 | 1226.82 | 1187.52 |
| Shear Strength Parameters c′ (kPa), φ′ (°) | Bare Soil | Roots-Soil Composite | ||||
|---|---|---|---|---|---|---|
| Dr—1 mm | Dr—2 mm | Dr—3 mm | Dr—4 mm | Dr—5 mm | ||
| c′ | 0.00 | 20.30 | 8.85 | 6.23 | 5.12 | 4.71 |
| Δcr′ | — | 20.30 | 8.85 | 6.23 | 5.12 | 4.71 |
| φ′ | 35.45 | 41.40 | 37.44 | 37.07 | 36.89 | 36.38 |
| Δφr′ | — | 5.96 | 1.99 | 1.63 | 1.44 | 0.93 |
| Confining Pressure (kPa) | Bare Soil | Soil + 1 mm Roots | Soil + 2 mm Roots | Soil + 3 mm Roots | Soil + 4 mm Roots | Soil + 5 mm Roots |
|---|---|---|---|---|---|---|
| 15 | 1.89 | 0.33 | 1.00 | 0.71 | 1.12 | 1.39 |
| 30 | 2.83 | 0.56 | 1.55 | 1.37 | 1.78 | 1.88 |
| 50 | 3.34 | 1.00 | 1.19 | 1.92 | 2.32 | 2.36 |
| 100 | 4.42 | 2.06 | 2.92 | 3.00 | 3.10 | 3.25 |
| 150 | 5.23 | 2.82 | 3.48 | 3.61 | 3.78 | 3.98 |
| 200 | 5.75 | 3.90 | 4.20 | 4.25 | 4.58 | 4.80 |
| 300 | 6.17 | 4.53 | 4.87 | 4.96 | 5.54 | 5.75 |
| 400 | 6.95 | 5.14 | 5.39 | 5.75 | 6.07 | 6.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, X.; Jiang, Y.; Hu, X.; Zhu, Y.; Shah, I. The Influence of the Root Diameter of Cunninghamia lanceolata (Chinese Fir) on the Strength and Deformation Behavior of Sand. Forests 2025, 16, 135. https://doi.org/10.3390/f16010135
Xia X, Jiang Y, Hu X, Zhu Y, Shah I. The Influence of the Root Diameter of Cunninghamia lanceolata (Chinese Fir) on the Strength and Deformation Behavior of Sand. Forests. 2025; 16(1):135. https://doi.org/10.3390/f16010135
Chicago/Turabian StyleXia, Xin, Yuanjun Jiang, Xiaobo Hu, Yuanjia Zhu, and Ismail Shah. 2025. "The Influence of the Root Diameter of Cunninghamia lanceolata (Chinese Fir) on the Strength and Deformation Behavior of Sand" Forests 16, no. 1: 135. https://doi.org/10.3390/f16010135
APA StyleXia, X., Jiang, Y., Hu, X., Zhu, Y., & Shah, I. (2025). The Influence of the Root Diameter of Cunninghamia lanceolata (Chinese Fir) on the Strength and Deformation Behavior of Sand. Forests, 16(1), 135. https://doi.org/10.3390/f16010135





