PosE-Enhanced Point Transformer with Local Surface Features (LSF) for Wood–Leaf Separation
Abstract
1. Introduction
2. Study Area and Dataset Construction
2.1. Study Area and Data Acquisition
2.2. Data Preprocessing and Dataset Construction
3. Segmentation Network
- Randomly select an initial point: Start by randomly choosing a point from the point cloud as the first point in the sampled set.
- Calculate distances: For each remaining point in the point cloud, calculate the distance to the nearest point in the already selected set of points.
- Select the farthest point: Choose the point with the maximum distance from the points already selected. This point is then added to the set of sampled points.
- Repeat until the desired number of points is reached: Continue steps 2 and 3 until the desired number of points (in this case, 4096) has been selected. This ensures that the points are evenly distributed and well represent the structure of the original point cloud.
3.1. Local Surface Features Extraction (LSFE)
3.2. Feature Abstraction (FA)
3.3. PosE
3.4. RFFT
3.5. Point Transformer Block
3.6. Feature Propagation
4. Computational Experiments
4.1. Computational Environments
4.2. Local Surface Features
- Constructing the High-Dimensional Graph: UMAP begins by constructing a k-nearest neighbor (kNN) graph in high-dimensional space. For each point in the dataset, the algorithm identifies its k-nearest neighbors. The similarity weight between each pair of neighboring points and is then calculated as follows:
- 2.
- Constructing the Low-Dimensional Graph: In the low-dimensional space, UMAP initializes a graph structure and calculates similarity weights for each pair of points in a manner similar to the high-dimensional graph. The goal is to maintain the local similarity relationships found in the high-dimensional space within the low-dimensional structure. The calculation is as follows:
- 3.
- Optimizing the Low-Dimensional Embedding: UMAP optimizes the low-dimensional embedding by minimizing the difference between the high-dimensional and low-dimensional graphs. Specifically, it seeks to find the optimal set of low-dimensional feature vectors . The objective function for this optimization is typically defined using cross-entropy loss as follows:
- 4.
- Projection and Visualization: After optimization, the resulting low-dimensional feature are mapped onto the axes (e.g., Component 1, Component 2, and Component 3) for three-dimensional visualization, preserving the data’s local structure and distributional characteristics.
4.3. Results of RFFT
4.4. Wood–Leaf Separation
4.5. Ablation Studies
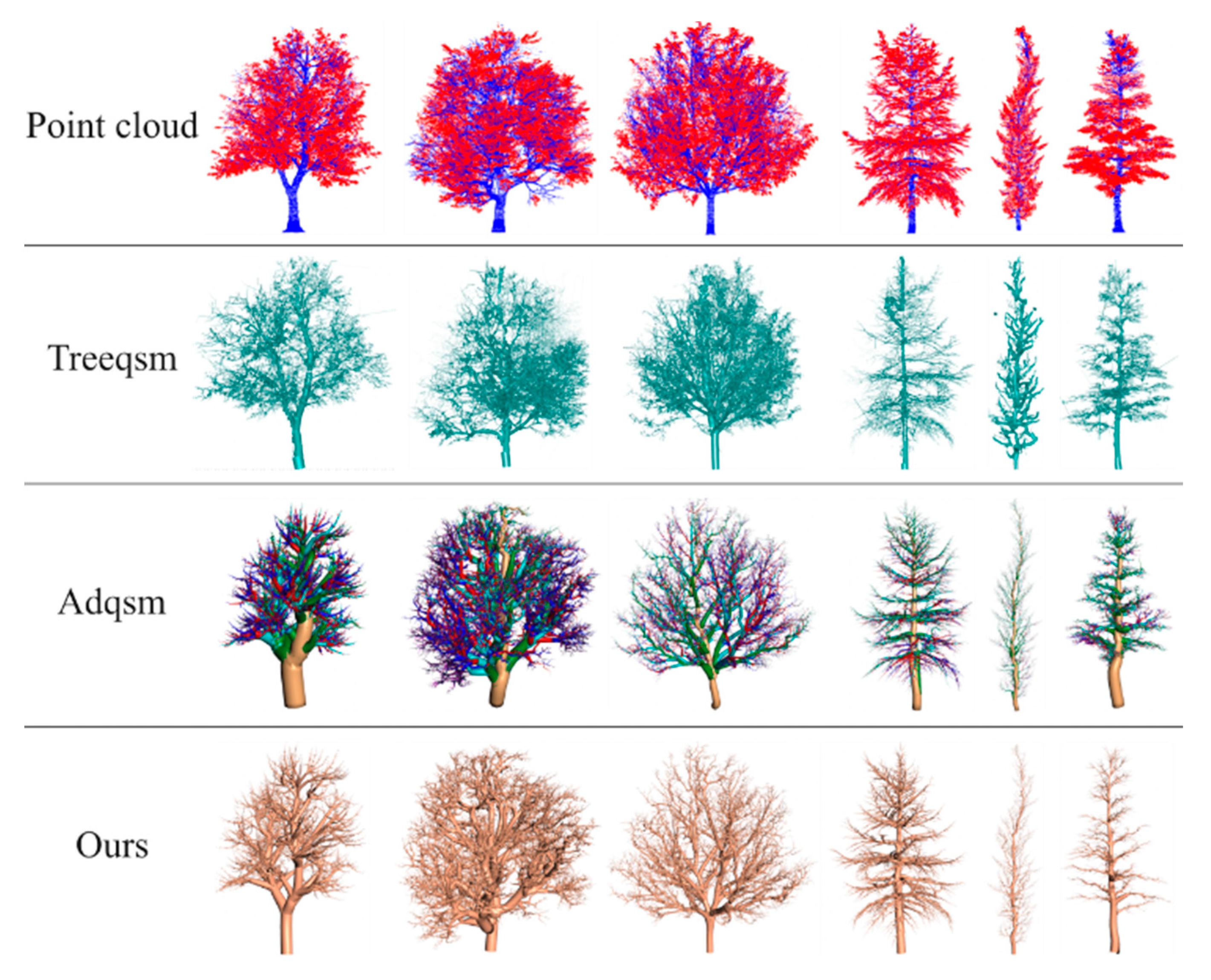
4.6. Comparison with Existing Methods
5. Discussion
5.1. Collaborative Synergy Between LSF and PosE: A Paradigm Shift in Wood–Leaf Separation
5.2. Design Principles of Local Surface Features
5.3. Discussion on the Effectiveness of PosE
5.4. Performance Analysis of Wood–Leaf Separation
5.5. A Path Forward for the Realization of the Digital Twins of Trees
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Hyperparameter | Value | Hyperparameter | Value |
| 10 | learning rate | 0.0015 | |
| 100 | weight decay | 0.0004 | |
| 500 | learning rate decay | 0.8 | |
| 156 | step size | 20 | |
| 1 | optimizer | Adamw | |
| batch size | 2 | point number | 4096 |
| epoch | 30 | 16 (in FA)/3 (in FP) |
References
- Qiu, H.; Zhang, H.; Lei, K.; Zhang, H.; Hu, X. Forest digital twin: A new tool for forest management practices based on Spatio-Temporal Data, 3D simulation Engine, and intelligent interactive environment. Comput. Electron. Agric. 2023, 215, 108416. [Google Scholar] [CrossRef]
- Gao, D.; Ou, L.; Liu, Y.; Yang, Q.; Wang, H. DeepSpoof: Deep Reinforcement Learning-Based Spoofing Attack in Cross-Technology Multimedia Communication. IEEE Trans. Multimed. 2024, 26, 10879–10891. [Google Scholar] [CrossRef]
- Zhang, W.; Li, W. Construction of Environment-Sensitive Digital Twin Plant Model for Ecological Indicators Analysis. J. Digit. Landsc. Archit. 2024, 9, 18–28. [Google Scholar]
- Silva, J.R.; Artaxo, P.; Vital, E. Forest Digital Twin: A Digital Transformation Approach for Monitoring Greenhouse Gas Emissions. Polytechnica 2023, 6, 2. [Google Scholar] [CrossRef]
- Feng, W.; Jiao, M.; Liu, N.; Yang, L.; Zhang, Z.; Hu, S. Realistic reconstruction of trees from sparse images in volumetric space. Comput. Graph. 2024, 121, 103953. [Google Scholar] [CrossRef]
- Li, Y.; Kan, J. CGAN-Based Forest Scene 3D Reconstruction from a Single Image. Forests 2024, 15, 194. [Google Scholar] [CrossRef]
- Li, W.; Tang, B.; Hou, Z.; Wang, H.; Bing, Z.; Yang, Q.; Zheng, Y. Dynamic Slicing and Reconstruction Algorithm for Precise Canopy Volume Estimation in 3D Citrus Tree Point Clouds. Remote Sens. 2024, 16, 2142. [Google Scholar] [CrossRef]
- Shan, P.; Sun, W. Research on landscape design system based on 3D virtual reality and image processing technology. Ecol. Inform. 2021, 63, 101287. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, J.; Benes, B.; Deussen, O.; Zhang, X.; Huang, H. TreePartNet: Neural decomposition of point clouds for 3D tree reconstruction. Comput. Electron. Agric. 2021, 40, 232. [Google Scholar] [CrossRef]
- Kok, E.; Wang, X.; Chen, C. Obscured tree branches segmentation and 3D reconstruction using deep learning and geometrical constraints. Comput. Electron. Agric. 2023, 210, 107884. [Google Scholar] [CrossRef]
- Tan, K.; Ke, T.; Tao, P.; Liu, K.; Duan, Y.; Zhang, W.; Wu, S. Discriminating forest leaf and wood components in TLS point clouds at single-scan level using derived geometric quantities. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Hao, W.; Ran, M. Dynamic region growing approach for leaf-wood separation of individual trees based on geometric features and growing patterns. Int. J. Remote Sens. 2024, 45, 6787–6813. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, Z.; Xu, F.; Chen, F. Unsupervised Semantic Segmenting TLS Data of Individual Tree Based on Smoothness Constraint Using Open-Source Datasets. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Arrizza, S.; Marras, S.; Ferrara, R.; Pellizzaro, G. Terrestrial Laser Scanning (TLS) for tree structure studies: A review of methods for wood-leaf classifications from 3D point clouds. Remote Sens. Appl. Soc. Environ. 2024, 36, 101364. [Google Scholar] [CrossRef]
- Spadavecchia, C.; Campos, M.B.; Piras, M.; Puttonen, E.; Shcherbacheva, A. Wood-Leaf Unsupervised Classification of Silver Birch Trees for Biomass Assessment Using Oblique Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 1795–1802. [Google Scholar] [CrossRef]
- Zhu, F.; Gao, J.; Yang, J.; Ye, N. Neighborhood linear discriminant analysis. Pattern Recognit. 2022, 123, 108422. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z.; Zhang, L.; Fan, X.; Ye, Q.; Fu, L. Global superpixel-merging via set maximum coverage. Eng. Appl. Artif. Intell. 2024, 127, 107212. [Google Scholar] [CrossRef]
- Tang, H.; Li, S.; Su, Z.; He, Z. Cluster-Based Wood–Leaf Separation Method for Forest Plots Using Terrestrial Laser Scanning Data. Remote Sens. 2024, 16, 3355. [Google Scholar] [CrossRef]
- Han, B.; Li, Y.; Bie, Z.; Peng, C.; Huang, Y.; Xu, S. MIX-NET: Deep Learning-Based Point Cloud Processing Method for Segmentation and Occlusion Leaf Restoration of Seedlings. Plants 2022, 11, 3342. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, J.; Xiang, S.; Pan, A. PSegNet: Simultaneous semantic and instance segmentation for point clouds of plants. Plant Phenomics 2022, 2022, 9787643. [Google Scholar] [CrossRef]
- Kim, D.-H.; Ko, C.-U.; Kim, D.-G.; Kang, J.-T.; Park, J.-M.; Cho, H.-J. Automated Segmentation of Individual Tree Structures Using Deep Learning over LiDAR Point Cloud Data. Forests 2023, 14, 1159. [Google Scholar] [CrossRef]
- Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.; Elhoseiny, M.; Ghanem, B. Pointnext: Revisiting pointnet++ with improved training and scaling strategies. Adv. Neural Inf. Process. Syst. 2022, 35, 23192–23204. [Google Scholar]
- Jiang, T.; Zhang, Q.; Liu, S.; Liang, C.; Dai, L.; Zhang, Z.; Sun, J.; Wang, Y. LWSNet: A Point-Based Segmentation Network for Leaf-Wood Separation of Individual Trees. Forests 2023, 14, 1303. [Google Scholar] [CrossRef]
- Akagi, T.; Masuda, K.; Kuwada, E.; Takeshita, K.; Kawakatsu, T.; Ariizumi, T.; Kubo, Y.; Ushijima, K.; Uchida, S. Genome-wide cis-decoding for expression design in tomato using cistrome data and explainable deep learning. Plant Cell 2022, 34, 2174–2187. [Google Scholar] [CrossRef] [PubMed]
- Pu, L.; Xv, J.; Deng, F. An automatic method for tree species point cloud segmentation based on deep learning. J. Indian Soc. Remote Sens. 2021, 49, 2163–2172. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 16259–16268. [Google Scholar]
- Shu, J.; Zhang, C.; Yu, K.; Shooshtarian, M.; Liang, P. IFC-based semantic modeling of damaged RC beams using 3D point clouds. Struct. Concr. 2023, 24, 389–410. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, K.; Zhu, Y.; Wang, X.; Yun, T. Individual tree crown segmentation directly from UAV-borne LiDAR data using the PointNet of deep learning. Forests 2021, 12, 131. [Google Scholar] [CrossRef]
- Yun, T.; An, F.; Li, W.; Sun, Y.; Cao, L.; Xue, L. A Novel Approach for Retrieving Tree Leaf Area from Ground-Based LiDAR. Remote Sens. 2016, 8, 942. [Google Scholar] [CrossRef]
- Wang, D.; Momo Takoudjou, S.; Casella, E. LeWoS: A universal leaf-wood classification method to facilitate the 3D modelling of large tropical trees using terrestrial LiDAR. Methods Ecol. Evol. 2020, 11, 376–389. [Google Scholar] [CrossRef]
- Tang, S.; Ao, Z.; Li, Y.; Huang, H.; Xie, L.; Wang, R.; Wang, W.; Guo, R. TreeNet3D: A large scale tree benchmark for 3D tree modeling, carbon storage estimation and tree segmentation. Int. J. Appl. Earth Obs. Geoinf. 2024, 130, 103903. [Google Scholar] [CrossRef]
- Michałowska, M.; Rapiński, J.; Janicka, J. Tree position estimation from TLS data using hough transform and robust least-squares circle fitting. Remote Sens. Appl. Soc. Environ. 2023, 29, 100863. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar]
- Gan, Z.; Ma, B.; Ling, Z. PCA-based fast point feature histogram simplification algorithm for point clouds. Eng. Rep. 2024, 6, e12800. [Google Scholar] [CrossRef]
- Do, Q.-T.; Chang, W.-Y.; Chen, L.-W. Dynamic workpiece modeling with robotic pick-place based on stereo vision scanning using fast point-feature histogram algorithm. Appl. Sci. 2021, 11, 11522. [Google Scholar] [CrossRef]
- Özdemir, C. Avg-topk: A new pooling method for convolutional neural networks. Expert Syst. Appl. 2023, 223, 119892. [Google Scholar] [CrossRef]
- Tancik, M.; Srinivasan, P.; Mildenhall, B.; Fridovich-Keil, S.; Raghavan, N.; Singhal, U.; Ramamoorthi, R.; Barron, J.; Ng, R. Fourier features let networks learn high frequency functions in low dimensional domains. Adv. Neural Inf. Process. Syst. 2020, 33, 7537–7547. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; pp. 5998–6008. [Google Scholar]
- Zhang, R.; Wang, L.; Guo, Z.; Wang, Y.; Gao, P.; Li, H.; Shi, J. Parameter is not all you need: Starting from non-parametric networks for 3d point cloud analysis. arXiv 2023, arXiv:2303.08134. [Google Scholar]
- Yao, J.; Erichson, N.B.; Lopes, M.E. Error estimation for random Fourier features. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 25–27 April 2023; pp. 2348–2364. [Google Scholar]
- Ghojogh, B.; Crowley, M.; Karray, F.; Ghodsi, A. Uniform Manifold Approximation and Projection (UMAP). In Elements of Dimensionality Reduction and Manifold Learning; Springer International Publishing: Cham, Switzerland, 2023; pp. 479–497. [Google Scholar]
- Zhuang, Z.; Liu, M.; Cutkosky, A.; Orabona, F. Understanding AdamW through Proximal Methods and Scale-Freeness. arXiv 2022, arXiv:2202.00089. [Google Scholar]
- Ran, H.; Liu, J.; Wang, C. Surface representation for point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18942–18952. [Google Scholar]
- Wang, Z.; Yu, X.; Rao, Y.; Zhou, J.; Lu, J. Take-a-photo: 3d-to-2d generative pre-training of point cloud models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 5640–5650. [Google Scholar]
- Zeid, K.A.; Schult, J.; Hermans, A.; Leibe, B. Point2vec for self-supervised representation learning on point clouds. In Proceedings of the DAGM German Conference on Pattern Recognition, Heidelberg, Germany, 19–22 September 2023; pp. 131–146. [Google Scholar]
- Owen Melia, E.J. Rotation-Invariant Random Features Provide a Strong Baseline for Machine Learning on 3D Point Cloud. arXiv 2023, arXiv:2308.06271. [Google Scholar]
- Mei, J.; Zhang, L.Q.; Wu, S.H.; Wang, Z.; Zhang, L. 3D tree modeling from incomplete point clouds via optimization and L-1-MST. Int. J. Geogr. Inf. Sci. 2017, 31, 999–1021. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Fan, G.; Nan, L.; Dong, Y.; Su, X.; Chen, F. AdQSM: A new method for estimating above-ground biomass from TLS point clouds. Remote Sens. 2020, 12, 3089. [Google Scholar] [CrossRef]
- Åkerblom, M.; Raumonen, P.; Casella, E.; Disney, M.I.; Danson, F.M.; Gaulton, R.; Schofield, L.A.; Kaasalainen, M. Non-intersecting leaf insertion algorithm for tree structure models. Interface Focus 2018, 8, 20170045. [Google Scholar] [CrossRef]
- Wang, Y.; Rong, Q.; Hu, C. Ripe Tomato Detection Algorithm Based on Improved YOLOv9. Plants 2024, 13, 3253. [Google Scholar] [CrossRef]
- Chi, Y.; Wang, C.; Chen, Z.; Xu, S. TCSNet: A New Individual Tree Crown Segmentation Network from Unmanned Aerial Vehicle Images. Forests 2024, 15, 1814. [Google Scholar] [CrossRef]
- Fischer, K.; Simon, M.; Olsner, F.; Milz, S.; Gross, H.-M.; Mader, P. Stickypillars: Robust and efficient feature matching on point clouds using graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 313–323. [Google Scholar]
- Cui, Y.; Zhang, Y.; Dong, J.; Sun, H.; Chen, X.; Zhu, F. Link3d: Linear keypoints representation for 3d lidar point cloud. IEEE Robot. Autom. Lett. 2024, 9, 2128–2135. [Google Scholar] [CrossRef]
- Bornand, A.; Abegg, M.; Morsdorf, F.; Rehush, N. Completing 3D point clouds of individual trees using deep learning. Methods Ecol. Evol. 2024, 15, 2010–2023. [Google Scholar] [CrossRef]
- Ge, B.; Chen, S.; He, W.; Qiang, X.; Li, J.; Teng, G.; Huang, F. Tree Completion Net: A Novel Vegetation Point Clouds Completion Model Based on Deep Learning. Remote Sens. 2024, 16, 3763. [Google Scholar] [CrossRef]
- Wang, Q.; Fan, X.; Zhuang, Z.; Tjahjadi, T.; Jin, S.; Huan, H.; Ye, Q. One to All: Toward a Unified Model for Counting Cereal Crop Heads Based on Few-Shot Learning. Plant Phenomics 2024, 6, 0271. [Google Scholar] [CrossRef] [PubMed]



| Private Dataset | Public Dataset | ||||
|---|---|---|---|---|---|
| Rubber Tree Plantations | Mixed Forest | Urban Forest | LeWoS | TreeNet3D (Flamboyant Tree) | |
| Type | TLS | TLS | ALS | TLS | Synthetic |
| Age (Years) | 10 | 15 | 10 | - | - |
| Quantity (Training / Test) | 285/122 | 167/70 | 66/28 | 43/18 | 490/210 |
| Avg. Height (m) | 9.72 | 11.65 | 11.86 | 33.7 | 133.19 |
| Avg. Diameter at Breast Height (cm) | 16.7 | 23.46 | 31.08 | 58.4 | 359 |
| Avg. Crown Width (m) (N–S)/ (E–W) | 2.91/3.74 | 3.05/3.11 | 6.82/7.12 | 14.0/14.57 | 102.89/104.03 |
| Density (m) | 0.02 | 0.13 | 0.06 | 0.05 | 0.01 |
| Data Size (GB) | 10.8 | 1.2 | 0.4 | 10.4 | 47.6 |
| Local Surface Features | PosE (in FA) | PosE (in PTB) | NPTB | Precision (%) | mIoU (%) | Time (s/per Tree) |
|---|---|---|---|---|---|---|
| × | × | × | 10 | 87.31 | 79.07 | 2.90 |
| × | √ | × | 10 | 89.01 | 81.27 | 3.25 |
| × | × | √ | 10 | 89.14 | 81.35 | 3.28 |
| × | √ | √ | 10 | 91.13 | 82.77 | 4.07 |
| √ | × | × | 10 | 89.21 | 81.52 | 3.32 |
| √ | √ | × | 10 | 91.34 | 83.00 | 4.08 |
| √ | × | √ | 10 | 91.52 | 83.32 | 3.99 |
| √ | √ | √ | 6 | 91.06 | 83.01 | 3.86 |
| √ | √ | √ | 8 | 92.59 | 83.81 | 4.30 |
| √ | √ | √ | 12 | 92.62 | 83.93 | 5.17 |
| √ | √ | √ | 14 | 91.35 | 81.80 | 5.68 |
| √ | √ | √ | 10 | 94.36 | 85.48 | 4.62 |
| Position Encoding | Precision (%) | mIoU (%) | Time (s/per Tree) |
|---|---|---|---|
| none | 83.02 | 76.29 | 2.76 |
| absolute | 85.34 | 78.67 | 2.89 |
| relative | 89.21 | 81.52 | 3.32 |
| relative for attention | 86.17 | 78.60 | 3.36 |
| relative for feature | 87.44 | 79.65 | 3.93 |
| PosE | 94.36 | 85.48 | 4.62 |
| Rubber Tree Plantations | Mixed Forest | Urban Forest | LeWoS | TreeNet3D | ||
|---|---|---|---|---|---|---|
| Machine learning [30] | Precision (%) | 84.94 | 71.01 | 85.02 | 85.87 | 86.47 |
| mIoU (%) | 74.01 | 63.69 | 75.31 | 75.92 | 77.86 | |
| PointNet++ [21] | Precision (%) | 86.34 | 71.99 | 87.33 | 87.83 | 88.23 |
| mIoU (%) | 75.96 | 65.19 | 77.43 | 78.21 | 80.19 | |
| PSegNet [20] | Precision (%) | 89.97 | 75.81 | 90.23 | 90.79 | 91.97 |
| mIoU (%) | 80.69 | 69.19 | 82.99 | 83.27 | 85.01 | |
| PT [26] | Precision (%) | 89.71 | 75.00 | 89.91 | 90.26 | 91.70 |
| mIoU (%) | 80.99 | 68.92 | 81.31 | 82.94 | 85.00 | |
| RepSurf-U [44] | Precision (%) | 89.22 | 74.43 | 89.24 | 89.95 | 91.33 |
| mIoU (%) | 79.01 | 66.94 | 79.01 | 79.50 | 84.75 | |
| PointNeXt [22] | Precision (%) | 89.50 | 74.81 | 89.65 | 90.41 | 91.58 |
| mIoU (%) | 80.97 | 68.89 | 81.32 | 81.79 | 83.06 | |
| PointMLP + TAP [45] | Precision (%) | 92.11 | 78.09 | 91.55 | 91.90 | 92.44 |
| mIoU (%) | 84.41 | 71.26 | 84.52 | 84.93 | 86.07 | |
| Point2vec [46] | Precision (%) | 89.47 | 74.69 | 89.60 | 90.71 | 92.06 |
| mIoU (%) | 80.66 | 68.48 | 81.00 | 82.85 | 85.77 | |
| Enhanced PT | Precision (%) | 94.69 | 80.43 | 94.88 | 95.31 | 96.23 |
| mIoU (%) | 86.65 | 73.51 | 86.76 | 87.02 | 91.51 | |
| Rubber Tree Plantations | Mixed Forest | Urban Forest | LeWos | TreeNet3D | |
|---|---|---|---|---|---|
| Avg. Height (m) | 9.38 | 10.75 | 11.10 | 31.5 | 126.91 |
| Avg. Diameter at Breast Height (cm) | 16.1 | 22.16 | 30.18 | 56.4 | 342 |
| Avg. Crown Width (m) (N–S)/(E–W) | 2.32/3.01 | 2.83/2.99 | 6.32/6.87 | 13.4/13.01 | 97.94/99.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Wang, R.; Zhang, H.; Zhou, J.; Yun, T. PosE-Enhanced Point Transformer with Local Surface Features (LSF) for Wood–Leaf Separation. Forests 2024, 15, 2244. https://doi.org/10.3390/f15122244
Lu X, Wang R, Zhang H, Zhou J, Yun T. PosE-Enhanced Point Transformer with Local Surface Features (LSF) for Wood–Leaf Separation. Forests. 2024; 15(12):2244. https://doi.org/10.3390/f15122244
Chicago/Turabian StyleLu, Xin, Ruisheng Wang, Huaiqing Zhang, Ji Zhou, and Ting Yun. 2024. "PosE-Enhanced Point Transformer with Local Surface Features (LSF) for Wood–Leaf Separation" Forests 15, no. 12: 2244. https://doi.org/10.3390/f15122244
APA StyleLu, X., Wang, R., Zhang, H., Zhou, J., & Yun, T. (2024). PosE-Enhanced Point Transformer with Local Surface Features (LSF) for Wood–Leaf Separation. Forests, 15(12), 2244. https://doi.org/10.3390/f15122244









