Preliminary Insights on Moisture Content Measurement in Square Timbers Using GPR Signals and 1D-CNN Models
Abstract
1. Introduction
2. Materials and Methods
2.1. GPR Data Acquisition
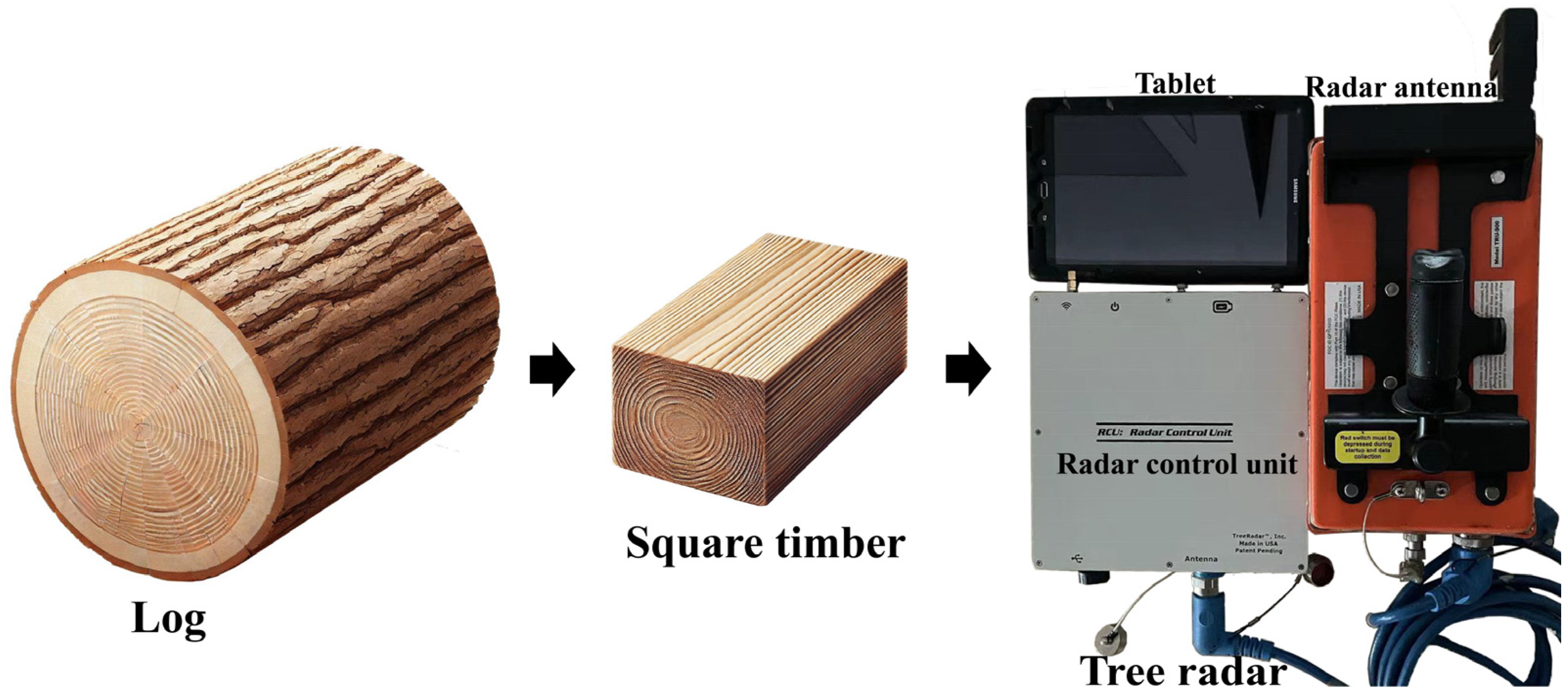
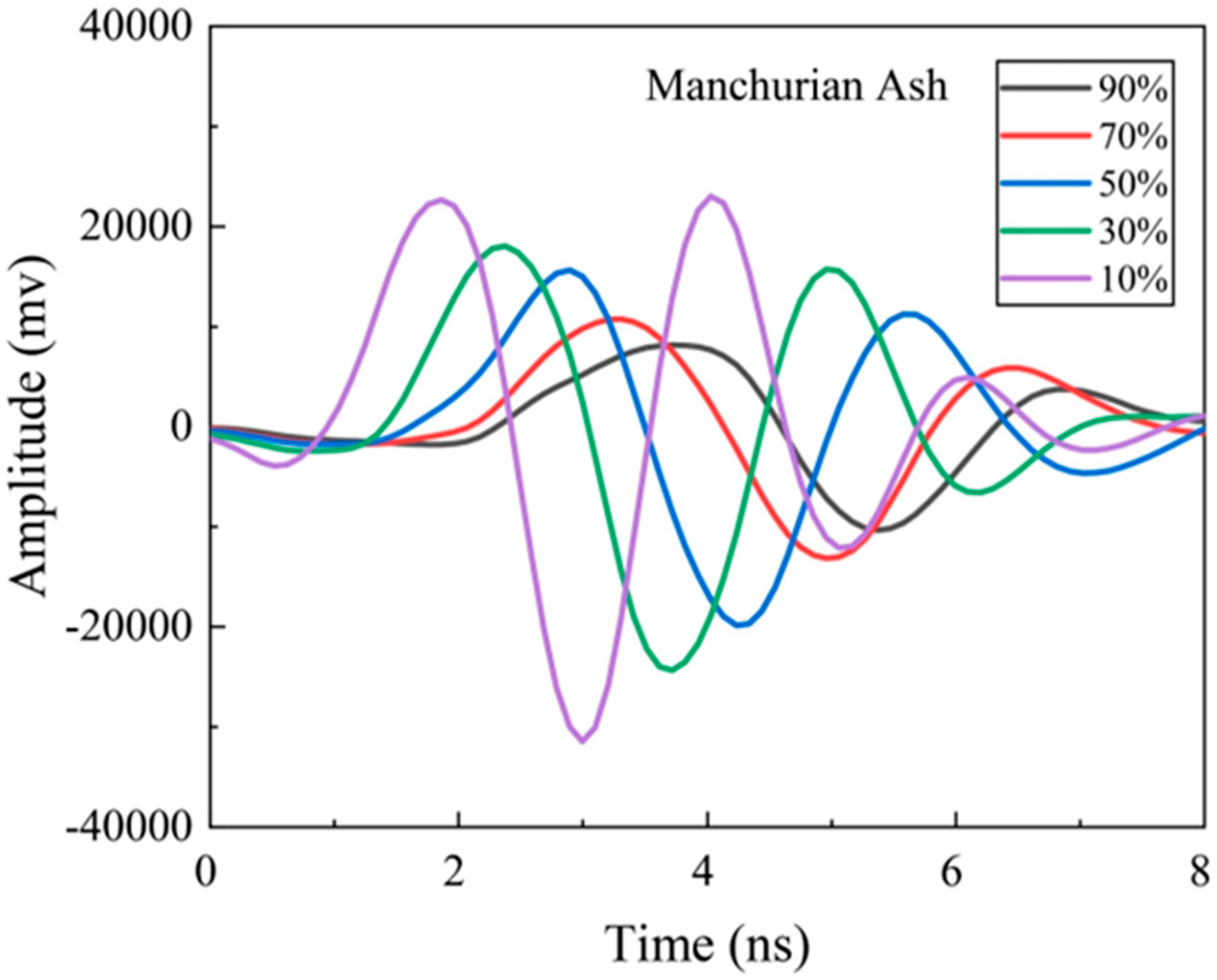
2.2. Signal Feature Analysis
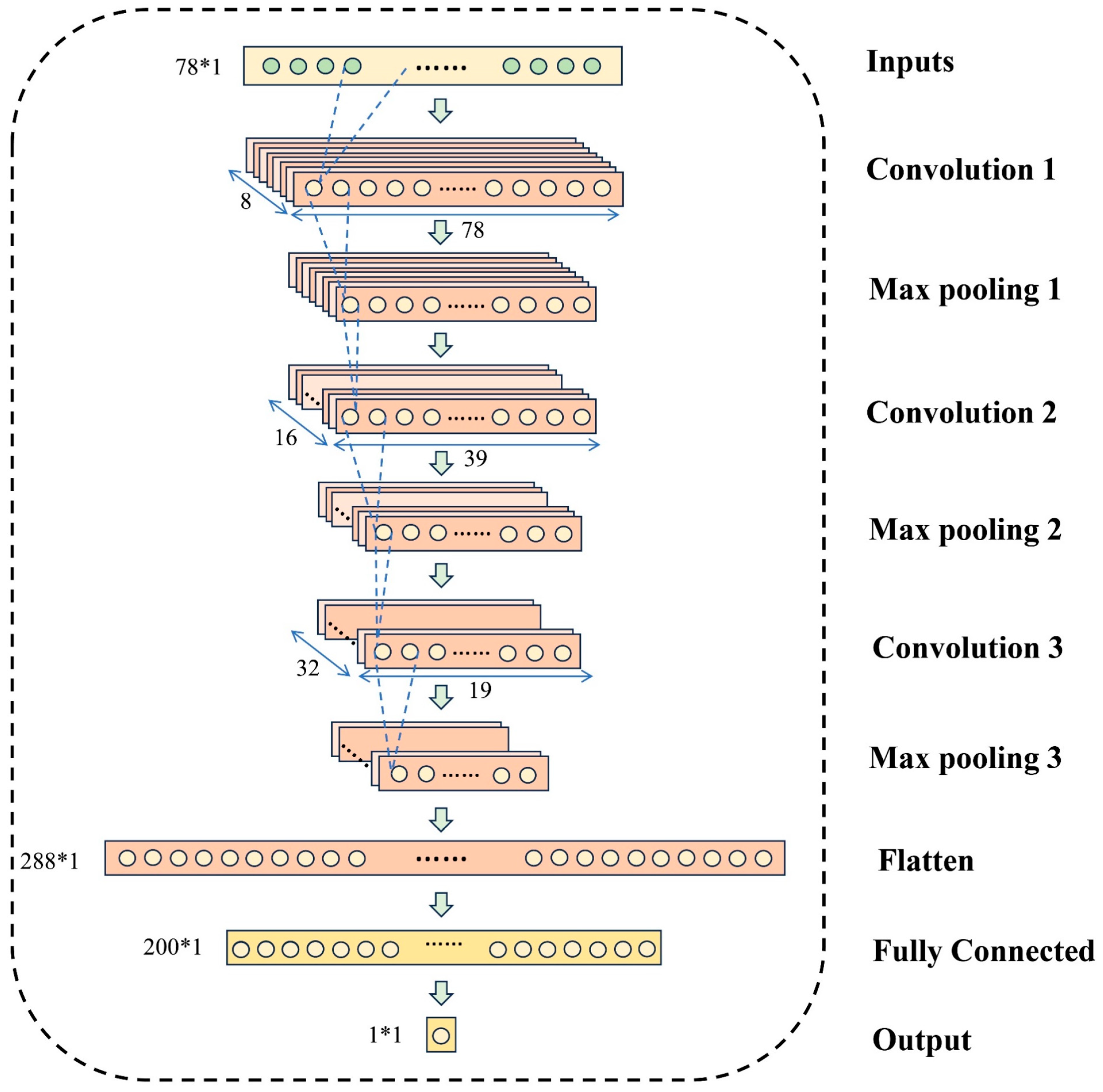
2.3. 1D-CNN Model Construction
| Category | Dataset | Min (%) | Max (%) | Mean (%) | Median (%) | Std (%) | Number |
|---|---|---|---|---|---|---|---|
| Mixed-species | All selected set | 0 | 133.1 | 53.5 | 51 | 34.2 | 2208 |
| Training set | 0 | 133.1 | 53.5 | 51 | 34.4 | 1545 | |
| Testing set | 0 | 133.1 | 53.7 | 51 | 33.8 | 663 | |
| Red spruce | All selected set | 0 | 106.8 | 50.4 | 49.0 | 31.4 | 568 |
| Training set | 0 | 106.8 | 50.2 | 48.9 | 32.2 | 397 | |
| Testing set | 0 | 104.1 | 51.1 | 49.1 | 29.5 | 171 | |
| Dahurian larch | All selected set | 0 | 107 | 46.4 | 44.4 | 30.6 | 404 |
| Training set | 0 | 107 | 46.1 | 44.4 | 29.9 | 283 | |
| Testing set | 0 | 107 | 47.1 | 44.4 | 32.2 | 122 | |
| White birch | All selected set | 0 | 133.1 | 61.7 | 60.5 | 39.2 | 596 |
| Training set | 0 | 133.1 | 61.7 | 59.2 | 38.4 | 417 | |
| Testing set | 0 | 133.1 | 61.6 | 61.3 | 41.1 | 179 | |
| Manchurian ash | All selected set | 0 | 110.6 | 53.2 | 51.7 | 32.3 | 640 |
| Training set | 0 | 110.6 | 52.9 | 51 | 32.2 | 448 | |
| Testing set | 0 | 110.6 | 53.8 | 51.7 | 32.8 | 192 |
2.4. Comparative Analysis of Different Algorithms for Time–Frequency Parameters and Full-Waveform Amplitude Based on GPR Signals
2.5. Square Timber MC Models for Different Tree Species
3. Result and Discussion
3.1. Construction of 1D-CNN for Mixed-Species Trees
3.2. Comparison of Different Algorithms for Time–Frequency Parameters and Full-Waveform Amplitude from GPR Signals
3.3. D-CNN Model Construction for Different Tree Species
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Forsén, H.; Tarvainen, V. Accuracy and Functionality of Hand Held Wood Moisture Content Meters; Technical Research Centre of Finland: Espoo, Finland, 2000; pp. 2–79. [Google Scholar]
- Redman, J.; Hans, G.; Diamanti, N. Impact of Wood Sample Shape and Size on Moisture Content Measurement Using a GPR-Based Sensor. IEEE J.-STARS 2016, 9, 221–227. [Google Scholar] [CrossRef]
- Guo, J.; Wang, P.; Qin, R.; Zhao, L.; Tang, X.; Zeng, J.; Xu, H. Detection of moisture content in logs using multi-parameter GPR signal analysis and neural network models. Holzforschung 2023, 77, 240–247. [Google Scholar] [CrossRef]
- Gereke, T.; Hass, P.; Niemz, P. Moisture-induced stresses and distortions in spruce cross-laminates and composite laminates. Holzforschung 2010, 64, 127–133. [Google Scholar] [CrossRef]
- Hänsel, A.; Sandak, J.; Sandak, A.; Mai, J.; Niemz, P. Selected previous findings on the factors influencing the gluing quality of solid wood products in timber construction and possible developments: A review. Wood Mater. Sci. Eng. 2022, 17, 230–241. [Google Scholar] [CrossRef]
- Govett, R.; Mace, T.; Bowe, S. A Practical Guide for the Determination of Moisture Content of Woody Biomass; University of Wisconsin: Madison, WI, USA, 2010; Volume 20. [Google Scholar]
- Dietsch, P.; Franke, S.; Franke, B.; Gamper, A.; Winter, S. Methods to determine wood moisture content and their applicability in monitoring concepts. J. Civ. Struct. Health Monit. 2015, 5, 115–127. [Google Scholar] [CrossRef]
- Dahlen, J.; Schimleck, L.; Schilling, E. Modeling and Monitoring of Wood Moisture Content Using Time-Domain Reflectometry. Forests 2020, 11, 479. [Google Scholar] [CrossRef]
- Dos Santos, L.M.; Amaral, E.A.; Nieri, E.M.; Costa, E.V.S.; Trugilho, P.F.; Calegário, N.; Hein, P.R.G. Estimating wood moisture by near infrared spectroscopy: Testing acquisition methods and wood surfaces qualities. Wood Mater. Sci. Eng. 2021, 16, 336–343. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, B.; Sandhu, B.S. A gamma-ray scattering technique for estimation of density and moisture content of wood. Radiat. Eff. Defects Solids 2017, 172, 286–295. [Google Scholar] [CrossRef]
- He, X.; Qi, D. Density and moisture content forecasting based on X-ray computed tomography. Eur. J. Wood Wood Prod. 2013, 71, 647–652. [Google Scholar] [CrossRef]
- Wolter, B.; Krus, M. Moisture Measuring with Nuclear Magnetic Resonance (NMR). In Electromagnetic Aquametry: Electromagnetic Wave Interaction with Water and Moist Substances; Kupfer, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 491–515. [Google Scholar]
- Pajewski, L.; Benedetto, A.; Derobert, X.; Giannopoulos, A.; Loizos, A.; Manacorda, G.; Marciniak, M.; Plati, C.; Schettini, G.; Trinks, I. Applications of Ground Penetrating Radar in civil engineering—COST action TU1208. In Proceedings of the 2013 7th International Workshop on Advanced Ground Penetrating Radar, Nantes, France, 2–5 July 2013; pp. 1–6. [Google Scholar]
- Zhang, J.; Zhang, C.; Lu, Y.; Zheng, T.; Dong, Z.; Tian, Y.; Jia, Y. In-situ recognition of moisture damage in bridge deck asphalt pavement with time-frequency features of GPR signal. Constr. Build. Mater. 2020, 244, 118295. [Google Scholar] [CrossRef]
- Sbartaï, Z.M.; Laurens, S.; Balayssac, J.P.; Arliguie, G.; Ballivy, G. Ability of the direct wave of radar ground-coupled antenna for NDT of concrete structures. NDT&E Int. 2006, 39, 400–407. [Google Scholar]
- Li, F.; Yang, F.; Qiao, X.; Hu, Z.; Wu, X.; Xing, H. 3D ground penetrating radar road underground target identification algorithm using time-frequency statistical features of data. NDT&E Int. 2023, 137, 102860. [Google Scholar]
- Shirmohammadi, M.; Leggate, W.; Redman, A. Effects of moisture ingress and egress on the performance and service life of mass timber products in buildings: A review. Constr. Build. Mater. 2021, 290, 123176. [Google Scholar] [CrossRef]
- Mai, T.C.; Razafindratsima, S.; Sbartaï, Z.M.; Demontoux, F.; Bos, F. Non-destructive evaluation of moisture content of wood material at GPR frequency. Constr. Build. Mater. 2015, 77, 213–217. [Google Scholar] [CrossRef]
- Rodríguez-Abad, I.; Martínez-Sala, R.; García-García, F.; Capuz-Lladró, R. Ability of the Direct Wave Amplitude of Ground-penetrating Radar for Assessing the Moisture Content Variation of Timber. In Proceedings of the 16th EAGE European Meeting of Environmental and Engineering Geophysics, Zurich, Switzerland, 6–8 September 2010; pp. 2214–4609. [Google Scholar]
- Rodríguez-Abad, I.; Martínez-Sala, R.; García-García, F.; Capuz-Lladró, R. Non-destructive methodologies for the evaluation of moisture content in sawn timber structures: Ground-penetrating radar and ultrasound techniques. Near Surf. Geophys. 2010, 8, 475–482. [Google Scholar] [CrossRef]
- Marques Duarte da Paz, A.M. Water Content Measurement in Woody Biomass: Using Dielectric Constant at Radio Frequencies. Ph.D. Thesis, Mälardalen University, Västerås, Sweden, 2008. [Google Scholar]
- Hans, G.; Redman, D.; Leblon, B.; Nader, J.; La Rocque, A. Determination of log moisture content using early-time ground penetrating radar signal. Wood Mater. Sci. Eng. 2015, 10, 112–129. [Google Scholar] [CrossRef]
- Zhang, W.; Yan, J.; Yan, Y. Measurement of the moisture content in woodchips through capacitive sensing and data driven modelling. Measurement 2021, 186, 110205. [Google Scholar] [CrossRef]
- Zheng, S.; Gao, P.; Wang, W.; Zou, X. A Highly Accurate Forest Fire Prediction Model Based on an Improved Dynamic Convolutional Neural Network. Appl. Sci. 2022, 12, 6721. [Google Scholar] [CrossRef]
- You, X.; Zheng, Z.; Yang, K.; Yu, L.; Liu, J.; Chen, J.; Lu, X.; Guo, S. A PSO-CNN-Based Deep Learning Model for Predicting Forest Fire Risk on a National Scale. Forests 2024, 15, 86. [Google Scholar] [CrossRef]
- Egli, S.; Höpke, M. CNN-Based Tree Species Classification Using High Resolution RGB Image Data from Automated UAV Observations. Remote Sens. 2020, 12, 3892. [Google Scholar] [CrossRef]
- Jiao, L.; Dong, S.; Zhang, S.; Xie, C.; Wang, H. AF-RCNN: An anchor-free convolutional neural network for multi-categories agricultural pest detection. Comput. Electron. Agric. 2020, 174, 105522. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Hamila, R.; Gabbouj, M. Convolutional Neural Networks for patient-specific ECG classification. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 2608–2611. [Google Scholar]
- Zheng, J.; Teng, X.; Liu, J.; Qiao, X. Convolutional Neural Networks for Water Content Classification and Prediction with Ground Penetrating Radar. IEEE Access 2019, 7, 185385–185392. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J.; Sun, W. Recognition of the Typical Distress in Concrete Pavement Based on GPR and 1D-CNN. Remote Sens. 2021, 13, 2375. [Google Scholar] [CrossRef]
- Ferrara, C.; Barone, P.M.; Steelman, C.M.; Pettinelli, E.; Endres, A.L. Monitoring Shallow Soil Water Content Under Natural Field Conditions Using the Early-Time GPR Signal Technique. Vadose Zone J. 2013, 12, vzj2012.0202. [Google Scholar] [CrossRef]
- Su, H.; Shen, W.; Wang, J.; Ali, A.; Li, M. Machine learning and geostatistical approaches for estimating aboveground biomass in Chinese subtropical forests. For. Ecosyst. 2020, 7, 64. [Google Scholar] [CrossRef]
- Shin, J.; Temesgen, H.; Strunk, J.L.; Hilker, T. Comparing modeling methods for predicting forest attributes using LiDAR metrics and ground measurements. Can. J. Remote Sens. 2016, 42, 739–765. [Google Scholar] [CrossRef]
- Zheng, Y.; Huang, J.; Chen, T.; Ou, Y.; Zhou, W. CNN classification based on global and local features. In Proceedings of the Real-Time Image Processing and Deep Learning 2019, Baltimore, MD, USA, 14–18 April 2019; pp. 96–108. [Google Scholar]


| Time Domain Parameters | Frequency Domain Parameters | ||||
|---|---|---|---|---|---|
| Name | Explanation | Name | Explanation | Name | Explanation |
| Maximum | Standard deviation | Amplitude average | |||
| Minimum | Skewness coefficient | Amplitude standard deviation | |||
| Mean | Kurtosis coefficient | Sample Skewness | |||
| Average absolute value | Peak factor | Sample Kurtosis | |||
| Peak-to-peak value | Peak-to-mean ratio | Frequency mean | |||
| Variance | Form factor | Frequency standard deviation | |||
| Skewness | Amplitude factor | Frequency Root Mean Square | |||
| Kurtosis | Frequency Fourth Root Mean Square | ||||
| Root mean square | Frequency Band Index | ||||
| Mean square amplitude | Frequency Bandwidth Index | ||||
| Total energy | Frequency skewness | ||||
| Average energy | Frequency kurtosis | ||||
| Parameter Class | Model | Hyperparameter Values | Testing Set | Training Set | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |||
| Full waveform amplitude | 1D-CNN | epochs = 300, batch_size = 16. | 0.9864 | 0.0393 | 0.0298 | 0.9907 | 0.0332 | 0.0255 |
| RF | n_estimators:900, max_depth: 9. | 0.9799 | 0.0479 | 0.0329 | 0.9972 | 0.0181 | 0.0122 | |
| KNN | n_neighbors: 3. | 0.9837 | 0.0430 | 0.0265 | 0.9945 | 0.0253 | 0.0151 | |
| BPNN | hidden_layer: (30,15) activation: relu. | 0.9686 | 0.0598 | 0.0446 | 0.9792 | 0.0496 | 0.0378 | |
| PLS | n_components: 14. | 0.9111 | 0.1006 | 0.0785 | 0.9189 | 0.0980 | 0.0755 | |
| Time–frequency domain parameters | RF | n_estimators:300, max_depth:9. | 0.9382 | 0.0840 | 0.0589 | 0.9917 | 0.0314 | 0.0224 |
| KNN | n_neighbors: 5. | 0.9254 | 0.0922 | 0.0620 | 0.9528 | 0.0747 | 0.0490 | |
| BPNN | hidden_layer: (20) activation: tanh. | 0.9130 | 0.0994 | 0.0748 | 0.9336 | 0.0886 | 0.0666 | |
| PLS | n_components: 14. | 0.8469 | 0.1345 | 0.1060 | 0.8543 | 0.1289 | 0.1013 | |
| Category | Hyperparameter Values | Testing Set | Training Set | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| Red spruce | epochs = 300, batch_size = 4. | 0.9902 | 0.0320 | 0.0263 | 0.9915 | 0.0284 | 0.0225 |
| Dahurian larch | epochs = 300, batch_size = 4. | 0.9876 | 0.0358 | 0.0282 | 0.9893 | 0.0310 | 0.0242 |
| European white birch | epochs = 300, batch_size = 8. | 0.9930 | 0.0343 | 0.0269 | 0.9942 | 0.0291 | 0.0237 |
| Manchurian ash | epochs = 300, batch_size = 4. | 0.9931 | 0.0271 | 0.0215 | 0.9939 | 0.0251 | 0.0197 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Xu, H.; Zhong, Y.; Yu, K. Preliminary Insights on Moisture Content Measurement in Square Timbers Using GPR Signals and 1D-CNN Models. Forests 2024, 15, 1800. https://doi.org/10.3390/f15101800
Guo J, Xu H, Zhong Y, Yu K. Preliminary Insights on Moisture Content Measurement in Square Timbers Using GPR Signals and 1D-CNN Models. Forests. 2024; 15(10):1800. https://doi.org/10.3390/f15101800
Chicago/Turabian StyleGuo, Jiaxing, Huadong Xu, Yan Zhong, and Kuanjie Yu. 2024. "Preliminary Insights on Moisture Content Measurement in Square Timbers Using GPR Signals and 1D-CNN Models" Forests 15, no. 10: 1800. https://doi.org/10.3390/f15101800
APA StyleGuo, J., Xu, H., Zhong, Y., & Yu, K. (2024). Preliminary Insights on Moisture Content Measurement in Square Timbers Using GPR Signals and 1D-CNN Models. Forests, 15(10), 1800. https://doi.org/10.3390/f15101800





