Leaf Moisture Content Detection Method Based on UHF RFID and Hyperdimensional Computing
Abstract
1. Introduction
2. Methodology
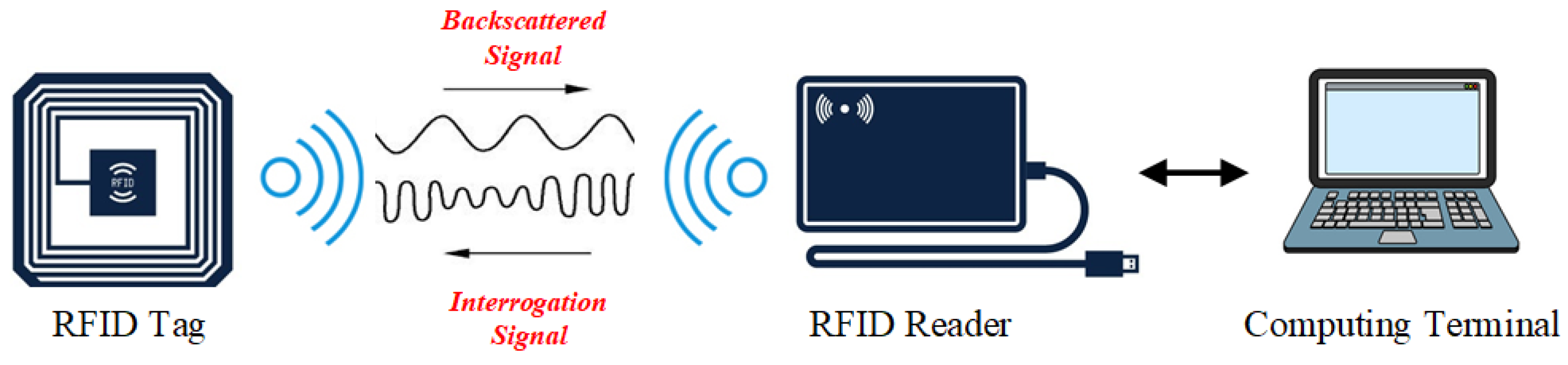
2.1. UHF RFID Communication Technology
- Read/Write Distance: Under ideal conditions, as indicated by (1), the received signal power at the antenna is directly influenced by the transmission distance. Considering real-world application scenarios, particularly in complex forest environments, the read/write distance cannot be considered a constant value. Therefore, it is essential to include read/write distance as a key indicator.
- RSSI: (1) represents the transmission under ideal conditions. When considering the insertion of a medium (in this study, leaves with different moisture content), we introduce a loss or gain factor caused by the presence of an object in the transmission path, as shown below:where represents the received power at the antenna after accounting for the losses in the actual environment, represents the attenuation due to the object, which includes the penetration loss caused by the blocking or transmission of electromagnetic waves and the absorption loss due to the object. This type of loss is typically challenging to quantify in real-world environments. The backscattered signal strength RSSI through the tag represents the loss of the signal during the transmission process. The relationship between RSSI and signal power is as follows:
- Phase: During the transmission process, due to the signal transmission characteristics of RFID, the total distance traveled by the radio-frequency signal during transmission is 2 d. The phase of the radio-frequency signal is also changing, which can be expressed as follows:
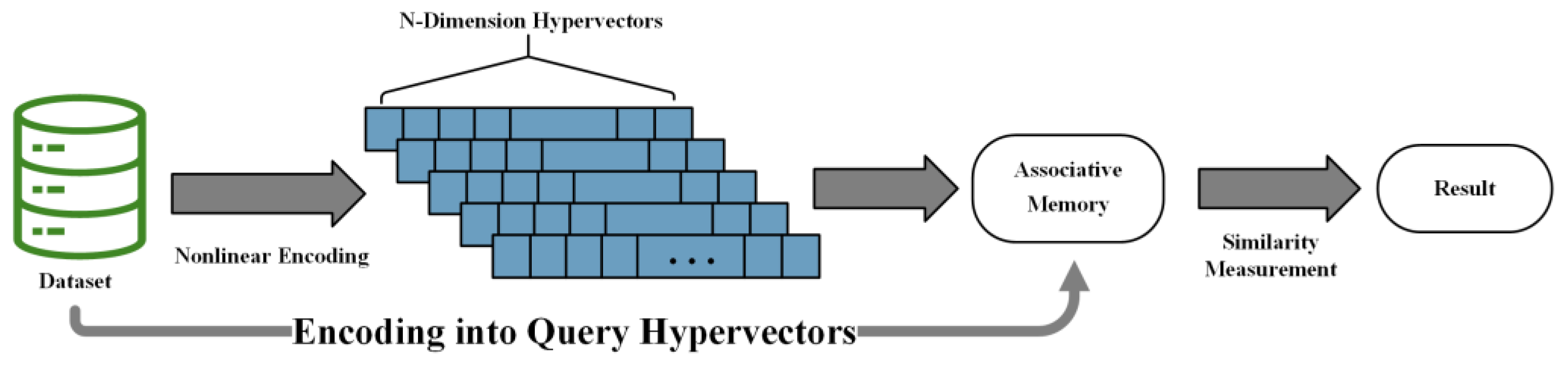
2.2. Hyperdimensional Computing
2.2.1. Hyperdimensional Characteristics of HDC
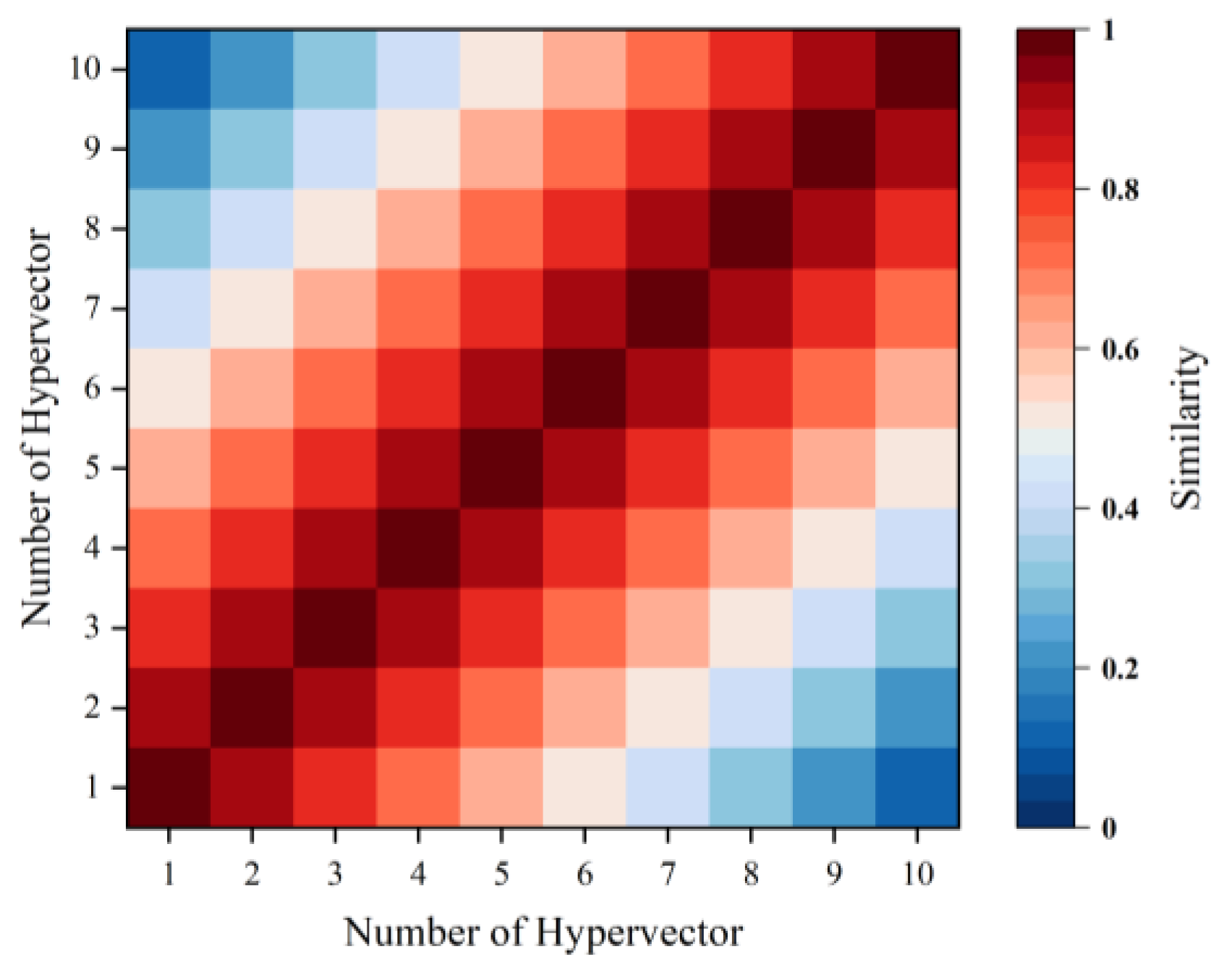
2.2.2. Similarity Criterion
2.2.3. Hyperdimensional Vector Operational Method
- Addition: Element-wise addition, also known as bundling operation, functions analogously to a majority vote mechanism. In this operation, when multiple hypervectors are added together, the element at each corresponding position in the newly generated hypervector is determined by the most frequently occurring element among all vectors at that position. The addition operation of three hypervectors using binary encoding is as follows:
- Multiplication: Element-wise multiplication, also referred to as binding, is primarily employed to establish an association between two hypervectors, such as binding a data value to its corresponding address. In the context of HDC, for hypervectors encoded in binary, element-wise multiplication is equivalent to the bitwise exclusive OR (XOR) operation, denoted by the symbol ⊕. When two vectors undergo multiplication, their corresponding elements are subjected to XOR, resulting in a new hypervector. In (9), we demonstrate the multiplication of two binary-coded hypervectors.
- Permutation: In the realm of HDC, the permutation constitutes a distinctive computational procedure. This operation systematically reorganizes the elements of a hypervector through a predefined transformation schema. To capitalize on the hardware-compatibility benefits intrinsic to HDC, permutations are typically executed via cyclic shifting mechanisms, denoted by the symbol Π. The 8-dimensional binary hypervector A is arranged as follows:
2.3. Encoding
- Randomly generate a binary hypervector as the encoded minimum value, also referred to as the initial hypervector.
- Randomly flip d/2/(L−1) bits of the hypervector corresponding to the previous encoded value to encode the next hypervector, ensuring that each bit is flipped only once and not repeatedly.
- Repeat step 2 until all L values are encoded into hypervectors.
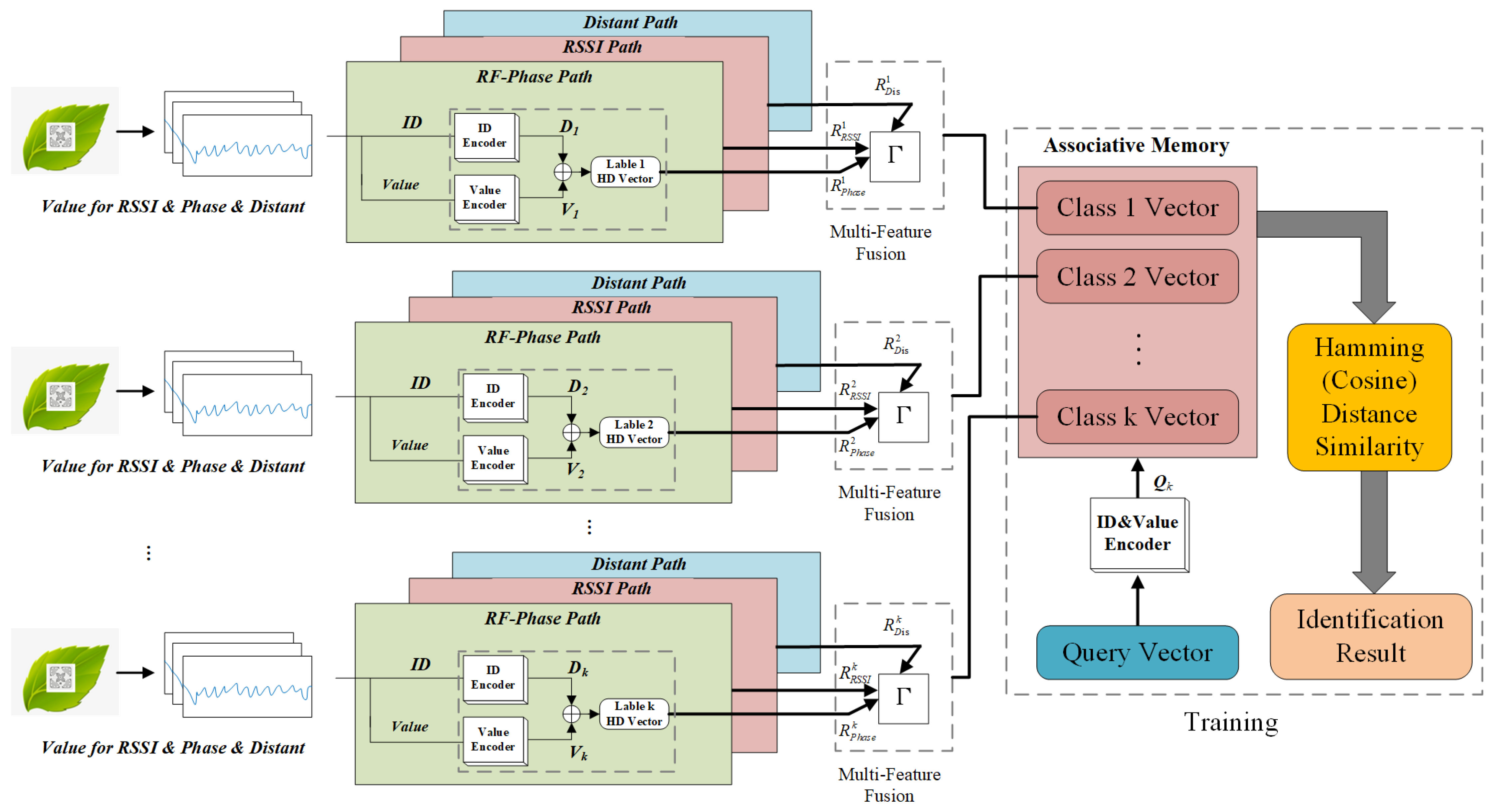
2.4. Multi-Feature Fusion
2.5. Re-Training
3. Experiment Methodology
3.1. Leaf Moisture Data Acquisition
3.2. Evaluation Metrics
4. Result and Discussion
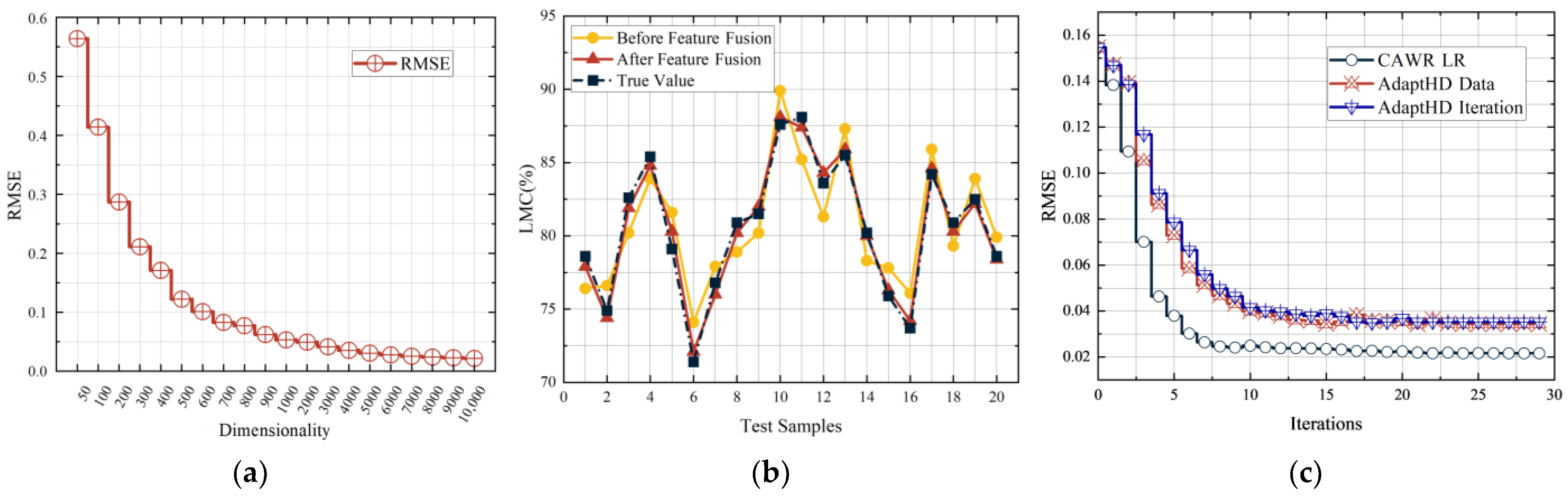
4.1. Paramaters Determined
4.2. Experimental Comparison before and after Multi-Feature Fusion
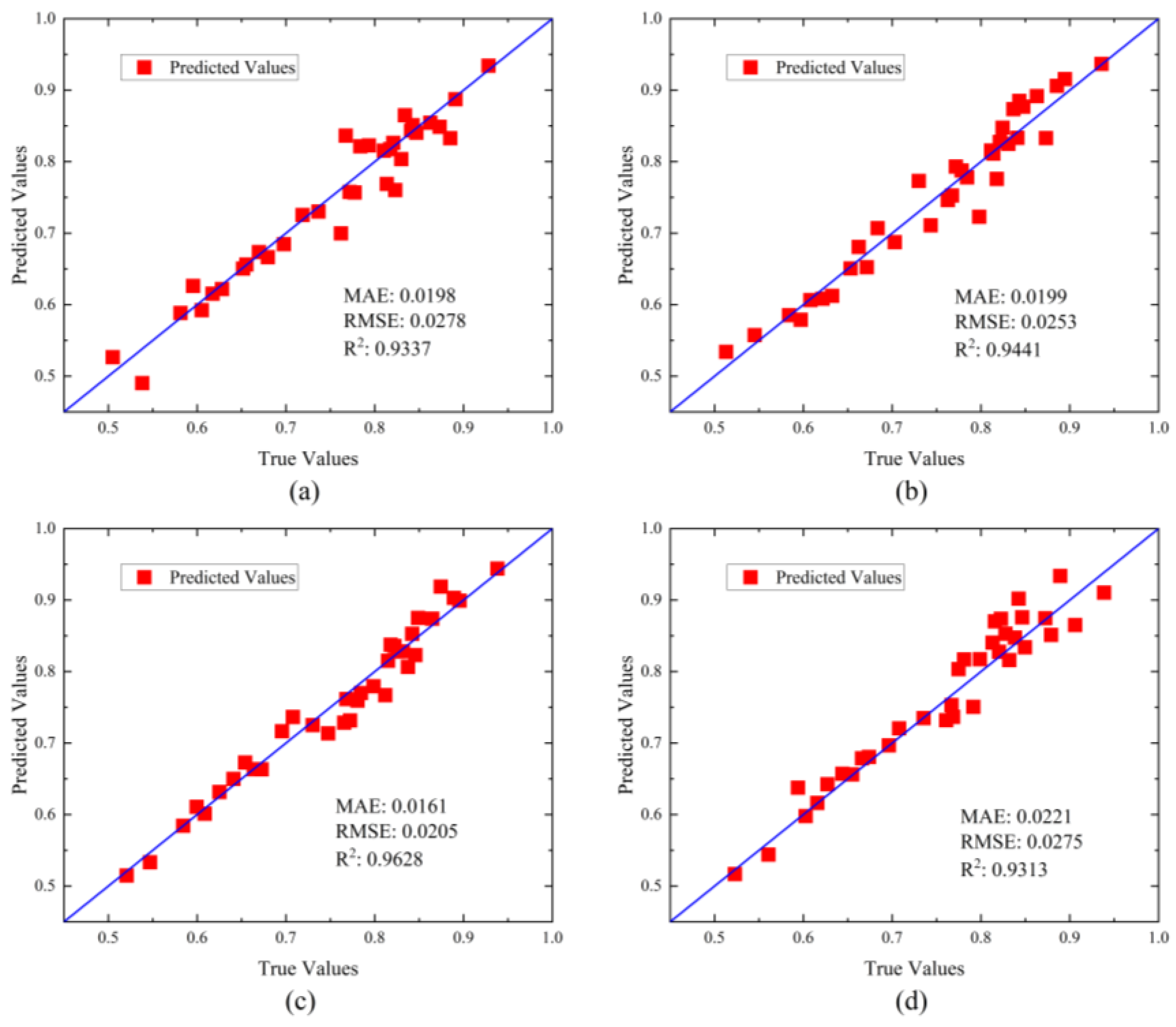
4.3. Re-Training Methods
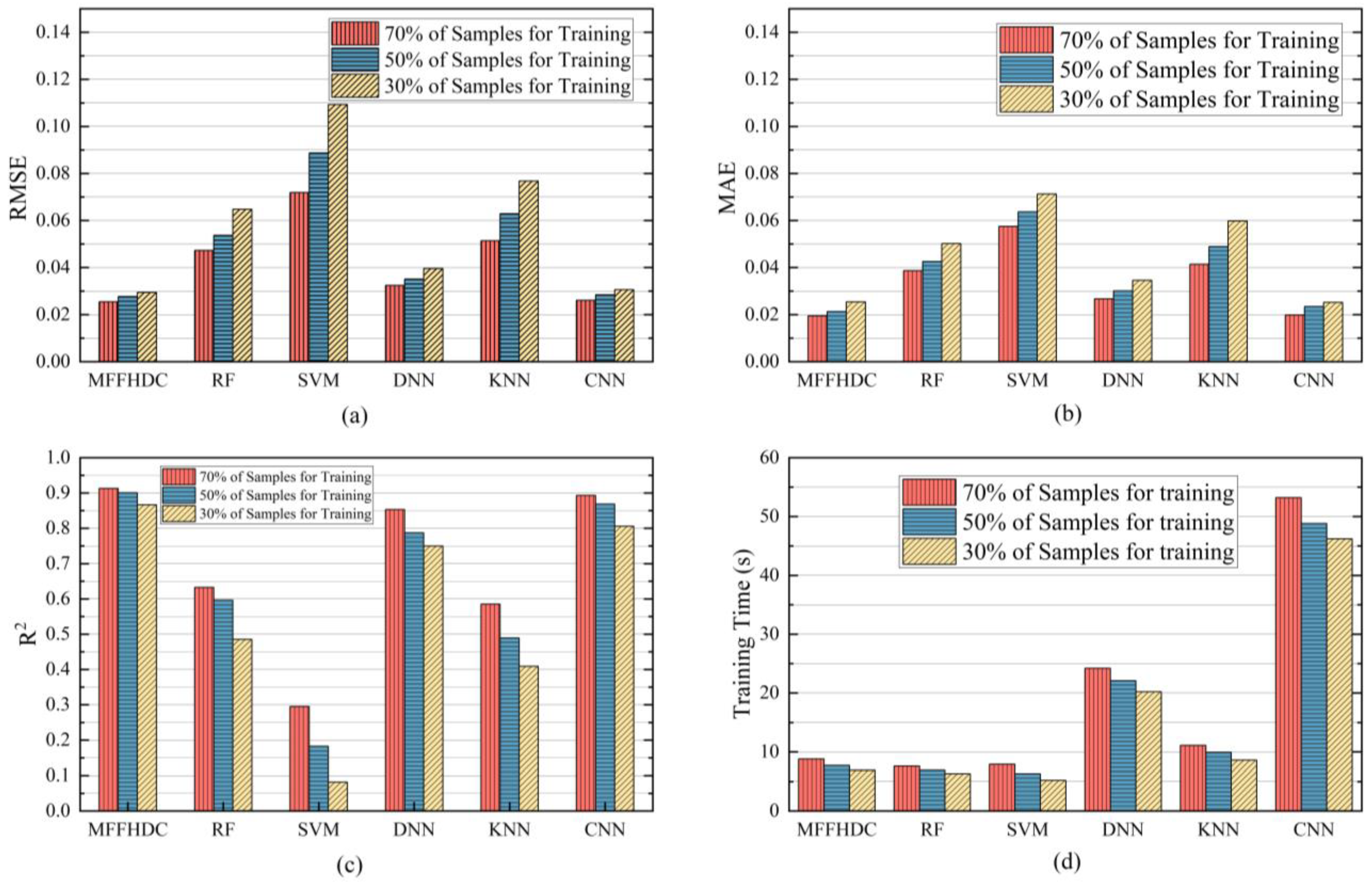
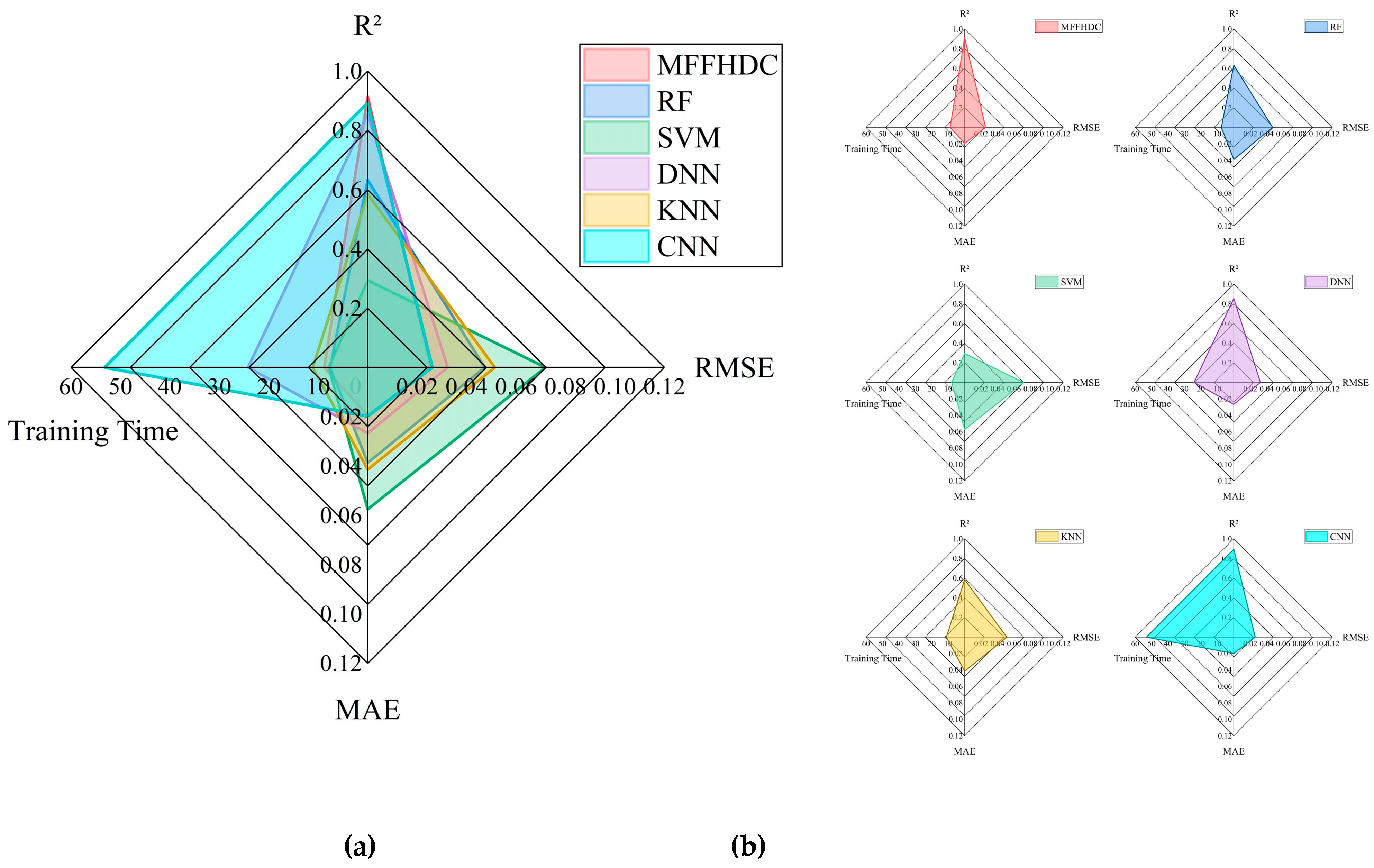
4.4. Performance Evaluation
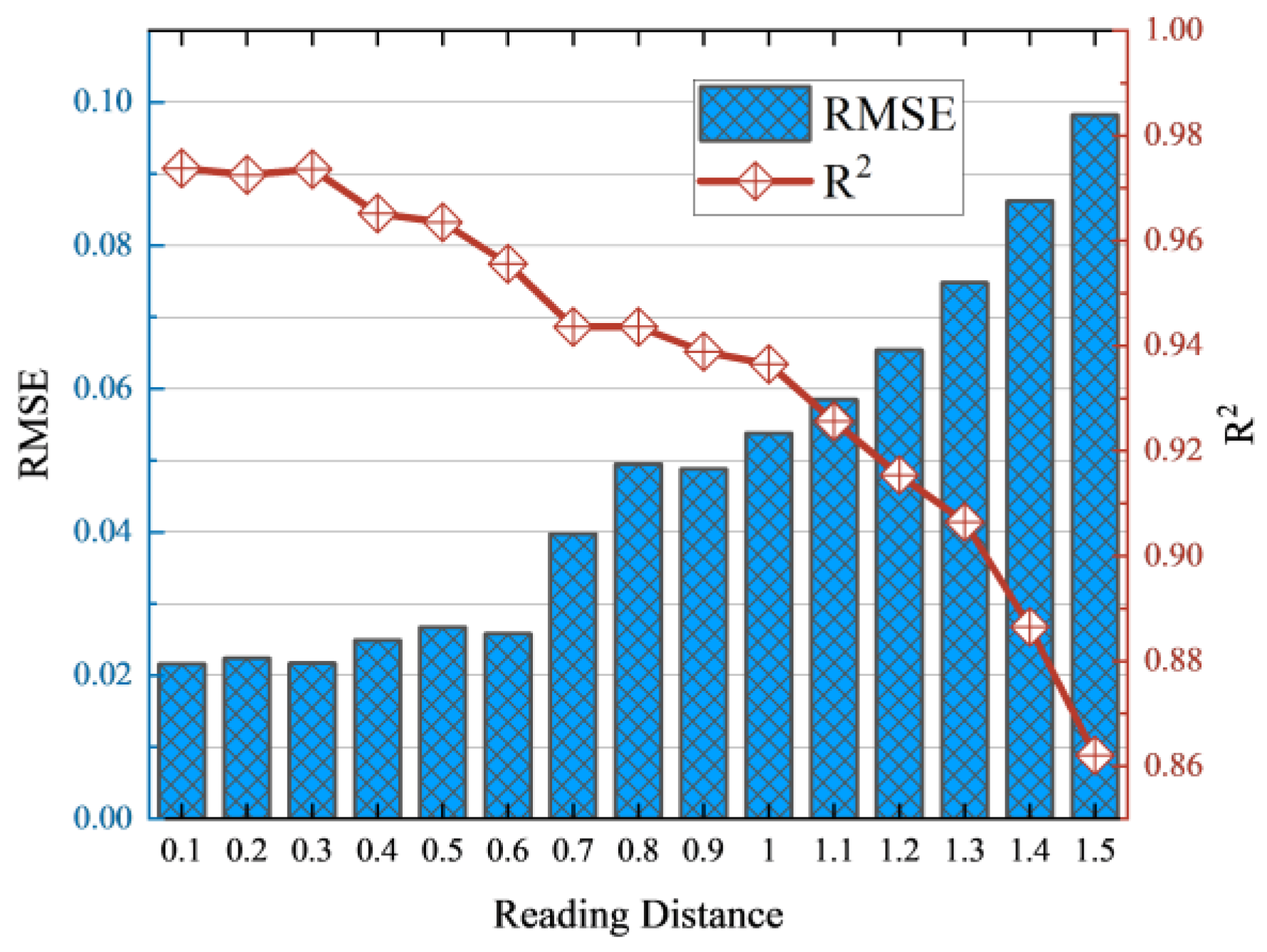
4.5. Farthest Distance Threshold Test
5. Conclusions
- Noise from environmental factors and the RFID reader can reduce detection accuracy. Future research should develop advanced noise filtering and signal processing algorithms to improve precision.
- Inconsistent alignment between tags and the reader in forest environments affects accuracy. Flexible mounting mechanisms or enhanced antenna systems can mitigate this. To further solve this problem, our next research focus will be on the design of the internal structure of the RFID tag suitable for most LMC detection. We believe that field effect transistors [55] are a good choice for applying them to label design, and we will continue to explore other possible methods to achieve further results in our research.
- Future studies could expand to measure moisture content across entire trees or plant areas, using multi-sensor data fusion for a comprehensive understanding of vegetation moisture and plant health.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, Y.L.; Zhao, Q.; Chen, L.R.; Yao, X.D.; Zhang, W.; Zhang, B.; Xie, F.T. Effect of drought stress on sugar metabolism in leaves and roots of soybean seedlings. Plant Physiol. Biochem. 2020, 146, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ramzan, R.; Omar, M.; Siddiqui, O.F.; Ksiksi, T.S.; Bastaki, N. Internet of Trees (IoTr) Implemented by Highly Dispersive Electromagnetic Sensors. IEEE Sens. J. 2021, 21, 642–650. [Google Scholar] [CrossRef]
- Babu, A.K.; Kumaresan, G.; Raj, V.A.A.; Velraj, R. Review of leaf drying: Mechanism and influencing parameters, drying methods, nutrient preservation, and mathematical models. Renew. Sustain. Energy Rev. 2018, 90, 536–556. [Google Scholar] [CrossRef]
- Shen, S.; Hua, J.J.; Zhu, H.K.; Yang, Y.Q.; Deng, Y.L.; Li, J.; Yuan, H.B.; Wang, J.J.; Zhu, J.Y.; Jiang, Y.W. Rapid and real-time detection of moisture in black tea during withering using micro-near-infrared spectroscopy. LWT-Food Sci. Technol. 2022, 155, 9. [Google Scholar] [CrossRef]
- Dong, C.W.; An, T.; Yang, M.; Yang, C.S.; Liu, Z.Y.; Li, Y.; Duan, D.D.; Fan, S.X. Quantitative prediction and visual detection of the moisture content of withering leaves in black tea (Camellia sinensis) with hyperspectral image. Infrared Phys. Technol. 2022, 123, 104118. [Google Scholar] [CrossRef]
- An, T.; Yu, S.Y.; Huang, W.Q.; Li, G.L.; Tian, X.; Fan, S.X.; Dong, C.W.; Zhao, C.J. Robustness and accuracy evaluation of moisture prediction model for black tea withering process using hyperspectral imaging. Spectrochim. Acta Part A-Mol. Biomol. Spectrosc. 2022, 269, 120791. [Google Scholar] [CrossRef]
- Wei, Y.Z.; Wu, F.Y.; Xu, J.; Sha, J.J.; Zhao, Z.F.; He, Y.; Li, X.L. Visual detection of the moisture content of tea leaves with hyperspectral imaging technology. J. Food Eng. 2019, 248, 89–96. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, X.; Hu, Y.G.; Wu, X.H.; Zhang, X.D.; Wang, P. Visualizing distribution of moisture content in tea leaves using optimization algorithms and NIR hyperspectral imaging. Comput. Electron. Agric. 2019, 160, 153–159. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, X.; Sun, J.; Li, B.; Ji, J.Y. A Method for Non-destructive Detection of Moisture Content in Oilseed Rape Leaves Using Hyperspectral Imaging Technology. J. Nondestruct. Eval. 2024, 43, 32. [Google Scholar] [CrossRef]
- Li, B.; Zhao, X.T.; Zhang, Y.; Zhang, S.J.; Luo, B. Prediction and monitoring of leaf water content in soybean plants using terahertz time-domain spectroscopy. Comput. Electron. Agric. 2020, 170, 105239. [Google Scholar] [CrossRef]
- Othman, Y.; Steele, C.; VanLeeuwen, D.; Heerema, R.; Bawazir, S.; St Hilaire, R. Remote sensing used to detect moisture status of pecan orchards grown in a desert environment. Int. J. Remote Sens. 2014, 35, 949–966. [Google Scholar] [CrossRef]
- Steele-Dunne, S.C.; Friesen, J.; van de Giesen, N. Using Diurnal Variation in Backscatter to Detect Vegetation Water Stress. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2618–2629. [Google Scholar] [CrossRef]
- Basyigit, I.B. The examination and modeling of moisture content effect of banana leaves on dielectric constant for remote sensing. Microw. Opt. Technol. Lett. 2020, 62, 1087–1092. [Google Scholar] [CrossRef]
- Tang, L.; Gao, S.D.; Wang, W.; Xiong, X.F.; Han, W.T.; Li, X.S. Moisture Content Detection of Tomato Leaves Based on Electrical Impedance Spectroscopy. Commun. Soil Sci. Plant Anal. 2024, 55, 609–623. [Google Scholar] [CrossRef]
- Jabbar, A.; Omar, M.; Ramzan, R.; Siddiqui, O.F. Internet of Trees (IoTr): A Low-Cost Single Stub Lorentz Resonator For Plant Moisture Sensing. In Proceedings of the 18th International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, 12–16 January 2021; pp. 979–982. [Google Scholar] [CrossRef]
- Han, W.T.; Yu, S.; Xu, T.F.; Chen, X.W.; Ooi, S.K. Detecting maize leaf water status by using digital RGB images. Int. J. Agric. Biol. Eng. 2014, 7, 45–53. [Google Scholar] [CrossRef]
- Yang, Z.Y.; He, W.Y.; Fan, X.J.; Tjahjadi, T. PlantNet: Transfer learning-based fine-grained network for high-throughput plants recognition. Soft Comput. 2022, 26, 10581–10590. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Sun, W.M.; Cao, X.Y.; Wang, C.Y.; Wu, D.Y.; Yang, Y.; Ye, N. TA-CNN: Two-way attention models in deep convolutional neural network for plant recognition. Neurocomputing 2019, 365, 191–200. [Google Scholar] [CrossRef]
- Rong, Q.J.; Hu, C.H.; Hu, X.D.; Xu, M.X. Picking point recognition for ripe tomatoes using semantic segmentation and morphological processing. Comput. Electron. Agric. 2023, 210, 107923. [Google Scholar] [CrossRef]
- Yu, Y.F.; Fu, L.Y.; Cheng, Y.W.; Ye, Q.L. Multi-view distance metric learning via independent and shared feature subspace with applications to face and forest fire recognition, and remote sensing classification. Knowl.-Based Syst. 2022, 243, 108350. [Google Scholar] [CrossRef]
- Lin, H.F.; Liu, X.Y.; Wang, X.Y.; Liu, Y.F. A fuzzy inference and big data analysis algorithm for the prediction of forest fire based on rechargeable wireless sensor networks. Sustain. Comput.-Inform. Syst. 2018, 18, 101–111. [Google Scholar] [CrossRef]
- Cheng, Y.W.; Fu, L.Y.; Luo, P.; Ye, Q.L.; Liu, F.; Zhu, W. Multi-view generalized support vector machine via mining the inherent relationship between views with applications to face and fire smoke recognition. Knowl.-Based Syst. 2020, 210, 106488. [Google Scholar] [CrossRef]
- Fan, X.J.; Luo, P.; Mu, Y.; Zhou, R.; Tjahjadi, T.; Ren, Y. Leaf image based plant disease identification using transfer learning and feature fusion. Comput. Electron. Agric. 2022, 196, 106892. [Google Scholar] [CrossRef]
- Shivling, V.D.; Singh, A.; Bansod, B.K.; Nag, U.; Meena, D.L. Feasibility study of patch antenna for monitoring moisture content of made tea. J. Microw. Power Electromagn. Energy 2022, 56, 192–200. [Google Scholar] [CrossRef]
- Colak, B. Moisture content effect of banana leaves to radio frequency absorbing. Microw. Opt. Technol. Lett. 2019, 61, 2591–2595. [Google Scholar] [CrossRef]
- Tein, S.Y.; Then, Y.L.; You, K.Y. Tea Leaves Moisture Measurement and Prediction Using RF Waveguide Antenna. In Proceedings of the 2017 IEEE Asia Pacific Microwave Conference (APMC), Kuala Lumpur, Malaysia, 13–16 November 2017; pp. 670–673. [Google Scholar] [CrossRef]
- Peng, B.; Liu, X.X.; Yao, Y.; Ping, J.F.; Ying, Y.B. A wearable and capacitive sensor for leaf moisture status monitoring. Biosens. Bioelectron. 2024, 245, 115804. [Google Scholar] [CrossRef]
- Colella, R.; Catarinucci, L.; Grassi, G. Battery-less RF-powered circuits for non-contact voltage monitoring of electric systems: Circuit modeling and SPICE analysis. Int. J. Circuit Theory Appl. 2024. (Early Access). [Google Scholar] [CrossRef]
- Daskalakis, S.N.; Assimonis, S.D.; Goussetis, G.; Tentzeris, M.M.; Georgiadis, A. The Future of Backscatter in Precision Agriculture. In Proceedings of the USNC-URSI Radio Science Meeting/IEEE International Symposium on Antennas and Propagation (AP-S), Atlanta, GA, USA, 7–12 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 647–648. [Google Scholar]
- Costa, F.; Genovesi, S.; Borgese, M.; Michel, A.; Dicandia, F.A.; Manara, G. A Review of RFID Sensors, the New Frontier of Internet of Things. Sensors 2021, 21, 3138. [Google Scholar] [CrossRef]
- Daskalakis, S.N.; Goussetis, G.; Assimonis, S.D.; Tentzeris, M.M.; Georgiadis, A. A uW Backscatter-Morse-Leaf Sensor for Low-Power Agricultural Wireless Sensor Networks. IEEE Sens. J. 2018, 18, 7889–7898. [Google Scholar] [CrossRef]
- Melià-Segní, J.; Vilajosana, X. Ubiquitous moisture sensing in automaker industry based on standard UHF RFID tags. In Proceedings of the IEEE International Conference on RFID (IEEE RFID), Phoenix, AZ, USA, 2–4 April 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, C.W.; Liu, W.B. Living Tree Moisture Content Detection Method Based on Intelligent UHF RFID Sensors and OS-PELM. Sensors 2022, 22, 6287. [Google Scholar] [CrossRef]
- Thomas, A.; Dasgupta, S.; Rosing, T. A Theoretical Perspective on Hyperdimensional Computing. J. Artif. Intell. Res. 2021, 72, 215–249. [Google Scholar] [CrossRef]
- Kanerva, P. Hyperdimensional Computing: An Introduction to Computing in Distributed Representation with High-Dimensional Random Vectors. Cogn. Comput. 2009, 1, 139–159. [Google Scholar] [CrossRef]
- Imani, M.; Kong, D.Q.; Rahimi, A.; Rosing, T. VoiceHD: Hyperdimensional Computing for Efficient Speech Recognition. In Proceedings of the IEEE International Conference on Rebooting Computing (ICRC), Washington, DC, USA, 8–9 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 97–104. [Google Scholar] [CrossRef]
- Imani, M.; Hwang, J.; Rosing, T.; Rahimi, A.; Rabaey, J.M. Low-Power Sparse Hyperdimensional Encoder for Language Recognition. IEEE Des. Test 2017, 34, 94–101. [Google Scholar] [CrossRef]
- Li, H.T.; Wu, T.F.; Rahimi, A.; Li, K.S.; Rusch, M.; Lin, C.H.; Hsu, J.L.; Sabry, M.M.; Eryilmaz, S.B.; Sohn, J.; et al. Hyperdimensional Computing with 3D VRRAM In-Memory Kernels: Device-Architecture Co-Design for Energy-Efficient, Error-Resilient Language Recognition. In Proceedings of the 62nd Annual IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016. [Google Scholar] [CrossRef]
- Chang, E.J.; Rahimi, A.; Benini, L.; Wu, A.Y. Hyperdimensional Computing-based Multimodality Emotion Recognition with Physiological Signals. In Proceedings of the 1st IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS), Hsinchu, Taiwan, 18–20 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 137–141. [Google Scholar] [CrossRef]
- Rahimi, A.; Kanerva, P.; Benini, L.; Rabaey, J.M. Efficient Biosignal Processing Using Hyperdimensional Computing: Network Templates for Combined Learning and Classification of ExG Signals. Proc. IEEE 2019, 107, 123–143. [Google Scholar] [CrossRef]
- Burrello, A.; Benatti, S.; Schindler, K.; Benini, L.; Rahimi, A. An Ensemble of Hyperdimensional Classifiers: Hardware-Friendly Short-Latency Seizure Detection With Automatic iEEG Electrode Selection. IEEE J. Biomed. Health Inform. 2021, 25, 935–946. [Google Scholar] [CrossRef]
- Watkinson, N.; Devineni, D.; Joe, V.; Givargis, T.; Nicolau, A.; Veidenbaum, A. Using Hyperdimensional Computing to Extract Features for the Detection of Type 2 Diabetes. In Proceedings of the 37th IEEE International Parallel and Distributed Processing Symposium (IPDPS), St. Petersburg, FL, USA, 15–19 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 149–156. [Google Scholar] [CrossRef]
- Yao, Y.R.; Liu, W.B.; Zhang, G.; Hu, W. Radar-Based Human Activity Recognition Using Hyperdimensional Computing. IEEE Trans. Microw. Theory Tech. 2022, 70, 1605–1619. [Google Scholar] [CrossRef]
- Wang, X.L.; Flores, R.; Brouwer, J.; Papaefthymiou, M. Real-time detection of electrical load anomalies through hyperdimensional computing. Energy 2022, 261, 125042. [Google Scholar] [CrossRef]
- Imani, M.; Morris, J.; Bosch, S.; Shu, H.; De Micheli, G.; Rosing, T. AdaptHD: Adaptive Efficient Training for Brain-Inspired Hyperdimensional Computing. In Proceedings of the IEEE Biomedical Circuits and Systems Conference (BioCAS), Nara, Japan, 17–19 October 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Taheri, F.; Bayat-Sarmadi, S.; Rastaghi, H. PartialHD: Toward Efficient Hyperdimensional Computing by Partial Processing. IEEE Internet Things J. 2024, 11, 987–994. [Google Scholar] [CrossRef]
- Karunaratne, G.; Le Gallo, M.; Cherubini, G.; Benini, L.; Rahimi, A.; Sebastian, A. In-memory hyperdimensional computing. Nat. Electron. 2020, 3, 327. [Google Scholar] [CrossRef]
- Salamat, S.; Imani, M.; Rosing, T. Accelerating Hyperdimensional Computing on FPGAs by Exploiting Computational Reuse. IEEE Trans. Comput. 2020, 69, 1159–1171. [Google Scholar] [CrossRef]
- Rahimi, A.; Tchouprina, A.; Kanerva, P.; Millan, J.D.; Rabaey, J.M. Hyperdimensional Computing for Blind and One-Shot Classification of EEG Error-Related Potentials. Mob. Netw. Appl. 2020, 25, 1958–1969. [Google Scholar] [CrossRef]
- Räsänen, O.J.; Saarinen, J.P. Sequence Prediction with Sparse Distributed Hyperdimensional Coding Applied to the Analysis of Mobile Phone Use Patterns. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1878–1889. [Google Scholar] [CrossRef] [PubMed]
- Ge, L.L.; Parhi, K.K. Classification Using Hyperdimensional Computing: A Review. IEEE Circuits Syst. Mag. 2020, 20, 30–47. [Google Scholar] [CrossRef]
- Huang, P.; Ye, Q.L.; Zhang, F.L.; Yang, G.W.; Zhu, W.; Yang, Z.J. Double L2,p- norm based PCA for feature extraction. Inf. Sci. 2021, 573, 345–359. [Google Scholar] [CrossRef]
- Ye, Q.L.; Fu, L.Y.; Zhang, Z.; Zhao, H.H.; Naiem, M. Lp- and Ls-Norm Distance Based Robust Linear Discriminant Analysis. Neural Netw. 2018, 105, 393–404. [Google Scholar] [CrossRef]
- Fu, L.Y.; Li, Z.C.; Ye, Q.L.; Yin, H.; Liu, Q.W.; Chen, X.B.; Fan, X.J.; Yang, W.K.; Yang, G.W. Learning Robust Discriminant Subspace Based on Joint L2,p- and L2,s- Norm Distance Metrics. Ieee Trans. Neural Netw. Learn. Syst. 2022, 33, 130–144. [Google Scholar] [CrossRef]
- Nawaz, A.; Merces, L.; Ferro, L.M.M.; Sonar, P.; Bufon, C.C.B. Impact of Planar and Vertical Organic Field-Effect Transistors on Flexible Electronics. Adv. Mater. 2023, 35, e2204804. [Google Scholar] [CrossRef]


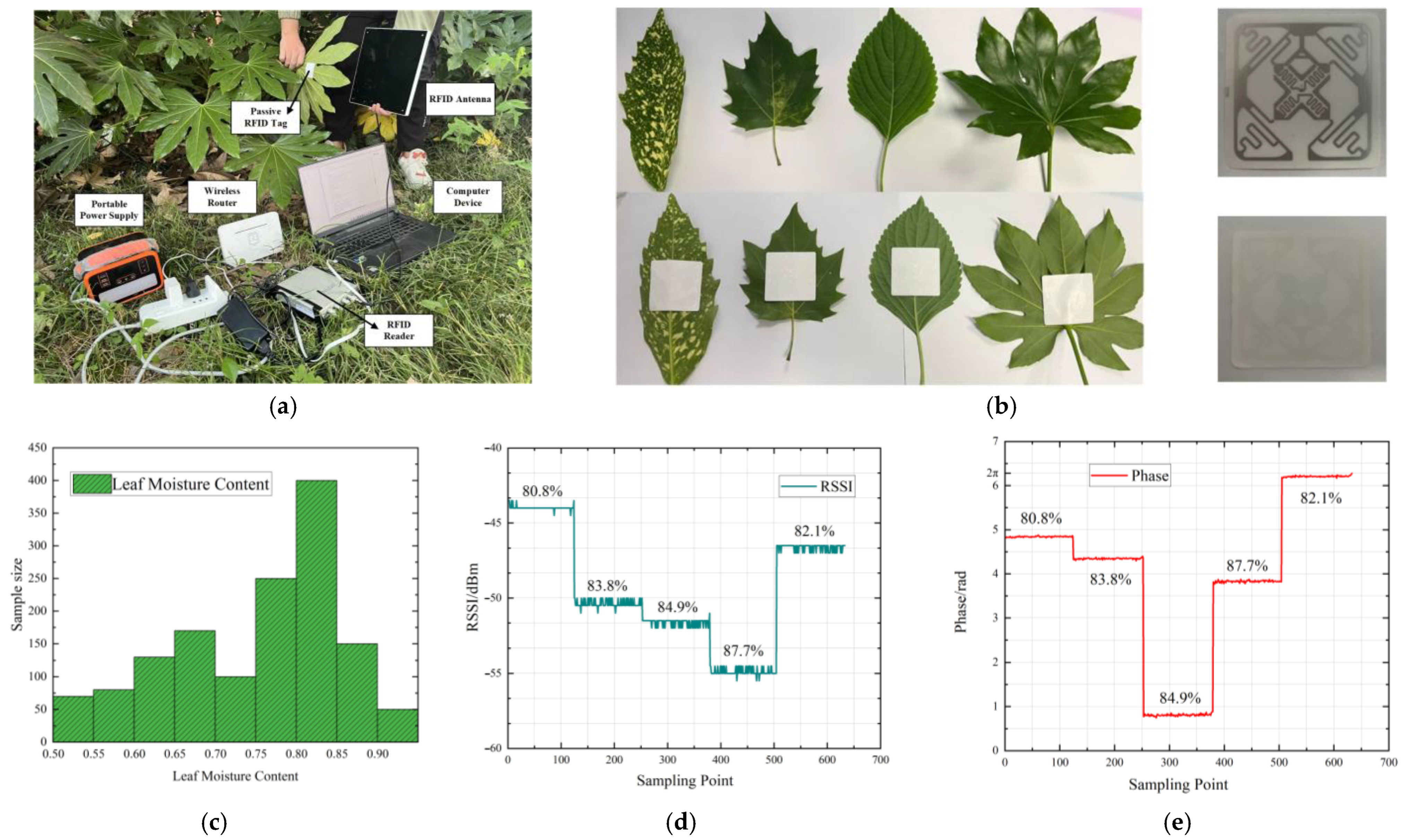
| Selected Materials | TSN |
|---|---|
| Fatsia japonica | 505935 |
| Aucuba japonica | 565023 |
| Perilla frutescens | 32634 |
| Firmiana simplex | 21578 |
| Maximum | Minimum | Average | Standard Deviation | |
|---|---|---|---|---|
| RSSI (dBm) | −24.0 | −75.5 | −44.05 | 5.857 |
| Phase (rad) | 6.277 | 0.006 | 3.149 | 2.022 |
| Real Moisture Content (%) | 91.28 | 47.65 | 80.29 | 7.138 |
| Algorithm Name | Details |
|---|---|
| MFFHDC | The dimensional of hypervector is 10,000. |
| Random Forest | The n_estimators is 100, the max_depth is 30, the min_samples_split is 2, and the min_samples_leaf is 1. |
| Support Vector Machine | The type of kernel function is linear kernel function, and the value of C parameter is 100. |
| KNN | The number of neighbors is set to 10, the algorithm is set to auto, and the weights select distance. |
| DNN | There are two fully connected layers, the number of neurons in each layer is 64, the activation function is ReLU, and the loss function is MSE. |
| CNN | There are 2 convolution layers, 32 convolution kernels, 2 pooling layers, and 2 fully connected layers. The activation function is ReLU, and MSE is the loss function. |
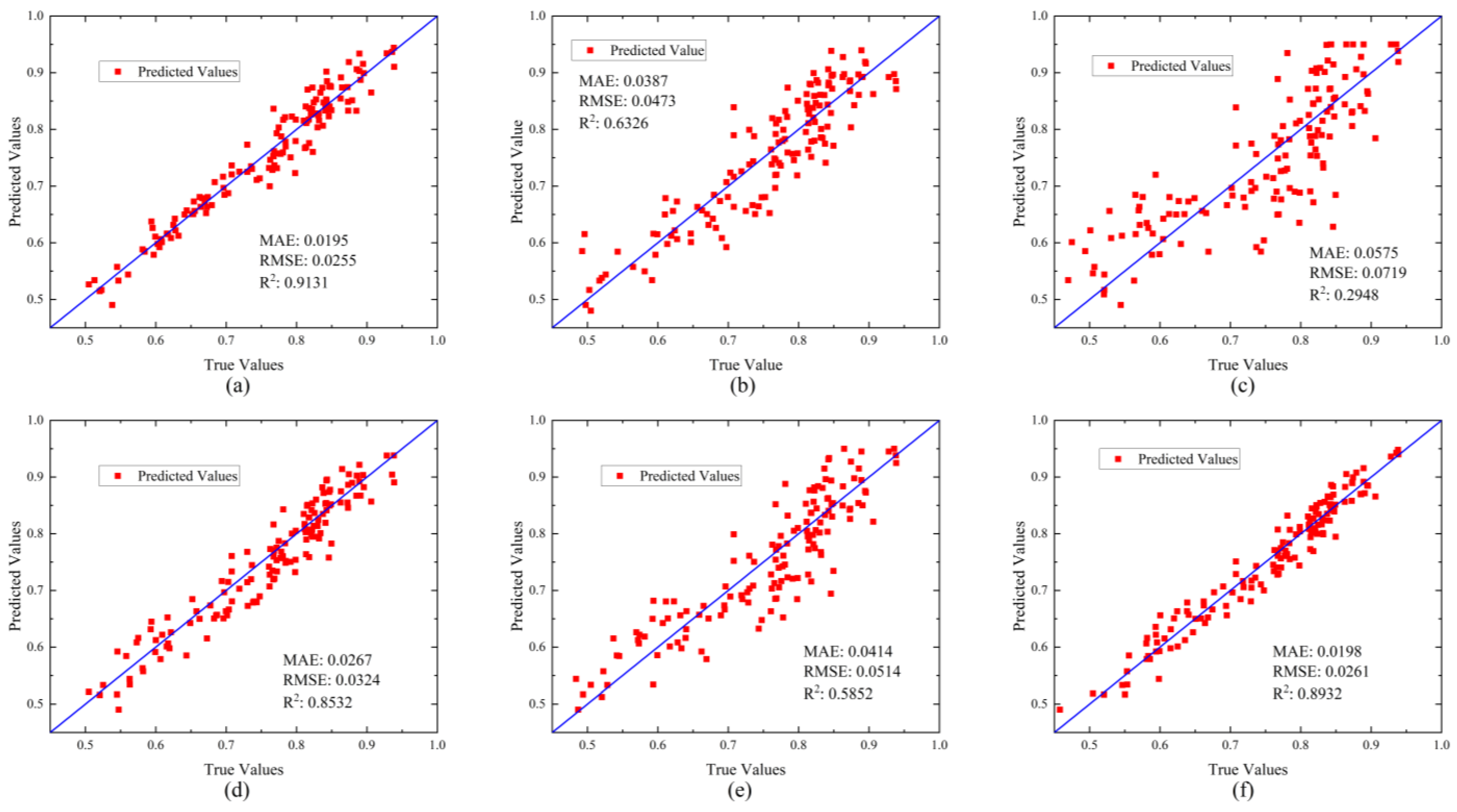
| Algorithm Model | MAE | RMSE | R2 | Training Time |
|---|---|---|---|---|
| MFFHDC | 0.0195 | 0.0255 | 0.9131 | 8.8 |
| RF | 0.0387 | 0.0473 | 0.6326 | 7.6 |
| SVM | 0.0575 | 0.0719 | 0.2948 | 7.9 |
| DNN | 0.0267 | 0.0324 | 0.8532 | 24.2 |
| KNN | 0.0414 | 0.0514 | 0.5852 | 11.1 |
| CNN | 0.0198 | 0.0261 | 0.8932 | 53.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Hou, Z.; Liu, Y.; Liu, W. Leaf Moisture Content Detection Method Based on UHF RFID and Hyperdimensional Computing. Forests 2024, 15, 1798. https://doi.org/10.3390/f15101798
Wu Y, Hou Z, Liu Y, Liu W. Leaf Moisture Content Detection Method Based on UHF RFID and Hyperdimensional Computing. Forests. 2024; 15(10):1798. https://doi.org/10.3390/f15101798
Chicago/Turabian StyleWu, Yin, Ziyang Hou, Yanyi Liu, and Wenbo Liu. 2024. "Leaf Moisture Content Detection Method Based on UHF RFID and Hyperdimensional Computing" Forests 15, no. 10: 1798. https://doi.org/10.3390/f15101798
APA StyleWu, Y., Hou, Z., Liu, Y., & Liu, W. (2024). Leaf Moisture Content Detection Method Based on UHF RFID and Hyperdimensional Computing. Forests, 15(10), 1798. https://doi.org/10.3390/f15101798







