Optimization of Vibration Parameters for Red Jujube Trees with Different Diameters

Abstract

Vibratory harvesting is the primary method used to harvest red jujubes. This study aimed to improve the efficiency of vibratory harvesting for red jujubes and identify the optimal parameters for harvesting at different jujube tree diameters. A model for the forced vibration dynamics of jujube trees was established, and a three-dimensional model was constructed for different diameter variations. A kinematic simulation analysis was then conducted to determine the inherent frequency and modal vibration patterns of jujube trees. Harmonic response analysis was performed to study the displacement and acceleration responses of jujube trees with different diameters to different vibration factors. Subsequently, vibration tests were carried out on the jujube trees. The results showed that the vibration characteristics of trees with different diameters were distinct at each vibration order, and the maximum number of vibrating branches differed at different orders of vibration. The vibration frequency ranges for vibration harvesting of jujube trees with 30 mm, 50 mm, and 70 mm diameters were determined as 4–30 Hz, 6–25 Hz, and 17–29 Hz, respectively. Furthermore, the study obtained the optimal vibration parameters for jujube trees by establishing the regression equations of harvest rate and each vibration factor. For jujube trees with a diameter of 30 mm, the optimal parameters included a vibration frequency of 30 Hz and a vibration amplitude of 15 mm. For jujube trees with a diameter of 50 mm, the optimal parameters included a vibration frequency of 18.55 Hz and a vibration amplitude of 12.52 mm. Lastly, for jujube trees with a diameter of 70 mm, the optimal parameters included a vibration frequency of 6 Hz and a vibration amplitude of 15 mm. This study provides a theoretical foundation and technical support for improving the efficiency of vibratory harvesting and identifying the optimal vibration harvesting parameters for jujube trees with different diameters.

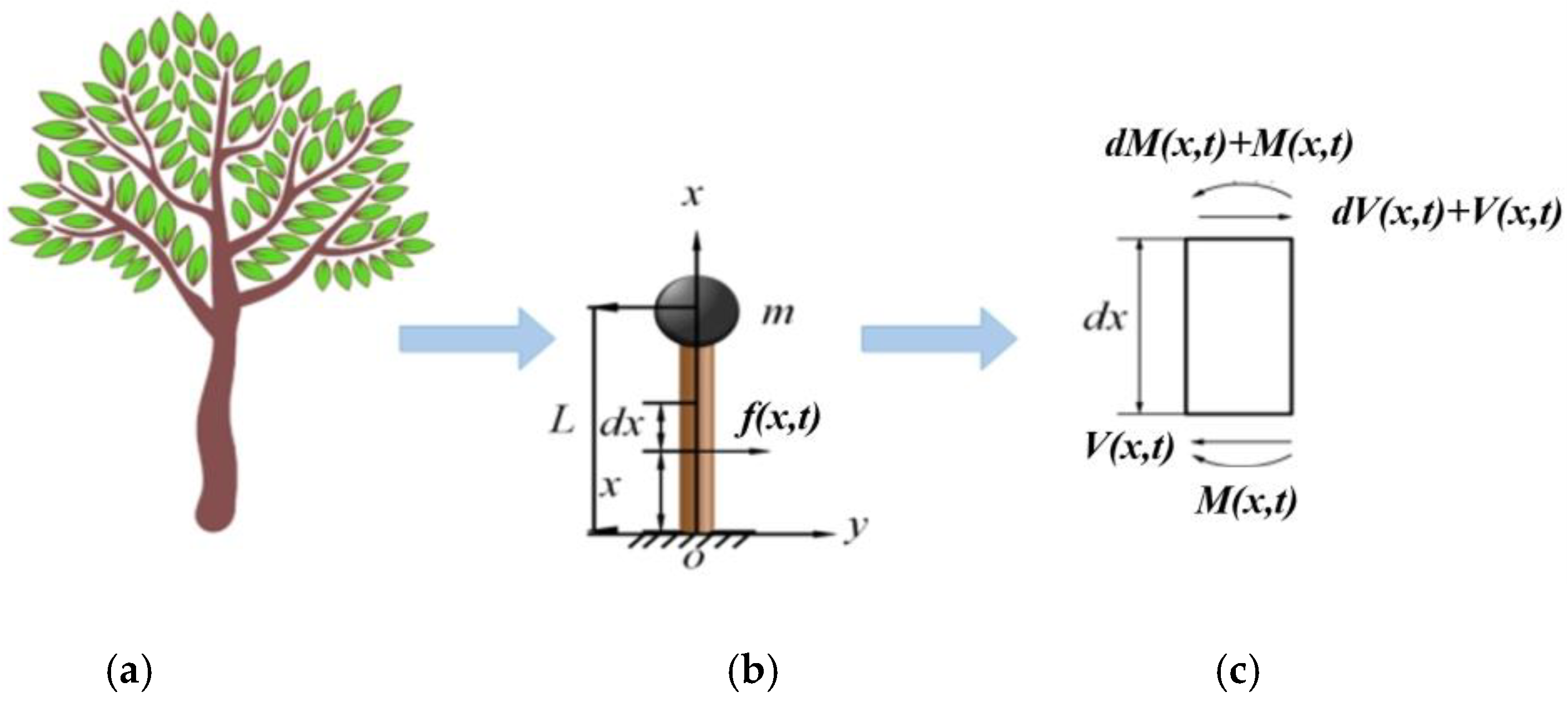
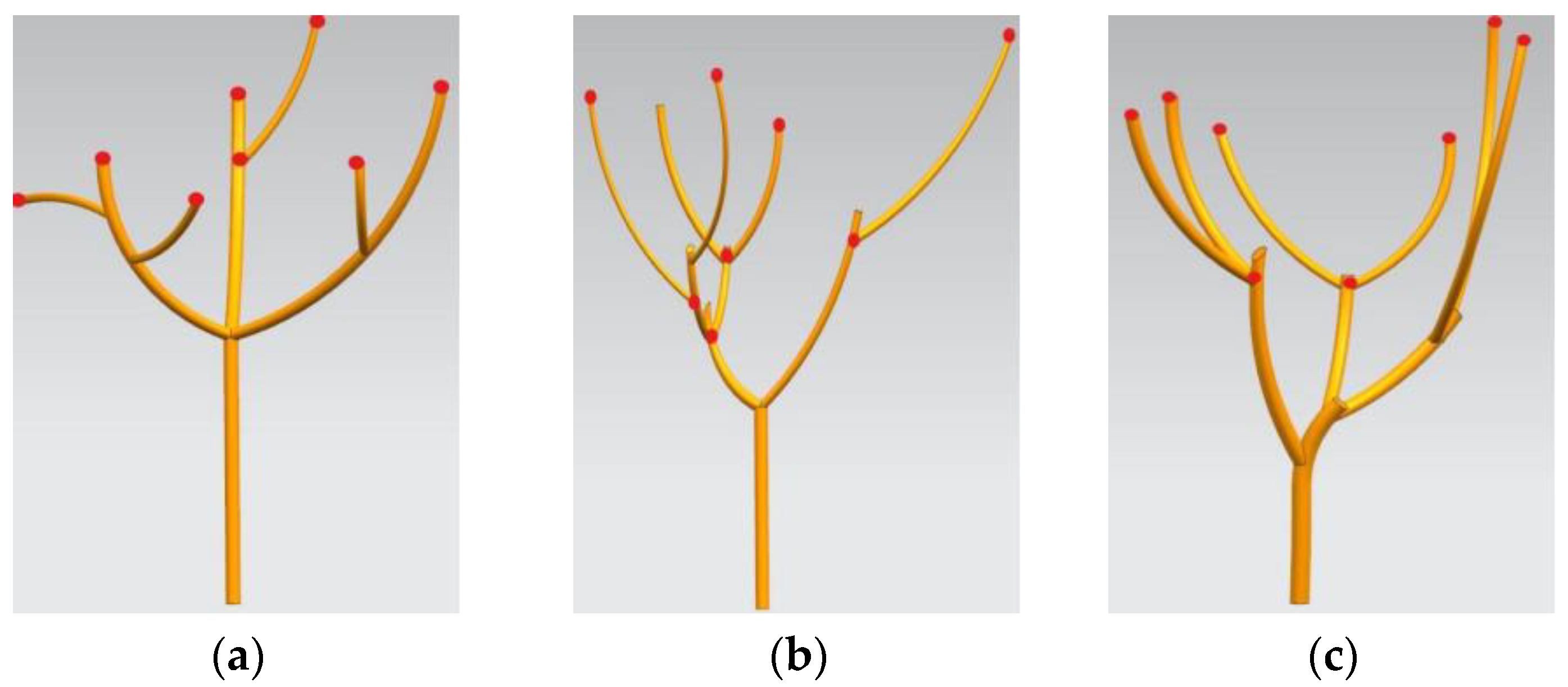
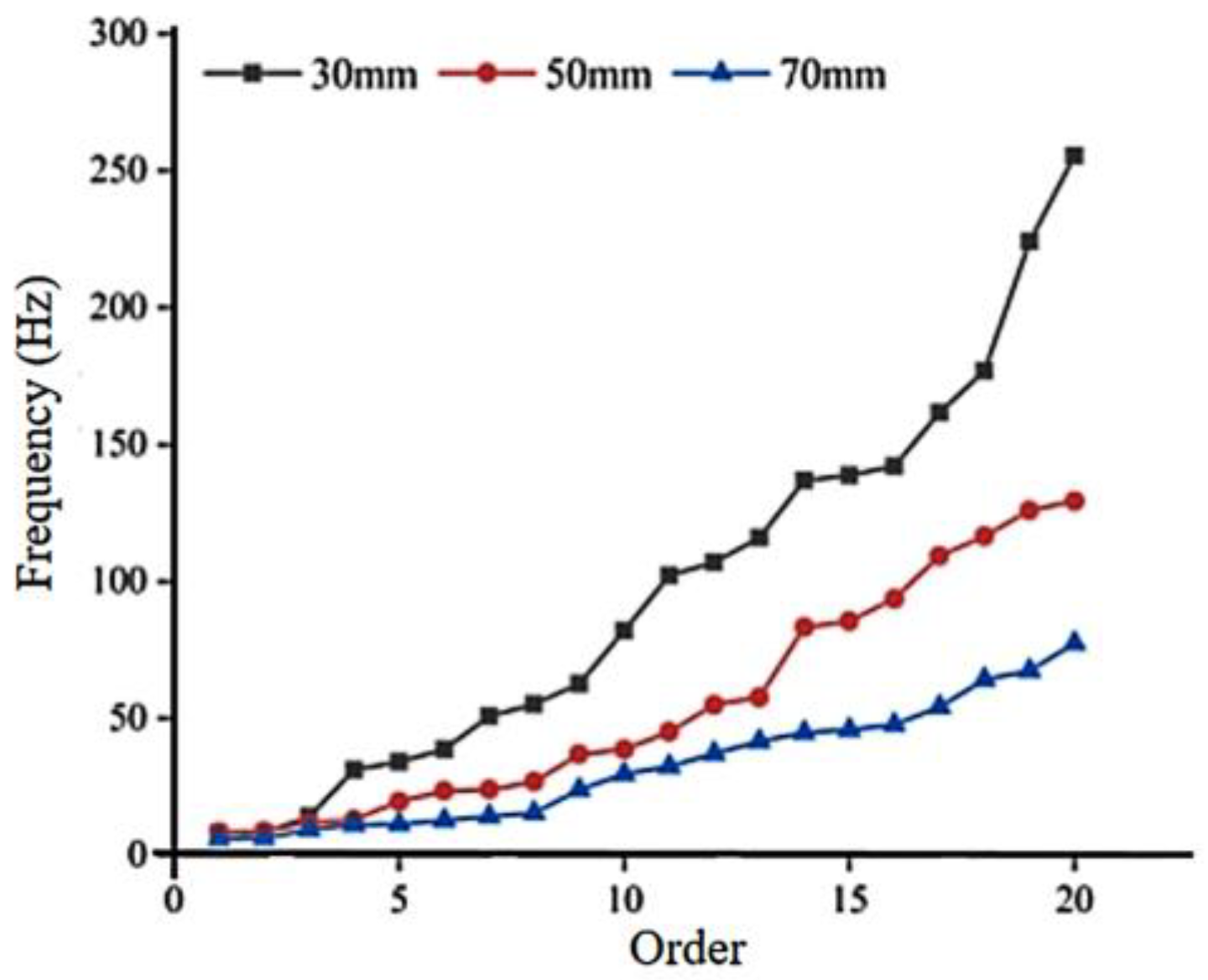
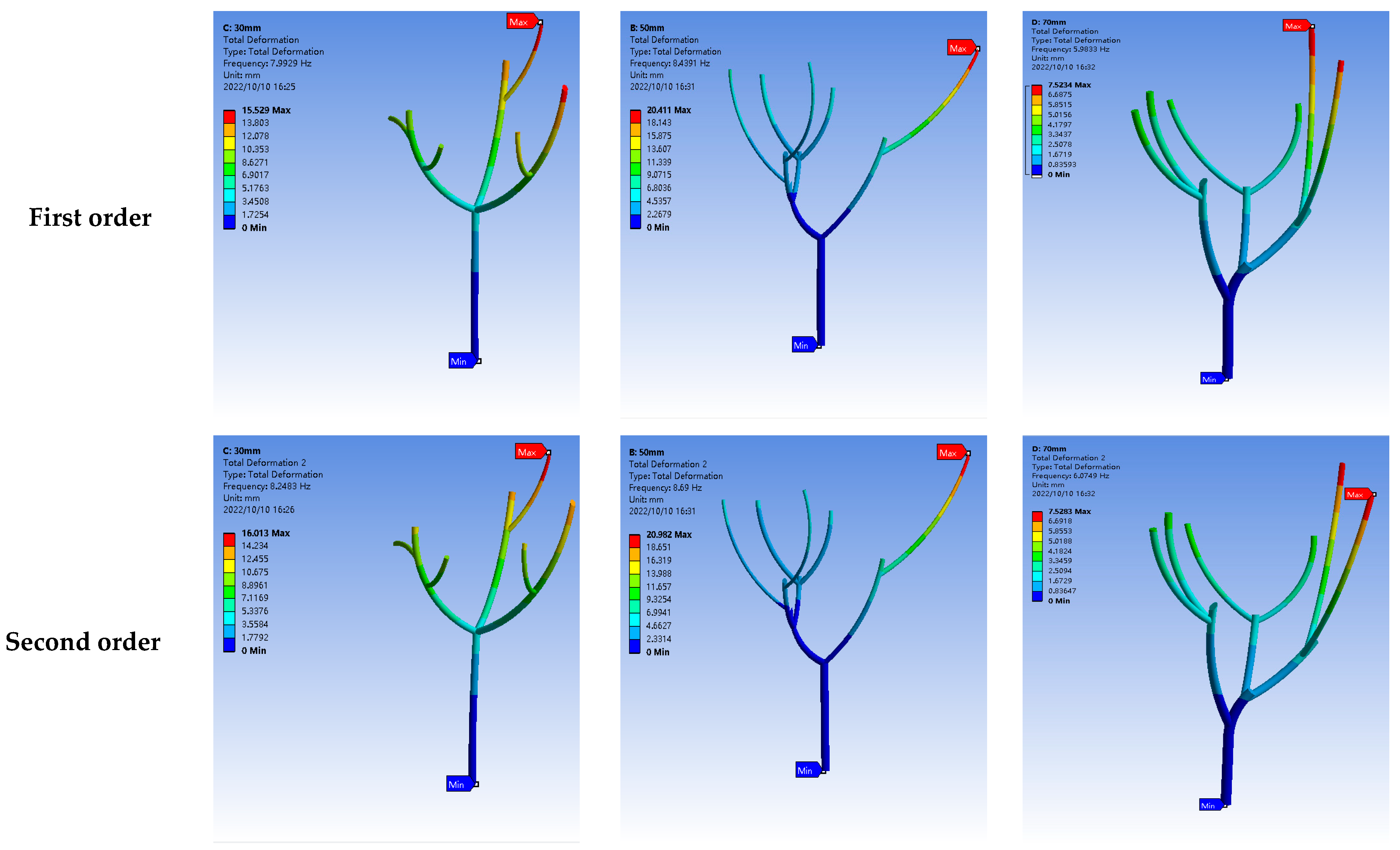
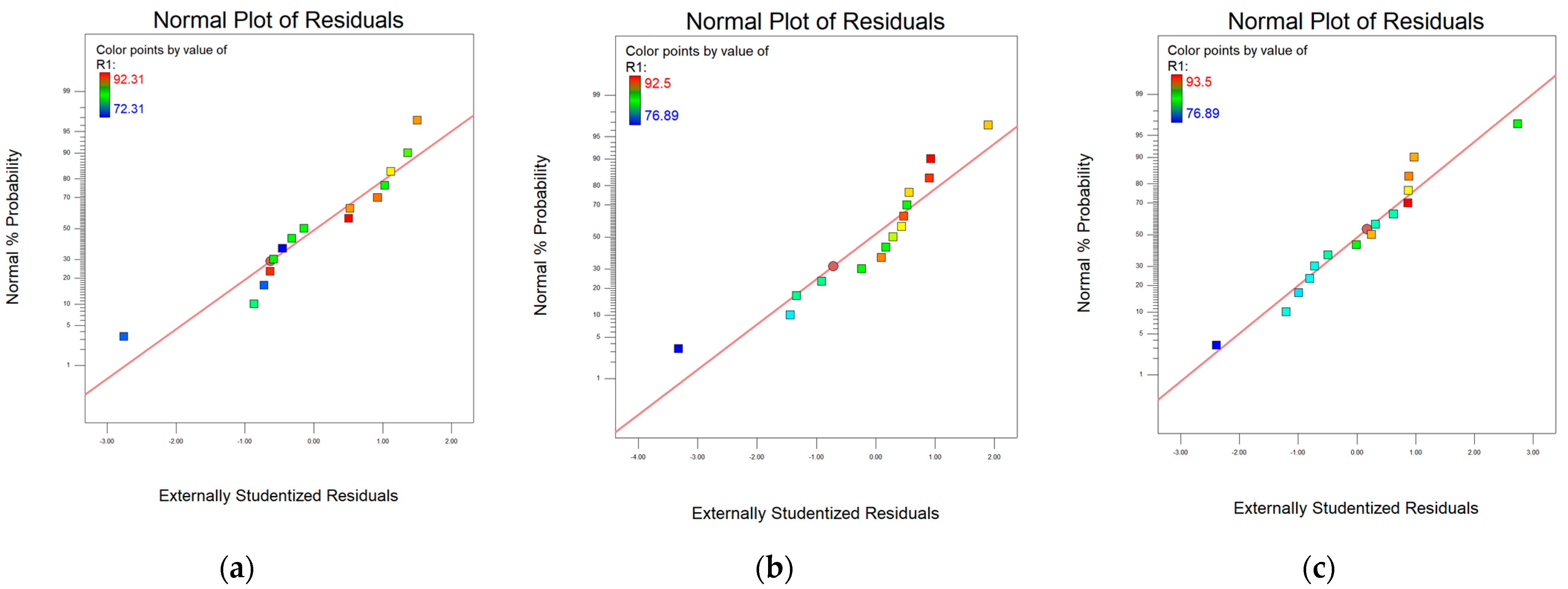
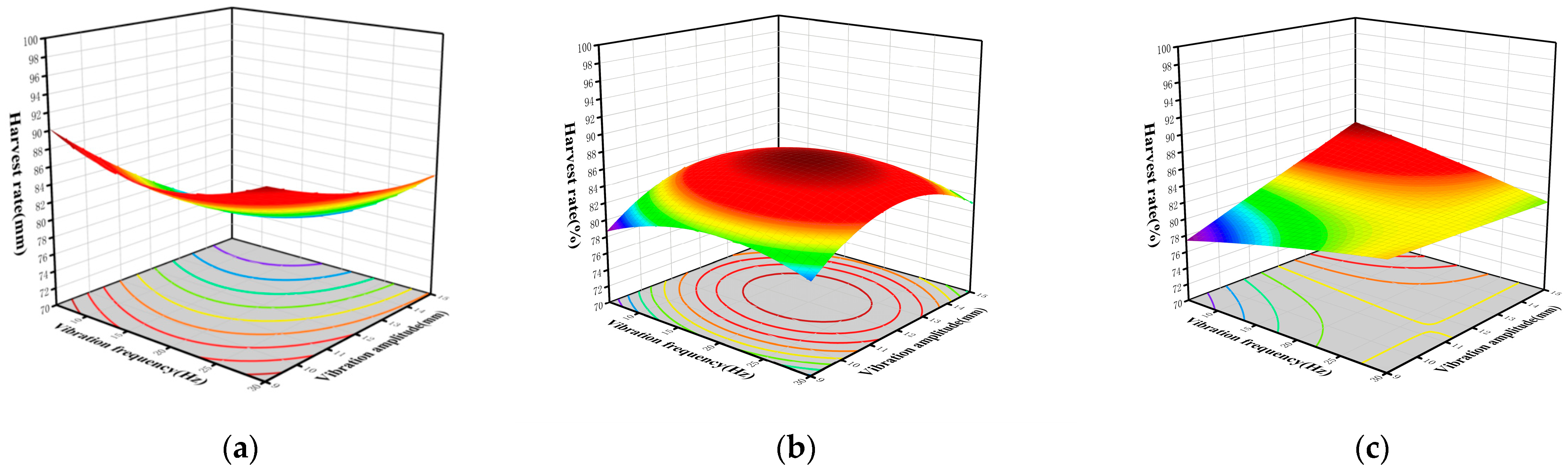
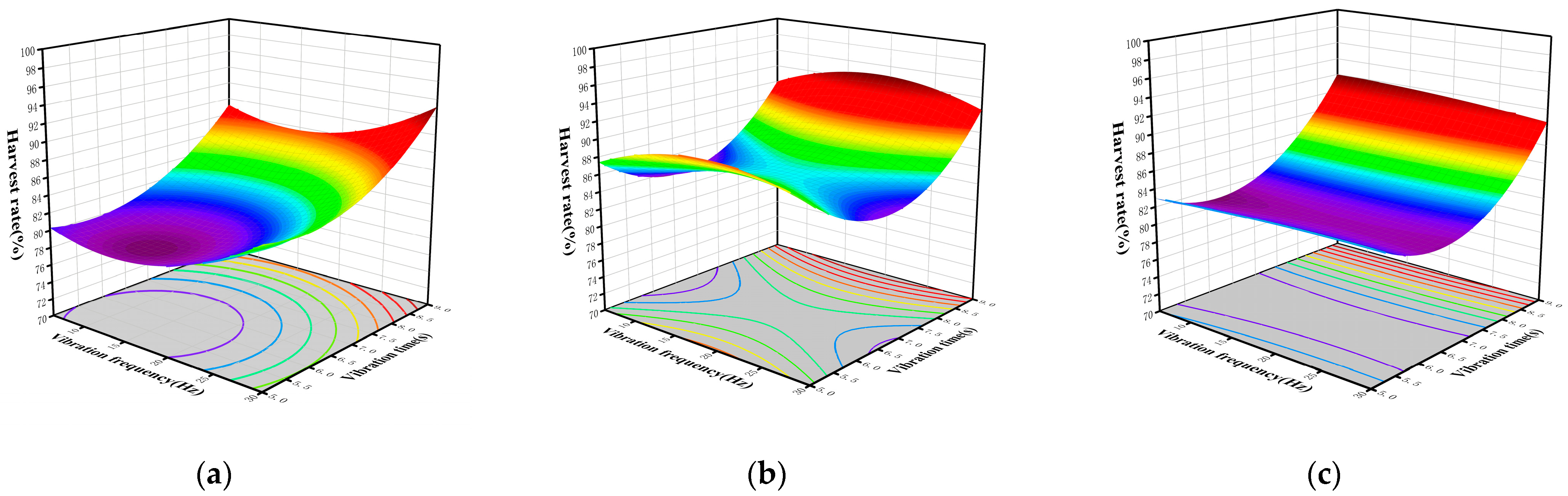
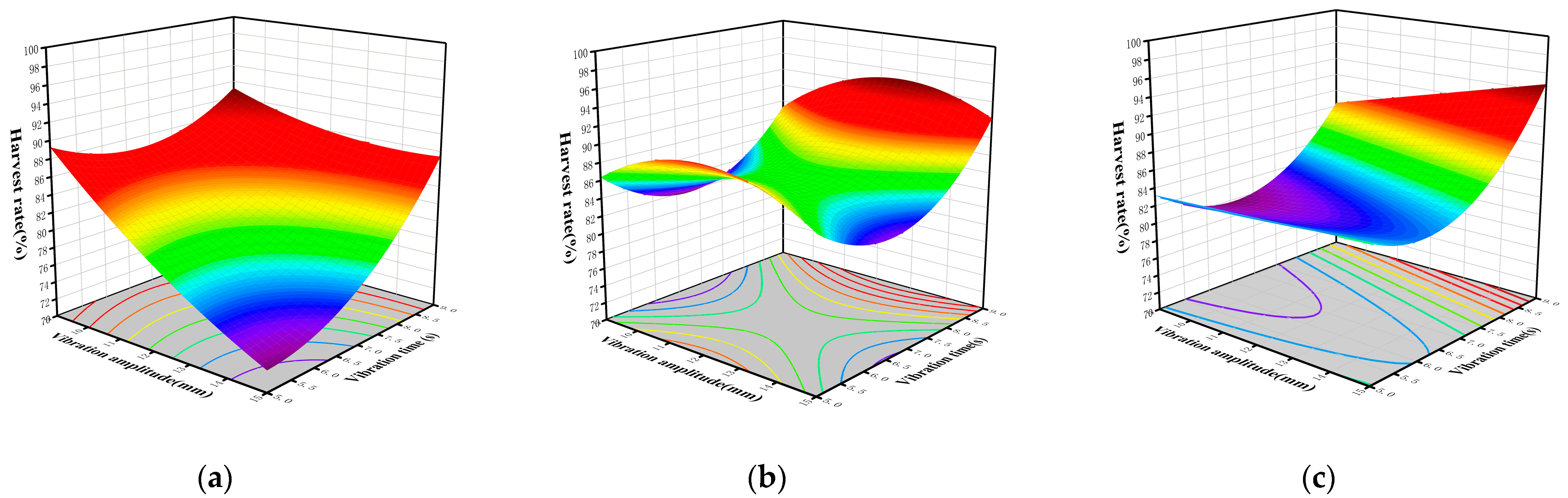
1. Introduction

Red jujube is a fruit that holds immense economic value in China [1] and is considered significant in the country’s food supply [2]. Although the cultivation of red jujubes has developed into large-scale production involving standardized techniques [3], the traditional method of harvesting still relies predominantly on manual labor [4], making it time-consuming, labor-intensive, and expensive [5]. However, significant advancements have been made in mechanized harvesting methods over the past few decades [6]. Vibratory harvesting is regarded as one of the most effective means to reduce harvesting costs [7].

Vibratory harvesting is a method of harvesting crops that involves applying mechanical vibrations to the branches of fruit trees to cause them to vibrate and facilitate fruit removal [8]. This method has been widely adopted for harvesting various crops. Researchers have developed many vibratory harvesters, such as the vibratory coffee harvester designed by Yu et al. [9] where the harvesting rate of mature and immature coffee was 92.22% and 8.33%, respectively, and the hazard rate was 5.23%. For red jujube harvesting, Zheng et al. [10] designed a catch-and-shake robot to identify tree trunks with RGB-D cameras and find suitable vibration shaking points for vibrating and harvesting jujube trees by manipulators. Meng et al. [11] created a 4YS-24 red jujube harvester that uses mechanical vibratory fruit drop principles, achieving a fruit harvesting rate of 91.40% in field tests. Fu et al. [12] designed a fully hydraulic self-propelled red jujube harvester, achieving a ground red jujube harvesting rate of 45.1%, a tree red jujube harvesting rate of 93.2%, a loss rate of 2.9%, and a damage rate of 0.9%. Despite these successes, vibratory harvesting still faces challenges, including low efficiency, high fruit damage rates, and low fruit removal efficiency caused by either too little or too much vibration energy. These factors can lead to fruit leakage harvesting or damage to both fruit and tree trunks [13].

To enhance the efficiency of vibratory harvesting, it is necessary to study the fruit vibration mechanism. Zhao et al. [14] used physical tests to establish a three-dimensional model of a shrub and a material mechanics model of its branches. They conducted a modal analysis of the shrub using the finite element method and modal experiments with acceleration sensors and impact hammers to determine the optimized resonant frequency of 2 Hz. Field experiments demonstrated that vibrating branches at this frequency resulted in fruit shedding. Zhang et al. [15] investigated the dynamic response characteristics of grape berries in the X, Y, and Z directions using a dynamic model and finite element analysis. They found that the optimal vibration frequency of the harvesting mechanism should be around 10 Hz to avoid resonance that leads to multiple fruit shedding. Bentaher et al. [16] utilized the finite element method to simulate the process of vibration harvesting for the “Chemlali” olive tree. They developed an equation for the excitation force as a function of the shaker characteristics, including the eccentricity value, unbalanced weight, and rotation frequency. The structural response of the olive tree was also analyzed in relation to the type, position, and excitation frequency of the shaker. Liu et al. [17] developed a theoretical model of walnut vibration during harvesting, analyzed vibration response in terms of motion morphology and separation force, and verified the model through field tests. Theoretical and experimental results showed that the response amplitude and frequency of walnuts are proportional to the vibration amplitude and frequency of the equipment, respectively, while the separation force is proportional to the square of both parameters. Yan et al. [18] examined the influence of the ginkgo canopy structure on its vibration characteristics. Two representative ginkgo canopy structures, monopodial branching and sympodial branching, were chosen by assessing 273 ginkgo tree canopies. Subsequently, their vibration spectra were meticulously analyzed. Vibration models were established for ginkgo trees with different canopy shapes, allowing for an in-depth analysis of their vibration states at various frequencies. The results suggest that the spectral curve of dromedary ginkgo trees exhibits a prominent intrinsic frequency above 30 Hz, corresponding to the frequency of maximum acceleration. On the other hand, y-branch ginkgo trees display a maximum acceleration frequency ranging from 20 to 30 Hz, which falls within the typical excitation range observed in fruit trees. These findings highlight the superior vibration characteristics of the y-shaped canopy structure in ginkgo trees. Lang et al. [19,20] analyzed the relationship between the height of excitation, vibration frequency, and the vibration response characteristics of cherry trees by measuring parameters such as the rotational center, simplified mass, elastic modulus, and dynamic damping coefficient of the cherry tree. They also identified the most effective clamping height for the vibration sieve. These studies provide a theoretical basis for designing the optimal input vibration parameters for harvesting devices to improve fruit harvesting rates.

Several studies have investigated the vibration mechanism of jujube trees. Wang et al. [21] developed a model to examine the relationship between the harvesting rate of red jujubes and factors such as vibration amplitude, vibration frequency, and vibration time. They utilized a quadratic regression generalized rotational combination test method for constructing the model and investigated the essential parameters of compact dwarf red jujube harvesting machinery. Fu et al. [22] simplified the jujube “branch-stalk-fruit” system as a double pendulum vibration model to analyze natural frequencies and obtain the natural vibration frequencies of the system (14.69 Hz and 17.26 Hz). Constant-frequency vibration tests were conducted on jujube tree samples at various amplitudes (3 mm, 5 mm, and 7 mm) and frequencies (12–24 Hz) to investigate the effects of vibration frequency and amplitude on the instantaneous acceleration of each branch. DHDAS analysis showed a correlation between vibration frequency and instantaneous acceleration, while amplitude did not have a significant effect. Peng et al. [23] utilized a finite element method to anticipate the response of jujube trees to shaker excitation and to determine the relationship between the response and excitation frequency. They conducted field experiments on three jujube trees, replicating five different shaker frequencies (5, 10, 15, 20, and 25 Hz). The researchers modeled the trees using Autodesk Inventor 2014 and then simulated them in ANSYS 15.0 using the finite element method. The results showed that the average correlation coefficient between the experimental and simulated accelerations was 0.62. The measured and simulated derived average accelerations showed good agreement in terms of variation trends. The researchers concluded that the simulation method could be employed to investigate the vibration response of jujube trees under shaking table excitation. Peng et al. [24] used spectral analysis to find the optimal frequency range for vibrational harvesting of winter jujube, and the first three orders of intrinsic frequencies were in the frequency range of 5–25 Hz. Finally, the fruit shedding rate was tested in the resonance frequency range, and the maximum shedding rate of crisp ripe fruits was found when the frequency was between 12.5 and 17.5 Hz. Yang et al. [25] developed a dynamics model of the jujube tree and theoretically solved the resonant frequencies and corresponding modes of the jujube tree system. ANSYS finite element analysis was performed on the established solid model of the jujube tree. The analysis of the modal vibration response of the jujube tree revealed that the motions of different branches were significantly different and independent, and the response of the jujube tree showed good consistency at the low frequency of 5.47 Hz. The harmonic response analysis shows that the excitation frequency is within 0–10 Hz, and the acceleration response increases with the increase of the excitation position height at the same vibration frequency but the overall change pattern and trend of the acceleration response remains the same, and the maximum acceleration response frequency is 5.2 Hz. The selected frequency range of the vibration device and fruit tree rigid-flexible coupling is 4–8 Hz. Zhuo et al. [26] studied the vibration response characteristics of jujube branches and evaluated the vibration effect of jujube branches based on different excitation parameters using a response surface method, obtaining an optimized vibration effect. The low-order natural frequencies of dense jujube branches were mainly concentrated in the range of 6–22 Hz, and the strongest vibration responses were found at 17.5 Hz, 18.0 Hz, and 22.5 Hz. Li et al. [27] conducted a comprehensive finite element modeling and simulation analysis of the jujube tree. Initially, SolidWorks 2016 software was utilized to create a 3D model of the jujube tree, which was then imported into ANSYS 18.0. Subsequently, modal and harmonic response analyses were performed using ANSYS 18.0. The analysis results indicated that each branch of the jujube tree exhibited a certain level of independence, implying that the vibration of the tree primarily occurred at the branch level. Moreover, it was observed that the vibration acceleration of the jujube tree was significantly higher at excitation frequencies of 12 Hz, 17 Hz, and 19 Hz. At excitation frequencies of 12 Hz, 17 Hz, or 19 Hz, the jujube tree demonstrated substantial stress-deformation responses. Consequently, it is feasible to conduct vibration harvesting tests at a frequency of 12 Hz or 17 Hz. For the harvesting test, a vibration frequency within the range of 12–20 Hz can be selected. These studies specifically examined the vibration mechanisms of jujube trees or jujube branches. By conducting simulation analyses and field experiments, researchers successfully identified vibration parameters that yield superior effects on jujube trees. These findings provide valuable insights for designing the optimal input vibration parameters for vibratory harvesting devices to improve the harvesting rate of jujubes.

In summary, compared with other harvesting methods, the vibration harvesting method can harvest red jujubes uninterruptedly with a certain vibration frequency and vibration amplitude, which is important to improve the mechanized harvesting efficiency of red jujubes. However, the current research primarily concentrates on the equipment for harvesting red jujubes through vibration. There is a limited amount of research on the vibration mechanism of jujube trees, which is mainly based on simplified models of jujube trees and branches. The effects of intrinsic frequency of jujube trees, various vibration frequencies, and different vibration amplitudes generated by the excitation device on the vibration characteristics and instantaneous acceleration of jujube branches are examined through finite element analysis and harmonic response analysis to seek a range of jujube tree vibration parameters with better vibration effects. In the domain of red jujube vibration harvesting devices, prevailing studies employ fixed vibration frequencies and amplitudes to vibrate jujube trees. While this approach endeavors to select optimal vibration parameters for red jujube harvesting by delving into the vibration mechanism of jujube trees and their branches, it fails to account for the diverse diameters among individual jujube trees, which easily results in tree trunk damage, thereby affecting the subsequent year’s red jujube yield. Moreover, jujube trees with distinct diameters exhibit substantial discrepancies in inherent frequencies and branch vibration characteristics. Consequently, the adoption of fixed vibration frequencies and amplitudes for red jujube harvesting leads to a diminished harvest rate. This study introduces a novel vibration parameter optimization method that takes into consideration the different diameters of jujube trees. It aims to adjust the vibration frequency and amplitude of the red jujube vibration harvesting device based on the optimal vibration parameters specific to each jujube tree diameter. This endeavor seeks to attain better vibration effects and enhance the jujube harvest rate. The findings of this study serve as a theoretical foundation for determining the optimal vibration harvesting parameters for jujube trees of diverse diameters, while also providing technical support for improving the vibration harvesting device of red jujube and improving the vibration harvesting efficiency. This study will be conducted in the following three aspects:

• To establish a model of the forced vibration dynamics of jujube trees to identify the key factors in the vibration process and provide a theoretical basis for modal analysis and harmonious response analysis;
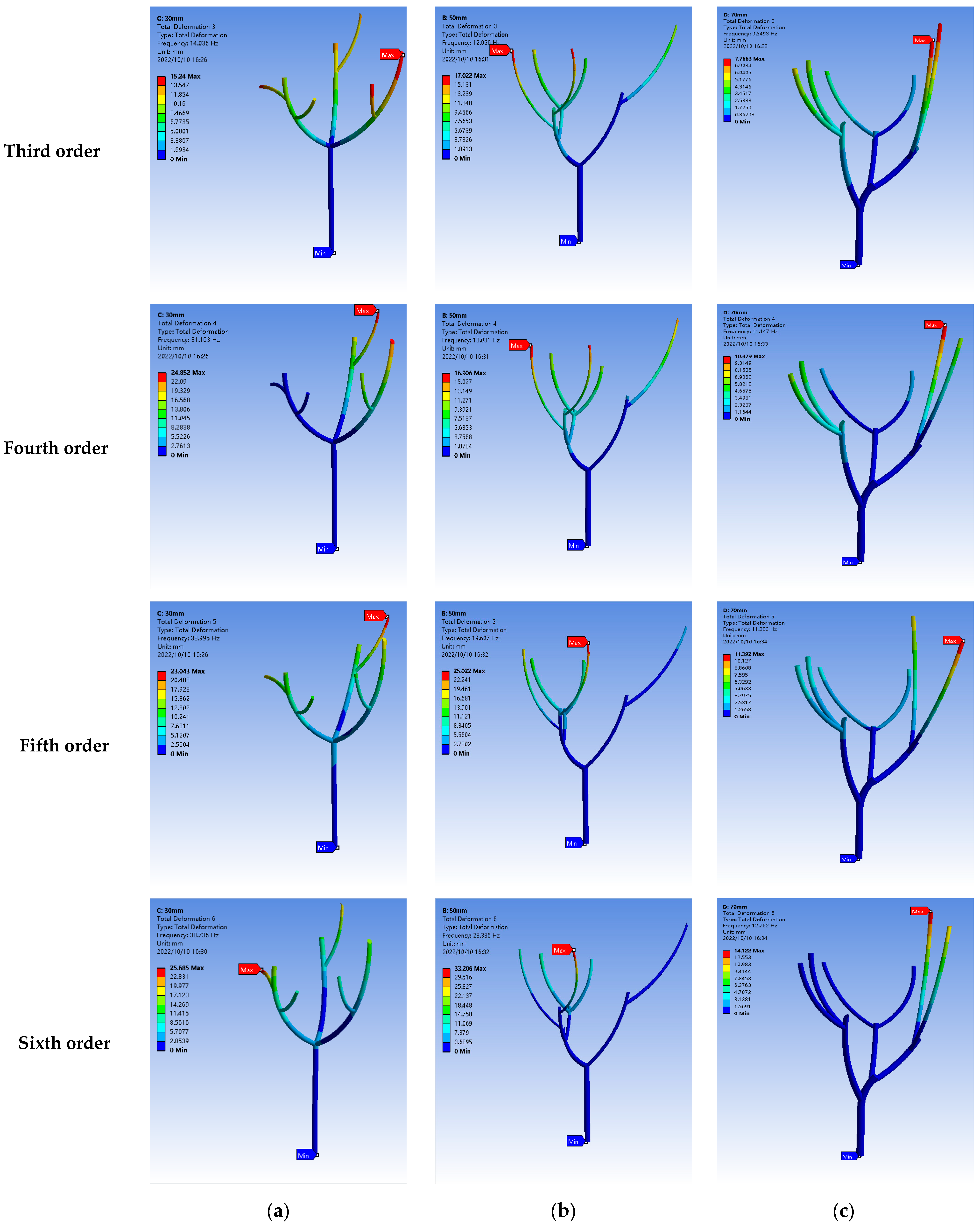
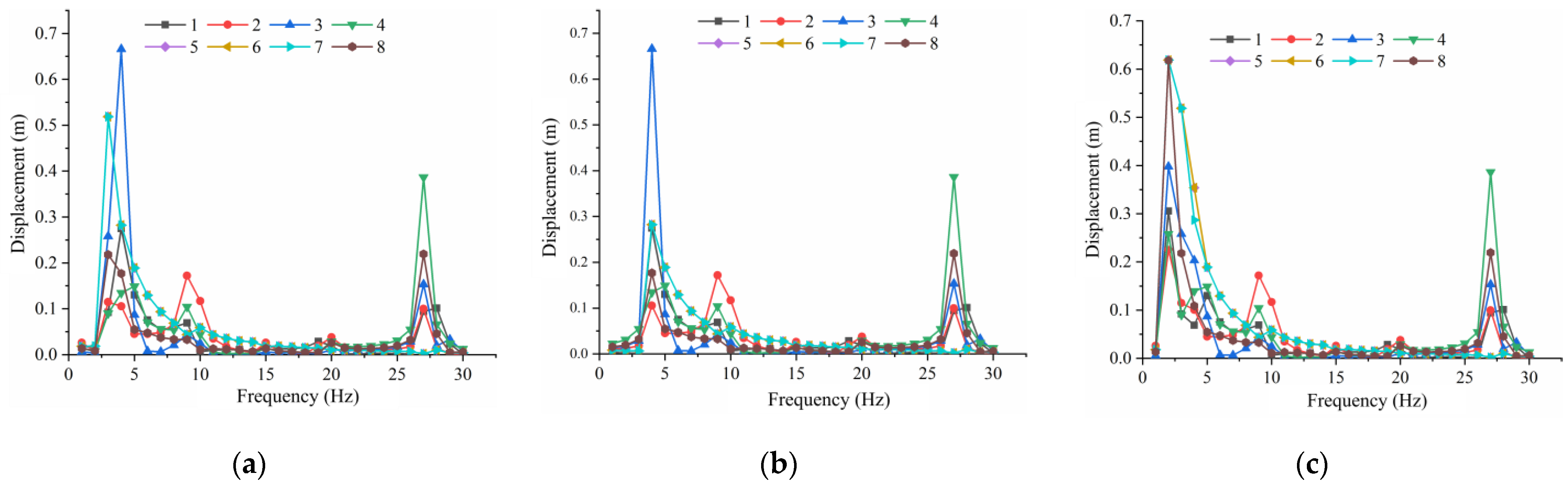
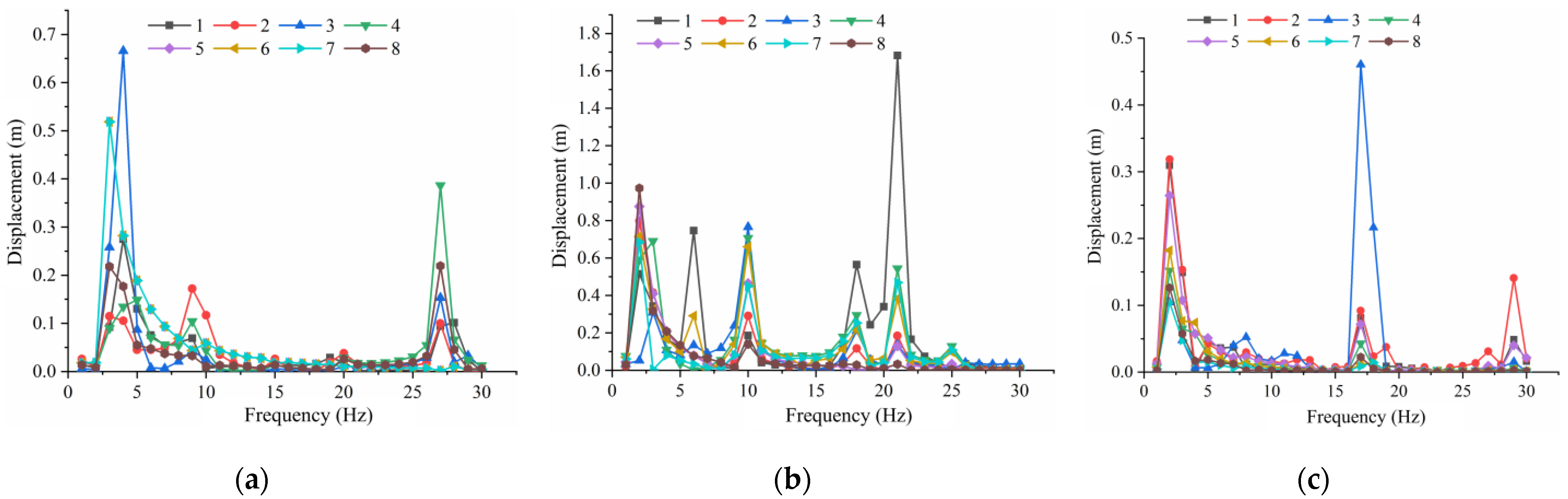
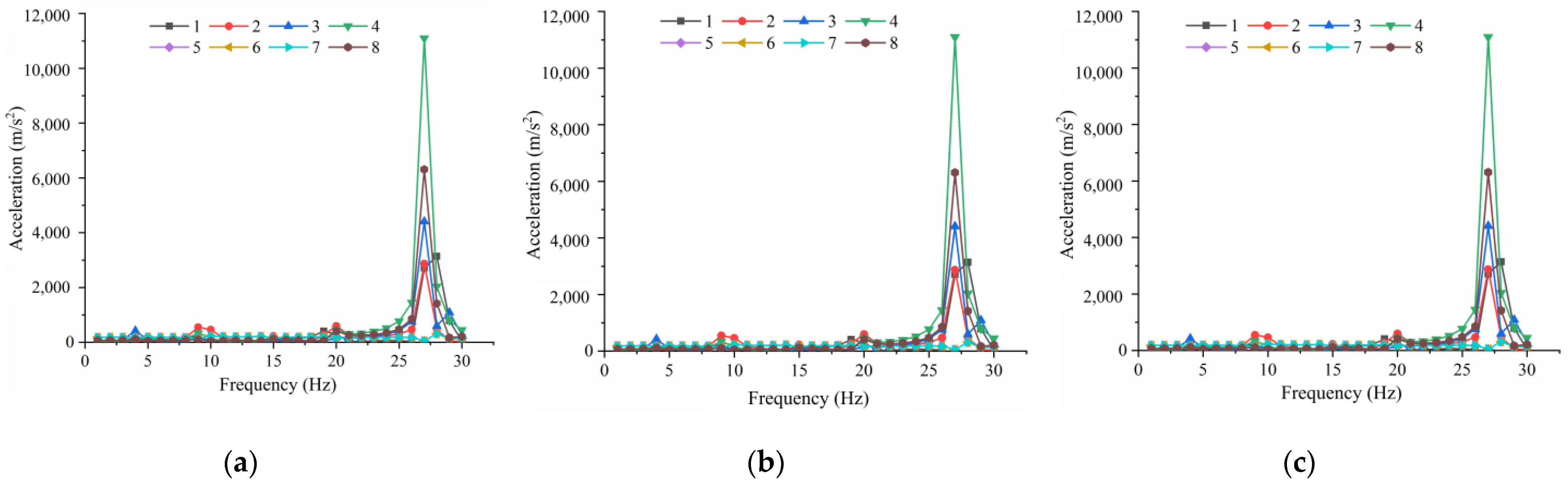
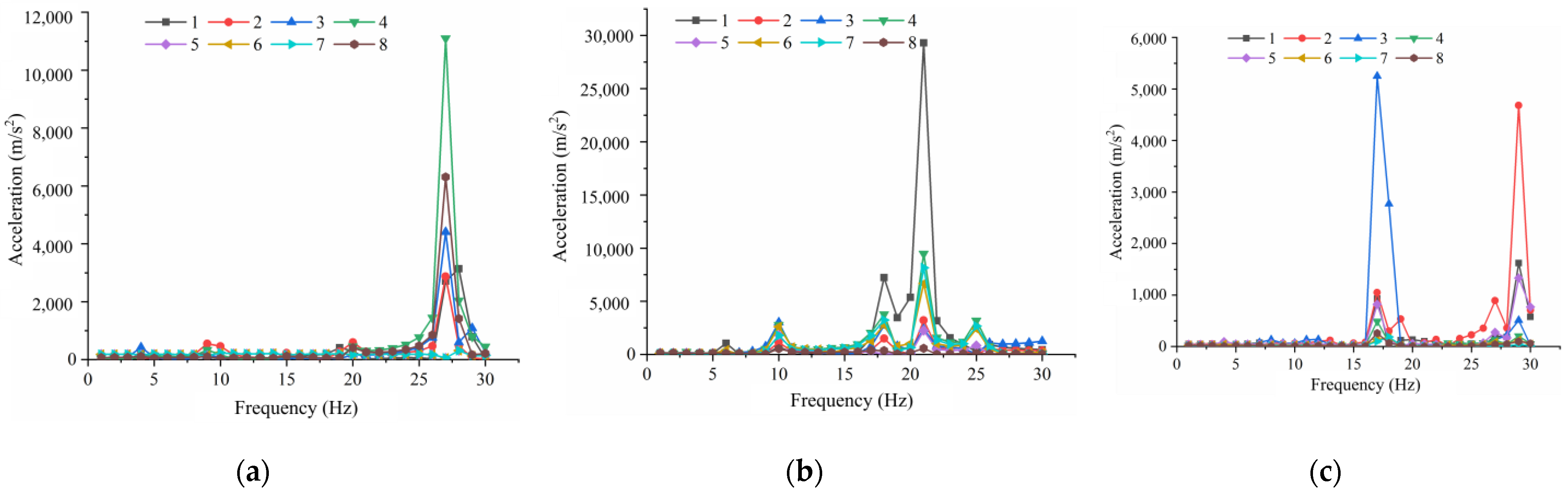
• To investigate the intrinsic frequency characteristics of jujube trees of different diameters by constructing 3D models and conducting modal analysis, and conducting harmonic response analysis to investigate the displacement response relationship and acceleration response relationship of red jujube trees using different vibration factors at different diameters;
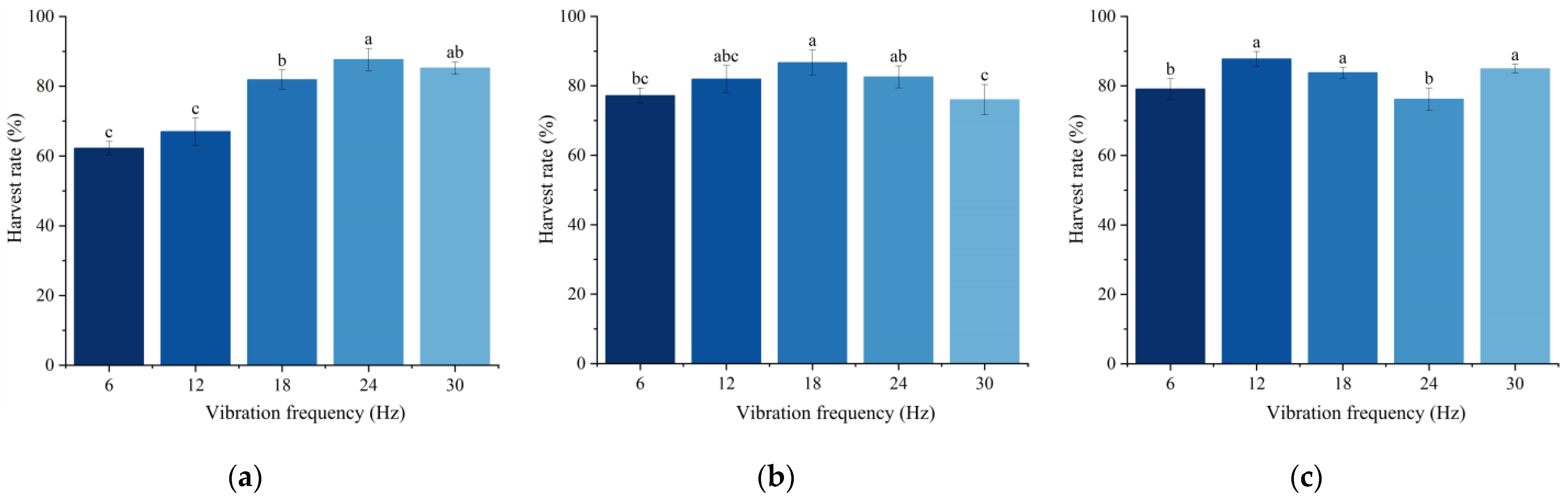
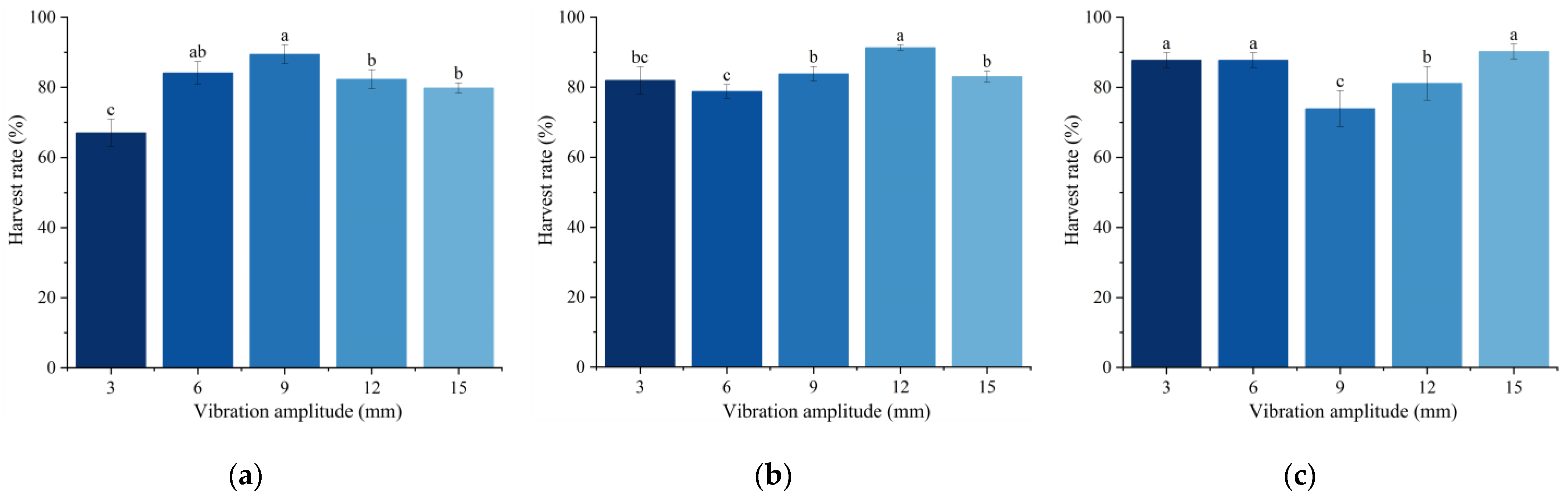
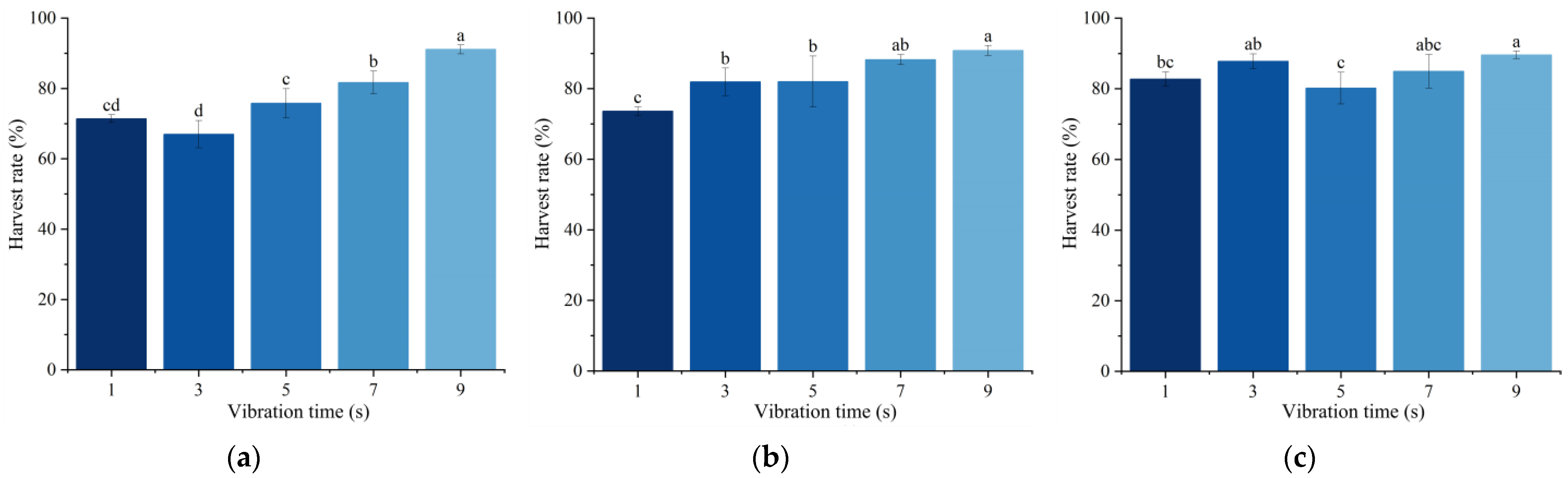
• To investigate the effect of different vibration factors on the harvesting efficiency of jujube trees with varying diameters, single-factor tests of vibration parameters were conducted to determine the impact of each factor on the jujube harvesting rate. Furthermore, multi-factor tests were carried out to identify the optimal vibration parameters for jujube trees of different diameters.

2. Materials and Methods

2.1. Principle of Vibration Harvesting of Red Jujube

Vibration harvesting involves using machinery to clamp and secure fruit trees into a rigid structure, and then inducing simple harmonic vibration through a vibration device to transfer energy to the fruit, resulting in accelerated motion. As the inertial force of the red jujube during this motion surpasses the bonding force between the fruit and the fruit stalk, the fruit separates naturally from the tree. To investigate the factors that affect vibration during the harvesting of red jujube, this study developed a dynamics model of the jujube tree and analyzed the vibration-influencing factors of the tree during the vibration process.

Since the growth characteristics of fruit trees conform to the Euler–Bernoulli beam [28,29], where the length is more than five times the cross-section, this study simplified the trunk to a beam model with an equal cross-section, where one end is fixed and the other end is free, and a concentrated mass is present at the free end [30,31,32,33]. The coordinate system xoy was constructed with the root of the tree trunk as the origin O, and a unit length of the beam unit was used for force analysis, as shown in Figure 1. By analyzing the forces acting on the simplified beam model, a better understanding of the mechanical characteristics of the fruit tree during the vibration harvesting process can be obtained.

The jujube tree model is simplified to a beam model with a concentrated mass at the end, which intercepts an arbitrary section dx at x with mass ρSdx, a shear force of V(x,t), and a bending moment of M(x,t) on the micro end, and according to Newton’s second law, Equation (1) can be obtained as follows:

$$\rho Sdx\frac{{\mathsf{\partial }}^{2}y(x,t)}{\mathsf{\partial }{t}^2}=-(V_{(x,t)}+\frac{\mathsf{\partial }V(x,t)}{\mathsf{\partial }x}dx)+V(x,t)+f(x,t)$$

(1)

where ρ is the density of the tree trunk, kg/m³; S is the cross-sectional area of the tree trunk, m²; and y(x,t) is the displacement of the trunk along the y-axis direction, m.

Rectifying Equation (1) yields Equation (2):

$$\rho S\frac{{\mathsf{\partial }}^{2}y(x,t)}{\mathsf{\partial }{t}^2}+\frac{\mathsf{\partial }V(x,t)}{\mathsf{\partial }x}=f(x,t)$$

(2)

Since the rotational moment of inertia of the cross-section is neglected, the equation can be simplified to Equation (3) according to the momentum moment theorem:

$$(M(x,t)+\frac{\mathsf{\partial }M(x,t)}{\mathsf{\partial }x}dx)-(M(x,t)+V(x,t)dx)=0$$

(3)

Rectifying Equation (3) yields Equation (4):

$$\frac{\mathsf{\partial }M(x,t)}{\mathsf{\partial }x}=V(x,t)$$

(4)

Substituting Equation (4) into Equation (2) yields Equation (5):

$$\rho S\frac{{\mathsf{\partial }}^{2}y(x,t)}{\mathsf{\partial }{t}^2}+\frac{{\mathsf{\partial }}^{2}M(x,t)}{\mathsf{\partial }{x}^2}=f(x,t)$$

(5)

According to the relationship between bending moment and deflection of material mechanics, Equation (5) can be organized to obtain Equation (6):

$$M(x,t)=EI\frac{{\mathsf{\partial }}^{2}y(x,t)}{\mathsf{\partial }{x}^2}$$

(6)

where E is Young’s modulus of the jujube tree trunk, Pa; I is the moment of inertia of the jujube tree cross-section around the central axis, mm⁴.

Substituting Equation (6) into Equation (5) yields Equation (7):

$$\rho S\frac{{\mathsf{\partial }}^{2}y}{\mathsf{\partial }{t}^2}+\frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{x}^2}(EI\frac{{\mathsf{\partial }}^{2}y}{\mathsf{\partial }{x}^2})=f(x,t)$$

(7)

The differential equation for the forced vibration of the jujube tree, Equation (8), is obtained by collapsing Equation (7):

$$EI\frac{{\mathsf{\partial }}^{4}y(x,t)}{\mathsf{\partial }{x}^4}+\rho S\frac{{\mathsf{\partial }}^{2}y(x,t)}{\mathsf{\partial }{t}^2}=f(x,t)$$

(8)

Then the differential equation for the free vibration of the jujube tree is shown in Equation (9):

$$\frac{{\mathsf{\partial }}^{4}y(x,t)}{\mathsf{\partial }{x}^4}+\frac{1}{a^2}\frac{{\mathsf{\partial }}^{2}y(x,t)}{\mathsf{\partial }{t}^2}=0$$

(9)

where $a^2=\frac{EI}{\rho S}$.

Since y(x,t) is a function of x concerning time t, the separation of variables method is used to find the solution of its sub-equation, and the solution of the equation is set to Equation (10):

$$y(x,t)=Y(x)T(t)$$

(10)

Substituting Equation (10) into Equation (9) and organizing gives Equation (11):

$$\frac{a^2}{Y(x)}\frac{d^{4}Y(x)}{d{x}^4}=-\frac{1}{T(t)}\frac{d^{2}T(t)}{d{t}^2}=c=w^2$$

(11)

where c = w² is a constant.

Solving for Equation (11), the vibration function of the jujube tree is shown in Equation (12):

$$Y(x)=C_1\cos \beta x+C_2\sin \beta x+C_3\cosh \beta x+C_4\sinh \beta x$$

(12)

Then the intrinsic frequency of the jujube tree is shown in Equation (13):

$$w={(\beta L)}^2\sqrt{\frac{EI}{\rho S{L}^2}}$$

(13)

Since one fixed section of the model has a concentrated mass at one end, its boundary condition is shown in Equation (14):

$$\left\{\begin{array}{l}Y(0)=0\\ \frac{dY(0)}{dx}=0\\ \frac{d^{2}Y(L)}{d{x}^2}=0\\ EI\frac{d^{3}Y(L)}{d{x}^3}=-M{w}^{2}Y(L)\end{array}\right.$$

(14)

Substituting the boundary conditions into the equation yields the equation as shown in Equation (15):

$$\left\{\begin{array}{l}{C}_1+C_3=0\\ \beta (C_2+C_4)=0\\ -{\beta }^2\cos (\beta L)C_1-{\beta }^2\sin (\beta L)C_2+{\beta }^2\cosh (\beta L)C_3+{\beta }^2\sinh (\beta L)C_4=0\\ (EI{\beta }^3\sin (\beta L)+M{w}^2\cos (\beta L))C_1+(EI{\beta }^3\cos (\beta L)+M{w}^2\sin (\beta L))C_2+\\ (EI{\beta }^3\sinh (\beta L)+M{w}^2\cosh (\beta L))C_3+(EI{\beta }^3\cosh (\beta L)+M{w}^2\sinh (\beta L))C_4=0\end{array}\right.$$

(15)

Then the parameter matrices of C₁, C₂, C₃, and C₄ are:

$$\left|\begin{array}{cccc}1& 0& 1& 0\\ 0& 1& 0& 1\\ -{\beta }^2\cos (\beta L)& -{\beta }^2\sin (\beta L)& {\beta }^2\cosh (\beta L)& {\beta }^2\sinh (\beta L)\\ EI{\beta }^3\sin (\beta L)+M{w}^2\cos (\beta L)& EI{\beta }^3\cos (\beta L)+M{w}^2\sin (\beta L)& EI{\beta }^3\sinh (\beta L)+M{w}^2\cosh (\beta L)& EI{\beta }^3\cosh (\beta L)+M{w}^2\sinh (\beta L)\end{array}\right|=0$$

Based on the analysis of the jujube tree’s vibration function, the factors that affect the shedding effect when the tree is vibrated by the excitation force include (1) vibration position, (2) vibration frequency, (3) vibration amplitude, (4) Young’s modulus of the jujube tree trunk, and (5) moment of inertia of the jujube tree cross-section around the central axis. However, in the process of jujube tree vibration harvesting, the farther the vibration position is from the root of the tree, the better the vibration effect, and the higher the harvesting efficiency. In this study, Young’s modulus of the jujube tree trunk was considered to be the same, and the vibration could be selected at a fixed height according to the growth characteristics of jujube trees. Therefore, the main influencing factors when the jujube tree is forced to vibrate are the vibration frequency and vibration amplitude.

2.2. Modal Analysis Methods of Jujube Tree Models with Different Diameters

2.2.1. Three-Dimensional Modeling of Jujube Trees with Different Diameters

This study aimed to investigate the impact of various vibration frequencies and amplitudes on jujube trees with different diameters. To achieve this, 3D models were created for jujube trees with varying diameters. The measurements were conducted at the Jujube Tree Experimental Station of Northwest Agriculture and Forestry University of Science and Technology in Qingjian County, Yulin City, Shaanxi Province, for different growth years of jujube trees. The diameter of the jujube trees was measured using vernier calipers, and the length of the jujube trees was measured using a tape measure. The results of the diameter measurements of the jujube trees are shown in

Table 1. Diameter measurement results of jujube trees of different ages.

Tree Age (Year)	Quantity (Trees)	Maximum Diameter (mm)	Minimum Diameter (mm)	Average Diameter (mm)	Coefficient of Variation (%)
3	10	31.26	29.15	30.18	2.86
5	10	52.34	49.56	50.71	2.34
8	10	73.25	65.23	69.78	4.82

.

In this study, 10 jujube trees each aged 3, 5, and 8 years were measured for diameter and the results are listed in Table 1. The smallest average diameter was observed in jujube trees aged three years (30.18 mm), while the largest average diameter was recorded in jujube trees aged eight years (69.78 mm). The coefficient of variation of diameter was the smallest for jujube trees aged five years (2.34%) and the largest for jujube trees aged eight years (4.82%). Thus, the diameter variation of jujube trees of the same age was found to be small. Three jujube trees of the same height but with different diameters of 30 mm, 50 mm, and 70 mm were randomly selected to study the vibration characteristics of different diameters. The main trunk and first-level branches of the selected trees were measured, and the height position distribution of the first-level branches was recorded. For 3D modeling and post-simulation analysis, the leaves and jujube fruit mass were not considered, and 3D models of the main trunk and first-level branches were constructed using UG NX 12.0 software. The main trunk and first-level branches were simplified to Euler–Bernoulli beam models, and their cross-sectional areas were assumed to be circular. The 3D models for the three different diameters of jujube trees were constructed, as shown in Figure 2. The specific environment settings for modeling in this study are shown in

Table 2. Experimental environment.

Configuration	Parameter
Operating system	Windows 11
CPU	Intel(R) i7-10870H
GPU	NVIDIA GeForce RTX2060
3D modeling software	UG NX 12.0

.

2.2.2. Modal Simulation of Jujube Tree Model

Performing modal analysis [34,35] of jujube trees can help understand their modal parameters, providing a theoretical basis for minimizing damage to trees during mechanical vibration-based red jujube harvesting. The intrinsic frequency of jujube trees is a material property-related characteristic, with a higher trunk stiffness producing a more prominent vibration effect. The modal vibration pattern is another intrinsic characteristic of the jujube tree, with influencing factors similar to intrinsic frequency. Vibrating the jujube tree at a frequency close to its intrinsic frequency can improve energy transfer and red jujube vibration harvesting efficiency. Referring to Castro-García et al., Niu et al., Wang et al., and Wei et al. for the modal analysis method of fruit trees [36,37,38,39], in this study, modal simulation analysis of the jujube tree model was conducted as follows.

(1)

Importing the three-dimensional model of the jujube tree

The three-dimensional model of the jujube tree was imported into ANSYS Workbench after constructing it using NX 12.0. To simplify the analysis process, physical property differences between the trunk and branches were ignored, and the model was defined materially. Physical property parameters of the jujube tree were referred to in the study of Zhiyuan Zhang [40], with the model’s physical property parameters shown in

Table 3. Physical parameters of jujube trees.

Physical Property Parameters	Values
Modulus of elasticity (MPa)	6658
Density (kg/m3)	478
Poisson’s ratio	0.3

.

(2)

Meshing

To obtain more accurate analysis results, the mesh size was set to 5 mm, and tetrahedral and hexahedral meshes were used to divide the jujube tree model in this study. The meshing results for different diameters of jujube trees are shown in

Table 4. Results of meshing for different diameters of jujube trees.

Diameter (mm)	Mesh (Units)	Number of Nodes (Units)
30	26,502	50,563
50	39,928	74,809
70	86,495	157,756

.

(3)

Imposition of restraint

In studying the growth of jujube trees, the influence of gravity can be disregarded, with the tree primarily experiencing a fixed constraint effect from the surrounding soil. As such, in conducting modal analysis on a model of a jujube tree, fixed constraints in the form of a fixed support should be applied at the base of the tree trunk.

(4)

Modal analysis solution

In this study, the maximum modal order of the jujube tree is set to 20. Since the subiteration method uses the complete stiffness and mass matrices to solve the model with high accuracy, the sub-iteration method is used for solving the model. Total deformation is selected for the solution results and the model is solved.

2.3. Harmonic Response Analysis Method for Jujube Tree Model

The following section is dedicated to exploring the vibration effects of jujube trees with different diameters under various vibration factors. To analyze the displacement response and acceleration response of these trees, we have utilized the harmonic response method.

2.3.1. Introduction of Harmonic Response Analysis Method

Harmonic response analysis is a technique used to study the behavior of a system when it is in a resonant state [41,42,43]. It involves analyzing the frequency response characteristics of the system to determine resonant frequency and amplitude, among other parameters. By optimizing system design and performance based on these parameters, the system can be made more efficient. In this study, the harmonic response analysis is used to examine the displacement and acceleration responses of jujube tree branches subjected to different frequency excitation forces. Three jujube tree models with varying diameters are subjected to excitation forces of different vibration amplitudes. Eight random locations on the tree branches are selected as test points to monitor displacement and acceleration response between 0 and 30 Hz. The monitoring points are marked with red dots in Figure 3.

2.3.2. Design of Parameters for Harmonic Response Analysis

In this study, the Harmonic Response module in ANSYS Workbench was selected based on the modal analysis of the jujube tree. The model from the modal analysis stage was inherited and a harmonic response analysis was conducted by setting the harmonic frequency to 30 Hz and the step length to 30 steps.

To analyze the displacement and acceleration response curves of each monitoring point of the 50 mm diameter jujube tree model with different amplitudes, the diameter of the selected test tree model was 50 mm, the excitation force was set at 50 N, and the excitation position at 400 mm. Three different excitation amplitudes of 3 mm, 6 mm, and 9 mm were applied to the model.

To analyze the displacement and acceleration response curves of each monitoring point on the jujube tree model with different diameters under identical excitation conditions, the test tree models with diameters of 30 mm, 50 mm, and 70 mm were selected. The excitation force was set at 50 N, the excitation position at 400 mm, and the excitation amplitude at 3 mm.

2.4. Vibration Test

To investigate the effect of vibration frequency, amplitude, and time on red jujube harvesting of jujube trees with varying diameters, nine trees with diameters of 30 mm, 50 mm, and 70 mm were subjected to vibration tests. The tests were carried out at the Red Jujube Experiment Station of Northwest University of Agriculture and Forestry in Qingjian County, Shaanxi Province, using a homemade red jujube vibration device consisting of a clamping mechanism, an excitation mechanism, a frequency modulation motor, a walking mechanism, a fruit collection mechanism, and other components, along with a frequency modulator and an electronic balance. The process of the jujube tree vibration test was depicted in Figure 4.

Initially, the amplitude dial of the homemade red jujube vibration device was adjusted to achieve different vibration amplitudes. The trunk of the jujube tree was then secured using the clamping device of the homemade red jujube vibration harvesting device, forming a rigid body with the harvesting device. The jujube trees were then vibrated by adjusting the frequency regulator to different vibration frequencies and vibration times, and finally the vibration-shed jujubes were collected by the fruit collection mechanism, and the total mass of successfully harvested red jujubes and the total mass of unsuccessfully harvested red jujubes were counted and recorded. For each diameter of jujube trees, five vibration tests were performed, and the average value was taken as the final result. After completing one round of tests, the jujube trees of different diameters were replaced while maintaining the same clamping height for the next round of tests. The vibration parameters of jujube trees with different diameters were obtained, providing an experimental basis for selecting the optimal parameters for harvesting red jujubes from jujube trees of different diameters.

2.5. Vibration Test Index

The purpose of the jujube tree vibration harvesting test is to achieve an optimal harvesting effect of red jujubes, and the performance of the vibration device is directly related to the harvesting results of red jujubes. The harvest rate is a critical indicator used to evaluate the best vibration factor, and it has a significant impact on the assessment of the red jujube harvesting effect. During the vibration harvesting process, the fruits that detached from the branches were considered successfully harvested, while those that remained on the tree were considered unsuccessfully harvested. In this test, the total mass of successfully harvested red jujubes and the total mass of unsuccessfully harvested red jujubes were recorded separately, and the harvesting rate was calculated using Equation (16) as follows:

$$R=\frac{Q_{\mathrm{a}}}{Q_{\mathrm{a}}+Q_n}\times 100\%$$

(16)

where R is the harvest rate of red jujube fruit; Q_a is the mass of successfully harvested red jujubes; Q_n is the mass of unsuccessfully harvested red jujubes.

3. Results and Discussion

3.1. Modal Simulation Results and Analysis of the Jujube Tree Model

The sub-iterative method was used to solve the 3D model of the jujube tree. The inherent frequencies of the model obtained by solving for different diameters of jujube trees are shown in Figure 5. The first six orders of modal analysis were also performed, and the modal vibration patterns of different diameters of jujube trees are shown in Figure 6.

Figure 5 illustrates the modal analysis results for different diameters of jujube trees, revealing that the intrinsic frequencies of jujube trees increase gradually with the order. In the 20-order modal analysis, the minimum intrinsic frequency for different diameters of jujube trees is the first-order modal, which are 7.99 Hz, 8.44 Hz, and 5.98 Hz, respectively. The curves from the first to the 20th order reveal that the increase in intrinsic frequencies tends to be consistent across different orders. Notably, the number of intrinsic frequency maxima at different orders is significantly higher for the jujube tree with a diameter of 70 mm than for the other two diameters, while the jujube tree with a diameter of 30 mm has the least number of intrinsic frequency maxima at different orders. Thus, the intrinsic frequency of the jujube tree increases with increasing diameter.

Based on Figure 6, it can be observed that the deformation of branches in the same mode varies significantly for jujube trees of different diameters. Additionally, the deformation increases gradually from the bifurcation to the end of the branch on the same branch, reaching its maximum value at the end of the branch where the vibration effect is strongest. For instance, the maximum deformation in the first-, second-, fourth-, and fifth-order vibration patterns occurred on the same branches for jujube trees with a diameter of 30 mm, whereas for jujube trees with a diameter of 50 mm, the maximum deformation in the first- and second-order vibration patterns occurred on the same branches, and the maximum deformation in the third- and fourth-order vibration patterns occurred on other branches. Moreover, for jujube trees with a diameter of 70 mm, the maximum deformation in the first-, third-, fourth-, and sixth-order vibration patterns also occurred on the same branches. In the first six orders of vibration, there were differences in the vibration characteristics of jujube trees of different diameters at each order of vibration, and the maximum number of vibrating branches occurred at different orders of vibration. For example, the maximum number of resonant branches was reached at the third order of vibration for jujube trees with a diameter of 30 mm, whereas it was reached at the fourth order of vibration for jujube trees with a diameter of 50 mm, and at the third order of vibration for jujube trees with a diameter of 70 mm. Therefore, the excitation force frequency can be adjusted for jujube trees of different diameters to maximize the number of vibrating branches and improve the efficiency of red jujube vibration harvesting.

3.2. Harmonic Response Analysis of Jujube Tree Model Based on Different Diameters

3.2.1. Displacement Response Analysis

Based on the parameters set in Section 2.3.2 for harmonic response analysis, displacement response curves of various monitoring points on the 50 mm diameter jujube tree model under different amplitudes were obtained through the post-processing module, as shown in Figure 7. Under the same excitation conditions, displacement response curves of various monitoring points on jujube tree models with different diameters are shown in Figure 8.

When the vibration frequency approaches the intrinsic frequency of the jujube tree, resonance occurs, and the vibration displacement and acceleration increase significantly. Figure 7 shows that the displacement change trend of the jujube tree is approximately the same as the change of vibration frequency at different amplitudes. At low frequencies, the peak displacement of the jujube tree is higher, and it gradually decreases with increasing frequency. The displacement variation peaks at approximately 3–5 Hz, 8–10 Hz, and 25–27 Hz. The peak displacement for a 3 mm amplitude jujube tree was maximum at 0.666 m at 4 Hz and minimum at 0.172 m at 9 Hz. For a 6 mm amplitude jujube tree, the peak displacement was maximum at 0.676 m at 4 Hz and minimum at 0.173 m at 9 Hz. For a 9 mm amplitude jujube tree, the peak displacement was maximum at 0.618 m at 4 Hz and minimum at 0.173 m at 9 Hz. The frequency range of maximum displacement is the same for jujube trees with the same diameter but different amplitudes and the same excitation position.

Based on Figure 8, there are significant differences in the resonance displacement changes of jujube trees with different diameters under the condition of a 400 mm excitation height from the root and a 3 mm amplitude. At low-frequency vibration, the peak resonance displacement of the jujube tree is higher, and it decreases gradually with an increase in frequency. The peak resonance displacement of the 30 mm diameter jujube tree was maximum at 4 Hz, while that of the 70 mm diameter jujube tree was maximum at 17 Hz. Additionally, the 50 mm diameter jujube tree produced the widest range of resonance displacement frequencies and the highest peak resonance displacement. Therefore, for different diameters of jujube trees, different vibration frequencies and amplitudes should be selected to maximize harvesting efficiency.

3.2.2. Acceleration Response Analysis

Based on the parameters established in the experimental design for harmonic response analysis in Section 2.3.2, the post-processing module was used to generate acceleration response curves for each monitoring point of the 50 mm diameter jujube tree model at different amplitudes, as illustrated in Figure 9. Meanwhile, Figure 10 displays the acceleration response curves of each monitoring point for jujube tree models with various diameters under the same excitation conditions.

As shown in Figure 9, the variation in the resonant acceleration of the jujube tree was relatively consistent when different amplitudes were used for harmonic response analysis at the same diameter. The acceleration response of the jujube trees under different amplitudes was approximately the same as the vibration frequency changed. At low-frequency vibrations, the acceleration response of the jujube trees was relatively consistent, while at high-frequency vibrations, the acceleration response varied more. The acceleration response of jujube trees with different amplitudes peaked around 3–5 Hz, 8–10 Hz, 19–21 Hz, and 26–28 Hz with changes in frequency. At an amplitude of 3 mm, the red jujube’s acceleration response reached a maximum peak of 11,100 m/s² at around 27 Hz and a minimum peak of 421 m/s² at around 4 Hz. At an amplitude of 6 mm, the acceleration response reached a maximum peak of 11,500 m/s² around 26 Hz and a minimum peak of 411 m/s² around 5 Hz. At an amplitude of 9 mm, the acceleration response reached a maximum peak of 11,200 m/s² around 27 Hz and a minimum peak of 421 m/s² around 4 Hz. Therefore, the variation in amplitude has less effect on the acceleration response of jujube trees with the same diameter because the mechanical properties are the same. The acceleration variations produced by the jujube trees with amplitudes of 3 mm, 6 mm, and 9 mm at monitoring points 2, 3, 4, and 8 were larger than those at the remaining detection points, possibly because monitoring points 2, 3, 4, and 8 were farther away from the excitation and had larger moments.

The results of the harmonic response analysis for jujube trees of different diameters under the same excitation conditions (excitation height of 400 mm from the root and amplitude of 3 mm) are presented in Figure 10. The acceleration response of the jujube trees showed a significant variation among different diameters. The jujube tree with a diameter of 50 mm exhibited the widest range of resonant frequencies for the acceleration response, while the jujube trees with diameters of 30 mm and 70 mm had the narrowest range of resonant frequencies. The variation of acceleration response for different diameters of jujube trees also differed at specific frequencies. For instance, the 30 mm diameter jujube tree had a minimum acceleration response of 421 m/s² at 4 Hz and a maximum peak value of 11,100 m/s² at 27 Hz. Similarly, the 50 mm diameter jujube tree had a minimum acceleration response of 1060 m/s² at 6 Hz and a maximum peak value of 29,300 m/s² at 21 Hz. The 70 mm diameter jujube tree had a maximum peak value of 5250 m/s² at 17 Hz and a minimum value of 891 m/s² at 27 Hz. Moreover, there were variations in acceleration at different monitoring points for different diameters of jujube trees, which could be attributed to the different distances between the monitoring points and the excitation locations, leading to the generation of different moments and energies. Hence, a suitable vibration frequency range should be selected for different diameters of jujube trees to improve the efficiency of vibration harvesting. For 30 mm diameter jujube trees, the vibration frequency range can be chosen from 4–30 Hz; for 50 mm diameter jujube trees, from 6–25 Hz; and for 70 mm diameter jujube trees, from 17–29 Hz.

3.3. Single-Factor Test and Analysis

3.3.1. Effect of Vibration Frequency of Jujube Trees with Different Diameters

In this study, vibration harvesting tests were conducted on jujube trees with diameters of 30 mm, 50 mm, and 70 mm. The vibration position was set at 0.4 m, and the vibration amplitude and time were fixed at 3 mm and 3 s, respectively. In a single-factor test, vibration frequencies of 6 Hz, 12 Hz, 18 Hz, 24 Hz, and 30 Hz were set. The experimental results of the harvesting rate at different vibration frequencies are presented in

Table 5. Test results of harvest rate under different vibration frequencies.

Vibration Frequency (Hz)	Diameter 30 mm		Diameter 50 mm		Diameter 70 mm
	Average Value (%)	Standard Deviation (%)	Average Value (%)	Standard Deviation (%)	Average Value (%)	Standard Deviation (%)
6	62.24	1.92	77.21	2.15	79.09	2.98
12	67.01	3.88	81.93	3.89	87.77	2.10
18	81.90	2.74	86.69	3.64	83.78	1.57
24	87.66	3.19	82.58	3.17	76.16	3.26
30	85.20	1.80	75.99	4.38	84.95	1.29

.

Table 5 shows the results of the harvest rate tests conducted under the same vibration position, amplitude, and time conditions for jujube trees with diameters of 30 mm, 50 mm, and 70 mm. It was observed that as the vibration frequency increased from 6 Hz to 30 Hz, the average harvest rate of red jujubes initially increased and then decreased, indicating a bell-shaped trend. The increase in vibration frequency led to more energy being transferred to the jujube fruit, resulting in increased movement and easier shedding. However, as the vibration frequency continued to increase, the harvest rate decreased due to a decrease in energy transfer and weaker movement, making shedding difficult. Furthermore, differences in the harvest rates of red jujubes with different diameters were observed under the same vibration conditions, possibly due to variations in the growth state and energy absorption capacity of the jujube trees, leading to different energy transfer to the red jujube fruits and affecting their abscission.

Figure 11 displays the outcome of a single-factor analysis on the impact of vibration frequency on the harvest rate for jujube trees of different diameters. For jujube trees with a diameter of 30 mm, the harvest rate significantly increased within the 12–24 Hz range of vibration frequency, but gradually decreased beyond 24 Hz. Figure 11a shows significant differences between 12 Hz, 18 Hz, and 24 Hz. For jujube trees with a diameter of 50 mm, the harvest rate initially increased and then decreased with increasing vibration frequency, with significant differences between 18 Hz and 30 Hz, 6 Hz and 18 Hz, and 24 Hz and 30 Hz, as shown in Figure 11b. In the case of jujube trees with a diameter of 70 mm, the harvest rate significantly increased and then decreased with increasing vibration frequency, followed by a significant increase again. Figure 11c shows no significant difference between 12 Hz, 18 Hz, and 30 Hz, but a significant difference between 6 Hz and 24 Hz. These findings indicate that in the process of vibration harvesting, the appropriate vibration frequency should be selected based on the diameter of the jujube trees to enhance the harvest rate.

3.3.2. Effect of Vibration Amplitude for Different Diameters of Jujube Trees

In the single-factor test, with the vibration position set at 0.4 m, the vibration frequency at 12 Hz, and the vibration time at 3 s, the vibration amplitude was set at 3 mm, 6 mm, 9 mm, 12 mm, and 15 mm for jujube trees with diameters of 30 mm, 50 mm, and 70 mm. The results of the harvest rate under different vibration amplitudes are shown in

Table 6. Test results of harvest rate under different vibration amplitudes.

Vibration Amplitude (mm)	Diameter 30 mm		Diameter 50 mm		Diameter 70 mm
	Average Value (%)	Standard Deviation (%)	Average Value (%)	Standard Deviation (%)	Average Value (%)	Standard Deviation (%)
3	67.01	3.88	81.93	3.89	87.77	2.10
6	84.10	3.29	78.78	1.97	80.37	1.07
9	89.40	2.70	83.83	2.09	73.89	5.13
12	82.31	2.67	91.30	0.77	81.14	4.81
15	79.77	1.47	83.04	1.62	90.25	2.10

.

Table 6 presents the results of a single-factor test conducted with the vibration amplitude set at 3 mm, 6 mm, 9 mm, 12 mm, and 15 mm, while keeping vibration position, vibration frequency, and vibration time constant for jujube trees with diameters of 30 mm, 50 mm, and 70 mm. The mean harvest rate initially increased with increasing vibration amplitude but then gradually decreased. This can be attributed to the excitation force on the jujube trees and fruit increasing with vibration amplitude, leading to fruit separation from the tree when the inertial force exceeded the bonding force between the fruit and stalk. However, when the vibration amplitude continued to increase, the mean harvest rate decreased due to the increase in the ground binding force on the jujube tree with increased diameter, resulting in a decrease in force on the fruit and ultimately a decrease in the shedding rate. Furthermore, there were differences in the standard deviations of the harvest rates of jujube trees with different diameters and vibration amplitudes. The greatest difference in the harvest rate effect was observed for jujube trees with a diameter of 70 mm when the vibration amplitude was 9 mm, while the smallest difference was observed for jujube trees with a diameter of 50 mm when the vibration amplitude was 12 mm.

Figure 12 illustrates the results of a single-factor analysis investigating the impact of vibration amplitude on the harvest rate for jujube trees with different diameters. For jujube trees with a 30 mm diameter, the harvest rate significantly increased between vibration amplitude values of 3 mm and 6 mm, while it significantly decreased between vibration amplitude values of 9 mm and 12 mm. Significant differences were observed between vibration amplitudes of 3 mm, 9 mm, and 12 mm, and also between vibration amplitudes of 3 mm, 9 mm, and 15 mm, as shown in Figure 12a.

For jujube trees with a 50 mm diameter, the harvest rate decreased within the vibration amplitude range of 3–6 mm, and significantly increased within the vibration amplitude range of 6–12 mm as the vibration amplitude increased. The harvest rate decreased significantly within the vibration amplitude range of 12–15 mm. Significant differences were found between vibration amplitude values of 6 mm, 9 mm, and 12 mm, and also between vibration amplitude values of 6 mm, 12 mm, and 15 mm, as shown in Figure 12b.

For jujube trees with a diameter of 70 mm, the harvest rate significantly decreased with increasing vibration amplitude within the range of 6–9 mm, and significantly increased within the range of 9–15 mm. No significant differences were observed between vibration amplitude values of 3 mm, 6 mm, and 15 mm, but significant differences were observed with vibration amplitude values of 9 mm and 12 mm, as well as between vibration amplitude values of 9 mm and 12 mm, as shown in Figure 12c.

The observed differences may be attributed to the variations in the growth state and structure of jujube trees with different diameters, resulting in varying effects of vibration amplitudes on the trees. Therefore, selecting an appropriate vibration amplitude according to the diameter of the jujube tree is crucial to improving the harvest rate.

3.3.3. Effect of Vibration Time on Different Diameters of Jujube Trees

The study conducted a single-factor test on jujube trees with diameters of 30 mm, 50 mm, and 70 mm. The vibration position was set at 0.4 m, the vibration frequency was 12 Hz, and the vibration amplitude was 3 mm. Vibration time was varied between 1 s, 3 s, 5 s, 7 s, and 9 s, and the harvest rates were recorded accordingly.

Table 7. Test results of harvest rate under different vibration times.

Vibration Time (s)	Diameter 30 mm		Diameter 50 mm		Diameter 70 mm
	Average Value (%)	Standard Deviation (%)	Average Value (%)	Standard Deviation (%)	Average Value (%)	Standard Deviation (%)
1	71.40	1.10	73.60	1.19	82.75	2.03
3	67.01	3.88	81.93	3.89	87.77	2.10
5	75.81	4.14	82.00	7.24	80.18	4.50
7	81.71	3.25	88.24	1.41	84.95	4.76
9	91.11	1.27	90.82	1.41	89.59	1.06

shows the results of the harvest rate tests for different vibration times.

Based on the results presented in Table 7, it is evident that when the vibration position, vibration frequency, and vibration amplitude were held constant, the average harvest rate of jujube trees increased gradually with an increase in vibration time. This is because the vibration of the tree causes the fruits to move unevenly, and those with a greater acceleration are detached from the fruit stalk first. This changes the vibration state of the branches and the motion state of the fruits. When the inertial force acting on the fruits exceeds the force combined with the fruit stalk, the fruits detach from the tree. Moreover, the standard deviations of the harvesting rate varied for different diameters and vibration time conditions. The standard deviations increased initially and then decreased with increasing vibration time. The most significant difference in harvest rate was observed at a vibration time of 5 s for jujube trees with a diameter of 50 mm, while the least significant difference was observed at a vibration time of 9 s for jujube trees with a diameter of 70 mm.

Figure 13 illustrates the outcomes of a single-factor analysis conducted to examine the impact of vibration time on the harvest rate of jujube trees with different diameters.

For jujube trees with a diameter of 30 mm, the harvest rate decreased within the vibration time range of 1–3 s and significantly increased within the range of 3–9 s. Notably, significant differences were found between vibration times of 3 s, 5 s, 7 s, and 9 s, as depicted in Figure 13a.

For jujube trees with a diameter of 50 mm, the harvest rate significantly increased within the vibration time range of 1–3 s and showed a gradual increase within the range of 6–9 s. Furthermore, there were significant differences between vibration times of 1 s and 9 s, as illustrated in Figure 13b.

For jujube trees with a diameter of 70 mm, there was a significant difference between the vibration times of 5 s and 9 s. The harvest rate showed an initial increase, then a decrease, and finally an increase again. Additionally, there was a significant difference between the vibration times of 1 s and 9 s, as indicated in Figure 13c.

3.4. Multi-Factorial Experimental Design and Analysis

To find the optimal parameters for different diameters of jujube trees, a three-factor, three-level response surface analysis [44] was used in this study for jujube trees with diameters of 30 mm, 50 mm and 70 mm. Vibration frequency, vibration amplitude and vibration time were selected as the test factors, and harvest rate was used as the test index. The levels of the test factors were set as shown in

Table 8. Table of test factor levels.

Level	Vibration Frequency (Hz)	Vibration Amplitude (mm)	Vibration Time (s)
−1	6	9	5
0	18	12	7
1	30	15	9

.

Design-Expert.V8.0.6 was used to design a multi-factorial experiment for 30 mm, 50 mm, and 70 mm diameter jujube trees, respectively, and the results of the design are shown in

Table 9. Multi-factor test table.

Vibration Frequency (Hz)	Vibration Amplitude (mm)	Vibration Time (s)	Harvest Rates at Different Diameters (%)
			30 mm	50 mm	70 mm
6	9	7	89.34	76.89	76.89
6	12	5	81.33	89.46	82.31
6	12	9	90.11	91.66	90.53
6	15	7	74.21	80.57	89.23
18	9	5	89.33	85.96	84.56
18	9	9	91.35	91.25	90.75
18	15	5	72.31	84.31	82.15
18	15	9	87.56	92.50	93.50
18	12	7	81.23	87.89	82.42
18	12	7	82.43	82.53	84.32
18	12	7	83.25	89.12	81.24
18	12	7	80.02	85.46	80.57
18	12	7	74.23	88.55	81.56
30	12	9	92.31	90.45	91.34
30	15	7	85.32	82.54	81.56

.

In this experiment, a multiple regression equation was fitted using Design-Expert V8.0.6 software for the relationship between three factors and harvest rate for three different diameters of jujube trees. The results were analyzed to obtain regression equations between vibration frequency, vibration amplitude, vibration time, and harvest rate. In addition, the established regression models were analyzed for reliability and significance testing.

3.4.1. Residual Analysis of Harvesting Rate at Different Diameters

The regression equations between vibration frequency, vibration amplitude, vibration time, harvest rate for three different diameters of jujube trees were established by analyzing the experimental data, as shown in Equations (17)–(19).

$$\begin{array}{l}{Y}_{30}=215.41588-1.40402x_1-10.48233x_2-16.70400x_3+0.069028x_1{x}_2\\ -7.5\times {10}^{-3}{x}_1{x}_3+0.55125x_2{x}_3+0.022484x_1{}^2+0.15281x_2{}^2+0.88256x_3{}^2\end{array}$$

(17)

$$\begin{array}{l}{Y}_{50}=84.01688+0.81312x_1+10.55833x_2-21.00313x_3-8.68056\times {10}^{-3}{x}_1{x}_2\\ -5.20833\times {10}^{-3}{x}_1{x}_3+0.12083x_2{x}_3-0.017734x_1{}^2-0.45875x_2{}^2+1.48094x_3{}^2\end{array}$$

(18)

$$\begin{array}{l}{Y}_{70}=130.06463+1.079x_1+0.391x_2-20.17713x_3-0.069514x_1{x}_2\\ -0.026458x_1{x}_3+0.215x_2{x}_3-1.99479\times {10}^{-3}{x}_1{}^2-8.05556\times {10}^{-4}{x}_2{}^2+1.43131x_3{}^2\end{array}$$

(19)

where Y₃₀ is the harvesting rate of 30 mm diameter jujube tree; Y₅₀ is the harvesting rate of 50 mm diameter jujube tree; Y₇₀ is the harvesting rate of 70 mm diameter jujube tree; x₁ is the vibration frequency; x₂ is the vibration amplitude; and x₃ is the vibration time.

In this study, the normal distribution plots of the residuals for red jujube harvest rates with different diameters were analyzed to evaluate the reliability of the regression model. Figure 14a illustrates the normal distribution plot of the residuals for a diameter of 30 mm, and it is evident that the majority of residual values are distributed along a straight line, indicating a good fit of the regression model. Similarly, Figure 14b demonstrates the normal distribution plot of the residual values for a diameter of 50 mm, which shows that the residual values are uniformly distributed around a straight line, further confirming the model’s good fit. Figure 14c shows the normal distribution plot of the residuals for a diameter of 70 mm, which reveals that the residual values are distributed along a straight line, signifying that the regression model is also a good fit for this diameter. Thus, it can be concluded that the established regression model based on this dataset is reliable.

3.4.2. Analysis of Variance

Analysis of variance (ANOVA) was performed on the harvest rates of different diameters as shown in

Table 10. Analysis of variance for different diameter harvest rates.

Diameter	Source	Sum of Squares	Degree of Freedom	Mean Square	F−Value	p−Value
30 mm	Model	578.28	9	64.25	7.83	0.0064 **
	Residual	57.47	7	8.21
	Lack of fit	6.46	3	2.15	0.17	0.9121
	Pure error	51.00	4	12.75
	Cor total	635.75	16
50 mm	Model	280.50	9	31.17	4.14	0.0372 *
	Residual	52.71	7	7.53
	Lack of fit	23.09	3	7.70	1.04	0.4657
	Pure error	29.62	4	7.41
	Cor total	333.21	16
70 mm	Model	323.60	9	35.96	5.36	0.0188 *
	Residual	46.95	7	6.71
	Lack of fit	38.58	3	12.86	6.14	0.0559
	Pure error	8.37	4	2.09
	Cor total	370.55	16

** indicates p < 0.01, highly significant; * indicates p < 0.05, significant.

.

Based on the regression models fitted for harvesting rates at different diameters as presented in Table 10, it can be observed that for the model fitted with a diameter of 30 mm, all p values are less than 0.01, indicating high significance of the fitted model and practical meaningfulness of the fitted equations. Similarly, for the models fitted with diameters of 50 mm and 70 mm, all p values are less than 0.05, suggesting a good fitting effect and a better reflection of the actual situation.

3.4.3. Response Surface Analysis

The significance analysis indicated that among the three factors affecting the harvesting rate of red jujubes, there was a significant interaction between vibration frequency and vibration amplitude. Additionally, similar relationships were observed between vibration frequency and vibration time, as well as between vibration amplitude and vibration time. Both vibration frequency and vibration amplitude had a direct impact on the inertia force during the vibration harvesting of red jujubes, with higher inertia force resulting in a higher harvesting rate.

The results shown in Figure 15 indicate that for a diameter of 30 mm, the red jujube harvesting rate initially decreases and then increases with increasing vibration frequency at any vibration amplitude. Meanwhile, an increase in vibration amplitude at any vibration frequency causes a gradual decrease in the red jujube harvesting rate. The harvesting rate reaches its minimum value when the vibration frequency is 6 Hz and the vibration amplitude is 15 mm, while the maximum value is reached when the vibration frequency is 30 Hz and the vibration amplitude is 9 mm. For a 50 mm diameter jujube tree, increasing the vibration frequency at any vibration amplitude initially results in an increase and then a decrease in the red jujube harvest, while increasing the vibration amplitude at any vibration frequency initially results in an increase and then a decrease in the red jujube harvest. The maximum harvest rate is achieved when the vibration frequency is 12 Hz and the vibration amplitude is 19 mm, while the minimum harvest rate is reached when the vibration frequency is 7 Hz and the vibration amplitude is 9 mm. When the jujube tree diameter is 70 mm, increasing the vibration frequency at any vibration amplitude results in a gradual increase in the red jujube harvest rate, while increasing the vibration amplitude at any vibration frequency results in a gradual increase in the red jujube harvest rate. The harvest rate reaches its minimum value when the vibration frequency is 6 Hz and the vibration amplitude is 9 mm, while the maximum value is reached when the vibration frequency is 6 Hz and the vibration amplitude is 15 mm.

Figure 16 shows that for a 30 mm diameter, the harvesting rate of red jujube increased gradually as the vibration time increased at any vibration frequency, and it also increased gradually as the vibration frequency increased at any vibration time. The highest harvesting rate was achieved at a vibration frequency of 30 Hz and a vibration time of 9 s, while the lowest harvesting rate occurred at a vibration frequency of 6 Hz and a vibration time of 5 s.

For a 50 mm diameter, the harvesting rate of red jujube initially decreased and then increased with increasing vibration time at any vibration frequency. Additionally, the harvesting rate increased and then decreased with an increasing vibration frequency at any vibration time. The highest harvesting rate was achieved at a vibration frequency of 20 Hz and a vibration time of 6 s, while the lowest harvesting rate occurred at a vibration frequency of 6 Hz and a vibration time of 7 s.

For a 70 mm diameter, the harvesting rate of red jujube increased gradually as the vibration time increased at any vibration frequency, but slowly decreased as the vibration frequency increased at any vibration time. The highest harvesting rate was achieved at a vibration frequency of 6 Hz and a vibration time of 9 s, while the lowest harvesting rate occurred at a vibration frequency of 6 Hz and a vibration time of 5 s.

According to Figure 17, for a 30 mm diameter, the harvesting rate of red jujube gradually increased with increasing vibration time at any vibration amplitude, while it gradually decreased with increasing vibration amplitude at any vibration time. The highest harvesting rate was achieved at a vibration amplitude of 9 mm and a vibration time of 9 s, while the lowest harvesting rate occurred at a vibration amplitude of 15 mm and a vibration time of 5 s.

For a 50 mm diameter, the harvesting rate of red jujubes initially decreased and then increased with increasing vibration time at any vibration amplitude, while it increased and then decreased with increasing vibration amplitude at any vibration time. The lowest harvesting rate was achieved at a vibration amplitude of 9 mm and a vibration time of 6 s, while the highest harvesting rate occurred at a vibration amplitude of 12 mm and a vibration time of 5 s.

For a 70 mm diameter, the harvesting rate of red jujubes initially decreased and then increased with increasing vibration time at any vibration amplitude, and gradually increased with increasing vibration amplitude at any vibration time. The highest harvesting rate was achieved at a vibration amplitude of 15 mm and a vibration time of 9 s, while the lowest harvesting rate occurred at a vibration amplitude of 9 mm and a vibration time of 6 s.

3.4.4. Optimal Vibration Parameters for Different Diameters of Jujube Trees

To improve the vibration harvesting efficiency and increase the vibration harvesting rate of red jujubes, this experiment used the Optimization function in Design-Expert.V8.0.6 software to determine the optimal vibration parameters for different diameters. The best vibration parameters for jujube trees with a diameter of 30 mm were a vibration frequency of 30.00 Hz, a vibration amplitude of 15.00 mm, and a vibration time of 9 s. For trees with a diameter of 50 mm, the optimal parameters were a vibration frequency of 18.55 Hz, a vibration amplitude of 12.52 mm, and a vibration time of 9 s. Additionally, for a 70 mm diameter tree, the optimal vibration parameters were a vibration frequency of 6.00 Hz, a vibration amplitude of 15.00 mm, and a vibration time of 9 s.

3.5. Discussion and Analysis of Results

The objective of this study was to investigate the effect of vibration parameters on the effect of harvesting jujube trees. Initially, we investigated the key factors influencing jujube fruit shedding, focusing primarily on vibration frequency and vibration amplitude, then analyzed the displacement response relationship and the acceleration response relationship of red jujube branches’ monitoring points under different vibration factors by the harmonic response analysis method. Subsequently, the vibration parameters for different tree diameters were optimized by using a three-factor, three-level response surface analysis method. By analyzing the data, we determined the optimal combination of vibration parameters for different jujube tree diameters.

In related studies, Fu et al. [22], Yang et al. [25], Zhuo et al. [26] and Li et al. [27] conducted earlier research on the vibration mechanisms of jujube trees and their branches, which provided a valuable theoretical foundation for the vibration harvesting of jujube trees. Fu et al. [22] carried out experiments involving constant-frequency vibrations on samples of jujube tree branches, utilizing different amplitudes (3 mm, 5 mm, and 7 mm) and frequencies (12–24 Hz). The test results revealed a correlation between vibration frequency and instantaneous acceleration, while the effect of amplitude on instantaneous acceleration was found to be insignificant. Our harmonic response analysis corroborated these findings, demonstrating that the acceleration response of jujube tree branches varied less at low-frequency vibrations and more at high-frequency vibrations. The acceleration response variation of jujube tree branches with different amplitudes peaked at frequencies around 3–5 Hz, 8–10 Hz, 19–21 Hz, and 26–28 Hz. However, unlike the study by Yang et al. [25], who carried out a subsequent harmonic response analysis with a vibration frequency of 0–10 Hz to investigate the relationship between vibration height and branch node acceleration through the results of modal analysis, our study fully investigated the displacement response and acceleration of jujube tree branches within a vibration frequency of 0–30 Hz through harmonic response analysis on the basis of modal analysis response and, based on the results, we obtained vibration ranges of 4–30 Hz, 6–25 Hz, and 17–29 Hz for 30, 50, and 70 mm diameter jujube trees, respectively. Furthermore, in contrast to the studies of Zhuo et al. [26] and Li et al. [27] who determined the optimal frequency range for vibratory harvesting of jujubes by spectral analysis, our results also showed that the optimal combination of vibration parameters for a specific diameter significantly improved the efficiency of jujube harvesting. The difference is that our research primarily focused on the overall vibration harvesting effect of jujube trees. Utilizing a three-factor, three-level response surface analysis method, we established a mathematical model correlating vibration frequency, vibration amplitude, and vibration time with the harvesting rate. This allowed us to determine the optimal parameter combination for vibrating jujube trees of various diameters. Instead of obtaining the vibration characteristics of specific branches under different vibration parameters using sensors to theoretically identify the optimal vibration frequency range, we relied on the harvest rate as the experimental index in our approach.

Our research findings bring innovation and valuable insights to the field of red jujube harvesting. We have developed a method that enhances the efficiency of red jujube harvesting by optimizing the combination of vibration parameters for jujube trees with varying diameters. This methodology provides practical guidance for the design and utilization of red jujube harvesting equipment. Our results highlight the significance of vibration frequency, vibration amplitude, and vibration time in the red jujube harvesting process, offering recommendations for optimal parameters suitable for different diameters of jujube trees. Furthermore, optimal vibration parameters for different diameters of jujube trees were also obtained by single-factor test and analysis and multi-factor test and analysis, while further field tests and data collection in turn helped to verify the reliability and applicability of our findings.

It should be noted that there are still some limitations in our study. Specifically, our research solely concentrated on examining the impact of vibration parameters on the effectiveness of red jujube harvesting, while disregarding other influential factors such as red jujube maturity and fruit shape. In future investigations, it would be valuable to include more variables to enhance theoretical studies on jujube harvesting and the design and parameterization of harvesting equipment.

4. Conclusions

This study proposes a vibration parameter optimization method that considers the influence of jujube tree diameter on the vibration harvesting effect. The study establishes a model of forced vibration dynamics of jujube trees and constructs a three-dimensional model of three different diameters of jujube trees (30 mm, 50 mm, and 70 mm) using field measurements. Vibration tests are conducted on the three different diameters, and single-factor and multi-factor test analyses are performed. The following conclusions were obtained:

(1)

A kinetic model of forced vibration of jujube trees is established using Lagrange’s equation. The main factors affecting fruit shedding of the jujube tree system in forced vibration are analyzed and calculated as vibration frequency and vibration amplitude, providing a theoretical basis for modal analysis and harmonious response analysis of jujube trees.

(2)

Kinematic simulation analysis of the three different diameters yields intrinsic frequencies and vibration models of jujube trees. The simulation results reveal that the vibration characteristics of different diameters of jujube trees differ at each order of vibration in the first six orders of vibration, and the maximum number of vibrating branches appears at different orders of vibration. Through harmonic response analysis, vibration frequency ranges for vibration harvesting are determined as 4–30 Hz, 6–25 Hz, and 17–29 Hz for jujube trees with diameters of 30 mm, 50 mm, and 70 mm, respectively. For jujube trees of different diameters, when the excitation frequency of the excitation force is in the corresponding range, the branches of jujube trees can produce larger vibration acceleration and displacement, which is beneficial to the vibration harvest of jujube trees. By determining the range of vibration frequencies that cause the desired response, we can establish the appropriate frequency range for conducting vibration acquisition tests, and then determine the optimal vibration frequencies for different diameters of jujube trees through the tests.

(3)

By designing a three-factor, three-level response surface test, the regression models of vibration frequency, vibration amplitude, vibration time, and harvest rate for different diameters were established and solved to obtain the optimal vibration parameters. The optimal vibration parameters for 30 mm diameter jujube trees are a vibration frequency of 30.00 Hz, a vibration amplitude of 15.00 mm, and a vibration time of 9 s; for 50 mm diameter jujube trees, the optimal vibration parameters are a vibration frequency of 18.55 Hz, a vibration amplitude of 12.52 mm, and a vibration time of 9 s; and for 70 mm diameter jujube trees, the optimal vibration parameters are a vibration frequency of 6.00 Hz, a vibration amplitude of 15.00 mm, and a vibration time of 9 s. These results validate the simulation results and provide useful references for improving the efficiency of red jujube vibration harvesting and finding the best parameters for vibration harvesting of red jujubes from jujube trees with different diameters.