Abstract
The first commercial thinning usually entails a high cost in harvest operations and a low resulting income. From a practical forestry perspective, a schematic spatial selection might be more efficient than a selective approach. Therefore, this study aimed to compare basal area, total and standing volumes, and periodic annual increment (PAI), as well as stand structure, between different thinning designs (selective and schematic thinning) and strategies (thinning once or more than once) over a long-term monitoring period of Scots pine (Pinus sylvestris) plantations in Sweden. We also evaluated the relevancy of distance-dependent competition indices (CIs) in individual tree growth models by comparing growth model predictions with the use of distance-dependent and distance-independent CIs. Despite higher heterogeneity in schematically thinned stands, there were no significant differences in standing and total volumes (m3·ha−1) among treatments in the short or long term. Although the inclusion of a distance-dependent CI improved the model slightly, distance-independent models predicted diameter growth just as effectively. Schematic thinning could be a viable option for a first commercial thinning or one-time thinning if, at least, one more thinning is included in the management plan, or if the motivating interest is mainly volume.
1. Introduction
Thinning is one of the main management practices in forestry, as it plays a key part in the increase in individual tree growth and the regulation of wood quality [1]. Important reasons for thinning include removing low-quality stems [2], increasing resource availability (e.g., water, light, and nutrients) for the remaining trees [1,3], diversifying forest structure and generating income before final felling [4], and reducing mortality rates due to self-thinning [5,6]. In Swedish forestry, the first commercial thinning usually entails thinning selectively from below, i.e., the biggest, most productive trees are kept on the stand and the smallest and/or damaged trees are harvested, when the dominant trees reach a height of over 11–12 m [7]. The 1960s saw an increase in mechanization in harvest operations, accompanied by a higher thinning intensity in early stages, consequently reducing intensity as the stands got older [1,8]. In that particular context, the possibility of having complete systematized thinning operations became a topic of interest [1]. When it comes to the first commercial thinning specifically, forest owners are still often reluctant to perform systematized thinning due to the high cost of harvest operations and the low income derived from it [9]. The importance of finding a more cost-efficient thinning method is, therefore, as prevalent now as it was decades ago, a fact shown by various other studies [1,9,10,11]. In their study, for example, the authors of [12] showed that mechanized line thinning increased productivity and enabled low-cost thinning operations in comparison to conventional single-tree selection thinning.
Schematic thinning, i.e., boom-corridor cuttings, can lower the number of damaged trees and reduce fuel consumption and emissions, offering not only an attractive economical alternative, but a more environmental friendly one [13]. Potentially, schematic thinning also increases biodiversity due to a more heterogeneous stand structure developing [11,14], especially if it is a mixed forest or if there is ingrowth of other tree species.
Scots pine (Pinus sylvestris) is the most well-distributed conifer species worldwide [15]. It is considered to be a shade-intolerant, light-demanding species [16], and it has been reported that competition leads to reduced diameter increment in stands of this species [17]. While using another study’s [18] competition index (CI), the authors of [19] found that competition in four types of Scots pine stand structures (a mature even-aged stand, a plantation, one with oak understory, and an uneven-aged stand) presented a negative relationship to stem diameter in all stands. When evaluating the relationship between current diameter increment and the CI, the authors suggested that, in low stand densities (<1000 stems·ha−1), the competition between trees may not cause severe growth limitation [19].
The success of the first commercial thinning in Scots pine stands and further stand development is highly dependent on precommercial thinning (PCT), with early and intensive PCT generally increasing merchantable volume and the profitability of harvested wood during the first commercial thinning [20]. However, the maintenance of a high stem density, e.g., >3000 stems·ha−1, in the early development of Scots pine stands has been shown to promote good external wood quality with smaller branches [21].
Thinning can be selective, systematic, or half-systematic [1,10]. The first is generally applied on the basis of size selection, i.e., dominant and codominant trees are prioritized, with the removal of smaller and/or damaged trees (thinning from below), or bigger trees are removed from the stand to allow the suppressed, subdominant trees to grow better (thinning from above) [8,10]. Schematic thinning, on the other hand, refers to when the thinning design is chosen on the basis of a spatial selection, e.g., thinning in corridors, regardless of tree size; it can be implemented in different ways and have different nomenclatures, such as row thinning [22], corridor thinning [11], systematic thinning [1], and boom-corridor thinning (BCT) [23,24], with trees of all sizes being removed proportionally [25]. If the distance between rows is small, an alternative to this is to use narrow harvesting machines or to increase the number of adjacent rows to be removed [22].
Growth rates vary considerably within different diametric classes in a stand, and one cause of that is the variation in competition by other trees [26,27]. A larger crown will generally result in high increment performance for a tree, while also reducing light availability for its neighbors [28].
Having a better understanding of what impacts growth variation is essential for predicting stand development and evaluating forest resistance and resilience to environmental change [27]. Other authors have previously suggested that the effect of competition on the growth of individual trees and stand development can be best predicted if the coordinates for all trees are known, potentially making the model more accurate and enabling the effective evaluation of different spatial distribution designs derived from, for example, systematic thinning, half-systematic thinning, or selective thinning [26,29]. Individual-tree-based growth models generally include an index designed to quantify the degree of competitive stress on individual trees in a stand [18]. The models can be distance-dependent or distance-independent. The former requires that the model has information on the location of the trees [30]. CIs depend on the position, dimensions, and number of trees, and they can be based on the weighted distance of neighboring trees (competitors), selected through an empirical rule, which are located within a certain distance from the subject tree [30,31]; CIs are usually included in individual tree growth models as an explanatory variable [32].
CIs are important tools in forest management and help determine how much of the growing space of an individual is occupied by others, potentially reflecting more successfully the growth of individual trees [33,34,35]. CIs can assume asymmetry or symmetry when it comes to the partitioning of resources and neighborhood effects [31], i.e., “the tree with the highest influence captures all the resources available at that spot” (asymmetric distribution), or the opposite, when the resources are assumed to be shared among the trees proportionally, depending on their local influence function values (symmetric distribution) [36]. CIs generally assume that there is asymmetry on the effects caused by the neighboring trees and the way that the tree responds to them [33].
Within this context, this study compares different thinning designs (selective and schematic thinning) and strategies (by thinning once or more than once), using long-term monitoring of a set of Scots pine stands in Sweden. Furthermore, we enquire whether or not the spatial arrangement of trees influences single tree growth.
From a practical forestry perspective, it could be economically relevant for forest owners to know if the spatial selection of thinned trees significantly affects productivity, rather than a size selection. Therefore, this study aimed to investigate if spatial selection affects stand growth. We hypothesized the following:
H1.
There will be no significant differences among thinning treatments in pine stand basal area, periodic annual increment (PAI), or in mean diameter growth.
H2.
Distance-independent models will be as effective for predicting diameter growth as the distance-dependent model.
2. Materials and Methods
2.1. Experimental Design
The data were obtained from a long-term thinning experiment established in Sweden [7] in young Scots pine plantations, using a site for each block, with three exceptions in which there were two blocks on the same site. Each block contained two randomized plots with the respective treatments (selective and schematic thinning). The stands were planted between 1949 and 1958 as a provenance trial, and the thinning experiment was then established between 1974 and 1981, when the stands were, on average, 25 years old, in a total of 16 blocks. The original spacing and stem density from the planting were maintained, and ingrowth was removed in blocks where it had appeared. The spacing between the trees was 1.5 m × 1.5 m; on the basis of the planting design, we created coordinate systems for each treatment plot with the spatial location of each tree (Figure 1). The treatment plots ranged from 0.05 to 0.2 ha in size. Surrounding the treatment plots was also a buffer zone of trees with the same treatment (varying 2–5 m in width), but none of the trees in the buffer zone were measured. In this study, we reduced the net plots by trimming at least 3 m of distance off the plot edges, such that all subject trees had known size and distance to all neighboring trees within at least 3 m.
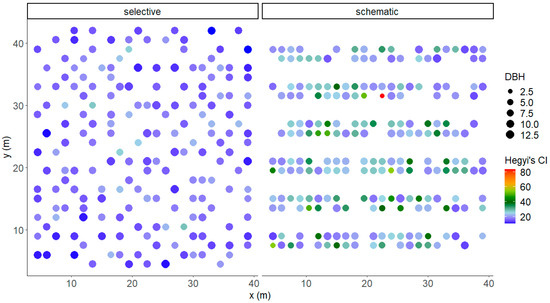
Figure 1.
Representation of the spatial location of the trees for one of the sites after establishing the thinning treatments (selective or schematic). The size of the points is based on the diameter at breast height (DBH), i.e., bigger points represent bigger trees. The colors in the scale express the competition based on one of the calculated distance-dependent competition indices in this study (Hegyi’s in this case). Higher CIs indicate that the tree is suffering from more competition.
The 16 blocks were located In eight regions in Sweden, between latitudes 56°40′ N and 66°04′ N (the counties Kronoberg, Västerbotten, Västernorrland, Norrbotten, Dalarna, Jämtland, Kalmar, and Halland) (Figure 2, Table 1). The experimental design consisted of two levels of thinning treatments, selective and schematic thinning, randomized within blocks during first thinning. Over time, the blocks were managed with two different experimental plans, where 10 of the blocks had no further thinning, only measurements of living and dead trees. The other six blocks were thinned more than once, according to a thinning template and with the same thinning strategy for both treatments. This resulted in two different experiments.
Figure 2.
Map of the sites included in the study.

Table 1.
Description of the study sites.
In the first thinning, both treatments had a basal area removal of the same intensity (50% intensity), with the selective thinning being performed from below and the schematic thinning being applied on the basis of a spatial selection (two rows were harvested, two rows were kept).
The thinning ratio, i.e., the ratio of mean diameter between harvested trees and retained trees, describes the used thinning type [8]. Since thinning from below consists of harvesting, mostly, the smallest trees, the ratio is lower than 1.0. In contrast, in thinning from above, the thinning ratio is over 1.0 [8]. Schematic thinning, however, is based on spatial selection, regardless of tree size, e.g., corridor thinning; the thinning ratio should theoretically be 1, or close to 1. Mean thinning ratios for the treatments were 0.72 and 0.97, respectively.
Later thinning, if applied, was performed as selective thinning from below with 25% intensity for both treatments.
All trees with a height over 1.3 m were numbered and registered for remeasurements over all revisions, starting with the first revision at the time of conducting the thinning treatments, prior to harvest. Stem diameter at 1.3 m height (dbh) was measured on every tree together with height on 20 sample trees. Each revision provided data on the dbh of all trees, status of the trees (e.g., thinned or not, dead or alive), and height of sample trees. The experiments were measured at minimum three times and at most seven times, with the monitoring period from 1974 to 2022 (Table 1). The time for remeasurements varied among sites, with an increased interval across revisions as the stands got older. On average, it ranged from 8 to 10 years.
2.2. Treatment Comparisons
The treatment effect on stand level was tested by comparing PAI between the first two revisions, and standing and total volumes for the second and the last revisions. On average, the time between the first and second revisions was 6 years. Additionally, we also compared the mean annual increment (MAI) between the selective and schematic thinning treatments. PAI establishes a relation between tree growth (in this case, specifically volume growth) “over a certain period to the length of the period” [37], whereas MAI refers to the current size of a tree in relation to its age [37].
A visual representation of the data was obtained by plotting the diameter distribution of the different blocks, the treatments (selective or schematic), and thinning strategies (thinning once or more than once). Additionally, to test the heterogeneity, we calculated the Gini coefficient [38,39] to measure the heterogeneity of forests as a function of certain variables, e.g., diameter, basal area, and growth. In the case of our study, we used arithmetic mean diameter. As a way to further showcase the heterogeneity, the coefficient of variation (CV) was calculated. We also compared quadratic mean diameter (QMD) among the thinning treatments in the short term (first revision at the time of thinning). For the long-term analysis, we compared both the treatments and the thinning strategies, i.e., blocks that were only thinned once with treatments maintained after first thinning, and blocks that were thinned more than once, using data from the last revision.
The data were analyzed using the statistical and graphics software R (version 4.0.4) (R Core Team 2021). To test for potential statistical difference among treatments on a stand level, the data were computed with mixed-effects models using the nmle package in R. Plots within sites were considered a random effect. We tested PAI (m3·ha−1·a−1) between the first two revisions (revision 1 after thinning and revision 2 before thinning), and standing volume (m3·ha−1) between the second (before second thinning) and last revisions as response variables. The Tukey test (0.95 level of confidence) was used to test the difference in basal area, total and standing volumes, and QMD among the different treatments.
2.3. Comparing Growth Predictions with and without Competition Indices
The measured growth between revisions 1 and 2 was used for the development of 5 year interval growth functions with and without CIs. Thereafter, the functions were applied for dbh increment over 5 and 10 years, respectively, after first commercial thinning. We used the individual tree models with no CI (BA-base), with distance-dependent CI (BA-DDCI), and with distance-independent CI (BA-DICI) to predict diameter growth and, subsequently, basal area on a stand level to see how well the models performed in comparison to the original stand-level data (BA-stand) (Figure 3).
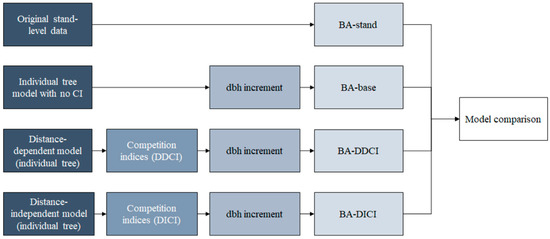
Figure 3.
Description of the model comparison process.
The individual tree dbh growth base model was fitted to the data (Equation (1)), with no CI, using the 5 year diameter growth as the response variable. Only trees within the net plots were used as subject trees. Plots within sites were used as random effects using the lme function in the nlme package. Treatment (selective and schematic thinning) was initially tested, but was proven to be nonsignificant and, therefore, removed from the final model.
where Idbh5 is the 5 year diameter increment (cm), dbh is the diameter at breast height (cm), SI is the scaled site index ranging from 0 to 1 (lowest to highest SI, respectively), BA is the basal area (m2·ha−1), bi is a random factor, and ei is the error term. β0 is a constant and βi denotes coefficients.
Idbh5 = β0 + (β1dbh) + (β2SI) + (β3BA) + bi + ei,
Thereafter, the CIs were added to the base model, creating a total of five models (Equation (2)).
where CI is the added competition index.
Idbh5 = β0 + (β1dbh) + (β2SI) + (β3BA) + (β4CI) + bi + ei,
Additionally, we created a final function in which we included age at last revision as a covariate (Equation (3)).
where age refers to the age of the trees at the last revision.
Idbh5 = β0 + (β1dbh) + (β2SI) + (β3BA) + (β4CI) + (β5age) + bi + ei,
The models met the normality assumptions. To correct for heteroscedasticity, we used an exponential weight function. Since the models did not have the same fixed effects, we used the maximum likelihood (ML) method. R2 values for all models were calculated with the MuMIn package. To check for multicollinearity amongst the explanatory variables in the model, we calculated the variance inflation factor (VIF).
We calculated and implemented two distance-dependent and three distance-independent CIs into the base growth model. The neighboring trees (competitors, j) were selected regardless of their distances to the subject tree (i), i.e., every tree that was not the subject tree was selected as a competitor, with the distances between the trees being incorporated into the calculation of the distance-dependent CIs. Five models using asymmetric competition were developed [40]. In total, there were 3267 and 3240 subject trees in the net plots in revisions 2 and 3, respectively, excluding outliers and dead trees. We used Spearman’s rank correlation to examine the relationship between the CIs and 5 year diameter increment for individual trees.
The evaluation of model performance for predicting 5 year diameter increment was initially conducted using the Akaike information criterion (AIC). The same models were used for predicting 10 year diameter growth and final growth. The model comparisons were then used to test the second hypothesis.
3. Results
3.1. Treatment Effect on Stand and Individual Tree Growth
Basal area (m2·ha−1) did not differ among treatments in the short term, on average, 6 years after thinning (p = 0.214), nor did it differ in the long term, on average, 35 years after first thinning, for stands that were thinned once (p = 0.092) or more than once (p = 0.736). Although there was no significant difference, mean basal area was higher for the schematic thinning than in the selective thinning in the short and long terms. There were no statistical differences among the treatments on stand-level data for PAI between the first two revisions (p = 0.850) or standing volume on the second revision (p = 0.768). Conditional R2 values for the models were 0.936 and 0.931, respectively, i.e., the variance was well explained by the fixed and random effects. Additionally, no significant difference among treatments was found when evaluating MAI over a long term for either thinning strategy, i.e., sites that were thinned only once (p = 0.230) and more than once (p = 0.661). Total volume in the last revision did not present significant differences among treatments for the blocks that were thinned only once (p = 0.060) (Figure 4). The same can be said for the blocks that received more than one thinning (p = 0.673) (Figure 4). Standing volume also did not differ significantly among treatments at the last revision.
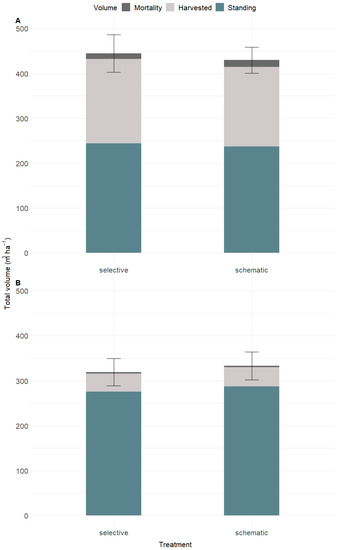
Figure 4.
Total volume production (m3·ha−1) of the blocks thinned more than once (A) and only once (B), expressed on stacked bar charts with mortality, harvested, and standing volumes. The error bar represents the standard error of the total volume among the thinning treatments. The site index ranged from 23 to 29 for blocks that were thinned once and from 24 to 32 for blocks that were thinned more.
Mean arithmetic diameter growth (cm·year−1) was significantly higher for the selective thinning treatment (0.32 cm·year−1) in comparison to the schematic thinning (0.29 cm·year−1) for sites that were thinned only once (p = 0.012). On the other hand, for sites that had more than one thinning, that difference was not significant (p = 0.948), with mean diameter growth being 0.42 cm·year−1 for both thinning treatments.
3.2. Stand Structure
For the sites that maintained the initial treatment, i.e., those that were thinned only once, stand structure was more heterogeneous for the schematic thinning treatment, since there were a higher number of smaller trees, as well as greater stem density, in general, along with a higher Gini coefficient and CV (Figure 5, Table 2). As a result, mean dbh was mostly concentrated in bigger diameter classes for the selective thinning, in comparison to the schematic thinning (Figure 5). For sites that were thinned more than once, that tendency started to disappear and heterogeneity was no longer significant among treatments (Figure 6, Table 2).
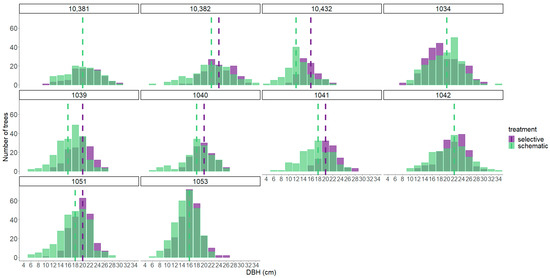
Figure 5.
Diameter distribution for sites that were thinned only once. The x-axis value represents the upper limit of the dbh class. The y-axis represents the number of trees on the plot. The dashed lines represent the mean dbh value for each treatment. When only one dashed line appears, it means that the dbh means for both treatments were in the same class.

Table 2.
Coefficient of variation and Gini coefficient calculated in the first and last revisions. N is the number of blocks, and sd is standard deviation.
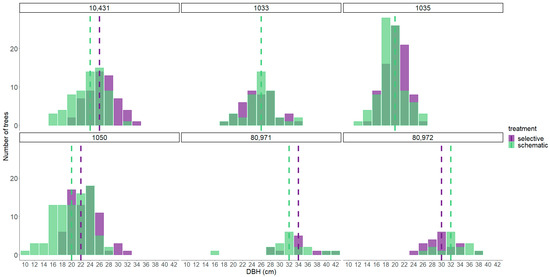
Figure 6.
Diameter distribution for sites that were thinned more than once. Each number on the x-axis represents the upper number of the diameter class. The y-axis represents the number of trees on the plot. The dashed lines represent the mean dbh value for each treatment. When only one dashed line appears, it means that the dbh means for both treatments were in the same class.
QMD was significantly different between treatments at the time of first thinning due to the thinning designs that were established and the thinning ratios derived from them (p < 0.0001) (Figure 7). When evaluating QMD at the time of the last revision, the thinning strategies differed significantly (p < 0.0001), as did the treatments in blocks that had only one thinning (p = 0.0147) (Figure 8). There was no significant difference between treatments when there was more than one thinning (p = 0.3735).
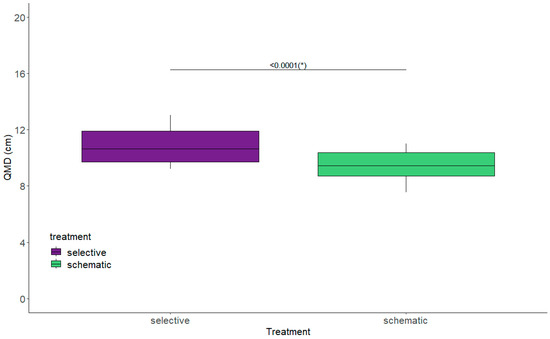
Figure 7.
Evaluation of quadratic mean diameter between treatments (selective and schematic) and different thinning strategies (one thinning and more than one thinning) at the time of the first thinning. (*) indicates significant differences using the Tukey test (p < 0.05).
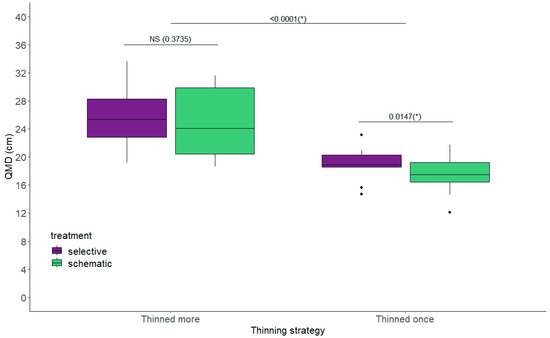
Figure 8.
Evaluation of quadratic mean diameter between treatments (selective and schematic) and different thinning strategies (one thinning and more than one thinning) in the last revision. NS means “not significant” (p ≥ 0.05); (*) indicates significant differences using the Tukey test (p < 0.05).
3.3. Competition Indices and Model Performance
All of the computed CIs (distance-dependent and distance-independent), using Spearman’s rank correlation coefficient (rho), presented a negative relationship with 5 year individual tree diameter increment (Table 3).

Table 3.
Spearman’s rank correlation coefficient between 5 year individual tree increment and the competition indices.
Model performance did not differ across treatments. However, the addition of CIs to the growth model slightly improved its performance according to AICc. The model that best predicted 5 year dbh increment and best explained the variation in the data was a distance-dependent model using Hegyi’s CI (BA_DDCI_Hey, Table 4 and Table 5, Figure 9), which differed significantly to other models. The model with no CI (BA_BASE) and one of the distance-independent ones (BA_DICI_Lor2) were ranked as less suitable models. The CI in the latter was not significant (Table 4).

Table 4.
Models for predicting 5 year dbh increment for individual trees.

Table 5.
Ranking of the tested models, from best to worst, based on the Akaike information criterion.
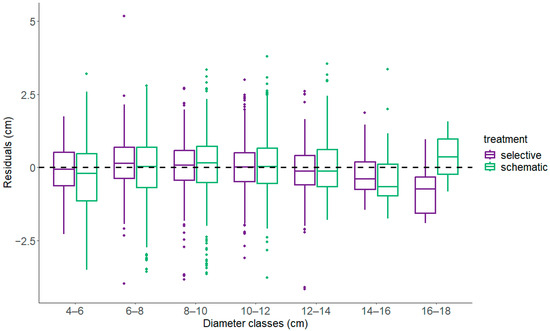
Figure 9.
Residual plot of the distance-dependent model using Hegyi’s competition index (BA_DDCI_Hey), considering only trees with dbh ≥ 4 cm.
When comparing the predictions of basal area (m2·ha−1) for 5, 10, and 35 years after thinning (average time at the last revision), they did not significantly differ among all tested models, with and without CIs (Figure 10).
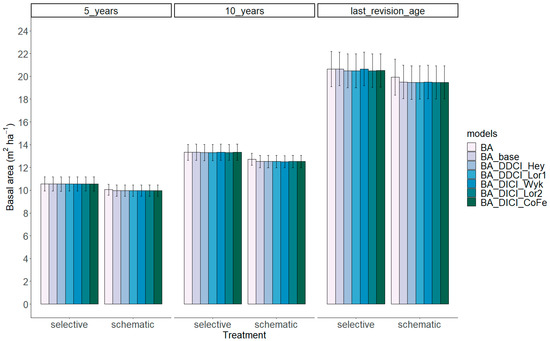
Figure 10.
Basal area (m2·ha−1) predictions using different models and over time (5, 10, and 35 years (last revision age) (average time)) after thinning. The last graph had age included in the model, considering the latest revision. “BA” indicates the real basal area value. “BA_base” has no competition index. “BA_DDCI_Hey” and “BA_DDCI_Lor1” are distance-dependent models. “BA_DICI_Wyk”, “BA_DICI_Lor2”, and “BA_DICI_CoFe” are distance-independent models.
The analysis using VIF presented no major multicollinearity issues, with similar studies suggesting that a value of less than 10 is acceptable [41,42]. The highest value was close to 6 for one of the distance-independent models (BA_DICI_Wyk), with the initial dbh and DICI presenting values of 5.52 and 5.63, respectively. All other models and their explanatory variables presented a VIF of less than 3.
4. Discussion
We show in this study that both selective and schematic thinning are useful strategies in early harvests. In this experiment, by design, only the thinning ratio differed among the treatments after thinning, but not the remaining basal area. With this approach, a schematic thinning will create stands with more stems, albeit smaller. This resulted in no significant difference in stand basal area, over a short or long term. It also resulted in an increased mean diameter in the selective thinning. However, when later thinnings were performed (selective thinning from below), the difference between the early treatment of selective and schematic disappeared.
Unlike what we found in our study, despite the selective thinning treatment having a higher mean diameter increment, the authors of [1] found no statistical differences in mean diameter growth among the thinned treatments (selective, half-systematic, and systematic) when working with Scots pine and Norway spruce stands in Finland. The authors argued, however, that a higher mean diameter increment for a selective thinning based on basal area removal, as was the case in our study, makes sense since “the growing space released by the removed trees is more evenly distributed among all the trees remaining on a plot”. When working with a 35 year old Douglas fir stand to compare growth among unthinned, strip-thinned, and selectively thinned, the authors of [43] also found that individual tree growth was higher in the selective thinning than in the plots with strip thinning. Our first hypothesis was, therefore, partly rejected, since, although there were no significant differences among treatments in stand basal area and PAI, arithmetic diameter growth was significantly higher for the selective thinning treatment.
Different management goals and thinning strategies can result in a varied stand structure and resource distribution in the short term, potentially also affecting forest development in the long term [44]. The authors of [11] argued that different thinning treatments will promote “very different effects on vertical stand structure, habitat diversity, and light conditions”. In a different study, the authors of [45] found that crown attributes in Scots pine were significantly larger in intensive thinning from below (66% of basal area removal) in comparison to the systematic thinning and thinning from above treatments, which could be one reason to explain the higher individual tree diameter growth found in the selective thinning i.e., potentially higher photosynthetic rates, due to a larger crown. The authors of [44], who did not specifically work with corridors on their thinning simulations, argued that light distribution may not vary so much among different stand structures, which could be the reason why, in our study, we did not see significant differences in basal area in the short and long terms after thinning.
Furthermore, a higher number of stems in the schematic thinning and the potential that some trees have to benefit from the increased resource availability along the corridors end up making the treatments comparable when it comes to total stand volume [7], compensating for the lower growth [1]. The forests look structurally different, i.e., the plots with corridors have higher stem density and a higher number of smaller trees, making them more heterogeneous, while the plots with selective thinning present a more homogenous structure, even though both treatments had the same amount of basal area removed in the first thinning and in subsequent thinning (for six of the blocks). Other studies have shown that schematic thinning treatments, such as BCT, resulted in a more heterogeneous forest, similar to the results from [9,14,46,47]. Schematic thinning will generally not improve the external wood quality of the remaining trees [25].
Our models with CIs for comparison of stand basal area performed very well in the short term, regardless of being spatially dependent or not, especially for the plots with selective thinning. Despite the AICc showing a significantly higher efficiency in prediction and explanation of the variation in the data for one of distance-dependent models (BA_DDCI_Hey), we saw that estimated stand basal area using the predicted diameter growth did not differ among the models (distance-dependent or -independent), thus confirming our second hypothesis. The slightly better, but not significant, performance for the selective thinning treatment was probably due to the fact that the models underperformed for trees in smaller diameter classes, which were mostly found in the schematic thinning treatment. In their study, the authors [48] also found little difference in predictive ability between distance-dependent and distance-independent models, when working on 11 year old Pinus radiata plantations in Italy with different thinning intensities; they argued that the costs to obtain the coordinates of trees “may be unjustified for growth prediction, at least in young conifer plantations”.
By not choosing a specific method for competitor selection, such as the fixed radius method, one of the potential consequences in our analysis would be the presence of spatial autocorrelation among samples, since the trees were not independent from each other and were repeatedly analyzed, producing pseudo-replicates. To account for that, we included plots within sites as random effects in the models. Additionally, the authors of [34] went into detail about overlapping samples in their study, and one of their conclusions was that spatial autocorrelation was only detected for a very short search radius (3–4 m) and that “on average, this effect does not seem to introduce any type I statistical error”.
With advances in technology and the continuing development of precision forestry [49], cheaper and less time-consuming methods could be implemented to obtain tree coordinates. However, perhaps, even more important for long-term predictions would be to use methods that could give us more information on crown development over a period of years; this was one of the limitations in our study, since changes in morphology could be important to understand growth patterns after competition release due to thinning [50]. When working with unevenly sized Norway spruce stands in Sweden, the authors of [51] mentioned that their model could have possibly been improved if they had a “more representative measure for the crown ratio”.
5. Conclusions
Accordingly, on the basis of our findings, if production is the main goal, in addition to selective thinning, schematic thinning could also be a viable option for the first commercial thinning. If working with a one-time thinning system, schematic thinning will result in a longer rotation to get to a specific target diameter in the stand. However, if the main motivation is volume, the thinning design one chooses—selective or schematic—will amount to nonsignificant differences between treatments. If thinning is performed more than once, trees can be selectively thinned from below in later thinning, thereby promoting fast-growing, good-quality trees at a later stage. Nevertheless, it is important to highlight that the first commercial thinning in our study was performed when dominant height ranged 7–11.8 m among the different sites, i.e., there was no late first commercial thinning. In that way, codominant trees at this range of dominant height tend to develop really well after thinning, because of their live crown ratio, which is especially important for the schematically thinned stands due to a generally higher number of codominant trees in growing stock, in comparison to the selectively thinned ones. If the first thinning was applied later, the crown of codominant trees would suffer more to recover, consequently affecting growth. Therefore, further investigation would have to be conducted at sites in which first commercial thinning was performed at a later stage to evaluate if similar results to our study would be found.
Author Contributions
Conceptualization, E.H., A.C.S., S.H. and N.F.; methodology, A.C.S., E.H., S.H. and N.F.; formal analysis, A.C.S.; writing—original draft preparation, A.C.S.; writing—review and editing, A.C.S., E.H., S.H. and N.F.; visualization, A.C.S. and E.H.; supervision, E.H. All authors have read and agreed to the published version of the manuscript.
Funding
The experiments were measured and funded by the Unit for Field-Based Research, SLU. The project was financed by the Swedish University of Agricultural Sciences (SLU) and Stora Enso AB as part of their long-term strategic collaboration.
Data Availability Statement
The data presented in this study are openly available in https://www.silvaboreal.com, accessed on 25 April 2023.
Acknowledgments
The authors would like to thank the staff and managers at the Unit for Field-Based Research, SLU involved in the data collection and the researchers responsible for designing the experiment. The authors would like to thank Stora Enso AB for their financial support. The authors also thank the Bo Rydin Foundation for their support of Amanda’s attendance of the IUFRO conference ABIES & PINUS 2022 in Sarajevo.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mäkinen, H.; Isomäki, A.; Hongisto, T. Effect of half-systematic and systematic thinning on the increment of Scots pine and Norway spruce in Finland. For. Int. J. For. Res. 2005, 79, 103–121. [Google Scholar] [CrossRef]
- Niemistö, P.; Kilpeläinen, H.; Poutiainen, E. Effect of first thinning type and age on growth, stem quality and financial performance of a Scots pine stand in Finland. Silva Fenn. 2018, 52, 7816. [Google Scholar] [CrossRef]
- Saarinen, N.; Kankare, V.; Yrttimaa, T.; Viljanen, N.; Honkavaara, E.; Holopainen, M.; Hyyppä, J.; Huuskonen, S.; Hynynen, J.; Vastaranta, M. Assessing the effects of thinning on stem growth allocation of individual Scots pine trees. For. Ecol. Manag. 2020, 474, 118344. [Google Scholar] [CrossRef]
- Bianchi, S.; Huuskonen, S.; Hynynen, J.; Siipilehto, J.; Niemistö, P. Tree-level differences in Norway spruce and Scots pine growth after extreme thinning treatments. Scand. J. For. Res. 2022, 37, 109–118. [Google Scholar] [CrossRef]
- Hynynen, J. Self-thinning models for even-aged stands of Pinus sylvestris, Picea abies and Betula pendula. Scand. J. For. Res. 1993, 8, 326–336. [Google Scholar] [CrossRef]
- Siipilehto, J.; Allen, M.; Nilsson, U.; Brunner, A.; Huuskonen, S.; Haikarainen, S.; Subramanian, N.; Antón-Fernández, C.; Holmström, E.; Andreassen, K.; et al. Stand-level mortality models for Nordic boreal forests. Silva Fenn. 2020, 54, 10414. [Google Scholar] [CrossRef]
- Karlsson, L.; Bergsten, U.; Ulvcrona, T.; Elfving, B. Long-term effects on growth and yield of corridor thinning in young Pinus sylvestris stands. Scand. J. For. Res. 2013, 28, 28–37. [Google Scholar] [CrossRef]
- Nilsson, U.; Agestam, E.; Ekö, P.-M.; Elfving, B.; Fahlvik, N.; Johansson, U.; Karlsson, K.; Lundmark, T.; Wallentin, C. Thinning of Scots pine and Norway spruce monocultures in Sweden. Stud. For. Suec. 2010, 219, 1–46. [Google Scholar]
- Nuutinen, Y.; Miina, J.; Saksa, T.; Bergström, D.; Routa, J. Comparing the characteristics of boom-corridor and selectively thinned stands of Scots pine and birch. Silva Fenn. 2021, 55, 10462. [Google Scholar] [CrossRef]
- Hamilton, G.J. Forestry Commission Leafle; Line Thinning: Oxford, UK, 1980; Volume 77, ISBN 0-11-710229-6. Available online: https://www.forestresearch.gov.uk/publications/archive-line-thinning-fc-leaflet-77-1980/ (accessed on 7 June 2023).
- Witzell, J.; Bergström, D.; Bergsten, U. Variable corridor thinning—A cost-effective key to provision of multiple ecosystem services from young boreal conifer forests? Scand. J. For. Res. 2019, 34, 497–507. [Google Scholar] [CrossRef]
- Cho, M.-J.; Choi, Y.-S.; Oh, J.-H.; Mun, H.-S.; Han, S.-K. Comparison of harvesting productivity, cost, and residual stand damages between single-tree selection thinning and mechanized line thinning using a small-scale grapple-saw. For. Sci. Technol. 2022, 18, 45–55. [Google Scholar] [CrossRef]
- de la Fuente, T.; Bergström, D.; Fernandez-Lacruz, R.; Hujala, T.; Krajnc, N.; Laina, R.; Nordfjell, T.; Triplat, M.; Tolosana, E. Environmental Impacts of Boom-Corridor and Selectively Thinned Small-Diameter-Tree Forests. Sustainability 2022, 14, 6075. [Google Scholar] [CrossRef]
- Ahnlund Ulvcrona, K.; Bergström, D.; Bergsten, U. Stand structure after thinning in 1–2 m wide corridors in young dense stands. Silva Fenn. 2017, 51, 1563. [Google Scholar] [CrossRef]
- del Río, M.; Bravo-Oviedo, A.; Pretzsch, H.; Löf, M.; Ruiz-Peinado, R. A review of thinning effects on Scots pine stands: From growth and yield to new challenges under global change. For. Syst. 2017, 26, 9. [Google Scholar] [CrossRef]
- Pretzsch, H.; del Río, M.; Ammer, C.; Avdagic, A.; Barbeito, I.; Bielak, K.; Brazaitis, G.; Coll, L.; Dirnberger, G.; Drössler, L.; et al. Growth and yield of mixed versus pure stands of Scots pine (Pinus sylvestris L.) and European beech (Fagus sylvatica L.) analysed along a productivity gradient through Europe. Eur. J. For. Res. 2015, 134, 927–947. [Google Scholar] [CrossRef]
- Jäghagen, K.; Albrektson, A. Induced competition among scots pine seedlings and its effect on future timber quality. New For. 1996, 12, 163–174. [Google Scholar] [CrossRef]
- Lorimer, C.G. Tests of age-independent competition indices for individual trees in natural hardwood stands. For. Ecol. Manag. 1983, 6, 343–360. [Google Scholar] [CrossRef]
- García-Abril, A.; Martin-Fernández, S.; Grande, M.A.; Manzanera, J.A. Stand structure, competition and growth of Scots pine (Pinus sylvestris L.) in a Mediterranean mountainous environment. Ann. For. Sci. 2007, 64, 825–830. [Google Scholar] [CrossRef]
- Huuskonen, S.; Hynynen, J. Timing and intensity of precommercial thinning and their effects on the first commercial thinning in Scots pine stands. Silva Fenn. 2006, 40, 645–662. [Google Scholar] [CrossRef]
- Fahlvik, N.; Ekö, P.-M.; Pettersson, N. Influence of precommercial thinning grade on branch diameter and crown ratio in Pinus sylvestris in southern Sweden. Scand. J. For. Res. 2005, 20, 243–251. [Google Scholar] [CrossRef]
- Suadicani, K.; Nordfjell, T. Operational aspects of row and selective Thinning in the establishing of a shelterwood in a 50-year-old Norway Spruce stand. Int. J. For. Eng. 2003, 14, 25–37. [Google Scholar] [CrossRef]
- Bergström, D. Techniques and Systems for Boom-Corridor Thinning in Young Dense Forests. Ph.D. Thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2009. [Google Scholar]
- Sängstuvall, L.; Bergström, D.; Lämås, T.; Nordfjell, T. Simulation of harvester productivity in selective and boom-corridor thinning of young forests. Scand. J. For. Res. 2012, 27, 56–73. [Google Scholar] [CrossRef]
- Amateis, R.L.; Carlson, C.A. Modeling diameter class removals for thinned loblolly pine (Pinus taeda) plantations. For. Ecol. Manag. 2014, 327, 26–30. [Google Scholar] [CrossRef]
- Pukkala, T.; Kolström, T. Competition indices and the prediction of radial growth in Scots pine. Silva Fenn. 1987, 21, 55–67. [Google Scholar] [CrossRef]
- Fraver, S.; D’Amato, A.W.; Bradford, J.B.; Jonsson, B.G.; Jönsson, M.; Esseen, P.-A. Tree growth and competition in an old-growth Picea abies forest of boreal Sweden: Influence of tree spatial patterning. J. Veg. Sci. 2014, 25, 374–385. [Google Scholar] [CrossRef]
- Assmann, E. Section C—The Constitution and Development of Stands. In The Principles of Forest Yield Study; Assmann, E., Ed.; Pergamon: Oxford, UK, 1970; pp. 83–205. [Google Scholar]
- Eriksson, L. Single-Tree Competition Models: Predicting Stand Development after Cleaning; Swedish University of Agricultural Sciences: Garpenberg, Sweden, 1977. [Google Scholar]
- Fukumoto, K.; Nishizono, T.; Kitahara, F.; Hosoda, K. Evaluation of individual distance-independent diameter growth models for Japanese Cedar (Cryptomeria japonica) trees under multiple thinning treatments. Forests 2020, 11, 344. [Google Scholar] [CrossRef]
- Soares, P.; Tomé, M. Distance-dependent competition measures for eucalyptus plantations in Portugal. Ann. For. Sci. 1999, 56, 307–319. [Google Scholar] [CrossRef]
- Kahriman, A.; Şahin, A.; Sönmez, T.; Yavuz, M. A novel approach to selecting a competition index: The effect of competition on individual-tree diameter growth of Calabrian pine. Can. J. For. Res. 2018, 48, 1217–1226. [Google Scholar] [CrossRef]
- Burton, P.J. Some limitations inherent to static indices of plant competition. Can. J. For. Res. 1993, 23, 2141–2152. [Google Scholar] [CrossRef]
- Pedersen, R.Ø.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. On the evaluation of competition indices—The problem of overlapping samples. For. Ecol. Manag. 2013, 310, 120–133. [Google Scholar] [CrossRef]
- McTague, J.P.; Weiskittel, A.R. Individual-Tree Competition Indices and Improved Compatibility with Stand-Level Estimates of Stem Density and Long-Term Production. Forests 2016, 7, 238. [Google Scholar] [CrossRef]
- García, O. Plasticity as a link between spatially explicit, distance-independent, and whole-stand forest growth models. For. Sci. 2021, 68, 1–7. [Google Scholar] [CrossRef]
- Maltamo, M.; Vartiainen, P.; Packalen, P.; Korhonen, L. Estimation of periodic annual increment of tree ring widths by airborne laser scanning. Can. J. For. Res. 2022, 52, 644–651. [Google Scholar] [CrossRef]
- Bourdier, T.; Cordonnier, T.; Kunstler, G.; Piedallu, C.; Lagarrigues, G.; Courbaud, B. Tree size inequality reduces forest productivity: An analysis combining inventory data for ten European species and a light competition model. PLoS ONE 2016, 11, e0151852. [Google Scholar] [CrossRef] [PubMed]
- Pretzsch, H.; Bravo-Oviedo, A.; Hilmers, T.; Ruiz-Peinado, R.; Coll, L.; Löf, M.; Ahmed, S.; Aldea, J.; Ammer, C.; Avdagić, A.; et al. With increasing site quality asymmetric competition and mortality reduces Scots pine (Pinus sylvestris L.) stand structuring across Europe. For. Ecol. Manag. 2022, 520, 120365. [Google Scholar] [CrossRef]
- Cattaneo, N.; Bravo-Oviedo, A.; Bravo, F. Analysis of tree interactions in a mixed Mediterranean pine stand using competition indices. Eur. J. For. Res. 2018, 137, 109–120. [Google Scholar] [CrossRef]
- Maleki, K.; Kiviste, A.; Korjus, H. Analysis of individual tree competition on diameter growth of Silver Birch in Estonia. For. Syst. 2015, 24, e023. [Google Scholar] [CrossRef]
- Soares, P.; Tomé, M. A tree crown ratio prediction equation for eucalypt plantations. Ann. For. Sci. 2001, 58, 193–202. [Google Scholar] [CrossRef]
- McCreary, D.D.; Perry, D.A. Strip Thinning and Selective Thinning in Douglas-Fir. J. For. 1983, 81, 375–377. [Google Scholar]
- Sprugel, D.G.; Rascher, K.G.; Gersonde, R.; Dovčiak, M.; Lutz, J.A.; Halpern, C.B. Spatially explicit modeling of overstory manipulations in young forests: Effects on stand structure and light. Ecol. Model. 2009, 220, 3565–3575. [Google Scholar] [CrossRef]
- Saarinen, N.; Kankare, V.; Huuskonen, S.; Hynynen, J.; Bianchi, S.; Yrttimaa, T.; Luoma, V.; Junttila, S.; Holopainen, M.; Hyyppä, J.; et al. Effects of stem density on crown architecture of Scots Pine trees. Front. Plant Sci. 2022, 13, 817792. [Google Scholar] [CrossRef] [PubMed]
- Kankare, V.; Saarinen, N.; Pyörälä, J.; Yrttimaa, T.; Hynynen, J.; Huuskonen, S.; Hyyppä, J.; Vastaranta, M. Assessing the dependencies of Scots Pine (Pinus sylvestris L.) structural characteristics and internal wood property variation. Forests 2022, 13, 397. [Google Scholar] [CrossRef]
- Ronoud, G.; Poorazimy, M.; Yrttimaa, T.; Luoma, V.; Huuskonen, S.; Hynynen, J.; Hyyppä, J.; Saarinen, N.; Kankare, V.; Vastaranta, M. Terrestrial laser scanning in assessing the effect of different thinning treatments on the competition of Scots Pine (Pinus sylvestris L.) forests. Remote Sens. 2022, 14, 5196. [Google Scholar] [CrossRef]
- Corona, P.; Ferrara, A. Individual competition indices for conifer plantations. Agric. Ecosyst. Environ. 1989, 27, 429–437. [Google Scholar] [CrossRef]
- Saksa, T.; Uusitalo, J.; Lindeman, H.; Häyrynen, E.; Kulju, S.; Huuskonen, S. Decision support tool for tree species selection in forest regeneration based on harvester data. Forests 2021, 12, 1329. [Google Scholar] [CrossRef]
- Wimberly, M.C.; Bare, B.B. Distance-dependent and distance-independent models of Douglas-fir and western hemlock basal area growth following silvicultural treatment. For. Ecol. Manag. 1996, 89, 1–11. [Google Scholar] [CrossRef]
- Fagerberg, N.; Olsson, J.-O.; Lohmander, P.; Andersson, M.; Bergh, J. Individual-tree distance-dependent growth models for uneven-sized Norway spruce. For. Int. J. For. Res. 2022, 95, 634–646. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).