Patterns of Forest Species Association in a Broadleaf Forest in Romania
Abstract
1. Introduction
2. Materials and Methods
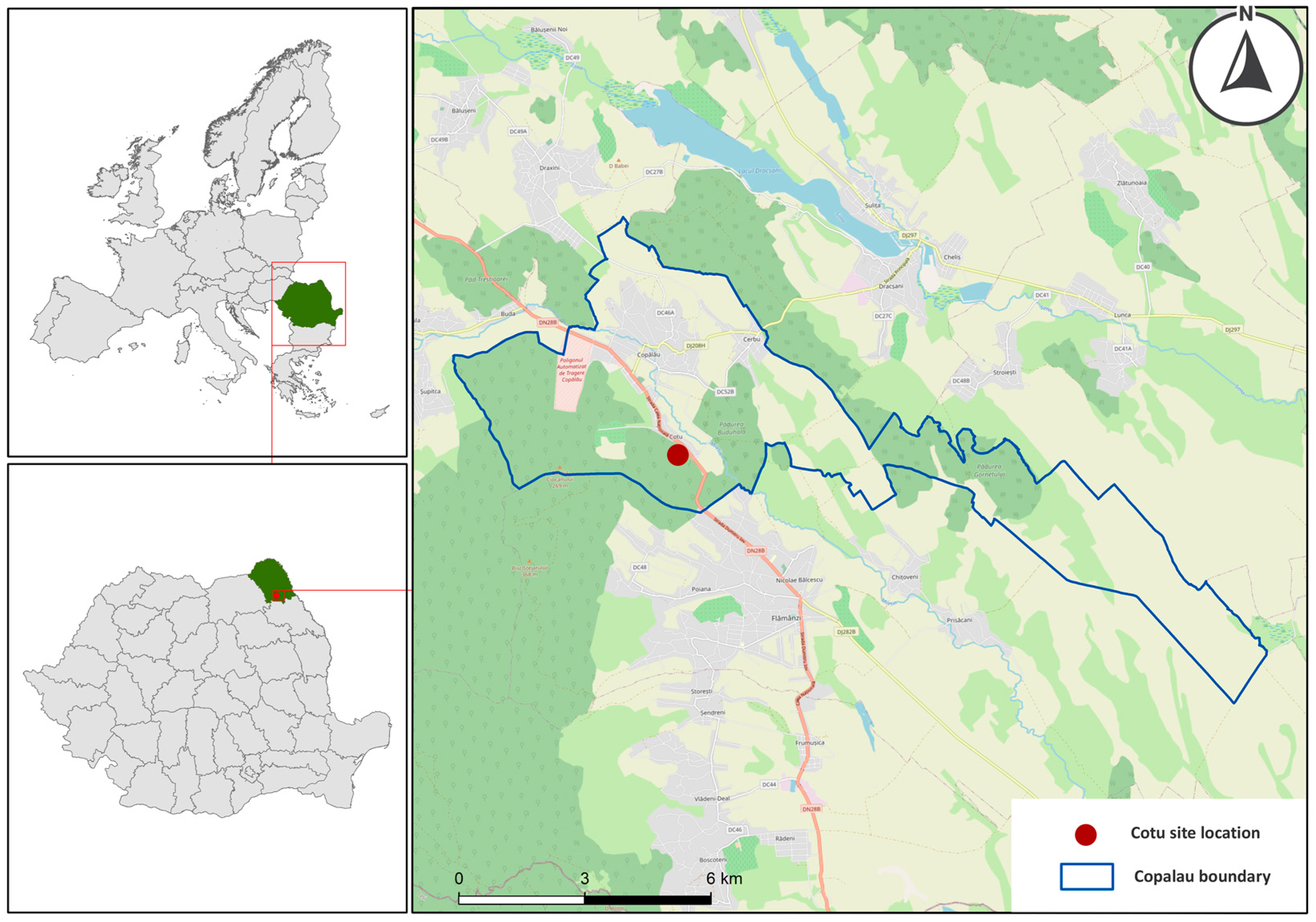
2.1. Study Site
2.2. Data Collection
2.3. Data Analysis
3. Results
3.1. The Analysis Based on Binary Indices
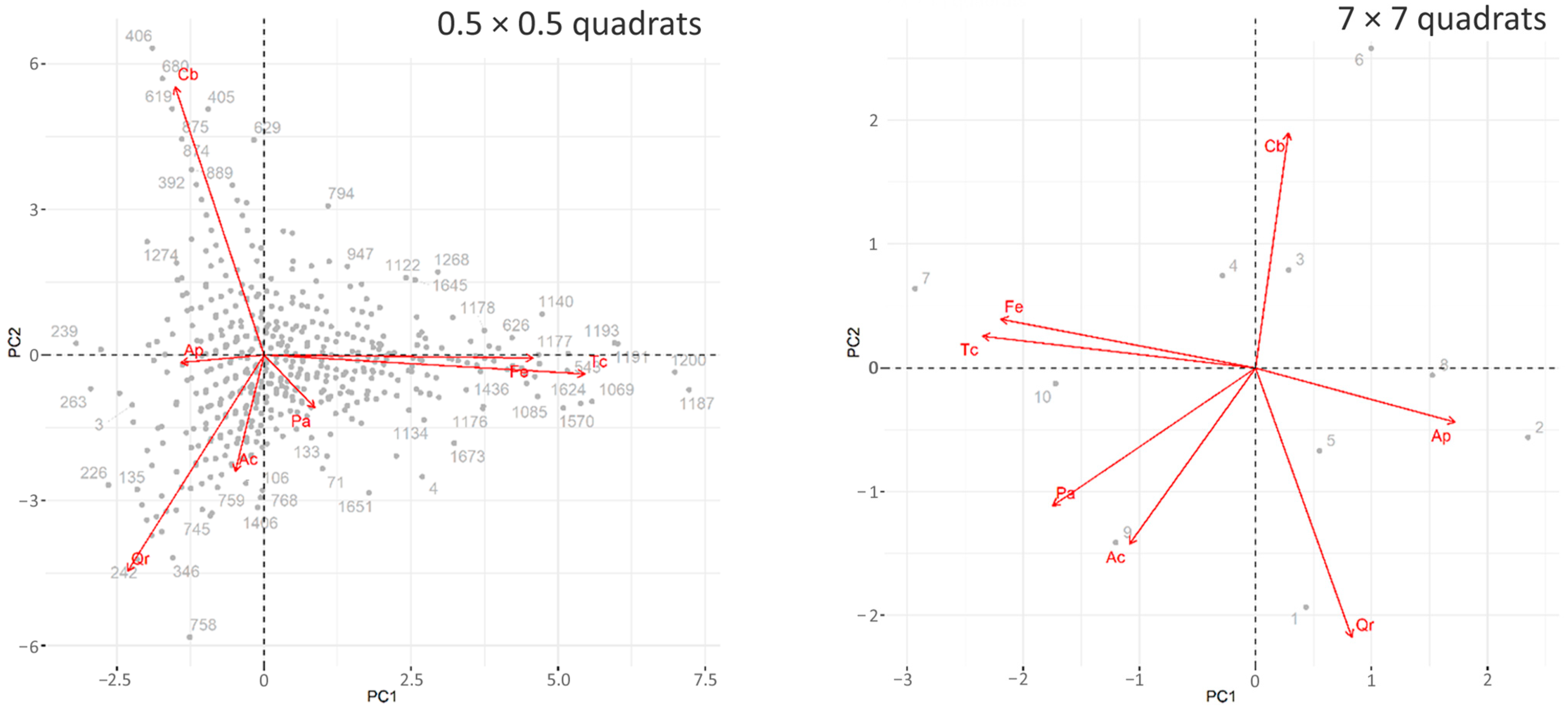
3.2. The Analysis Based on the Relationship between Quadrat-Specific Abundances
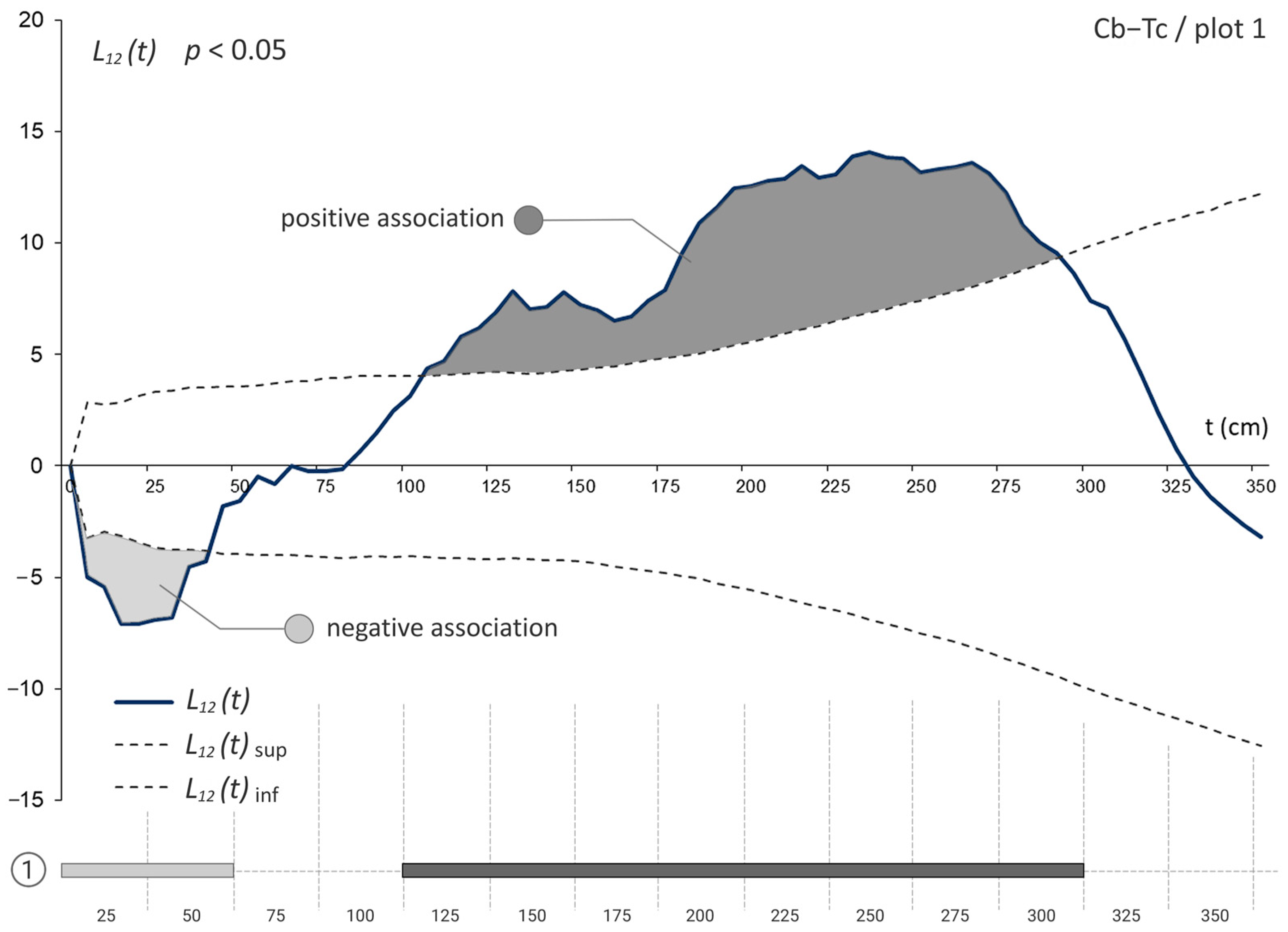
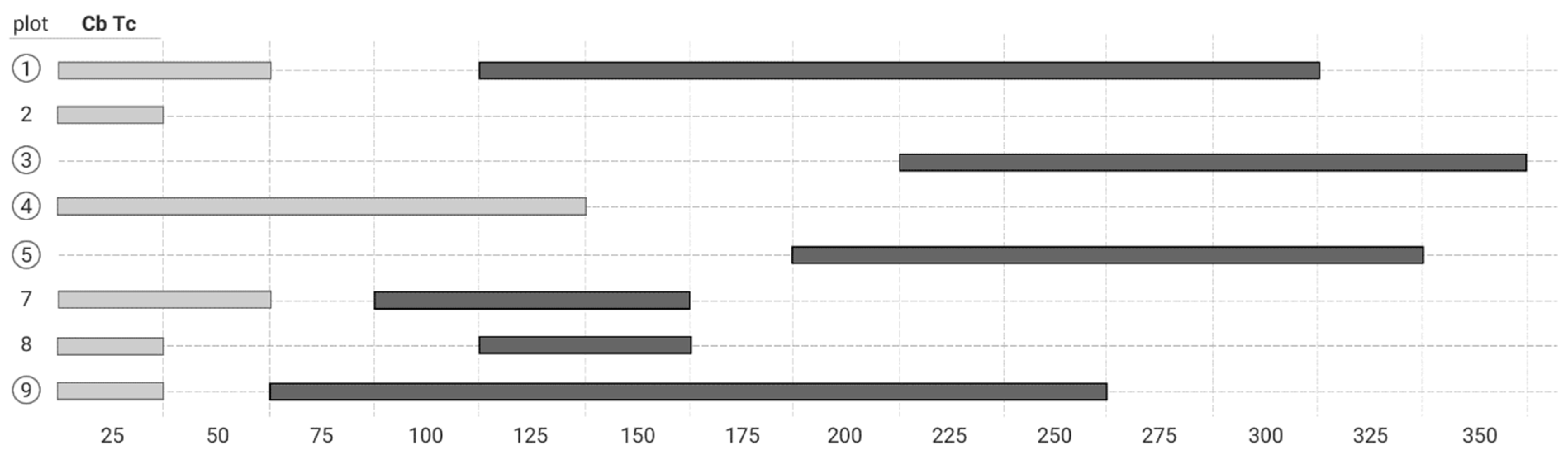
3.3. The Bivariate Analysis
4. Discussion
4.1. Specific Co-Occurrence Patterns
4.2. Co-Occurrence Patterns at Different Scale
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jost, L.; Chao, A.; Chazdon, R.L. Compositional Similarity and β (Beta) Diversity. In Biological Diversity: Frontiers in Measurement and Assessment; Magurran, A.E., McGill, B.J., Eds.; Oxford University Press: New York, NY, USA, 2011; pp. 66–84. ISBN 9780199580668. [Google Scholar]
- Legendre, P.; Legendre, L. Numerical Ecology, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 9780444538697. [Google Scholar]
- Mainali, K.P.; Slud, E.; Singer, M.C.; Fagan, W.F. A Better Index for Analysis of Co-Occurrence and Similarity. Sci. Adv. 2022, 8, eabj9204. [Google Scholar] [CrossRef] [PubMed]
- Sritharan, M.S.; Scheele, B.C.; Blanchard, W.; Lindenmayer, D.B. Spatial Associations between Plants and Vegetation Community Characteristics Provide Insights into the Processes Influencing Plant Rarity. PLoS ONE 2021, 16, e0260215. [Google Scholar] [CrossRef]
- Blanchet, F.G.; Cazelles, K.; Gravel, D. Co-occurrence Is Not Evidence of Ecological Interactions. Ecol. Lett. 2020, 23, 1050–1063. [Google Scholar] [CrossRef] [PubMed]
- Keil, P. Z-scores Unite Pairwise Indices of Ecological Similarity and Association for Binary Data. Ecosphere 2019, 10, e02933. [Google Scholar] [CrossRef]
- Brusco, M.; Cradit, J.D.; Steinley, D. A Comparison of 71 Binary Similarity Coefficients: The Effect of Base Rates. PLoS ONE 2021, 16, e0247751. [Google Scholar] [CrossRef]
- MacGregor-Fors, I.; Escobar, F.; Escobar-Ibáñez, J.F.; Mesa-Sierra, N.; Alvarado, F.; Rueda-Hernández, R.; Moreno, C.E.; Falfán, I.; Corro, E.J.; Pineda, E.; et al. Shopping for Ecological Indices? On the Use of Incidence-Based Species Compositional Similarity Measures. Diversity 2022, 14, 384. [Google Scholar] [CrossRef]
- Chirigati, F. Co-Occurrence and Similarity Revisited. Nat. Comput. Sci. 2022, 2, 67. [Google Scholar] [CrossRef]
- Jaccard, P. The Distribution of the Flora in the Alpine Zone. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Arita, H.T. Multisite and Multispecies Measures of Overlap, Co-Occurrence, and Co-Diversity. Ecography 2017, 40, 709–718. [Google Scholar] [CrossRef]
- Griffith, D.M.; Veech, J.A.; Marsh, C.J. Cooccur: Probabilistic Species Co-Occurrence Analysis in R. J. Stat. Softw. 2016, 69, 1–17. [Google Scholar] [CrossRef]
- Chung, N.C.; Miasojedow, B.; Startek, M.; Gambin, A. Jaccard/Tanimoto Similarity Test and Estimation Methods for Biological Presence-Absence Data. BMC Bioinform. 2019, 20, 644. [Google Scholar] [CrossRef]
- Snijders, T.A.B.; Dormaar, M.; van Schuur, W.H.; Dijkman-Caes, C.; Driessen, G. Distribution of Some Similarity Coefficients for Dyadic Binary Data in the Case of Associated Attributes. J. Classif. 1990, 7, 5–31. [Google Scholar] [CrossRef]
- Real, R.; Vargas, J.M. The Probabilistic Basis of Jaccard’s Index of Similarity. Syst. Biol. 1996, 45, 380–385. [Google Scholar] [CrossRef]
- Janson, S.; Vegelius, J. Measures of Ecological Association. Oecologia 1981, 49, 371–376. [Google Scholar] [CrossRef] [PubMed]
- Wilson, M.V.; Shmida, A. Measuring Beta Diversity with Presence-Absence Data. J. Ecol. 1984, 72, 1055–1064. [Google Scholar] [CrossRef]
- Cairns, S.J.; Schwager, S.J. A Comparison of Association Indices. Anim. Behav. 1987, 35, 1454–1469. [Google Scholar] [CrossRef]
- Koleff, P.; Gaston, K.J.; Lennon, J.J. Measuring Beta Diversity for Presence-Absence Data. J. Anim. Ecol. 2003, 72, 367–382. [Google Scholar] [CrossRef]
- Fortin, M.-J.; Drapeau, P.; Legendre, P. Spatial Autocorrelation and Sampling Design in Plant Ecology. In Progress in Theoretical Vegetation Science; Springer: Dordrecht, The Netherlands, 1990; pp. 209–222. [Google Scholar]
- Jonsson, B.G.; Moen, J. Patterns in Species Associations in Plant Communities: The Importance of Scale. J. Veg. Sci. 1998, 9, 327–332. [Google Scholar] [CrossRef]
- Sanaei, A.; Sayer, E.J.; Saiz, H.; Yuan, Z.; Ali, A. Species Co-occurrence Shapes Spatial Variability in Plant Diversity–Biomass Relationships in Natural Rangelands under Different Grazing Intensities. Land Degrad. Dev. 2021, 32, 4390–4401. [Google Scholar] [CrossRef]
- Roxburgh, S.H.; Chesson, P. A New Method for Detecting Species Associations with Spatially Autocorrelated Data. Ecology 1998, 79, 2180–2192. [Google Scholar] [CrossRef]
- Gu, L.; O’Hara, K.L.; Li, W.; Gong, Z. Spatial Patterns and Interspecific Associations among Trees at Different Stand Development Stages in the Natural Secondary Forests on the Loess Plateau, China. Ecol. Evol. 2019, 9, 6410–6421. [Google Scholar] [CrossRef]
- Silva, L.A.E.; Siqueira, M.F.; Pinto, F.d.S.; Barros, F.S.M.; Zimbrão, G.; Souza, J.M. Applying Data Mining Techniques for Spatial Distribution Analysis of Plant Species Co-Occurrences. Expert Syst. Appl. 2016, 43, 250–260. [Google Scholar] [CrossRef]
- Araújo, M.B.; Rozenfeld, A.; Rahbek, C.; Marquet, P.A. Using Species Co-Occurrence Networks to Assess the Impacts of Climate Change. Ecography 2011, 34, 897–908. [Google Scholar] [CrossRef]
- Cazelles, K.; Araújo, M.B.; Mouquet, N.; Gravel, D. A Theory for Species Co-Occurrence in Interaction Networks. Theor. Ecol. 2016, 9, 39–48. [Google Scholar] [CrossRef]
- Julio Camarero, J.; Gutierrez, E.; Fortin, M.-J.; Ribbens, E. Spatial Patterns of Tree Recruitment in a Relict Population of Pinus Uncinata: Forest Expansion through Stratified Diffusion. J. Biogeogr. 2005, 32, 1979–1992. [Google Scholar] [CrossRef]
- Wiegand, T.; Gunatilleke, S.; Gunatilleke, N. Species Associations in a Heterogeneous Sri Lankan Dipterocarp Forest. Am. Nat. 2007, 170, E77–E95. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Hu, F.; Zeng, F.; Wang, K.; Peng, W.; Zhang, H.; Zeng, Z.; Zhang, F.; Song, T. Spatial Distribution of Tree Species in Evergreen-Deciduous Broadleaf Karst Forests in Southwest China. Sci. Rep. 2017, 7, 15664. [Google Scholar] [CrossRef]
- Bastias, C.C.; Truchado, D.A.; Valladares, F.; Benavides, R.; Bouriaud, O.; Bruelheide, H.; Coppi, A.; Finér, L.; Gimeno, T.E.; Jaroszewicz, B.; et al. Species Richness Influences the Spatial Distribution of Trees in European Forests. Oikos 2020, 129, 380–390. [Google Scholar] [CrossRef]
- Ripley, B.D. Modelling Spatial Patterns. J. R. Stat. Soc. Ser. B 1977, 39, 172–192. [Google Scholar] [CrossRef]
- Ripley, B.D. The Second-Order Analysis of Stationary Point Processes. J. Appl. Probab. 1976, 13, 255–266. [Google Scholar] [CrossRef]
- Webb, C.O.; Peart, D.R. Habitat Associations of Trees and Seedlings in a Bornean Rain Forest. J. Ecol. 2000, 88, 464–478. [Google Scholar] [CrossRef]
- Yamazaki, M.; Iwamoto, S.; Seiwa, K. Distance- and Density-Dependent Seedling Mortality Caused by Several Diseases in Eight Tree Species Co-Occurring in a Temperate Forest. In Forest Ecology; Van der Valk, A.G., Ed.; Springer: Dordrecht, The Netherlands, 2008; pp. 181–196. [Google Scholar]
- Zhang, J.; Hao, Z.; Song, B.; Li, B.; Wang, X.; Ye, J. Fine-Scale Species Co-Occurrence Patterns in an Old-Growth Temperate Forest. For. Ecol. Manag. 2009, 257, 2115–2120. [Google Scholar] [CrossRef]
- Dale, M.R.T. Spatial Pattern Analysis in Plant Ecology; Cambridge University Press: Cambridge, UK, 2000; ISBN 9780521794374. [Google Scholar]
- Ulrich, W.; Kryszewski, W.; Sewerniak, P.; Puchałka, R.; Strona, G.; Gotelli, N.J. A Comprehensive Framework for the Study of Species Co-Occurrences, Nestedness and Turnover. Oikos 2017, 126, 1607–1616. [Google Scholar] [CrossRef]
- Real, R. Tables of Significant Values of Jaccard’s Index of Similarity. Misc. Zool. 1999, 22, 29–40. [Google Scholar]
- Bro, R.; Smilde, A.K. Principal Component Analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef]
- Shlens, J. A Tutorial on Principal Component Analysis. arXiv 2014, arXiv:1404.1100. [Google Scholar]
- Eriksson, L.; Byrne, T.; Johansson, E.; Trygg, J.; Vikström, C. Multi-and Megavariate Data Analysis Basic Principles and Applications; MKS Umetrics: Malmo, Sweden, 2013; Volume 1. [Google Scholar]
- Legendre, P.; Gallagher, E.D. Ecologically Meaningful Transformations for Ordination of Species Data. Oecologia 2001, 129, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Zhu, S.; Chen, H.Y.H.; John, R.; Zhou, G.; Zhang, D.; Zhang, Q.; Ye, Q. Are Functional Traits a Good Predictor of Global Change Impacts on Tree Species Abundance Dynamics in a Subtropical Forest? Ecol. Lett. 2015, 18, 1181–1189. [Google Scholar] [CrossRef]
- Restuccia, A.; Scavo, A.; Lombardo, S.; Pandino, G.; Fontanazza, S.; Anastasi, U.; Abbate, C.; Mauromicale, G. Long-Term Effect of Cover Crops on Species Abundance and Diversity of Weed Flora. Plants 2020, 9, 1506. [Google Scholar] [CrossRef]
- Bin, Y.; Spence, J.; Wu, L.; Li, B.; Hao, Z.; Ye, W.; He, F. Species-Habitat Associations and Demographic Rates of Forest Trees. Ecography 2016, 39, 9–16. [Google Scholar] [CrossRef]
- R Core Team. The R Project for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 6 March 2023).
- Lotwick, H.W.; Silverman, B.W. Methods for Analysing Spatial Processes of Several Types of Points. J. R. Stat. Soc. Ser. B 1982, 44, 406–413. [Google Scholar] [CrossRef]
- Diggle, P.J. Statistical Analysis of Spatial Point Patterns; Academic Press: London, UK, 1983; ISBN 9780122158506. [Google Scholar]
- Haase, P. Spatial Pattern Analysis in Ecology Based on Ripley’s K-Function: Introduction and Methods of Edge Correction. J. Veg. Sci. 1995, 6, 575–582. [Google Scholar] [CrossRef]
- Andersen, M. Spatial Analysis of Two-Species Interactions. Oecologia 1992, 91, 134–140. [Google Scholar] [CrossRef]
- Martens, S.N.; Breshears, D.D.; Meyer, C.W.; Barnes, F.J. Scales of Aboveground and Below-Ground Competition in a Semi-Arid Woodland Detected from Spatial Pattern. J. Veg. Sci. 1997, 8, 655–664. [Google Scholar] [CrossRef]
- Haase, P. Can Isotropy vs. Anisotropy in the Spatial Association of Plant Species Reveal Physical vs. Biotic Facilitation? J. Veg. Sci. 2001, 12, 127–136. [Google Scholar] [CrossRef]
- Goreaud, F.; Pélissier, R. Avoiding Misinterpretation of Biotic Interactions with the Intertype K 12 -function: Population Independence vs. Random Labelling Hypotheses. J. Veg. Sci. 2003, 14, 681–692. [Google Scholar] [CrossRef]
- Hai, N.H.; Erfanifard, Y.; Bui, V.B.; Mai, T.H.; Petritan, A.M.; Petritan, I.C. Topographic Effects on the Spatial Species Associations in Diverse Heterogeneous Tropical Evergreen Forests. Sustainability 2021, 13, 2468. [Google Scholar] [CrossRef]
- Haase, P. SPPA ver. 2.03—A Program for Spatial Point Pattern Analysis 2004. Available online: http://haasep.homepage.t-online.de/ (accessed on 6 July 2008).
- Liu, Z.; Zhu, Y.; Wang, J.; Ma, W.; Meng, J. Species Association of the Dominant Tree Species in an Old-Growth Forest and Implications for Enrichment Planting for the Restoration of Natural Degraded Forest in Subtropical China. Forests 2019, 10, 957. [Google Scholar] [CrossRef]
- O’Reilly, E.; Gregory, R.D.; Aunins, A.; Brotons, L.; Chodkiewicz, T.; Escandell, V.; Foppen, R.P.B.; Gamero, A.; Herrando, S.; Jiguet, F.; et al. An Assessment of Relative Habitat Use as a Metric for Species’ Habitat Association and Degree of Specialization. Ecol. Indic. 2022, 135, 108521. [Google Scholar] [CrossRef]
- Chuyong, G.B.; Kenfack, D.; Harms, K.E.; Thomas, D.W.; Condit, R.; Comita, L.S. Habitat Specificity and Diversity of Tree Species in an African Wet Tropical Forest. Plant Ecol. 2011, 212, 1363–1374. [Google Scholar] [CrossRef]
- Garzon-Lopez, C.X.; Jansen, P.A.; Bohlman, S.A.; Ordonez, A.; Olff, H. Effects of Sampling Scale on Patterns of Habitat Association in Tropical Trees. J. Veg. Sci. 2014, 25, 349–362. [Google Scholar] [CrossRef]
- Yin, D.; Liu, Y.; Ye, Q.; Cadotte, M.W.; He, F. Trait Hierarchies Are Stronger than Trait Dissimilarities in Structuring Spatial Co-occurrence Patterns of Common Tree Species in a Subtropical Forest. Ecol. Evol. 2021, 11, 7366–7377. [Google Scholar] [CrossRef]
- Modrý, M.; Hubený, D.; Rejšek, K. Differential Response of Naturally Regenerated European Shade Tolerant Tree Species to Soil Type and Light Availability. For. Ecol. Manag. 2004, 188, 185–195. [Google Scholar] [CrossRef]
- Hou, J.H.; Mi, X.C.; Liu, C.R.; Ma, K.P. Spatial Patterns and Associations in a Quercus-Betula Forest in Northern China. J. Veg. Sci. 2004, 15, 407–414. [Google Scholar] [CrossRef]
- Fajardo, A.; Goodburn, J.M.; Graham, J. Spatial Patterns of Regeneration in Managed Uneven-Aged Ponderosa Pine/Douglas-Fir Forests of Western Montana, USA. For. Ecol. Manag. 2006, 223, 255–266. [Google Scholar] [CrossRef]
- Ray, D.G.; Nyland, R.D.; Yanai, R.D. Patterns of Early Cohort Development Following Shelterwood Cutting in Three Adirondack Northern Hardwood Stands. For. Ecol. Manag. 1999, 119, 1–11. [Google Scholar] [CrossRef]
- Gaudio, N.; Balandier, P.; Perret, S.; Ginisty, C. Growth of Understorey Scots Pine (Pinus Sylvestris L.) Saplings in Response to Light in Mixed Temperate Forest. Forestry 2011, 84, 187–195. [Google Scholar] [CrossRef]
- Penttinen, A.; Stoyan, D. Recent Applications of Point Process Methods in Forestry Statistics. Stat. Sci. 2000, 15, 61–78. [Google Scholar] [CrossRef]
- Gotelli, N.J.; Ulrich, W. Statistical Challenges in Null Model Analysis. Oikos 2012, 121, 171–180. [Google Scholar] [CrossRef]
- Ulrich, W.; Gotelli, N.J. Pattern Detection in Null Model Analysis. Oikos 2013, 122, 2–18. [Google Scholar] [CrossRef]
- Harris, D.J. Inferring Species Interactions from Co-occurrence Data with Markov Networks. Ecology 2016, 97, 3308–3314. [Google Scholar] [CrossRef]
- Pacala, S.W. Dynamics of Plant Communities. In Plant Ecology; Crawley, M.J., Ed.; Blackwell Publishing Ltd.: Oxford, UK, 1996; pp. 532–555. [Google Scholar]
- Zhou, Q.; Shi, H.; Shu, X.; Xie, F.; Zhang, K.; Zhang, Q.; Dang, H. Spatial Distribution and Interspecific Associations in a Deciduous Broad-leaved Forest in North-central China. J. Veg. Sci. 2019, 30, 1153–1163. [Google Scholar] [CrossRef]
- Peters, H.A. Neighbour-Regulated Mortality: The Influence of Positive and Negative Density Dependence on Tree Populations in Species-Rich Tropical Forests. Ecol. Lett. 2003, 6, 757–765. [Google Scholar] [CrossRef]
- Seiwa, K.; Miwa, Y.; Sahashi, N.; Kanno, H.; Tomita, M.; Ueno, N.; Yamazaki, M. Pathogen Attack and Spatial Patterns of Juvenile Mortality and Growth in a Temperate Tree, Prunus Grayana. Can. J. For. Res. 2008, 38, 2445–2454. [Google Scholar] [CrossRef]
- Szwagrzyk, J.; Czerwczak, M. Spatial Patterns of Trees in Natural Forests of East-Central Europe. J. Veg. Sci. 1993, 4, 469–476. [Google Scholar] [CrossRef]
- Lieberman, M.; Lieberman, D. Nearest-Neighbor Tree Species Combinations in Tropical Forest: The Role of Chance, and Some Consequences of High Diversity. Oikos 2007, 116, 377–386. [Google Scholar] [CrossRef]
- Xie, L.; Chen, H.; Wei, L.; Chen, S.; Wang, L.; Xu, B.; Yi, X.; Wang, X.; Ding, H.; Fang, Y. Scale-dependent Effects of Species Diversity on Aboveground Biomass and Productivity in a Subtropical Broadleaved Forest on Mt. Huangshan. Ecol. Evol. 2023, 13, e9786. [Google Scholar] [CrossRef]
- Hurlbert, S.H. Spatial Distribution of the Montane Unicorn. Oikos 1990, 58, 257–271. [Google Scholar] [CrossRef]
- Liu, P.; Wang, W.; Bai, Z.; Guo, Z.; Ren, W.; Huang, J.; Xu, Y.; Yao, J.; Ding, Y.; Zang, R. Competition and Facilitation Co-Regulate the Spatial Patterns of Boreal Tree Species in Kanas of Xinjiang, Northwest China. Ecol. Manag. 2020, 467, 118167. [Google Scholar] [CrossRef]
- Paquette, A.; Messier, C. The Effect of Biodiversity on Tree Productivity: From Temperate to Boreal Forests. Glob. Ecol. Biogeogr. 2011, 20, 170–180. [Google Scholar] [CrossRef]
- Ratcliffe, S.; Wirth, C.; Jucker, T.; van der Plas, F.; Scherer-Lorenzen, M.; Verheyen, K.; Allan, E.; Benavides, R.; Bruelheide, H.; Ohse, B.; et al. Biodiversity and Ecosystem Functioning Relations in European Forests Depend on Environmental Context. Ecol. Lett. 2017, 20, 1414–1426. [Google Scholar] [CrossRef] [PubMed]
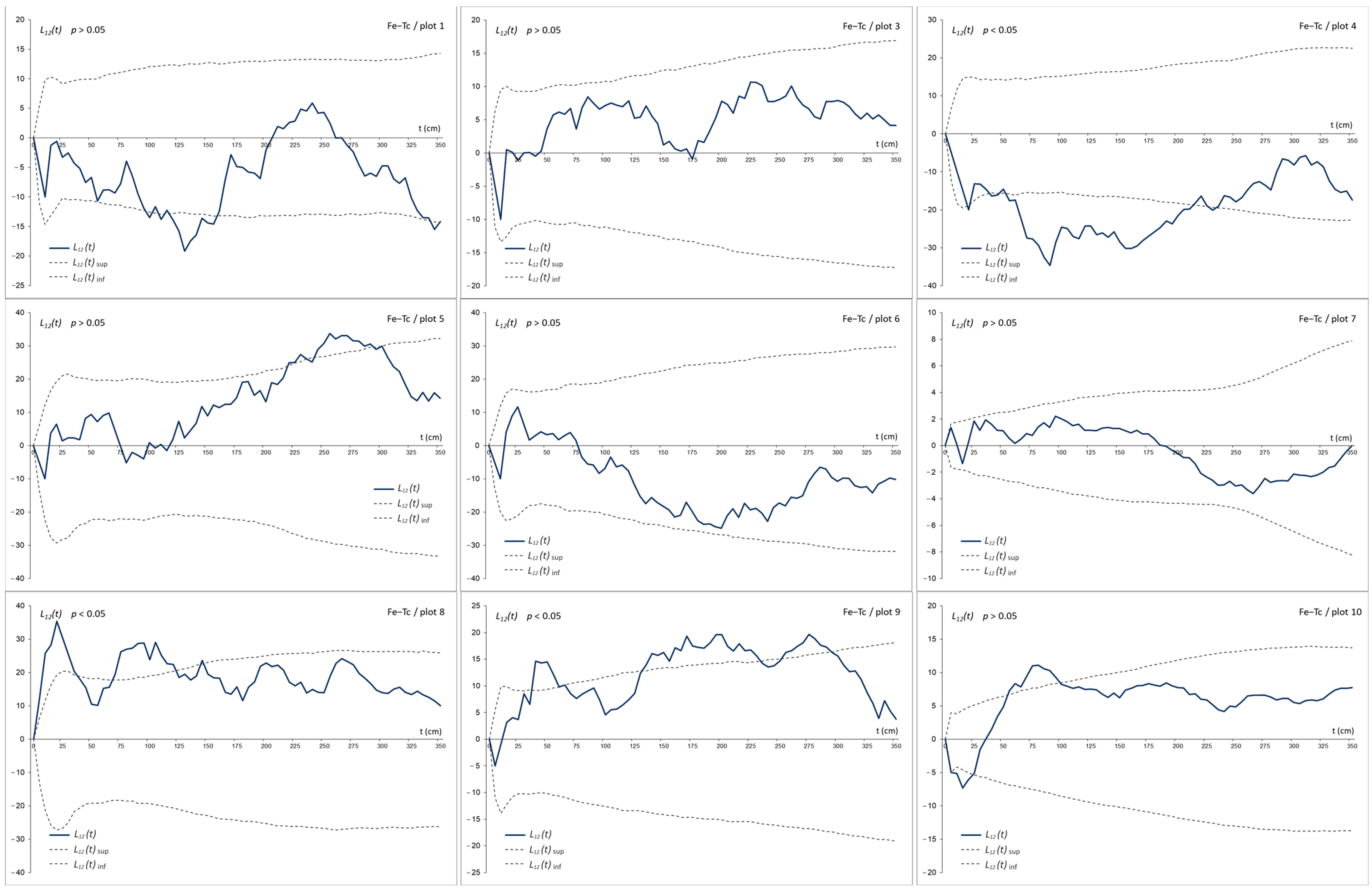
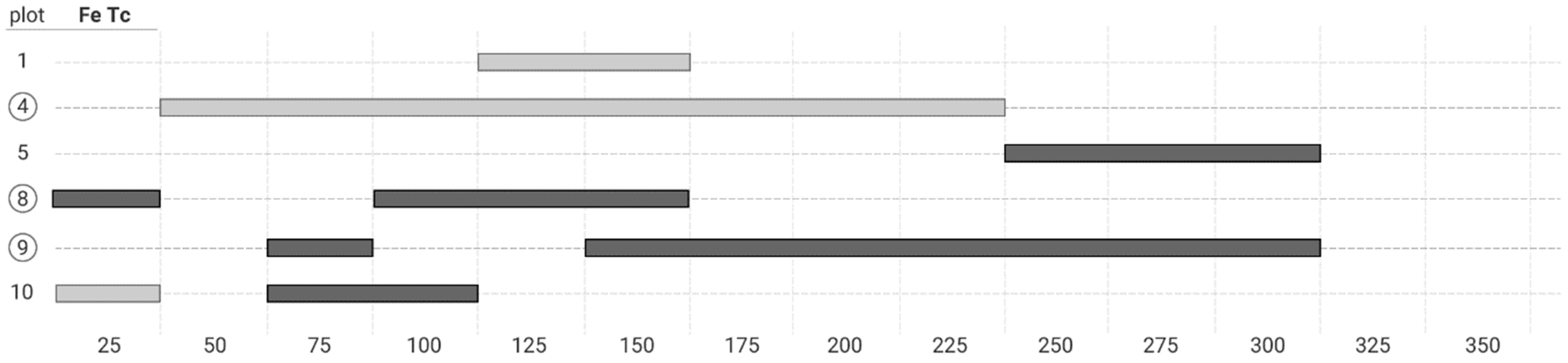
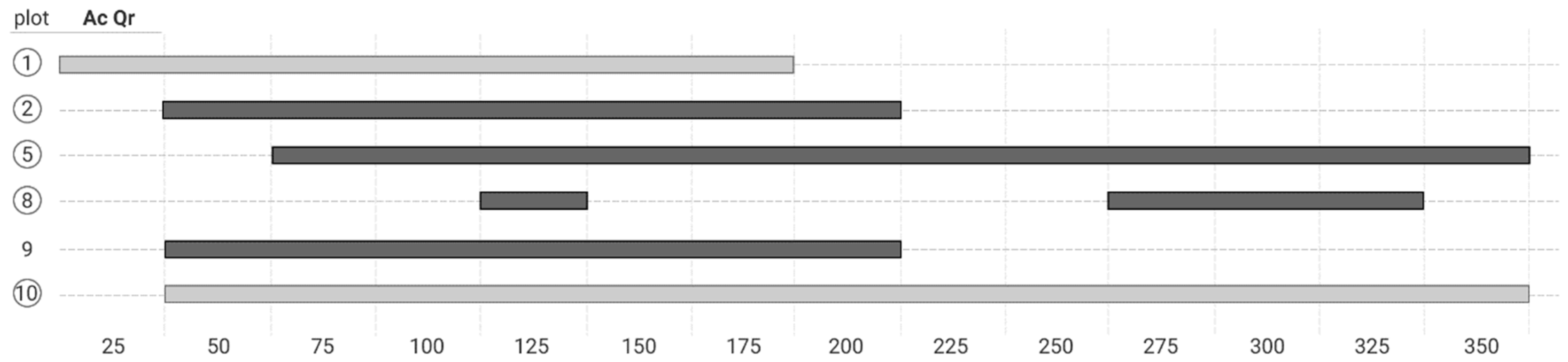

| Qdrt. Size | Cb–Pa | Cb–Fe | Cb–Ac | Cb–Ap | Cb–Qr | Cb–Tc | Pa–Fe | Pa–Ac | Pa–Ap | Pa–Qr | Pa–Tc |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 × 7 m | 1.000 | 1.000 | 1.000 | 0.700 | 1.000 | 1.000 | 1.000 | 1.000 | 0.700 | 1.000 | 1.000 |
| 3.5 × 3.5 m | 0.800 | 0.950 | 0.925 | 0.525 | 0.950 | 1.000 | 0.795 | 0.816 | 0.432 | 0.842 | 0.800 |
| 2.33 × 2.33 m | 0.567 | 0.744 | 0.722 | 0.322 | 0.922 | 0.967 | 0.532 | 0.487 | 0.250 | 0.576 | 0.551 |
| 1.75 × 1.75 m | 0.381 | 0.638 | 0.594 | 0.238 | 0.813 | 0.850 | 0.336 | 0.322 | 0.165 | 0.404 | 0.387 |
| 1.4 × 1.4 m | 0.272 | 0.548 | 0.488 | 0.160 | 0.740 | 0.732 | 0.235 | 0.250 | 0.091 | 0.278 | 0.287 |
| 1 × 1 m | 0.183 | 0.384 | 0.337 | 0.089 | 0.606 | 0.524 | 0.181 | 0.196 | 0.063 | 0.201 | 0.185 |
| 0.5 × 0.5 m | 0.051 | 0.187 | 0.131 | 0.031 | 0.284 | 0.203 | 0.045 | 0.048 | 0.000 | 0.051 | 0.056 |
| Qdrt. size | Fe–Ac | Fe–Ap | Fe–Qr | Fe–Tc | Ac–Ap | Ac–Qr | Ac–Tc | Ap–Qr | Ap–Tc | Qr–Tc | |
| 7 × 7 m | 1.000 | 0.700 | 1.000 | 1.000 | 0.700 | 1.000 | 1.000 | 0.700 | 0.700 | 1.000 | |
| 3.5 × 3.5 m | 0.875 | 0.475 | 0.900 | 0.950 | 0.568 | 0.974 | 0.925 | 0.553 | 0.525 | 0.950 | |
| 2.33 × 2.33 m | 0.610 | 0.215 | 0.705 | 0.750 | 0.306 | 0.721 | 0.727 | 0.318 | 0.303 | 0.889 | |
| 1.75 × 1.75 m | 0.470 | 0.167 | 0.589 | 0.630 | 0.198 | 0.585 | 0.604 | 0.273 | 0.234 | 0.739 | |
| 1.4 × 1.4 m | 0.385 | 0.113 | 0.464 | 0.546 | 0.117 | 0.476 | 0.473 | 0.172 | 0.155 | 0.586 | |
| 1 × 1 m | 0.262 | 0.073 | 0.297 | 0.413 | 0.071 | 0.340 | 0.281 | 0.110 | 0.066 | 0.382 | |
| 0.5 × 0.5 m | 0.102 | 0.018 | 0.124 | 0.198 | 0.006 | 0.134 | 0.092 | 0.026 | 0.019 | 0.128 |
| Quadrat Size | 0.5 m | 1.0 m | 1.4 m | 1.75 m | 2.33 m | 3.5 m | 7 m |
|---|---|---|---|---|---|---|---|
| no. of positive associations | 0 | 3 | 9 | 10 | 15 | 19 | 15 |
| no. of negative associations | 20 | 12 | 8 | 5 | 1 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palaghianu, C.; Coșofreț, C. Patterns of Forest Species Association in a Broadleaf Forest in Romania. Forests 2023, 14, 1118. https://doi.org/10.3390/f14061118
Palaghianu C, Coșofreț C. Patterns of Forest Species Association in a Broadleaf Forest in Romania. Forests. 2023; 14(6):1118. https://doi.org/10.3390/f14061118
Chicago/Turabian StylePalaghianu, Ciprian, and Cosmin Coșofreț. 2023. "Patterns of Forest Species Association in a Broadleaf Forest in Romania" Forests 14, no. 6: 1118. https://doi.org/10.3390/f14061118
APA StylePalaghianu, C., & Coșofreț, C. (2023). Patterns of Forest Species Association in a Broadleaf Forest in Romania. Forests, 14(6), 1118. https://doi.org/10.3390/f14061118







