Accuracy of Double Bark Thickness Estimation Methods Used in Spruce—(Picea abies L. Karst) Timber Production in Czechia
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yilmaz, E.; Ozdemir, E.; Makineci, E. Bark Thickness Models for Oak Forests Being Converted from Coppice to High Forests in Northwestern Turkey. Environ. Monit. Assess. 2021, 193, 728. [Google Scholar] [CrossRef] [PubMed]
- Mosaffaei, Z.; Jahani, A. Modeling of Ash (Fraxinus excelsior) Bark Thickness in Urban Forests Using Artificial Neural Network (ANN) and Regression Models. Model. Earth Syst. Environ. 2021, 7, 1443–1452. [Google Scholar] [CrossRef]
- Bauer, R.; Billard, A.; Mothe, F.; Longuetaud, F.; Houballah, M.; Bouvet, A.; Cuny, H.; Colin, A.; Colin, F. Modelling Bark Volume for Six Commercially Important Tree Species in France: Assessment of Models and Application at Regional Scale. Ann. For. Sci. 2022, 78, 104. [Google Scholar] [CrossRef]
- Sherrill, J.R.; Mullin, T.J.; Bullock, B.P.; Mckeand, S.E.; Purnell, R.C.; Gumpert, M.L.; Isik, F. An Evaluation of Selection for Volume Growth in Loblolly Pine. Silvae Genet. 2008, 57, 22–28. [Google Scholar] [CrossRef]
- Cellini, J.M.; Galarza, M.; Burns, S.L.; Martinez-Pastur, G.J.; Lencinas, M.V. Equations of Bark Thickness and Volume Profiles at Different Heights with Easy-Measurement Variables. For. Syst. 2012, 21, 23–30. [Google Scholar] [CrossRef]
- Wilson, B.G.; Witkowski, E.T.F. Seed Banks, Bark Thickness and Change in Age and Size Structure (1978–1999) of the African Savanna Tree, Burkea Africana. Plant Ecol. 2003, 167, 151–162. [Google Scholar] [CrossRef]
- Graves, S.J.; Rifai, S.W.; Putz, F.E. Outer Bark Thickness Decreases More with Height on Stems of Fire-Resistant than Fire-Sensitive Floridian Oaks (Quercus spp.; Fagaceae). Am. J. Bot. 2014, 101, 2183–2188. [Google Scholar] [CrossRef]
- Biggs, A.R.; Merrill, W.; Davis, D.D. Discussion: Response of Bark Tissues to Injury and Infection. Can. J. For. Res. 1984, 14, 351–356. [Google Scholar] [CrossRef]
- Pausas, J.G. Bark Thickness and Fire Regime. Funct. Ecol. 2015, 29, 315–327. [Google Scholar] [CrossRef]
- Paine, C.E.T.; Stahl, C.; Courtois, E.A.; Patiño, S.; Sarmiento, C.; Baraloto, C. Functional Explanations for Variation in Bark Thickness in Tropical Rain Forest Trees. Funct. Ecol. 2010, 24, 1202–1210. [Google Scholar] [CrossRef]
- Adams, D.C.; Jackson, J.F. Estimating the Allometry of Tree Bark. Am. Midl. Nat. 1995, 134, 99–106. [Google Scholar] [CrossRef]
- Hoffmann, W.A.; Adasme, R.; Haridasan, M.; de Carvalho, M.T.; Geiger, E.L.; Pereira, M.A.B.; Gotsch, S.G.; Franco, A.C. Tree Topkill, Not Mortality, Governs the Dynamics of Savanna—Forest Boundaries under Frequent Fire in Central Brazil. Ecology 2009, 90, 1326–1337. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.-I.; Radtke, P.J. Predicting Bark Thickness with One- and Two-Stage Regression Models for Three Hardwood Species in the Southeastern US. For. Ecol. Manag. 2022, 503, 119778. [Google Scholar] [CrossRef]
- Helfter, C.; Shephard, J.D.; Martínez-Vilalta, J.; Mencuccini, M.; Hand, D.P. A Noninvasive Optical System for the Measurement of Xylem and Phloem Sap Flow in Woody Plants of Small Stem Size. Tree Physiol. 2007, 27, 169–179. [Google Scholar] [CrossRef] [PubMed]
- Scholz, F.G.; Bucci, S.J.; Goldstein, G.; Meinzer, F.C.; Franco, A.C.; Miralles-Wilhelm, F. Biophysical Properties and Functional Significance of Stem Water Storage Tissues in Neotropical Savanna Trees. Plant Cell Environ. 2007, 30, 236–248. [Google Scholar] [CrossRef] [PubMed]
- Lendzian, K.J. Survival Strategies of Plants during Secondary Growth: Barrier Properties of Phellems and Lenticels towards Water, Oxygen, and Carbon Dioxide. J. Exp. Bot. 2006, 57, 2535–2546. [Google Scholar] [CrossRef]
- Rosell, J.A.; Olson, M.E.; Aguirre-Hernández, R.; Sánchez-Sesma, F.J. Ontogenetic Modulation of Branch Size, Shape, and Biomechanics Produces Diversity across Habitats in the Bursera Simaruba Clade of Tropical Trees. Evol. Dev. 2012, 14, 437–449. [Google Scholar] [CrossRef]
- Ilek, A.; Kucza, J.; Morkisz, K. Hygroscopicity of the Bark of Selected Forest Tree Species. IForest Biogeosciences For. 2016, 10, 220. [Google Scholar] [CrossRef]
- Muhairwe, C.K. Bark Thickness Equations for Five Commercial Tree Species in Regrowth Forests of Northern New South Wales. Aust. For. 2000, 63, 34–43. [Google Scholar] [CrossRef]
- Wilms, F.; Duppel, N.; Cremer, T.; Berendt, F. Bark Thickness and Heights of the Bark Transition Area of Scots Pine. Forests 2021, 12, 1386. [Google Scholar] [CrossRef]
- Heath, S.L.; Hansen, H.M.; Smith, E.J.; Smith, W.B.; Miles, P.D. Nvestigation into Calculating Tree Biomass and Carbon in the FIADB Using a Biomass Expansion Factor Approach. In Proceedings of the Forest Inventory and Analysis (FIA) Symposium, Fort Collins, CO, USA, 21–23 October 2008; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Park City, UT, USA; Volume 56, p. 26. [Google Scholar]
- Schreuder, H.T.; Gregoire, T.G.; Wood, G.B. Sampling Methods for Multiresource Forest Inventory, 1st ed.; John Wiley & Sons: New York, NY, USA, 1993; ISBN 0-471-55245-3. [Google Scholar]
- Laasasenaho, J.; Melkas, T.; Aldén, S. Modelling Bark Thickness of Picea Abies with Taper Curves. For. Ecol. Manag. 2005, 206, 35–47. [Google Scholar] [CrossRef]
- Akossou, A.Y.J.; Arzouma, S.; Attakpa, E.Y.; Fonton, N.H.; Kokou, K. Scaling of Teak (Tectona grandis) Logs by the Xylometer Technique: Accuracy of Volume Equations and Influence of the Log Length. Diversity 2013, 5, 99–113. [Google Scholar] [CrossRef]
- Berendt, F.; de Miguel-Diez, F.; Wallor, E.; Blasko, L.; Cremer, T. Comparison of Different Approaches to Estimate Bark Volume of Industrial Wood at Disc and Log Scale. Sci. Rep. 2021, 11, 15630. [Google Scholar] [CrossRef]
- Cremer, T.; Berendt, F.; Diez, F.d.M.; Wolfgramm, F.; Blasko, L. Accuracy of Photo-Optical Measurement of Wood Piles. Environ. Sci. Proc. 2020, 3, 90. [Google Scholar] [CrossRef]
- Bauhaus, J.; Kouki, J.; Paillet, Y.; Asbeck, T.; Marchetti, M. Towards a Sustainable European Forest-Based Bioeconomy—Assessment and the Way Forward; What Science Can Tell us, no. 8; European Forest Institute: Joensuu, Finland, 2017; pp. 67–77. [Google Scholar]
- Routa, J.; Brännström, H.; Hellström, J.; Laitila, J. Influence of Storage on the Physical and Chemical Properties of Scots Pine Bark. BioEnergy Res. 2021, 14, 575–587. [Google Scholar] [CrossRef]
- Musić, J.; Halilović, V.; Knežević, J.; Avdagić, A.; Ibrahimspahić, A.; Balić, B.; Lojo, A. Modelling Bark Thickness of Norway Spruce (Picea abies Karst). South-East Eur. For. 2019, 10, 125–135. [Google Scholar] [CrossRef]
- Marshall, H.; Murphy, G.; Lachenbruch, B. Effects of Bark Thickness Estimates on Optimal Log Merchandising. For. Prod. J. 2006, 56, 87–92. [Google Scholar]
- Beltrán-Rodríguez, L.; Valdez-Hernández, J.I.; Saynes-Vásquez, A.; Blancas, J.; Sierra-Huelsz, J.A.; Cristians, S.; Martínez-Ballesté, A.; Romero-Manzanares, A.; Luna-Cavazos, M.; Borja de la Rosa, M.A.; et al. Sustaining Medicinal Barks: Survival and Bark Regeneration of Amphipterygium Adstringens (Anacardiaceae), a Tropical Tree under Experimental Debarking. Sustainability 2021, 13, 2860. [Google Scholar] [CrossRef]
- Stängle, S.M.; Weiskittel, A.R.; Dormann, C.F.; Brüchert, F. Measurement and Prediction of Bark Thickness in Picea Abies: Assessment of Accuracy, Precision, and Sample Size Requirements. Can. J. For. Res. 2016, 46, 39–47. [Google Scholar] [CrossRef]
- Li, R.; Weiskittel, A.R. Estimating and Predicting Bark Thickness for Seven Conifer Species in the Acadian Region of North America Using a Mixed-Effects Modeling Approach: Comparison of Model Forms and Subsampling Strategies. Eur. J. For. Res. 2011, 130, 219–233. [Google Scholar] [CrossRef]
- Zacco, P. Barktjockleken Hos Sågtimmer (the Bark Thickness of Saw Logs); Swedish Royal College of Forestry, Department of Forest Products: Uppsala, Sweden, 1974; p. 87. [Google Scholar]
- Fachagentur Nachwachsende Rohstoffe e.V. (FNR); Rahmenvereinbarung Für Den Rohholzhandel in Deutschland (RVR). Available online: https://www.fnr.de/fileadmin/kiwuh/broschueren/Broschuere_RVR2020_Nachdruck_web.pdf (accessed on 22 February 2023).
- Černý, M.; Pařez, J. Tabulky a Polynomy pro Výpočet Objemu Kulatiny Bez Kůry Podle Středové Tloušťky Měřené v Kůře; Lesnická práce: Kostelec nad Černými lesy, Czech Republic, 2009; ISBN 80-86386-26-0. [Google Scholar]
- ČSN. Tabulky Objemu Kulatiny Bez k Ůry Podle Středové Tloušťky Měřené v Kůře (Tables of Roundwood inside Bark Volume According to Midspan Diameter Measured over Bark); Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 1977; p. 18. [Google Scholar]
- Jankovský, M.; Allman, M.; Allmanová, Z.; Ferenčík, M.; Vlčková, M. Changes of Key Soil Parameters Five Years after Forest Harvesting Suggest Slow Regeneration of Disturbed Soil. J. Sustain. For. 2019, 38, 369–380. [Google Scholar] [CrossRef]
- Lundbäck, M.; Häggström, C.; Nordfjell, T. Worldwide Trends in the Methods and Systems for Harvesting, Extraction and Transportation of Roundwood. In Proceedings of the 6th International Forest Engineering Conference “Quenching Our Thirst for New Knowledge”, Rotorua, New Zealand, 16–19 April 2018; p. 12. [Google Scholar]
- Löwe, R.; Sedmíková, M.; Natov, P.; Jankovský, M.; Hejcmanová, P.; Dvořák, J. Differences in Timber Volume Estimates Using Various Algorithms Available in the Control and Information Systems of Harvesters. Forests 2019, 10, 388. [Google Scholar] [CrossRef]
- Dvořák, J.; Bystrickỳ, R.; Hošková, P.; Hrib, M.; Jarkovská, M.; Kováč, J.; Krilek, J.; Natov, P.; Natovová, L. The Use of Harvester Technology in Production Forests, 1st ed.; Lesnická Práce: Kostelec nad Černỳmi Lesy, Czech Republic, 2011. [Google Scholar]
- Sladek, P.; Neruda, J. Analysis of Volume Differences in Measuring Timber in Forestry and Wood Industry. In Proceedings of the Austro 2007/FORMEC’07: Meeting the Needs of Tomorrows’ Forests—New Developments in Forest Engineering, Vienna, Austria, 7 October 2007; p. 11. [Google Scholar]
- Nieuwenhuis, M.; Dooley, T. The Effect of Calibration on the Accuracy of Harvester Measurements. Int. J. For. Eng. 2006, 17, 25–33. [Google Scholar] [CrossRef]
- Macek, J.; Kořínek, J. Další Krok k Racionalizaci Těžby Dříví (Another Step towards Forest Harvesting Rationalization). Lesn. Práce 1972, 51, 299–301. [Google Scholar]
- Bundesministerium für Verbraucherschutz, Ernährung und Landwirtschaft Gesetzliche Handelsklassensortierung Für Rohholz Mit Ergänzungsbestimmungen Für Baden-Würtemberg (Forst-HKS). 1983. Available online: https://silo.tips/download/fr-rohholz-forst-hks (accessed on 11 February 2023).
- IPCC. Climate Change 2014; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Gleason, K.E.; Bradford, J.B.; Bottero, A.; D’Amato, A.W.; Fraver, S.; Palik, B.J.; Battaglia, M.A.; Iverson, L.; Kenefic, L.; Kern, C.C. Competition Amplifies Drought Stress in Forests across Broad Climatic and Compositional Gradients. Ecosphere 2017, 8, e01849. [Google Scholar] [CrossRef]
- Stängle, S.M.; Sauter, U.H.; Dormann, C.F. Comparison of Models for Estimating Bark Thickness of Picea Abies in Southwest Germany: The Role of Tree, Stand, and Environmental Factors. Ann. For. Sci. 2017, 74, 16. [Google Scholar] [CrossRef]
- Pellegrini, M.; Grigolato, S.; Cavalli, R. Spatial Multi-Criteria Decision Process to Define Maintenance Priorities of Forest Road Network: An Application in the Italian Alpine Region. Croat. J. For. Eng. J. Theory Appl. For. Eng. 2013, 34, 31–42. [Google Scholar]
- Skogforsk the Forest Research Institute of Sweden Standard for Forest Data and Communications 2007. Available online: https://www.skogforsk.se/cd_20190114161714/contentassets/b063db555a664ff8b515ce121f4a42d1/stanford_maindoc_070327.pdf (accessed on 9 May 2022).
- Jankovskỳ, M.; Natov, P.; Dvořák, J.; Szala, L. Norway Spruce Bark Thickness Models Based on Log Midspan Diameter for Use in Mechanized Forest Harvesting in Czechia. Scand. J. For. Res. 2019, 34, 617–626. [Google Scholar] [CrossRef]
- Natov, P.; Dvořák, J.; Jankovský, M. Guidelines for Scaling Timber ByHarvesters in the Czech Republic, 1st ed.; Czech University of Life Sciences Prague: Prague, Czech Republic, 2018. [Google Scholar]
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1977; ISBN 0-471-16240-X. [Google Scholar]
- Wojnar, T. Doporučená Pravidla pro Měření a Třídění Dříví v ČR 2008; Lesnická Práce: Kostelec nad Černỳmi Lesy, Czech Republic, 2007; ISBN 978-80-87154-01-4. [Google Scholar]
- Berendt, F.; Pegel, E.; Blasko, L.; Cremer, T. Bark Proportion of Scots Pine Industrial Wood. Eur. J. Wood Wood Prod. 2021, 79, 749–752. [Google Scholar] [CrossRef]
- Neumann, M.; Lawes, M.J. Quantifying Carbon in Tree Bark: The Importance of Bark Morphology and Tree Size. Methods Ecol. Evol. 2021, 12, 646–654. [Google Scholar] [CrossRef]
- Gordon, A. Estimating Bark Thickness of Pinus Radiata. NZJ For. Sci. 1983, 13, 340–348. [Google Scholar]
- Stängle, S.M.; Nakoi, A.; Brüchert, F.; Sauter, U.H.; Kohnle, U. Modeling Bark Thickness of Norway Spruce. In Proceedings of the Abstracts of XXIV IUFRO World Congress, Salt Lake City, UT, USA, 5 October 2014; p. 427. [Google Scholar]
- Sonmez, T.; Keles, S.; Tilki, F. Effect of Aspect, Tree Age and Tree Diameter on Bark Thickness of Picea Orientalis. Scand. J. For. Res. 2007, 22, 193–197. [Google Scholar] [CrossRef]
- ČSN EN 1315 (480053); Dimensional Classification of Round Timber. Czech Office for Standards, Metrology and Testing: Czech Republic, Prague, 2010.
- Sedmíková, M.; Löwe, R.; Jankovský, M.; Natov, P.; Linda, R.; Dvořák, J. Estimation of Over- and Under-Bark Volume of Scots Pine Timber Produced by Harvesters. Forests 2020, 11, 626. [Google Scholar] [CrossRef]

| Variable | Descriptive Statistics | ||||||
|---|---|---|---|---|---|---|---|
| Valid N | Mean | Median | Minimum | Maximum | Std. Dev. | Coef. Var. | |
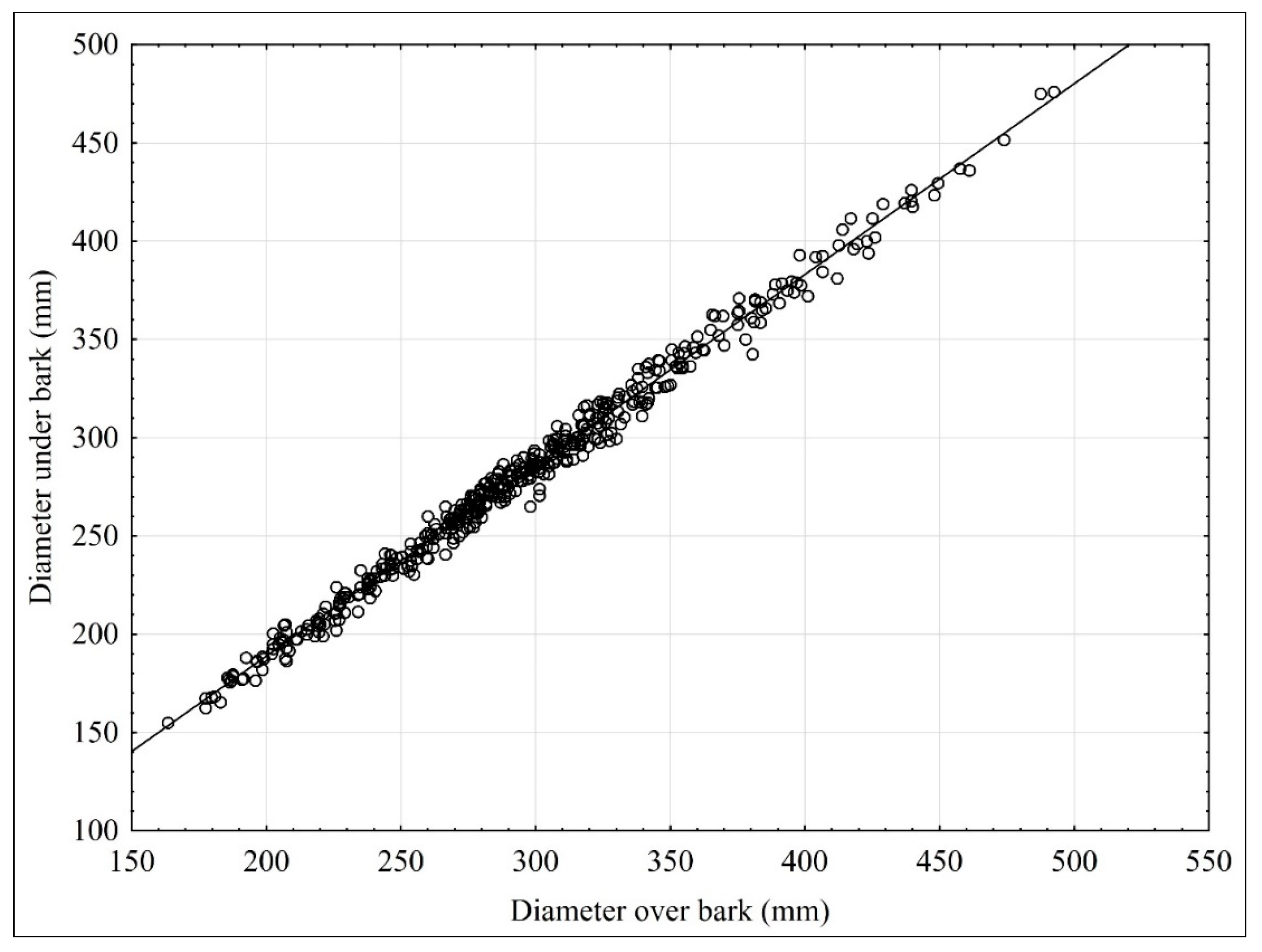
| DOB (mm) | 438 | 294.8 | 290.5 | 163.0 | 492.0 | 60.7 | 20.6 |
| DUB (mm) | 438 | 280.8 | 278.2 | 155.0 | 476.0 | 59.3 | 21.1 |
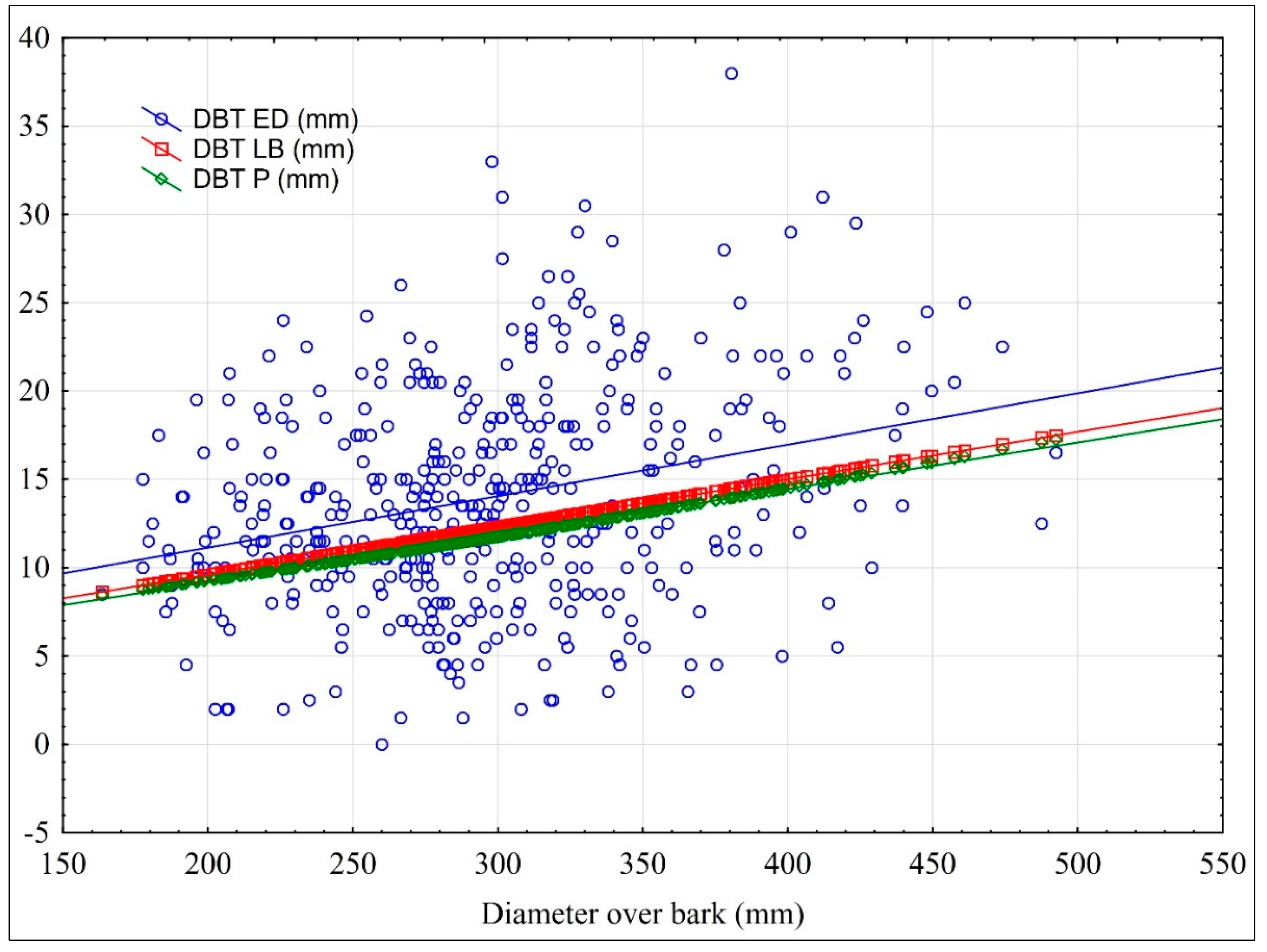
| DBT ED (mm) | 438 | 13.9 | 13.0 | 1.5 | 38.0 | 6.1 | 43.6 |
| DBT LB (mm) | 438 | 12.1 | 12.0 | 8.6 | 17.4 | 1.6 | 13.4 |
| DBT P (mm) | 438 | 11.6 | 11.5 | 8.4 | 17.2 | 1.6 | 13.7 |
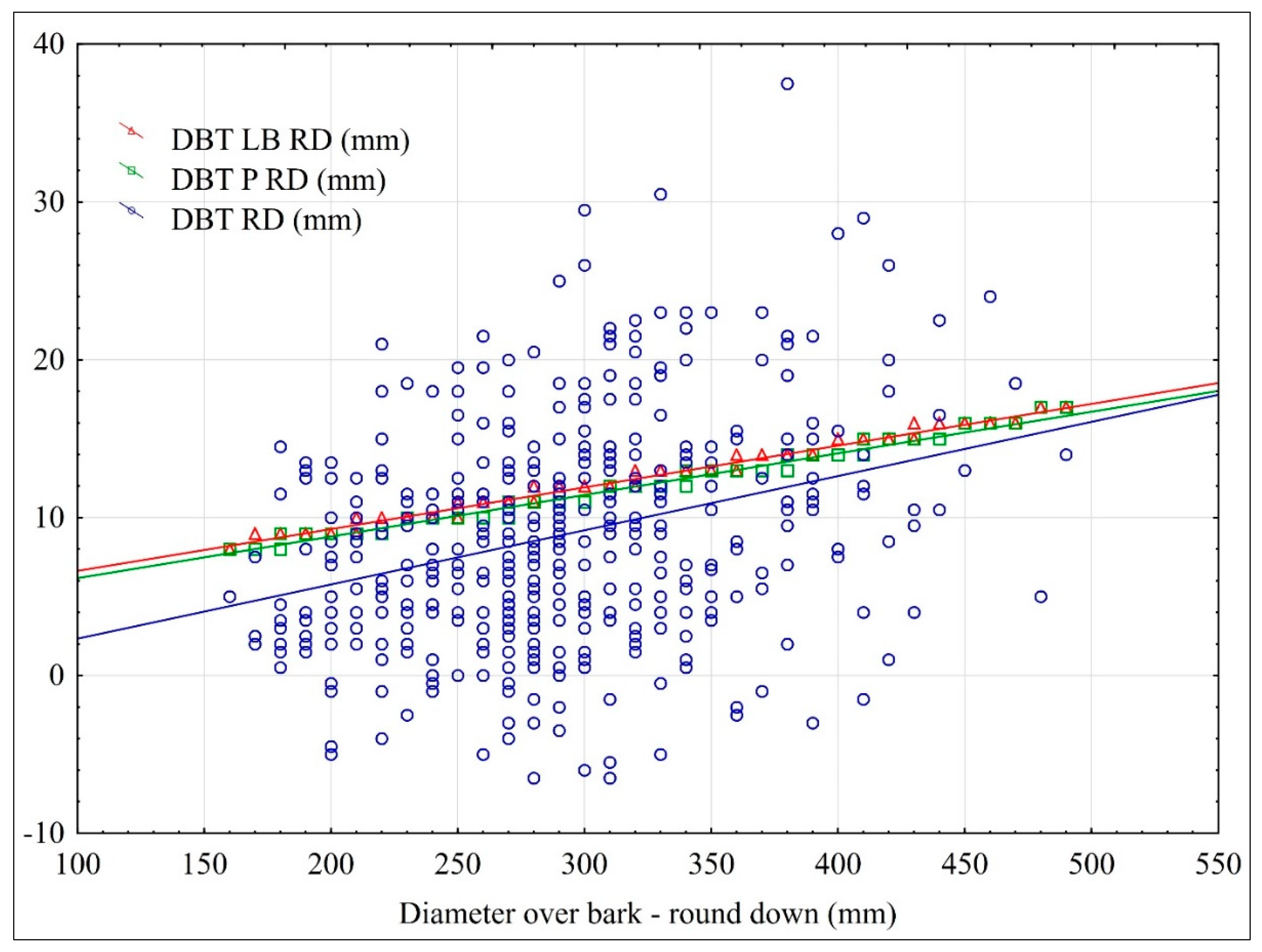
| DBT RD (mm) | 438 | 8.8 | 8.5 | −6.5 * | 37.5 | 6.8 | 77.9 |
| DBT RD LB (mm) | 438 | 11.6 | 12 | 8 | 17 | 1.6 | 14.1 |
| DBT RD P (mm) | 438 | 11.2 | 11 | 8 | 17 | 1.6 | 14.7 |
| N = 438 | Regression Summary of Dependent Variable: DBT ED (mm) R = 0.28 R2 = 0.08; F(1436) = 39.715; p < 0.00000; Std. Error of Estimate: 5.8179 | |||||
|---|---|---|---|---|---|---|
| b* | Std. Err. of b* | b | Std. Err. of b | t(436) | p-Value | |
| Intercept | 5.404130 | 1.379508 | 3.917432 | 0.000104 | ||
| DOB (mm) | 0.288937 | 0.045849 | 0.028884 | 0.004583 | 6.301970 | 0.000000 |
| N = 438 | Regression Summary for Dependent Variable: DBT RD (mm) R = 0.30 R2 = 0.09; F(1436) = 44.440; p < 0.00000; Std. Error of Estimate: 6.5675 | |||||
|---|---|---|---|---|---|---|
| b* | Std. Err. of b* | b | Std. Err. of b | t(436) | p-Value | |
| Intercept | −1.11161 | 1.525205 | −0.728829 | 0.466498 | ||
| DOB RD (mm) | 0.304135 | 0.045623 | 0.03434 | 0.005152 | 6.666316 | 0.000000 |
| Paired-Samples t-Test Differences Are Significant on a Level of p < 0.05000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variables | Mean | SD | N | Difference | SD Differences | t | SV | p | CI −95.0% | CI +95% |
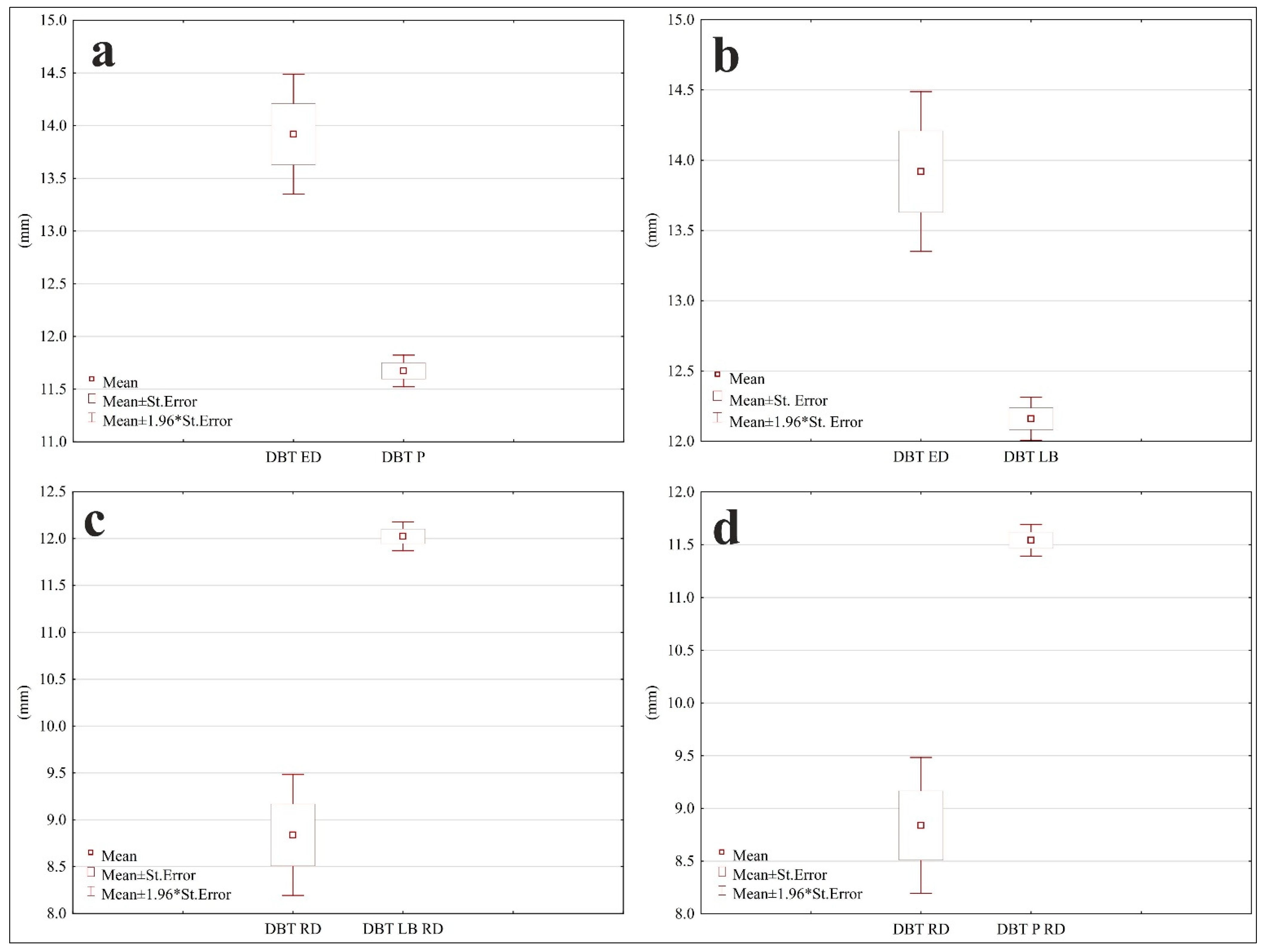
| DBT ED (mm) | 13.919 | 6.070 | ||||||||
| DBT RD (mm) | 8.838 | 6.886 | 438 | 5.081 | 2.883 | 36.87 | 438 | 0.00 | 4.810 | 5.351 |
| Paired-Samples t-Test Fifferences Are Significant on a Level of p < 0.05000 | ||||||||||
| Variables | Mean | SD | N | Difference | SD Differences | t | SV | p | CI −95.0% | CI +95% |
| DBT ED (mm) | 13.919 | 6.070 | ||||||||
| DBT LB (mm) | 12.160 | 1.633 | 438 | 1.759 | 5.812 | 6.33 | 437 | 0.00 | 1.213 | 2.304 |
| DBT ED (mm) | 13.919 | 6.070 | ||||||||
| DBT P (mm) | 11.672 | 1.599 | 438 | 2.247 | 5.810 | 8.09 | 437 | 0.00 | 1.701 | 2.792 |
| Paired-Samples t-Test Differences Are Significant on a Level of p < 0.05000 | ||||||||||
| Variables | Mean | SD | N | Difference | SD Differences | t | SV | p | CI −95.0% | CI +95% |
| DBT RD (mm) | 8.838 | 6.886 | ||||||||
| DBT LB RD (mm) | 12.023 | 1.640 | 438 | −3.185 | 6.575 | −10.13 | 437 | 0.000 | −3.802 | −2.567 |
| DBT RD (mm) | 8.838 | 6.886 | ||||||||
| DBT P RD (mm) | 11.541 | 1.597 | 438 | −2.703 | 6.578 | −8.59 | 437 | 0.00 | −3.320 | −2.085 |
| Dataset | Error Metric | DBT P (mm) | DBT LB (mm) |
|---|---|---|---|
| DBT ED (mm) | MAE(a) | 4.835932 | 4.777381 |
| MBE(b) | −2.24719 | −1.7591 | |
| MAPE(c) | 46.13819 | 47.04241 | |
| RMSE(d) | 6.223826 | 6.066472 | |
| Dataset | Error metric | DBT P RD (mm) | DBT LB RD (mm) |
| DBT RD (mm) | MAE(a) | 5.720047 | 5.89026484 |
| MBE(b) | 2.702997 | 3.185274 | |
| MAPE(c) | 65.19454385 | 68.8024884 | |
| RMSE(d) | 7.105576 | 7.29973099 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jankovský, M.; Dudáková, Z.; Allman, M.; Dvořák, J.; Peseu, P.O.; Jácome, S.P.G. Accuracy of Double Bark Thickness Estimation Methods Used in Spruce—(Picea abies L. Karst) Timber Production in Czechia. Forests 2023, 14, 1026. https://doi.org/10.3390/f14051026
Jankovský M, Dudáková Z, Allman M, Dvořák J, Peseu PO, Jácome SPG. Accuracy of Double Bark Thickness Estimation Methods Used in Spruce—(Picea abies L. Karst) Timber Production in Czechia. Forests. 2023; 14(5):1026. https://doi.org/10.3390/f14051026
Chicago/Turabian StyleJankovský, Martin, Zuzana Dudáková, Michal Allman, Jiří Dvořák, Prince Opoku Peseu, and Sandra Paola García Jácome. 2023. "Accuracy of Double Bark Thickness Estimation Methods Used in Spruce—(Picea abies L. Karst) Timber Production in Czechia" Forests 14, no. 5: 1026. https://doi.org/10.3390/f14051026
APA StyleJankovský, M., Dudáková, Z., Allman, M., Dvořák, J., Peseu, P. O., & Jácome, S. P. G. (2023). Accuracy of Double Bark Thickness Estimation Methods Used in Spruce—(Picea abies L. Karst) Timber Production in Czechia. Forests, 14(5), 1026. https://doi.org/10.3390/f14051026







