Should Government Play a Strict or Lenient Role? An Evolutionary Game Analysis of Implementing the Forest Ecological Bank Policy
Abstract
1. Introduction
2. Evolutionary Game Analysis of the FEB Policy
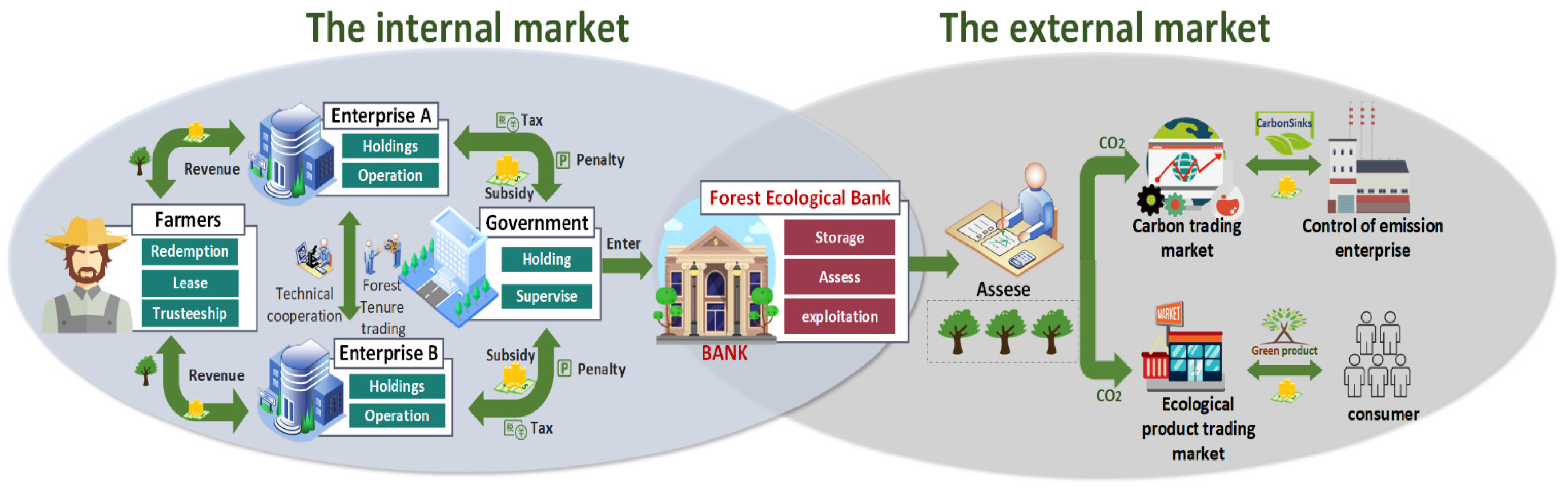
2.1. The Operating Mechanism of the FEB
2.2. Model Description
- (1)
- The dynamic game between government and companies
- (2)
- The dynamic game between forestry enterprises
2.3. Base Assumptions and Parameter Settings
- (1)
- In the evolutionary game system, the three stakeholders are finite and rational, and all start with the goal of maximizing their own benefits. With limited policy knowledge and limited decision-making information, each player continuously adjusts its strategic choices around the actions of other stakeholders. When the government implements regulatory strategies with a negative attitude, media reports become an important channel for companies to understand the progress of ecological bank policy implementation.
- (2)
- First, the probability that the local government will choose a positive regulatory strategy is x, and the probability that it will choose a negative regulation strategy is 1 − x. Second, the probability that company A will choose to participate in the FEB policy is y, and the probability that it will choose to refuse to join is 1 − y. Third, the probability that company B will choose to participate in the policy is z, and the probability that it will choose to refuse to participate is 1 − z. It is worth noting that 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, and 0 ≤ z ≤ 1.
- (3)
- Cooperation mechanisms exist between companies, where companies in the same industry reduce the additional costs of joining the FEB policy by establishing cooperation. Meanwhile, the revenue and costs of each company are proportional to that company’s size.
2.4. Evolutionary Game Analysis That Replicates Dynamic Equations
- (1)
- The equations for the replication dynamics of “active regulation” (C) and “negative regulation” (D) of local governments are as follows:
- (2)
- The equations for the replication dynamics of “participation policy” (P) and “refusal to participate” (R) for company A are as follows:
- (3)
- The equations for the replication dynamics of “participation policy” (P) and “refusal to participate” (R) for firm B are as follows:
3. Evolutionary Game Stability Analysis
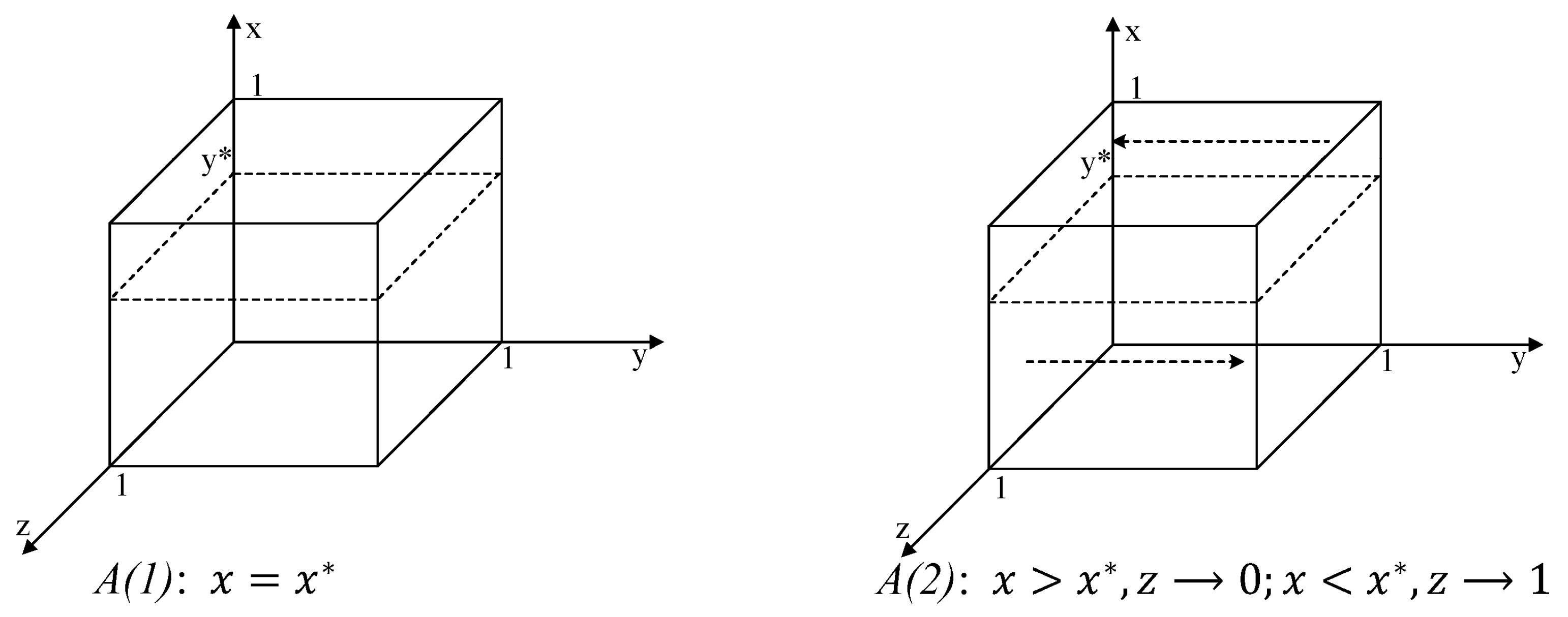
- (1)
- When or ; , this causes all behavioral strategies to be in a steady state.
- (2)
- When , assuming , then there exist and are two stable solutions.
- (1)
- When time, , all game strategies are in a steady state.
- (2)
- When , assuming , then there exist and , which are two stable solutions.
- (1)
- When time, , all game strategies are in a steady state.
- (2)
- When , suppose , and then has the two stable solutions of the existence of and .
4. Simulation of the Three-Way Evolutionary Game
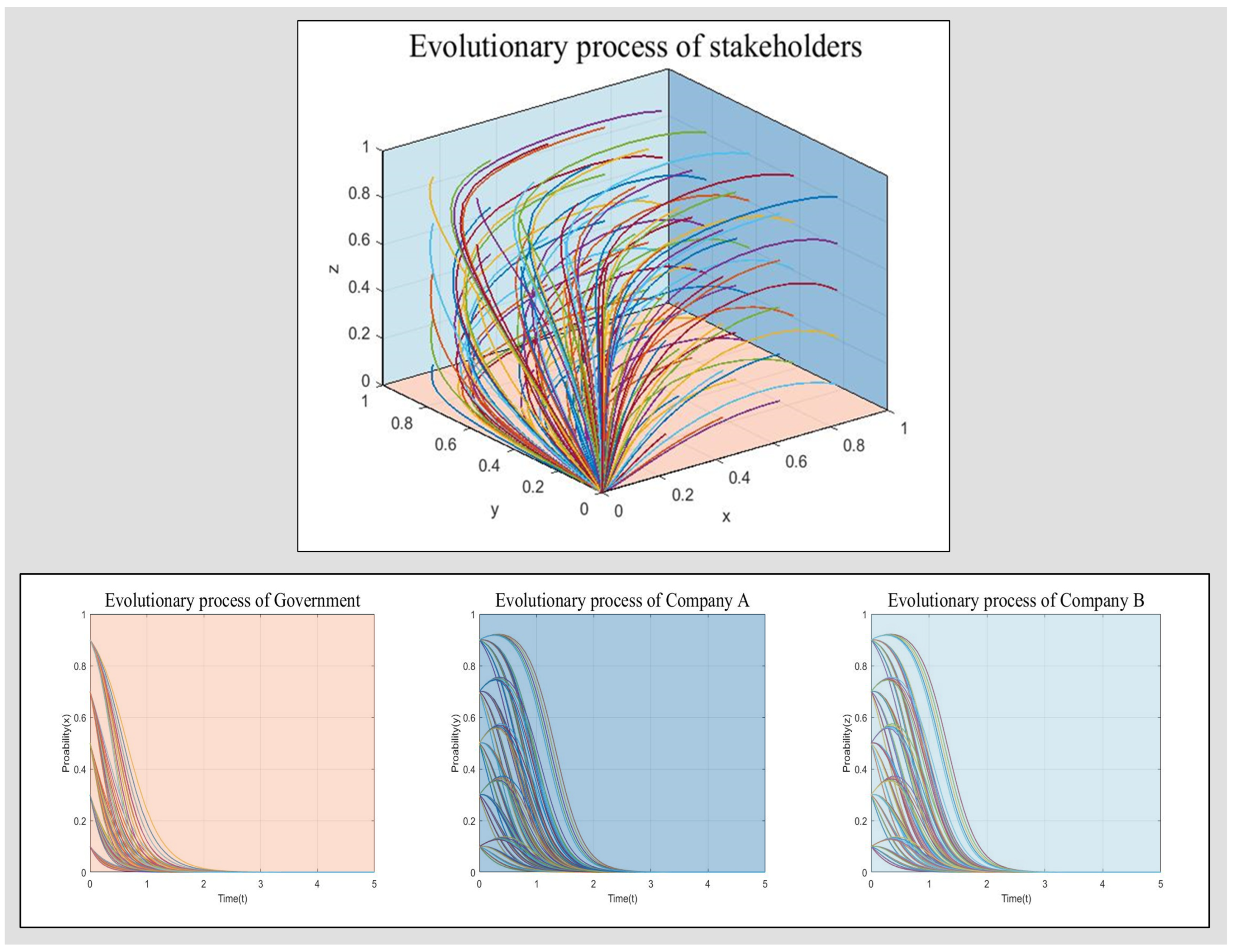
4.1. ESS in Different Game Scenarios
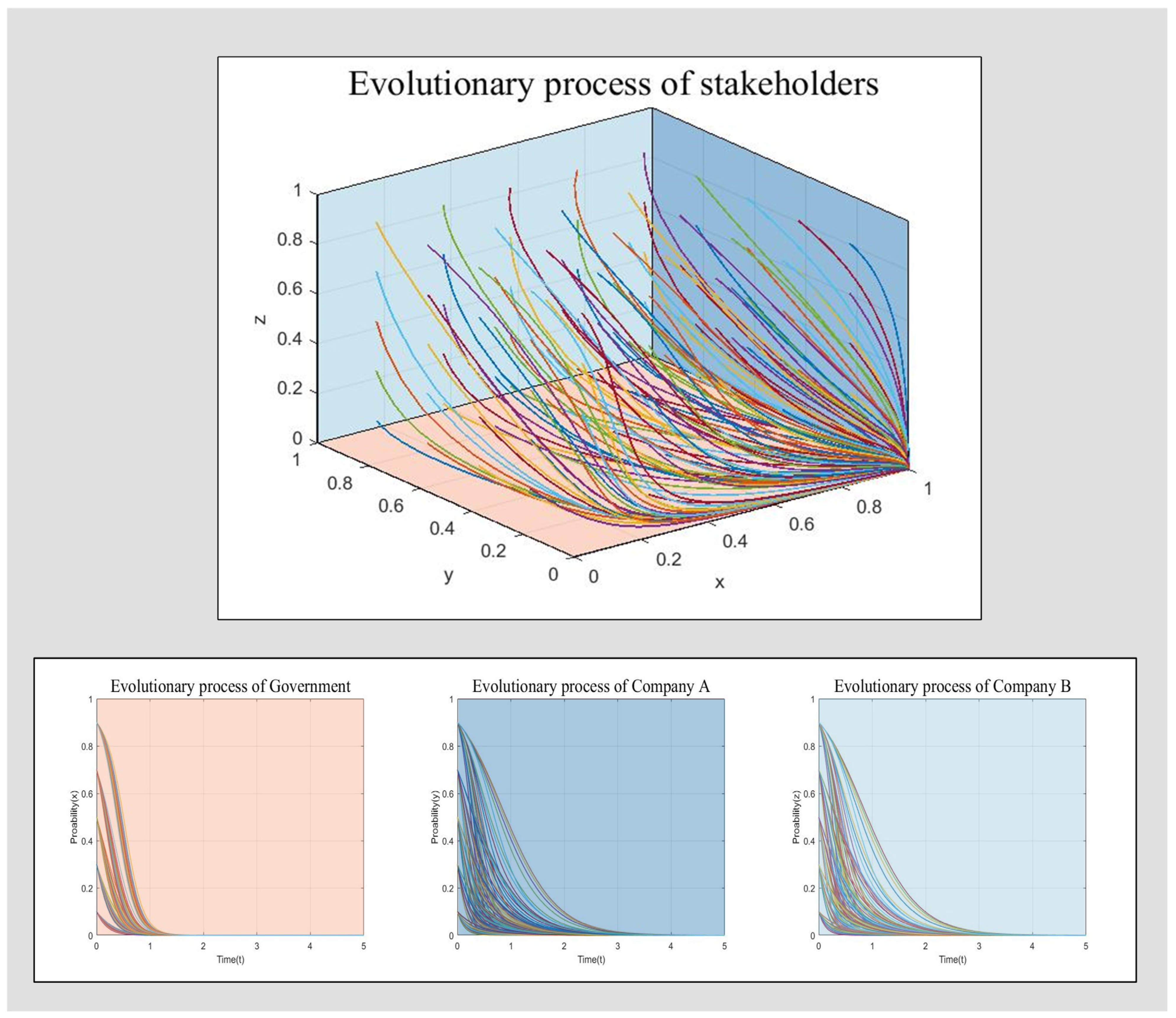
4.1.1. ESS in Scenario 1
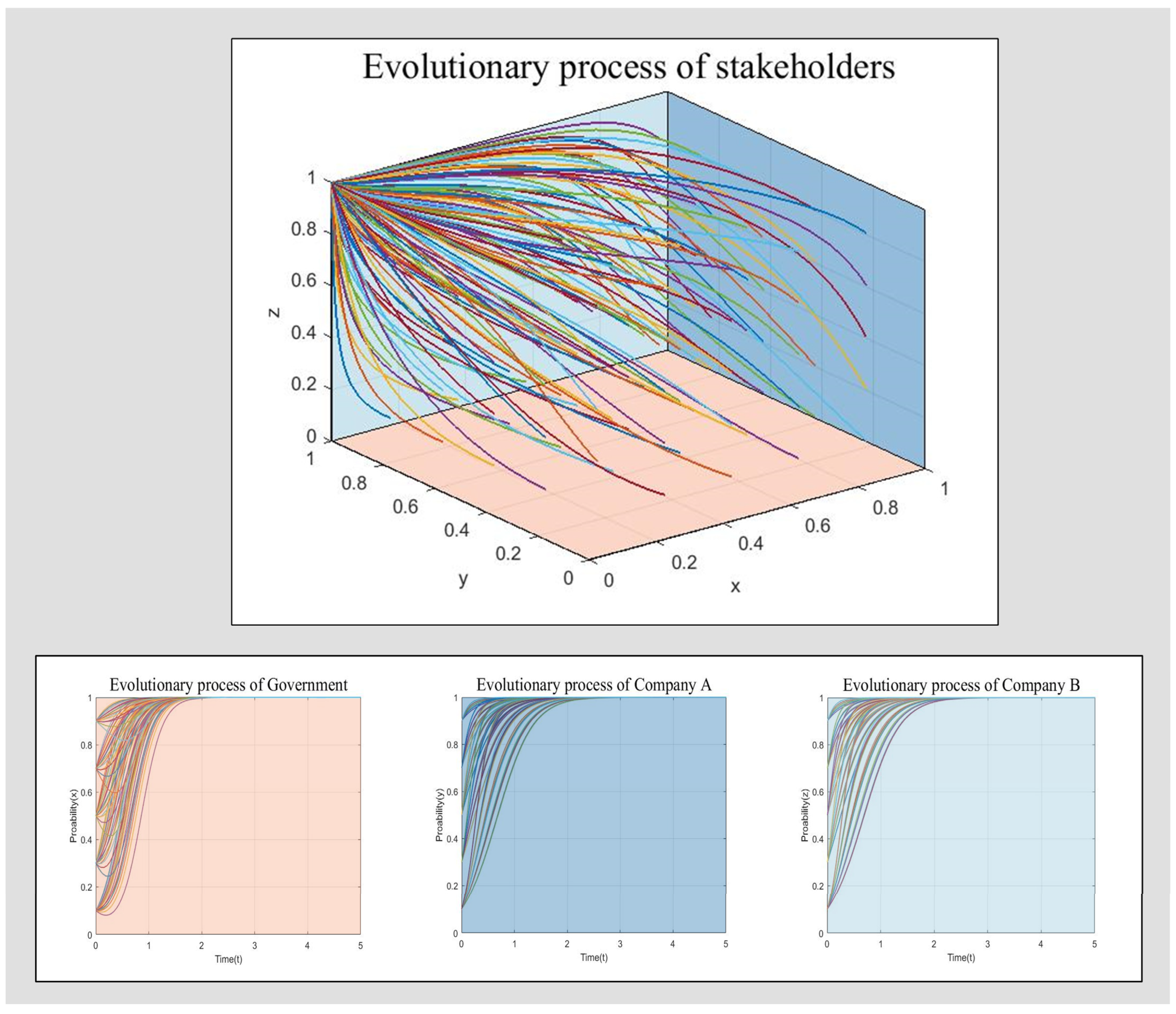
4.1.2. ESS in Scenario 2
4.1.3. ESS in Scenario 3
4.2. The Influence of Key Factors on Evolutionary Outcomes
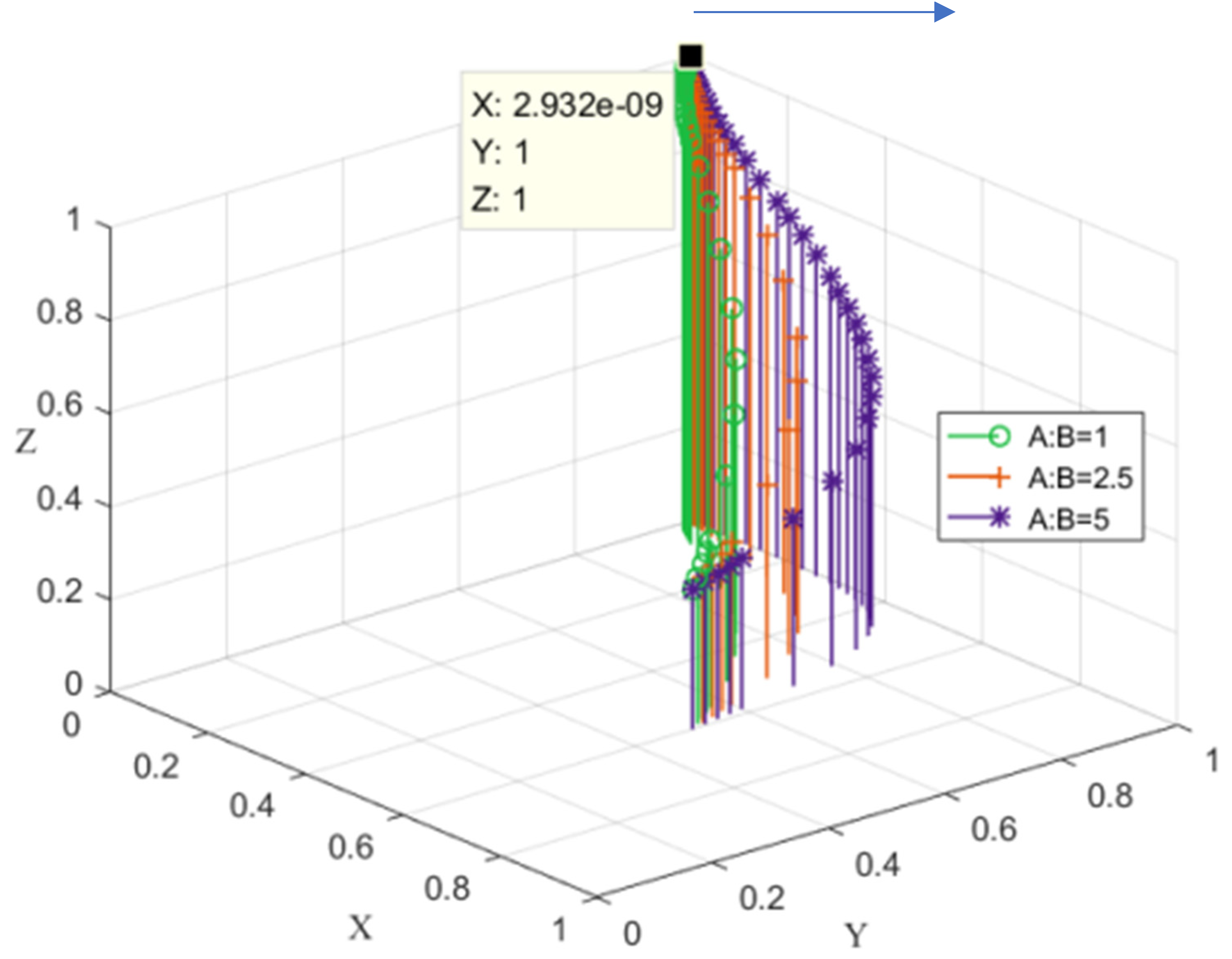
4.2.1. The Size of the Relevant Company
4.2.2. Government Fines
4.2.3. The Probability of Media Exposure
5. Discussion
6. Conclusions
- 1.
- Different governmental attitudes and approaches to policy implementation (i.e., playing different roles) influence the state in which the evolutionary stabilization strategy is ultimately achieved. Specifically, the following were found:
- (1)
- The strict government role motivates firms to participate in the FEB policy through intense government regulatory actions. In other words, a firm’s choice to “participate” is positively correlated with the severity of the penalty and the probability of joining the policy increases in line with the expected risk of loss. Therefore, the government adopted strict regulatory measures at the initial stage of the implementation of the forest ecological bank policy to motivate to participate by means of increasing administrative penalties and raising subsidies for policy participation.
- (2)
- As the policy continues, the impact of harsh regulatory actions on the companies’ “participation” behavior diminishes. Instead, the relaxed government role allows the companies’ autonomy to be fully utilized by creating a favorable market environment. This, in turn, leads to higher ecological benefits. When most enterprises participate in the forest ecological bank policy, the government deregulates, giving greater weight to market-based instruments in the management process, improving compensation mechanisms, and establishing links between the internal and external markets.
- 2.
- The effect of different initial probabilities on the ESS convergence state of the government-firm A-firm B evolutionary game model is not significant enough. In addition, the decreasing effect of initial probabilities on the stable strategy of the model with increasing iterations indicates that the proportion of intersubjective strategy choices tends to reach the same decision as the generation of opinion leaders.
- 3.
- In the process of FEB policy implementation, cooperative behavior between companies of different scales reduces the cost of technological innovation, and both share technological dividends. This promotes the transformation of ecological products into ecological capital and forms economies of scale, this leads to the achievement of a stabilization strategy, thus promoting the sustainable development of the FEB policy. At the same time, the relevant media’s social responsibility to track the progress of the policy’s implementation has become one of the important motivations for companies to make the decision to participate. Companies are also more inclined to make the decision to participate in the policy after weighing the pros and cons of either public opinion condemnation or building a positive company image.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Description |
|---|---|
| EGAB | Companies A and B both participate in the forest eco-banking (FEB) policy, and the government benefits |
| EGA | Company A participates separately in the FEB policy, and the government benefits. |
| EGB | Company B participates separately in the FEB policy, and the government benefits. |
| CG1 | Cost of active government regulation |
| CG2 | Cost of negative government regulation |
| PA | “A Penalty”, payable for refusal to participate in the FEB policy |
| PB | “B Penalty”, payable for refusal to participate in the FEB policy |
| TA | Revenue from Company A’s development and operation using traditional methods |
| TB | Revenue from Company B’s development and operation using traditional methods |
| SA | Company A’s carbon sink income |
| SB | Company B’s carbon sink income |
| VA | Additional benefits from Company A’s participation in the FEB policy (ecological benefits and prestige benefits) |
| VB | Additional benefits from Company B’s participation in the FEB policy (ecological benefits and prestige benefits) |
| QA | Additional costs for Company A to participate in the FEB policy |
| QB | Additional costs for Company B to participate in the FEB policy |
| Θ | Exposure of relevant media for policy implementation |
| M | A subsidizes the cost of participating in the policy to B. |
| N | B subsidizes the cost of participating in the policy to A. |
| X | Probability of active government regulation of policy implementation |
| Y | Probability of participation of company A in the FEB policy |
| Z | Probability of participation of firm B in the FEB policy |
Appendix B
Appendix C

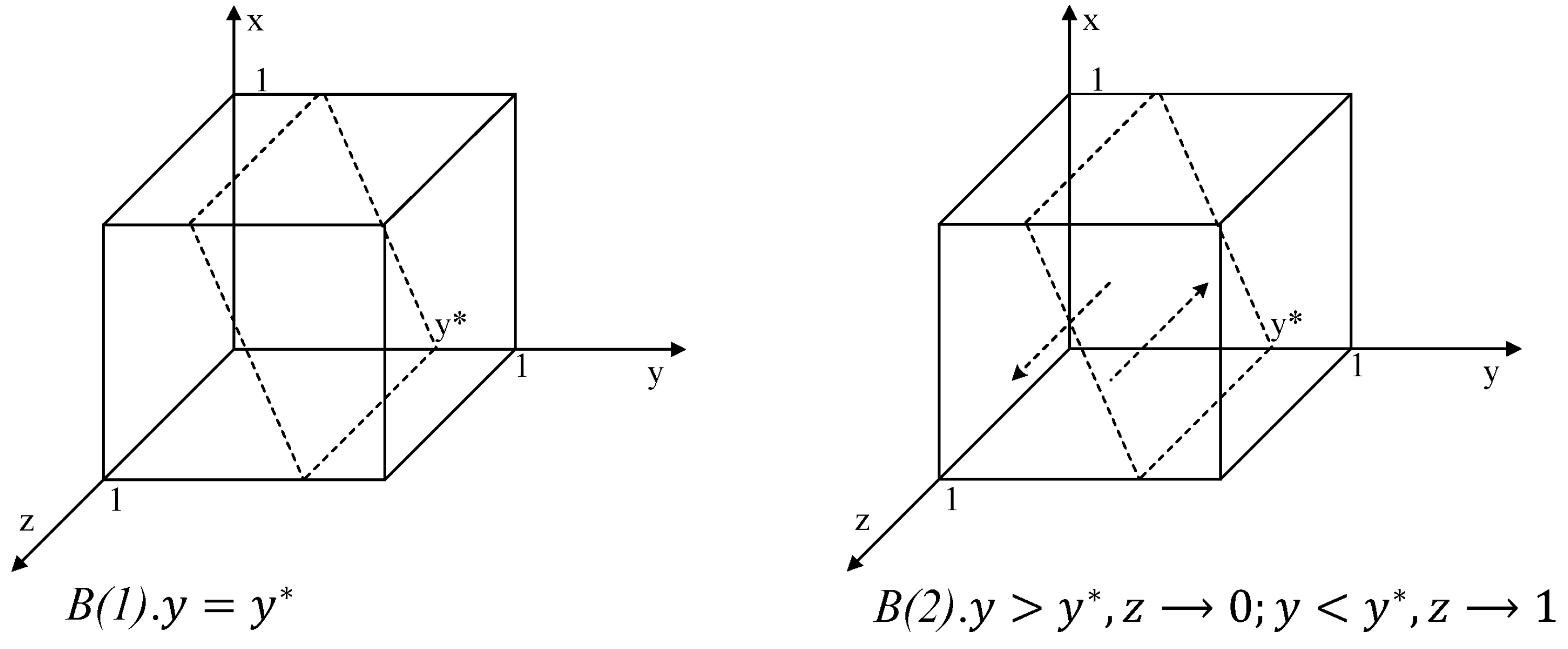
References
- Fan, W.; Wang, S.; Gu, X.; Zhou, Z.; Zhao, Y.; Huo, W. Evolutionary game analysis on industrial pollution control of local government in China. J. Environ. Manag. 2021, 298, 113499. [Google Scholar] [CrossRef] [PubMed]
- Ju, F.; Zhou, J.; Jiang, K. Evolution of stakeholders’ behavioral strategies in the ecological compensation mechanism for poverty alleviation. Resour. Conserv. Recycl. 2022, 176, 105915. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, B.; Fan, J.; Qiao, Q. The multi-player evolutionary game analysis for the protective development of ecotourism. Environ. Sci. Policy 2021, 126, 111–121. [Google Scholar] [CrossRef]
- Hiironen, J.; Riekkinen, K. Agricultural impacts and profitability of land consolidations. Land Use Policy 2016, 55, 309–317. [Google Scholar] [CrossRef]
- Pruetz, R.; Standridge, N. What Makes Transfer of Development Rights Work?: Success Factors From Research and Practice. J. Am. Plan. Assoc. 2008, 75, 78–87. [Google Scholar] [CrossRef]
- Burnett, P. Land Use Regulations and Regional Economic Development. Land Econ. 2016, 92, 237–255. [Google Scholar] [CrossRef]
- Wang, H.; He, C.; Li, W.; Nie, X.; Zhong, H.; Wen, L. Will transferable development rights (TDR) increase regional economic imbalance?—A quota transaction case of cultivated land conversion and reclamation in Guangxi, China. Habitat Int. 2020, 104, 102254. [Google Scholar] [CrossRef]
- Rosegrant, M.; Binswanger, H.P. Markets in tradable water rights: Potential for efficiency gains in developing country water resource allocation. World Dev. 1994, 22, 1613–1625. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, Y.; Zhao, J. Understanding water rights and water trading systems in China: A systematic framework. Water Secur. 2021, 13, 100094. [Google Scholar] [CrossRef]
- Keohane, N.; Petsonk, A.; Hanafi, A. Toward a club of carbon markets. Clim. Chang. 2015, 144, 81–95. [Google Scholar] [CrossRef]
- Weng, Q.; Xu, H. A review of China’s carbon trading market. Renew. Sustain. Energy Rev. 2018, 91, 613–619. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Wu, X.; Nie, X. Can a carbon trading system promote the transformation of a low-carbon economy under the framework of the porter hypothesis?—Empirical analysis based on the PSM-DID method. Energy Policy 2019, 129, 930–938. [Google Scholar] [CrossRef]
- Sullivan, J.; Amacher, G.S.; Chapman, S. Forest banking and forest landowners forgoing management rights for guaranteed financial returns. For. Policy Econ. 2003, 7, 381–392. [Google Scholar] [CrossRef]
- Wei, G.; Kong, X.; Wang, Y.; Gao, Q. China’s Forest Eco-Bank Project: An Analysis Based on the Actor-Network Theory. Forests 2022, 13, 944. [Google Scholar] [CrossRef]
- Pirard, R. Market-based instruments for biodiversity and ecosystem services: A lexicon. Environ. Sci. Policy 2012, 19–20, 59–68. [Google Scholar] [CrossRef]
- Bramwell, B.; Lane, B. Critical research on the governance of tourism and sustainability. J. Sustain. Tour. 2011, 19, 411–421. [Google Scholar] [CrossRef]
- Jamal, T.; Camargo, B.A. Tourism governance and policy: Whither justice? Tour. Manag. Perspect. 2018, 25, 205–208. [Google Scholar] [CrossRef]
- Althor, G.; Witt, B. A quantitative systematic review of distributive environmental justice literature: A rich history and the need for an enterprising future. J. Environ. Stud. Sci. 2019, 10, 91–103. [Google Scholar] [CrossRef]
- Schaafsma, M.; Eigenbrod, F.; Gasparatos, A.; Gross-Camp, N.; Hutton, C.; Nunan, F.; Schreckenberg, K.; Turner, K. Trade-off decisions in ecosystem management for poverty alleviation. Ecol. Econ. 2021, 187, 107103. [Google Scholar] [CrossRef]
- Moledina, A.A.; Coggins, J.S.; Polasky, S.; Costello, C. Dynamic environmental policy with strategic firms: Prices versus quantities. J. Environ. Econ. Manag. 2003, 45, 356–376. [Google Scholar] [CrossRef]
- Zheng, S.; Yu, L. The government’s subsidy strategy of carbon-sink fishery based on evolutionary game. Energy 2022, 254, 124282. [Google Scholar] [CrossRef]
- Dong, J.; Jiang, Y.; Liu, D.; Dou, X.; Liu, Y.; Peng, S. Promoting dynamic pricing implementation considering policy incentives and electricity retailers’ behaviors: An evolutionary game model based on prospect theory. Energy Policy 2022, 167, 113059. [Google Scholar] [CrossRef]
- Lin, B.; Ge, J. Carbon sinks and output of China’s forestry sector: An ecological economic development perspective. Sci. Total. Environ. 2019, 655, 1169–1180. [Google Scholar] [CrossRef] [PubMed]
- Sandra, D.A.; Otto, A.R. Cognitive capacity limitations and Need for Cognition differentially predict reward-induced cognitive effort expenditure. Cognition 2018, 172, 101–106. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wang, T. Photovoltaic subsidy withdrawal: An evolutionary game analysis of the impact on Chinese stakeholders’ strategic choices. Sol. Energy 2022, 241, 302–314. [Google Scholar] [CrossRef]
- Cressman, R.; Tao, Y. The replicator equation and other game dynamics. Proc. Natl. Acad. Sci. USA 2014, 111, 10810–10817. [Google Scholar] [CrossRef]
- Ritzberger, K.; Weibull, J.W. Evolutionary Selection in Normal-Form Games. Econometrica 1995, 63, 1371. [Google Scholar] [CrossRef]
- Xu, X.; Yang, Y. Analysis of the Dilemma of Promoting Circular Logistics Packaging in China: A Stochastic Evolutionary Game-Based Approach. Int. J. Environ. Res. Public Health 2022, 19, 7363. [Google Scholar] [CrossRef]
- Liu, X.; Lin, K.; Wang, L. Stochastic evolutionary game analysis of e-waste recycling in environmental regulation from the perspective of dual governance system. J. Clean. Prod. 2021, 319, 128685. [Google Scholar] [CrossRef]
- Vaissière, A.-C.; Levrel, H. Biodiversity offset markets: What are they really? An empirical approach to wetland mitigation banking. Ecol. Econ. 2015, 110, 81–88. [Google Scholar] [CrossRef]
- Gao, X.; Shen, J.; He, W.; Sun, F.; Zhang, Z.; Guo, W.; Zhang, X.; Kong, Y. An evolutionary game analysis of governments’ decision-making behaviors and factors influencing watershed ecological compensation in China. J. Environ. Manag. 2019, 251, 109592. [Google Scholar] [CrossRef] [PubMed]
- Spreafico, C.; Landi, D. Investigating students’ eco-misperceptions in applying eco-design methods. J. Clean. Prod. 2022, 342, 130866. [Google Scholar] [CrossRef]




| Active Regulation by Local Governments (x) | Negative Regulation by Local Governments (1 − x) | |||
|---|---|---|---|---|
| Company A Chooses to Participate in (y) | Company A Refuses to Participate (1 − y) | Related Companies Opt-in (y) | Related Companies Refuse to Join (1 − y) | |
| Company B chooses to participate in (z) | EGAB − CG1 | EGB + PA − CG1 | EGAB | EGB + θ(PA − CG2) + (1 − θ)EGA |
| TA + SA + VA − QA | TA − PA − m | TA + SA + VA − QA | TA − θPA − m | |
| TB + SB + VB − QB | TB + SB + VB − QB + m | TB + SB + VB − QB | TB + SB + VB − QB + m | |
| Company B refuses to participate (1 − z) | EGA + PB − CG1 | PA + PB − CG1 | EGA + θ(PB − CG2) + (1 − θ) EGB | (1 − θ)EGAB + θ(PA + PB − 2CG2) |
| TA + SA + VA − QA + n | TA − PA | TA + SA + VA − QA + n | TA − θPA | |
| TB − PB − n | TB − PB | TB − θPB − n | TB − θPB | |
| Eigenvalue 1λ1 | Eigenvalue 2λ2 | Eigenvalue 3λ3 | |
|---|---|---|---|
| (0, 0, 0) | (1 − θ)(PA + PB − EGAB) − CG1 + 2θCG2 | SA + VA − QA + θPA + n | SB + VB − QB + θPB + m |
| (0, 0, 1) | (θ − 1)EGA + (1 − θ) PA − CG1 + θCG2 | SA + VA − QA + θPA + m | QB − SB − VB − θPB − m |
| (0, 1, 0) | (θ − 1)EGB + (1 − θ) PB − CG1 + θCG2 | QA − SA − VA − θPA − n | SB + VB − QB + θPB + n |
| (0, 1, 1) | −CG1 | QA − SA − VA − θPA − m | QB − SB − VB − θPB − n |
| (1, 0, 0) | (1 − θ)(EGAB − PA − PB) + CG1 − 2θCG2 | SA + VA − QA + PA + n | SB + VB − QB + PB + m |
| (1, 0, 1) | (1 − θ)EGA − (1 − θ) PA + CG1 − θCG2 | SA + VA − QA + PA + m | QB − SB − VB − PB − m |
| (1, 1, 0) | (1 − θ)EGB − (1 − θ) PB + CG1 − θCG2 | QA − SA − VA − PA − n | SB + VB − QB + PB + n |
| (1, 1, 1) | CG1 | QA − SA − VA − PA − m | QB − SB − VB − PB − n |
| λ1 | λ2 | λ3 | Stable Condition | Stable Conditions | |
|---|---|---|---|---|---|
| F1 (0, 0, 0) | − | − | − | ESS | (1 − θ) (PA + PB − EGAB) + 2θCG2 < CG1 QA > SA + VA + θPA + m QB > SB + VB + θPB + n |
| F2 (0, 0, 1) | +, − | +, − | +, − | No ESS | / |
| F3 (0, 1, 0) | +, − | +, − | +, − | No ESS | / |
| F4 (0, 1, 1) | − | − | − | ESS | QA < SA + VA + θPA + m QB < SB + VB + θPB + n |
| F5 (1, 0, 0) | − | − | − | ESS | CG1 < 2θCG2 − (1− θ) (EGAB − PA − PB) QA > SA + VA + PA + m QB > SB + VB + PB + n |
| F6 (1, 0, 1) | +, − | +, − | +, − | No ESS | / |
| F7 (1, 1, 0) | +, − | +, − | +, − | No ESS | / |
| F8 (1, 1, 1) | + | +, − | +, − | No ESS | / |
| Parameters | EGA | EGB | PA | PB | CG1 | CG2 | SA | SB | VA | VB | QA | QB | m | n | θ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Values | 3 | 3 | 4 | 4 | 6 | 2 | 5 | 5 | 4 | 4 | 18 | 18 | 3 | 3 | 0.5 |
| Parameters | EGA | EGB | PA | PB | CG1 | CG2 | SA | SB | VA | VB | QA | QB | m | n | θ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Values | 3 | 3 | 4 | 4 | 6 | 2 | 5 | 5 | 3 | 3 | 10 | 10 | 3 | 3 | 0.5 |
| Parameters | EGA | EGB | PA | PB | CG1 | CG2 | SA | SB | VA | VB | QA | QB | m | n | θ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Values | 3 | 3 | 5 | 5 | 3 | 6 | 2 | 2 | 4 | 4 | 21 | 21 | 3 | 3 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, X.; Yang, M.; Chen, Z.; Li, W.; Zang, R.; Wang, H. Should Government Play a Strict or Lenient Role? An Evolutionary Game Analysis of Implementing the Forest Ecological Bank Policy. Forests 2023, 14, 1002. https://doi.org/10.3390/f14051002
Nie X, Yang M, Chen Z, Li W, Zang R, Wang H. Should Government Play a Strict or Lenient Role? An Evolutionary Game Analysis of Implementing the Forest Ecological Bank Policy. Forests. 2023; 14(5):1002. https://doi.org/10.3390/f14051002
Chicago/Turabian StyleNie, Xin, Mengshi Yang, Zhoupeng Chen, Weijuan Li, Ran Zang, and Han Wang. 2023. "Should Government Play a Strict or Lenient Role? An Evolutionary Game Analysis of Implementing the Forest Ecological Bank Policy" Forests 14, no. 5: 1002. https://doi.org/10.3390/f14051002
APA StyleNie, X., Yang, M., Chen, Z., Li, W., Zang, R., & Wang, H. (2023). Should Government Play a Strict or Lenient Role? An Evolutionary Game Analysis of Implementing the Forest Ecological Bank Policy. Forests, 14(5), 1002. https://doi.org/10.3390/f14051002






