An Estimation Model of the Ultimate Shear Strength of Root-Permeated Soil, Fully Considering Interface Bonding
Abstract
1. Introduction
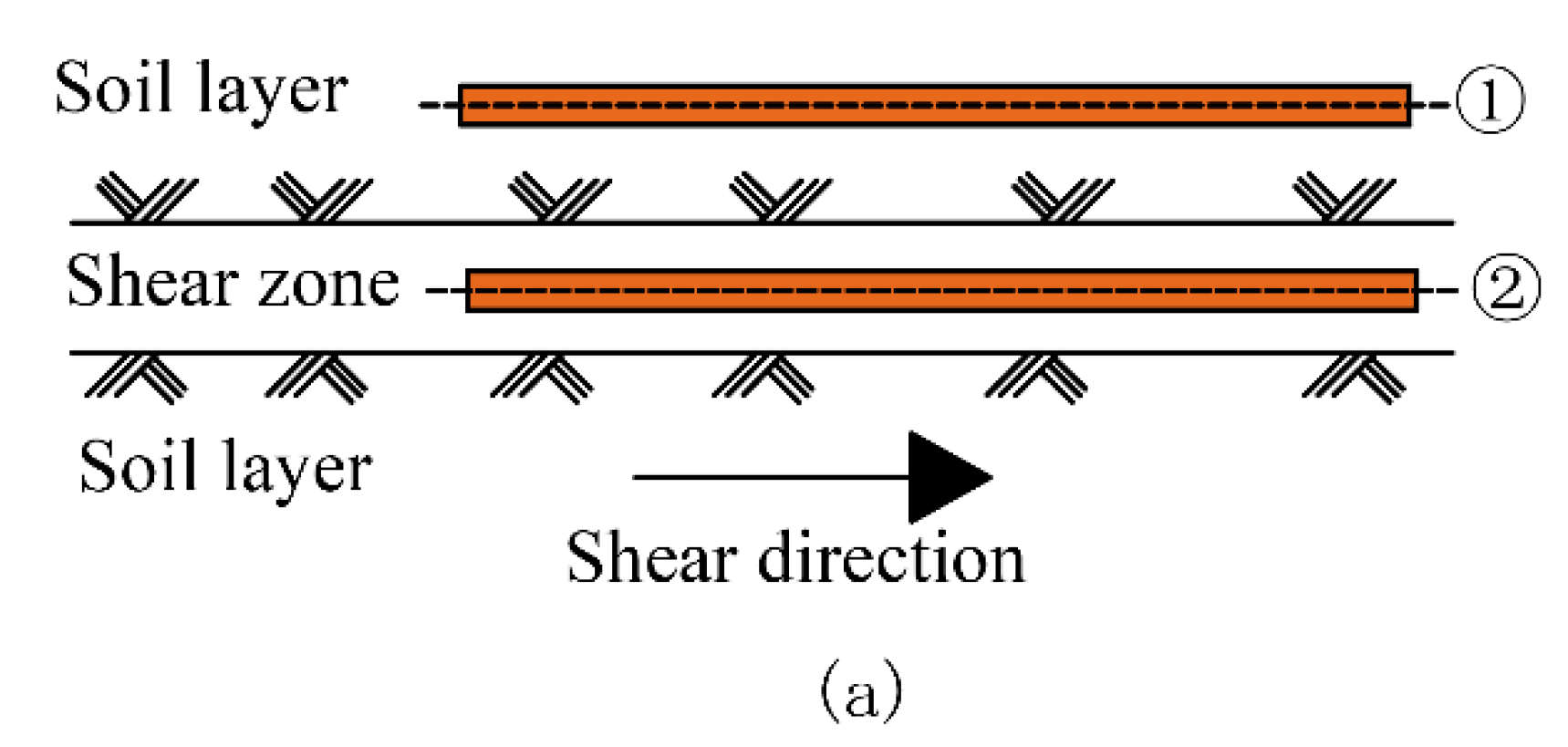
2. Theoretical Background of Rooted-Permeated Soil
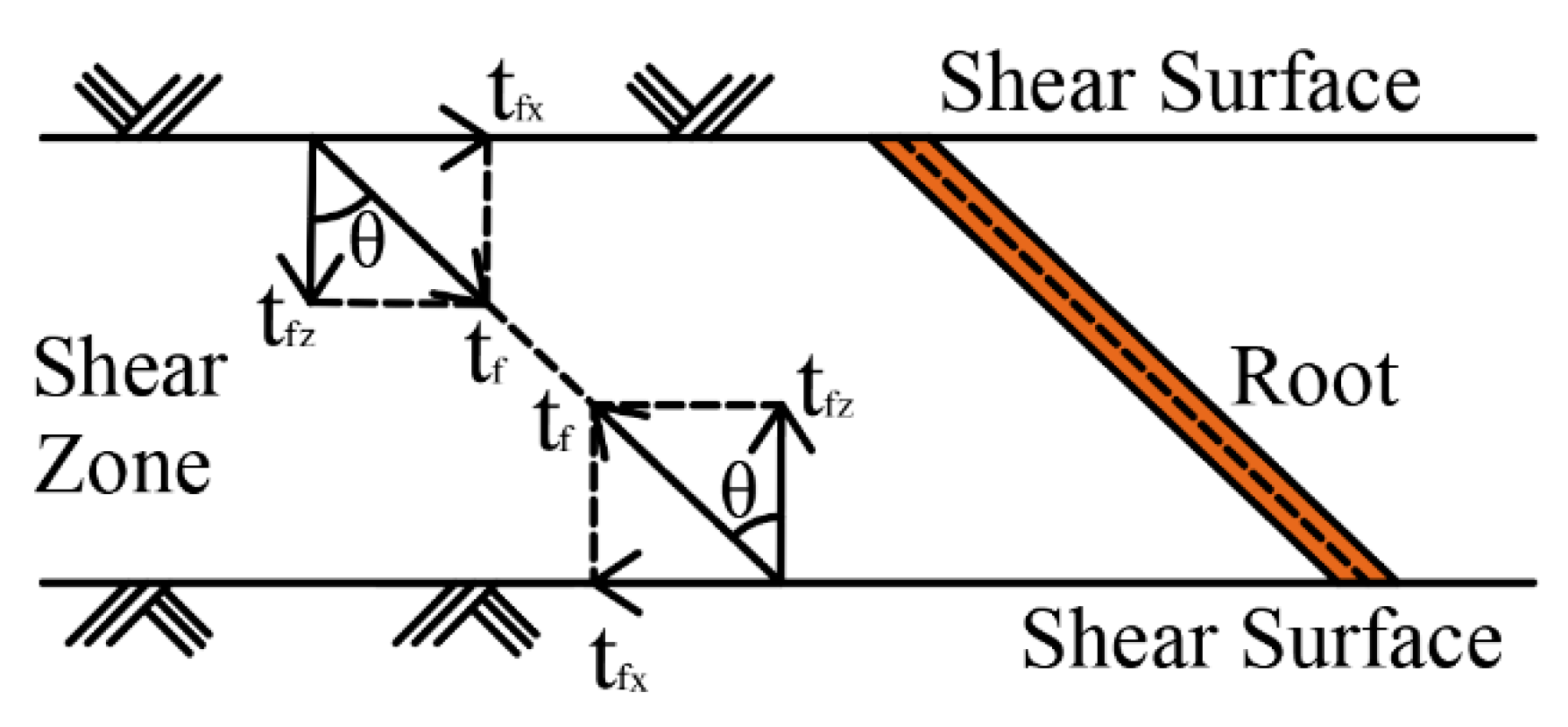
2.1. Wu’s Model
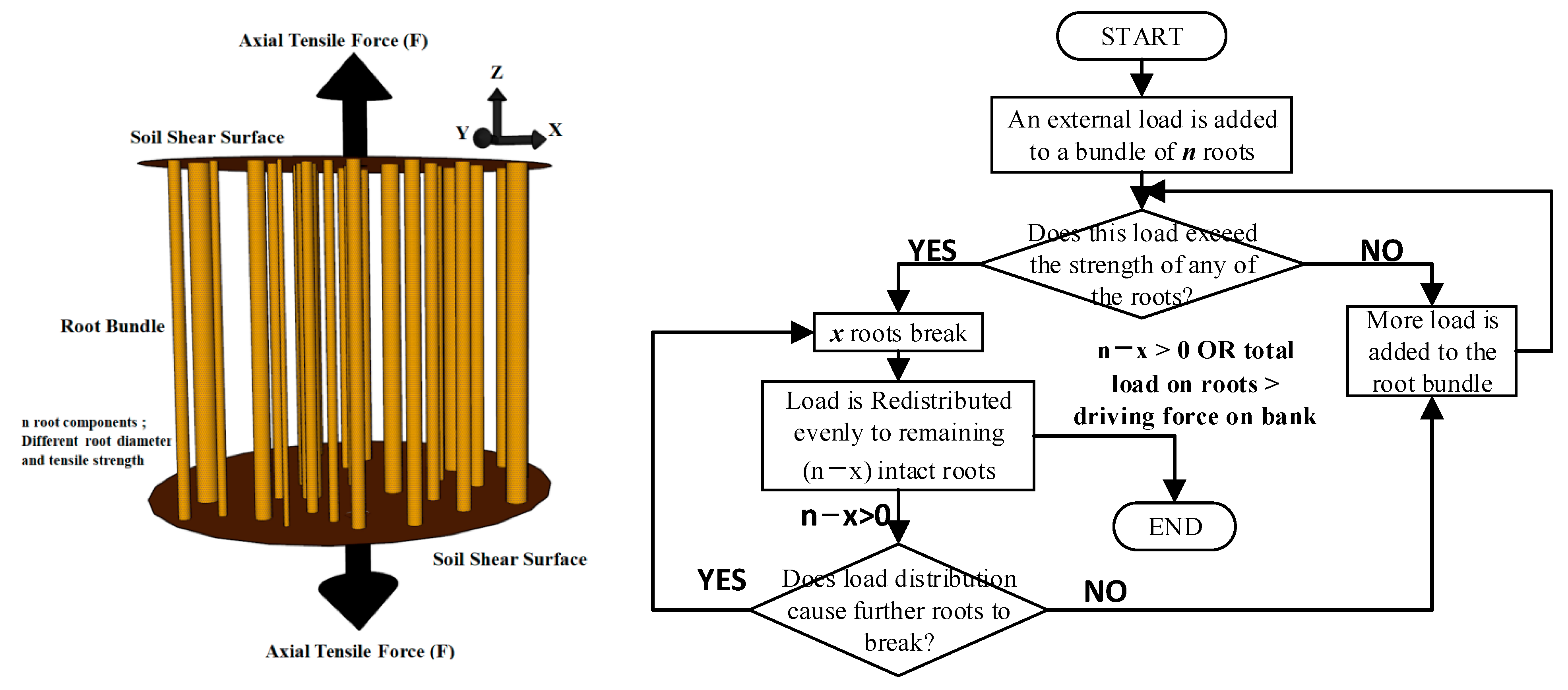
2.2. Fiber Bundle Model
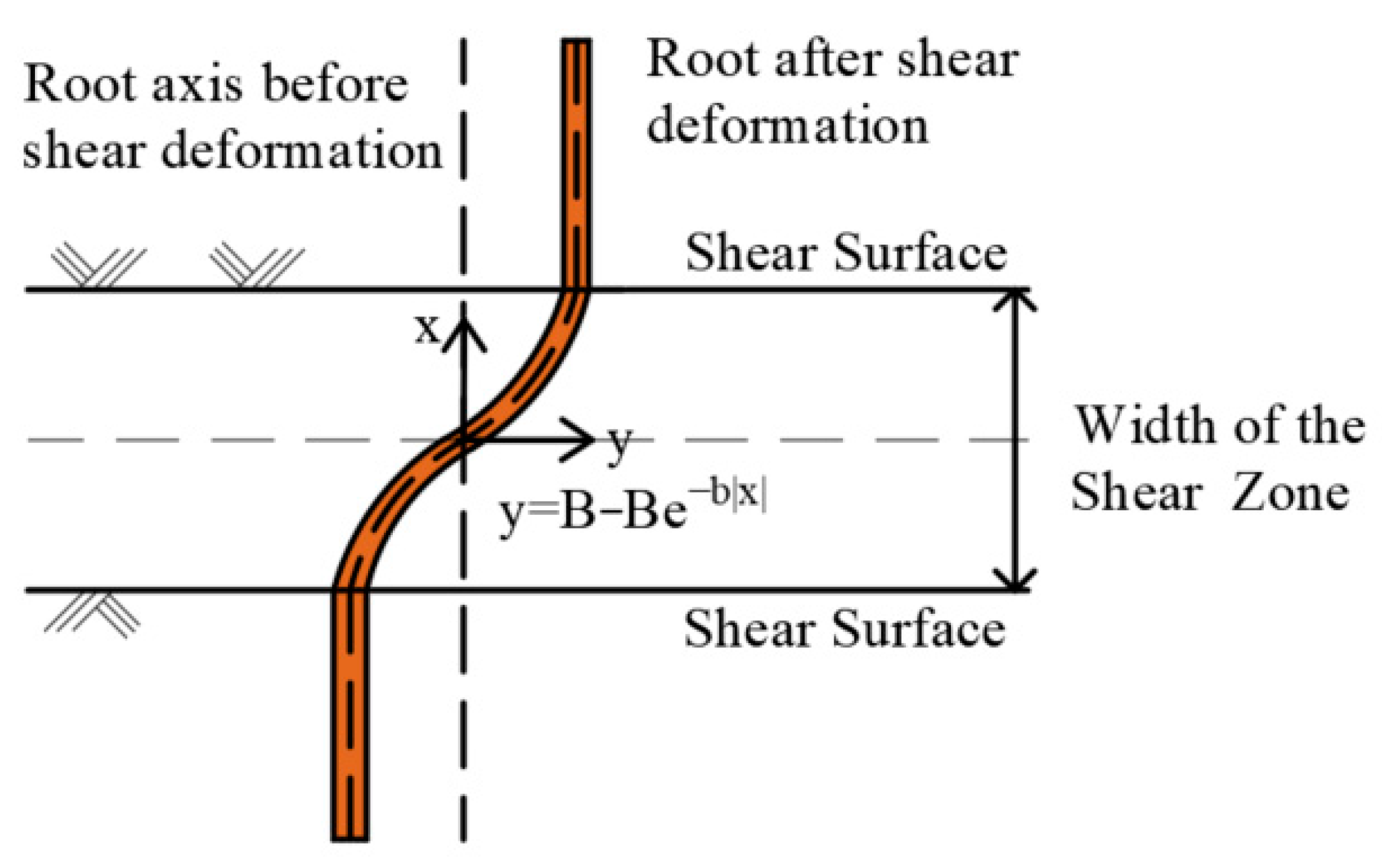
2.3. Displacement-Based Model
3. Experiments Method
3.1. Materials
- (1)
- Overview of the Study Area
- (2)
- Plant roots
- (3)
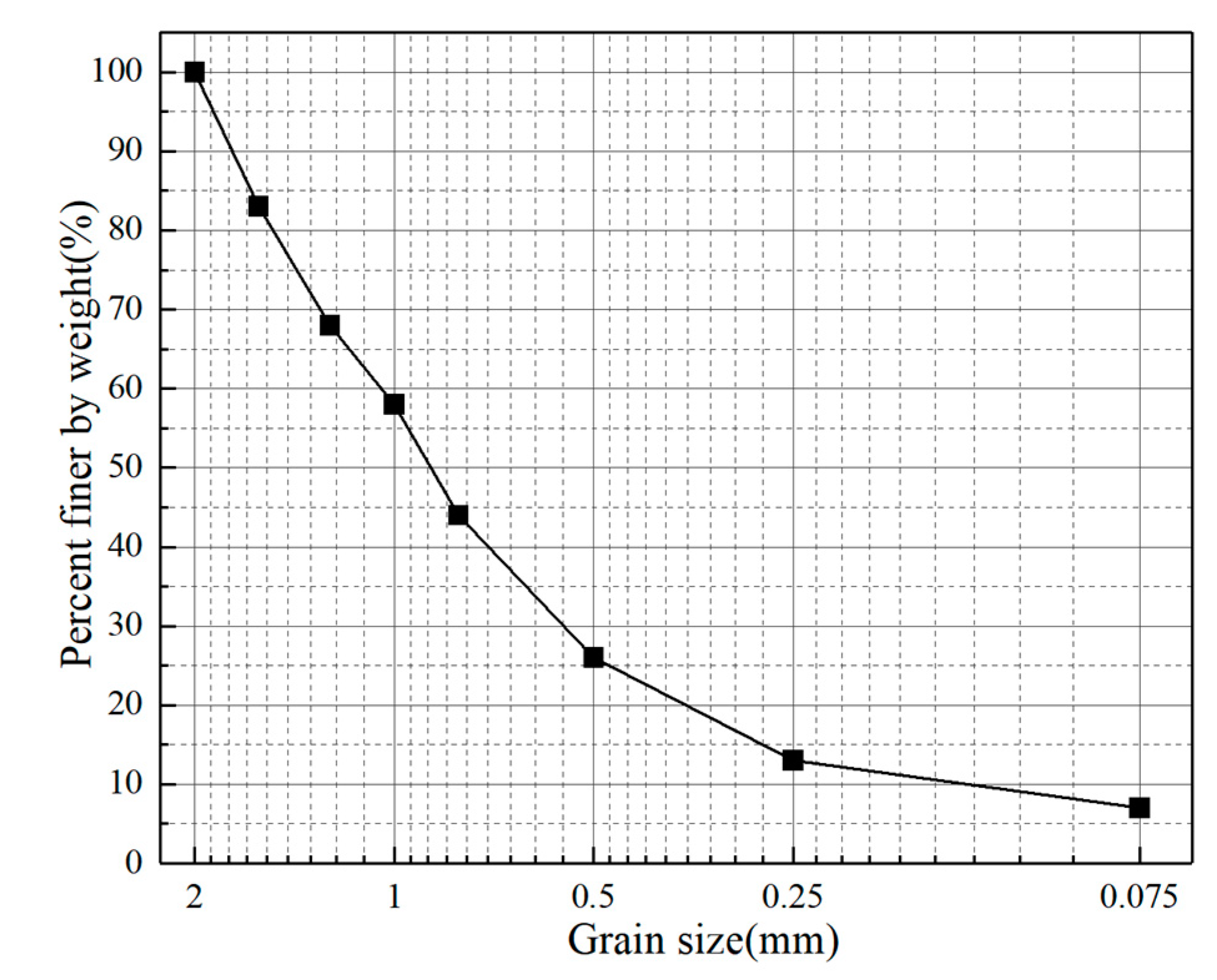
- Soil material
3.2. Scheme and Procedure
- (1)
- Root tensile test
- (2)
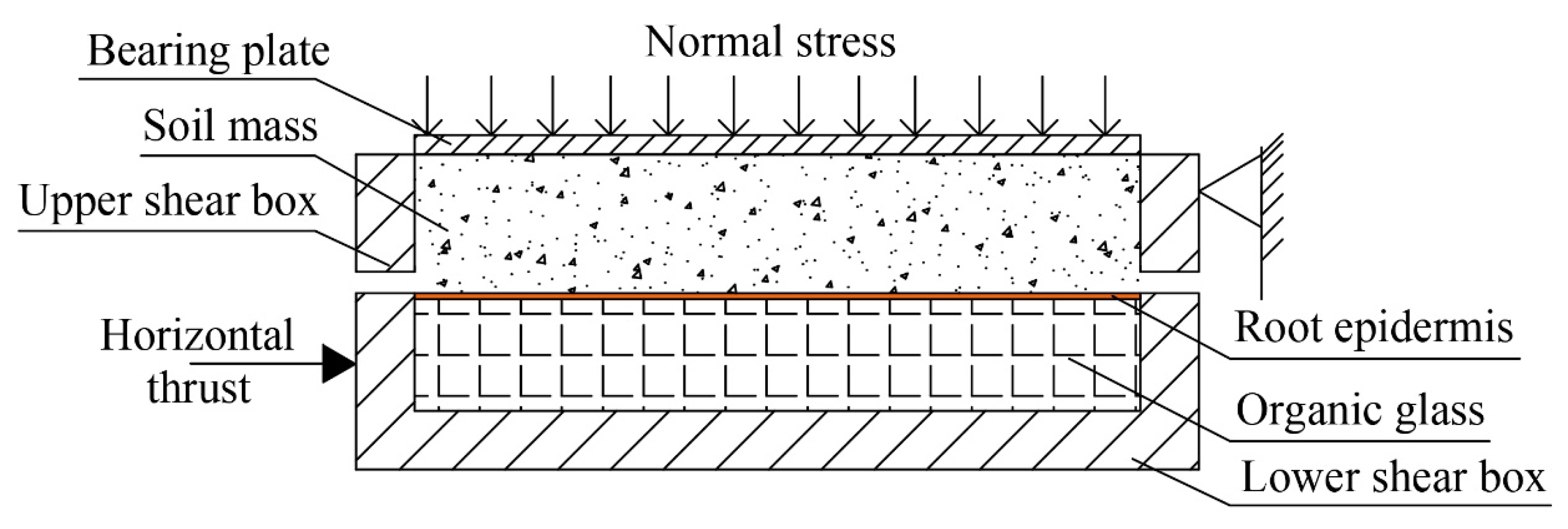
- Shear resistance test of the root–soil interface bonding strength
- (1)
- Test principle and instrument
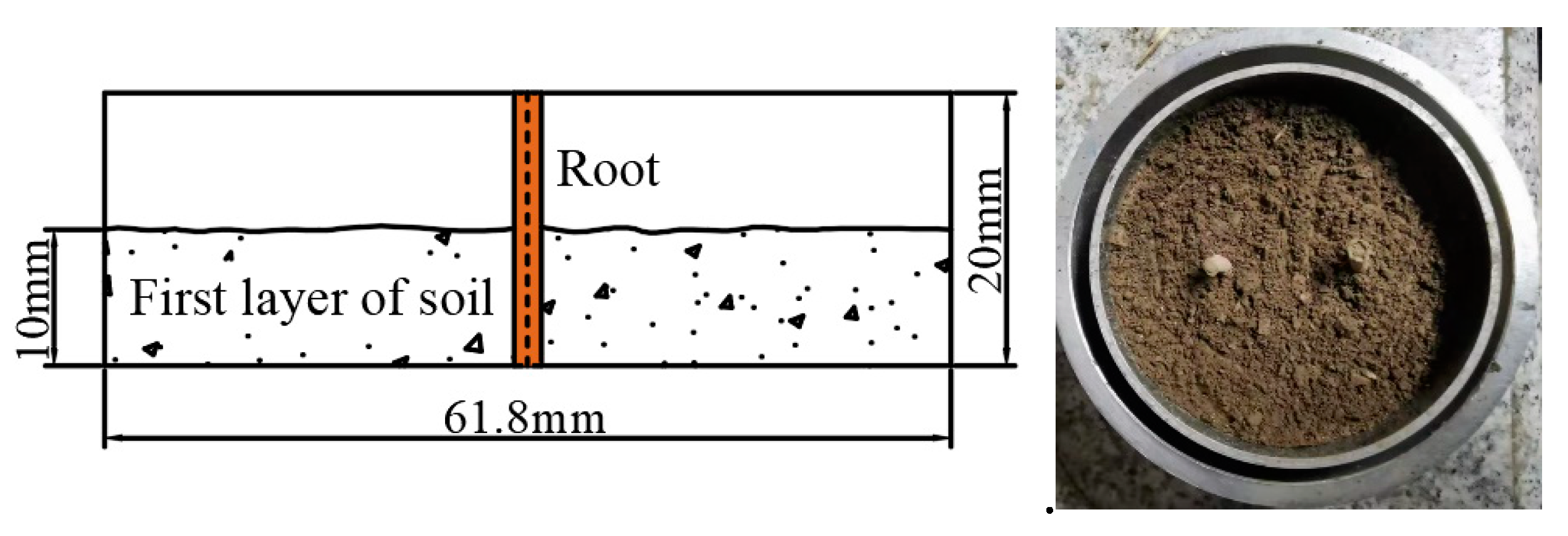
- (2)
- Specimens preparation and shearing
- (3)
- Direct shear test of root-permeated soil
4. Experiments Results
4.1. Root Tensile Strength
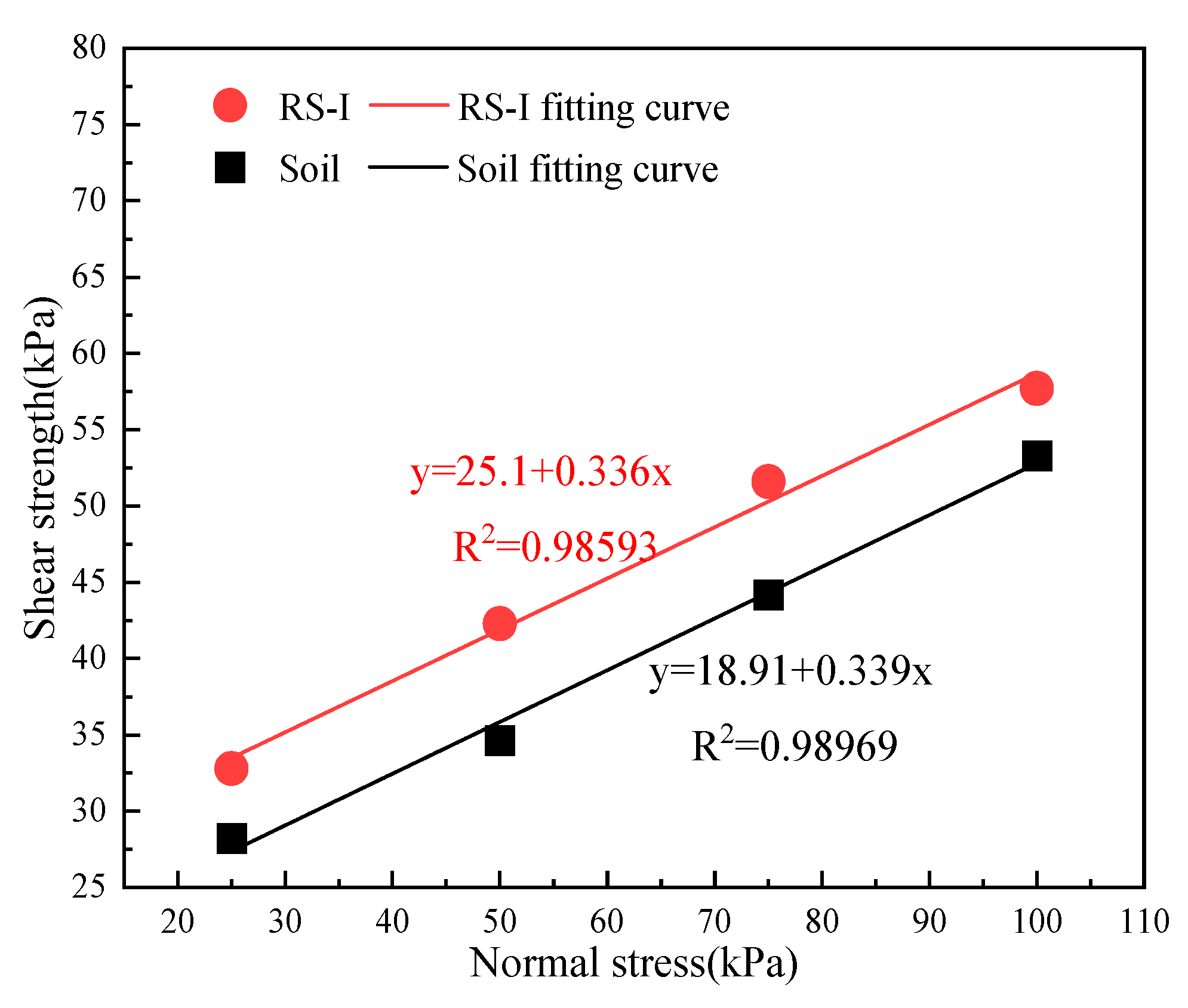
4.2. Bond Strength of Root–Soil Interface
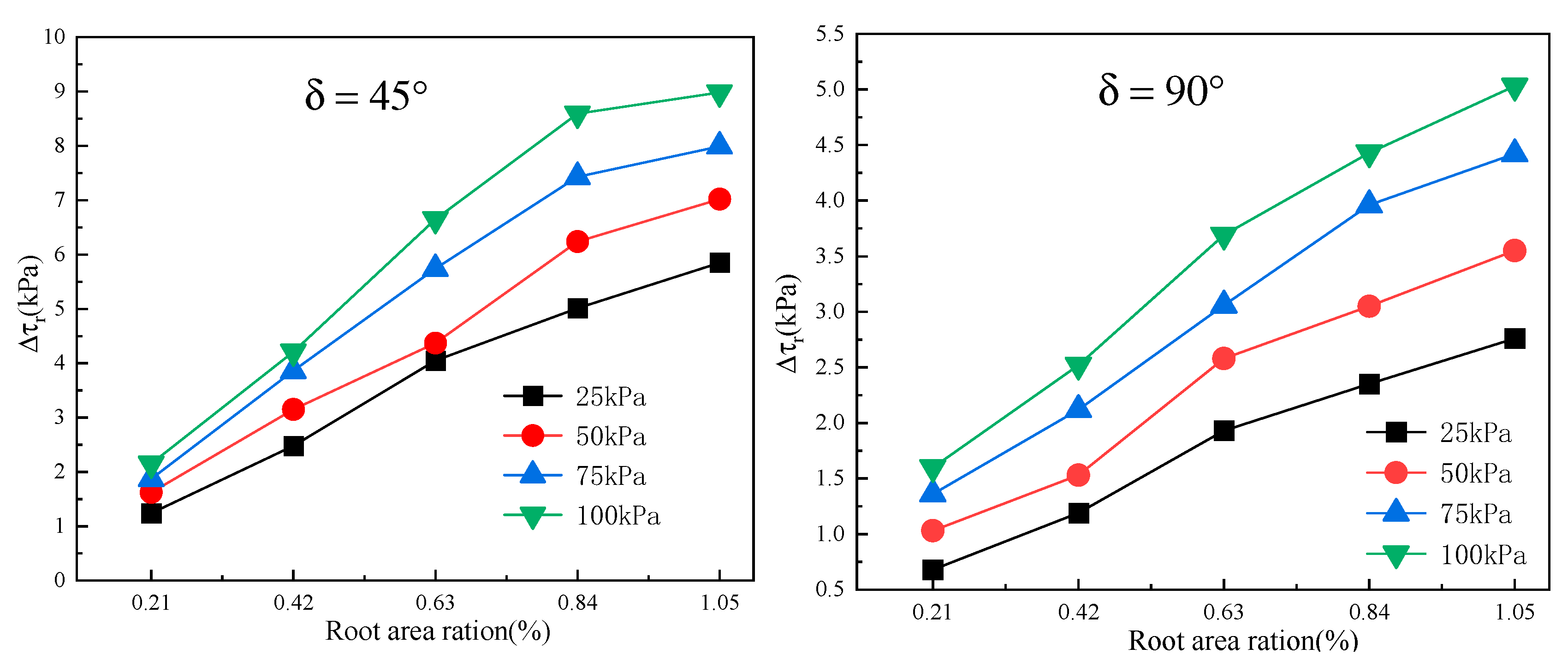
4.3. Shear Strength of Root-Permeated Soil
5. Establishment and Validation of Estimation Model of the Ultimate Shear Strength of Root-Permeated Soil Fully Considering Interface Bonding
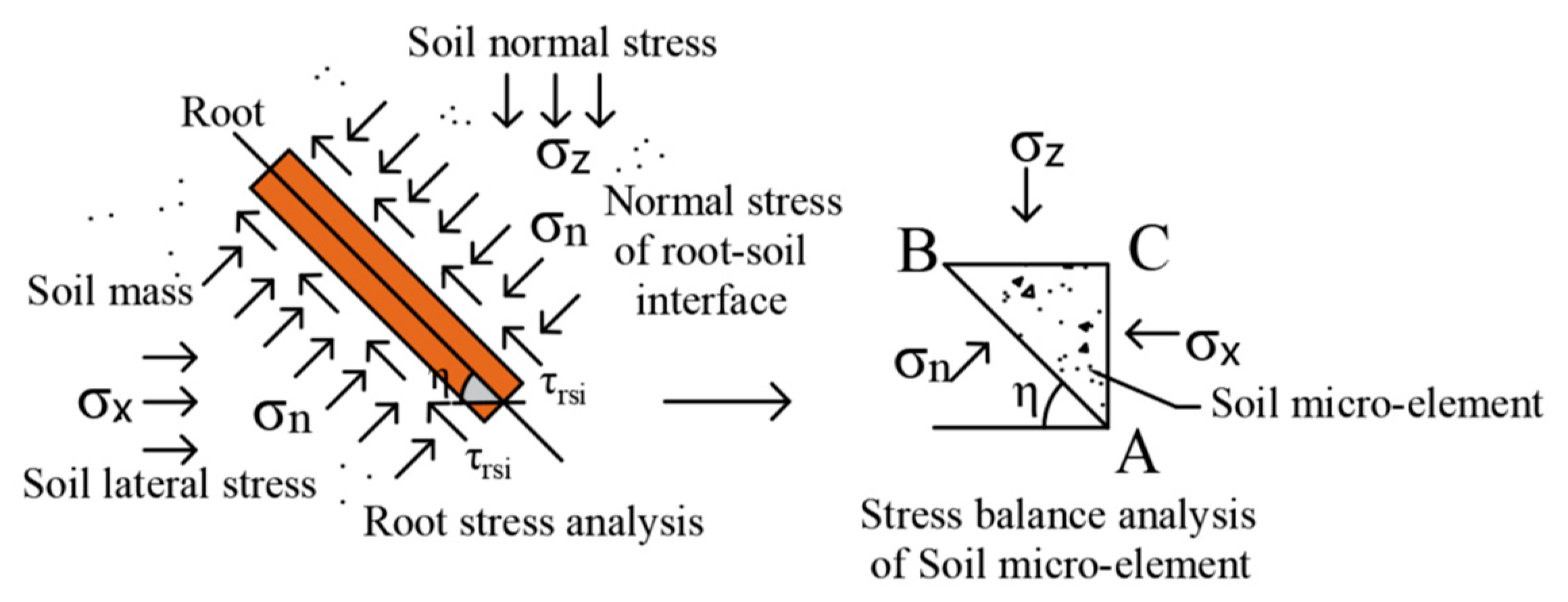
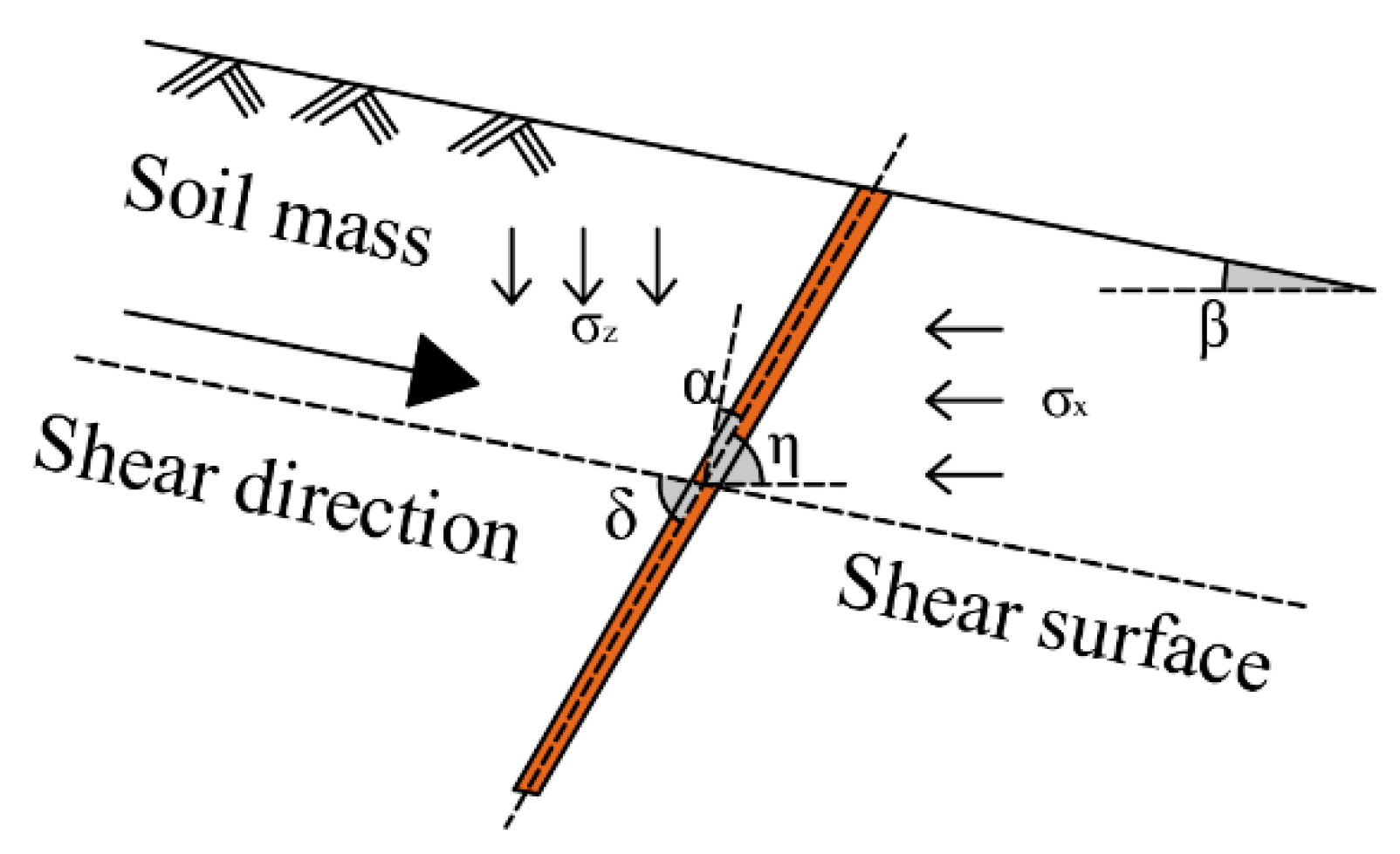
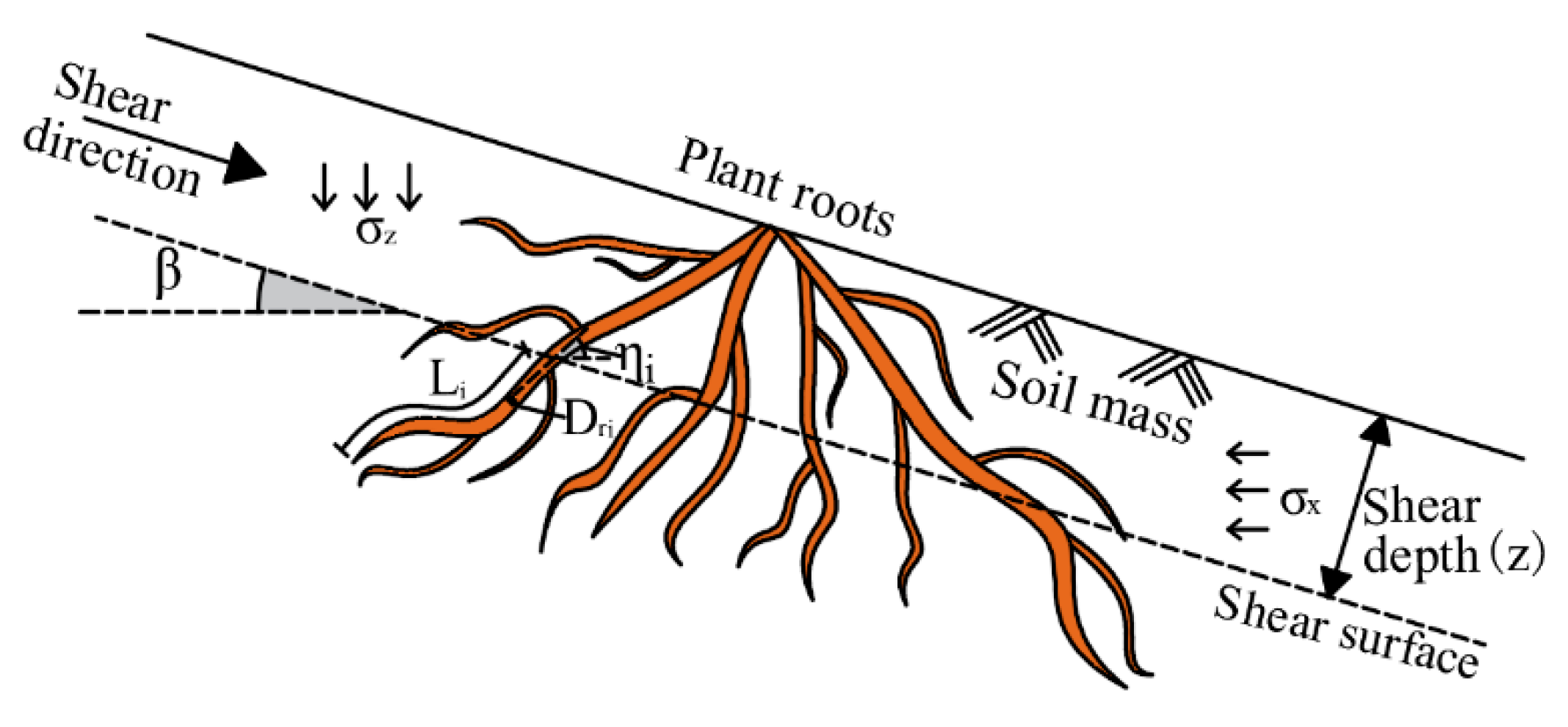
5.1. Model Establishment
- (1)
- When analyzing the interaction between plant roots and soil, the three-dimensional reinforcement was simplified to a two-dimensional plane state.
- (2)
- Due to the great difference in deformation modulus and material properties between plant roots and soil, the soil-permeated root could be regarded as anisotropic composite materials, and the roots were equivalent to flexible tensile components in the soil.
- (3)
- The tensile stress of roots could be decomposed into the normal stress and tangential stress on the shear surface of the soil, where the normal stress enhanced the friction strength on the shear surface, and the tangential stress could be directly involved in resisting the shear deformation of soil on both sides of the shear surface.
- (1)
- Maximum
- (2)
- Minimum
- ①
- When , the minimum value of is sinφ as shown in Figure 18a, then the minimum value of is:
- ②
- When , the value of is shown in Figure 18b. When , the minimum value of is , then the minimum value of is shown in Equation (22); when , the minimum value of is , then the minimum value of is shown in Equation (21).
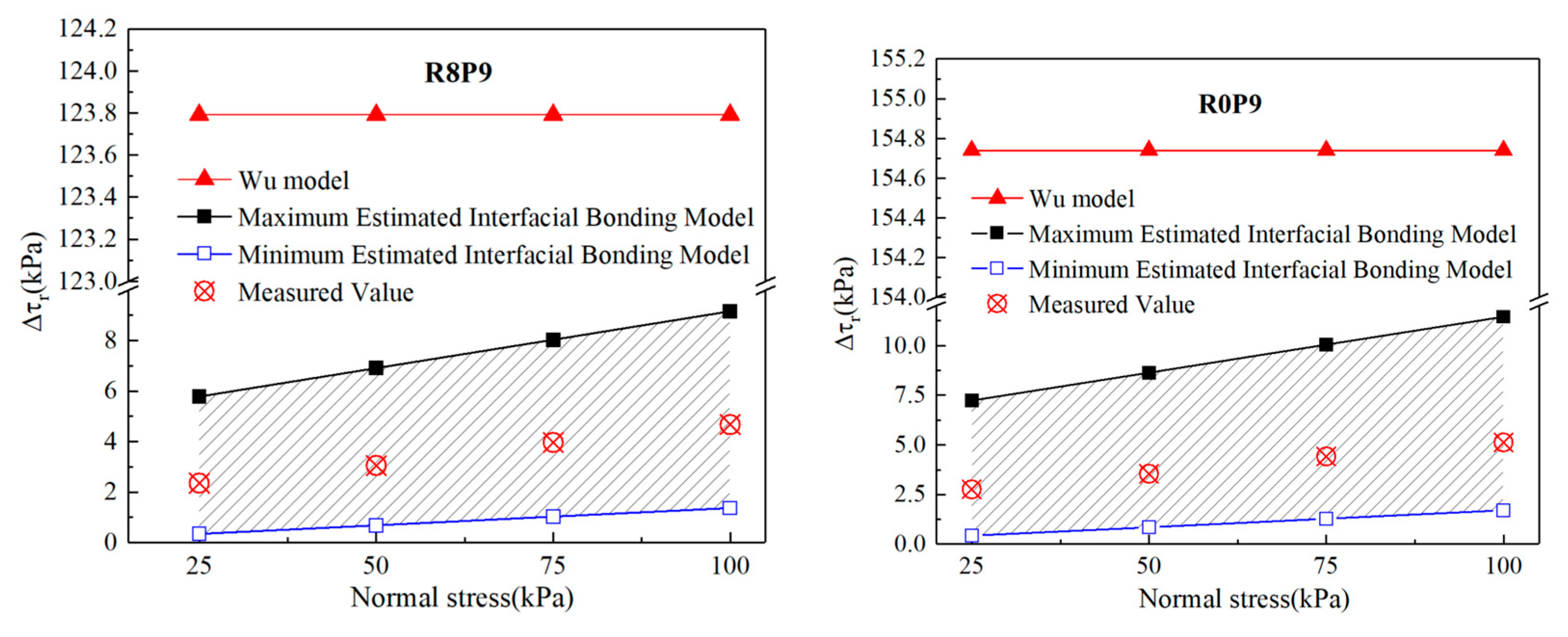
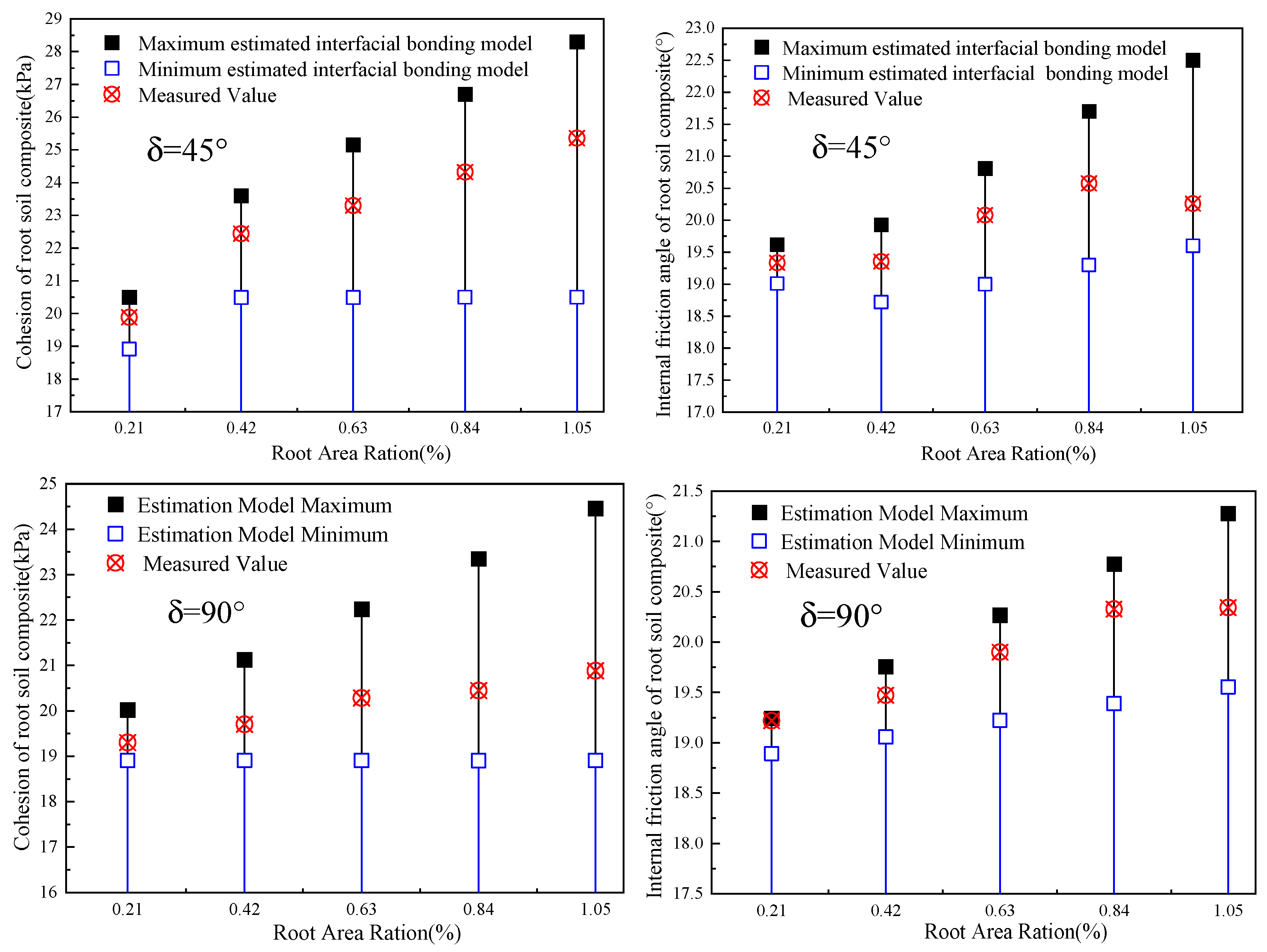
5.2. Model Validation
6. Discussion
6.1. Scope of Application of the Estimation Model
- (1)
- Mechanical properties of roots
- (2)
- Orientation of roots relative to the shear plane
6.2. Model Parameters
- (1)
- Soil strength parameters
- (2)
- Bond strength parameters of root–soil interface
- (3)
- Tensile strength of roots
- (4)
- Spatial geometric characteristic parameters of roots
7. Conclusions
- (1)
- Experimental results of bond strength of root–soil interface and shear strength of root-permeated soil: The shear resistance tests of root–soil interface bonding strength showed that the interface bond strength and the interface normal stress were in accordance with the Coulomb’s law, which could be quantified by the interface cohesion and the interface friction angle. The indoor direct shear test results showed that the mechanical reinforcement of roots in the root-permeated soil increased with the root area ratio and normal stress. The shear strength of root-permeated soil in the condition of a 45° Angle between the root system and shear direction was greater than that in a 90° Angle.
- (2)
- The characteristics and application range of the proposed shear strength model of root-permeated soil: The bond effect of root–soil interface was fully considered, and the estimation model of ultimate shear strength of root-permeated soil was established by combining with Wu’s model. The estimation model realizes the estimation of ultimate shear strength (maximum and minimum) of root-permeated soil considering soil stress, root diameter, root length and initial angle between root and shear direction. The model is suitable for herbaceous roots and lateral roots of woody plants with small stiffness and sharp angle across the shear plane.
- (3)
- Verification of rationality and advancement of the proposed estimation model: The proposed estimation model was quantitatively compared with the results of the direct shear test and Wu’s model. The results showed that the measured root reinforcement and the shear strength parameters of root-permeated soil were within the range of the calculated values of the estimation model. Moreover, the accuracy of the estimation model was five times higher than that of Wu’s model on average. Therefore, the established estimation model can reasonably and effectively estimate the shear strength of the root-permeated soil and be used to calculate the stability of biotechnical reinforcement landslides.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fowze, J.S.M.; Bergado, D.T.; Soralump, S.; Voottipreux, P.; Dechasakulsom, M. Rain-triggered landslide hazards and mitigation measures in Thailand: From research to practice. Geotext. Geomembr. 2012, 30, 50–64. [Google Scholar] [CrossRef]
- Shen, P.; Zhang, L.M.; Chen, H.X.; Gao, L. Role of vegetation restoration in mitigating hillslope erosion and debris flows. Eng. Geol. 2017, 216, 122–133. [Google Scholar] [CrossRef]
- Lotfalian, M.; Nasiri, M.; Modarres, A.; Wu, W. Slope stability analysis considering weight of trees and root reinforcement. J. Environ. Eng. Landsc. Manag. 2019, 27, 201–208. [Google Scholar] [CrossRef]
- Tan, H.; Chen, F.; Chen, J.; Gao, Y. Direct shear tests of shear strength of soils reinforced by geomats and plant roots. Geotext. Geomembr. 2019, 47, 780–791. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, L.M. Field investigation of erosion resistance of common grass species for soil bioengineering in Hong Kong. Acta Geotech. 2016, 11, 1047–1059. [Google Scholar] [CrossRef]
- Zydroń, T.; Gruchot, A. Influence of root systems of deciduous trees on soil reinforcement—A case study from the carpathians, poland. Environ. Eng. Manag. J. 2021, 20, 419–433. [Google Scholar] [CrossRef]
- Gonzalez-Ollauri, A.; Mickovski, S.B. Plant-soil reinforcement response under different soil hydrological regimes. Geoderma 2017, 285, 141–150. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Ni, J.J.; Leung, A.K. Effects of plant growth and spacing on soil hydrological changes: A field study. Geotechnique 2020, 70, 867–881. [Google Scholar] [CrossRef]
- Yildiz, A.; Graf, F.; Rickli, C.; Springman, S.M. Assessment of plant-induced suction and its effects on the shear strength of rooted soils. Proc. Inst. Civ. Eng. Geotech. Eng. 2019, 172, 507–519. [Google Scholar] [CrossRef]
- Zhu, H.; Indupriya, M.; Gadi, V.K.; Sreedeep, S.; Mei, G.X.; Garg, A. Assessment of the coupled effects of vegetation leaf and root characteristics on soil suction: An integrated numerical modeling and probabilistic approach. Acta Geotech. 2020, 15, 1331–1339. [Google Scholar] [CrossRef]
- Mao, Z.; Saint-André, L.; Genet, M.; Mine, F.X.; Jourdan, C.; Rey, H.; Courbaud, B.; Stokes, A. Engineering ecological protection against landslides in diverse mountain forests: Choosing cohesion models. Ecol. Eng. 2012, 45, 55–69. [Google Scholar] [CrossRef]
- Bordoloi, S.; Ng, C.W.W. The effects of vegetation traits and their stability functions in bio-engineered slopes: A perspective review. Eng. Geol. 2020, 275, 105742. [Google Scholar] [CrossRef]
- Leung, A.K.; Garg, A.; Ng, C.W.W. Effects of plant roots on soil-water retention and induced suction in vegetated soil. Eng. Geol. 2015, 193, 183–197. [Google Scholar] [CrossRef]
- Schmaltz, E.M.; Mergili, M. Integration of root systems into a GIS-based slip surface model: Computational experiments in a generic hillslope environment. Landslides 2018, 15, 1561–1575. [Google Scholar] [CrossRef]
- Vannoppen, W.; De Baets, S.; Keeble, J.; Dong, Y.; Poesen, J. How do root and soil characteristics affect the erosion-reducing potential of plant species? Ecol. Eng. 2017, 109, 186–195. [Google Scholar] [CrossRef]
- Stokes, A.; Douglas, G.B.; Fourcaud, T.; Giadrossich, F.; Gillies, C.; Hubble, T.; Kim, J.H.; Loades, K.W.; Mao, Z.; McIvor, I.R.; et al. Ecological mitigation of hillslope instability: Ten key issues facing researchers and practitioners. Plant Soil 2014, 377, 1–23. [Google Scholar] [CrossRef]
- Mahannopkul, K.; Jotisankasa, A. Influences of root concentration and suction on Chrysopogon zizanioides reinforcement of soil. Soils Found. 2019, 59, 500–516. [Google Scholar] [CrossRef]
- Yildiz, A.; Graf, F.; Rickli, C.; Springman, S.M. Determination of the shearing behaviour of root-permeated soils with a large-scale direct shear apparatus. Catena 2018, 166, 98–113. [Google Scholar] [CrossRef]
- Fan, C.C.; Tsai, M.H. Spatial distribution of plant root forces in root-permeated soils subject to shear. Soil Tillage Res. 2016, 156, 1–15. [Google Scholar] [CrossRef]
- Meijer, G.J.; Knappett, J.A.; Bengough, A.G.; Bull, D.J.; Liang, T.; Muir Wood, D. DRAM: A three-dimensional analytical model for the mobilisation of root reinforcement in direct shear conditions. Ecol. Eng. 2022, 179, 106621. [Google Scholar] [CrossRef]
- Meijer, G.J.; Bengough, G.; Knappett, J.; Loades, K.; Nicoll, B.; Mukov, I.; Zhang, M. In situ root identification through blade penetrometer testing—Part 1: Interpretative models and laboratory testing. Géotechnique 2018, 68, 303–319. [Google Scholar] [CrossRef]
- Meijer, G.J.; Bengough, G.; Knappett, J.; Loades, K.; Nicoll, B.; Mukov, I.; Zhang, M. In situ root identification through blade penetrometer testing—Part 2: Field testing. Géotechnique 2018, 68, 320–331. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. Earth Surf. 2010, 115, 1–19. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Pullout tests of root analogs and natural root bundles in soil: Experiments and modeling. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Burak, E.; Dodd, I.C.; Quinton, J.N. Do root hairs of barley and maize roots reinforce soil under shear stress? Geoderma 2021, 383, 114740. [Google Scholar] [CrossRef]
- Comino, E.; Marengo, P. Root tensile strength of three shrub species: Rosa canina, Cotoneaster dammeri and Juniperus horizontalis. Soil reinforcement estimation by laboratory tests. Catena 2010, 82, 227–235. [Google Scholar] [CrossRef]
- Meena, S.K.; Sahu, R.; Ayothiraman, R. Utilization of Waste Wheat Straw Fibers for Improving the Strength Characteristics of Clay. J. Nat. Fibers 2021, 18, 1404–1418. [Google Scholar] [CrossRef]
- Sivakumar Babu, G.L.; Vasudevan, A.K.; Sayida, M.K. Use of coir fibers for improving the engineering properties of expansive soils. J. Nat. Fibers 2008, 5, 61–75. [Google Scholar] [CrossRef]
- Laio, F.; D’Odorico, P.; Ridolfi, L. An analytical model to relate the vertical root distribution to climate and soil properties. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Gonzalez-Ollauri, A.; Mickovski, S.B. Using the root spread information of pioneer plants to quantify their mitigation potential against shallow landslides and erosion in temperate humid climates. Ecol. Eng. 2016, 95, 302–315. [Google Scholar] [CrossRef]
- Wu, T.H.; McKinnell, W.P.; Swanston, D.N. Strength of Tree Roots and Landslides on Prince-Of-Wales-Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Fan, C.C. A displacement-based model for estimating the shear resistance of root-permeated soils. Plant Soil 2012, 355, 103–119. [Google Scholar] [CrossRef]
- Liang, T.; Knappett, J.A.; Leung, A.; Carnaghan, A.; Bengough, A.G.; Zhao, R. A critical evaluation of predictive models for rooted soil strength with application to predicting the seismic deformation of rooted slopes. Landslides 2020, 17, 93–109. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour. Res. 2005, 41, 1–11. [Google Scholar] [CrossRef]
- Schwarz, M.; Giadrossich, F.; Cohen, D. Modeling root reinforcement using a root-failure Weibull survival function. Hydrol. Earth Syst. Sci. 2013, 17, 4367–4377. [Google Scholar] [CrossRef]
- Schwarz, M.; Lehmann, P.; Or, D. Quantifying lateral root reinforcement in steep slopes—from a bundle of roots to tree stands. Earth Surf. Process. Landforms 2010, 35, 354–367. [Google Scholar] [CrossRef]
- Zydroń, T.; Gruchot, A.; Kluba, M. Spatial variability of reinforcement provided by juvenile root systems of black locust and black poplar. Polish J. Environ. Stud. 2019, 28, 4027–4037. [Google Scholar] [CrossRef] [PubMed]
- Ji, J.; Mao, Z.; Qu, W.; Zhang, Z. Energy-based fibre bundle model algorithms to predict soil reinforcement by roots. Plant Soil 2020, 446, 307–329. [Google Scholar] [CrossRef]
- Meijer, G.J. A generic form of fibre bundle models for root reinforcement of soil. Plant Soil 2021, 468, 45–65. [Google Scholar] [CrossRef]
- Docker, B.B.; Hubble, T.C.T. Quantifying root-reinforcement of river bank soils by four Australian tree species. Geomorphology 2008, 100, 401–418. [Google Scholar] [CrossRef]
- Waldron, L.J.; Dakessian, S. Effect of Grass, Legume, and Tree Roots on Soil Shearing Resistance. Soil Sci. Soc. Am. J. 1982, 46, 894–899. [Google Scholar] [CrossRef]
- Wen, W.; Li, G.; Hu, W.; Liu, H.; Xiang, W. Modification of reinforcement effect model of herbs root system in soil. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2016, 35, 4211–4217. [Google Scholar] [CrossRef]
- Kong, Y.; Zhou, A.; Shen, F.; Yao, Y. Stress–dilatancy relationship for fiber-reinforced sand and its modeling. Acta Geotech. 2019, 14, 1871–1881. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Zhang, Q.; Ni, J.; Li, Z. A new three-dimensional theoretical model for analysing the stability of vegetated slopes with different root architectures and planting patterns. Comput. Geotech. 2021, 130, 103912. [Google Scholar] [CrossRef]
- Tosi, M. Root tensile strength relationships and their slope stability implications of three shrub species in the Northern Apennines (Italy). Geomorphology 2007, 87, 268–283. [Google Scholar] [CrossRef]
- Vergani, C.; Werlen, M.; Conedera, M.; Cohen, D.; Schwarz, M. Investigation of root reinforcement decay after a forest fire in a Scots pine (Pinus sylvestris) protection forest. For. Ecol. Manag. 2017, 400, 339–352. [Google Scholar] [CrossRef]
- Fan, C.C.; Su, C.F. Role of roots in the shear strength of root-reinforced soils with high moisture content. Ecol. Eng. 2008, 33, 157–166. [Google Scholar] [CrossRef]
- Liang, T.; Knappett, J.A.; Bengough, A.G.; Ke, Y.X. Small-scale modelling of plant root systems using 3D printing, with applications to investigate the role of vegetation on earthquake-induced landslides. Landslides 2017, 14, 1747–1765. [Google Scholar] [CrossRef]
- Meijer, G.J.; Muir Wood, D.; Knappett, J.A.; Bengough, G.A.; Liang, T. Analysis of coupled axial and lateral deformation of roots in soil. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 684–707. [Google Scholar] [CrossRef]
- Abe, K.; Ziemer, R.R. Effect of tree roots on a shear zone: Modeling reinforced shear stress. Can. J. For. Res. 1991, 21, 1012–1019. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; He, Y. Sensitivity analysis of debris flow to environmental factors: A case of Longxi River basin. Chin. J. Geol. Hazard Control 2020, 31, 32–39. [Google Scholar] [CrossRef]
- Li, J.; Qiu, H.; Cao, M.; Xur, B.; Hu, S.; Cui, P. Spatial-temporal process and characteristics of vegetation recovery after Wenchuan earthquake: A case study in Longxi River basin of Dujiangyan, China. Chin. J. Appl. Ecol. 2016, 27, 3479–3486. [Google Scholar] [CrossRef]
- Yang, Q.C.; Hao, Z.; Cheng, W.; Lei, S.Y.; Zhang, Y.; Teng, D.; Zhang, Q.; Wang, X.M. Study on the cohesive shear characteristics and intrinsic modelling of the root–tailing soil interface of Amorpha fruticosa. Sci. Rep. 2022, 12. [Google Scholar] [CrossRef] [PubMed]
- Naveed, M.; Brown, L.K.; Raffan, A.C.; George, T.S.; Bengough, A.G.; Roose, T.; Sinclair, I.; Koebernick, N.; Cooper, L.; Hallett, P.D. Rhizosphere-Scale Quantification of Hydraulic and Mechanical Properties of Soil Impacted by Root and Seed Exudates. Vadose Zo. J. 2018, 17, 1–12. [Google Scholar] [CrossRef]
- Jaky, J. The coefficient of earth pressure at rest. J. Hung. Soc. Archit. Eng. 1944, 25, 355–358. [Google Scholar]
- Li, Y.; Wang, Y.; Wang, Y.; Ma, C. Effects of Vitex negundo root properties on soil resistance caused by pull-out forces at different positions around the stem. Catena 2017, 158, 148–160. [Google Scholar] [CrossRef]
- Su, L.J.; Hu, B.L.; Xie, Q.J.; Yu, F.W.; Zhang, C.L. Experimental and theoretical study of mechanical properties of root-soil interface for slope protection. J. Mt. Sci. 2020, 17, 2784–2795. [Google Scholar] [CrossRef]
- Xin, Z.; Jing, L.; Jingli, H.; Hao, R.; Tiejun, L.I.U.; Honghui, Z.; Ruishen, L. Study on Friction Characteristics of Root-soil Interface of two Types of Soil. IOP Conf. Ser. Earth Environ. Sci. 2019, 304. [Google Scholar] [CrossRef]









| Geographic Location | Altitude (m) | Trunk Diameter (mm) | Slope (°) |
|---|---|---|---|
| 31°12′33″ N | 1700 | 360 | 7 |
| 103°36′31″ E |
| Specimen Number | Material Composition | |
|---|---|---|
| Shear Box (Diameter: 61.8 mm; Height: 20 mm) | ||
| Top Box | Lower Box | |
| RS-I | Soil | Organic glass block with root epidermis |
| Soil | Soil | Soil |
| Specimen Number | δ (°) | RAR (%) | Root Quantity |
|---|---|---|---|
| R2P4 | 45 | 0.21 | 2 |
| R4P4 | 0.42 | 4 | |
| R6P4 | 0.63 | 6 | |
| R8P4 | 0.84 | 8 | |
| R0P4 | 1.05 | 10 | |
| R2P9 | 90 | 0.21 | 2 |
| R4P9 | 0.42 | 4 | |
| R6P9 | 0.63 | 6 | |
| R8P9 | 0.84 | 8 | |
| R0P9 | 1.05 | 10 |
| Root Diameter (mm) | Tensile Force (N) | Tensile Strength (MPa) |
|---|---|---|
| 2 | 38.68 | 12.3 |
| Specimen Number | Shear Strength (kPa) | |||
|---|---|---|---|---|
| σ1 = 25 kPa | σ2 = 50 kPa | σ3 = 75 kPa | σ4 = 100 kPa | |
| Soil | 28.24 | 34.64 | 44.2 | 53.3 |
| RS-I | 32.8 | 43.3 | 51.6 | 57.7 |
| Specimen Number | Strength Parameters | |
|---|---|---|
| Cohesion Stress (kPa) | Internal Friction Angle (°) | |
| Soil | 18.91 | 18.71 |
| RS-I | 25.1 | 18.57 |
| Specimen Number | Strength Parameters | |||||
|---|---|---|---|---|---|---|
| σ1 25 kPa | σ2 50 kPa | σ3 75 kPa | σ4 100 kPa | Cohesion Stress (kPa) | Internal Friction Angle (°) | |
| R2P4 | 29.48 | 36.26 | 46.07 | 55.45 | 19.89 | 19.33 |
| R4P4 | 30.72 | 40.75 | 48.8 | 57.31 | 22.44 | 19.36 |
| R6P4 | 32.29 | 41.97 | 50.68 | 59.75 | 23.30 | 20.08 |
| R8P4 | 33.25 | 44.33 | 52.63 | 61.97 | 24.33 | 20.58 |
| R0P4 | 33.59 | 44.96 | 53.18 | 62.06 | 25.36 | 20.26 |
| R2P9 | 28.92 | 35.67 | 45.56 | 54.9 | 19.30 | 19.36 |
| R4P9 | 29.43 | 36.17 | 45.99 | 55.62 | 19.73 | 19.47 |
| R6P9 | 30.17 | 37.22 | 47.26 | 56.99 | 20.28 | 19.90 |
| R8P9 | 30.59 | 37.69 | 48.16 | 57.97 | 20.45 | 20.33 |
| R0P9 | 31.01 | 38.19 | 48.62 | 58.42 | 20.88 | 20.34 |
| Specimen Number | RAR (%) | α (°) | η (°) | L (mm) | K0 | tf (MPa) | Shear Strength Parameters of Soil | Bond Strength Parameters of Root–Soil Interface | ||
|---|---|---|---|---|---|---|---|---|---|---|
| C (kPa) | φ (°) | Crsi (kPa) | φrsi (°) | |||||||
| R2P4 | 0.21 | 45 | 45 | 14 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R4P4 | 0.42 | 45 | 45 | 14 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R6P4 | 0.63 | 45 | 45 | 14 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R8P4 | 0.84 | 45 | 45 | 14 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R0P4 | 1.05 | 45 | 45 | 14 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R2P9 | 0.21 | 0 | 90 | 10 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R4P9 | 0.42 | 0 | 90 | 10 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R6P9 | 0.63 | 0 | 90 | 10 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R8P9 | 0.84 | 0 | 90 | 10 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
| R0P9 | 1.05 | 0 | 90 | 10 | 0.68 | 12.3 | 18.91 | 18.71 | 25.1 | 18.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, P.; Xia, X.; Jiang, Y. An Estimation Model of the Ultimate Shear Strength of Root-Permeated Soil, Fully Considering Interface Bonding. Forests 2023, 14, 819. https://doi.org/10.3390/f14040819
Ning P, Xia X, Jiang Y. An Estimation Model of the Ultimate Shear Strength of Root-Permeated Soil, Fully Considering Interface Bonding. Forests. 2023; 14(4):819. https://doi.org/10.3390/f14040819
Chicago/Turabian StyleNing, Po, Xin Xia, and Yuanjun Jiang. 2023. "An Estimation Model of the Ultimate Shear Strength of Root-Permeated Soil, Fully Considering Interface Bonding" Forests 14, no. 4: 819. https://doi.org/10.3390/f14040819
APA StyleNing, P., Xia, X., & Jiang, Y. (2023). An Estimation Model of the Ultimate Shear Strength of Root-Permeated Soil, Fully Considering Interface Bonding. Forests, 14(4), 819. https://doi.org/10.3390/f14040819






