Estimation of the Three-Dimension Green Volume Based on UAV RGB Images: A Case Study in YueYaTan Park in Kunming, China
Abstract
1. Introduction
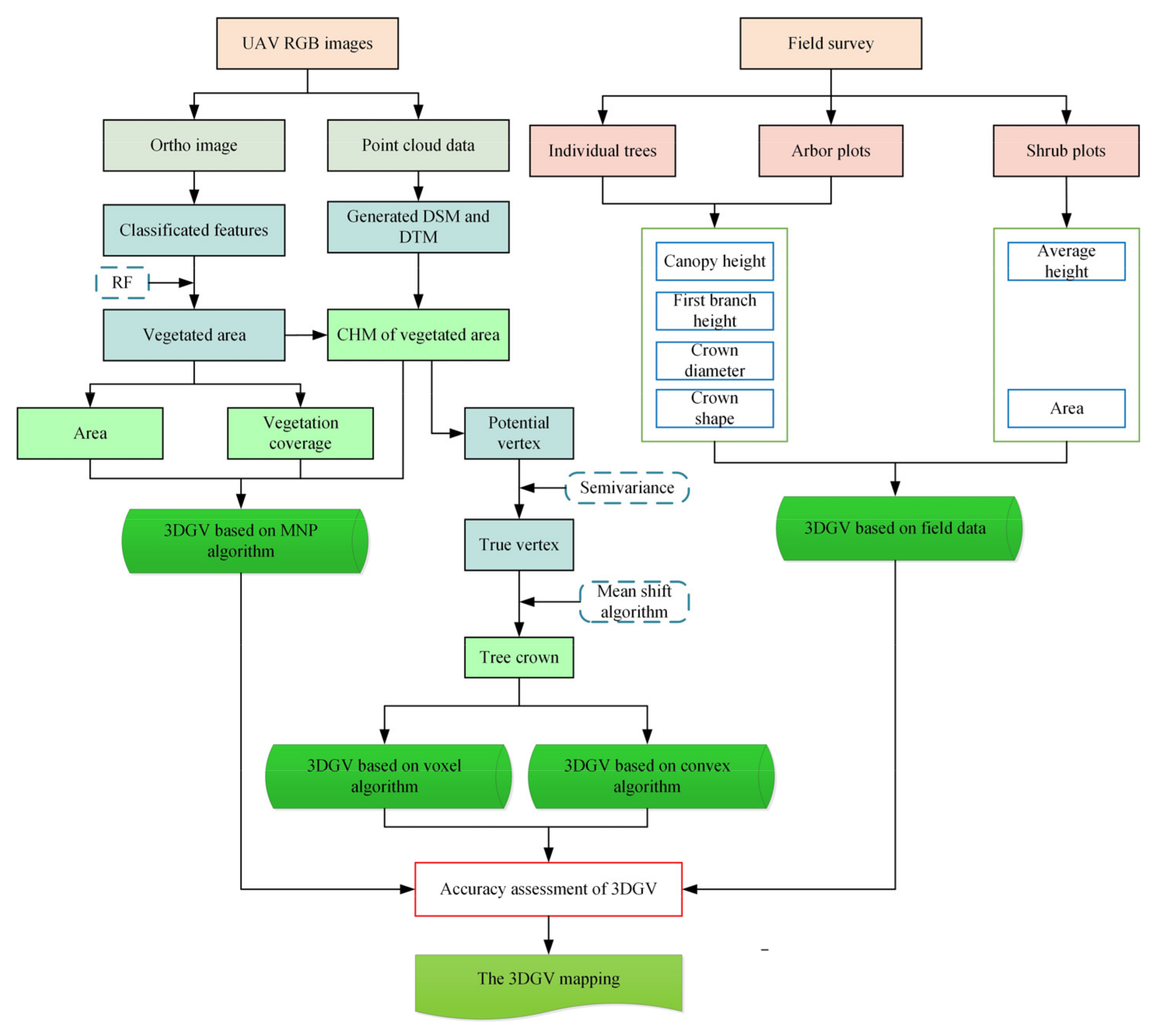
2. Materials and Methods
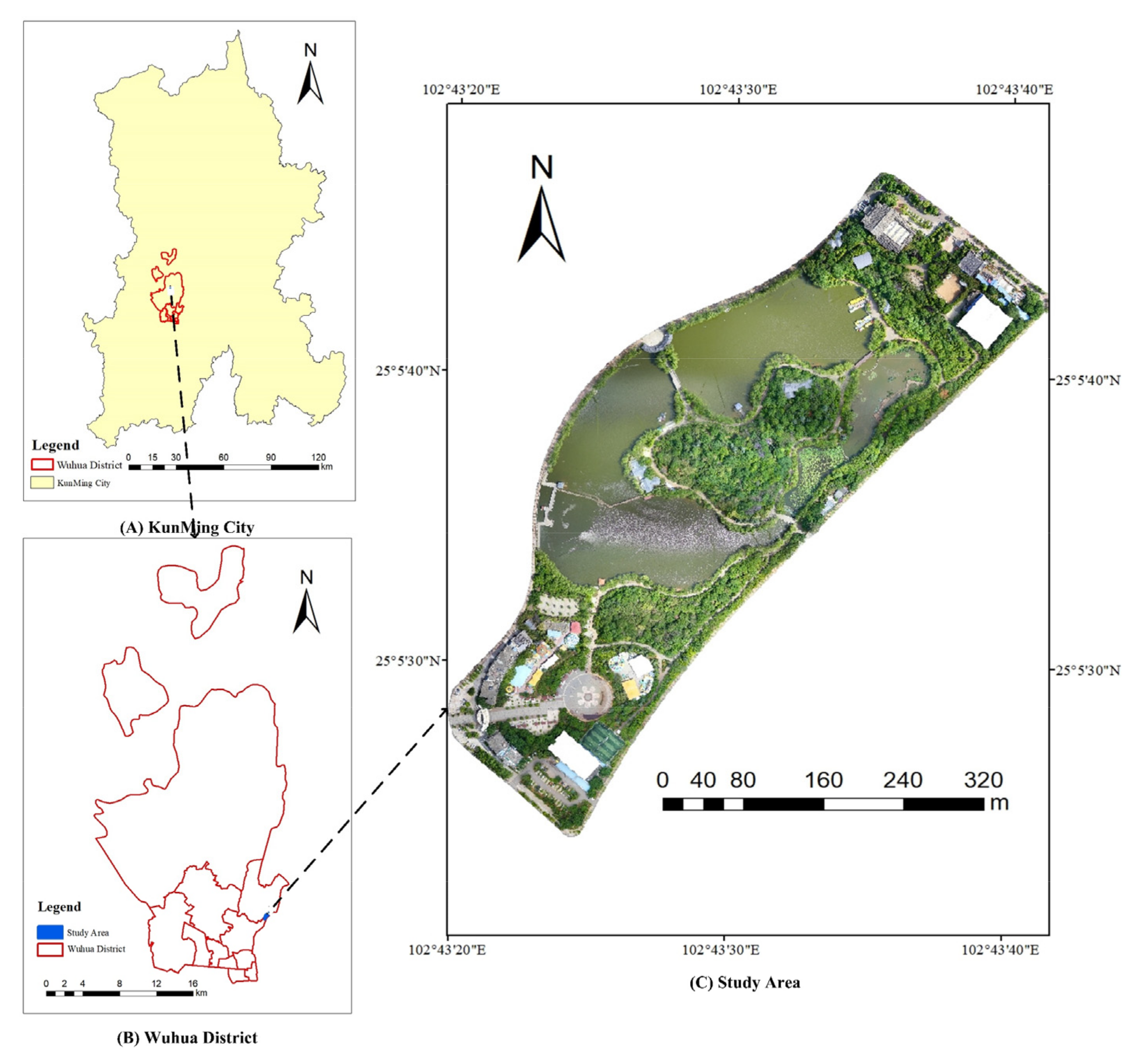
2.1. Study Area
2.2. Data Acquisition
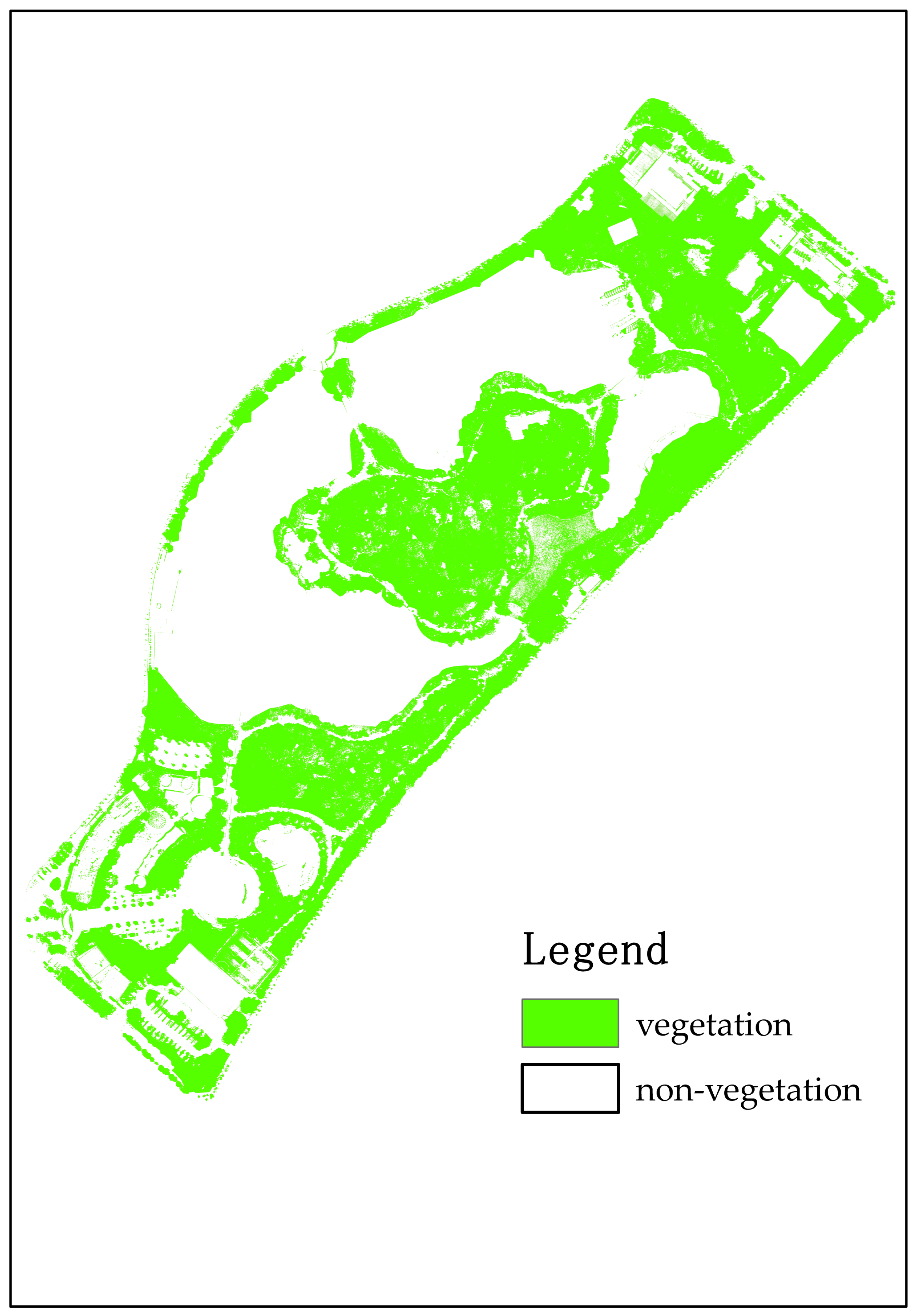
2.3. Vegetation Extraction
2.4. Estimation of 3DGV Based on the MNP Algorithm
2.5. Estimation of 3DGV Based on Tree Detection
2.5.1. Semi Variance Local Maximum Filtering
2.5.2. Segmentation by Mean Shift Algorithm
2.5.3. Estimation of 3DGV Based on the Convex Hull Algorithm
2.5.4. Estimation of 3DGV Based on the Voxel Algorithm
2.6. Accuracy Assessment
3. Results
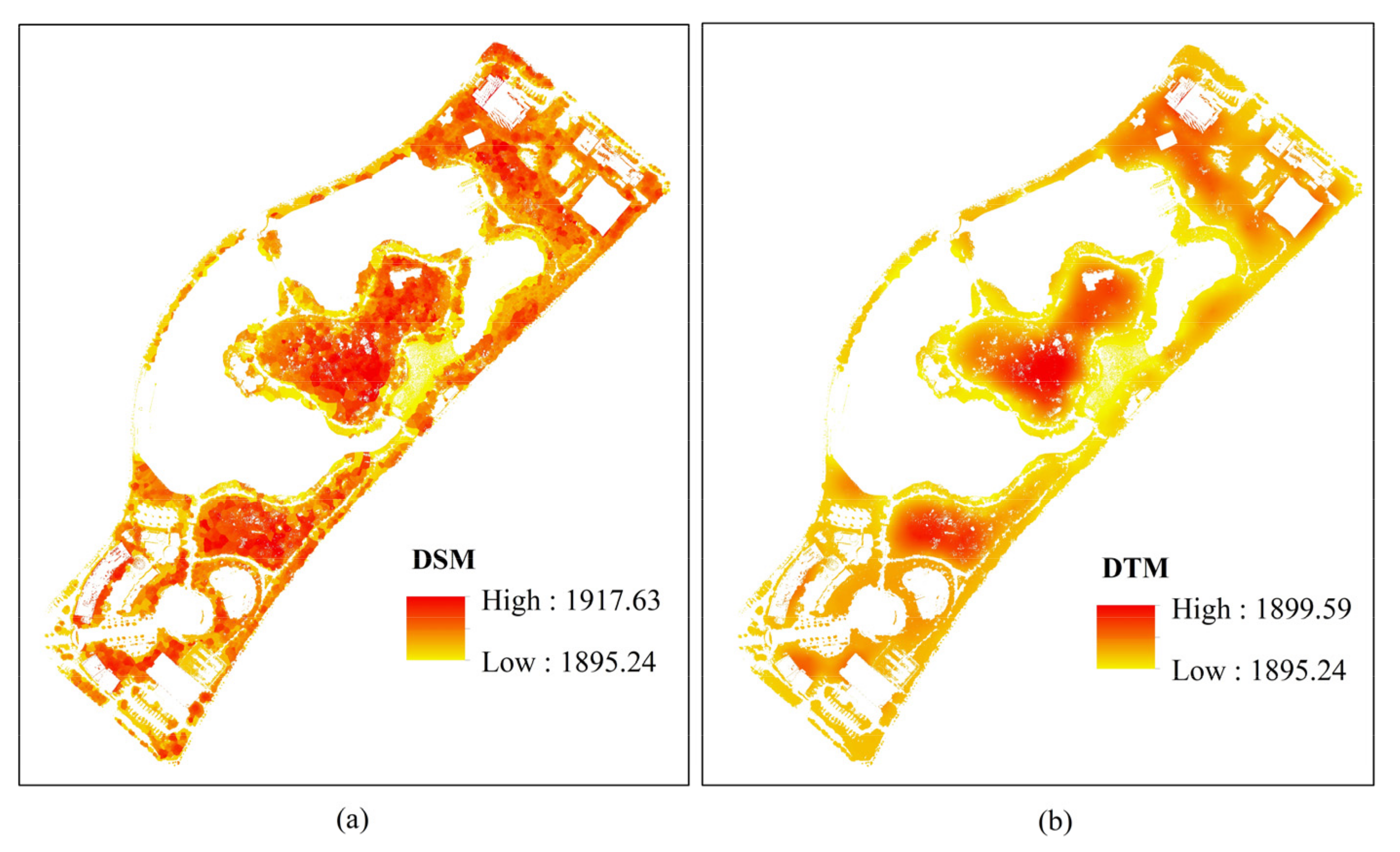
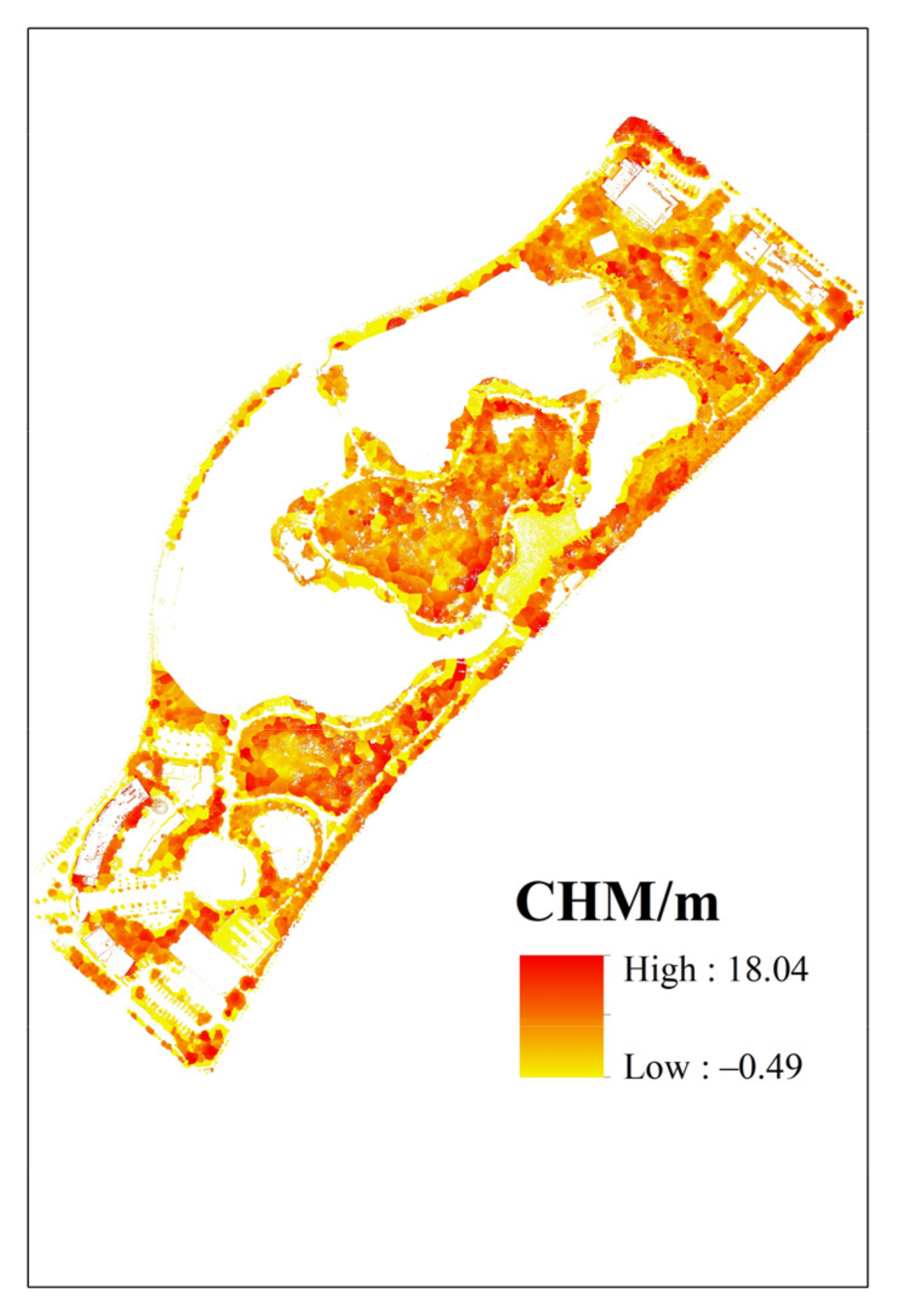
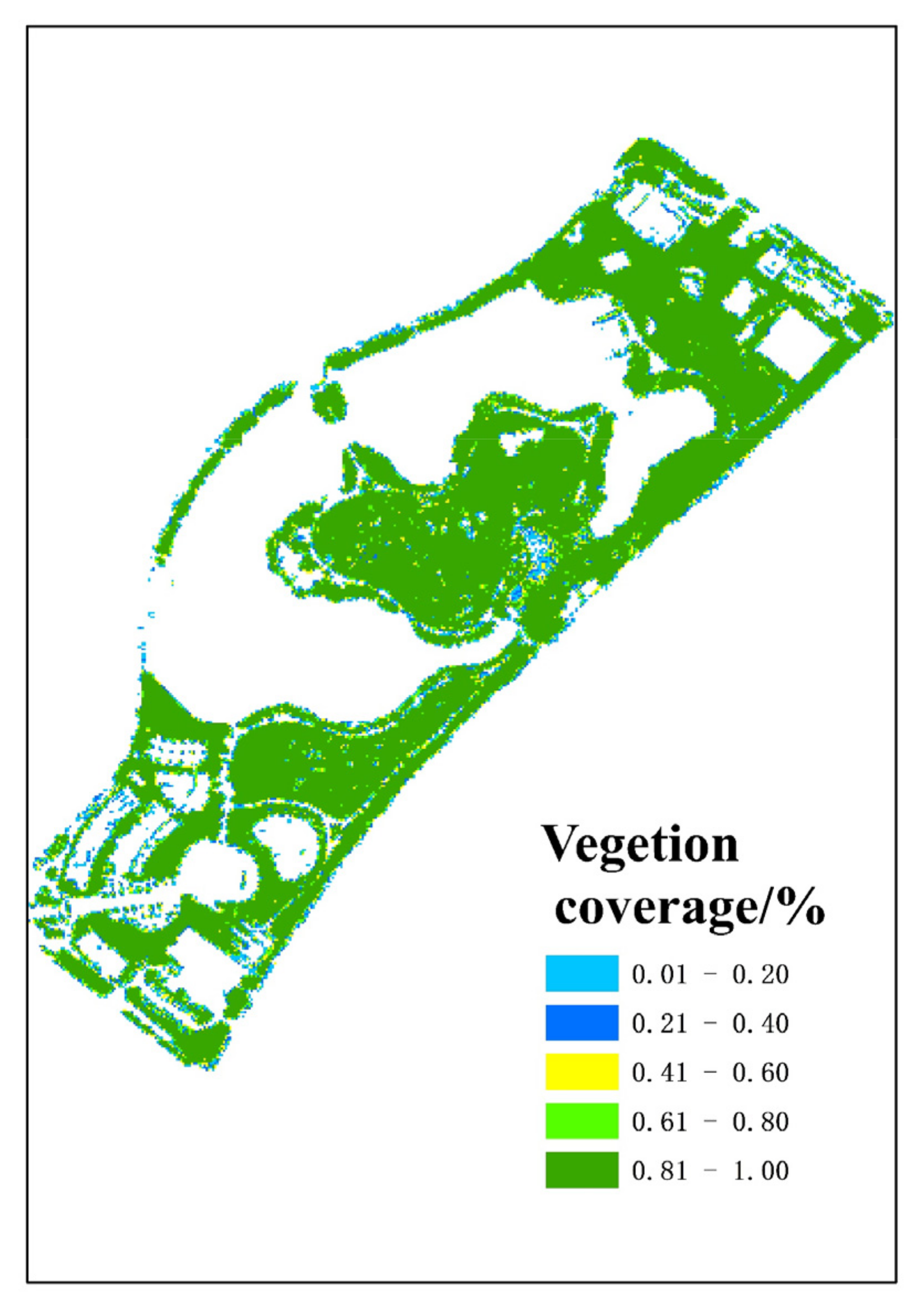
3.1. The Canopy Height and Vegetation Coverage
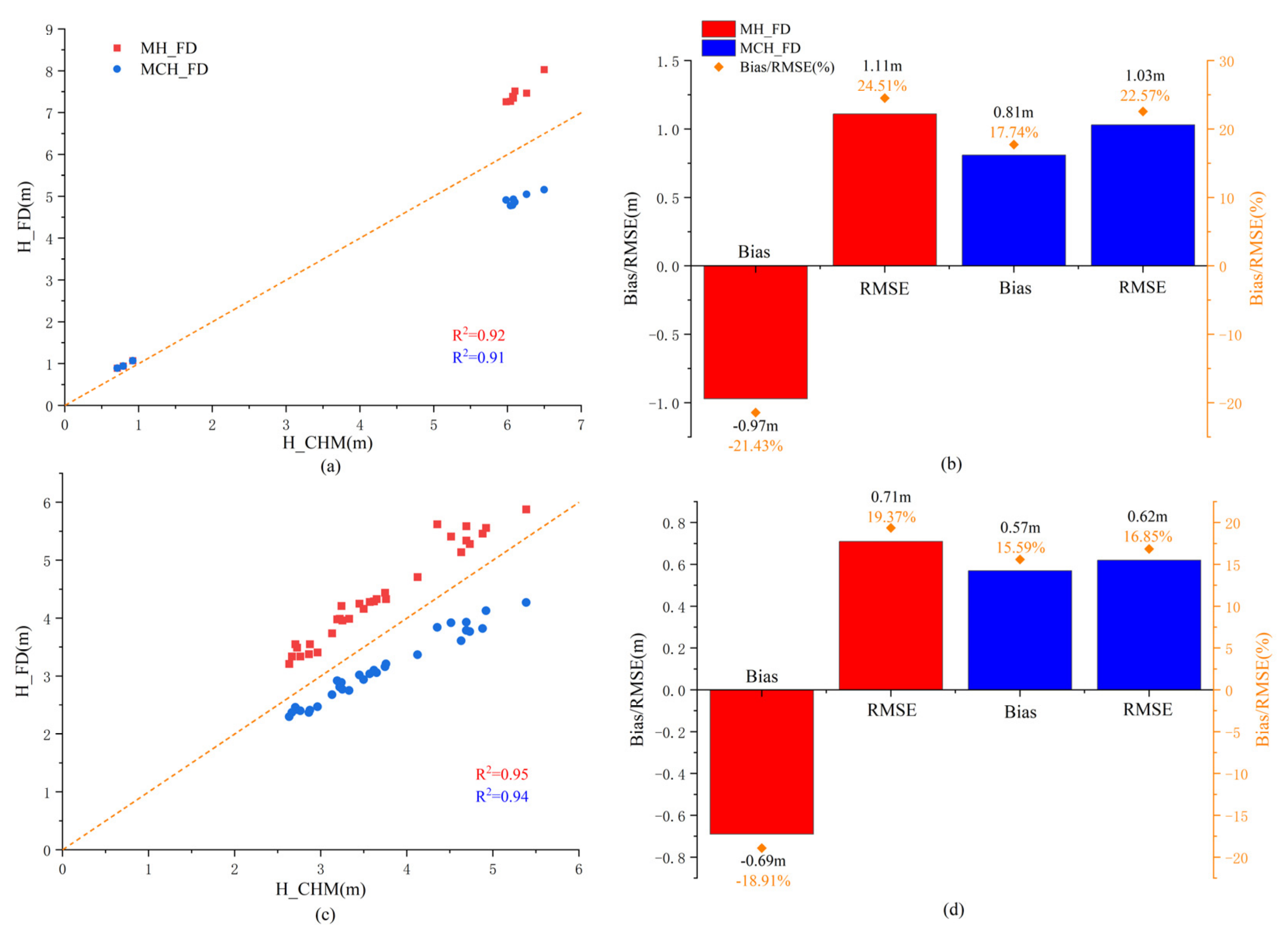
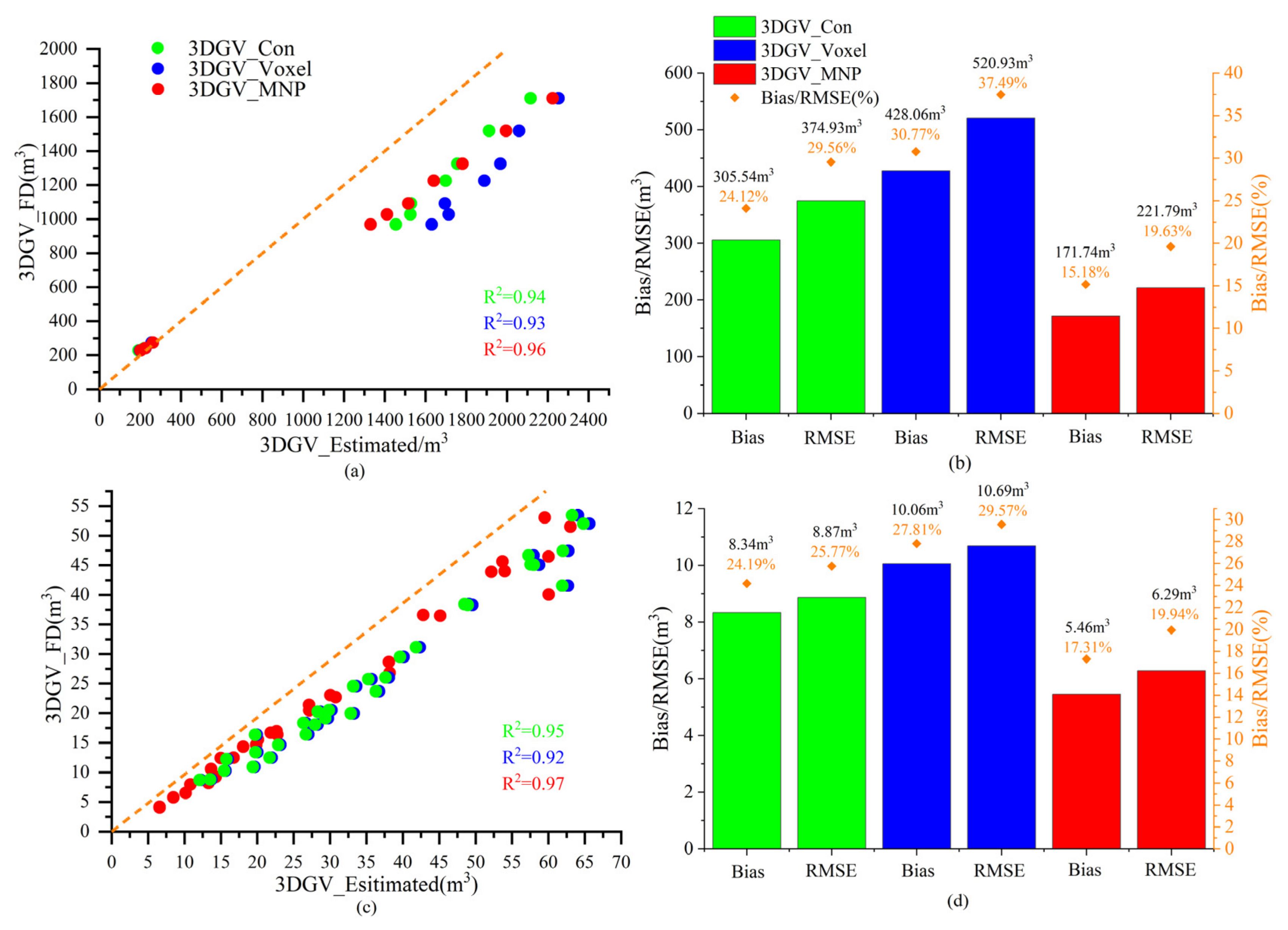
3.2. Accuracy Assessment of 3DGV
3.3. The Maps of 3DGV
4. Discussion
4.1. The Process of Tree Detection
4.2. Innovations and Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiong, Y.; Zhao, S.; Yan, C.; Qiu, G.; Sun, H.; Wang, Y.; Qin, L. A comparative study of methods for monitoring and assessing urban green space resources at multiple scales. Remote Sens. Land Resour. 2021, 33, 54–62. [Google Scholar]
- Kondo, M.C.; Fluehr, J.M.; McKeon, T.; Branas, C.C. Urban green space and its impact on human health. Int. J. Environ. Res. Public Health 2018, 15, 445. [Google Scholar] [CrossRef] [PubMed]
- Nath, T.K.; Han, S.S.Z.; Lechner, A.M. Urban green space and well-being in Kuala Lumpur, Malaysia. Urban For. Urban Green. 2018, 36, 34–41. [Google Scholar] [CrossRef]
- Bertram, C.; Rehdanz, K. The role of urban green space for human well-being. Ecol. Econ. 2015, 120, 139–152. [Google Scholar] [CrossRef]
- Richardson, E.A.; Pearce, J.; Mitchell, R.; Kingham, S. Role of physical activity in the relationship between urban green space and health. Public Health 2013, 127, 318–324. [Google Scholar] [CrossRef] [PubMed]
- Wolch, J.R.; Byrne, J.; Newell, J.P. Urban green space, public health, and environmental justice: The challenge of making cities ‘just green enough’. Landsc. Urban Plan. 2014, 125, 234–244. [Google Scholar] [CrossRef]
- Dobbs, C.; Kendal, D.; Nitschke, C. The effects of land tenure and land use on the urban forest structure and composition of Melbourne. Urban For. Urban Green. 2013, 12, 417–425. [Google Scholar] [CrossRef]
- Kendal, D.; Williams, N.S.G.; Williams, K.J.H. Drivers of diversity and tree cover in gardens, parks and streetscapes in an Australian city. Urban For. Urban Green. 2012, 11, 257–265. [Google Scholar] [CrossRef]
- Chen, Z. Research on the ecological benefits of urban landscaping in Beijing (2). China Gard. 1998, 14, 51–54. [Google Scholar]
- Zhou, J.H. Research on the green quantity group of urban living environment (5)—Research on greening 3D volume and its application. China Gard. 1998, 14, 61–63. [Google Scholar]
- Zhou, T.; Luo, H.; Guo, D. Remote sensing image based quantitative study on urban spatial 3D Green Quantity Virescence three dimension quantity. Acta Ecol. Sin. 2005, 25, 415–420. [Google Scholar]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Williams, J.; Schonlieb, C.-B.; Swinfield, T.; Lee, J.; Cai, X.; Qie, L.; Coomes, D.A. 3D Segmentation of Trees Through a Flexible Multiclass Graph Cut Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 754–776. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, S.; Chu, S.; Li, S.; Yuan, Y.; Wang, Y.; Li, M. LiDAR-based three-dimensional street landscape indices for urban habitability. Earth Sci. Inform. 2017, 10, 457–470. [Google Scholar] [CrossRef]
- He, C.; Convertino, M.; Feng, Z.; Zhang, S. Using LiDAR data to measure the 3D green biomass of Beijing urban forest in China. PLoS ONE 2013, 8, e75920. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, B.; Zhou, J.; Hu, C.; Tan, W.; Hu, Z.; Wu, J. Toward automatic estimation of urban green volume using airborne LiDAR data and high resolution remote sensing images. Front. Earth Sci. 2013, 7, 43–54. [Google Scholar] [CrossRef]
- Li, X.; Tang, L.; Peng, W.; Chen, J. Estimation method of urban green space living vegetation volume based on backpack light detection and ranging. Chin. J. Appl. Ecol. 2021, 33, 2777–2784. [Google Scholar]
- Wang, J.; Yang, H.; Feng, Z. Tridimensional Green Biomass Measurement for Trees Using 3-D Laser Scanning. Trans. Chin. Soc. Agric. Mach. 2013, 44, 229–233. [Google Scholar]
- Cabo, C.; Del Pozo, S.; Rodríguez-Gonzálvez, P.; Ordóñez, C.; González-Aguilera, D. Comparing terrestrial laser scanning (TLS) and wearable laser scanning (WLS) for individual tree modeling at plot level. Remote Sens. 2018, 10, 540. [Google Scholar] [CrossRef]
- Huo, L.; Zhang, N.; Zhang, X.; Wu, Y. Tree defoliation classification based on point distribution features derived from single-scan terrestrial laser scanning data. Ecol. Indic. 2019, 103, 782–790. [Google Scholar] [CrossRef]
- Hyyppä, E.; Kukko, A.; Kaijaluoto, R.; White, J.C.; Wulder, M.A.; Pyörälä, J.; Liang, X.; Yu, X.; Wang, Y.; Kaartinen, H. Accurate derivation of stem curve and volume using backpack mobile laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 161, 246–262. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating individual tree height and diameter at breast height (DBH) from terrestrial laser scanning (TLS) data at plot level. Forests 2018, 9, 398. [Google Scholar] [CrossRef]
- Sun, Y. A Estimation Model of Tridimensional Green Biosmass Established on GF-2 Remote Sensing Data. Master’s Thesis, University of Geosciences, Beijing, China, 2017. [Google Scholar]
- Wang, P. The Esimation of Living Vegetation Volume in the Ring Park around Hefei City Based on TLS and Landsat8. Master’s Thesis, Anhui Agricultural University, Hefei, China, 2018. [Google Scholar]
- Xie, L.; Zhang, X.; Song, J. Estimation for tridimensional green biomass based on TM remote sensing image. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2015, 39, 104–108. [Google Scholar]
- Yi, Y.; Zhang, G.; Zhang, L. Research of 3D Green Quantity of Urban Vegetation Based on GF-2 Remote Sensing Image. Intell. Constr. Urban Green Space 2020, 2–7. [Google Scholar]
- Feng, Q.; Liu, J.; Gong, J. UAV Remote Sensing for Urban Vegetation Mapping Using Random Forest and Texture Analysis. Remote Sens. 2015, 7, 1074–1094. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; Peña, J.M.; de Castro, A.I.; López-Granados, F. Multi-temporal mapping of the vegetation fraction in early-season wheat fields using images from UAV. Comput. Electron. Agric. 2014, 103, 104–113. [Google Scholar] [CrossRef]
- Xu, E.; Guo, Y.; Chen, E.; Li, Z.; Zhao, L.; Liu, Q. Deep learning remote sensing estimation method (UnetR) for regional forest canopy closure combined with UAV LiDAR and high spatial resolution satellite remote sensing data. Geomat. Inf. Sci. Wuhan Univ. 2021, 47, 1298–1308. [Google Scholar]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR system with application to forest inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Xu, W.; Deng, S.; Liang, D.; Cheng, X. A crown morphology-based approach to individual tree detection in subtropical mixed broadleaf urban forests using UAV LiDAR data. Remote Sens. 2021, 13, 1278. [Google Scholar] [CrossRef]
- Zhou, L.; Meng, R.; Tan, Y.; Lv, Z.; Zhao, Y.; Xu, B.; Zhao, F. Comparison of UAV-based LiDAR and digital aerial photogrammetry for measuring crown-level canopy height in the urban environment. Urban For. Urban Green. 2022, 69, 127489. [Google Scholar] [CrossRef]
- Ge, H.; Xiang, H.; Ma, F.; Li, Z.; Qiu, Z.; Tan, Z.; Du, C. Estimating plant nitrogen concentration of rice through fusing vegetation indices and color moments derived from UAV-RGB images. Remote Sens. 2021, 13, 1620. [Google Scholar] [CrossRef]
- Li, L.; Chen, J.; Mu, X.; Li, W.; Yan, G.; Xie, D.; Zhang, W. Quantifying understory and overstory vegetation cover using UAV-based RGB imagery in forest plantation. Remote Sens. 2020, 12, 298. [Google Scholar] [CrossRef]
- Liang, Y.; Kou, W.; Lai, H.; Wang, J.; Wang, Q.; Xu, W.; Wang, H.; Lu, N. Improved estimation of aboveground biomass in rubber plantations by fusing spectral and textural information from UAV-based RGB imagery. Ecol. Indic. 2022, 142, 109286. [Google Scholar] [CrossRef]
- Marcial-Pablo, M.d.J.; Gonzalez-Sanchez, A.; Jimenez-Jimenez, S.I.; Ontiveros-Capurata, R.E.; Ojeda-Bustamante, W. Estimation of vegetation fraction using RGB and multispectral images from UAV. Int. J. Remote Sens. 2019, 40, 420–438. [Google Scholar] [CrossRef]
- Schiefer, F.; Kattenborn, T.; Frick, A.; Frey, J.; Schall, P.; Koch, B.; Schmidtlein, S. Mapping forest tree species in high resolution UAV-based RGB-imagery by means of convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2020, 170, 205–215. [Google Scholar] [CrossRef]
- Nykiel, G.; Barbasiewicz, A.; Widerski, T.; Daliga, K. The analysis of the accuracy of spatial models using photogrammetric software: Agisoft Photoscan and Pix4D. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 26. [Google Scholar]
- Amani, M.; Ghorbanian, A.; Ahmadi, S.A.; Kakooei, M.; Moghimi, A.; Mirmazloumi, S.M.; Moghaddam, S.H.A.; Mahdavi, S.; Ghahremanloo, M.; Parsian, S.; et al. Google Earth Engine Cloud Computing Platform for Remote Sensing Big Data Applications: A Comprehensive Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5326–5350. [Google Scholar] [CrossRef]
- Xu, W.; Feng, Z.; Su, Z.; Xu, H.; Jiao, Y.; Fan, J. Development and experiment of handheld digitalized and multi-functional forest measurement gun. Trans. Chin. Soc. Agric. Eng. 2013, 29, 90–99. [Google Scholar]
- Di Salvatore, U.; Marchi, M.; Cantiani, P. Single-tree crown shape and crown volume models for Pinus nigra J. F. Arnold in central Italy. Ann. For. Sci. 2021, 78, 76. [Google Scholar]
- Xu, W.; Su, Z.; Feng, Z.; Xu, H.; Jiao, Y.; Yan, F. Comparison of conventional measurement and LiDAR-based measurement for crown structures. Comput. Electron. Agric. 2013, 98, 242–251. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, J. Fast method to detect and calculate LVV. Acta Ecol. Sin. 2006, 26, 4204–4211. [Google Scholar]
- Liang, H.; Li, W.; Zhang, Q.; Zhu, W.; Chen, D.; Liu, J.; Shu, T. Using unmanned aerial vehicle data to assess the three-dimension green quantity of urban green space: A case study in Shanghai, China. Landsc. Urban Plan. 2017, 164, 81–90. [Google Scholar] [CrossRef]
- Chen, F.; Zhou, Z.X.; Xiao, R.B.; Wang, P.C.; Li, H.F.; Guo, E.X. Estimation of ecosystem services of urban green-land in industrial areas: A case study on green-land in the workshop area of the Wuhan Iron and Steel Company. Acta Ecol. Sin. 2006, 26, 2230–2236. [Google Scholar]
- Wang, X.; Wang, M.; Wang, S.; Wu, Y. Extraction of vegetation information from visible unmanned aerial vehicle images. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2015; 31, 152–159. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Zhang, T.; Zhang, L. Two phase Land Use Classification Method for Village scale UAV Imagery Based on Multi-features Fusion. Geomat. Spat. Inf. Technol. 2022, 45, 43–49. [Google Scholar]
- Hayes, M.M.; Miller, S.N.; Murphy, M.A. High-resolution landcover classification using Random Forest. Remote Sens. Lett. 2014, 5, 112–121. [Google Scholar] [CrossRef]
- Puissant, A.; Rougier, S.; Stumpf, A. Object-oriented mapping of urban trees using Random Forest classifiers. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 235–245. [Google Scholar] [CrossRef]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local maximum filtering for the extraction of tree locations and basal area from high spatial resolution imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, J.; Wang, Q. Mean-shift-based color segmentation of images containing green vegetation. Comput. Electron. Agric. 2009, 65, 93–98. [Google Scholar] [CrossRef]
- Luo, J.; Zhou, Y.; Leng, H.; Meng, C.; Hou, Z.; Song, T.; Hu, Z.; Zhang, C. Quick estimation of three-dimensional vegetation volume based on images from an unmanned aerial vehicle: A case study on Shanghai Botanical Garden. J. East China Norm. Univ. (Nat. Sci.) 2022, 2022, 122. [Google Scholar]
- Li, F.; Li, M.; Feng, X.-g. High-Precision Method for Estimating the Three-Dimensional Green Quantity of an Urban Forest. J. Indian Soc. Remote Sens. 2021, 49, 1407–1417. [Google Scholar] [CrossRef]
- Bai, M.; Zhang, C.; Chen, Q.; Wang, J.; Li, H.; Shi, X.; Tian, X.; Zhang, Y. Study on the Extraction of Individual Tree Height Based on UAV Visual Spectrum Remote Sensing. For. Resour. Manag. 2021, 1, 164. [Google Scholar]
- Bian, R.; Nian, Y.; Gou, X.; He, Z.; Tian, X. Analysis of Forest Canopy Height based on UAV LiDAR: A Case Study of Picea Crassifolia in the East and Central of the Qilian Mountains. Remote Sens. Technol. Appl. 2021, 36. [Google Scholar]
- Li, Q.; Zheng, J.; Zhou, H.; Shu, Y.; Xu, B. Three-dimensional green biomass measurement for individual tree using mobile two-dimensional laser scanning. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2018, 42, 127–132. [Google Scholar]




| Abbreviation | Meaning |
|---|---|
| H_FD | The tree height of measured field data. |
| H_CHM | The canopy height of CHM in our works. |
| MH_FD | The mean tree height derived from field data. |
| MCH_FD | The mean canopy height derived from field data. |
| 3DGV_FD | The 3DGV calculated by geometrical formulas. |
| 3DGV_Con | The 3DGV estimated based Convex hull algorithm. |
| 3DGV_Voxel | The 3DGV estimated based Voxel algorithm. |
| 3DGV_MNP | The 3DGV estimated based on the Mean neighboring of pixels algorithm. |
| Plots | Total Number | Plots Size/m2 | Vegetation Size/m |
|---|---|---|---|
| Arbor plots | 7 | 256 | Tree height > 3 |
| Shrub plots | 3 | 256 | Tree height < 3 |
| Individual trees | 31 |
| Tree Species | Geometrical Morphology | Calculation Equation | Description |
|---|---|---|---|
| Metasequoia glyptostroboides Hu and W. | cone | represents crown diameter and represents crown height. | |
| Salix babylonica L. Elaeis guineensis Jacq. | ovoid | ||
| Osmanthus fragrans Makino. Cinnamomum japonicum Sieb. Ficus microcarpa L.f. | sphere | ||
| Elaeocarpus decipiens Linn. Cycas revoluta Thunb. | flabellate |
| Vegetation Indices | Description |
|---|---|
| represent the three bands of red, green, blue, respectively reflectance. | |
| Texture Features | Description |
|---|---|
| is the gray level; and are the gray value of two neighboring resolution cells separated by the distance occurring in the image, respectively; stands for the times the number of the gray value and were neighbors; is the normalized gray value spatial dependence matrix. | |
| | |
| Classes | Vegetation | Non-Vegetation | UA/% |
|---|---|---|---|
| Vegetation | 1010 | 14 | 98.63 |
| Non-Vegetation | 18 | 1309 | 98.64 |
| PA/% | 98.24 | 98.94 | |
| OA/% | 98.64 | ||
| Kappa | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Z.; Xu, W.; Liu, Y.; Wang, L.; Ou, G.; Lu, N.; Dai, Q. Estimation of the Three-Dimension Green Volume Based on UAV RGB Images: A Case Study in YueYaTan Park in Kunming, China. Forests 2023, 14, 752. https://doi.org/10.3390/f14040752
Hong Z, Xu W, Liu Y, Wang L, Ou G, Lu N, Dai Q. Estimation of the Three-Dimension Green Volume Based on UAV RGB Images: A Case Study in YueYaTan Park in Kunming, China. Forests. 2023; 14(4):752. https://doi.org/10.3390/f14040752
Chicago/Turabian StyleHong, Zehu, Weiheng Xu, Yun Liu, Leiguang Wang, Guanglong Ou, Ning Lu, and Qinling Dai. 2023. "Estimation of the Three-Dimension Green Volume Based on UAV RGB Images: A Case Study in YueYaTan Park in Kunming, China" Forests 14, no. 4: 752. https://doi.org/10.3390/f14040752
APA StyleHong, Z., Xu, W., Liu, Y., Wang, L., Ou, G., Lu, N., & Dai, Q. (2023). Estimation of the Three-Dimension Green Volume Based on UAV RGB Images: A Case Study in YueYaTan Park in Kunming, China. Forests, 14(4), 752. https://doi.org/10.3390/f14040752







