Comparison of Global and Local Poisson Models for the Number of Recruitment Trees in Natural Forests
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Ground-Observed Data
2.3. Remote Sensing Data
2.4. Variable Selection
2.5. Poisson Regression (PR)
2.6. Linear Mixed Poisson Regression (LMPR)
2.7. Geographically Weighted Poisson Regression (GWPR)
2.8. Semiparametric GWPR (SGWPR)
2.9. Model Evaluation
3. Results
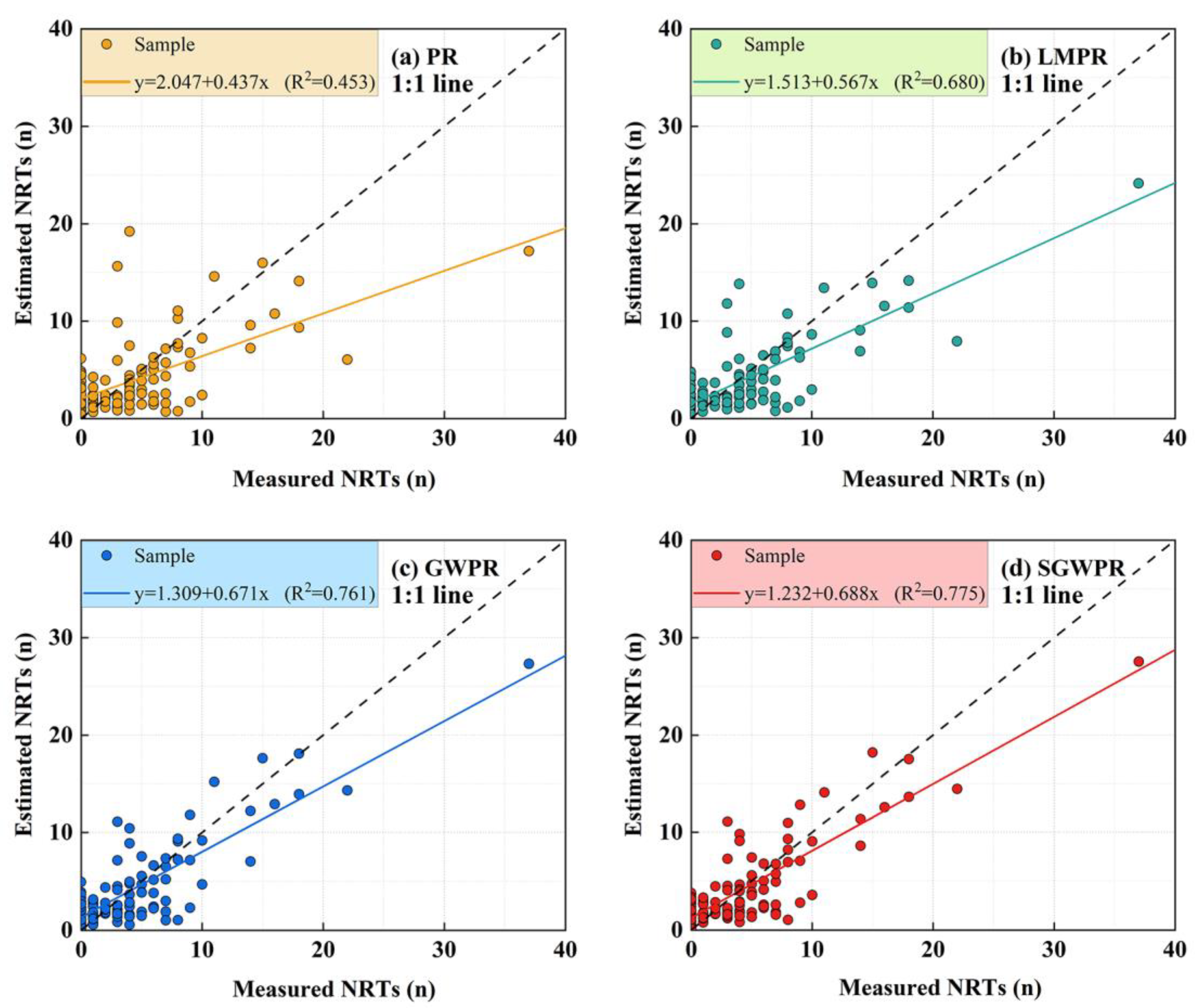
3.1. Parameter Estimation
3.2. Model Evaluation
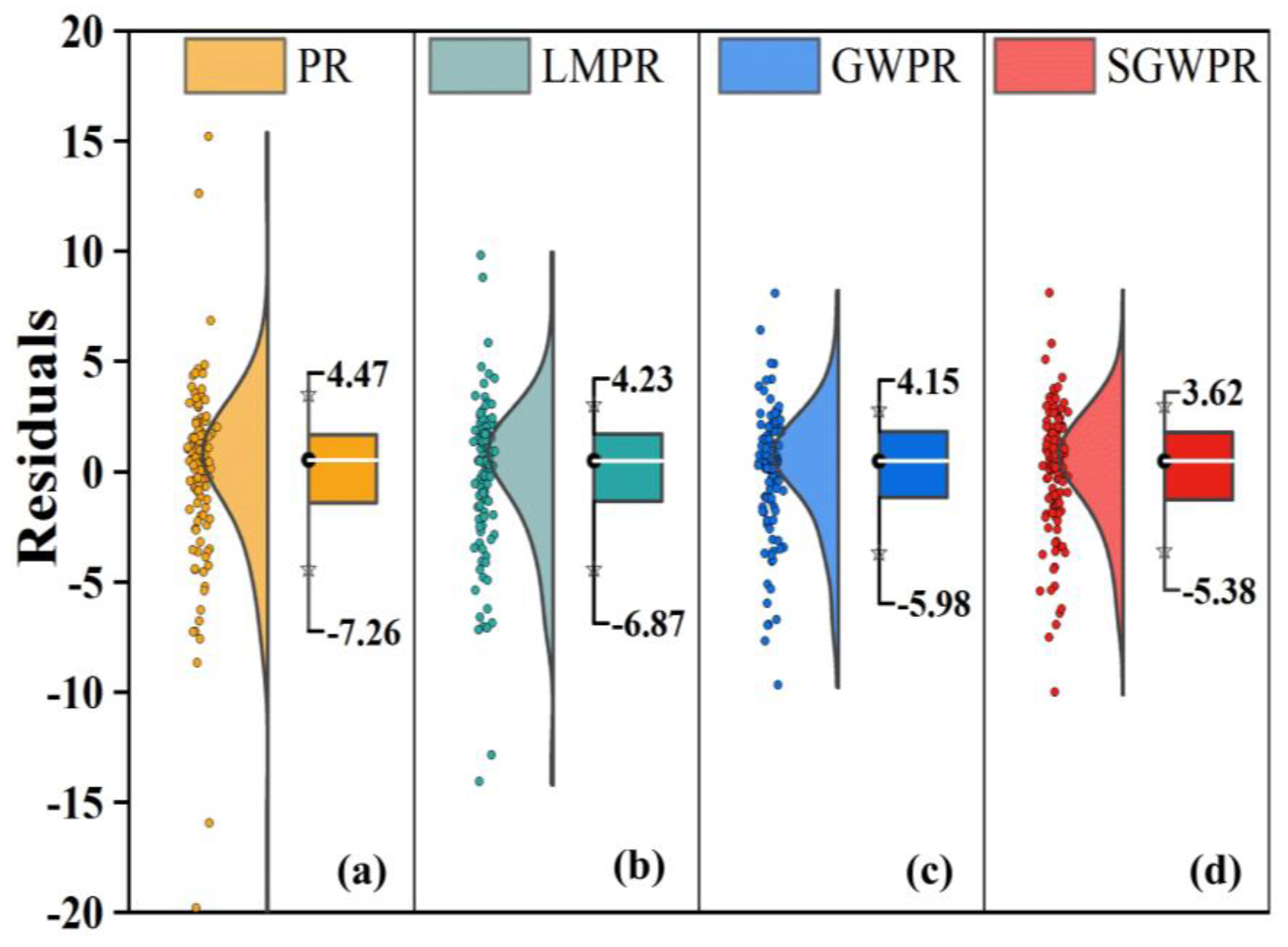
3.3. Residual Analysis
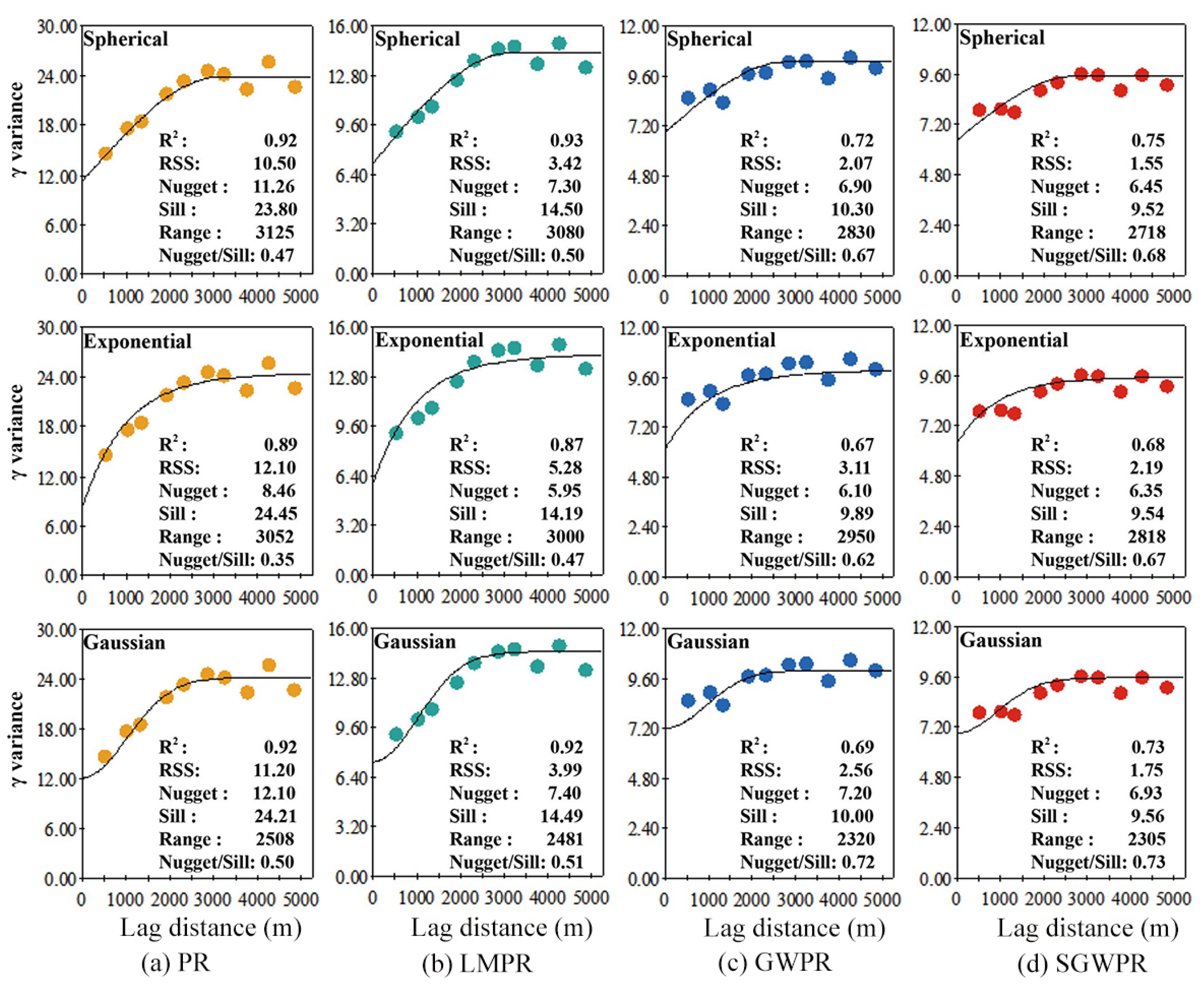
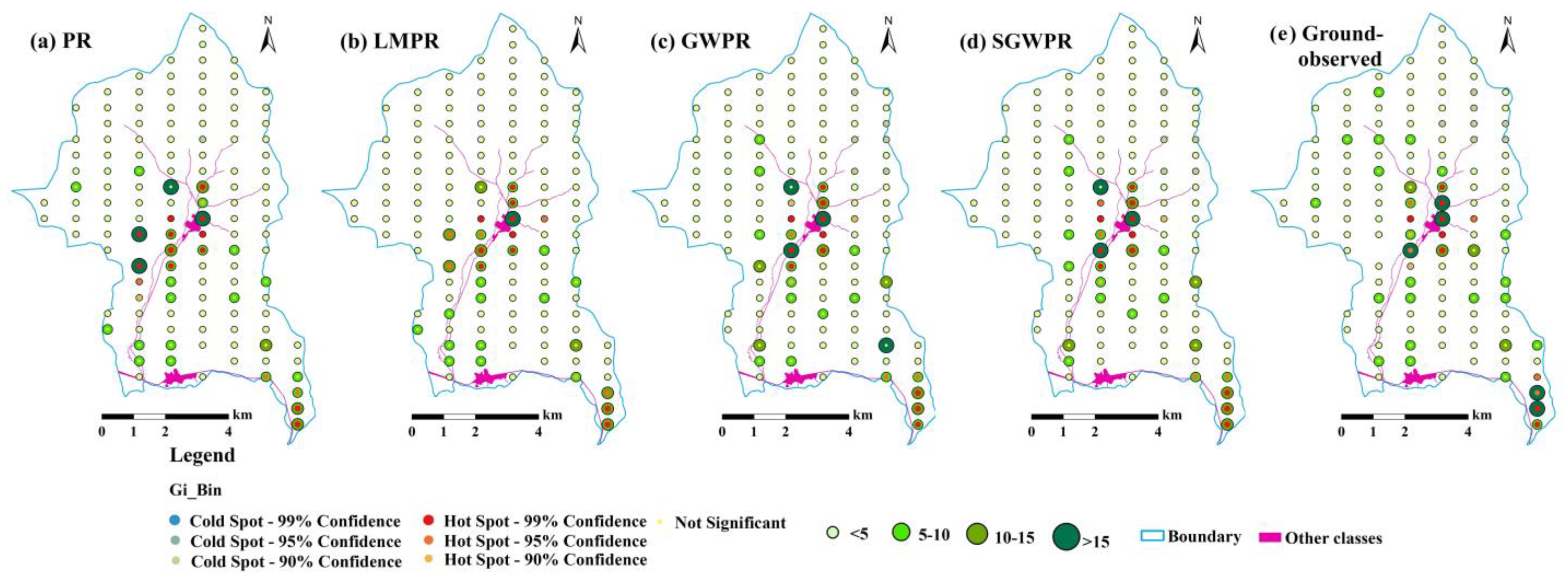
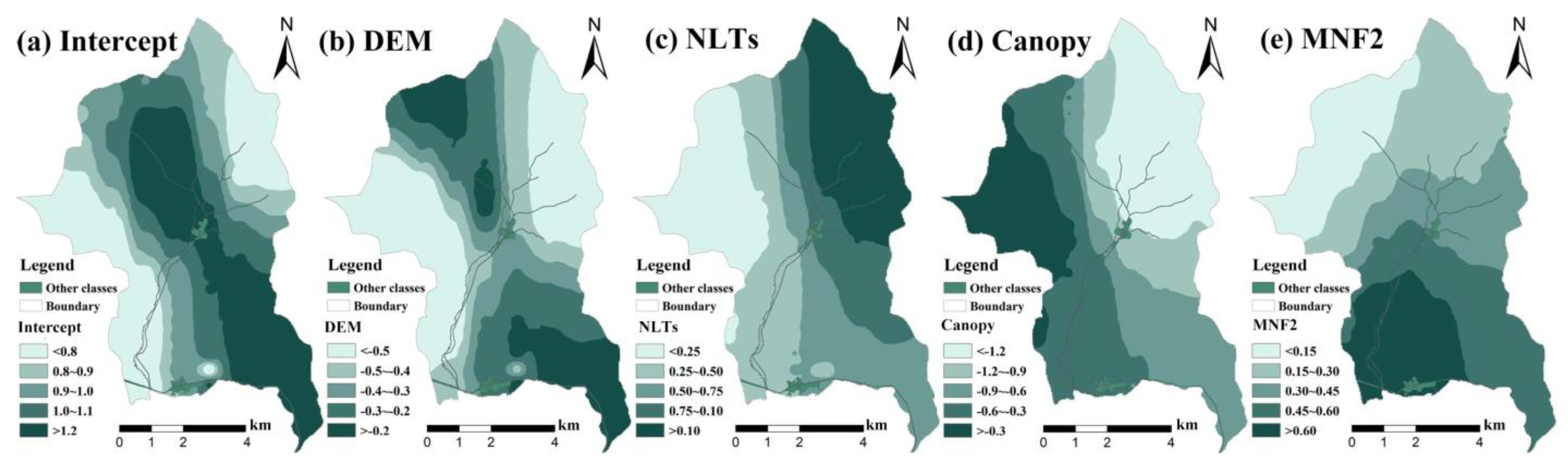
3.4. Visual Analysis
4. Discussion
4.1. Model Variables
4.2. Model Comparisons
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhen, Z.; Li, F.; Liu, Z.; Liu, C.; Zhao, Y.; Ma, Z.; Zhang, L. Geographically Local Modeling of Occurrence, Count, and Volume of Downwood in Northeast China. Appl. Geogr. 2013, 37, 114–126. [Google Scholar] [CrossRef]
- Chen, S.; Lu, N.; Fu, B.; Wang, S.; Deng, L.; Wang, L. Current and Future Carbon Stocks of Natural Forests in China. For. Ecol. Manag. 2022, 511, 120137. [Google Scholar] [CrossRef]
- Gauthier, M.; Guillemette, F.; Bédard, S. On the Relationship between Saplings and Ingrowth in Northern Hardwood Stands. For. Ecol. Manag. 2015, 358, 261–271. [Google Scholar] [CrossRef]
- Fortin, M.; DeBlois, J. Modeling Tree Recruitment with Zero-Inflated Models: The Example of Hardwood Stands in Southern Quebec, Canada. For. Sci. 2007, 53, 529–539. [Google Scholar]
- Xiang, W.; Lei, X.; Zhang, X. Modelling Tree Recruitment in Relation to Climate and Competition in Semi-Natural Larix-Picea-Abies Forests in Northeast China. For. Ecol. Manag. 2016, 382, 100–109. [Google Scholar] [CrossRef]
- Zhang, X.; Lei, Y.; Cai, D.; Liu, F. Predicting Tree Recruitment with Negative Binomial Mixture Models. For. Ecol. Manag. 2012, 270, 209–215. [Google Scholar] [CrossRef]
- Silla, F.; Camison, A.; Solana, A.; Hernandez, H.; Rios, G.; Cabrera, M.; Lopez, D.; Morera-Beita, A. Does the Persistence of Sweet Chestnut Depend on Cultural Inputs? Regeneration, Recruitment, and Mortality in Quercus- and Castanea-Dominated Forests. Ann. For. Sci. 2018, 75, 95. [Google Scholar] [CrossRef]
- Manso, R.; Ligot, G.; Fortin, M. A Recruitment Model for Beech-Oak Pure and Mixed Stands in Belgium. Forestry 2020, 93, 124–132. [Google Scholar] [CrossRef]
- Pardos, M.; Madrigal, G.; de Dios-García, J.; Gordo, J.; Calama, R. Sapling Recruitment in Mixed Stands in the Northern Plateau of Spain: A Patch Model Approach. Trees-Struct. Funct. 2021, 35, 2043–2058. [Google Scholar] [CrossRef]
- Russell, M.B.; Westfall, J.A.; Woodall, C.W. Modeling Browse Impacts on Sapling and Tree Recruitment across Forests in the Northern United States. Can. J. For. Res. 2017, 47, 1474–1481. [Google Scholar] [CrossRef]
- Russell, M.B. Influence of Prior Distributions and Random Effects on Count Regression Models: Implications for Estimating Standing Dead Tree Abundance. Environ. Ecol. Stat. 2015, 22, 145–160. [Google Scholar] [CrossRef]
- Zhang, X.-Q.; Lei, Y.-C.; Liu, X.-Z. Modeling Stand Mortality Using Poisson Mixture Models with Mixed-Effects. iForest 2015, 8, 333–338. [Google Scholar] [CrossRef]
- Zhou, X.; Fu, L.; Sharma, R.P.; He, P.; Lei, Y.; Guo, J. Generalized or General Mixed-Effect Modelling of Tree Morality of Larix Gmelinii Subsp. Principis-Rupprechtii in Northern China. J. For. Res. 2021, 32, 2447–2458. [Google Scholar] [CrossRef]
- Wei, Q.; Zhang, L.; Duan, W.; Zhen, Z. Global and Geographically and Temporally Weighted Regression Models for Modeling PM2.5 in Heilongjiang, China from 2015 to 2018. Int. J. Environ. Res. Public. Health 2019, 16, 5107. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Ma, Z.; Guo, L. An Evaluation of Spatial Autocorrelation and Heterogeneity in the Residuals of Six Regression Models. For. Sci. 2009, 55, 533–548. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Foody, G.M. Geographical Weighting as a Further Refinement to Regression Modelling: An Example Focused on the NDVI-Rainfall Relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E.J. Predictive Relations of Tropical Forest Biomass from Landsat TM Data and Their Transferability between Regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Propastin, P.A. Spatial Non-Stationarity and Scale-Dependency of Prediction Accuracy in the Remote Estimation of LAI over a Tropical Rainforest in Sulawesi, Indonesia. Remote Sens. Environ. 2009, 113, 2234–2242. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Zhang, L.; Bi, H.; Cheng, P.; Davis, C.J. Modeling Spatial Variation in Tree Diameter–Height Relationships. For. Ecol. Manag. 2004, 189, 317–329. [Google Scholar] [CrossRef]
- Sun, Y.; Ao, Z.; Jia, W.; Chen, Y.; Xu, K. A Geographically Weighted Deep Neural Network Model for Research on the Spatial Distribution of the down Dead Wood Volume in Liangshui National Nature Reserve (China). iForest 2021, 14, 353–361. [Google Scholar] [CrossRef]
- Sun, Y.; Jia, W.; Zhu, W.; Zhang, X.; Saidahemaiti, S.; Hu, T.; Guo, H. Local Neural-Network-Weighted Models for Occurrence and Number of down Wood in Natural Forest Ecosystem. Sci. Rep. 2022, 12, 6375. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Sun, Y.; Jia, W.; Wang, F.; Guo, H.; Ao, Z. Research on the Temporal and Spatial Distributions of Standing Wood Carbon Storage Based on Remote Sensing Images and Local Models. Forests 2022, 13, 346. [Google Scholar] [CrossRef]
- Propastin, P. Modifying Geographically Weighted Regression for Estimating Aboveground Biomass in Tropical Rainforests by Multispectral Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 82–90. [Google Scholar] [CrossRef]
- Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Marais Sicre, C.; Le Dantec, V.; Demarez, V. Estimating Maize Biomass and Yield over Large Areas Using High Spatial and Temporal Resolution Sentinel-2 like Remote Sensing Data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 Imagery for Forest Variable Prediction in Boreal Region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- SNAP. Sentinels Application Platform, Software Version 4.0.0; European Space Agency: Paris, France, 2016. [Google Scholar]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Xi, Y. Estimation of Forest Above-Ground Biomass by Geographically Weighted Regression and Machine Learning with Sentinel Imagery. Forests 2018, 9, 582. [Google Scholar] [CrossRef]
- Puliti, S.; Breidenbach, J.; Schumacher, J.; Hauglin, M.; Klingenberg, T.F.; Astrup, R. Above-Ground Biomass Change Estimation Using National Forest Inventory Data with Sentinel-2 and Landsat. Remote Sens. Environ. 2021, 265, 112644. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Chen, Z. Comparison of Broad-Band and Narrow-Band Red and near-Infrared Vegetation Indices. Remote Sens. Environ. 1995, 54, 38–48. [Google Scholar] [CrossRef]
- Myneni, R.B.; Tucker, C.J.; Asrar, G.; Keeling, C.D. Interannual Variations in Satellite-Sensed Vegetation Index Data from 1981 to 1991. J. Geophys. Res. Atmos. 1998, 103, 6145–6160. [Google Scholar] [CrossRef]
- Salas, E.A.L.; Henebry, G.M. A New Approach for the Analysis of Hyperspectral Data: Theory and Sensitivity Analysis of the Moment Distance Method. Remote Sens. 2014, 6, 20–41. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Examining the Potential of Sentinel-2 MSI Spectral Resolution in Quantifying above Ground Biomass across Different Fertilizer Treatments. ISPRS J. Photogramm. Remote Sens. 2015, 110, 55–65. [Google Scholar] [CrossRef]
- Haralick, R.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC3, 610–621. [Google Scholar] [CrossRef]
- Yang, C.; Lu, L.; Lin, H.; Guan, R.; Shi, X.; Liang, Y. A Fuzzy-Statistics-Based Principal Component Analysis (FS-PCA) Method for Multispectral Image Enhancement and Display. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3937–3947. [Google Scholar] [CrossRef]
- Wulder, M.A.; Franklin, S.E.; Lavigne, M.B. High Spatial Resolution Optical Image Texture for Improved Estimation of Forest Stand Leaf Area Index. Can. J. Remote Sens. 1996, 22, 441–449. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved Forest Biomass Estimates Using ALOS AVNIR-2 Texture Indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
- Klopcic, M.; Poljanec, A.; Boncina, A. Modelling Natural Recruitment of European Beech (Fagus sylvatica L.). For. Ecol. Manag. 2012, 284, 142–151. [Google Scholar] [CrossRef]
- Axer, M.; Martens, S.; Schlicht, R.; Wagner, S. Modelling Natural Regeneration of European Beech in Saxony, Germany: Identifying Factors Influencing the Occurrence and Density of Regeneration. Eur. J. For. Res. 2021, 140, 947–968. [Google Scholar] [CrossRef]
- Guisan, A.; Edwards, T.C.; Hastie, T. Generalized Linear and Generalized Additive Models in Studies of Species Distributions: Setting the Scene. Ecol. Model. 2002, 157, 89–100. [Google Scholar] [CrossRef]
- Podur, J.J.; Martell, D.L.; Stanford, D. A Compound Poisson Model for the Annual Area Burned by Forest Fires in the Province of Ontario. Environmetrics 2010, 21, 457–469. [Google Scholar] [CrossRef]
- Ma, Z.; Zuckerberg, B.; Porter, W.F.; Zhang, L. Spatial Poisson Models for Examining the Influence of Climate and Land Cover Pattern on Bird Species Richness. For. Sci. 2012, 58, 61–74. [Google Scholar] [CrossRef]
- Schabenberger, O. Introducing the GLIMMIX Procedure for Generalized Linear Mixed Models. Statistics and Data Analysis. Statistics and Data Analysis. SUGI 2008, 30, 196–230. [Google Scholar]
- Zhang, L.; Gove, J.H.; Heath, L.S. Spatial Residual Analysis of Six Modeling Techniques. Ecol. Model. 2005, 186, 154–177. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, L. Comparison of Spatial and Non-Spatial Logistic Regression Models for Modeling the Occurrence of Cloud Cover in North-Eastern Puerto Rico. Appl. Geogr. 2013, 37, 52–62. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, L.; Liu, J. A New Spatial-Attribute Weighting Function for Geographically Weighted Regression. Can. J. For. Res. 2006, 36, 996–1005. [Google Scholar] [CrossRef]
- Griffith, D.A. Spatial-Filtering-Based Contributions To A Critique Of Geographically Weighted Regression (Gwr). Environ. Plan. 2008, 40, 2751–2769. [Google Scholar] [CrossRef]
- Usman, U.; Yelwa, S.A.; Gulumbe, S.U.; Danbaba, A. Modelling Relationship between NDVI and Climatic Variables Using Geographically Weighted Regression. J. Math. Sci. Appl. 2013, 1, 24–28. [Google Scholar] [CrossRef]
- Shin, J.; Temesgen, H.; Strunk, J.L.; Hilker, T. Comparing Modeling Methods for Predicting Forest Attributes Using LiDAR Metrics and Ground Measurements. Can. J. Remote Sens. 2016, 42, 739–765. [Google Scholar] [CrossRef]
- Nakaya, T. Geographically Weighted Generalised Linear Modelling. In Geocomputation: A Practical Primer; SAGE Publications Ltd.: New York, NY, USA, 2015; pp. 201–220. ISBN 978-1-4462-7292-3. [Google Scholar]
- Anselin, L. Spatial Effects in Econometric Practice in Environmental and Resource Economics. Am. J. Agric. Econ. 2001, 83, 705–710. [Google Scholar] [CrossRef]
- de Jong, P.; Sprenger, C.; van Veen, F. On Extreme Values of Moran’s I and Geary’s c. Geogr. Anal. 1984, 16, 17–24. [Google Scholar] [CrossRef]
- Sawada, M. Rookcase: An Excel 97/2000 Visual Basic (VB) Add-in for Exploring Global and Local Spatial Autocorrelation. Bull. Ecol. Soc. Am. 1999, 80, 231–234. [Google Scholar] [CrossRef]
- Hu, T.; Sun, Y.; Jia, W.; Li, D.; Zou, M.; Zhang, M. Study on the Estimation of Forest Volume Based on Multi-Source Data. Sensors 2021, 21, 7796. [Google Scholar] [CrossRef]
- Barnes, R.J. The Variogram Sill and the Sample Variance. Math. Geol. 1991, 23, 673–678. [Google Scholar] [CrossRef]
- Solana-Gutiérrez, J.; Merino-de-Miguel, S. A Variogram Model Comparison for Predicting Forest Changes. Procedia Environ. Sci. 2011, 7, 383–388. [Google Scholar] [CrossRef]
- Bachmaier, M.; Backes, M. Variogram or Semivariogram? Understanding the Variances in a Variogram. Precis. Agric. 2008, 9, 173–175. [Google Scholar] [CrossRef]
- Strîmbu, V.F.; Ene, L.T.; Næsset, E. Spatially Consistent Imputations of Forest Data under a Semivariogram Model. Can. J. For. Res. 2016, 46, 1145–1156. [Google Scholar] [CrossRef]
- Propastin, P. Multiscale Analysis of the Relationship between Topography and Aboveground Biomass in the Tropical Rainforests of Sulawesi, Indonesia. Int. J. Geogr. Inf. Sci. 2011, 25, 455–472. [Google Scholar] [CrossRef]
- Sprintsin, M.; Karnieli, A.; Berliner, P.; Rotenberg, E.; Yakir, D.; Cohen, S. The Effect of Spatial Resolution on the Accuracy of Leaf Area Index Estimation for a Forest Planted in the Desert Transition Zone. Remote Sens. Environ. 2007, 109, 416–428. [Google Scholar] [CrossRef]
- Taureau, F.; Robin, M.; Proisy, C.; Fromard, F.; Imbert, D.; Debaine, F. Mapping the Mangrove Forest Canopy Using Spectral Unmixing of Very High Spatial Resolution Satellite Images. Remote Sens. 2019, 11, 367. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.; Brunsdon, C. Two Techniques for Exploring Non-Stationarity in Geographical Data. Geogr. Syst. 1997, 4, 59–82. [Google Scholar]
- Demšar, U.; Fotheringham, S.A.; Charlton, M. Combining Geovisual Analytics with Spatial Statistics: The Example of Geographically Weighted Regression. Cartogr. J. 2008, 45, 182–192. [Google Scholar] [CrossRef]
- Packer, A.; Clay, K. Soil Pathogens and Prunus Serotina Seedling and Sapling Growth Near Conspecific Trees. Ecology 2003, 84, 108–119. [Google Scholar] [CrossRef]
- Peñuelas, J.; Ogaya, R.; Boada, M.; Jump, A.S. Migration, Invasion and Decline: Changes in Recruitment and Forest Structure in a Warming-Linked Shift of European Beech Forest in Catalonia (NE Spain). Ecography 2007, 30, 829–837. [Google Scholar] [CrossRef]
- Vitasse, Y.; Hoch, G.; Randin, C.F.; Lenz, A.; Kollas, C.; Körner, C. Tree Recruitment of European Tree Species at Their Current Upper Elevational Limits in the Swiss Alps. J. Biogeogr. 2012, 39, 1439–1449. [Google Scholar] [CrossRef]
- Dyderski, M.K.; Paź, S.; Frelich, L.E.; Jagodziński, A.M. How Much Does Climate Change Threaten European Forest Tree Species Distributions? Glob. Chang. Biol. 2018, 24, 1150–1163. [Google Scholar] [CrossRef]
- Jones, M.T.; Niemi, G.J.; Hanowski, J.M.; Regal, R.R. Poisson Regression: A Better Approach to Modeling Abundance Data. In Predicting Species Occurrences: Issues of Accuracy and Scale, 1st ed.; Scott, J.M., Heglund, P.J., Morrison, M.L., Haufler, J.B., Raphael, M.G., Wall, W.A., Samson, F.B., Eds.; Island Press: Washington, DC, USA, 2002; pp. 411–418. [Google Scholar]
- Rathbun, S.L.; Fei, S. A Spatial Zero-Inflated Poisson Regression Model for Oak Regeneration. Environ. Ecol. Stat. 2006, 13, 409. [Google Scholar] [CrossRef]
- Zuur, A.F.; Ieno, E.N.; Elphick, C.S. A Protocol for Data Exploration to Avoid Common Statistical Problems. Methods Ecol. Evol. 2010, 1, 3–14. [Google Scholar] [CrossRef]
- Li, R.; Weiskittel, A.R.; Kershaw, J.A. Modeling Annualized Occurrence, Frequency, and Composition of Ingrowth Using Mixed-Effects Zero-Inflated Models and Permanent Plots in the Acadian Forest Region of North America. Can. J. For. Res. 2011, 41, 2077–2089. [Google Scholar] [CrossRef]
- Cunningham, R.B.; Lindenmayer, D.B. Modeling Count Data of Rare Species: Some Statistical Issues. Ecology 2005, 86, 1135–1142. [Google Scholar] [CrossRef]
- Lindén, A.; Mäntyniemi, S. Using the Negative Binomial Distribution to Model Overdispersion in Ecological Count Data. Ecology 2011, 92, 1414–1421. [Google Scholar] [CrossRef]
- Kéry, M.; Royle, J.A.; Schmid, H. Modeling Avian Abundance from Replicated Counts Using Binomial Mixture Models. Ecol. Appl. 2005, 15, 1450–1461. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, Z.; Guo, L. Spatially Assessing Model Errors of Four Regression Techniques for Three Types of Forest Stands. Forestry 2008, 81, 209–225. [Google Scholar] [CrossRef]
- Zhang, L.; Gove, J.H. Spatial Assessment of Model Errors from Four Regression Techniques. For. Sci. 2005, 51, 334–346. [Google Scholar]
- Guo, H.; Jia, W.; Li, D.; Sun, Y. Modeling Knot Geometry from Scanned Images of Korean Pine Plantations. Can. J. For. Res. 2022, 52, 845–859. [Google Scholar] [CrossRef]
- Harris, P.; Brunsdon, C. Exploring Spatial Variation and Spatial Relationships in a Freshwater Acidification Critical Load Data Set for Great Britain Using Geographically Weighted Summary Statistics. Comput. Geosci. 2010, 36, 54–70. [Google Scholar] [CrossRef]
- Johnson, D.J.; Magee, L.; Pandit, K.; Bourdon, J.; Broadbent, E.N.; Glenn, K.; Kaddoura, Y.; Machado, S.; Nieves, J.; Wilkinson, B.E.; et al. Canopy Tree Density and Species Influence Tree Regeneration Patterns and Woody Species Diversity in a Longleaf Pine Forest. For. Ecol. Manag. 2021, 490, 119082. [Google Scholar] [CrossRef]
- Carl, G.; Kühn, I. Analyzing Spatial Autocorrelation in Species Distributions Using Gaussian and Logit Models. Ecol. Model. 2007, 207, 159–170. [Google Scholar] [CrossRef]
- Dormann, C.F.; McPherson, J.M.; Araújo, M.B.; Bivand, R.; Bolliger, J.; Carl, G.; Davies, R.G.; Hirzel, A.; Jetz, W.; Kissling, W.D.; et al. Methods to Account for Spatial Autocorrelation in the Analysis of Species Distributional Data: A Review. Ecography 2007, 30, 609–628. [Google Scholar] [CrossRef]
- Griffith, D.; Chun, Y. Spatial Autocorrelation and Spatial Filtering. In Handbook of Regional Science; Fischer, M.M., Nijkamp, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1477–1507. ISBN 978-3-642-23430-9. [Google Scholar]


| Remote Sensing Factors | Description | Abbreviation | |
|---|---|---|---|
| VI | Ratio VI | B8/B4 | RVI |
| Atmospheric Ratio VI | [B8 − (2 × B4 − B2)]/[B8 + (2 × B4 − B2)] | ARVI | |
| Difference VI | B8 − B4 | DVI | |
| Weighted Difference VI | B8 − 0.8 × B4 | WDVI | |
| Perpendicular VI | sin 45° × B8 − cos 45° × B4 | PVI | |
| Infrared Percentage VI | B8/(B8 + B4) | IPVI | |
| Normalized Difference VI | (B8 − B4)/(B8 − B4) | NDVI | |
| Soil-Adjusted VI | 1.5 × (B8 − B4)/8 × (B8 + B4 + 0.5) | SAVI | |
| Modified Soil-Adjusted VI | (2 − NDVI × WDVI) × (B8 − B4)/8 × (B8 + B4 + 1 − NDVI × WDVI) | MSAVI | |
| Modified Soil-Adjusted VI2 | 0.5 × (2 × (B8 + 1)) − sqrt[(2 × B8 + 1)2 − 8 × (B8 − B4)] | MSAVI2 | |
| Textural | Mean | B4 and B8 | MeanB4 and MeanB8 |
| Variance | B4 and B8 | VarB4 and VarB8 | |
| Homogeneity | B4 and B8 | HomoB4 and HomoB8 | |
| Contrast | B4 and B8 | ConB4 and ConB8 | |
| Entropy | B4 and B8 | EntrB4 and EntrB8 | |
| Second moment | B4 and B8 | SMB4 and SMB8 | |
| Correlation | B4 and B8 | CorrB4 and CorrB8 | |
| Image enhancement | Minimum noise fraction | The first three minimum noise fraction | MNF1, MNF2 and MNF3 |
| Principal component analysis | The first three principal components analysis | PCA1, PCA2 andPCA3 |
| Variable | Mean | Median | Std | Min | Max | CV | VIF |
|---|---|---|---|---|---|---|---|
| DEM (m) | 402.12 | 390.00 | 76.72 | 270.00 | 638.00 | 19.08 | 1.04 |
| Number of living trees (NLTs, nha-1) | 702.63 | 633.33 | 406.56 | 83.33 | 2716.67 | 57.86 | 1.79 |
| Canopy | 0.53 | 0.50 | 0.14 | 0.30 | 0.90 | 25.49 | 1.81 |
| IPVI | 0.78 | 0.78 | 0.06 | 0.69 | 0.89 | 7.031 | 1.02 |
| MeanB8 | 24.54 | 24.56 | 2.04 | 19.78 | 30.78 | 8.33 | 1.02 |
| MNF2 | 0.17 | 0.16 | 5.75 | 15.09 | 11.93 | 3422.25 | 1.02 |
| Number of recruitment trees (NRTs, n) | 3.73 | 2.00 | 5.29 | 0.00 | 37.00 | 141.79 | - |
| Models | Statistics | Intercept | DEM | NLTs | Canopy | IPVI | MeanB8 | MNF2 |
|---|---|---|---|---|---|---|---|---|
| PR | Estimate | 0.952 | −0.353 | 0.600 | −0.615 | −0.322 | −0.401 | 0.331 |
| p value | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | |
| LMPR | Estimate | 0.930 | −0.368 | 0.601 | −0.620 | −0.283 | −0.382 | 0.255 |
| p value | <0.0001 | 0.003 | <0.0001 | 0.002 | 0.005 | 0.016 | 0.047 | |
| GWPR | Mean | 0.947 | −0.468 | 0.643 | −0.686 | −0.248 | −0.372 | 0.271 |
| Min | 0.527 | −1.189 | −0.159 | −1.627 | −0.458 | −0.619 | −0.095 | |
| Q1 | 0.788 | −0.659 | 0.290 | −1.165 | −0.360 | −0.446 | 0.099 | |
| Median | 0.984 | −0.433 | 0.673 | −0.589 | −0.264 | −0.367 | 0.336 | |
| Q3 | 1.090 | −0.227 | 0.999 | −0.311 | −0.151 | −0.286 | 0.406 | |
| Max | 1.374 | −0.106 | 1.476 | 0.351 | 0.094 | −0.149 | 0.612 | |
| SGWPR | Mean | 0.944 | −0.455 | 0.645 | −0.693 | −0.306 | −0.377 | 0.239 |
| Min | 0.520 | −1.184 | −0.153 | −1.579 | −0.094 | |||
| Q1 | 0.746 | −0.632 | 0.302 | −1.170 | 0.113 | |||
| Median | 0.955 | −0.421 | 0.649 | −0.616 | 0.205 | |||
| Q3 | 1.123 | −0.223 | 1.043 | −0.308 | 0.393 | |||
| Max | 1.370 | −0.113 | 1.371 | 0.347 | 0.599 |
| ∆DOF | |||
|---|---|---|---|
| Intercept | 14.445 | 1.772 | −8.488 |
| DEM | 19.298 | 1.416 | −14.515 |
| NLTs | 38.787 | 1.282 | −34.449 |
| Canopy | 30.684 | 1.706 | −24.942 |
| IPVI | 8.798 | 2.514 | −0.427 |
| MeanB8 | 1.935 | 1.600 | 3.457 |
| MNF2 | 10.055 | 1.814 | −3.960 |
| Models | Training Set | Validation Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | AICc | BIC | R2 | RMSE | MAE | P% | |
| PR | 0.453 | 4.587 | 2.699 | 366.967 | 383.645 | 0.440 | 3.279 | 2.558 | 67.488 |
| LMPR | 0.695 | 3.429 | 2.287 | - | - | 0.450 | 3.248 | 2.534 | 68.587 |
| GWPR | 0.797 | 2.796 | 1.919 | 266.176 | 308.989 | 0.457 | 3.227 | 2.446 | 71.721 |
| SGWPR | 0.803 | 2.782 | 1.918 | 262.402 | 298.907 | 0.511 | 3.062 | 2.413 | 72.335 |
| Models | PR | LMPR | GWPR | SGWPR |
|---|---|---|---|---|
| Moran’s I | 0.196 | 0.092 | 0.021 | 0.011 |
| Z-statistic | 2.178 | 1.069 | 0.314 | 0.201 |
| p value | 0.029 | 0.285 | 0.754 | 0.841 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Jia, W.; Guo, H.; Zhang, X.; Wang, F.; Zhao, H.; Li, T.; Zhao, Z. Comparison of Global and Local Poisson Models for the Number of Recruitment Trees in Natural Forests. Forests 2023, 14, 739. https://doi.org/10.3390/f14040739
Sun Y, Jia W, Guo H, Zhang X, Wang F, Zhao H, Li T, Zhao Z. Comparison of Global and Local Poisson Models for the Number of Recruitment Trees in Natural Forests. Forests. 2023; 14(4):739. https://doi.org/10.3390/f14040739
Chicago/Turabian StyleSun, Yuman, Weiwei Jia, Haotian Guo, Xiaoyong Zhang, Fan Wang, Haiping Zhao, Tianyu Li, and Zipeng Zhao. 2023. "Comparison of Global and Local Poisson Models for the Number of Recruitment Trees in Natural Forests" Forests 14, no. 4: 739. https://doi.org/10.3390/f14040739
APA StyleSun, Y., Jia, W., Guo, H., Zhang, X., Wang, F., Zhao, H., Li, T., & Zhao, Z. (2023). Comparison of Global and Local Poisson Models for the Number of Recruitment Trees in Natural Forests. Forests, 14(4), 739. https://doi.org/10.3390/f14040739






