Next Article in Journal
Tree Genetics: Molecular and Functional Characterization of Genes
Next Article in Special Issue
Effect of Geometry Precision and Load Distribution on Branch Mechanical Response
Previous Article in Journal
Lessons from A Degradation of Planted Kandelia obovata Mangrove Forest in the Pearl River Estuary, China
Previous Article in Special Issue
Tomographic Images Generated from Measurements in Standing Trees Using Ultrasound and Postprocessed Images: Methodological Proposals for Cutting Velocity, Interpolation Algorithm and Confusion Matrix Metrics Focusing on Image Quality
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 14
Issue 3
10.3390/f14030533
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Experimental Test of Non-Destructive Methods to Assess the Anchorage of Trees

by
Andreas Detter
1,*,†,
Steffen Rust
2,† and
Oskars Krišāns
3
1
Brudi & Partner Tree Consult, Berengariastr. 9, 82131 Gauting, Germany
2
Faculty of Resource Management, University of Applied Science and Art, Büsgenweg 1A, 37077 Göttingen, Germany
3
Latvian State Forest Research Institute ‘Silava’, 111 Rigas Street, LV-2169 Salaspils, Latvia
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Forests 2023, 14(3), 533; https://doi.org/10.3390/f14030533
Submission received: 13 February 2023 / Revised: 2 March 2023 / Accepted: 7 March 2023 / Published: 8 March 2023
(This article belongs to the Special Issue Tree Stability and Tree Risk Analysis)
Browse Figures
Versions Notes

Abstract

:
More than 280 trees were uprooted in winching tests monitored by high resolution inclinometers at the base of the trees and a forcemeter mounted in the winching line. The dataset comprises trees growing on different urban and forest sites in Europe and North America and mainly consists of fifteen widespread tree species. For the first time, a large number of trees were measured non-destructively prior to uprooting failure, as commonly practiced by consulting arborists in static load tests. With these tests, the bending moment required to cause 0.25° root plate inclination (rotational stiffness) was determined and used to predict the strength of the root system from equations described in two evaluation methods currently used in arboriculture. The predictions were tested against the measured anchorage strength, i.e., the maximum bending moment that was required to uproot the trees. Both methods delivered good estimates, which indicates that rotational stiffness at 0.25° inclination of the stem base is a suitable proxy for anchorage strength. Both equations can be considered valid for assessing the likelihood of uprooting failure, as they systematically underestimate and rarely overestimate the actual resistance to failure of a tree’s root system. As a trend, the differences between predicted and measured anchorage strength were larger for small trees, for which the resistance of the root system was overcome at larger inclination angles. While the quality of the predictions differed for species, it did not differ between sites. The angles of stem inclination at which the anchorage strength was overcome for all trees in our dataset support models for the mechanics involved in uprooting failure that previously have been described only for conifers with a shallow root system.

1. Introduction

The failure of urban trees with root systems compromised by decay or mechanical damage (e.g., resulting from root severance [1,2]) can pose risks to significant targets, such as infrastructure and residents in urban settings [3,4]. Tree owners can be held liable for accidents caused by trees that have experienced root injury in cases where the effect on stability was not adequately assessed after the damage occurred.
Especially in urban sites, potential restrictions on root development and hints at former construction work are frequently evident in the trees’ rooting areas, causing considerable uncertainties with regard to the visual assessment of tree stability [5]. However, assessing the anchorage of a tree is very difficult, because neither the size of a particular tree’s root system nor the presence of below-ground damage to structural roots are ascertainable during a basic tree risk assessment [6].
Often, removal is recommended when a tree is observed to have significant root issues or when roots have been severed during construction work. While this mitigates risk, it removes the stream of valuable social, environmental, and economic benefits that a tree provides [7,8,9,10,11]. Moreover, removal may endanger the climbers who carry out the dismantling operations if the residual anchorage strength is not properly addressed prior to undertaking arboricultural work [12,13,14].
In forest stands, wind-induced forces may uproot trees during severe storms. The economic damage caused by such failures can be disastrous [15]. Below-ground damage to structural roots can often occur due to root decay, and may be caused by overloading during wind and snow loads or even by heavy impacts (e.g. during avalanches) [16,17]. New pathogens (e.g., Ash Dieback Disease, which is currently affecting ash trees in Europe) can dramatically reduce tree stability as well [18,19].
For decades, destructive tests have been used in forest science to assess tree stability and determine the best time for harvesting [20,21,22,23]. This procedure is not possible for individual urban trees. There, as well as in forestry, non-destructive tests could speed up and enlarge the experiments required to study stand stability, thereby informing management decisions.
Root systems are complex subterranean structures that direct a major portion of the wind load collected by the crown into the ground [24]. The mechanics of root and soil interaction have been the subject of biomechanical research for decades [25]. Conclusions are sometimes drawn from the architecture [26] or size [27] of root systems on tree stability; however, the validity of simple rules for required root zone diameter is questioned [28,29]. Furthermore, reliable detection of roots requires costly and damaging excavations, which often are impossible in urban sites [30].
Static load tests, as introduced by [31], are frequently utilized to non-destructively inform tree managers about the stability of trees with compromised root systems. The underlying hypothesis is that a tree’s resistance to uprooting can be assessed by applying and measuring a moderate non-destructive load with a winch, simultaneously monitoring the tree’s response with a high-precision inclinometer at the stem base, and extrapolating these data to determine the minimum anchorage strength of the root system [32,33,34]. Estimates of stability in storms are based on comparing this load bearing capacity with modeled wind loads for a tree at its actual location based on statistical wind data and local wind conditions [35].
The anchorage of trees has been studied in many scientific experiments (for an overview, see [24,25]), and has been modeled by several authors, e.g., [36,37,38]. Tree uprooting is often described as a progressive failure process that occurs in different stages [39], with a number of components playing different roles [22]. Rather early in the tipping process, the applied force cannot be increased beyond a maximum force (the tree’s anchorage strength) because the root–soil system yields. Afterwards, the tipping continues at gradually decreasing loads until the tree is completely uprooted [22,34,40,41]. When the change in stem base inclination does not exceed 0.5° during pulling tests, the process is fully reversible and can be considered non-destructive [22,42,43].
To date, there have been no studies testing and comparing the predictive abilities of the methods used in arboricultural static load tests [44,45] on a larger number of trees (though for a small study, cf. [46]). In this paper, we test the hypothesis that failure loads can be successfully estimated using the non-destructive range of pulling tests.
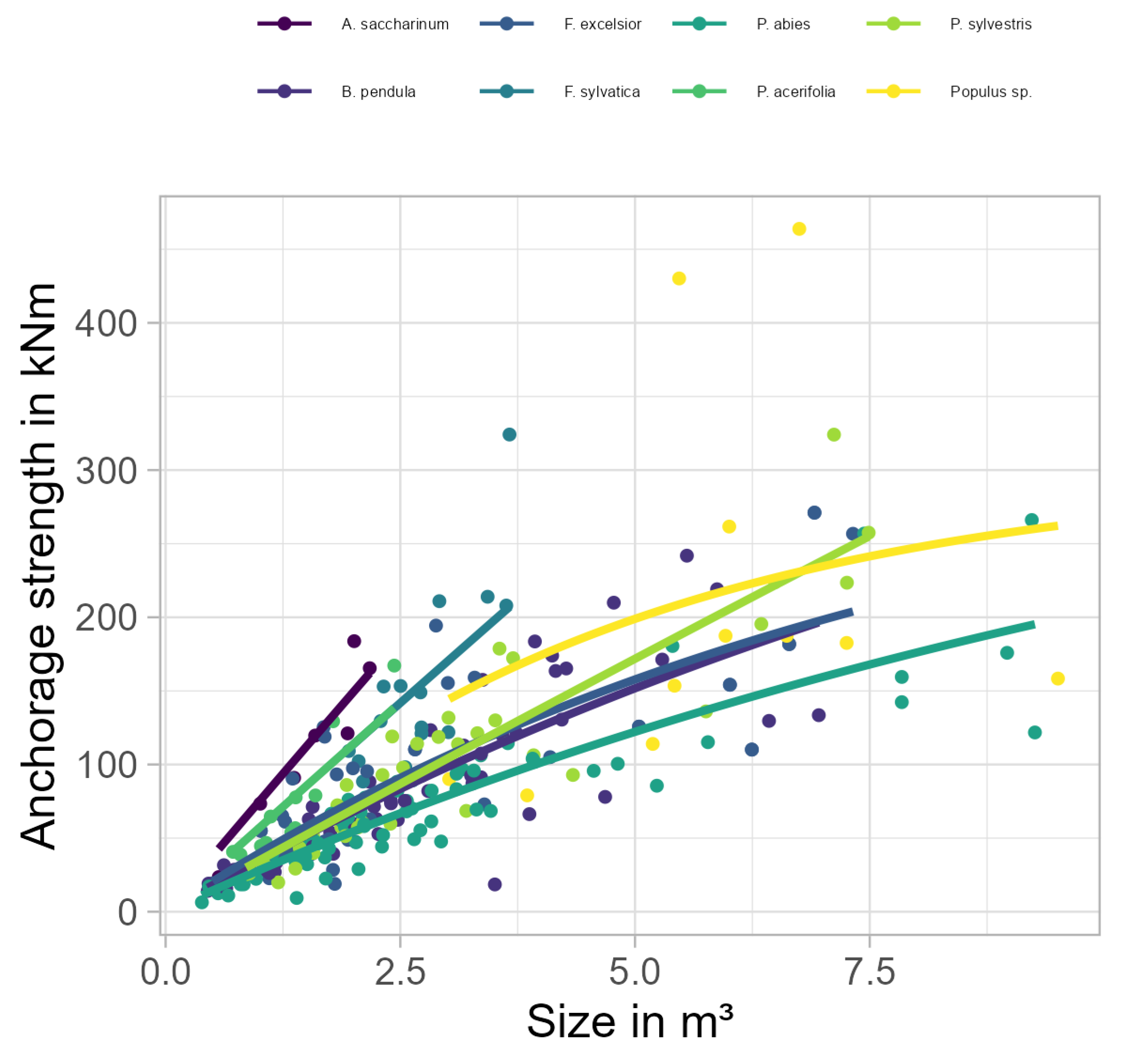
We compare the estimated anchorage strength with the measured resistance to uprooting failure for more than 280 trees of fifteen species frequently found in European and North American urban and peri-urban forests growing on a wide range of sites, including forests, parks, and roadsides.

2. Materials and Methods

The experiments described in this paper were undertaken at several sites across Germany, Austria, the USA, and Latvia between 2010 and 2019. Table 1 summarizes the trees used and lists their average diameter and height by species. All trees were pulled non-destructively to 0.25° of inclination at the stem base before being pulled to up-rooting failure. While the winching tests were underway, the applied force was measured continuously with a force meter (load cell) in the pulling line and the resulting root plate rotation ( ϕ ) was measured with a bi-axial inclinometer at the side of the stem base. The instruments used were part of the TreeQinetic system (IML Electronic GmbH, Rostock, Germany). The inclinometers had a resolution of 0.001° (accuracy 0.005°) and the forcemeter had a resolution of 0.1 kN (accuracy 0.3 kN). The rope angle from the horizontal was measured either using a digital level or using data provided by a built-in clinometer in the forcemeter.
The test was configured according to the Static Integrated Method or Pulling Test Method [31,33]. The applied force was converted into its lateral component by the cosine of the rope angle. The bending moment was determined as the product of the lateral force component (in kN) and the lever arm length as the vertical distance from the stem base to the anchor point of the rope (in m).
Prior to testing, tree crowns were removed to eliminate the influence of the unknown weight of the crown and to prevent errors caused by wind impact or branches becoming caught in adjacent trees. Anchorage strength ( M a ) was defined as the maximum bending moment that occurred during the winching tests. Within the non-destructive portion of the trials, the applied force and current rope angle were determined at an inclination of 0.25° and used to calculate the root–soil rotational stiffness ( k r ) as the respective bending moment at that instant (cf. [31,33]). The rotational stiffness k r was then used to estimate the anchorage strength M a according to two published methods: either multiplying rotational stiffness at 0.25° with a constant factor of 2.5 (Equation (1)) [34], or iteratively fitting the formula published by [45] (Equation (2)) to the data measured at 0.25° basal inclination in order to derive a prediction for M a .
M a = 2.5 k r
ϕ = 1 3 t a n ( M M a ) + 1 2 M M a 2 − 0.1 M M a
The first evaluation of our dataset showed strong deviations of the predictions generated by Equation (2) from the measured data [47]. The anchorage strength was systematically overestimated, which could potentially generate false positive results in tree stability assessments. After discussing this finding, F. Divos (pers. comm., 2019) provided a revised version of Equation (2), which was used for subsequent analyses in the present study:
ϕ = 1 3 t a n 100 M M a 73.85 + 1 2 M M a 2 − 0.09 M M a
The sample sizes in the results vary because Equations (2) and (3) could not be solved for M a analytically. Therefore, a fitting routine had to be applied to derive an estimate of M a from Equations (2) and (3), which was not always successful and sometimes generated unrealistically high results. Due to this problem, six trees had to be excluded from the dataset for Equations (2) and (3).
In several analyses, tree size is used as a parameter. In analogy to prior studies, size was calculated as the product of height and diameter at breast height squared.

Data Analysis

Data were analyzed using the R software environment for statistical computing and graphics [48]. Linear mixed-effects models were used to incorporate random effects of sites or repeated measurements of individual trees. Variance structures were adjusted to deal with heterogeneity. Results of analyses were added directly to graphics in concise form or printed in the appendix. Where species effects were analyzed, a subset of data with at least five individuals per species was used. Robust linear regression models were used, as OLS and model II (MA, RMA) assumptions were not satisfied.

3. Results

3.1. Indicators of Anchorage Strength

3.1.1. Tree Size

In our dataset, anchorage strength correlated significantly with tree size (Figure 1), and a linear model explained 80% of the variation (Table A1). The correlation was non-linear, as anchorage strength M a did not generally improve proportionally with increasing tree size. The slope differed significantly between species. The accuracy of estimations of anchorage strength based on tree size alone would therefore suffer from large residuals from the average and the implications of non-linear extrapolations, especially beyond the range of tree sizes contained in our dataset.

3.1.2. Soil–Root Rotational Stiffness k r

The fundamental principle of the static load test method for assessing the likelihood of uprooting in a storm is that the maximum restoring moment generated during the uprooting process (anchorage strength M a ) is related to properties measurable in the non-destructive range, here represented by the bending moment required to generate 0.25° of the stem base inclination (rotational stiffness). This hypothesis was true for the dataset presented here. For all species combined, anchorage strength was closely and linearly correlated with rotational stiffness measured at 0.25° change of inclination at the stem base (Figure 2).

3.2. Testing the Estimations of Anchorage Strength

3.2.1. Linear Extrapolation of Rotational Stiffness (Equation (1))

Using Equation (1), rotational stiffness k r (bending moment at 0.25°) is multiplied by a fixed factor of 2.5 to obtain values for estimated anchorage strength. Thus, the linear correlation and its statistical characteristics are very similar to Figure 2. However, in contrast to the algorithm proposed by [34], the slope (ratio of the bending moments at failure and at 0.25°) of a linear model without intercept differed significantly from 2.5 (2.95 ± 0.14 (se)), and the relationship was significantly non-linear for certain species (Figure 3). Multiplying rotational stiffness by a factor of 2.5 systematically underestimates anchorage strength, especially in small trees. For larger trees, the ratio approaches roughly 2.5 (Figure 4), which confirms that Equation (1) may be used for larger trees with greater accuracy than for small trees.

3.2.2. Non-Linear Extrapolation (Equation (3))

Fitting the formula of [45] to the first portion of the data resulted in a poor fit and systematic overestimation of anchorage strength (data not shown), while the corrected version (Equation (3)) produced an excellent fit (Figure 5). Again, the relationship was significantly nonlinear for certain species (Figure 6). For six trees, the fitting routine for Equation (3) failed or produced estimated bending moments beyond 1000 kNm which were considered unrealistic and were excluded from the dataset. This failure prevented the application of Equation (3) or would have generated a severe overestimation of anchorage strength if unnoticed. If the same failure rate persisted in arboricultural practice, Equation (3) would have to be replaced by other methods in more than 2% of non-destructive pulling tests to enable assessment of anchorage strength and the likelihood of uprooting.
It may be the case that urban trees cannot be pulled to a basal inclination of 0.25°. To test whether this affects the estimate of M a , we used subsets of the data limited to a range between 0.05° and 0.25°. This resulted in a highly significant interaction effect of the range of data used for the extrapolation and estimated M a . The further the maximum ϕ fell below 0.25°, the lower the estimate of M a was.

3.2.3. Comparison between Predictors

Both methods provided very similar results (Figure 7), with a coefficient of correlation of 0.97 and a slope of 1.05 ± 0.002 (se). The presence of a non-zero intercept indicates slightly different estimates for smaller trees.

3.3. Species Effect on Anchorage Strength

In our study, samples of individual tree species consisted of trees of different sizes on several different sites. Therefore, it was not possible to draw conclusions on the typical anchorage strength of trees from one species or on specific soil conditions directly. Instead, we scaled anchorage strength by tree size and plotted the results for nine tree species that were represented in our dataset with more than five samples. Here, the mean scaled anchorage strength of P. abies trees was much lower than that of B. pendula, F. excelsior, F. sylvatica, and P. sylvestris (Figure 8), even though average diameter and tree height were similar for those species (Table 1). The anchorage strength of Populus. sp. was towards the low end of the range after scaling for size, which was due to the fact that the mean diameter and height were the greatest in our dataset. On the contrary, trees of A. saccharinum in our dataset had a small diameter on average, and were rather short, which placed their mean scaled anchorage strength at the top of our sample. Rather than a species-dependent difference, the latter two results mirror only the more generic result that smaller trees have a higher scaled anchorage strength than larger trees.
P. abies again proved to be special when anchorage strength was compared to tree size separately for four individual tree species that contributed more than 25 samples each to our data set (Figure 1). While trees of the three other species (B. pendula, F. excelsior, P. sylvestris) showed consistent data with similar and rather linear correlations, for P. abies we found a much less linear correlation, with the anchorage strength falling below that of the other three species for trees of similar size.

4. Discussion

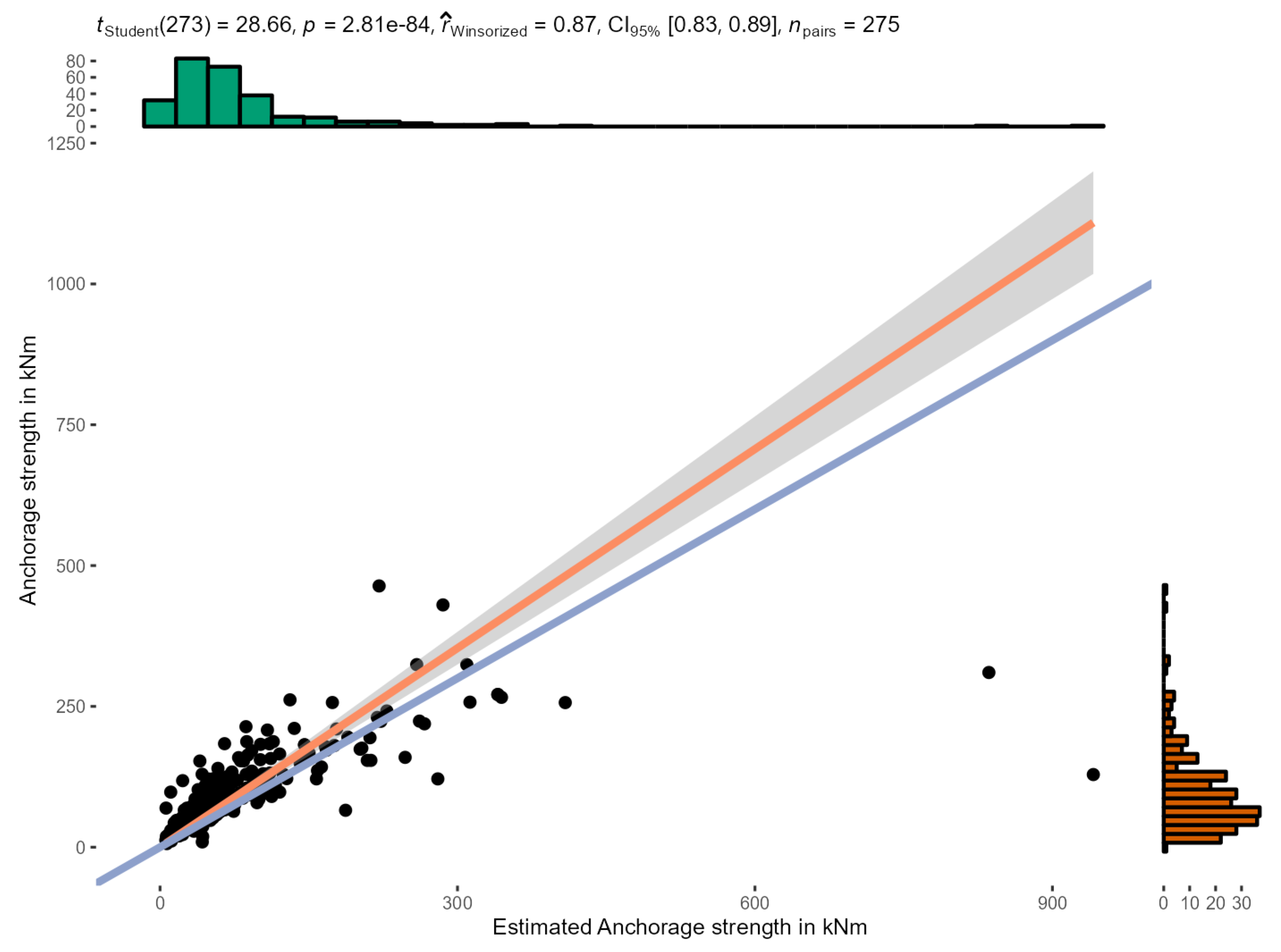
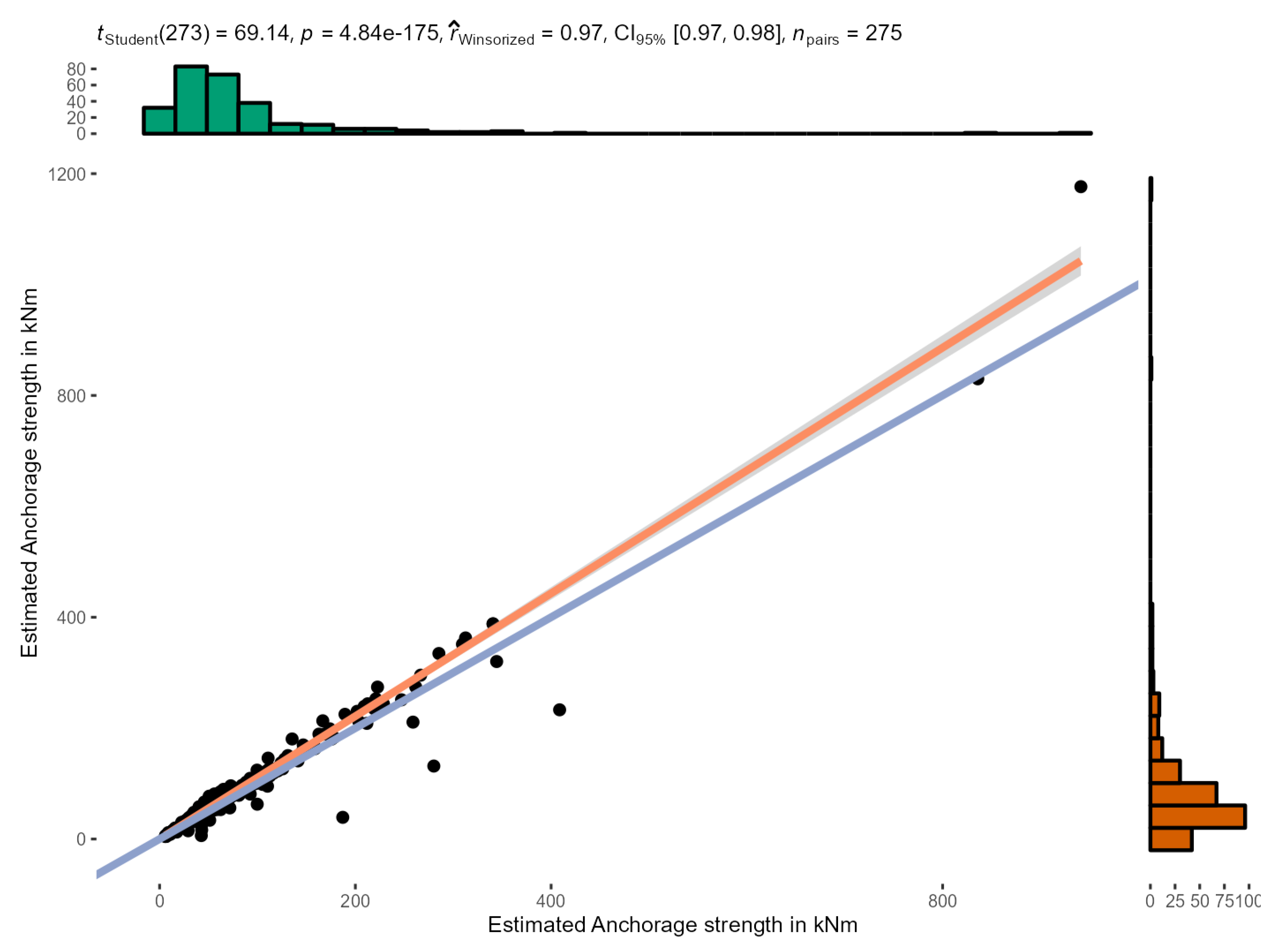
Our data show that both methods of evaluation can reliably extrapolate from non-destructive pulling tests to anchorage strength. They systematically underestimate anchorage strength by one third on average, providing users with a margin of safety for tree assessment. Especially in smaller trees, the errors are sometimes greater and may underrate the anchorage strength by a factor of up to two.
The critical bending moments measured in this study are comparable to many other reports [41,49,50,51,52,53], as is the correlation between anchorage and the parameters of tree size [53,54,55]. A nonlinear relationship between tree size and maximum bending moments has already been proposed by [54]. According to our results, the factor that should be used in a linear extrapolation (Equation (1)) approximates 2.5 with increasing tree size. Therefore, it is likely, that anchorage of trees larger than those in our sample can be assessed with pulling tests by applying Equation (1) as well. Yet, extrapolation beyond the range of tree sizes tested here must be treated with caution. An increased level of uncertainty should be balanced with adequate factors of safety when used in the context of risk assessments.
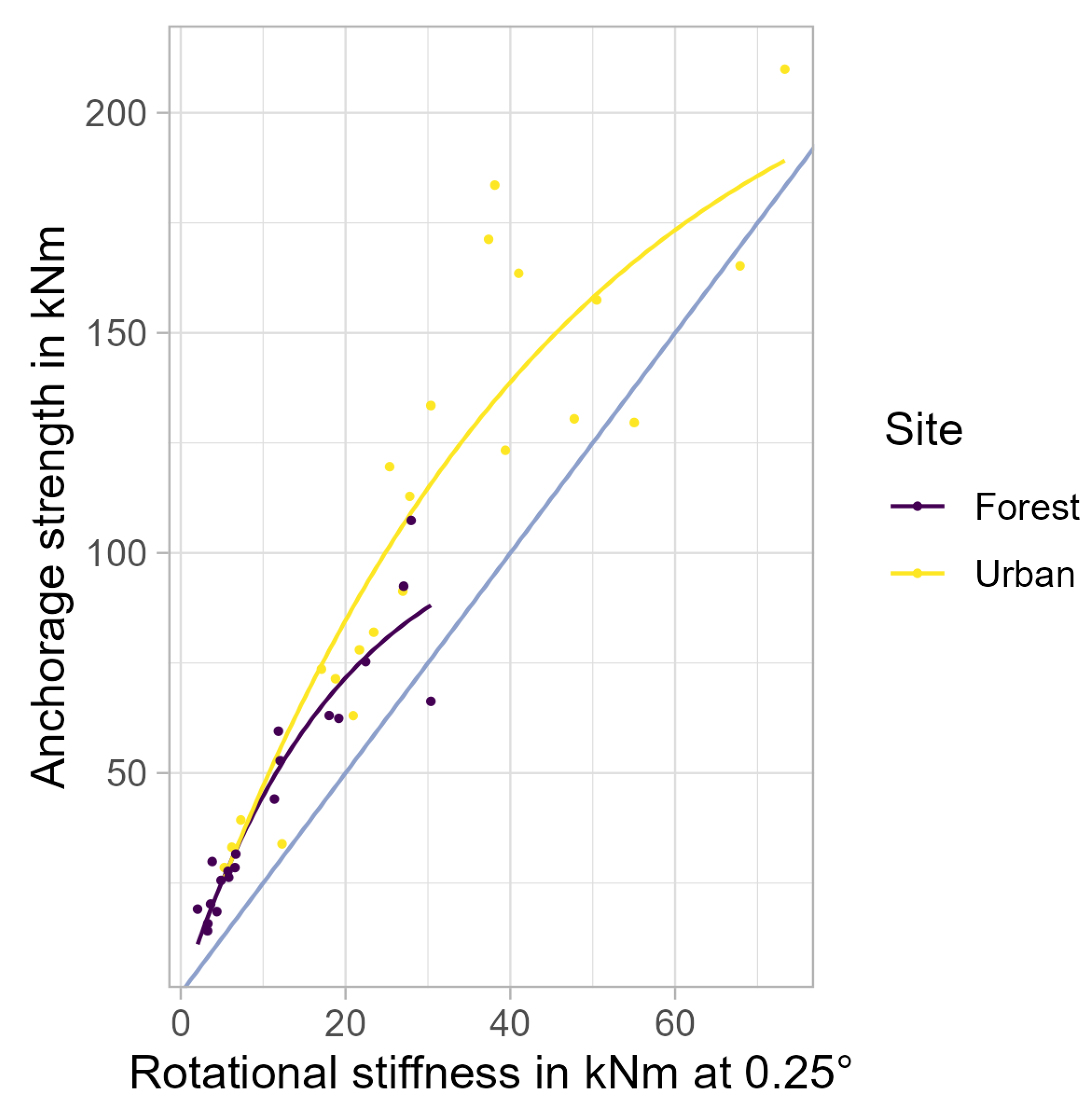
Trees were sampled on a wide range of sites, including forests, parks, and roadsides; there was no systematic difference in anchorage or in its extrapolation from non-destructive tests between urban and woodland trees, as illustrated for birch in Figure 9 and Table A2. Therefore, it seems viable to apply the findings from testing trees in forests to urban trees of similar size. Furthermore, we did not observe significant differences between sites with very different types of soil, such as loam and sand. In accordance with other sources [56], we did not find significant deviations in the extrapolation of anchorage strength from the non-destructive rotational stiffness on sites with high water table or others where the groundwater level had recently fallen [57]. Static load tests may therefore be applicable regardless of the growing site.
There were small but significant differences between tree species, several of which are represented only by small samples in this study. Further research could allow species- and size-specific models to be introduced that extrapolate anchorage strength from non-destructive pulling tests. The lack of data on certain species that are very common in urban areas as well as on species outside temperate regions should be addressed in subsequent studies. Yet, the present study illustrates for a wide range of temperate tree species that anchorage strength may be reliably estimated from measurements in the non-destructive range. The observed underestimation of the anchorage strength for trees of smaller size may stimulate adaptions in evaluation methods for pulling tests currently used in arboriculture.
Equation (1) allows linear extrapolation to be applied. A solution to Equation (3), however, can only be found by iteration, and bears the risk of providing a local instead of a global optimum. This should be safeguarded against in any practical application. Equation (1), on the contrary, requires the pulling test to be continued until 0.25° inclination is obtained. This may require the application of high forces, especially for larger trees, and often involves elaborate precautions with regard to occupational safety and accident prevention. Sufficient load-bearing capacity in all parts of the winching apparatus must be ensured.
Equation (3) allows for extrapolating from lower to higher degrees of inclination. Because lower maximum ϕ reduces the estimate of M a , the error is on the safe side for consultants; however, it could result in unnecessary measures, including tree removal. Currently, all established methods for pulling test evaluation are able to accommodate lower inclinations as well. In order to achieve this, they use unpublished mathematical functions [33] or statistical characteristics from a great number of pulling tests (Arbosafe GmbH, Training materials for mandatory Qualification Training for Licensing Arbostat Evaluation Software, 2008). Their reliability could be tested against our dataset, which could increase their credibility and improve their predictions.
Trees in our dataset reached their anchorage strength at rather low inclination. This is in accordance with findings by many other authors referred to earlier in this paper. As long as stem base rotation angles are very low, the roots on the windward side can hardly experience a high degree of tension, as the curvature of the soil surface is yet very small [58,59]. On all trees uprooted for this study, a visibly pronounced line formed directly next to the stem base on the side where the force was applied very early in the uprooting process. At this position, the soil did not sink in very much; instead, it kinked and behaved similar to a hinge. While the formation of a hinge has primarily been described for trees with shallow root systems of lateral and sinker roots [58,60], we found this to be typical for all tree species and soil types in our dataset. These observations may help to change the focus of risk assessments from defects located on the roots on the windward side only, which are exposed to tensile forces [27,61], to the structural integrity of the roots close to the stem base on the leeward side as well. This idea was postulated as early as in 1933 in forest research [62]; however, it is not yet widely acknowledged among consulting arborists.
As the anchorage strength is overcome early in the uprooting process, it is more likely that the roots located at the hinge yield than that the tensile strength of roots on the windward side is already exceeded at such low inclinations. Anchorage strength is mainly generated from roots close to the trunk [63] before they rapidly taper [26,64]. In response to wind loading, roots near the stem base experience great strains [65], grow in diameter within the Zone of Rapid Taper, and increase the rotational stiffness [66]. At the same time, this incremental growth improves the anchorage strength [67]. Our results confirm a strong correlation between rotational stiffness and anchorage strength. Therefore, the importance of the leeward hinge in providing anchorage for trees should be a subject of further research.
Trees of small size often fail at significantly higher degrees of basal inclination than 2.5° (Figure 10). This, together with the slight non-linearity in the relationship between rotational stiffness and anchorage, contradicts the notion of uniform tipping behavior for all trees, be presumed by the “generalized tipping curve” [44]. Our results indicate that this generalization may be based on a lower envelope of many tipping curves; the extrapolation from Equation (1) systematically underestimated the anchorage strength and, on average, the inclination at the stem base was greater than 2.5° when the anchorage strength was reached.
Originally, a graphical solution for application to tree stability assessments was used instead of a mathematical function [68]. Because the rotation angle continuously increases, while the restoring moment of the root system reaches a maximum and then gradually decreases again, any mathematical solution can only describe the first part of that curve where the load increases and must show asymptotic behavior against x = 1 . While Equation (3) mimics this behavior to a degree, it does not fulfill this requirement entirely. Therefore, errors are to be expected as loads approach the anchorage strength. For the non-destructive range, this does not necessarily cause critical deviations. Because Equations (1) and (3) often provide similar results, it is very likely that both were developed on the basis of a number of tipping curves, as stated for the ”generalized tipping curve” [34].
Our results support the general observation that the strength of younger trees is usually underrated in non-destructive pulling tests. The systematic underestimation of anchorage strength in pulling tests on small trees reaches a similar magnitude as the omission of pre-stresses [69,70,71,72] in assessing the bending strength of their stems (which is an integral part of the pulling test method [31]). This would explain why pulling tests on young trees often indicate low but similar safety margins against stem fracture and anchorage failure [73]. For anchorage strength, the contribution of those pre-stresses was never tested, tough it likely would not apply to a similar degree [74].
Why the extrapolations deviate for smaller trees is not obvious from our data. We suspect that this is due to changes in the flexural rigidity of the roots as their diameters increase. For larger trees, the diameter of roots at a certain distance from the stem may easily reach a multiple of root diameters found on smaller trees. Their resistance to bending is governed by the second moment of inertia of their cross-section, which for a circular shape increases with the fourth power of the diameter [75]. As long as the flexural stiffness of the roots is distinctly lower than soil stiffness, their presence does not increase the rigidity of the root plate, and only increases root plate size and weight because of cohesion and friction between the roots and soil. Therefore, as long as roots are rather small in diameter and very flexible, deformations of the root–soil matrix under load are governed by soil parameters, e.g., the weight of the soil held by the roots and the soil shear modulus, rather than the root architecture.
As a tree ages, the flexural stiffness of the roots grows exponentially. As soon as it exceeds soil stiffness, the overall rigidity of the root–soil matrix begins to gradually increase. This rigidity is tested in a non-destructive pulling test, and is described as a key trait for anchorage strength [76]. Through a three-dimensional network of more rigid roots, wind energy may be dissipated over a greater distance into the soil. Stiffer roots on the leeward side are able to withstand applied bending moments under smaller deflections, thereby distributing compressive forces over a larger area of the root–soil matrix. Soil is usually able to withstand compression much better than tension. Unless the stem splits, the lifting action on the windward side is restricted as long as roots on the leeward side do not yield [59]. Greater lifting than 2 to 4 cm on the opposite side of the force application, accompanied by stretching and tensile failure of roots, was only visible at loads clearly beyond the anchorage strength [22,77]. This is an indicator that the bending strength of the roots at the leeward hinge could be decisive for anchorage strength.
In the same respect, [22] reported that the rotation measured at the stem base was greater than the inclination of the root plate. To allow for such a difference, the curvature must be greatest close to the stem base, though not necessarily on both sides. Bending roots upwards on the windward side is only restricted by soil weight and cohesion, and usually occurs over a larger distance than any downward movement on the leeward side [22,77]. Here, the curvature of the roots is restricted by the low compactibility of the soil. Therefore, stresses are concentrated in the area close to the stem base, where the hinge forms during the uprooting process. Roots located here bend to the greatest degree where they rapidly taper, causing them to buckle and yield before the anchorage strength is overcome. At greater inclinations, these roots obviously break and are often truncated entirely [77].
On larger trees, the correlation between rotational stiffness and anchorage strength presented in this paper should mainly depend on the proportion of bending stiffness and bending strength of major roots in the zone of rapid tapering. In younger trees, where soil properties are dominant and roots easily bend as the soil deforms around a more rigid central part of the root system [78], this correlation may obviously change. The transition to another mechanism of anchorage might happen gradually; however, because the major strengthening elements of a root system are already present in young trees [79], the uprooting behavior may change distinctively as soon as their rigidity exceeds the stiffness of the surrounding soil. The greater flexibility of roots can account for the greater inclination angles at which the anchorage strength of younger trees is overcome compared to larger trees [41]. This should be subject to future research. Nonetheless, the present data should already be regarded as representing a caveat that correlations between rotational stiffness and anchorage strength determined from younger trees should not be applied to larger trees without adaption; otherwise, the likelihood of failure of larger trees could be underrated.
The pulling tests in our experiments were static; naturally, however, trees are faced with dynamic impacts in the form of storms and heavy rain. Gusts overturning trees are in effect quasi-static [80], and dynamic effects of fatigue are restricted to rare soil conditions [81], and were reported here only for trees with very slender growth and shallow root systems [34]. The root plates of trees overturned by the wind do not appear different from those that failed in winching tests [22]. Previous cyclic loading tests have demonstrated a reduction of rotational stiffness between the first and the last of a series of cycles, though similar anchorage strength was measured under static and cyclic testing [39]. Furthermore, at maximum force, the reduction of rotational stiffness under cyclic loading was smaller by a magnitude than that caused by trenching near the stem. This implies that at least an increased likelihood of failure due to defects on roots can be identified adequately with static load tests. Cyclic experiments on different species growing in different soils should be conducted to further investigate the suspected role of dynamic effects on anchorage.
In urban tree assessment, non-destructive methods are essential, as tests are often applied to preserve trees (which excludes destructive methods) and measurements need to be repeated at intervals during the remaining lifetime of trees in order to monitor trends in their stability. Apart from dynamic methods, which are experimental and require wind events of certain severity to provide adequate information on stability [42,82,83], non-destructive static load tests are currently the only way to assess the anchorage of trees quantitatively in order to immediately inform management decisions. Although such tests have been used to assess the safety of urban trees for more than 30 years [31], studies testing their fundamental hypothesis are scarce [46,84]. Destructive winching tests have been applied as a research tool for decades [20,21,22,23]; however, to date, non-destructive load tests have rarely been used in scientific experiments [1].
Our results can provide a wider scientific basis for this method. They could help to validate risk assessments and studies based on static load tests and increase their credibility and acceptance, thereby contributing significantly to the efficacy of research experiments as well as to the prospects of conserving valuable trees.

Author Contributions

Conceptualization, A.D. and S.R.; methodology, A.D. and S.R.; formal analysis, S.R.; investigation, A.D., S.R. and O.K.; data curation, S.R.; writing—original draft preparation, S.R.; writing—review and editing, A.D., S.R. and O.K.; visualization, S.R.; funding acquisition, S.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partly funded by the German Federal Ministry of Education and Research, grant number FKZ 17021X11.

Data Availability Statement

Restrictions apply to the availability of these data. Part of the data were obtained from third parties.

Acknowledgments

A large number of colleagues provided additional data for this paper. We apologize for only mentioning those who contributed a larger dataset. In alphabetical order, we would like to thank F. Collet, T. Dapfer, R. Gschwandtner, R. Prosenz, C. Rust, A. Vögeli, P. van Wassenaer, D. Wolferz, and everyone else who supported data acquisition.

Conflicts of Interest

O.K. and S.R. have no relevant financial or non-financial interests to disclose. A.D. is general manager of Arbosafe GmbH, a company offering hardware and software for tree assessment.

Abbreviations

The following abbreviations are used in this manuscript:
MBending moment
M a Anchorage strength
k r Root–soil rotational stiffness
ϕ Root plate rotation
dStem diameter in m
hTree height in m

Appendix A

Table
Table A1. ANOVA of a linear model l n ( M a ) i = β 0 + β 1 × Species i + β 2 × l n ( Size ) i + β 3 × Species i × l n ( Size ) i + ϵ i .
Table A1. ANOVA of a linear model l n ( M a ) i = β 0 + β 1 × Species i + β 2 × l n ( Size ) i + β 3 × Species i × l n ( Size ) i + ϵ i .
DFSum SqMean SqF-ValuePr (>F)
Species722.383.2028.930.0000
Size1100.90100.90913.030.0000
Species:Size71.140.161.470.1771
Residuals26729.510.11
Table
Table A2. ANOVA of a linear model l n ( M a ) i = β 0 + β 1 × Species i + β 2 × l n ( k r ) i + β 3 × Species i × l n ( k r ) i + ϵ i .
Table A2. ANOVA of a linear model l n ( M a ) i = β 0 + β 1 × Species i + β 2 × l n ( k r ) i + β 3 × Species i × l n ( k r ) i + ϵ i .
DFSum SqMean SqF-ValuePr (>F)
Species722.43.259.90.00
l n ( k r ) 1116.4116.42178.40.00
Species: l n ( k r ) 70.90.12.50.02
Residuals26714.30.1
Table
Table A3. ANOVA of model l n ( 2.5 k r M a ) = β 0 + β 1 Species + β 2 l n ( Size ) + β 3 Species × l o g ( Size ) + ϵ i .
Table A3. ANOVA of model l n ( 2.5 k r M a ) = β 0 + β 1 Species + β 2 l n ( Size ) + β 3 Species × l o g ( Size ) + ϵ i .
DFSum SqMean SqF-ValuePr (>F)
fSpecies75.360.779.080.000
logSize16.296.2974.570.000
fSpecies:logSize71.080.151.830.081
Residuals26722.530.08
Table
Table A4. ANOVA of a linear mixed-effects model M a i j = β 0 + β 1 × k r i j + β 2 × Site i j + γ 0 i + γ 1 i × Site i j + ϵ i j with ϵ i j modeled as a power function of k r .
Table A4. ANOVA of a linear mixed-effects model M a i j = β 0 + β 1 × k r i j + β 2 × Site i j + γ 0 i + γ 1 i × Site i j + ϵ i j with ϵ i j modeled as a power function of k r .
DFF-ValuePr (>F)
(Intercept)68297.730.00
k r 68157.160.00
Site70.340.58
Table
Table A5. ANOVA of model l o g ( M est M a ) = Species × l o g ( Size ) .
Table A5. ANOVA of model l o g ( M est M a ) = Species × l o g ( Size ) .
DFSum SqMean SqF-ValuePr (>F)
Species75.360.779.080.000
log(Size)16.296.2974.570.000
Species:log(Size)71.080.151.830.081
Residuals26722.530.08
Table
Table A6. ANOVA of model l o g ( ϕ a ) = Species × l o g ( Size ) .
Table A6. ANOVA of model l o g ( ϕ a ) = Species × l o g ( Size ) .
DFF-ValuePr (>F)
(Intercept)12108.160.00
Species52.400.04
log(Size)146.950.00
Species:log(Size)53.190.01
Table
Table A7. ANOVA of model M a Size = Species .
Table A7. ANOVA of model M a Size = Species .
DFF-ValuePr (>F)
(Intercept)13482.600.00
Species821.810.00

References

  1. Smiley, E.T.; Holmes, L.; Fraedrich, B.R. Pruning of Buttress Roots and Stability Changes of Red Maple (Acer Rubrum). Arboric. Urban For. 2014, 40, 230–236. [Google Scholar] [CrossRef]
  2. Ghani, M.A.; Stokes, A.; Fourcaud, T. The Effect of Root Architecture and Root Loss through Trenching on the Anchorage of Tropical Urban Trees (Eugenia Grandis Wight). Trees-Struct. Funct. 2009, 23, 197–209. [Google Scholar] [CrossRef]
  3. Schmidlin, T.W. Human Fatalities from Wind-Related Tree Failures in the United States, 1995-2007. Nat. Hazards 2009, 50, 13–25. [Google Scholar] [CrossRef]
  4. Heneka, P.; Hofherr, T.; Ruck, B.; Kottmeier, C. Winter Storm Risk of Residential Structures–Model Development and Application to the German State of Baden-Württemberg. Nat. Hazards Earth Syst. Sci. 2006, 6, 721–733. [Google Scholar] [CrossRef] [Green Version]
  5. Pomnitz, M. Mangelnde Standsicherheit von Bäumen nach Baumaßnahmen—Gründe für einen sinnvollen Baumschutz. In Proceedings of the Jahrbuch der Baumpflege; Dujesiefken, D., Ed.; Haymarket Media GmbH: Augsburg, Germany, 2016; pp. 183–190. [Google Scholar]
  6. Smiley, E.T.; Matheny, N.P.; Lilly, S. Tree Risk Assessment; Best Management Practices, International Society of Arboriculture: Champaign, IL, USA, 2011. [Google Scholar]
  7. Kim, D.; Jin, J. Does Happiness Data Say Urban Parks Are Worth It? Landsc. Urban Plan. 2018, 178, 1–11. [Google Scholar] [CrossRef]
  8. Kuo, M. The Role of Arboriculture in a Healthy Social Ecology. J. Arboric. 2003, 29, 148–155. [Google Scholar]
  9. Na, H.R.; Heisler, G.M.; Nowak, D.J.; Grant, R.H. Modeling of Urban Trees’ Effects on Reducing Human Exposure to UV Radiation in Seoul, Korea. Urban For. Urban Green. 2014, 13, 785–792. [Google Scholar] [CrossRef]
  10. Price, C. Putting a Value on Trees: An Economist’s Perspective. Arboric. J. 2007, 30, 7–19. [Google Scholar] [CrossRef]
  11. Bratman, G.N.; Anderson, C.B.; Berman, M.G.; Cochran, B.; de Vries, S.; Flanders, J.; Folke, C.; Frumkin, H.; Gross, J.J.; Hartig, T.; et al. Nature and Mental Health: An Ecosystem Service Perspective. Sci. Adv. 2019, 5, eaax0903. [Google Scholar] [CrossRef] [Green Version]
  12. Bridge, M. Risk and Hazard Assement for Arborists. In Trees in Tune, Proceedings of the ISA 2005 Annual Conference and Trade Show; International Society of Arboriculture: Nashville, TN, USA, 2005. [Google Scholar]
  13. Detter, A.; Cowell, C.; McKeown, L.; Howard, P. Evaluation of Current Rigging and Dismantling Practices Used in Arboriculture; HSE Books: Norwich, UK, 2008. [Google Scholar]
  14. Mazzocchi, F.; Cecchini, M.; Monarca, D.; Colantoni, A.; Caruso, L.; Colopardi, F.; Cipollari, G.; Rapiti, R. An Overview of Risk Assessment for Tree Climber Arborists. Contemp. Eng. Sci. 2015, 8, 1171–1177. [Google Scholar] [CrossRef]
  15. Gardiner, B. Wind Damage to Forests and Trees: A Review with an Emphasis on Planted and Managed Forests. J. For. Res. 2021, 26, 248–266. [Google Scholar] [CrossRef]
  16. Stokes, A.; Salin, F.; Kokutse, A.D.; Berthier, S.; Jeannin, H.; Mochan, S.; Dorren, L.; Kokutse, N.; Abd Ghani, M.; Fourcaud, T. Mechanical Resistance of Different Tree Species to Rockfall in the French Alps. Plant Soil 2005, 278, 107–117. [Google Scholar] [CrossRef]
  17. Jonsson, M.J.; Volkwein, A.; Ammann, W. Quantification of Energy Absorption Capacity of Trees against Rockfall Using Finite Elements; Technical Report; WSL Swiss Federal Institute for Snow and Avalanche Research SLF: Davos, Switzerland, 2006. [Google Scholar]
  18. Chandelier, A.; Gerarts, F.; San Martin, G.; Herman, M.; Delahaye, L. Temporal Evolution of Collar Lesions Associated with Ash Dieback and the Occurrence of Armillaria in Belgian Forests. Forest Pathol. 2016, 46, 289–297. [Google Scholar] [CrossRef]
  19. Kehr, R. Eschentriebsterben—Aktuelles zur Schadensdynamik. In Jahrbuch der Baumpflege; Dujesiefken, D., Ed.; Haymarket Media: Braunschweig, Germany, 2018; pp. 192–201. [Google Scholar]
  20. Tamate, S.; Kashiyama, T.; Sasanuma, T. A Trial of Pulling down Standing Trees. J. Jpn. For. Res. 1965, 47, 210–213. [Google Scholar] [CrossRef]
  21. Fraser, A.I. The Soil and Roots as Factors in Tree Stability. Forestry 1962, 35, 117–127. [Google Scholar] [CrossRef]
  22. Coutts, M.P. Root Architecture and Tree Stability. Plant Soil 1983, 71, 171–188. [Google Scholar] [CrossRef]
  23. Ylinen, A. Über die mechanische Schaftformtheorie der Bäume; Technical Report 76; Technische Hochschule in Finnland: Helsinki, Finland, 1952. [Google Scholar]
  24. Stubbs, C.J.; Cook, D.D.; Niklas, K.J. A General Review of the Biomechanics of Root Anchorage. J. Exp. Bot. 2019, 70, 3439–3451. [Google Scholar] [CrossRef] [PubMed]
  25. Dahle, G.A.; James, K.R.; Kane, B.; Grabosky, J.C.; Detter, A. A Review of Factors That Affect the Static Load-Bearing Capacity of Urban Trees. Arboric. Urban For. 2017, 43, 89–106. [Google Scholar] [CrossRef]
  26. Danjon, F.; Fourcaud, T.; Bert, D. Root Architecture and Wind-Firmness of Mature Pinus Pinaster. New Phytol. 2005, 168, 387–400. [Google Scholar] [CrossRef]
  27. Weber, K.; Mattheck, C. Die Doppelnatur der Wurzelplatte. Allg. Forst Jagdztg. 2005, 176, 77–85. [Google Scholar]
  28. Gruber, F. Die VTA-Rw/R-Grenzregel zum Baumwurf, ein weiteres wissenschaftlich nicht nachvollziehbares und praktisch inadäquates Versagenskriterium der Standsicherheit. Agrar Umweltr. 2007, 3, 74–79. [Google Scholar]
  29. Vanomsen, P. Der Einfluss der Durchforstung auf die Verankerung der Fichte Hinsichtlich ihrer Sturmresistenz. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2006. [Google Scholar] [CrossRef]
  30. Comin, S.; Vigevani, I.; Fini, A. Non-Invasive Methods for the Investigation of Trees’ Root System in the Urban Environment. Italus Hortus 2021, 28, 37–57. [Google Scholar] [CrossRef]
  31. Sinn, G.; Wessolly, L. A Contribution to the Proper Assessment of the Strength and Stability of Trees. Arboric. J. 1989, 13, 45–65. [Google Scholar] [CrossRef]
  32. Sinn, G. Baumstatik; Thalacker Medien: Braunschweig, Germany, 2003. [Google Scholar]
  33. Brudi, E.; van Wassenaer, P. Trees and Statics: Nondestructive Failure Analysis. In How Trees Stand up and Fall Down Proceedings of the Tree Structure and Mechanics Conference; Smiley, E.T., Coder, K.D., Eds.; International Society of Arboriculture: Savannah, GA, USA, 2002; pp. 53–70. [Google Scholar]
  34. Wessolly, L.; Erb, M. Handbuch der Baumstatik und Baumkontrolle; Patzer Verlag: Berlin, Germany, 1998. [Google Scholar]
  35. Esche, D.; Schumacher, P.; Detter, A.; Rust, S. Experimentelle Überprüfung der Windlastanalyse für statische Zugversuche. In Proceedings of the Jahrbuch der Baumpflege; Dujesiefken, D., Ed.; Haymarket Media: Augsburg, Germany, 2018; pp. 229–236. [Google Scholar]
  36. Dupuy, L.; Fourcaud, T.; Stokes, A.; Danjon, F. A Density-Based Approach for the Modelling of Root Architecture: Application to Maritime Pine (Pinus Pinaster Ait.) Root Systems. J. Theor. Biol. 2005, 236, 323–334. [Google Scholar] [CrossRef]
  37. Dupuy, L.X.; Fourcaud, T.; Lac, P.; Stokes, A. A Generic 3d Finite Element Model of Tree Anchorage Integrating Soil Mechanics and Real Root System Architecture. Am. J. Bot. 2007, 94, 1506–1514. [Google Scholar] [CrossRef] [PubMed]
  38. Rahardjo, H.; Harnas, F.R.; Indrawan, I.G.B.; Leong, E.C.; Tan, P.Y.; Fong, Y.K.; Owc, L.F. Understanding the Stability of Samanea Saman Trees through Tree Pulling, Analytical Calculations and Numerical Models. Urban For. Urban Green. 2014, 13, 355–364. [Google Scholar] [CrossRef]
  39. Osullivan, M.; Ritchie, R. Tree Stability in Relation to Cyclic Loading. Forestry 1993, 66, 69–82. [Google Scholar] [CrossRef]
  40. Jonsson, M.J.; Foetzki, A.; Kalberer, M.; Lundström, T.; Ammann, W.; Stöckli, V. Root-Soil Rotation Stiffness of Norway Spruce (Picea Abies (L.) Karst) Growing on Subalpine Forested Slopes. Plant Soil 2006, 285, 267–277. [Google Scholar] [CrossRef] [Green Version]
  41. Lundström, T.; Jonas, T.; Stöckli, V.; Ammann, W. Anchorage of Mature Conifers: Resistive Turning Moment, Root–Soil Plate Geometry and Root Growth Orientation. Tree Physiol. 2007, 27, 1217–1227. [Google Scholar] [CrossRef] [Green Version]
  42. James, K.; Hallam, C.; Spencer, C. Measuring Tilt of Tree Structural Root Zones under Static and Wind Loading. Agric. For. Meteorol. 2013, 168, 160–167. [Google Scholar] [CrossRef]
  43. Marchi, L.; Mologni, O.; Trutalli, D.; Scotta, R.; Cavalli, R.; Montecchio, L.; Grigolato, S. Safety Assessment of Trees Used as Anchors in Cable-Supported Tree Harvesting Based on Experimental Observations. Biosyst. Eng. 2019, 186, 71–82. [Google Scholar] [CrossRef]
  44. Wessolly, L. Standsicherheit von Bäumen. Der Kippvorgang ist geklärt. Stadt Grün 1996, 4, 268–272. [Google Scholar]
  45. Buza, Á.K.; Divós, F.; Divos, F. Root Stability Evaluation with Non-Destructive Techniques. ActaSilv Lign Hung 2016, 12, 125–134. [Google Scholar] [CrossRef] [Green Version]
  46. Detter, A.; van Wassenaer, P.; Rust, S. Stability Recovery in London Plane Trees Eight Years After Primary Anchorage Failure. Arboric. Urban For. 2019, 45, 279–288. [Google Scholar] [CrossRef]
  47. Detter, A.; Rust, S. Experimental Test of Non-Destructive Methods to Assess the Anchorage of Urban Trees. In Proceedings of the 21st International Non-Destructive Testing and Evaluation of Wood Symposium; Wang, X., Sauter, U., Ross, R.J., Eds.; Forest Products Laboratory: Madison, WI, USA, 2019; General Technical Report FPL-GTR-272; pp. 417–421. [Google Scholar]
  48. R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021.
  49. Urata, T.; Shibuya, M.; Koizumi, A.; Torita, H.; Cha, J. Both Stem and Crown Mass Affect Tree Resistance to Uprooting. J. For. Res. 2012, 17, 65–71. [Google Scholar] [CrossRef] [Green Version]
  50. Ribeiro, G.H.P.M.; Chambers, J.Q.; Peterson, C.J.; Trumbore, S.E.; Magnabosco Marra, D.; Wirth, C.; Cannon, J.B.; Negron-Juarez, R.I.; Lima, A.J.N.; de Paula, E.V.C.M.; et al. Mechanical Vulnerability and Resistance to Snapping and Uprooting for Central Amazon Tree Species. For. Ecol. Manag. 2016, 380, 1–10. [Google Scholar] [CrossRef] [Green Version]
  51. Bergeron, C.; Ruel, J.C.; Elie, J.G.; Mitchell, S.J. Root Anchorage and Stem Strength of Black Spruce (Picea Mariana) Trees in Regular and Irregular Stands. Forestry 2009, 82, 29–41. [Google Scholar] [CrossRef] [Green Version]
  52. Sun, H.L.; Li, S.C.; Xiong, W.L.; Yang, Z.R.; Cui, B.S. Influence of Slope on Root System Anchorage of Pinus Yunnanensis. Ecol. Eng. 2008, 32, 60–67. [Google Scholar] [CrossRef]
  53. Nicoll, B.C.; Gardiner, B.A.; Rayner, B.; Peace, A.J. Anchorage of Coniferous Trees in Relation to Species, Soil Type, and Rooting Depth. Can. J. For.-Res.-Rev. Can. Rech. For. 2006, 36, 1871–1883. [Google Scholar] [CrossRef]
  54. Fraser, A.I.; Gardiner, J.B.H. Rooting and Stability in Sitka Spruce; Technical Report 40; Forestry Commision: London, UK, 1967. [Google Scholar]
  55. Cucchi, V.; Meredieu, C.; Stokes, A.; Berthier, S.; Bert, D.; Najar, M.; Denis, A.; Lastennet, R. Root Anchorage of Inner and Edge Trees in Stands of Maritime Pine (Pinus pinasterAit.) Growing in Different Podzolic Soil Conditions. Trees 2004, 18, 460–466. [Google Scholar] [CrossRef]
  56. Peterson, C.J.; Claassen, V. An Evaluation of the Stability of Quercus Lobata and Populus Fremontii on River Levees Assessed Using Static Winching Tests. Forestry 2013, 86, 201–209. [Google Scholar] [CrossRef] [Green Version]
  57. Detter, A.; Rust, S.; Böttcher, J.; Bouillon, J. Ambient Influences on the Results of Non-Destructive Pulling Tests. In Proceedings of the 21st International Nondestructive Testing and Evaluation of Wood Symposium; General Technical Report; Wang, X., Sauter, U.H., Ross, R.J., Eds.; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2019; Volume 272, pp. 422–436. [Google Scholar]
  58. Coutts, M.P. Components of Tree Stability in Sitka Spruce on Peaty Gley Soil. Forestry 1986, 59, 173–197. [Google Scholar] [CrossRef]
  59. Mergen, F. Mechanical Aspects of Wind-Breakage and Windfirmness. J. For. 1954, 52, 119–125. [Google Scholar]
  60. England, A.H.; Baker, C.J.; Saunderson, S.E.T. A Dynamic Analysis of Windthrow of Trees. Forestry 2000, 73, 225–237. [Google Scholar] [CrossRef]
  61. Mattheck, C.; Bethge, K. Wind Breakage of Trees Initiated by Root Delamination. Trees-Struct. Funct. 1990, 4, 2–4. [Google Scholar] [CrossRef]
  62. Fritzsche, K. Sturmgefahr und Anpassung: (Physiologische und technische Fragen des Sturmschutzes); Parey: Berlin, Germany, 1933; p. 94. [Google Scholar]
  63. Crook, M.J.J.; Ennos, A.R.R. The Anchorage Mechanics of Deep Rooted Larch, Larix Europea× L. Japonica. J. Exp. Bot. 1996, 47, 1509–1517. [Google Scholar] [CrossRef] [Green Version]
  64. Day, S.D.; Wiseman, P.E.; Dickinson, S.B.; Harris, J.R. Contemporary Concepts of Root System Architecture of Urban Trees. Arboric. Urban For. 2010, 36, 149–159. [Google Scholar] [CrossRef]
  65. Stokes, A. Strain Distribution during Anchorage Failure of Pinus Pinaster Ait. at Different Ages and Tree Growth Response to Wind-Induced Root Movement. Plant Soil 1999, 217, 17–27. [Google Scholar] [CrossRef]
  66. Saint Cast, C.; Meredieu, C.; Défossez, P.; Pagès, L.; Danjon, F. Correction to: Modelling Root System Development for Anchorage of Forest Trees up to the Mature Stage, Including Acclimation to Soil Constraints: The Case of Pinus Pinaster. Plant Soil 2019, 444, 537–538. [Google Scholar] [CrossRef] [Green Version]
  67. Yang, M.; Defossez, P.; Danjon, F.; Fourcaud, T. Analyzing Key Factors of Roots and Soil Contributing to Tree Anchorage of Pinus Species. Trees-Struct. Funct. 2018, 32, 703–712. [Google Scholar] [CrossRef] [Green Version]
  68. Wessolly, L. Verfahren zur Bestimmung der Stand- und Bruchsicherheit von Bäumen. Holz Roh-Werkst. 1991, 49, 99–104. [Google Scholar] [CrossRef]
  69. Kubler, H. Growth Stresses in Trees and Related Wood Properties. For. Prod. Abstr. 1987, 10, 61–119. [Google Scholar]
  70. Gril, J.; Jullien, D.; Bardet, S.; Yamamoto, H. Tree Growth Stress and Related Problems. J. Wood Sci. 2017, 63, 411–432. [Google Scholar] [CrossRef]
  71. Brudi, E. Longitudinal Prestresses in Tilia Cordata and Acer Pseudoplatanus. Master Thesis, University of Aberdeen, UK. 2001.
  72. Wessolly, L. Die natürliche Konstruktion Baum als intelligentes statisch-dynamisches System. In Proceedings of the Beiträge zum Internationalen Symposium des SFB 230-Natürliche Konstruktionen, Leichtbau in Architektur und Natur; Mitteilungen des SFB 230; Universität Stuttgart: Stuttgart, Germany, 1988; Volume 2, pp. 203–212. [Google Scholar]
  73. Wessolly, L. Baumdiagnose – Eingehende Untersuchung mittels Zugversuch – Ergebnisse. ProBaum 2004, 1, 2–3. [Google Scholar]
  74. Gartner, B.L. Trees Have Higher Longitudinal Growth Strains in Their Stems Than in Their Roots. Int. J. Plant Sci. 1997, 158, 418–423. [Google Scholar] [CrossRef]
  75. Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain, 7th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
  76. Ray, D.; Nicoll, B.C.C. The Effect of Soil Water-Table Depth on Root-Plate Development and Stability of Sitka Spruce. Forestry 1998, 71, 169–182. [Google Scholar] [CrossRef] [Green Version]
  77. Lundström, T.; Jonsson, M.J.; Kalberer, M. The Root–Soil System of Norway Spruce Subjected to Turning Moment: Resistance as a Function of Rotation. Plant Soil 2007, 300, 35–49. [Google Scholar] [CrossRef]
  78. Dorval, A.D.; Meredieu, C.; Danjon, F. Anchorage Failure of Young Trees in Sandy Soils Is Prevented by a Rigid Central Part of the Root System with Various Designs. Annals Botany 2016, 118, 747–762. [Google Scholar] [CrossRef] [Green Version]
  79. Saint Cast, C.; Meredieu, C.; Defossez, P.; Pages, L.; Danjon, F. Clustering of Pinus Pinaster Coarse Roots, from Juvenile to Mature Stage. Plant Soil 2020, 457, 185–205. [Google Scholar] [CrossRef]
  80. Schindler, D.; Mohr, M. Non-Oscillatory Response to Wind Loading Dominates Movement of Scots Pine Trees. Agric. For. Meteorol. 2018, 250, 209–216. [Google Scholar] [CrossRef]
  81. Rodgers, M.; Casey, A.; McMenamin, C.; Hendrick, E. An Experimental Investigation of the Effects of Dynamic Loading on Coniferous Trees Planted on Wet Mineral Soils. In Wind and Trees; Coutts, M.P., Grace, J., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 204–219. [Google Scholar]
  82. Göcke, L.; Rust, S.; Ruhl, F. Assessing the Anchorage and Critical Wind Speed of Urban Trees Using Root-Plate Inclination in High Winds. Arboric. Urban For. 2018, 44, 1–11. [Google Scholar] [CrossRef]
  83. Fathi, S.; Bejo, L.; Divos, F. Investigating the Effect of Weather and Seasonal Factors on Root Stability Using Dynamic Measurements. Open J. For. 2020, 10, 124–134. [Google Scholar] [CrossRef] [Green Version]
  84. Smiley, E.T. Root Pruning and Stability of Young Willow Oak. Arboric. Urban For. 2008, 34, 123–128. [Google Scholar] [CrossRef]
Forests 14 00533 g001 550
Figure 1. Species effect on anchoring strength (fitted lines: M a = y 0 ( 1 − e − a Size ) , ANOVA: Table A1).
Figure 1. Species effect on anchoring strength (fitted lines: M a = y 0 ( 1 − e − a Size ) , ANOVA: Table A1).
Forests 14 00533 g001
Forests 14 00533 g002 550
Figure 2. Robust correlation of bending moments at a root plate inclination of 0.25° k r and at failure M a . The blue line illustrates Equation (1).
Figure 2. Robust correlation of bending moments at a root plate inclination of 0.25° k r and at failure M a . The blue line illustrates Equation (1).
Forests 14 00533 g002
Forests 14 00533 g003 550
Figure 3. The relationship between rotational stiffness and anchorage strength varied from linear to curved depending on species. The blue line illustrates Equation (1) (fitted lines: M a = y 0 ( 1 − e − a k r ) , ANOVA: Table A2).
Figure 3. The relationship between rotational stiffness and anchorage strength varied from linear to curved depending on species. The blue line illustrates Equation (1) (fitted lines: M a = y 0 ( 1 − e − a k r ) , ANOVA: Table A2).
Forests 14 00533 g003
Forests 14 00533 g004 550
Figure 4. Depending on the degree of non-linearity in the relationship between rotational stiffness and anchorage strength, the ratio between predicted (Equation (1)) and measured anchorage strength approaches 1 (red line) for larger trees. Fitted lines: 2.5 k r M a = y 0 e − a Size + b , ANOVA: Table A3.
Figure 4. Depending on the degree of non-linearity in the relationship between rotational stiffness and anchorage strength, the ratio between predicted (Equation (1)) and measured anchorage strength approaches 1 (red line) for larger trees. Fitted lines: 2.5 k r M a = y 0 e − a Size + b , ANOVA: Table A3.
Forests 14 00533 g004
Forests 14 00533 g005 550
Figure 5. Estimated (Equation (3)) and measured anchorage strength (with four outliers beyond 1000 kNm removed). The blue line illustrates 1:1.
Figure 5. Estimated (Equation (3)) and measured anchorage strength (with four outliers beyond 1000 kNm removed). The blue line illustrates 1:1.
Forests 14 00533 g005
Forests 14 00533 g006 550
Figure 6. The ratio of estimated (Equation (3)) and measured anchorage strength approaches 1 (red line) for large trees. Three outliers > 2 removed. Fitted curve: y = y 0 ∗ e − a ∗ Size + b . ANOVA: Table A5.
Figure 6. The ratio of estimated (Equation (3)) and measured anchorage strength approaches 1 (red line) for large trees. Three outliers > 2 removed. Fitted curve: y = y 0 ∗ e − a ∗ Size + b . ANOVA: Table A5.
Forests 14 00533 g006
Forests 14 00533 g007 550
Figure 7. Comparison of estimates from Equation (1) (x-axis) and Equation (3) (y-axis) with four outliers removed. The blue line illustrates 1:1.
Figure 7. Comparison of estimates from Equation (1) (x-axis) and Equation (3) (y-axis) with four outliers removed. The blue line illustrates 1:1.
Forests 14 00533 g007
Forests 14 00533 g008 550
Figure 8. Species effect on anchoring strength. ANOVA: Table A7.
Figure 8. Species effect on anchoring strength. ANOVA: Table A7.
Forests 14 00533 g008
Forests 14 00533 g009 550
Figure 9. Rotational stiffness and maximum bending moments of B. pendula in forests and urban sites. There is no difference between anchorage and the ratio of the two parameters (Table A4). The blue line indicates a slope of 2.5 [34]. Fitted lines: M a = a ( 1 − e − e b k r ) .
Figure 9. Rotational stiffness and maximum bending moments of B. pendula in forests and urban sites. There is no difference between anchorage and the ratio of the two parameters (Table A4). The blue line indicates a slope of 2.5 [34]. Fitted lines: M a = a ( 1 − e − e b k r ) .
Forests 14 00533 g009
Forests 14 00533 g010 550
Figure 10. Basal inclination at failure, depending on tree size and species. Fitted curve: ϕ a = b ( d 2 h ) α [77]. ANOVA: Table A6.
Figure 10. Basal inclination at failure, depending on tree size and species. Fitted curve: ϕ a = b ( d 2 h ) α [77]. ANOVA: Table A6.
Forests 14 00533 g010
Table
Table 1. Tree species and average tree sizes used in the experiment.
Table 1. Tree species and average tree sizes used in the experiment.
Speciesnd in cmh in m
Betula pendula783324
Picea abies653225
Fraxinus excelsior483425
Pinus sylvestris483125
Fagus sylvatica213326
Populus sp. 184430
Platanus acerifolia122818
Acer saccharinum72817
Acer pseudoplatanus52223
Prunus sp. 33313
Quercus robur35419
Tilia sp. 33214
Robinia pseudoaccacia24819
Alnus glutinosa17221
Acer platanoides13410
Pseudotsuga menziesii13122
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Detter, A.; Rust, S.; Krišāns, O. Experimental Test of Non-Destructive Methods to Assess the Anchorage of Trees. Forests 2023, 14, 533. https://doi.org/10.3390/f14030533

AMA Style

Detter A, Rust S, Krišāns O. Experimental Test of Non-Destructive Methods to Assess the Anchorage of Trees. Forests. 2023; 14(3):533. https://doi.org/10.3390/f14030533

Chicago/Turabian Style

Detter, Andreas, Steffen Rust, and Oskars Krišāns. 2023. "Experimental Test of Non-Destructive Methods to Assess the Anchorage of Trees" Forests 14, no. 3: 533. https://doi.org/10.3390/f14030533

APA Style

Detter, A., Rust, S., & Krišāns, O. (2023). Experimental Test of Non-Destructive Methods to Assess the Anchorage of Trees. Forests, 14(3), 533. https://doi.org/10.3390/f14030533

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop