Abstract
Accurate forest information on tree species, stand age, tree density, and stand volume is required to ensure effective forest management practices. In Japan, forest information is consolidated in forest yield tables and stand density management diagrams (SDMDs) that are specifically designed for major forest plantation species. In this study, we analyzed whether the current full density curve in the SDMD of Hinoki (Chamaecyparis obtusa) plantation stands in Kyushu Island aligns with the characteristics of the existing stands. Data from 18 Hinoki forests were used to measure tree heights, diameters, and densities. Equations were developed to establish relationships between stand factors, and various curves were derived for average height, competition ratio, full density, yield ratio, average diameter, and natural mortality. The results showed that the current full density curve in the SDMD for Hinoki plantation stands did not completely align with the characteristics of the existing Hinoki plantation stands in Kyushu Island. Thus, the full density curve in the SDMD for the Hinoki stands in this region should be significantly adjusted. These results can enhance forest management in Japan and advance SDMD modeling and its application in forest planning and management.
1. Introduction
Forest managers and planners require a wide range of forest data, such as tree species, stand age, tree density, and stand volume, which are crucial for understanding the present and future conditions of a forest and to plan effectively and implement appropriate forest management practices [1,2,3]. In Japan, forest information is consolidated in forest yield tables and stand density management diagrams (SDMDs) specifically designed for major forest plantation species. Forest yield tables present empirical relationships between stand age and stand stem volume [4], while SDMDs are average stand-level models that visually depict the inter-relationships between yield, density, and mortality in various stages of stand development [5,6,7,8,9,10,11,12,13,14].
The National Forest Inventory (NFI) is a comprehensive forest survey conducted at the national level that primarily focuses on estimating timber productivity. Typically, the NFI collects information regarding tree species composition and measures stem or timber volume on both the stand and individual tree scales in selected forests [4]. Moreover, the NFI accurately and reliably estimates carbon stocks and carbon uptake across the entire forested area of the country [4,15,16,17]. Numerous studies have utilized NFI data to examine historical forest carbon stocks and net carbon uptake [4,16,17,18,19,20,21,22,23] and to project future changes using forest growth models [4,24,25,26].
In Japan, NFI data have traditionally been based on forest registers using yield tables derived from observational data collected around 1970 [4]. However, in recent years, new yield tables incorporating mathematical formulas based on SDMDs have been developed for private forests in Japan [27,28,29,30,31,32,33].
As mentioned above, SDMDs visually represent the relationships between yield, density, and mortality in different stages of stand development [12,13,14,34,35,36,37]. A full density curve plays a significant role in SDMDs as an important functional and empirical quantitative element. It serves as the foundation for the yield index, which indicates the ratio of a specific stem volume on the equivalent height curve to the maximum stem volume per unit area (e.g., ha) at the intersection point of the full density curve and the equivalent height curve [6]. The yield index is a common criterion for determining relative stand density because it is directly related to the stem volume per unit area. Furthermore, the full density curve establishes the upper limit of stand density with respect to a given mean stem volume [7]. However, in recent years, Kondoh [38] reported practical data for long-term forest survey plots of Hinoki (Chamaecyparis obtusa) that exceeded the upper limit of stand density for a given mean stem volume.
Although the full density curve serves as the foundation for the yield index of the SDMD, a residual error can occur between the full density curve and practical forest survey plot data [27,28,29,30,38]. This can affect the accuracy of the yield index in the SDMD. Therefore, in this study, we analyzed data from long-term continuous survey plots of Hinoki stands located in national forests to address the following question:
Do the characteristics of the current full density curve in the SDMD for Hinoki plantation stands in national forests in Kyushu Island align with that of the existing Hinoki plantation stands?
Answering this question will allow for adjustments to the current full density curve in the SDMD for Hinoki plantation stands in the national forests in Kyushu Island and potentially lead to improvements in the SDMD for Hinoki stands in this region. Hinoki is one of the primary tree species used in forestry in Japan, along with Sugi (Cryptomeria japonica) [39]. In 2017, the artificial Hinoki plantation area accounted for 25.5% of the total plantation area in Japan. Specifically, in Kyushu Island, located in southwestern Japan, Hinoki plantations cover 34.5% of the area [40]. Notably, the timber price of Hinoki is generally higher than that of Sugi in Japan [41].
2. Materials and Methods
2.1. Materials
We used 118 datasets collected from 18 pure and uniformly aged Hinoki forests in Kyushu Island, southwestern Japan (Figure 1, Table 1). The latest measured ages for each survey plot ranged from 54 to 113 years (Table 1). The plot sizes varied from 0.065 ha to 0.493 ha (median: 0.168 ha; mean: 0.197 ha). Throughout the study period, the total tree height and diameter at breast height (DBH) of all living trees were measured multiple times, with intervals of approximately 5 years for young plots (approximately < 50 years) and approximately 10 years for older stands.
Figure 1.
Location of the study site (red circles). Numbers on the site name correspond to the stand numbers listed in Table 1.

Table 1.
Stand attributes of the pure Hinoki (Chamaecyparis obtusa) forests studied during the first and last measurement periods.
As shown in Table 1, the dominant height was calculated as the average height of the dominant trees within each plot. Dominant trees were determined based on the tallest 100 trees per hectare [42].
The relative index (Ry) shown in Table 1 represents a commonly used indicator for determining stand density utilized in SDMDs in Japan. Ry is a relative value, with higher values indicate denser stands and a theoretical value of 1.0 representing an overcrowded stand. The curve at which Ry equals 1.0 is referred to as the full density curve [7]. The relative index (Ry) was calculated as follows:
where V is the stem volume per hectare and Ves is the stem volume per hectare on the full density curves of the existing SDMDs, that have been used [43].
Ry = V/Ves
2.2. Methods
The development methods used for SDMDs are primarily based on the studies of Ando [6], Nagahama [27,28], and Nagahama and Kondoh [29].
In this study, we aimed to establish the expression for forest stand functions.
The relationship between stand form height, the mean height of dominant trees, and stand density was calculated as follows:
where HF represents stand form height; Ht denotes the mean height of the dominant trees; N represents the number of trees per hectare, that is, stand density; and a1, a2, and a3 are coefficients.
HF = a1 + a2 × Ht + a3 × N1/2 × (Ht/100)
The relationship between the mean DBH, quadratic mean diameter, and stand density was calculated as follows:
where D represents the mean DBH, Dg signifies quadratic mean diameter, and b1, b2, and b3 are the coefficients.
D = b1 + b2 × Dg + b3 × N1/2 × (Ht/100)
The relationship between the mean tree height at a survey stand (H), the mean height of dominant trees (Ht), and stand density (N) was calculated as follows:
where c1, c2, and c3 are the coefficients.
H = c1 + c2 × Ht + c3 × N1/2 × (Ht/100)
The relationship between the mean stem volume of an individual tree (v) in a survey stand, the mean height of dominant trees (Ht), and stand density (N) was calculated as follows:
where d1, d2, and d3 are the coefficients.
v = d1 × (Htd2) × Nd3
To derive the above-mentioned equations, 118 plot measurements were used. The residuals between the calculated values based on each stand factor and the observed values were obtained using the derived equations. These residuals were divided by the sum of the squared residuals, and data exceeding the 1% threshold in the t-distribution table were assigned a score of 2, whereas data falling between 5% and 1% were assigned a score of 1. Data with a total score of 4 or higher were identified as anomalous and excluded [44]. The residual standard deviation (S) was calculated as follows:
where yi represents each individual residual, Myi is the mean of the residuals, N is the total number of data points, and P is the number of parameters in the equation.
S = (Σ(yi − Myi)2)1/2/(N − P − 1)
2.2.1. Reciprocal Equation of Competition—Density Effect
The average height curve in SDMDs represents the relationship between the number of stems per hectare and stem volume and is called the reciprocal equation of the competition—density effect [45,46,47]:
where V is stem volume per hectare, and A and B are constants determined for each dominant height.
V−1 = A + B × N−1
Ando [6] assumed that stands with the same dominant height were in the same growth stage regardless of their site or stand age. He substituted A and B into the dominant height equation and transformed Equation (5) as follows:
where k1, k2, k3, and k4 are constants.
V = (k1 × Htk2 + k3 × Htk4 × N−1)−1
Equation (6) requires the coefficients (constants) to be determined using a nonlinear model. Manabe [48] applied the iterative method described by Marquardt [49].
2.2.2. Derivation of Various Curves
The coefficients (constants) were calculated using the iterative method proposed by Marquardt [49]. Using the acquired results, we obtained the average height curve, competition ratio, full density curve, yield ratio curve, average diameter curve, and natural mortality line.
The expressions of all forest stand functions were established, and an SDMD for Hinoki (C. obtusa) forests in the Kyushu region is presented here. The estimation accuracy of the SDMD was determined through hypothesis testing. All statistics were calculated using R. 4. 2. 1 [50].
3. Results
3.1. Calculation of Abnormal Data
Scores were obtained for each stand composition factor using Equations (1)–(4). For data from 42-year-old and 47-year-old stands in the Tankaino survey plot, the scores were ≥4. Therefore, data from these two sets were excluded from the analysis. Consequently, 116 datasets were used to calculate the stand composition factor relationships.
3.2. Relationship Equations of Stand Composition Factors
The relationship equations of the stand composition factors were calculated based on discarded data for the experimental site.
The relationship between stand shape height, the average height of dominant trees, and stand density was calculated as follows:
HF = 0.113013 + 0.399036 × Ht + 0.109946 × N1/2 × Ht/100
The coefficient of multiple determination was 0.978, and the residual standard deviation (S) was 0.2622.
The relationship between the mean DBH, quadratic mean diameter, and stand density was as follows:
D = 0.097290 + 0.988882 × Dg − 0.034098 × N1/2 × Ht/100
The quadratic mean diameter (Dg) was calculated based on the stand shape height (HF) using Equation (7) and the basal area per hectare (G) using Equations (9) and (10).
G = V/HF
Dg = 200 × (G × (pi × N)−1)1/2
The coefficient of multiple determination was 0.9994, and S was 0.1345.
The relationship between average tree height, the average height of dominant trees, and stand density was as follows:
H = −0.55205 + 0.95098 × Ht − 0.08986 × N1/2 × Ht/100
The coefficient of multiple determination was 0.9746 and S was 0.6288.
The relationship between average stem volume per tree, the average height of dominant trees, and stand density was:
v = 0.08917 × (Ht2.17785) × N−0.69803
The coefficient of multiple determination was 0.9528, and S was 0.06789.
3.3. Reciprocal Equation of Yield Density Effect
Using the Levenberg–Marquardt method [48,49,50], the coefficients were calculated using Equation (6), and subsequently, Equation (13) was constructed as follows:
V = (0.07839 × Ht−1.32287 + 256,036.07702 × Ht−4.44913 × N−1)−1
3.4. Derivation of Various Curves on Stand Structure Factors
3.4.1. Equivalent Height Curve
Using the inverse formula of the yield density effect (Equation (13)), the relationship between the number of trees per hectare (N) and stem volume per hectare (V) for a given dominant tree height (Ht) was determined. This relationship corresponds to an even-aged stand—height curve, as indicated by Ando [6].
3.4.2. Competition Index and Limit Competition Index
Following the method proposed by Ando [46], the competition index (Rc) and limit competition index (Rf) were calculated using the method proposed by Ando:
where V represents the stem volume calculated using Equation (13). Ando [6] stated that there is an upper limit to density depending on the growth stage of a pure stand. Therefore, Rc had a certain threshold value for a real forest stand. The competition index at this threshold is referred to as the threshold competition index. In this study, Rc was calculated for 116 survey datasets, and the minimum value was considered as Rf, which was found to be 0.05447.
Rc = 256,036.07702 × Ht−4.44913 × V × N−1
3.4.3. Full Density Curve
Using the previously mentioned Rf values, a full density curve was constructed following the methods proposed by Ando [6] and Nagahama [28], resulting in Equation (15):
V_Rf = 23,033.51908 × N_Rf−0.42315
3.4.4. Yield Index Curve
Based on the methods of Ando [6] and Nagahama [28], the yield index curve was formulated as follows:
where K is a constant. The values of K for each yield index are listed in Table 2.
V_Ry = K × N_Ry−0.42315

Table 2.
Values of constant K for each yield index.
3.4.5. Natural Thinning Curve
A stand starting from planting density N0 will gradually approach the full density curve while exhibiting a decrease in density during the growth process, without any artificial thinning or adjustment of its tree numbers. The natural mortality line for planting density N0 is a function of the average stem volume v and is expressed in Equation (17) [51]:
where A and B are constants determined from the full density curve and planting density, respectively. Therefore, the natural mortality line was derived based on the full density curve given in Equation (18):
where V represents the stem volume per ha, N represents the number of trees per hectare, and N0 represents the planting density.
1/N = Av + B
V = ((N/N0) − 1) × (−54,765.60847) × (N00.42315)
3.5. Estimation Accuracy
Previous studies have examined the estimation accuracy of constructed SDMDs [6,28,44]. In this study, the estimation accuracy was examined following the estimation accuracy evaluation methods of the Forestry Agency [44] and Nagahama [28]. Using a permissible error rate of 20%, the stem volume per hectare estimated from the SDMD was compared with the actual measured values of stem volume per hectare at a significance level of 5%. Denoting the 5% significance level as Χ2(0.05), the values obtained were Χ2 = 67.32339 and Χ2(0.05) = 142.07551. Because the calculated value did not exceed the critical value, it was deemed statistically insignificant and was within the permissible error rate.
3.6. Stand Density Management Diagram
Using the formulas representing the stand structure factors mentioned earlier, an SDMD for Hinoki (C. obtusa) forests in the Kyushu region is presented (Figure 2).
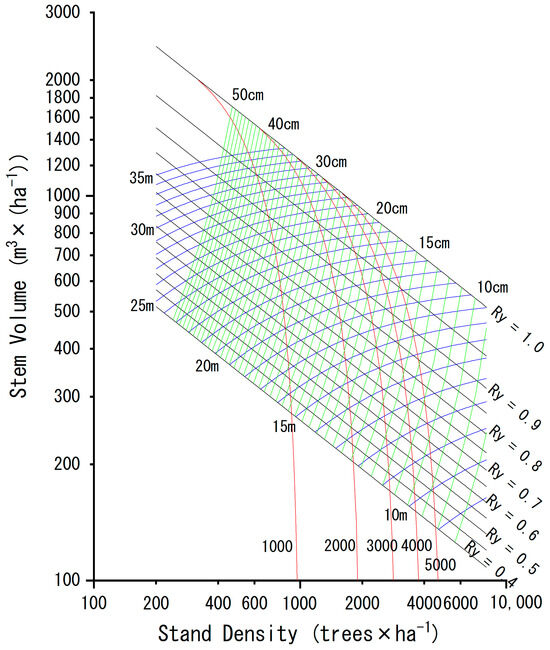
Figure 2.
Stand density management diagram for Hinoki (C. obtusa) plantation stands in national forests on Kyushu Island. Black, blue, green, and red isolines represent yield index (Ry) curve, equivalent height curve, quadratic mean diameter, and natural thinning curve, respectively.
3.7. Comparison with the Existing Full Density Curve
Figure 3 shows the existing full density curve and that calculated in this study. Up to a density of 167 trees × ha−1, the full density curve in this study was positioned above the existing curve. The corresponding stem volume at this point was 2644 m3 × (ha−1).
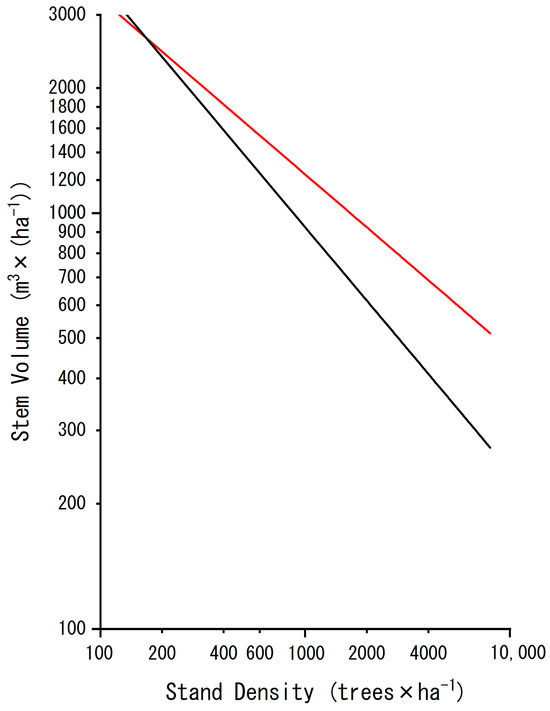
Figure 3.
Comparison with the existing full density curve (black isoline) and full density curve calculated in this study (red isoline). Up to a density of 167 trees × ha−1, the full density curve in this study was positioned above the existing curve. The corresponding stem volume at that point was 2644 m3 × (ha−1).
4. Discussion
The full density curve shows the upper limit of stand density with respect to the arbitrary mean stem volume [6,51]. It indicates the limit beyond which the density cannot increase further and is considered the most important factor in SDMDs. However, based on our forest resource surveys of the Hinoki cypress stands, it is evident that stands exceeding the full density curve exist. Moreover, this study revealed that compared to the existing SDMDs, the upper limit of stem volume per unit area is increased for high-density forests, as shown in Figure 3.
In Table 1, the mortality rates of the survey plots are shown. The average mortality rate is 4.4%, with a standard deviation of 4.0. The full density curve is adaptable to populations that exhibit mortality rates dependent on density. Given the low mortality rate in the study area used in this research, it is believed that it represents a population with mortality rates dependent on stand density. Therefore, it seems possible to adapt the full density curve.
In Japan, according to typical forest practice, Hinoki (C. obtusa) was planted at 3000 trees per hectare [52]. The natural mortality of Hinoki in a human-made forest with the typical planting pattern of 3000 trees per hectare would follow the trend along the natural thinning curve (red isoline) with competition for 3000 trees per hectare, as shown in Figure 1.
The following factors can explain the increase in the upper limit of the full density curve: First, there was a delay in the thinning of the Japanese cedar and Hinoki cypress plantations in Japan. In fact, in the fiscal year 2019, although thinning was planned for 452,000 ha nationwide, it was implemented in an area of only 365,000 ha [41]. Furthermore, considering the age structure of Japanese plantations, plantations exceeding the standard harvest age of 50 years accounted for 50% of the total plantation area [41]. In other words, there are many high-density, aging plantations in Japan where forest maintenance practices, such as thinning, are not conducted. This is likely the case in the Hinoki cypress forests in the Kyushu region, which were the focus of this study. We found an increase in the upper limit of stem volume per unit area in the Hinoki cypress forests in the Kyushu region. Therefore, the volume estimates for the Hinoki cypress in this region, calculated using the existing SDMDs, are believed to be underestimated. Egusa et al. [4] indicated that forest carbon storage estimated from yield tables created before 1970, which were used to estimate the total stem volume nationwide, accounted for only 58%–64% of the carbon storage estimated from the recent NFI, thus indicating a significant underestimation. These results support the conclusions of Egusa et al. [4].
According to the survey results of the NFI conducted by the Forestry Agency from the fiscal year 2014 to 2018, forest accumulation in Japan was approximately 8.6 billion m3 [53]. In contrast, the estimated forest accumulation based on the existing data, such as yield tables, was approximately 5.6 billion m3. Although the survey methods differed between the NFI and the estimates based on the existing data, such as yield tables, the total forest accumulation in Japan significantly differed. For basic reference materials for policy considerations, the estimated forest accumulation based on the existing data was utilized [54]. Owing to the large discrepancy between the NFI and existing data, it is necessary to improve the calculation accuracy of Japan’s forest accumulation.
Second, another possible factor for the change in the slope of the full density curve, as shown in Figure 2, is the age structure of the data used to create the SDMDs. In Japan, during and after World War II, many forests were harvested because of the high demand for timber. Widescale reforestation occurred from the 1950s to the 1960s [52]. The existing SDMDs [43,44] were adjusted for 1982. It is believed that there were hardly any old stands exceeding 50 years of age during the 1970s and 1980s. On examining the data used to create SDMDs for privately owned Hinoki cypress plantations in the Kyushu region, which were adjusted in 1982 [44], we found that the highest age was 79 years. Although this study focused on SDMDs in national forests, the age structure of national forests in the early 1980s was believed to be similar to that of private forests. Long-rotation management in Japan requires approximately double the standard harvest age. The standard harvest age for Hinoki cypress in the Kyushu region is 45 years [55], implying that the long-rotation management of Hinoki cypress forests in the Kyushu region would be 90 years or older. In this case, the existing SDMDs, which are assumed to lack data on old stands, would be difficult to implement for long-rotation management. Therefore, this condition is considered to be a reason for the underestimation of the full density curve in the SDMDs.
Third, the increase in the upper limit of the full density curve, as observed in this study, indicates that the growth of Hinoki cypress in the Kyushu region is greater than previously predicted. This increase in growth can be attributed to the recent increase in atmospheric CO2 concentrations and the effects of global warming [4,56].
Increasing temperatures promote plant growth [4,57,58]. Japan’s forests are located in a mid-latitude region and are part of the Asian Monsoon. In this region, the annual average temperature and solar radiation significantly influence the net primary productivity of forests [59,60,61]. Owing to recent climate change, temperatures have increased, along with an increase in the quantity of solar radiation due to reduced cloud cover. Therefore, forest growth in Japan is highly likely to have increased. Additionally, since the 1980s, increasing air pollutant emissions, particularly in China, have had a significant impact on nitrogen deposition in Japan [62,63]. Forest carbon uptake is greatly enhanced by nitrogen deposition [64,65,66,67]. Based on these factors, the increases in temperature and atmospheric CO2 concentration due to global warming and the increase in nitrogen deposition may contribute to an increase in net primary productivity and, subsequently, an increase in forest accumulation (forest stock) in Japan. Furthermore, the anthropogenic impacts of climate change, such as global warming and nitrogen deposition, may be factors contributing to the upward shift of the full density curve.
However, this study focused specifically on Hinoki plantation stands in Kyushu Island, and further research is needed to validate and generalize our findings to other regions and tree species. Future studies should also explore the applicability of the developed equations and their relationships with different stand types and forest management objectives.
5. Conclusions
By incorporating these new relationships and statistically significant equations into SDMDs, forest managers and planners will gain a more accurate tool for assessing and managing Hinoki plantation stands in the national forests of Kyushu Island. This improvement in the SDMDs could also contribute to improved forest management practices, leading to the more effective planning and implementation of forest management strategies.
Overall, this study provides valuable insights into the alignment between the current full density curve in the SDMD and the characteristics of existing Hinoki plantation stands. These results will contribute to ongoing efforts to enhance forest management practices in Japan, particularly in relation to Hinoki forestry, and pave the way for future advancements in SDMD modeling and its application in forest planning and management.
Funding
This study was supported by the program “Commissioned research project in FY2023 to study methods for promoting the advancement of forest information” of the Forest Agency, Japan, and by the program “Collecting of forest growth data in growth and yield experimental sites” of the Forestry and Forest Products Research Institute (FFPRI).
Data Availability Statement
The data that support the findings of this study are available from the FFPRI, but restrictions apply to the availability of these data, which were used under license for the current study and are thus not publicly available. However, data are available from the FFPRI upon reasonable request.
Acknowledgments
The author thanks the staff members of the Kyushu Research Center, FFPRI, who conducted the field survey. The author also thanks the staff members of the Kyushu Regional Forest Office, Forest Agency, Ministry of Agriculture, Forestry, and Fisheries, Japan, who installed the survey plots and maintained them over an extended period.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. Forestry 2008, 81, 13–31. [Google Scholar] [CrossRef]
- Socha, J.; Tymińska-Czabańska, L.; Grabska, E.; Orzeł, S. Site index models for main forest-forming tree species in Poland. Forests 2020, 11, 301. [Google Scholar] [CrossRef]
- Brandl, S.; Mette, T.; Falk, W.; Vallet, P.; Rötzer, T.; Pretzsch, H. Static site indices from different national forest inventories: Harmonization and prediction from site conditions. Ann. For. Sci. 2018, 75, 56. [Google Scholar] [CrossRef]
- Egusa, T.; Kumagai, T.; Shiraishi, N. Carbon stock in Japanese forests has been greatly underestimated. Sci. Rep. 2020, 10, 7895. [Google Scholar] [CrossRef] [PubMed]
- Ando, T. Growth analysis on the natural stands of Japanese red pine (Pinus densiflora Sieb. et Zucc). II. Analysis of stand density and growth. Bull. Govern. For. Exp. Stn. 1962, 147, 45–77, (In Japanese with English summary). [Google Scholar]
- Ando, T. Ecological studies on the stand density control in even-aged pure stand. Bull. Govern. For. Exp. Stn. 1968, 210, 1–153, (In Japanese with English summary). [Google Scholar]
- Tadaki, Y. The preestimating of stem yield based on the competition density effect. Bull. Govern. For. Exp. Stn. 1963, 154, 1–19, (In Japanese with English summary). [Google Scholar]
- Aiba, Y. Effects of cultural system on the growth of Sugi-plantations (Cryptomeria japonica). II. A tendency of the constant in final stem volume yield of stands under actual stand density. J. Jpn. For. Soc. 1975, 57, 39–44, (In Japanese with English summary). [Google Scholar]
- Aiba, Y. Effects of cultural system on the growth of Sugi-plantations (Cryptomeria japonica). III. Estimate of the stem volume yield under actual stand density (H-D-p-V diagram). J. Jpn. For. Soc. 1975, 57, 67–73, (In Japanese with English summary). [Google Scholar]
- Drew, T.J.; Flewelling, J.W. Some recent Japanese theories of yield-density relationship and their application to Monterey pine plantation. For. Sci. 1977, 23, 517–534. [Google Scholar] [CrossRef]
- Drew, T.J.; Flewelling, J.W. Stand density management: An alternative approach and its application to Douglas-fir plantations. For. Sci. 1979, 25, 518–532. [Google Scholar] [CrossRef]
- Newton, P.F.; Weetman, G.F. Stand density management diagrams and their development utility in black spruce management. For. Chron. 1993, 69, 421–430. [Google Scholar] [CrossRef]
- Newton, P.F.; Weetman, G.F. Stand density management diagram for managed black spruce stands. For. Chron. 1994, 70, 65–74. [Google Scholar] [CrossRef]
- Castedo-Dorado, F.; Crecente-Campo, F.; Alvarez-Alvarez, P.; Barrio-Anta, M. Development of a stand density management diagram for radiata pine stands including assessment of stand stability. Forestry 2009, 82, 1–16. [Google Scholar] [CrossRef]
- Goodale, C.L.; Apps, M.J.; Birdsey, R.A.; Field, C.B.; Heath, L.S.; Houghton, R.A.; Jenkins, J.C.; Kohlmaier, G.H.; Kurz, W.; Liu, S.; et al. Forest carbon sinks in the northern hemisphere. Ecol. Appl. 2002, 12, 891–899. [Google Scholar] [CrossRef]
- Kauppi, P.E.; Mielikäinen, K.; Kuusela, K. Biomass and carbon budget of European forests, 1971 to 1990. Science 1992, 256, 70–74. [Google Scholar] [CrossRef]
- Shvidenko, A.; Nilsson, S. Dynamics of Russian forests and the carbon budget in 1961–1998: An assessment based on long-term forest inventory data. Clim. Chang. 2002, 55, 5–37. [Google Scholar] [CrossRef]
- Birdsey, R.A.; Plantinga, A.J.; Heath, L.S. Past and prospective carbon storage in United States forests. For. Ecol. Manag. 1993, 58, 33–40. [Google Scholar] [CrossRef]
- Ciais, P.; Schelhaas, M.J.; Zaehle, S.; Piao, S.L.; Cescatti, A.; Liski, J.; Luyssaert, S.; Le-Maire, G.; Schulze, E.-D.; Bouriaud, O.; et al. Carbon accumulation in European forests. Nat. Geosci. 2008, 1, 425–429. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef]
- Kauppi, P.E.; Rautiainen, A.; Korhonen, K.T.; Lehtonen, A.; Liski, J.; Nöjd, P.; Tuominen, S.; Haakana, M.; Virtanen, T. Changing stock of biomass carbon in a boreal forest over 93 years. For. Ecol. Manag. 2010, 259, 1239–1244. [Google Scholar] [CrossRef]
- Kurz, W.A.; Apps, M.J.A. A 70-year retrospective analysis of carbon fluxes in the Canadian forest sector. Ecol. Appl. 1999, 9, 526–547. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent Carbon sink in the World’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Eggers, J.; Lindner, M.; Zudin, S.; Zaehle, S.; Liski, J. Impact of Changing wood demand, climate and land use on European forest resources and carbon stocks during the 21st century. Glob. Chang. Biol. 2008, 14, 2288–2303. [Google Scholar] [CrossRef]
- Hu, H.; Wang, S.; Guo, Z.; Xu, B.; Fang, J. The stage-classified matrix models project a significant increase in biomass carbon stocks in China’s forests between 2005 and 2050. Sci. Rep. 2015, 5, 11203. [Google Scholar] [CrossRef] [PubMed]
- Wear, D.N.; Coulston, J.W. From sink to source: Regional variation in U.S. forest carbon futures. Sci. Rep. 2015, 5, 16518. [Google Scholar] [CrossRef] [PubMed]
- Nagahama, T. Preparation of the original stand density control diagram for Sugi (Cryptomeria japonica) plantations in Kagoshima Prefecture. Bull. Kagoshima Prefect. For. Exp. Stn. 2003, 8, 1–11, (In Japanese with English summary). [Google Scholar]
- Nagahama, T. Management standard for Hinoki (Chamaecyparis obtusa) plantations applied to long-rotation management in Kagoshima Prefecture. Bull. Kagoshima Prefect. For. Exp. Stn. 2006, 9, 7–25, (In Japanese with English summary). [Google Scholar]
- Nagahama, T.; Kondoh, H. Improved yield prediction information for Sugi (Cryptomeria japonica) plantations applied to long-rotation management in Kagoshima Prefecture. J. Jpn. For. Soc. 2006, 88, 71–78, (In Japanese with English summary). [Google Scholar] [CrossRef][Green Version]
- Maeda, H. Management standard for Hinoki (Chamaecyparis obtusa) plantation applied to long-term management in Nagasaki Prefecture. Bull. Nagasaki Agric. For. Techn. Dev. Cent. 2012, 3, 53–65, (In Japanese with English summary). [Google Scholar]
- Narazaki, K.; Maeda, H.; Sasaki, S. Preparation of a stand density control diagram and a site index curve for Sugi (Cryptomeria japonica) plantation to construct a system yield table in Fukuoka Prefecture. Bull. Fukuoka Agric. For. Res. Cent. 2015, 1, 38–43, (In Japanese with English summary). [Google Scholar]
- Yamashita, Y.; Kondoh, H. Estimation of site index and yield tables and construction of a software of local yield tables for Sugi (Cryptomeria japonica D. Don) and hinoki (Chamaecyparis obtusa Sieb. et Zucc.) plantations in Wakayama Prefecture. Bull. Wakayama Prefect. Exp. Station. Agric. 2017, 5, 115–132. [Google Scholar]
- Ōita Prefecture. Report on the Survey of Revised Yield Tables for Ōita Prefecture; Obana Pringing Co.: Ōita, Japan, 2019; 29p. (In Japanese) [Google Scholar]
- Newton, P.F. Stand density management diagrams: Review of their development and utility in stand-level management planning. For. Ecol. Manag. 1997, 98, 251–265. [Google Scholar] [CrossRef]
- Newton, P.F.; Amponsah, I.G. Evaluation of Weibull-based parameter prediction equation systems for black spruce and jack pine stand types within the context of developing structural stand density management diagrams. Can. J. For. Res. 2005, 35, 2996–3010. [Google Scholar] [CrossRef]
- Newton, P.F.; Lei, Y.; Zhang, S.Y. Stand-level diameter distribution yield model for black spruce plantations. For. Ecol. Manag. 2005, 209, 181–192. [Google Scholar] [CrossRef]
- Tang, X.; Pérez-Cruzado, C.; Vor, T.; Fehrmann, L.; Álvarez-González, J.G.; Kleinn, C. Development of stand density management diagrams for Chinese fir plantations. Forestry 2016, 89, 36–45. [Google Scholar] [CrossRef]
- Kondoh, H. The adaptation of the complete enumeration data in the old-age forest to the stand density control diagram. J. For. Res. Kyushu 1998, 51, 9–10. (In Japanese) [Google Scholar]
- Fukuda, M.; Iehara, T.; Matsumoto, M. Carbon stock estimates for Sugi and Hinoki forests in Japan. For. Ecol. Manag. 2003, 184, 1–16. [Google Scholar] [CrossRef]
- Forestry Agency. Current Status of Forest Resources; Ministry of Agriculture, Forestry and Fisheries: Tokyo, Japan, 2023; Available online: https://www.rinya.maff.go.jp/j/keikaku/genkyou/h29/index.html (accessed on 8 May 2023). (In Japanese)
- Forestry Agency. Annual Report on Forest and Forestry in Japan. Fiscal Year 2021; Ministry of Agriculture, Forestry and Fisheries: Tokyo, Japan, 2022; 46p. [Google Scholar]
- Dzierzon, H.; Mason, E.G. Towards a nationwide growth and yield model for radiata pine plantations in New Zealand. Can. J. For. Res. 2006, 36, 2533–2543. [Google Scholar] [CrossRef]
- Forestry Agency. Stand Density Management Diagrams of Hinoki Artificial Forest Stands on National Forest in Kyushu District; Ministry of Agriculture, Forestry and Fisheries: Tokyo, Japan, 1982; 6p. (In Japanese) [Google Scholar]
- Forestry Agency. Stand Density Management Diagrams of Hinoki Artificial Forest Stands in Kyushu District; Ministry of Agriculture, Forestry and Fisheries: Tokyo, Japan, 1982; 25p. (In Japanese) [Google Scholar]
- Kira, T.; Ogawa, H.; Sakazaki, N. Intraspecific competition among higher plants. I. Competition-yield-density interrelationship in regularly dispersed populations. J. Polytech. Inst. Osaka City Univ. D 1953, 4, 1–16. [Google Scholar]
- Ando, T. Stand Density Management; Norinshuppan: Tokyo, Japan, 1982; 126p. (In Japanese) [Google Scholar]
- Japan Forest Technical Association. Stand Density Management Diagram of Artificial Forest; Japan Forest Technical Association: Tokyo, Japan, 1999; 15p. (In Japanese) [Google Scholar]
- Manabe, A. Constructing of stand density control diagram. Bull. Comput. Cent. Res. Agric. For. Fish. 1975, 11, 27–121. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 28 June 2023).
- Tadaki, Y. Effect of Thinning on Stem Volume Yield studied with Competition-Density Effect—On the case of Pinus densiflora. Bull. Govern. For. Exp. Stn. 1964, 166, 1–22, (In Japanese with English Summary). [Google Scholar]
- Sasse, J. The Forests of Japan; Japan Forest Technical Association: Tokyo, Japan, 1998; 75p. [Google Scholar]
- Forestry Agency. Forest Ecosystem Diversity Basic Survey; Ministry of Agriculture, Forestry and Fisheries: Tokyo, Japan, 2023; Available online: https://www.rinya.maff.go.jp/j/keikaku/tayouseichousa/attach/pdf/index-1.pdf (accessed on 30 May 2023). (In Japanese)
- Japan Forestry Investigation Committee 2023 RINSEI NEWS; Japan Forestry Investigation Committee: Tokyo, Japan, 2023; Volume 700, pp. 21–22. (In Japanese)
- Japan FAO Association. Forests and Forestry in Japan; Japan FAO Association: Tokyo, Japan, 1997; 64p. [Google Scholar]
- Booth, B.B.B.; Jones, D.C.; Collins, M.; Totterdell, J.I.; Cox, M.P.; Sitch, S.; Huntingford, C.; Betts, A.R.; Harris, A.R.; Harris, R.G.; et al. High sensitivity of future global warming to land carbon cycle processes. Environ. Res. Lett. 2012, 7, 021002. [Google Scholar] [CrossRef]
- Chung, H.; Muraoka, H.; Nakamura, M.; Han, S.; Muller, O.; Son, Y. Experimental warming studies on tree species and forest ecosystems: A literature review. J. Plant Res. 2013, 126, 447–460. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Kato, T.; Tang, Y. Spatial variability and major controlling factors of CO2 sink strength in Asia terrestrial ecosystems: Evidence from eddy covariance data. Glob. Chang. Biol. 2008, 14, 2333–2348. [Google Scholar] [CrossRef]
- Kondo, M.; Saitoh, T.M.; Sato, H.; Ichii, K. Comprehensive synthesis of spatial variability in carbon flux across monsoon Asian forests. Agric. For. Meteorol. 2017, 232, 623–634. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef]
- Oren, R.; Ellsworth, S.D.; Johnsen, H.K.; Phillips, N.; Ewers, E.B.; Maier, C.; Schäfer, V.R.K.; McCarthy, H.; Hendrey, G.; McNulty, G.S.; et al. Soil fertility limits carbon sequestration by forest ecosystems in a CO2-enriched atmosphere. Nature 2001, 411, 469–472. [Google Scholar] [CrossRef]
- Piao, S.; Sitch, S.; Ciais, P.; Friedlingstein, P.; Peylin, P.; Wang, X.; Ahlström, A.; Anav, A.; Canadell, J.G.; Cong, N.; et al. Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends. Glob. Chang. Biol. 2013, 19, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Magnani, F.; Mencuccini, M.; Borghetti, M.; Berbigier, P.; Berninger, F.; Delzon, S.; Grelle, A.; Hari, P.; Jarvis, P.G.; Kolari, P.; et al. The human footprint in the carbon cycle of temperate and boreal forests. Nature 2007, 447, 848–850. [Google Scholar] [CrossRef] [PubMed]
- Morino, Y.; Ohara, T.; Kurokawa, J.; Kuribayashi, M.; Uno, I.; Hara, H. Temporal variations of nitrogen wet deposition across Japan from 1989 to 2008. J. Geophys. Res. 2011, 116, D06307. [Google Scholar] [CrossRef]
- Norby, R.J.; Warren, J.M.; Iversen, C.M.; Medlyn, B.E.; McMurtrie, R.E. CO2 enhancement of forest productivity constrained by limited nitrogen availability. Proc. Natl Acad. Sci. USA 2010, 107, 19368–19373. [Google Scholar] [CrossRef]
- Wenzel, S.; Cox, P.M.; Eyring, V.; Friedlingstein, P. Projected land photosynthesis constrained by changes in the seasonal cycle of atmospheric CO2. Nature 2016, 538, 499–501. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).