Biological Rotation Age of Community Teak (Tectona grandis) Plantation Based on the Volume, Biomass, and Price Growth Curve Determined through the Analysis of Its Tree Ring Digitization
Abstract
1. Introduction
2. Materials and Methods
2.1. Tree Ring Circumference Digitization
2.2. Annual Tree Ring Elliptical Curve Fitting
2.3. Mathematical Prediction for the Reaction Wood Location
2.4. Tree Age-Related Dimension Estimation
2.5. Price and Dimension Inter-Correlation
2.6. Growth Curve, Increment, and Biological Rotation Age
3. Results
3.1. The Tree Ring Analysis
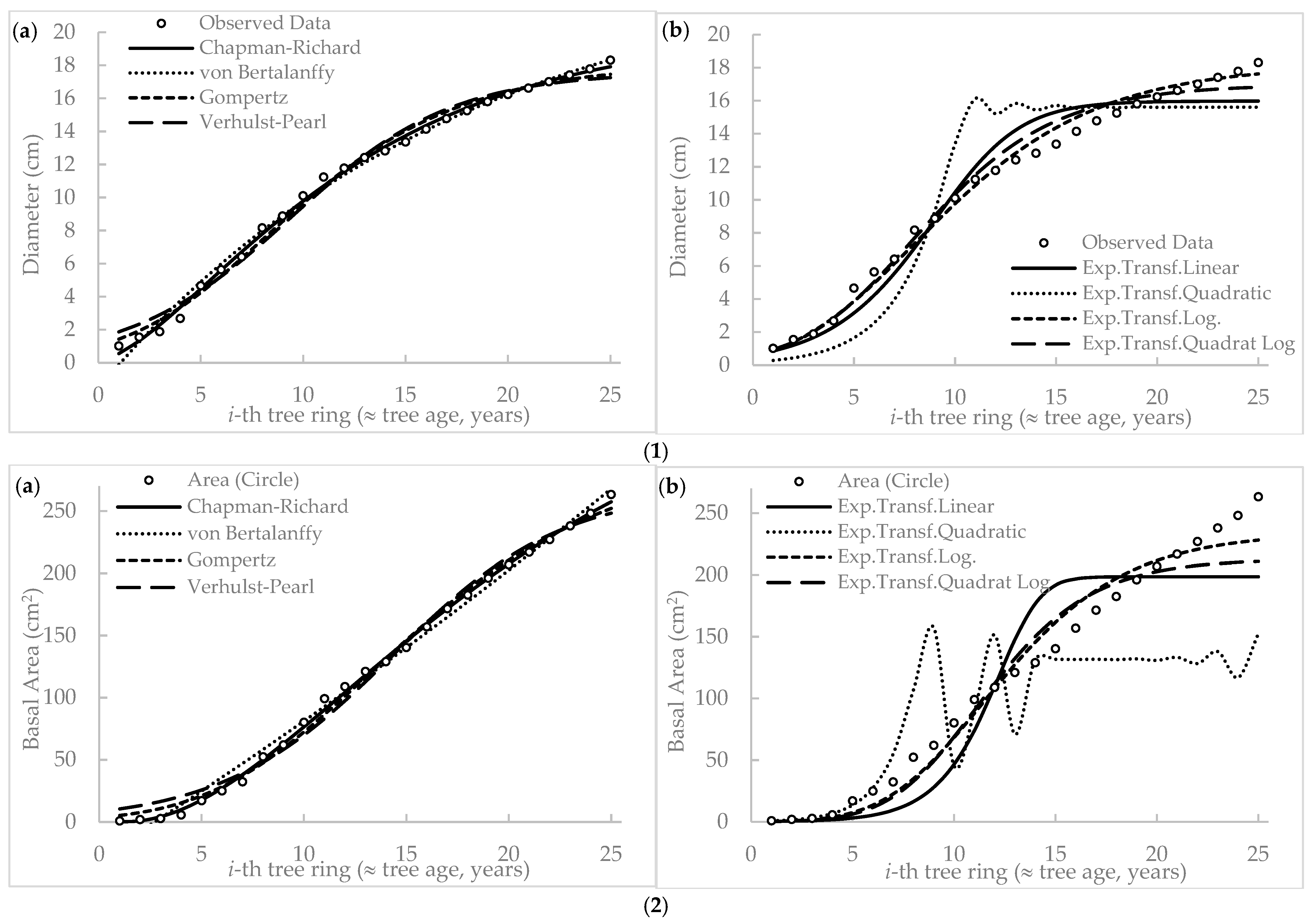
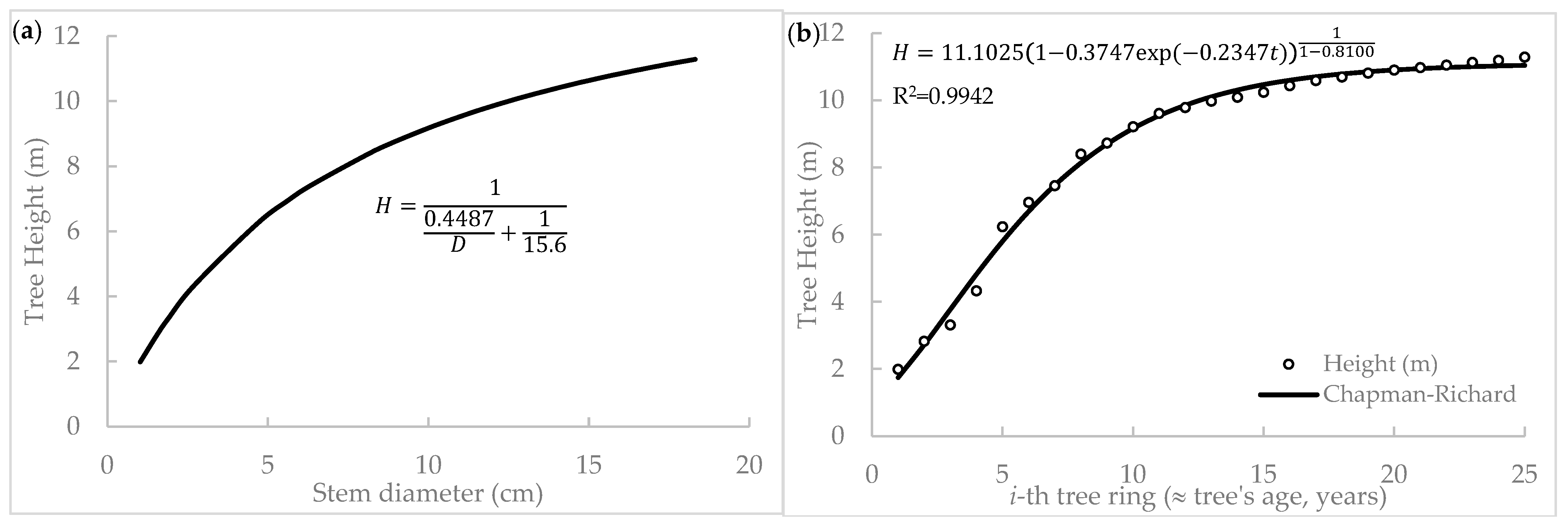
3.2. The Growth Curve Estimation
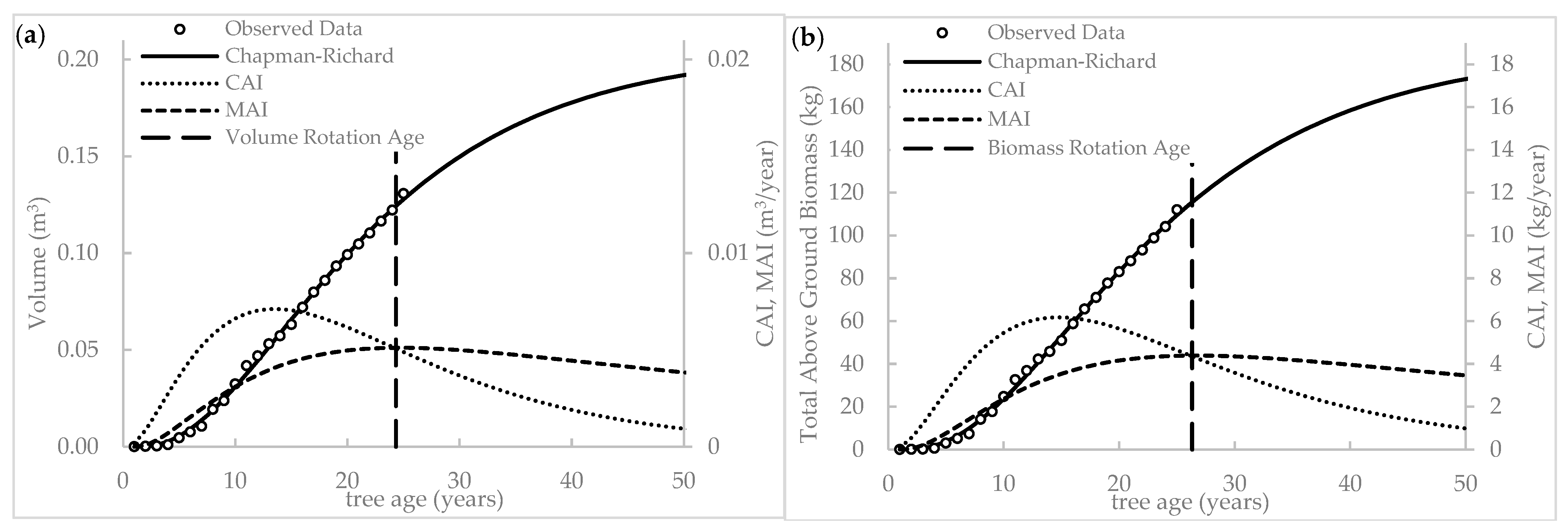
3.3. Biological Rotation Age Prediction
3.3.1. Volume- and Biomass-Based Rotation Age
3.3.2. Price-Based Rotation Age
4. Discussion
4.1. Community’s Teak Plantation
4.2. Tree Ring Analysis
4.3. Growth Curve
4.4. Increment and Biological Rotation Age
5. Future Work
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gua, B.; Pedersen, A.; Barstow, M. Tectona Grandis. The IUCN Red List of Threatened Species 2022: E.T62019830A62019832. Available online: https://www.iucnredlist.org/species/62019830/62019832#assessment-information (accessed on 25 June 2023).
- Budiono, R.; Nugroho, B.; Hardjanto; Nurrochmat, D.R. Dinamika Hegemoni Penguasaan Hutan Di Indonesia (The Dynamics of Forest Hegemony in Indonesia). J. Anal. Kebijak. Kehutan. 2018, 15, 113–125. [Google Scholar] [CrossRef]
- Nugroho, H.Y.S.H.; Indrajaya, Y.; Astana, S.; Murniati; Suharti, S.; Basuki, T.M.; Yuwati, T.W.; Putra, P.B.; Narendra, B.H.; Abdulah, L.; et al. A Chronicle of Indonesia’s Forest Management: A Long Step towards Environmental Sustainability and Community Welfare. Land 2023, 12, 1238. [Google Scholar] [CrossRef]
- Peluso, N.L. The History of State Forest Management in Colonial Java. For. Conserv. Hist. 1991, 35, 65–75. [Google Scholar] [CrossRef]
- Boomgaard, P. Forest Management and Exploitation in Colonial Java, 1677–1897. For. Conserv. Hist. 1992, 36, 4–14. [Google Scholar] [CrossRef]
- Moore, J.E.; Mascarenhas, A.; Bain, J.; Straus, S.E. Developing a Comprehensive Definition of Sustainability. Implement. Sci. 2017, 12, 110. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kamarulzaman, N.H.; Vijayan, G.; Vaiappuri, S.K.N. Sustainability: A Comprehensive Literature. In Handbook of Research on Global Supply Chain Management; Christiansen, B., Ed.; IGI Global: Hershey, PA, USA, 2016; pp. 248–268. ISBN 9781466696402. [Google Scholar]
- Gaitan-Alvarez, J.; Moya, R.; Berrocal, A. The Use of X-ray Densitometry to Evaluate the Wood Density Profile of Tectona Grandis Trees Growing in Fast-Growth Plantations. Dendrochronologia 2019, 55, 71–79. [Google Scholar] [CrossRef]
- Patel, V.R.; Pramod, S.; Rao, K.S. Cambial Activity, Annual Rhythm of Xylem Production in Relation to Phenology and Climatic Factors and Lignification Pattern during Xylogenesis in Drum-Stick Tree (Moringa oleifera). Flora-Morphol. Distrib. Funct. Ecol. Plants 2014, 209, 556–566. [Google Scholar] [CrossRef]
- Buajan, S.; Songtrirat, P.; Muangsong, C. Relationship of Cambial Activity and Xylem Production in Teak (Tectona Grandis) to Phenology and Climatic Variables in North-Western Thailand. J. Trop. For. Sci. 2023, 35, 141–156. [Google Scholar] [CrossRef]
- Karlinasari, L.; Bahtiar, E.T.; Kadir, A.S.A.; Adzkia, U.; Nugroho, N.; Siregar, I.Z. Structural Analysis of Self-Weight Loading Standing Trees to Determine Its Critical Buckling Height. Sustainability 2023, 15, 6075. [Google Scholar] [CrossRef]
- Dargahi, M.; Newson, T.; Moore, J. Buckling Behaviour of Trees under Self-Weight Loading. For. An Int. J. For. Res. 2019, 92, 393–405. [Google Scholar] [CrossRef]
- Leblicq, T.; Vanmaercke, S.; Ramon, H.; Saeys, W. Mechanical Analysis of the Bending Behaviour of Plant Stems. Biosyst. Eng. 2015, 129, 87–99. [Google Scholar] [CrossRef]
- Spatz, H.-C.; Bruechert, F. Basic Biomechanics of Self-Supporting Plants: Wind Loads and Gravitational Loads on a Norway Spruce Tree. For. Ecol. Manag. 2000, 135, 33–44. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Hsu, F.-L.; Lee, C.-M.; Juang, J.-Y. Failure Mechanism of Hollow Tree Trunks Due to Cross-Sectional Flattening. R. Soc. Open Sci. 2017, 4, 160972. [Google Scholar] [CrossRef]
- Bahtiar, E.T. Kekuatan Material: Teori, Contoh Kasus, Dan Penyelesaian, 1st ed.; Gumelar, A.D., Ed.; Penerbit IPB Press: Bogor, Indonesia, 2018; ISBN 978-602-440-576-2. [Google Scholar]
- Timoshenko, S. Strength of Materials. Nature 1942, 150, 645. [Google Scholar] [CrossRef]
- Akachuku, A.E.; Abolarin, D.A.O. Variations in Pith Eccentricity and Ring Width in Teak (Tectona grandis L. F.). Trees 1989, 3, 111–116. [Google Scholar] [CrossRef]
- Venugopal, N.; Khrisnamurthy, K.V. Seasonal Production of Secondary Phloem in the Twigs of Certain Tropical Timber Trees. Ann. Bot. 1987, 60, 61–67. [Google Scholar] [CrossRef]
- Denih, A.; Putra, G.R.; Kurniawan, Z.; Bahtiar, E.T. Developing a Model for Curve-Fitting a Tree Stem’s Cross-Sectional Shape and Sapwood–Heartwood Transition in a Polar Diagram System Using Nonlinear Regression. Forests 2023, 14, 1102. [Google Scholar] [CrossRef]
- Purwanto, R.H.; Silaban, M. Inventore Biomasa Dan Karbon Jenis Jati (Tectona grandis L.f.) Di Hutan Rakyat Desa Jatimulyo, Karanganyar. J. Ilmu Kehutan. 2011, 5, 40–50. [Google Scholar] [CrossRef]
- Samawal, M. Thoughts and Rectifications for Verhulst Growth Model: A Scientific Mathematization for a General Theory of Growth Led to a Fundamental Law of Growth. SSRN Electron. J. 2023. [CrossRef]
- Gatto, M.; Muratori, S.; Rinaldi, S. A Functional Interpretation of the Logistic Equation. Ecol. Modell. 1988, 42, 155–159. [Google Scholar] [CrossRef]
- Verhulst, P.F. Recherches Mathématiques Sur La Loi d’accroissement de La Population; Nouveaux Mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles: Bruxelles, Belgium, 1820; pp. 1–40. [Google Scholar]
- David, H.A.; Edwards, A.W.F. The Logistic Growth Curve. In Annotated Readings in the History of Statistics. Springer Series in Statistics; Springer: New York, NY, USA, 2001; pp. 65–67. [Google Scholar]
- Gompertz, B. On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies. In a Letter to Francis Baily, Esq. F. R. S. &C. Philos. Trans. R. Soc. London 1825, 115, 513–583. [Google Scholar] [CrossRef]
- Kyurkchiev, V.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. On a Piecewise Smooth Gompertz Growth Function. Applications. In Proceedings of the New Trends in the Applications of Differential Equations in Sciences, Sozopol, Bulgaria, 14–17 June 2022; NTADES 2022; Springer Proceedings in Mathematics & Statistics. Slavova, A., Ed.; Springer: Cham, Switzerland, 2022; Volume 412, pp. 461–472. [Google Scholar]
- Fang, S.-L.; Kuo, Y.-H.; Kang, L.; Chen, C.-C.; Hsieh, C.-Y.; Yao, M.-H.; Kuo, B.-J. Using Sigmoid Growth Models to Simulate Greenhouse Tomato Growth and Development. Horticulturae 2022, 8, 1021. [Google Scholar] [CrossRef]
- Tjørve, K.M.C.; Tjørve, E. The Use of Gompertz Models in Growth Analyses, and New Gompertz-Model Approach: An Addition to the Unified-Richards Family. PLoS ONE 2017, 12, e0178691. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Bartesaghi, P. From Networked SIS Model to the Gompertz Function. Appl. Math. Comput. 2022, 419, 126882. [Google Scholar] [CrossRef]
- Gultom, F.R.P.; Solimun, S.; Nurjannah, N. Bootstrap Resampling in Gompertz Growth Model with Levenberg–Marquardt Iteration. JTAM (Jurnal Teor. Apl. Mat.) 2022, 6, 810. [Google Scholar] [CrossRef]
- Lee, L.; Atkinson, D.; Hirst, A.G.; Cornell, S.J. A New Framework for Growth Curve Fitting Based on the von Bertalanffy Growth Function. Sci. Rep. 2020, 10, 7953. [Google Scholar] [CrossRef]
- Croll, J.C.; van Kooten, T. Accounting for Temporal and Individual Variation in the Estimation of Von Bertalanffy Growth Curves. Ecol. Evol. 2022, 12, e9619. [Google Scholar] [CrossRef]
- von Bertalanffy, L. Quantitative Laws in Metabolism and Growth. Q. Rev. Biol. 1957, 32, 217–231. [Google Scholar] [CrossRef]
- Simpson, M.J.; Browning, A.P.; Warne, D.J.; Maclaren, O.J.; Baker, R.E. Parameter Identifiability and Model Selection for Sigmoid Population Growth Models. J. Theor. Biol. 2022, 535, 110998. [Google Scholar] [CrossRef]
- Jannatizadeh, A.; Rezaei, M.; Rohani, A.; Lawson, S.; Fatahi, R. Towards Modeling Growth of Apricot Fruit: Finding a Proper Growth Model. Hortic. Environ. Biotechnol. 2023, 64, 209–222. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Darwis, A. Exponential Curve Modification by Linear and Nonlinear Function to Fit the Fiber Length of Teakwood (Tectona Grandis). J. Biol. Sci. 2014, 14, 183–194. [Google Scholar] [CrossRef]
- Cahyono, T.D.; Wahyudi, I.; Priadi, T.; Febrianto, F.; Darmawan, W.; Bahtiar, E.T.; Ohorella, S.; Novriyanti, E. The Quality of 8 and 10 Years Old Samama Wood (Anthocephalus macrophyllus). J. Indian Acad. Wood Sci. 2015, 12, 22–28. [Google Scholar] [CrossRef]
- Ferrero, M.E.; Villalba, R.; Rivera, S.M. An Assessment of Growth Ring Identification in Subtropical Forests from Northwestern Argentina. Dendrochronologia 2014, 32, 113–119. [Google Scholar] [CrossRef]
- Kanzow, C.; Yamashita, N.; Fukushima, M. Levenberg–Marquardt Methods with Strong Local Convergence Properties for Solving Nonlinear Equations with Convex Constraints. J. Comput. Appl. Math. 2004, 172, 375–397. [Google Scholar] [CrossRef]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Lourakis, M.I.A. A Brief Description of the Levenberg-Marquardt Algorithm Implemened by Levmar; Heraklion: Crete, Greece, 2005. [Google Scholar]
- Firmanti, A.; Bachtiar, E.T.; Surjokusumo, S.; Komatsu, K.; Kawai, S. Mechanical Stress Grading of Tropical Timbers without Regard to Species. J. Wood Sci. 2005, 51, 339–347. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Trujillo, D.; Nugroho, N. Compression Resistance of Short Members as the Basis for Structural Grading of Guadua Angustifolia. Constr. Build. Mater. 2020, 249, 118759. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Imanullah, A.P.; Hermawan, D.; Nugroho, N. Abdurachman Structural Grading of Three Sympodial Bamboo Culms (Hitam, Andong, and Tali) Subjected to Axial Compressive Load. Eng. Struct. 2019, 181, 233–245. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Nugroho, N.; Rahman, M.M.; Arinana; Kartika Sari, R.; Wirawan, W.; Hermawan, D. Estimation the Remaining Service-Lifetime of Wooden Structure of Geothermal Cooling Tower. Case Stud. Constr. Mater. 2017, 6, 91–102. [Google Scholar] [CrossRef]
- Nugroho, N.; Bahtiar, E.T. Nurmadina Grading Development of Indonesian Bamboo Culm: Case Study on Tali Bamboo (Gigantochloa apus). In Proceedings of the 2018 World Conference on TImber Engineering, Seoul, Republic of Korea, 20–23 August 2018; pp. 1–6. [Google Scholar]
- Bahtiar, E.T.; Denih, A.; Putra, G.R. Multi-Culm Bamboo Composites as Sustainable Materials for Green Constructions: Section Properties and Column Behavior. Results Eng. 2023, 17, 100911. [Google Scholar] [CrossRef]
- Sylvayanti, S.P.; Nugroho, N.; Bahtiar, E.T. Bamboo Scrimber’s Physical and Mechanical Properties in Comparison to Four Structural Timber Species. Forests 2023, 14, 146. [Google Scholar] [CrossRef]
- Cahyono, T.D.; Wahyudi, I.; Priadi, T.; Febrianto, F.; Bahtiar, E.T.; Novriyanti, E. Analysis on Wood Quality, Geometry Factor, and Their Effects on Lathe Check of Samama (Anthocephalus macrophyllus) Veneer. J. Korean Wood Sci. Technol. 2016, 44, 828–841. [Google Scholar] [CrossRef]
- Nugroho, N.; Kartini; Bahtiar, E.T. Cross-Species Bamboo Grading Based on Flexural Properties. IOP Conf. Ser. Earth Environ. Sci. 2021, 891, 012008. [Google Scholar] [CrossRef]
- Nurmadina; Nugroho, N.; Bahtiar, E.T. Structural Grading of Gigantochloa Apus Bamboo Based on Its Flexural Properties. Constr. Build. Mater. 2017, 157, 1173–1189. [Google Scholar] [CrossRef]
- Darwis, A.; Nurrochmat, D.R.; Massijaya, M.Y.; Nugroho, N.; Alamsyah, E.M.; Bahtiar, E.T.; Safei, R. Vascular Bundle Distribution Effect on Density and Mechanical Properties of Oil Palm Trunk. Asian J. Plant Sci. 2013, 12, 208–213. [Google Scholar] [CrossRef]
- Arinana; Philippine, I.; Koesmaryono, Y.; Nandika, D.; Rauf, A.; Harahap, I.S.; Sumertajaya, I.M.; Bahtiar, E.T. Coptotermes Curvignathus Holmgren (Isoptera: Rhinotermitidae) Capability to Maintain the Temperature Inside Its Nests. J. Entomol. 2016, 13, 199–202. [Google Scholar] [CrossRef][Green Version]
- Bahtiar, E.T.; Erizal, E.; Hermawan, D.; Nugroho, N.; Hidayatullah, R. Experimental Study of Beam Stability Factor of Sawn Lumber Subjected to Concentrated Bending Loads at Several Points. Forests 2022, 13, 1480. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Arinana; Nugroho, N.; Nandika, D. Daily Cycle of Air Temperature and Relative Humidity Effect to Creep Deflection of Wood Component of Low-Cost House in Cibeureum-Bogor, West Java, Indonesia. Asian J. Sci. Res. 2014, 7, 501–512. [Google Scholar] [CrossRef][Green Version]
- Bahtiar, E.T.; Nugroho, N.; Karlinasari, L.; Surjokusumo, S. Human Comfort Period Outside and Inside Bamboo Stands. J. Environ. Sci. Technol. 2014, 7, 245–265. [Google Scholar] [CrossRef]
- Nugroho, N.; Bahtiar, E.T. Buckling Formulas for Designing a Column with Gigantochloa Apus. Case Stud. Constr. Mater. 2021, 14, e00516. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Malkowska, D.; Trujillo, D.; Nugroho, N. Experimental Study on Buckling Resistance of Guadua Angustifolia Bamboo Column. Eng. Struct. 2021, 228, 111548. [Google Scholar] [CrossRef]
- Hermawan, D.; Budiman, I.; Febrianto, F.; Subyakto, S.; Pari, G.; Ghozali, M.; Bahtiar, E.T.; Sutiawan, J.; Azevedo, A.R.G. de Enhancement of the Mechanical, Self-Healing and Pollutant Adsorption Properties of Mortar Reinforced with Empty Fruit Bunches and Shell Chars of Oil Palm. Polymers 2022, 14, 410. [Google Scholar] [CrossRef] [PubMed]
- Hartavia, E. Pemodelan Volume Batang Tegakan Jati Umur 9-13 Tahun Untuk Penaksiran Potensi Hutan Rakyat Di Kabupaten Pati. Ph.D. Thesis, Gadjah Mada University, Yogyakarta, Indonesia, 2019. [Google Scholar]
- Du, S.; Yamamoto, F. An Overview of the Biology of Reaction Wood Formation. J. Integr. Plant Biol. 2007, 49, 131–143. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Iswanto, A.H. Annual Tree-Ring Curve-Fitting for Graphing the Growth Curve and Determining the Increment and Cutting Cycle Period of Sungkai (Peronema canescens). Forests 2023, 14, 1643. [Google Scholar] [CrossRef]
- Zhao-gang, L.; Feng-ri, L. The Generalized Chapman-Richards Function and Applications to Tree and Stand Growth. J. For. Res. 2003, 14, 19–26. [Google Scholar] [CrossRef]
- Shifley, S.R.; Brand, G.J. Chapman-Richards Growth Function Constrained for Maximum Tree Size. For. Sci. 1984, 30, 1066–1070. [Google Scholar] [CrossRef]
- Verhulst, P.-F. Notice Sur La Loi Que La Population Suit Dans Son Accroissement. Corresp. Math. Phys. 1838, 10, 113–129. [Google Scholar]
- Tjørve, E.; Tjørve, K.M.C. A Unified Approach to the Richards-Model Family for Use in Growth Analyses: Why We Need Only Two Model Forms. J. Theor. Biol. 2010, 267, 417–425. [Google Scholar] [CrossRef]
- Atherton, C. Simple Jewelry-Silver Bound Boxes. Des. Stud. 1927, 29, 185–188. [Google Scholar]
- Tiwari, A.K. Bastar Handicrafts: The Visible Cultural Symbol of Bastar Region of Chhattisgarh. Int. J. Res. Humanit. Arts Lit. 2015, 3, 43–48. [Google Scholar]
- Udaykumar, S. Initial Exploration of the Woodcraft Techniques of Tamil Nadu. Wood Is Good Grow More Use More 2021, 1, 47–50. [Google Scholar]
- Dumarçay, J. Wood and Carpentry. In Construction Techniques in South and Southeast Asia; BRILL: Leiden, The Netherlands, 2005; pp. 21–35. [Google Scholar]
- Lookose, S. Traditional Teak Wood Articles Used in Households of Nilambur and Malapuram Areas of Kerala. Indian J. Tradit. Knowl. 2008, 7, 108–111. [Google Scholar]
- Kongprasert, N. Emotional Design Approach to Design Teak Wood Furniture. In Proceedings of the Asia Pacific Industrial Engineering & Management Systems Conference 2012, Phuket, Thailand, 2–5 December 2012; Kachitvichyanukul, V., Luong, H.T., Pitakaso, R., Eds.; pp. 805–812. [Google Scholar]
- Chen, T.L.; Hong, P.F. Study on the Visual Image of Armchairs Furniture in Yangming Shu Wu. Adv. Mater. Res. 2010, 168–170, 2371–2375. [Google Scholar] [CrossRef]
- Puspita, A.A.; Sachari, A.; Sriwarno, A.B. Design Adaptation of Wooden Furniture through Sustainability Design Strategy (Case Studies: Five Furniture Industries in Central Java, Indonesia). Arts Des. Stud. 2016, 45, 1–13. [Google Scholar]
- Siahaan, H.; Wahyudi, I. Keragaan Permesinan Dan Keteguhan Rekat Kayu Jati Cepat Tumbuh Terdensifikasi. J. Ilmu Pertan. Indones. 2020, 26, 1–7. [Google Scholar] [CrossRef]
- Suranto, Y. Effect of Breeding Technology and Trunk Axial Position on Shrinkage and Quality of 10 Year Old Teak Wood as a Furniture’s Raw Material. IOP Conf. Ser. Mater. Sci. Eng. 2020, 935, 012037. [Google Scholar] [CrossRef]
- Afiyah, S.N.; Syaifuddin, M.; Aqromi, N.L. Optimization of Teak Wood Furniture Production Using Linear Programming Method at Sumenep East Java Indonesia. Numer. J. Mat. Pendidik. Mat. 2022, 6, 13–24. [Google Scholar] [CrossRef]
- Sushardi; Prayitno, T.A.; Suranto, Y.; Lukmandaru, G. Distribution of Certified Wood Teak Wood Machining Properties as Export Furniture Materials. Hutan Trop. 2022, 16, 15–25. [Google Scholar] [CrossRef]
- Rani, M.F.B.A.; Daud, P.S.D.S.N.I.M. The Role of Wood in Current Sustainable Building in Thailand as Architectural Ornaments. In The Importance of Wood and Timber in Sustainable Buildings; Springer: Berlin/Heidelberg, Germany, 2022; pp. 19–47. [Google Scholar]
- Christian, R.R. Challenges of Teak Architecture Conservation in Myanmar; Architectural Conservation Working Paper Series; Architectural Conservation: Singapore, 2020. [Google Scholar]
- Prajwal, S.; Akashaya Kumar, V.H.; Patil, N.N. Implementation of Sustainable Materials in an Existing Residential Building and Comparison. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1166, 012038. [Google Scholar] [CrossRef]
- Tripati, S.; Shukla, S.R.; Shashikala, S.; Sardar, A. Role of Teak and Other Hardwoods in Shipbuilding as Evidenced from Literature and Shipwrecks. Curr. Sci. 2016, 111, 1262–1268. [Google Scholar]
- Rudman, P.; Da Costa, E.W.B.; Gay, F.J.; Wetherly, A.H. Relationship of Tectoquinone to Durability in Tectona Grandis. Nature 1958, 181, 721–722. [Google Scholar] [CrossRef]
- Singh, R.; Verma, K.K.; Choudhary, A.; Veena, S. Screening of Heartwood of Tectona Grandis Linn for Antifungal Activity. Samriddhi A J. Phys. Sci. Eng. Technol. 2021, 13, 111–114. [Google Scholar] [CrossRef]
- Vyas, P.; Yadav, D.K.; Khandelwal, P. Tectona Grandis (Teak)—A Review on Its Phytochemical and Therapeutic Potential. Nat. Prod. Res. 2019, 33, 2338–2354. [Google Scholar] [CrossRef]
- Agrawal, A.; Chopra, S. Sustainable Dyeing of Selected Natural and Synthetic Fabrics Using Waste Teak Leaves (Tectona grandis L.). Res. J. Text. Appar. 2020, 24, 357–374. [Google Scholar] [CrossRef]
- Qadariyah, L.; Mahfud, M.; Sulistiawati, E.; Swastika, P. Natural Dye Extraction From Teak Leaves (Tectona grandis) Using Ultrasound Assisted Extraction Method for Dyeing on Cotton Fabric. MATEC Web Conf. 2018, 156, 05004. [Google Scholar] [CrossRef]
- Tibkawin, N.; Suphrom, N.; Nuengchamnong, N.; Khorana, N.; Charoensit, P. Utilisation of Tectona Grandis (Teak) Leaf Extracts as Natural Hair Dyes. Color. Technol. 2022, 138, 355–367. [Google Scholar] [CrossRef]
- Alamu, Q.A.; Adara, P.P.; Kofoworola, A.M.; Oyeshola, H.O. Utilization of Extracted Natural Dye from Tectona Grandis (Teak) as a Sensitizer for Dye-Sensitized Solar Cell. Int. J. Sci. Adv. 2022, 3, 577–580. [Google Scholar] [CrossRef]
- Charoensit, P.; Sawasdipol, F.; Tibkawin, N.; Suphrom, N.; Khorana, N. Development of Natural Pigments from Tectona Grandis (Teak) Leaves: Agricultural Waste Material from Teak Plantations. Sustain. Chem. Pharm. 2021, 19, 100365. [Google Scholar] [CrossRef]
- Haryanto, A.; Hidayat, W.; Hasanudin, U.; Iryani, D.A.; Kim, S.; Lee, S.; Yoo, J. Valorization of Indonesian Wood Wastes through Pyrolysis: A Review. Energies 2021, 14, 1407. [Google Scholar] [CrossRef]
- Siabi, W.K.; Owusu-Ansah, E.D.-J.; Essandoh, H.M.K.; Asiedu, N.Y. Modelling the Adsorption of Iron and Manganese by Activated Carbon from Teak and Shea Charcoal for Continuous Low Flow. Water-Energy Nexus 2021, 4, 88–94. [Google Scholar] [CrossRef]
- Berrocal-Mendéz, N.; Moya, R. Production, Cost and Properties of Charcoal Produced after Logging and Sawing, by the Earth Pit Method from Tectona Grandis Wood Residues. J. Indian Acad. Wood Sci. 2022, 19, 121–132. [Google Scholar] [CrossRef]
- Ratnani, R.D.; Purbacaraka, F.H.; Hartati, I.; Syafaat, I. Actived Carbon from Teak Wood, Jackfruit Wood, and Mango Wood Pyrolysis Process. J. Phys. Conf. Ser. 2019, 1217, 012055. [Google Scholar] [CrossRef]
- Kongnine, D.M.; Kpelou, P.; Attah, N.; Kombate, S.; Mouzou, E.; Djeteli, G.; Napo, K. Energy Resource of Charcoals Derived from Some Tropical Fruits Nuts Shells. Int. J. Renew. Energy Dev. 2020, 9, 29–35. [Google Scholar] [CrossRef]
- Siarudin, M.; Awang, S.A.; Sadono, R.; Suryanto, P. Renewable Energy from Secondary Wood Products Contributes to Local Green Development: The Case of Small-Scale Privately Owned Forests in Ciamis Regency, Indonesia. Energy. Sustain. Soc. 2023, 13, 4. [Google Scholar] [CrossRef] [PubMed]
- Iskandar, N.; Sulardjaka, S.; Munadi, M.; Nugroho, S.; Nidhom, A.S.; Fitriyana, D.F. The Characteristic of Bio-Pellet Made from Teak Wood Waste Due to the Influence of Variations in Material Composition and Compaction Pressure. J. Phys. Conf. Ser. 2020, 1517, 012017. [Google Scholar] [CrossRef]
- Wahyuni, H.; Aladin, A.; Kalla, R.; Nouman, M.; Ardimas, A.; Chowdhury, M.S. Utilization of Industrial Flour Waste as Biobriquette Adhesive: Application on Pyrolysis Biobriquette Sawdust Red Teak Wood. Int. J. Hydrol. Environ. Sustain. 2022, 1, 54–69. [Google Scholar] [CrossRef]
- Faisal, R.M.; Ardian, A.; Khoiriyah, V.; Chafidz, A. Production of Briquettes from a Blend of HDPE (High Density Polyethylene) Plastic Wastes and Teak (Tectona grandis Linn. f) Sawdust Using Different Natural Adhesives as the Binder. Key Eng. Mater. 2021, 882, 273–279. [Google Scholar] [CrossRef]
- Puspita, A.A.; Sachari, A.; Sriwarno, A.B. Jamaludin Knowledge from Javanese Cultural Heritage: How They Manage and Sustain Teak Wood. Cultura 2018, 15, 23–48. [Google Scholar] [CrossRef]
- Decuyper, M.; Chávez, R.O.; Čufar, K.; Estay, S.A.; Clevers, J.G.P.W.; Prislan, P.; Gričar, J.; Črepinšek, Z.; Merela, M.; de Luis, M.; et al. Spatio-Temporal Assessment of Beech Growth in Relation to Climate Extremes in Slovenia—An Integrated Approach Using Remote Sensing and Tree-Ring Data. Agric. For. Meteorol. 2020, 287, 107925. [Google Scholar] [CrossRef]
- Wang, Z.; Lyu, L.; Liu, W.; Liang, H.; Huang, J.; Zhang, Q.-B. Topographic Patterns of Forest Decline as Detected from Tree Rings and NDVI. Catena 2021, 198, 105011. [Google Scholar] [CrossRef]
- Bumann, E.; Awada, T.; Wardlow, B.; Hayes, M.; Okalebo, J.; Helzer, C.; Mazis, A.; Hiller, J.; Cherubini, P. Assessing Responses of Betula Papyrifera to Climate Variability in a Remnant Population along the Niobrara River Valley in Nebraska, U.S.A., through Dendroecological and Remote-Sensing Techniques. Can. J. For. Res. 2019, 49, 423–433. [Google Scholar] [CrossRef]
- Anderson-Teixeira, K.J.; Herrmann, V.; Rollinson, C.R.; Gonzalez, B.; Gonzalez-Akre, E.B.; Pederson, N.; Alexander, M.R.; Allen, C.D.; Alfaro-Sánchez, R.; Awada, T.; et al. Joint Effects of Climate, Tree Size, and Year on Annual Tree Growth Derived from Tree-ring Records of Ten Globally Distributed Forests. Glob. Chang. Biol. 2022, 28, 245–266. [Google Scholar] [CrossRef] [PubMed]
- Sevik, H.; Cetin, M.; Ozel, H.B.; Akarsu, H.; Zeren Cetin, I. Analyzing of Usability of Tree-Rings as Biomonitors for Monitoring Heavy Metal Accumulation in the Atmosphere in Urban Area: A Case Study of Cedar Tree (Cedrus Sp.). Environ. Monit. Assess. 2020, 192, 23. [Google Scholar] [CrossRef] [PubMed]
- Depardieu, C.; Gérardi, S.; Nadeau, S.; Parent, G.J.; Mackay, J.; Lenz, P.; Lamothe, M.; Girardin, M.P.; Bousquet, J.; Isabel, N. Connecting Tree-ring Phenotypes, Genetic Associations and Transcriptomics to Decipher the Genomic Architecture of Drought Adaptation in a Widespread Conifer. Mol. Ecol. 2021, 30, 3898–3917. [Google Scholar] [CrossRef]
- Housset, J.M.; Tóth, E.G.; Girardin, M.P.; Tremblay, F.; Motta, R.; Bergeron, Y.; Carcaillet, C. Tree-Rings, Genetics and the Environment: Complex Interactions at the Rear Edge of Species Distribution Range. Dendrochronologia 2021, 69, 125863. [Google Scholar] [CrossRef]
- Girardin, M.P.; Guo, X.J.; Metsaranta, J.; Gervais, D.; Campbell, E.; Arsenault, A.; Isaac-Renton, M.; Harvey, J.E.; Bhatti, J.; Hogg, E.H. A National Tree-Ring Data Repository for Canadian Forests (CFS-TRenD): Structure, Synthesis, and Applications. Environ. Rev. 2021, 29, 225–241. [Google Scholar] [CrossRef]
- Rodriguez-Zaccaro, F.D.; Valdovinos-Ayala, J.; Percolla, M.I.; Venturas, M.D.; Pratt, R.B.; Jacobsen, A.L. Wood Structure and Function Change with Maturity: Age of the Vascular Cambium Is Associated with Xylem Changes in Current-Year Growth. Plant. Cell Environ. 2019, 42, 1816–1831. [Google Scholar] [CrossRef]
- Ivković, M.; Gapare, W.; Wu, H.; Espinoza, S.; Rozenberg, P. Influence of Cambial Age and Climate on Ring Width and Wood Density in Pinus Radiata Families. Ann. For. Sci. 2013, 70, 525–534. [Google Scholar] [CrossRef]
- Xiang, W.; Leitch, M.; Auty, D.; Duchateau, E.; Achim, A. Radial Trends in Black Spruce Wood Density Can Show an Age- and Growth-Related Decline. Ann. For. Sci. 2014, 71, 603–615. [Google Scholar] [CrossRef]
- Plomion, C.; Leprovost, G.; Stokes, A. Wood Formation in Trees. Plant Physiol. 2001, 127, 1513–1523. [Google Scholar] [CrossRef]
- Ko, J.-H.; Kim, W.-C.; Keathley, D.E.; Han, K.-H. Genetic Engineering for Secondary Xylem Modification: Unraveling the Genetic Regulation of Wood Formation. In Secondary Xylem Biology; Elsevier: Amsterdam, The Netherlands, 2016; pp. 193–211. [Google Scholar]
- Kozlowski, T.T.; Pallardy, S.G. Environmental Regulation of Vegetative Growth. In Growth Control in Woody Plants; Elsevier: Amsterdam, The Netherlands, 1997; pp. 195–322. [Google Scholar]
- Telewski, F.W. Flexure Wood: Mechanical Stress Induced Secondary Xylem Formation. In Secondary Xylem Biology; Elsevier: Amsterdam, The Netherlands, 2016; pp. 73–91. [Google Scholar]
- Wheeler, E. Wood: Macroscopic Anatomy. In Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2001; pp. 9653–9657. [Google Scholar]
- Donaldson, L.; Nanayakkara, B.; Harrington, J. Wood Growth and Development. In Encyclopedia of Applied Plant Sciences; Elsevier: Amsterdam, The Netherlands, 2017; pp. 203–210. [Google Scholar]
- Gerttula, S.; Zinkgraf, M.; Muday, G.K.; Lewis, D.R.; Ibatullin, F.M.; Brumer, H.; Hart, F.; Mansfield, S.D.; Filkov, V.; Groover, A. Transcriptional and Hormonal Regulation of Gravitropism of Woody Stems in Populus. Plant Cell 2015, 27, 2800–2813. [Google Scholar] [CrossRef] [PubMed]
- Functional Mapping of Gravitropism and Phototropism for a Desert Tree, Populus Euphratica. Front. Biosci. 2021, 26, 988. [CrossRef]
- Christie, J.M.; Murphy, A.S. Shoot Phototropism in Higher Plants: New Light through Old Concepts. Am. J. Bot. 2013, 100, 35–46. [Google Scholar] [CrossRef] [PubMed]
- Tsutsumi, D.; Kosugi, K.; Mizuyama, T. Three-Dimensional Modeling of Hydrotropism Effects on Plant Root Architecture along a Hillslope. Vadose Zo. J. 2004, 3, 1017–1030. [Google Scholar] [CrossRef]
- Coutts, M.P.; Nicoll, B.C. Orientation of the Lateral Roots of Trees. New Phytol. 1993, 124, 277–281. [Google Scholar] [CrossRef]
- Mattheck, C.; Bethge, K. Biomechanical Study on The Interactions of Roots with Gas and Water Pipelines for the Evaluation of Tree Sites. Arboric. J. 1999, 23, 343–377. [Google Scholar] [CrossRef]
- Gul, M.U.; Paul, A.; Chehri, A. Hydrotropism: Understanding the Impact of Water on Plant Movement and Adaptation. Water 2023, 15, 567. [Google Scholar] [CrossRef]
- van Zanten, M.; Ai, H.; Quint, M. Plant Thermotropism: An Underexplored Thermal Engagement and Avoidance Strategy. J. Exp. Bot. 2021, 72, 7414–7420. [Google Scholar] [CrossRef]
- Aldrich-Blake, R.N. Recent Research on the Root Systems of Trees. For. An. Int. J. For. Res. 1929, 3, 66–70. [Google Scholar] [CrossRef][Green Version]
- Kojima, M.; Becker, V.K.; Altaner, C.M. An Unusual Form of Reaction Wood in Koromiko [Hebe Salicifolia G. Forst. (Pennell)], a Southern Hemisphere Angiosperm. Planta 2012, 235, 289–297. [Google Scholar] [CrossRef]
- Wilson, B.F.; Archer, R.R. Reaction Wood: Induction and Mechanical Action. Annu. Rev. Plant Physiol. 1977, 28, 23–43. [Google Scholar] [CrossRef]
- Winsor, C.P. The Gompertz Curve as a Growth Curve. Proc. Natl. Acad. Sci. USA 1932, 18, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Paine, C.E.T.; Marthews, T.R.; Vogt, D.R.; Purves, D.; Rees, M.; Hector, A.; Turnbull, L.A. How to Fit Nonlinear Plant Growth Models and Calculate Growth Rates: An Update for Ecologists. Methods Ecol. Evol. 2012, 3, 245–256. [Google Scholar] [CrossRef]
- Aggrey, S. Comparison of Three Nonlinear and Spline Regression Models for Describing Chicken Growth Curves. Poult. Sci. 2002, 81, 1782–1788. [Google Scholar] [CrossRef] [PubMed]
- Tjørve, K.M.C.; Tjørve, E. Shapes and Functions of Bird-Growth Models: How to Characterise Chick Postnatal Growth. Zoology 2010, 113, 326–333. [Google Scholar] [CrossRef] [PubMed]
- Makeham, W.M. On the Integral of Gompertz’s Function for Expressing the Values of Sums Depending upon the Contingency of Life. J. Inst. Actuar. Assur. Mag. 1873, 17, 305–327, 445–446. [Google Scholar] [CrossRef]
- Halmi, M.I.E.; Shukor, M.S.; Johari, W.L.W.; Shukor, M.Y. Evaluation of Several Mathematical Models for Fitting the Growth of the Algae Dunaliella Tertiolecta. Asian J. Plant Biol. 2014, 2, 1–6. [Google Scholar] [CrossRef]
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; van ’t Riet, K. Modeling of the Bacterial Growth Curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [CrossRef]
- Skinner, G.E.; Larkin, J.W.; Rhodehamel, E.J. Mathematical Modelling of Microbial Growth: A Review. J. Food Saf. 1994, 14, 175–217. [Google Scholar] [CrossRef]
- Halmi, M.I.E.; Shukor, M.S.; Masdor, N.A.; Shamaan, N.A.; Shukor, M.Y. Test of Randomness of Residuals for the Modified Gompertz Model Used in the Fitting the Growth of Sludge Microbes on PEG 600. J. Environ. Microbiol. Toxicol. 2015, 3, 9–11. [Google Scholar] [CrossRef]
- Laird, A.K. Dynamics of Tumor Growth. Br. J. Cancer 1964, 18, 490–502. [Google Scholar] [CrossRef] [PubMed]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.L.; Hlatky, L.; Hahnfeldt, P. Classical Mathematical Models for Description and Prediction of Experimental Tumor Growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef] [PubMed]
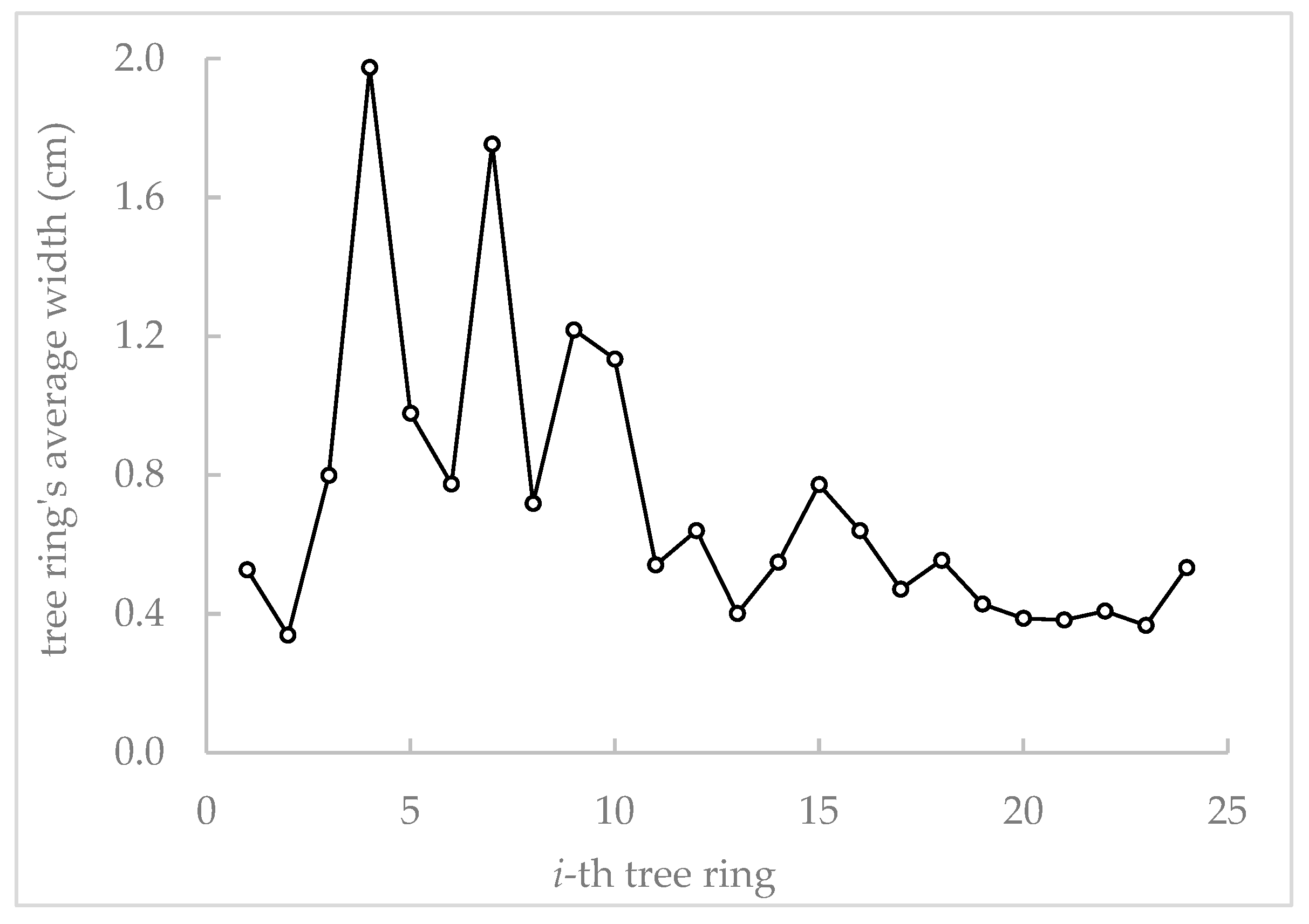
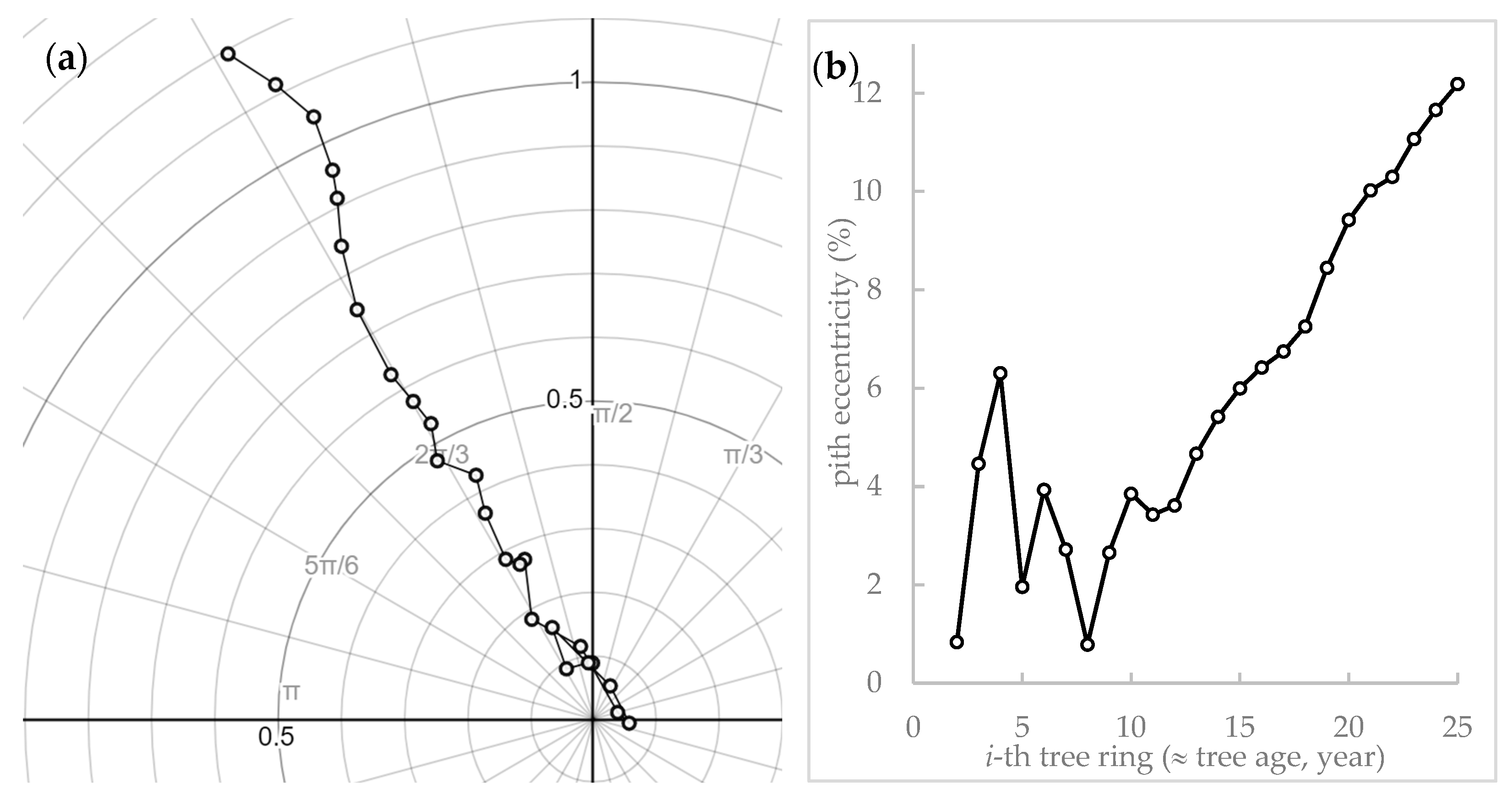

| Ring No. | Count of Digitized Point Coordinates | Estimated Parameters | R2 | MSE | ||||
|---|---|---|---|---|---|---|---|---|
| ro | a | b | k | θo | ||||
| 1 | 61 | −0.09 | 0.49 | 0.53 | −6.76 | 4.72 | 0.7158 | 0.00175 |
| 2 | 110 | −0.09 | 0.75 | 0.80 | −6.72 | 4.79 | 0.8589 | 0.00070 |
| 3 | 138 | −0.09 | 0.92 | 0.97 | −6.71 | 5.20 | 0.9106 | 0.00044 |
| 4 | 197 | −0.16 | 1.31 | 1.37 | −6.69 | 5.13 | 0.8850 | 0.00164 |
| 5 | 295 | −0.06 | 2.28 | 2.38 | −6.56 | 4.22 | 0.6787 | 0.00147 |
| 6 | 333 | 0.06 | 2.90 | 2.74 | −6.79 | −0.11 | 0.5643 | 0.00365 |
| 7 | 345 | 0.04 | 3.31 | 3.11 | −6.82 | 0.26 | 0.7953 | 0.00152 |
| 8 | 431 | 0.12 | 4.17 | 3.99 | −0.84 | 1.74 | 0.8128 | 0.00244 |
| 9 | 441 | 0.18 | 4.62 | 4.27 | −0.91 | 2.12 | 0.8365 | 0.00616 |
| 10 | 486 | 0.27 | 5.37 | 4.73 | −0.89 | 1.98 | 0.9540 | 0.00441 |
| 11 | 515 | 0.27 | 5.99 | 5.24 | −0.90 | 2.01 | 0.9335 | 0.00762 |
| 12 | 556 | 0.29 | 6.24 | 5.54 | −0.91 | 2.07 | 0.9614 | 0.00398 |
| 13 | 557 | 0.36 | 6.59 | 5.82 | −0.92 | 2.05 | 0.9500 | 0.00733 |
| 14 | 582 | 0.42 | 6.78 | 6.03 | −0.91 | 2.02 | 0.9343 | 0.01096 |
| 15 | 694 | 0.47 | 7.10 | 6.26 | −0.92 | 2.12 | 0.9232 | 0.01683 |
| 16 | 621 | 0.53 | 7.44 | 6.70 | −0.87 | 2.07 | 0.8754 | 0.03009 |
| 17 | 678 | 0.57 | 7.77 | 7.01 | −0.88 | 2.09 | 0.8803 | 0.03152 |
| 18 | 620 | 0.63 | 7.99 | 7.26 | −0.86 | 2.10 | 0.9006 | 0.02823 |
| 19 | 715 | 0.74 | 8.23 | 7.58 | −0.85 | 2.10 | 0.9307 | 0.02547 |
| 20 | 778 | 0.84 | 8.38 | 7.85 | −0.83 | 2.06 | 0.9429 | 0.02302 |
| 21 | 861 | 0.91 | 8.53 | 8.09 | −0.77 | 2.03 | 0.9519 | 0.02202 |
| 22 | 881 | 0.95 | 8.67 | 8.33 | −0.76 | 2.02 | 0.9578 | 0.02023 |
| 23 | 942 | 1.04 | 8.82 | 8.59 | −0.72 | 2.01 | 0.9605 | 0.02208 |
| 24 | 875 | 1.11 | 8.83 | 8.95 | −1.41 | 2.04 | 0.9414 | 0.03910 |
| 25 | 877 | 1.19 | 9.00 | 9.31 | −1.55 | 2.08 | 0.9346 | 0.05119 |
| Ring No. | Tree Ring Center Position | Reaction Wood Formation | Pith Distance from Centroid (cm) | Mean Radius (cm) | Pith Eccentricity (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| xo | yo | θrw | Start | End | ||||||
| xrw | yrw | xrw | yrw | |||||||
| 1 | −0.0003 | 0.0881 | - | - | - | - | - | - | 0.51 | - |
| 2 | −0.0068 | 0.0885 | 3.075 | −0.500 | 0.033 | −0.781 | 0.052 | 0.01 | 0.77 | 0.83 |
| 3 | −0.0414 | 0.0790 | 3.409 | −0.712 | −0.195 | −0.911 | −0.250 | 0.04 | 0.94 | 4.46 |
| 4 | −0.0640 | 0.1438 | 1.907 | −0.344 | 0.983 | −0.497 | 1.421 | 0.08 | 1.34 | 6.30 |
| 5 | 0.0278 | 0.0522 | 5.499 | 0.863 | −0.861 | 1.647 | −1.643 | 0.05 | 2.33 | 1.96 |
| 6 | 0.0577 | −0.0062 | 5.185 | 1.038 | −2.029 | 1.266 | −2.474 | 0.11 | 2.82 | 3.93 |
| 7 | 0.0395 | 0.0105 | 2.398 | −1.987 | 1.826 | −2.279 | 2.095 | 0.09 | 3.21 | 2.72 |
| 8 | −0.0191 | 0.1141 | 2.086 | −1.524 | 2.694 | −2.018 | 3.568 | 0.03 | 4.08 | 0.79 |
| 9 | −0.0961 | 0.1568 | 2.635 | −3.596 | 1.996 | −4.017 | 2.230 | 0.12 | 4.44 | 2.65 |
| 10 | −0.1074 | 0.2506 | 1.690 | −0.529 | 4.413 | −0.599 | 4.991 | 0.19 | 5.05 | 3.85 |
| 11 | −0.1149 | 0.2430 | 3.932 | −3.586 | −3.620 | −3.997 | −4.035 | 0.19 | 5.62 | 3.43 |
| 12 | −0.1373 | 0.2508 | 2.807 | −5.567 | 1.939 | −5.867 | 2.043 | 0.21 | 5.89 | 3.61 |
| 13 | −0.1697 | 0.3231 | 1.992 | −2.385 | 5.324 | −2.538 | 5.665 | 0.29 | 6.21 | 4.67 |
| 14 | −0.1843 | 0.3826 | 1.811 | −1.471 | 6.000 | −1.536 | 6.264 | 0.35 | 6.41 | 5.42 |
| 15 | −0.2454 | 0.4053 | 2.786 | −6.398 | 2.379 | −6.735 | 2.505 | 0.40 | 6.68 | 6.00 |
| 16 | −0.2554 | 0.4636 | 1.741 | −1.136 | 6.614 | −1.226 | 7.138 | 0.45 | 7.07 | 6.42 |
| 17 | −0.2835 | 0.4983 | 2.253 | −4.589 | 5.647 | −4.814 | 5.924 | 0.50 | 7.39 | 6.75 |
| 18 | −0.3187 | 0.5404 | 2.267 | −4.895 | 5.862 | −5.077 | 6.080 | 0.55 | 7.62 | 7.25 |
| 19 | −0.3723 | 0.6423 | 2.055 | −3.669 | 6.982 | −3.870 | 7.364 | 0.67 | 7.90 | 8.45 |
| 20 | −0.3970 | 0.7419 | 1.814 | −2.003 | 8.078 | −2.098 | 8.460 | 0.76 | 8.12 | 9.42 |
| 21 | −0.4036 | 0.8170 | 1.659 | −0.765 | 8.697 | −0.797 | 9.056 | 0.83 | 8.31 | 10.02 |
| 22 | −0.4110 | 0.8611 | 1.738 | −1.511 | 8.955 | −1.556 | 9.221 | 0.88 | 8.50 | 10.30 |
| 23 | −0.4408 | 0.9448 | 1.913 | −3.129 | 8.791 | −3.249 | 9.128 | 0.96 | 8.70 | 11.07 |
| 24 | −0.5010 | 0.9954 | 2.443 | −7.293 | 6.129 | −7.565 | 6.358 | 1.04 | 8.89 | 11.66 |
| 25 | −0.5761 | 1.0435 | 2.572 | −8.275 | 5.300 | −8.676 | 5.556 | 1.12 | 9.15 | 12.19 |
| Model | Estimated Formula | R2 | MSE |
|---|---|---|---|
| a. Continuous methods | |||
| Verhulst–Pearl | 0.9876 | 0.42744 | |
| Gompertz | 0.9931 | 0.23732 | |
| von Bertalanffy | 0.9942 | 0.20019 | |
| Chapman–Richards | 0.9972 | 0.09998 | |
| b. Discrete methods (Exponential transformation) | |||
| linear | 0.9517 | 1.6592 | |
| quadratic | 0.8327 | 6.0273 | |
| logarithmic | 0.9906 | 0.3234 | |
| quadratic logarithmic | 0.9823 | 0.6377 | |
| Model | Estimated Formula | R2 | MSE |
|---|---|---|---|
| a. Continuous methods | |||
| Verhulst–Pearl | 0.9900 | 84.3876 | |
| Gompertz | 0.9954 | 39.0051 | |
| von Bertalanffy | 0.9929 | 60.3875 | |
| Chapman–Richards | 0.9985 | 13.7107 | |
| b. Discrete methods (Exponential transformation) | |||
| linear | 0.8768 | 1041.261 | |
| quadratic | 0.5199 | 4249.377 | |
| logarithmic | 0.9748 | 212.568 | |
| quadratic logarithmic | 0.9534 | 412.479 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahtiar, E.T.; Kim, N.-H.; Iswanto, A.H. Biological Rotation Age of Community Teak (Tectona grandis) Plantation Based on the Volume, Biomass, and Price Growth Curve Determined through the Analysis of Its Tree Ring Digitization. Forests 2023, 14, 1944. https://doi.org/10.3390/f14101944
Bahtiar ET, Kim N-H, Iswanto AH. Biological Rotation Age of Community Teak (Tectona grandis) Plantation Based on the Volume, Biomass, and Price Growth Curve Determined through the Analysis of Its Tree Ring Digitization. Forests. 2023; 14(10):1944. https://doi.org/10.3390/f14101944
Chicago/Turabian StyleBahtiar, Effendi Tri, Nam-Hun Kim, and Apri Heri Iswanto. 2023. "Biological Rotation Age of Community Teak (Tectona grandis) Plantation Based on the Volume, Biomass, and Price Growth Curve Determined through the Analysis of Its Tree Ring Digitization" Forests 14, no. 10: 1944. https://doi.org/10.3390/f14101944
APA StyleBahtiar, E. T., Kim, N.-H., & Iswanto, A. H. (2023). Biological Rotation Age of Community Teak (Tectona grandis) Plantation Based on the Volume, Biomass, and Price Growth Curve Determined through the Analysis of Its Tree Ring Digitization. Forests, 14(10), 1944. https://doi.org/10.3390/f14101944







