Temperature Sensitivity of Soil Respiration in Two Temperate Forest Ecosystems: The Synthesis of a 24-Year Continuous Observation
Abstract
:1. Introduction
2. Materials and Methods
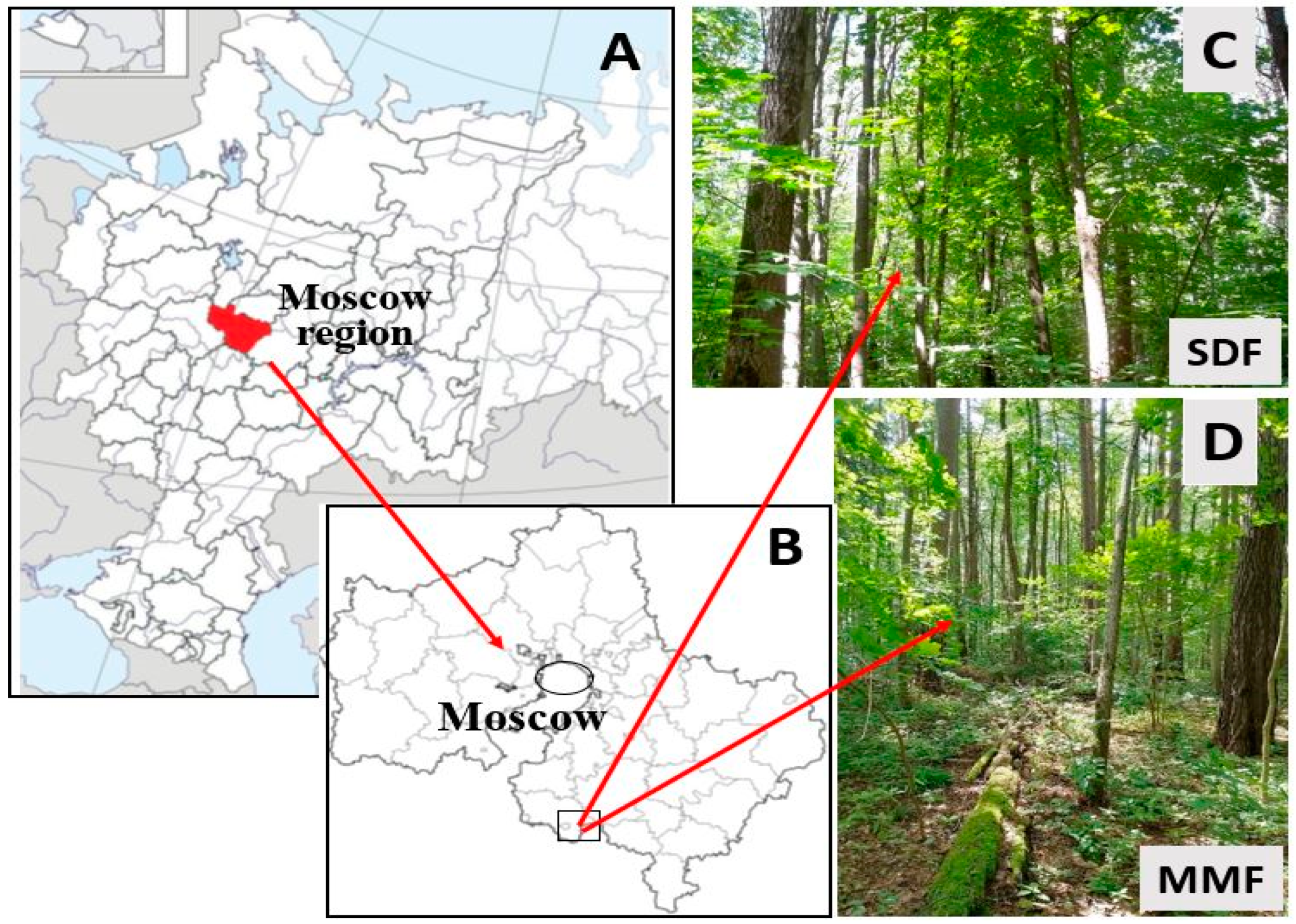
2.1. Study Area and Forest Sites
2.2. Soil Respiration Measurements
2.3. Data Processing
2.3.1. Calculation of the Meteorological Indexes
2.3.2. Calculation of the Temperature Coefficient Q10
2.3.3. Statistical Analyses
3. Results
3.1. Analysis of the Meteorological Indexes from 1998–2021
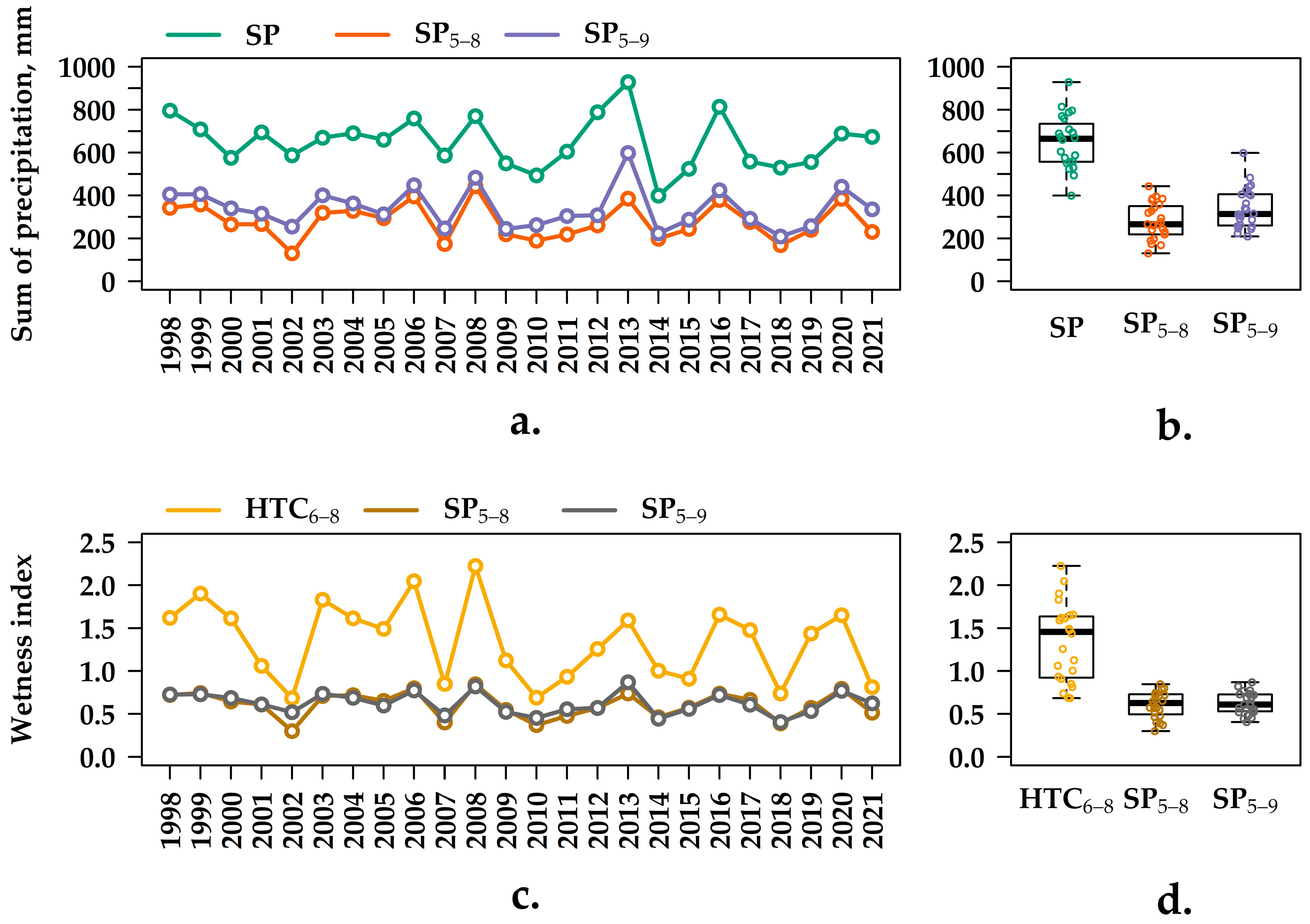
3.2. Q10 Values at Various Soil Temperature Intervals and at Different Levels of Humidity
3.3. Seasonal Variation of the Q10 Values in the Two Types of Forest
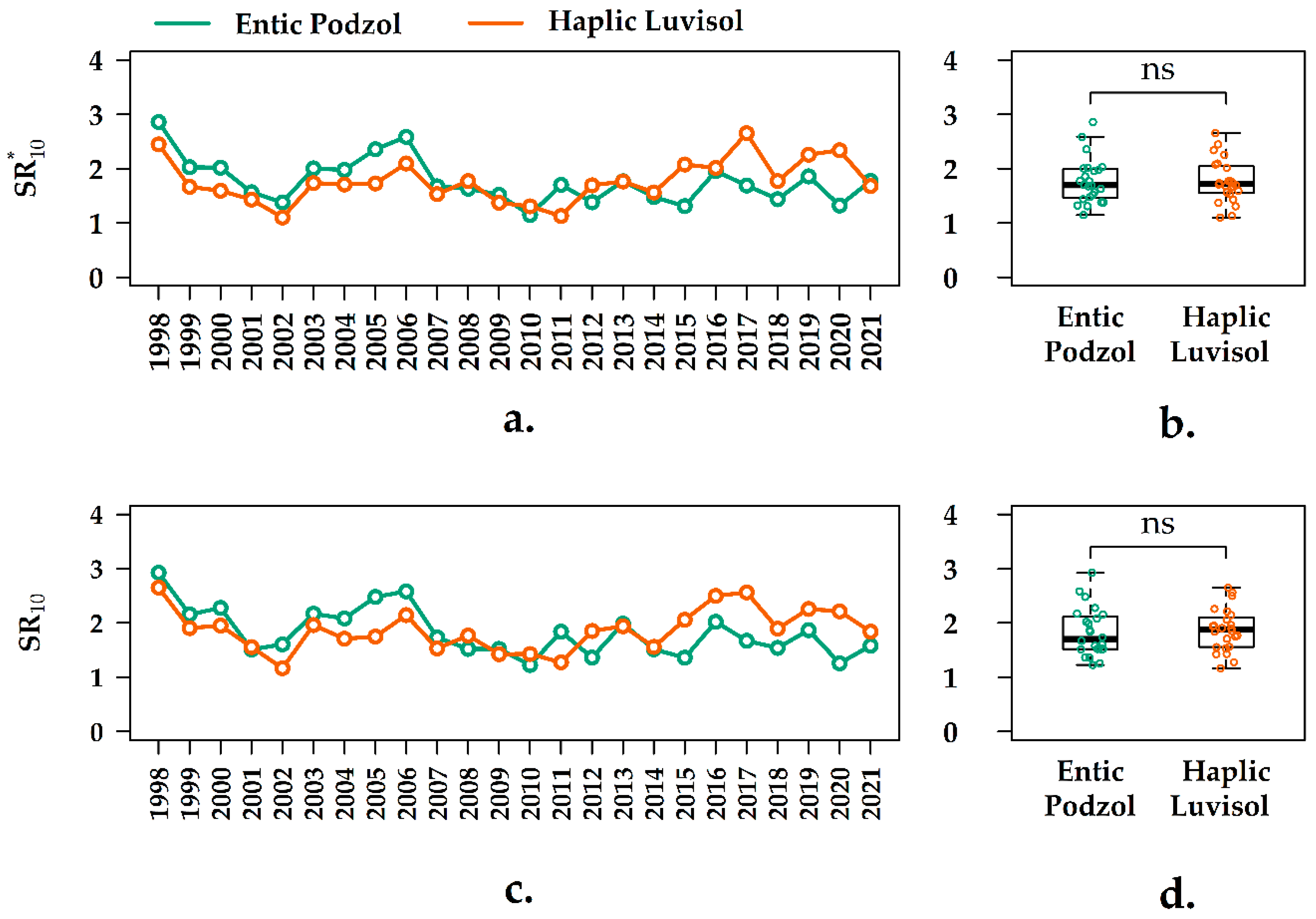
3.4. Interannual Variation of the Q10 Values in the Forest Ecosystems

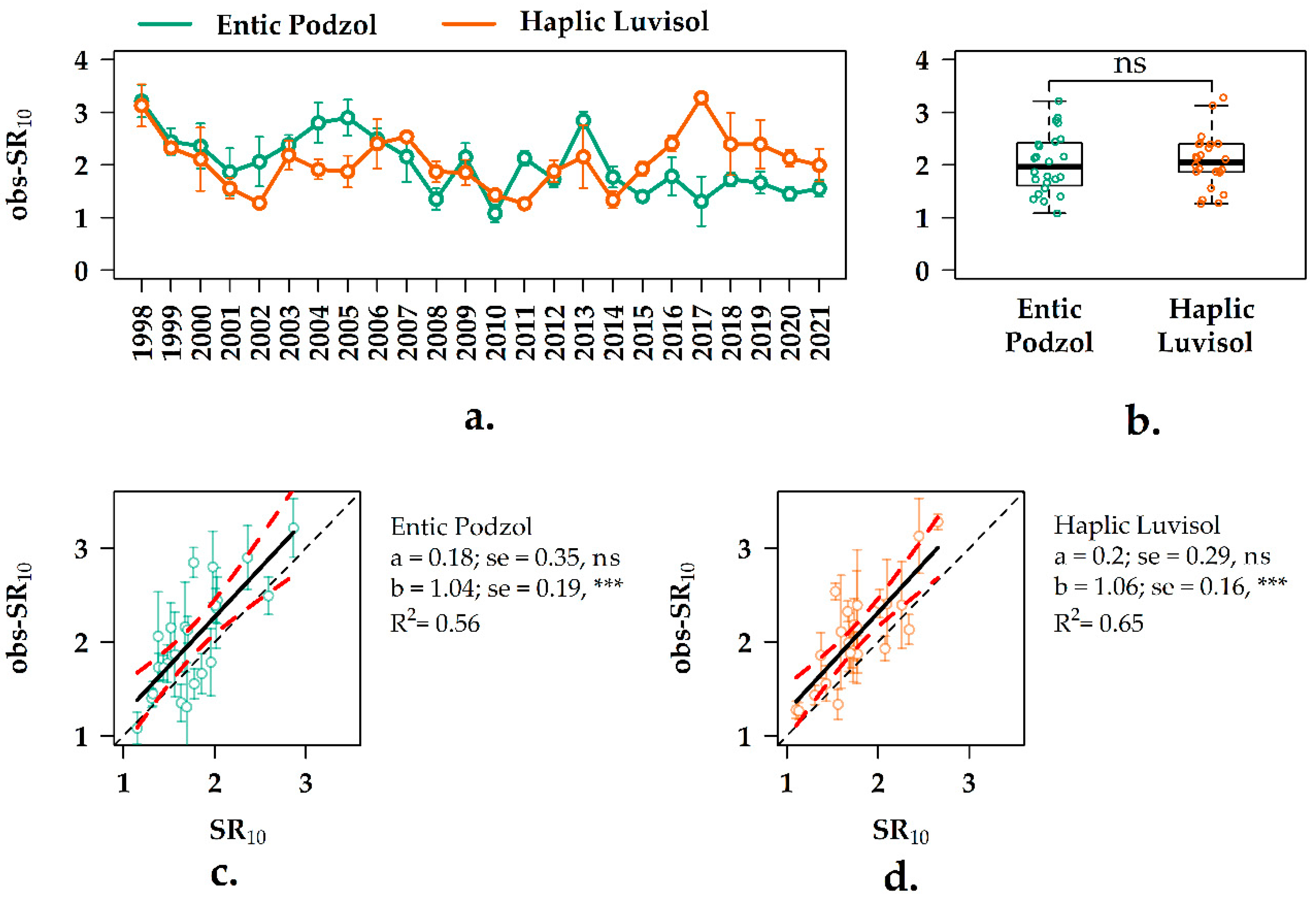
3.5. Interannual Variation of the SR10 Values in the Forest Ecosystems
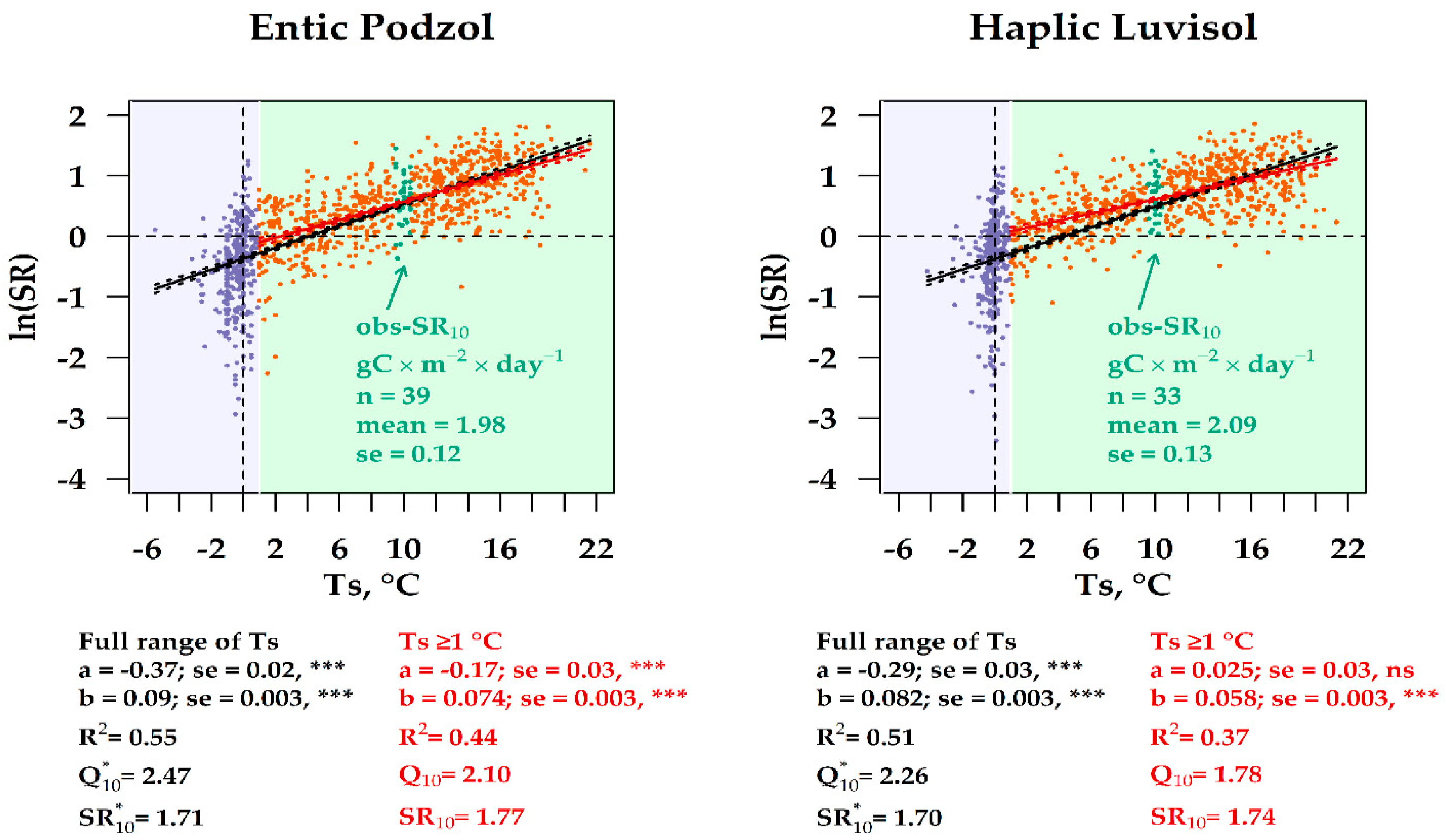
3.6. Experimental vs. Observation SR10 Values in the Two Forest Ecosystems
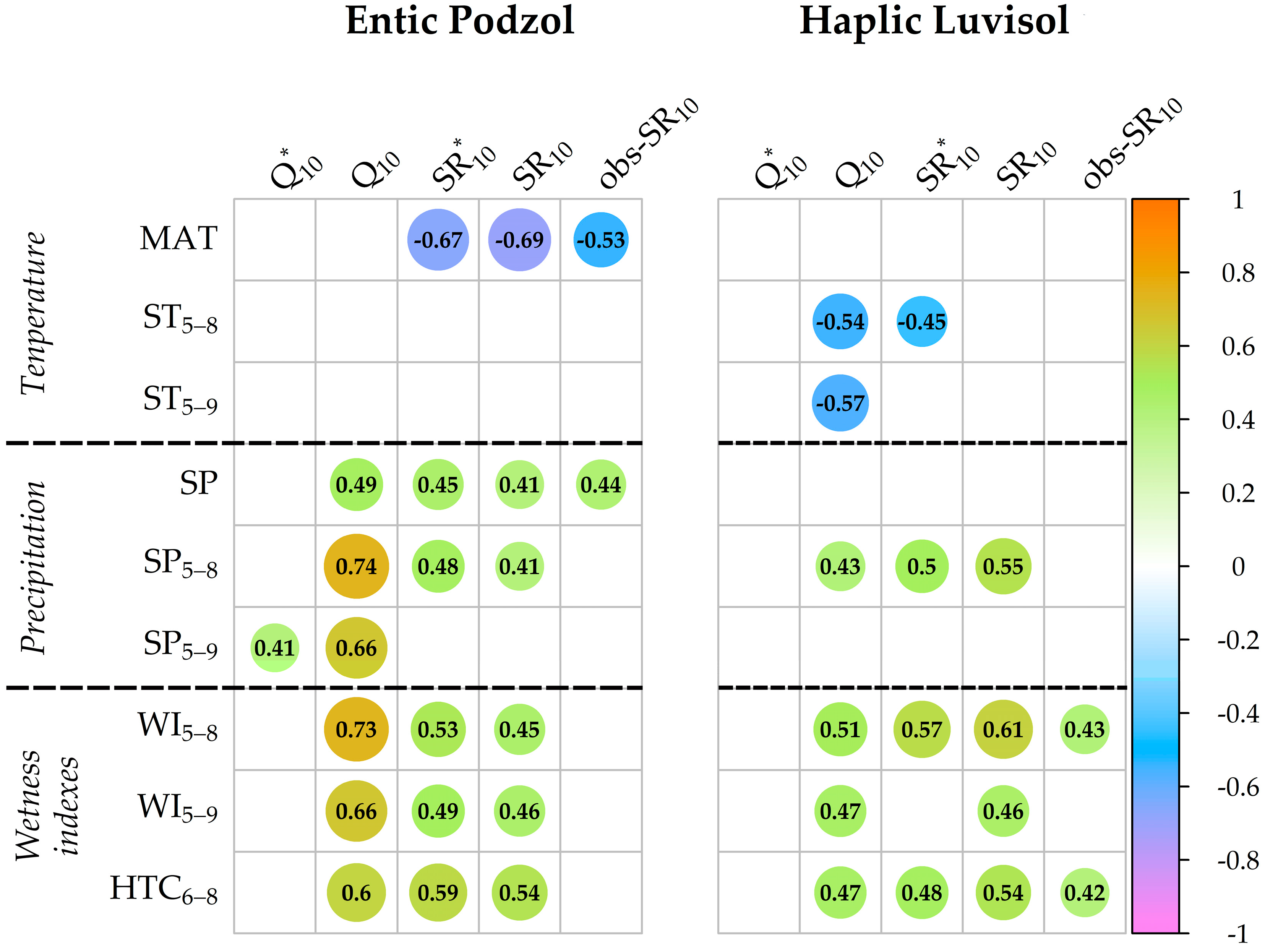
3.7. Relationship between the Q10 and SR10 Values and Meteorological Indexes over the 24-Year Observation Period
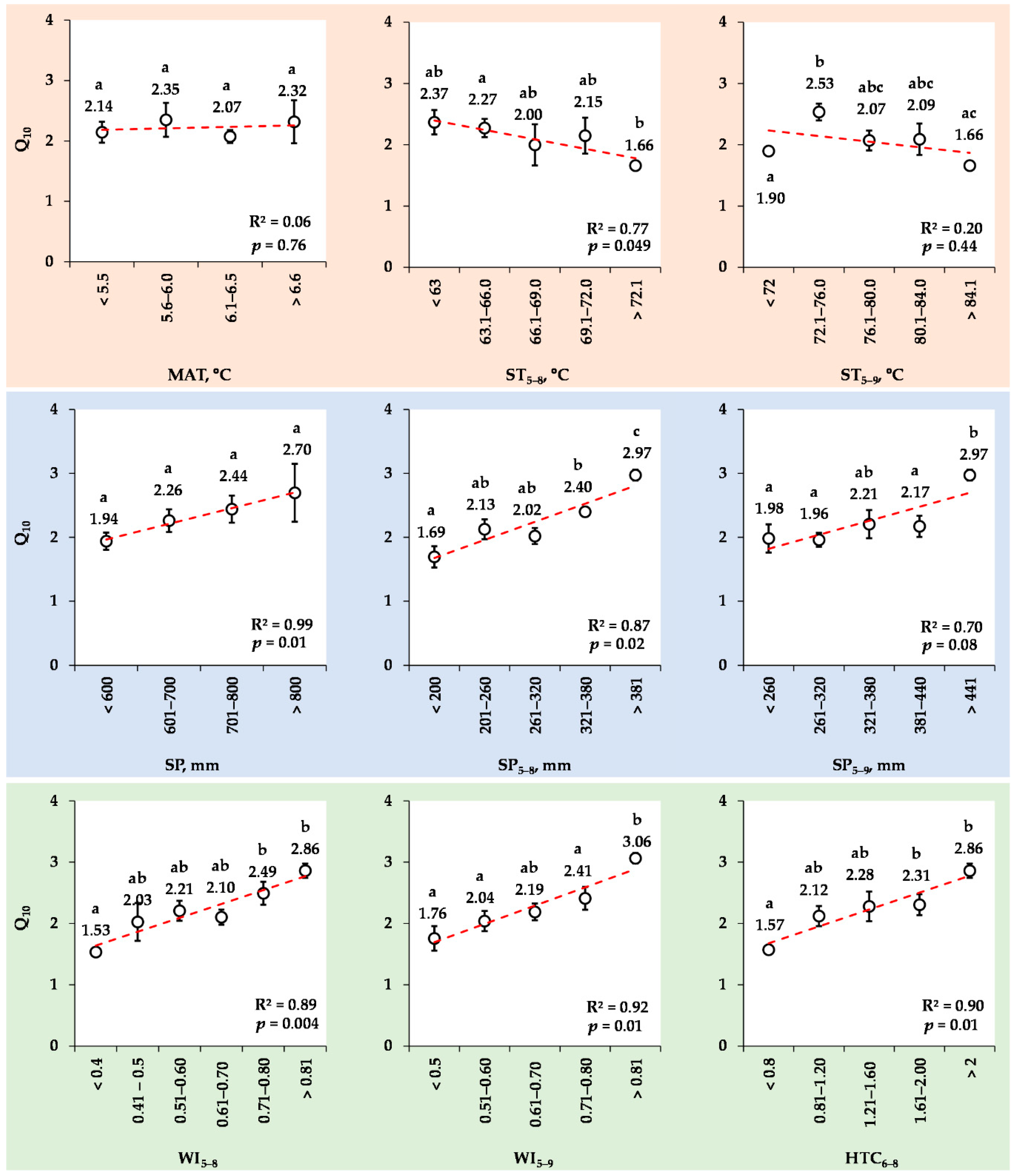
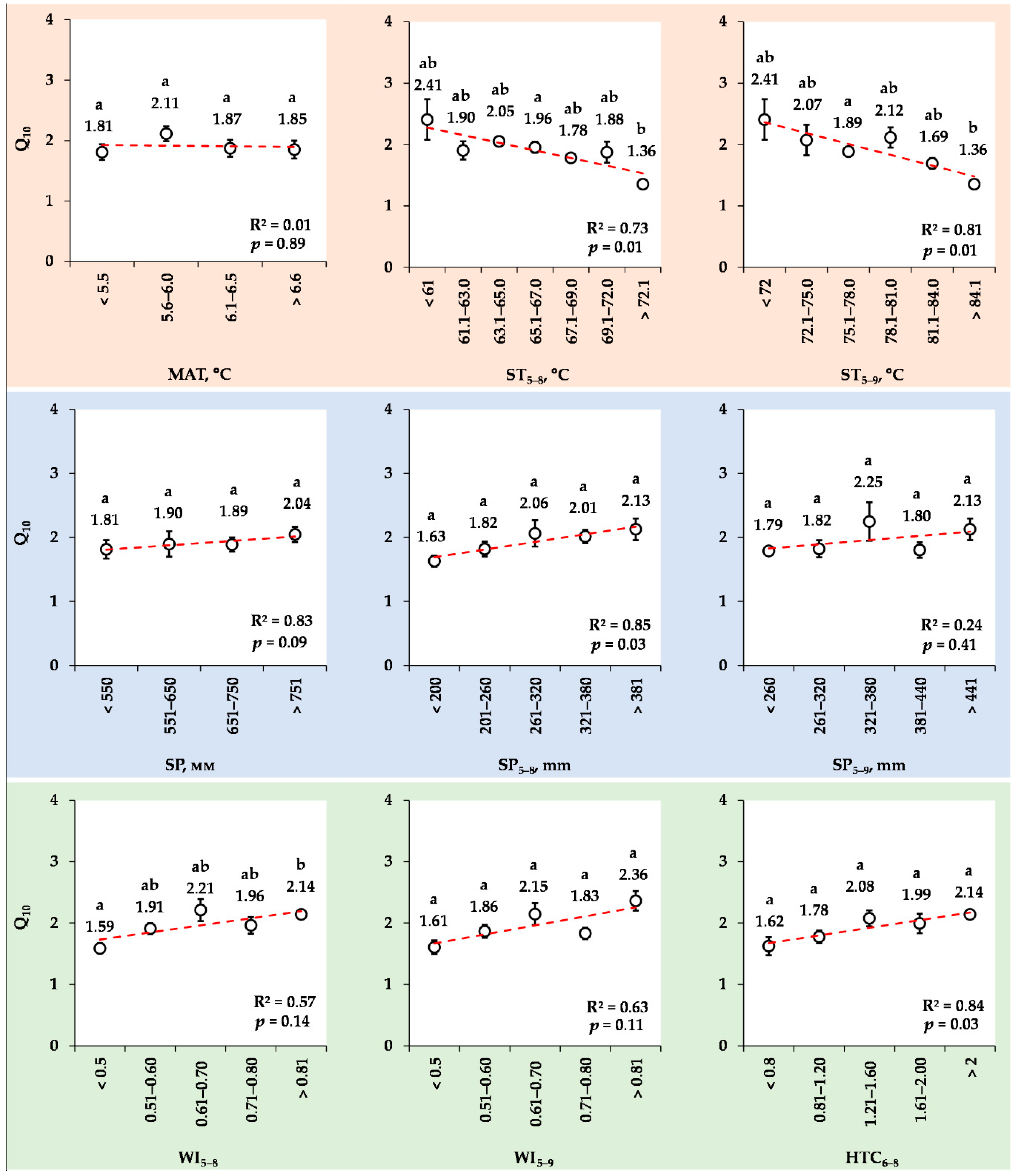
3.8. Changes in the Mean Q10 Values for Various Ranks of Meteorological Indexes
4. Discussion
4.1. Impacts of Internal and External Factors on the Temperature Sensitivity of Soil Respiration
4.2. Seasonal Variability of the Temperature Sensitivity of Soil Respiration
4.3. Interannual Variability of the Temperature Sensitivity of SR in the Forest Ecosystems
4.4. Research Perspectives in Light of the Current Climate Changes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Le Quéré, C.; Moriarty, R.; Andrew, R.M.; Peters, G.P.; Ciais, P.; Friedlingstein, P.; Jones, S.D.; Sitch, S.; Tans, P.; Arneth, A.; et al. Global carbon budget 2014. Earth Syst. Sci. Data 2015, 7, 47–85. [Google Scholar] [CrossRef]
- Gauthier, S.; Bernier, P.; Kuuluvainen, T.; Shvidenko, A.Z.; Schepaschenko, D.G. Boreal forest health and global change. Science 2015, 349, 819–822. [Google Scholar] [CrossRef] [PubMed]
- Shvidenko, A.Z.; Schepaschenko, D.G. Carbon Budget of Russian Forests. Sib. J. For. Sci. 2014, 1, 69–92. [Google Scholar]
- Ciais, P.; Soussana, J.F.; Vuichard, N.; Luyssaert, S.; Don, A.; Janssens, I.A.; Piao, S.L.; Dechow, R.; Lathière, J.; Maignan, F.; et al. The Greenhouse Gas Balance of European Grasslands. Biogeosci. Discuss. 2010, 7, 5997–6050. [Google Scholar] [CrossRef]
- Kurganova, I.N.; Kudeyarov, V.N. Ecosystems of Russia and Global Carbon Budget. Sci. Russ. 2012, 5, 25–32. [Google Scholar]
- Raich, J.W.; Tufekcioglu, A. Vegetation and soil respiration: Correlations and controls. Biogeochemistry 2000, 48, 71–90. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Andrews, J.A. Soil respiration and the global carbon cycle. Biogeochemistry 2000, 48, 7–20. [Google Scholar] [CrossRef]
- Xu, M.; Shang, H. Contribution of soil respiration to the global carbon equation. J. Plant Physiol. 2016, 203, 16–28. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Thomson, A. A global database of soil respiration data. Biogeosciences 2010, 7, 1915–1926. [Google Scholar] [CrossRef]
- Rustad, L.E.; Huntington, T.G.; Boone, R.D. Controls on soil respiration: Implications for climate change. Biogeochemistry 2000, 48, 1–6. [Google Scholar] [CrossRef]
- Zhou, T.; Shi, P.; Hui, D.; Luo, Y. Global pattern of temperature sensitivity of soil heterotrophic respiration (Q10) and its implications for carbon-climate feedback. J. Geophys. Res. Biogeosci. 2009, 114, G02016. [Google Scholar] [CrossRef]
- Han, M.; Jin, G. Seasonal variations of Q10 soil respiration and its components in the temperate forest ecosystems, northeastern China. Eur. J. Soil Biol. 2018, 85, 36–42. [Google Scholar] [CrossRef]
- Kudeyarov, V.N.; Kurganova, I.N. Respiration of Russian Soils: Database Analysis, Long-Term Monitoring, and General Estimates. Eurasian Soil Sci. 2005, 38, 983–992. [Google Scholar]
- Mukhortova, L.; Schepaschenko, D.; Moltchanova, E.; Shvidenko, A.; Khabarov, N.; See, L. Respiration of Russian soils: Climatic drivers and response to climate change. Sci. Total Environ. 2021, 785, 147314. [Google Scholar] [CrossRef]
- Giasson, M.-A.; Ellison, A.M.; Bowden, R.D.; Crill, P.M.; Davidson, E.A.; Drake, J.E.; Frey, S.D.; Hadley, J.L.; LaVine, M.; Melillo, J.M.; et al. Soil respiration in a northeastern US temperate forest: A 22-year synthesis. Ecosphere 2013, 4, art140. [Google Scholar] [CrossRef]
- Kurganova, I.N.; Lopes de Gerenyu, V.O.; Khoroshaev, D.A.; Myakshina, T.N.; Sapronov, D.V.; Zhmurin, V.A.; Kudeyarov, V.N. Analysis of the Long-Term Soil Respiration Dynamics in the Forest and Meadow Cenoses of the Prioksko-Terrasny Biosphere Reserve in the Perspective of Current Climate Trends. Eurasian Soil Sci. 2020, 53, 1421–1436. [Google Scholar] [CrossRef]
- Kurganova, I.N.; Lopes de Gerenyu, V.O.; Myakshina, T.N.; Sapronov, D.V.; Khoroshaev, D.A.; Zhmurin, V.A. The Temporal Variability of Respiration of a Soddy-Podzolic Soil in Forest and Meadow Coenoses of the South-Taiga Zone. Mosc. Univ. Soil Sci. Bull. 2022, 77, 74–82. [Google Scholar] [CrossRef]
- Reichstein, M.; Rey, A.; Freibauer, A.; Tenhunen, J.; Valentini, R.; Banza, J.; Casals, P.; Cheng, Y.; Grünzweig, J.M.; Irvine, J.; et al. Modeling temporal and large-scale spatial variability of soil respiration from soil water availability, temperature and vegetation productivity indices. Glob. Biogeochem. Cycles 2003, 17. [Google Scholar] [CrossRef]
- Davidson, E.A.; Janssens, I.A.; Luo, Y. On the variability of respiration in terrestrial ecosystems: Moving beyond Q10. Glob. Chang. Biol. 2006, 12, 154–164. [Google Scholar] [CrossRef]
- Suseela, V.; Conant, R.T.; Wallenstein, M.D.; Dukes, J.S. Effects of soil moisture on the temperature sensitivity of heterotrophic respiration vary seasonally in an old-field climate change experiment. Glob. Chang. Biol. 2012, 18, 336–348. [Google Scholar] [CrossRef]
- Bahn, M.; Reichstein, M.; Davidson, E.A.; Grünzweig, J.; Jung, M.; Carbone, M.S.; Epron, D.; Misson, L.; Nouvellon, Y.; Roupsard, O.; et al. Soil respiration at mean annual temperature predicts annual total across vegetation types and biomes. Biogeosciences 2010, 7, 2147–2157. [Google Scholar] [CrossRef] [PubMed]
- Friedlingstein, P.; Dufresne, J.-L.; Cox, P.M.; Rayner, P. How positive is the feedback between climate change and the carbon cycle? Tellus B Chem. Phys. Meteorol. 2003, 55, 692–700. [Google Scholar] [CrossRef]
- Luo, Y. Terrestrial Carbon-Cycle Feedback to Climate Warming. Annu. Rev. Ecol. Evol. Syst. 2007, 38, 683–712. [Google Scholar] [CrossRef] [Green Version]
- Kirschbaum, M.U.F. The temperature dependence of soil organic matter decomposition, and the effect of global warming on soil organic C storage. Soil Biol. Biochem. 1995, 27, 753–760. [Google Scholar] [CrossRef]
- Meyer, N.; Welp, G.; Amelung, W. The Temperature Sensitivity (Q10) of Soil Respiration: Controlling Factors and Spatial Prediction at Regional Scale Based on Environmental Soil Classes. Glob. Biogeochem. Cycles 2018, 32, 306–323. [Google Scholar] [CrossRef]
- Foereid, B.; Ward, D.S.; Mahowald, N.; Paterson, E.; Lehmann, J. The sensitivity of carbon turnover in the Community Land Model to modified assumptions about soil processes. Earth Syst. Dyn. 2014, 5, 211–221. [Google Scholar] [CrossRef]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef]
- Gritsch, C.; Zimmermann, M.; Zechmeister-Boltenstern, S. Interdependencies between temperature and moisture sensitivities of CO2 emissions in European land ecosystems. Biogeosciences 2015, 12, 5981–5993. [Google Scholar] [CrossRef]
- Hamdi, S.; Moyano, F.; Sall, S.; Bernoux, M.; Chevallier, T. Synthesis analysis of the temperature sensitivity of soil respiration from laboratory studies in relation to incubation methods and soil conditions. Soil Biol. Biochem. 2013, 58, 115–126. [Google Scholar] [CrossRef]
- Boone, R.D.; Nadelhoffer, K.J.; Canary, J.D.; Kaye, J.P. Roots exert a strong influence on the temperature sensitivityof soil respiration. Nature 1998, 396, 570–572. [Google Scholar] [CrossRef]
- Xu, M.; Qi, Y. Soil-surface CO2 efflux and its spatial and temporal variations in a young ponderosa pine plantation in northern California: Soil-Surface CO2 Efflux and Its Variation. Glob. Chang. Biol. 2001, 7, 667–677. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Chung, H.; Yu, L.; Mi, Z.; Geng, Y.; Jing, X.; Wang, S.; Zeng, H.; Cao, G.; et al. Non-growing-season soil respiration is controlled by freezing and thawing processes in the summer monsoon-dominated Tibetan alpine grassland. Glob. Biogeochem. Cycles 2014, 28, 1081–1095. [Google Scholar] [CrossRef]
- Chen, B.; Liu, S.; Ge, J.; Chu, J. Annual and seasonal variations of Q10 soil respiration in the sub-alpine forests of the Eastern Qinghai-Tibet Plateau, China. Soil Biol. Biochem. 2010, 42, 1735–1742. [Google Scholar] [CrossRef]
- Xu, M.; Qi, Y. Spatial and seasonal variations of Q10 determined by soil respiration measurements at a Sierra Nevadan Forest. Glob. Biogeochem. Cycles 2001, 15, 687–696. [Google Scholar] [CrossRef]
- Janssens, I.A.; Pilegaard, K. Large seasonal changes in Q10 of soil respiration in a beech forest. Glob. Chang. Biol. 2003, 9, 911–918. [Google Scholar] [CrossRef]
- Shabaga, J.A.; Basiliko, N.; Caspersen, J.P.; Jones, T.A. Seasonal controls on patterns of soil respiration and temperature sensitivity in a northern mixed deciduous forest following partial-harvesting. For. Ecol. Manag. 2015, 348, 208–219. [Google Scholar] [CrossRef]
- Noh, N.J.; Kuribayashi, M.; Saitoh, T.M.; Muraoka, H. Different responses of soil, heterotrophic and autotrophic respirations to a 4-year soil warming experiment in a cool-temperate deciduous broadleaved forest in central Japan. Agric. For. Meteorol. 2017, 247, 560–570. [Google Scholar] [CrossRef]
- Kurganova, I.N.; Lopes de Gerenyu, V.O.; Myakshina, T.N.; Sapronov, D.V.; Savin, I.Y.; Shorohova, E.V. Carbon Balance in Forest Ecosystems of Southern Part of Moscow Region under a Rising Aridity of Climate. Contemp. Probl. Ecol. 2017, 10, 748–760. [Google Scholar] [CrossRef]
- Larionova, A.A.; Rozanova, L.N.; Samoylov, T.I. Dynamics of Gas Exchange in the Profile of a Gray Forest Soil. Sov. Soil Sci. 1989, 21, 104–110. [Google Scholar]
- Kurganova, I.; Lopes de Gerenyu, V.; Rozanova, L.; Sapronov, D.; Myakshina, T.; Kudeyarov, V. Annual and seasonal CO2 fluxes from Russian southern taiga soils. Tellus B Chem. Phys. Meteorol. 2003, 55, 338–344. [Google Scholar] [CrossRef]
- Lopes de Gerenyu, V.O.; Kurganova, I.N.; Rozanova, L.N.; Kudeyarov, V.N. Annual Emission of Carbon Dioxide from Soils of the Southern Taiga Soils of Russia. Eurasian Soil Sci. 2001, 34, 931–944. [Google Scholar]
- Panikov, N.S.; Gorbenko, A.J. The Dynamics of Gas Exchange between Soil and Atmosphere in Relation to Plant-Microbe Interactions: Fluxes Measuring and Modelling. Ecol. Bull. 1992, 42, 53–61. [Google Scholar]
- Lei, Y.; Liu, Y.; Song, H.; Sun, B. A wetness index derived from tree-rings in the Mt. Yishan area of China since 1755 AD and its agricultural implications. Chin. Sci. Bull. 2014, 59, 3449–3456. [Google Scholar] [CrossRef]
- Pavelka, M.; Acosta, M.; Marek, M.V.; Kutsch, W.; Janouš, D. Dependence of the Q10 values on the depth of the soil temperature measuring point. Plant Soil 2007, 292, 171–179. [Google Scholar] [CrossRef]
- Humphreys, E.R.; Andrew Black, T.; Morgenstern, K.; Li, Z.; Nesic, Z. Net ecosystem production of a Douglas-fir stand for 3 years following clearcut harvesting. Glob. Chang. Biol. 2005, 11, 450–464. [Google Scholar] [CrossRef]
- Kurganova, I.N.; Tipe, P. The Effect of Freezing-Thawing Processes on Soil Respiration Activity. Eurasian Soil Sci. 2003, 36, 976–985. [Google Scholar]
- Kurganova, I.N.; Lopes De Gerenyu, V.O. Contribution of abiotic factors to CO2 emission from soils in the freeze–thaw cycles. Eurasian Soil Sci. 2015, 48, 1009–1015. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Wang, W.; Peng, S.; Wang, T.; Fang, J. Winter soil CO2 efflux and its contribution to annual soil respiration in different ecosystems of a forest-steppe ecotone, north China. Soil Biol. Biochem. 2010, 42, 451–458. [Google Scholar] [CrossRef]
- Kurganova, I.; Teepe, R.; Loftfield, N. Influence of freeze-thaw events on carbon dioxide emission from soils at different moisture and land use. Carbon Balance Manag. 2007, 2, 2. [Google Scholar] [CrossRef]
- Kurganova, I.; Lopes de Gerenyu, V.; Khoroshaev, D.; Blagodatskaya, E. Effect of snowpack pattern on cold-season CO2 efflux from soils under temperate continental climate. Geoderma 2017, 304, 28–39. [Google Scholar] [CrossRef]
- Xu, X. Effect of freeze-thaw disturbance on soil C and N dynamics and GHG fluxes of East Asia forests: Review and future perspectives. Soil Sci. Plant Nutr. 2022, 68, 15–26. [Google Scholar] [CrossRef]
- Du, E.; Zhou, Z.; Li, P.; Jiang, L.; Hu, X.; Fang, J. Winter soil respiration during soil-freezing process in a boreal forest in Northeast China. J. Plant Ecol. 2013, 6, 349–357. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Q.; Ma, Z.; Jin, H.; Chang, X.; Marchenko, S.S.; Spektor, V.V. Seasonal variations in temperature sensitivity of soil respiration in a larch forest in the Northern Daxing’an Mountains in Northeast China. J. For. Res. 2022, 33, 1061–1070. [Google Scholar] [CrossRef]
- Hashimoto, S. Q10 values of soil respiration in Japanese forests. J. For. Res. 2005, 10, 409–413. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, S.; Xiong, L.; Yang, W.; Yin, H.; Tu, L.; Wu, F.; Chen, L.; Tan, B. Temperature sensitivity of soil respiration in China’s forest ecosystems: Patterns and controls. Appl. Soil Ecol. 2015, 93, 105–110. [Google Scholar] [CrossRef]
- Osipov, A.F. Effect of Interannual Difference in Weather Conditions of the Growing Season on the CO2 Emission from the Soil Surface in the Middle-Taiga Cowberry–Lichen Pine Forest (Komi Republic). Eurasian Soil Sci. 2018, 51, 1419–1426. [Google Scholar] [CrossRef]
- Kurganova, I.N.; Lopes de Gerenyu, V.O.; Gallardo Lancho, J.F.; Oehm, C.T. Evaluation of the rates of soil organic matter mineralization in forest ecosystems of temperate continental, mediterranean, and tropical monsoon climates. Eurasian Soil Sci. 2012, 45, 68–79. [Google Scholar] [CrossRef]
- Schmidt, M.W.I.; Torn, M.S.; Abiven, S.; Dittmar, T.; Guggenberger, G.; Janssens, I.A.; Kleber, M.; Kögel-Knabner, I.; Lehmann, J.; Manning, D.A.C.; et al. Persistence of soil organic matter as an ecosystem property. Nature 2011, 478, 49–56. [Google Scholar] [CrossRef]
- Knorr, W.; Prentice, I.C.; House, J.I.; Holland, E.A. Long-term sensitivity of soil carbon turnover to warming. Nature 2005, 433, 298–301. [Google Scholar] [CrossRef]
- Conant, R.T.; Ryan, M.G.; Ågren, G.I.; Birge, H.E.; Davidson, E.A.; Eliasson, P.E.; Evans, S.E.; Frey, S.D.; Giardina, C.P.; Hopkins, F.M.; et al. Temperature and soil organic matter decomposition rates—Synthesis of current knowledge and a way forward. Glob. Chang. Biol. 2011, 17, 3392–3404. [Google Scholar] [CrossRef]
- Melillo, J.M.; Steudler, P.A.; Aber, J.D.; Newkirk, K.; Lux, H.; Bowles, F.P.; Catricala, C.; Magill, A.; Ahrens, T.; Morrisseau, S. Soil Warming and Carbon-Cycle Feedbacks to the Climate System. Science 2002, 298, 2173–2176. [Google Scholar] [CrossRef] [PubMed]
- Rey, A.; Jarvis, P. Modelling the effect of temperature on carbon mineralization rates across a network of European forest sites (FORCAST). Glob. Chang. Biol. 2006, 12, 1894–1908. [Google Scholar] [CrossRef]
- Bradford, M.A.; Davies, C.A.; Frey, S.D.; Maddox, T.R.; Melillo, J.M.; Mohan, J.E.; Reynolds, J.F.; Treseder, K.K.; Wallenstein, M.D. Thermal adaptation of soil microbial respiration to elevated temperature. Ecol. Lett. 2008, 11, 1316–1327. [Google Scholar] [CrossRef] [PubMed]
- Larionova, A.A.; Maltseva, A.N.; Lopes de Gerenyu, V.O.; Kvitkina, A.K.; Bykhovets, S.S.; Zolotareva, B.N.; Kudeyarov, V.N. Effect of temperature and moisture on the mineralization and humification of leaf litter in a model incubation experiment. Eurasian Soil Sci. 2017, 50, 422–431. [Google Scholar] [CrossRef]
- Fang, C.; Smith, P.; Moncrieff, J.B.; Smith, J.U. Similar response of labile and resistant soil organic matter pools to changes in temperature. Nature 2005, 433, 57–59. [Google Scholar] [CrossRef] [PubMed]
- Conen, F.; Leifeld, J.; Seth, B.; Alewell, C. Warming mineralizes young and old soil carbon equally. Biogeosciences 2006, 3, 515–519. [Google Scholar] [CrossRef]
- Drake, J.E.; Giasson, M.-A.; Spiller, K.J.; Finzi, A.C. Seasonal plasticity in the temperature sensitivity of microbial activity in three temperate forest soils. Ecosphere 2013, 4, art77. [Google Scholar] [CrossRef]
- Yang, S.; Wu, H.; Wang, Z.; Semenov, M.V.; Ye, J.; Yin, L.; Wang, X.; Kravchenko, I.; Semenov, V.; Kuzyakov, Y.; et al. Linkages between the temperature sensitivity of soil respiration and microbial life strategy are dependent on sampling season. Soil Biol. Biochem. 2022, 172, 108758. [Google Scholar] [CrossRef]
- Wallenstein, M.D.; Mcmahon, S.K.; Schimel, J.P. Seasonal variation in enzyme activities and temperature sensitivities in Arctic tundra soils. Glob. Chang. Biol. 2009, 15, 1631–1639. [Google Scholar] [CrossRef]
- Lopes de Gerenyu, V.; Kurganova, I.; Kuznetzov, M.; Osipov, A.; Myakshina, T.; Sapronov, D.; Kaganov, V.; Bobkova, K.; Kudeyarov, V. Organic Carbon Pools and CO2 Fluxes from Soils of Forest Ecosystems in the European Part of Russia. In Proceedings of the 1st Pan-Eurasian Experiment (PEEX) Conference and the 5th PEEX Meeting, Helsinki, Finland, 10–13 February 2015; Volume 163, pp. 250–255. [Google Scholar]
- Zheng, Z.-M.; Yu, G.-R.; Fu, Y.-L.; Wang, Y.-S.; Sun, X.-M.; Wang, Y.-H. Temperature sensitivity of soil respiration is affected by prevailing climatic conditions and soil organic carbon content: A trans-China based case study. Soil Biol. Biochem. 2009, 41, 1531–1540. [Google Scholar] [CrossRef]
- IPCC Climate Change 2014: Synthesis Report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014.
- Lopes de Gerenyu, V.O.; Kurganova, I.N.; Khoroshaev, D.A. The Effect of Contrasting Moistening Regimes on CO2 Emission from the Gray Forest Soil under a Grass Vegetation and Bare Fallow. Eurasian Soil Sci. 2018, 51, 1200–1213. [Google Scholar] [CrossRef]
- Arias, P.A.; Bellouin, N.; Coppola, E.; Jones, R.G.; Krinner, G.; Marotzke, J.; Naik, V.; Palmer, M.D.; Plattner, G.-K.; Rogelj, J.; et al. Technical Summary. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 33–144. [Google Scholar] [CrossRef]
- Roshydromet Second Assessment Report on Climate Change and Its Consequences in the Russian Federation (General Summary); Roshydromet: Moscow, Russia, 2014; ISBN 978-5-904206-13-0.
- Stefanidis, S.; Alexandridis, V. Precipitation and Potential Evapotranspiration Temporal Variability and Their Relationship in Two Forest Ecosystems in Greece. Hydrology 2021, 8, 160. [Google Scholar] [CrossRef]
- Stefanidis, S.P. Ability of Different Spatial Resolution Regional Climate Model to Simulate Air Temperature in a Forest Ecosystem of Central Greece. J. Environ. Prot. Ecol. 2021, 22, 1488–1495. [Google Scholar]
- Stefanidis, S.; Dafis, S.; Stathis, D. Evaluation of Regional Climate Models (RCMs) Performance in Simulating Seasonal Precipitation over Mountainous Central Pindus (Greece). Water 2020, 12, 2750. [Google Scholar] [CrossRef]
| Site | Soil | Sand:Silt:Clay | WHC, % | C | N | C/N | pHKCl |
|---|---|---|---|---|---|---|---|
| g/kg of Soil | |||||||
| MMF | Entic Podzol Arenic | 11.6:1.0:1.3 | 40.5 ± 2.7 | 12.2 ± 2.8 | 0.96 ± 0.15 | 15.3 | 3.67 ± 0.02 |
| SDF | Haplic Luvisol Siltic | 1.2:2.3:1.0 | 57.5 ± 2.3 | 30.0 ± 1.8 | 2.35 ± 0.10 | 12.8 | 5.56 ± 0.09 |
| Level of Humidity | Q*10 | n | R2 | SR*10 | Q10 | n | R2 | SR10 |
|---|---|---|---|---|---|---|---|---|
| Mixed mature forest, Entic Podzol | ||||||||
| Normal | 2.72 | 524 | 0.59 | 1.80 | 2.33 | 361 | 0.51 | 1.85 |
| Wet | 2.42 | 225 | 0.61 | 1.86 | 2.32 | 157 | 0.52 | 1.89 |
| Dry | 2.13 | 315 | 0.45 | 1.48 | 1.64 | 207 | 0.29 | 1.57 |
| Secondary deciduous forest, Haplic Luvisol | ||||||||
| Normal | 2.66 | 473 | 0.56 | 1.85 | 2.09 | 324 | 0.50 | 1.98 |
| Wet | 2.17 | 211 | 0.54 | 1.89 | 1.80 | 143 | 0.42 | 2.01 |
| Dry | 1.89 | 297 | 0.47 | 1.41 | 1.49 | 204 | 0.28 | 1.54 |
| Season | Q*10 | n | R2 | SR*10 | Q10 | n | R2 | SR10 |
|---|---|---|---|---|---|---|---|---|
| Mixed mature forest, Entic Podzol | ||||||||
| Spring | 2.47 | 272 | 0.34 | 1.76 | 1.82 | 154 | 0.26 | 1.70 |
| Fall | 2.33 | 281 | 0.40 | 1.79 | 2.14 | 259 | 0.34 | 1.77 |
| Winter | 3.23 | 241 | 0.07 | nd | 1.14 | 40 | ns | nd |
| Summer | 1.55 | 276 | 0.06 | nd | 1.55 | 276 | 0.06 | nd |
| Secondary deciduous forest, Haplic Luvisol | ||||||||
| Spring | 3.13 | 243 | 0.47 | 2.00 | 2.17 | 152 | 0.43 | 2.00 |
| Fall | 1.86 | 263 | 0.35 | 1.78 | 1.75 | 240 | 0.27 | 1.78 |
| Winter | 6.54 | 216 | 0.08 | nd | 2.14 | 20 | ns | nd |
| Summer | 1.03 | 249 | ns | nd | 1.03 | 249 | ns | nd |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurganova, I.; Lopes de Gerenyu, V.; Khoroshaev, D.; Myakshina, T.; Sapronov, D.; Zhmurin, V. Temperature Sensitivity of Soil Respiration in Two Temperate Forest Ecosystems: The Synthesis of a 24-Year Continuous Observation. Forests 2022, 13, 1374. https://doi.org/10.3390/f13091374
Kurganova I, Lopes de Gerenyu V, Khoroshaev D, Myakshina T, Sapronov D, Zhmurin V. Temperature Sensitivity of Soil Respiration in Two Temperate Forest Ecosystems: The Synthesis of a 24-Year Continuous Observation. Forests. 2022; 13(9):1374. https://doi.org/10.3390/f13091374
Chicago/Turabian StyleKurganova, Irina, Valentin Lopes de Gerenyu, Dmitry Khoroshaev, Tatiana Myakshina, Dmitry Sapronov, and Vasily Zhmurin. 2022. "Temperature Sensitivity of Soil Respiration in Two Temperate Forest Ecosystems: The Synthesis of a 24-Year Continuous Observation" Forests 13, no. 9: 1374. https://doi.org/10.3390/f13091374
APA StyleKurganova, I., Lopes de Gerenyu, V., Khoroshaev, D., Myakshina, T., Sapronov, D., & Zhmurin, V. (2022). Temperature Sensitivity of Soil Respiration in Two Temperate Forest Ecosystems: The Synthesis of a 24-Year Continuous Observation. Forests, 13(9), 1374. https://doi.org/10.3390/f13091374






