Abstract
The breeding of Norway spruce in northern Europe has substantially contributed to the production of high-quality wood. The vegetative propagation of robust elite clones could help to sustain the provision of high-quality timber in the face of changing climates. For the adequate evaluation of genetic gains, the altered tree growth dynamics of the clones need to be understood, yet essential information about the long-term growth dynamics of improvedboreal trees is still lacking. We examined a 50-year-old clonal plantation in Latvia to distinguish the clonal effects on diameter growth function parameters and estimate the genetic parameters. A mixed-effect modelling approach was used, in which the clones were applied as random effects on the parameters of the Chapman–Richard equation. All model parameters showed significant variance in the genotypic coefficients of variation CVg which ranged between 11.0 and 17.1%, with the highest being for the growth rate. The heritability (H2) of the diameter at breast height (DBH) reached 0.35 at the age of 40, while CVg decreased from 12.9% to 7.8% between the ages of 20 and 45. Age–age genotypic correlations were positive and were strong or very strong (>0.76). The realised genetic gain varied from −6.3 to +24.0% around the trial mean. A substantial improvement in DBH was indicated when elite clones were selected for vegetative propagation based not only on early measurements, but also considering the genetic variance in the model parameters.
1. Introduction
In the Baltic Sea region, the planting of forests has a substantial economic impact [1]. The breeding of Norway spruce (Picea abies (L.) Karst.) has taken place since the middle of the 20th century due to the financial importance of coniferous trees [2]. The profitability of long-term investment in genetic selection has been proven by increased productivity, quality and resistance to the risks of a changing environment, which has resulted in an improved monetary value [1,2,3,4,5]. The growing demand for wood-based biomass continues to maintain the significance of tree breeding in the future [1]. In addition, the financial performance of genetically improved material has been enhanced by the inclusion of carbon pricing [4], which indicates the additional benefits of breeding in terms of carbon sequestration.
When appropriately managed (e.g., in a sparsely planted plantation), Norway spruce can rapidly reach its target diameter [6], thereby shortening rotation time, reducing establishment costs and increasing financial outcomes [7,8]. In turn, a reduced rotation time can mitigate the risk of biotic and abiotic damage, such as that from wind, drought, root rot, bark beetle attacks, etc., which are commonly acknowledged threats for successful Norway spruce management in a changing climate [9,10,11,12,13].
Tree breeding has been estimated to advance production by 10–35% compared to unimproved material [14]. Substantial variations in genetic gains exist among the different improvement levels, including the combination of additive and non-additive genetic variance in clonal selection [15], which can increase the genetic gain for conifers by 5–20% compared to that from familial selection [16]. A recent study in Sweden showed a double genetic gain in diameter at breast height (DBH) for clonal deployment compared to improved seedlings [17]. The clonal propagation of Norway spruce is justified by a substantial growth improvement [1], the immediate transfer of genetic gains to new plantations, the flexibility to quickly adapt nursery production to various environmental conditions and management objectives [18] and its profitability [19]. Overall, considerable knowledge has been obtained from clone testing, which can be implemented in the practical management of clonal plantations [20]. Despite this, the relatively high initial investment that is required compared to more common types of reproductive materials (seedlings) restricts the wider deployment of vegetative propagation [1,19], even though it has a stable market share (for example, in Sweden, circa 1 million rooted cuttings are produced annually) and the interest of buyers is growing [19].
The substantial variation in genetic gains for growth has resulted in altered stand dynamics for improved planting stocks [21,22]. Growth and yield modelling is commonly used for the long-term estimation of forest development and the evaluation of alternative management options [23,24,25], although it is usually based on data from unimproved stands [26]. To avoid biased predictions, differences in the growth dynamics of different genetic entries must be understood to allow for the adequate inclusion of genetic gains in the growth functions [21,22,27]. Genetic improvement can affect height and diameter growth differently [28], and so the commonly applied site index adjustment alone [29,30,31,32] may not accurately account for the altered dynamics of the DBH, which is also an important component in reliable predictions of forest yield [33,34,35,36,37].
Overall, little is known about the long-term genetic effects of cloning on Norway spruce diameter growth. To ensure an efficient breeding cycle, the genetic gains are usually estimated from young field trials and the optimal selection time for Norway spruce is the age of 10–16 years [38]. This is justified by sufficiently high correlations between the early measurements and the resulting production at the end of the rotation [39], although the realised yield can be higher than was expected based on the early height [19]. Therefore, an exceptionally widely planted (5 × 5 m) clonal Norway spruce plantation at rotation age with presumably delayed inter-tree competition could provide insights into the diameter growth differences among the various genetic entries, which could indicate distinct clonal effects on the growth function parameters. The origin of the study material (vegetative propagation) was expected to demonstrate a large proportion of the genetic variations [17,40], with clones representing the highest level of genetic uniformity [41]. Although the utilisation of vegetatively propagated Norway spruce is still not a common practice in commercial forestry, this trial was expected to provide essential information about genetic effects up to rotation age, which is currently lacking, in order to obtain more precise predictions of diameter growth [18].
Thus, the aim of this study was (i) to determine the clone effect on the parameters of the Norway spruce diameter growth curve by applying a mixed-effect modelling approach and (ii) to estimate the dynamics of the genetic parameters for diameter at breast height up to the final harvest dimensions. We hypothesised that all model parameters would have significant genetic variance.
2. Materials and Methods
2.1. Study Site and Material
The study was carried out in a Norway spruce clonal plantation, which is located on fertile mineral soil under mesotrophic conditions in eastern Latvia (56°42′ N, 25°53′ E) at 119 m above sea level. The plantation is comparable to the Oxalidosa forest type [42]. The site index was 36.0 m. The mean annual temperature in the study area was circa +6.0 °C, with the mean monthly temperature ranging from −6.4 °C in February to +17.1 °C in July. The mean annual precipitation was circa 700 mm [43].
The plantation was established in 1964 using vegetatively propagated (grafted) planting material from 20 selected fast-growing plus trees of local origin, at a spacing of 5 × 5 m (400 trees ha−1). The rootstock material comprised seedlings of local origin. In total, 421 trees were planted in randomly distributed single-tree plots (11–31 replications (ramets) per clone). Weed control was carried out in the planting year and the first year after planting. No thinning was conducted prior to the sampling. No measurements had been performed before during the trial.
Both DBH and height were measured for all mature trees (i.e., 50 years old or more) in the plantation. The plantation growth and yield data for trees at the age of 50 years were published previously by Katrevičs et al. [6].
Cores from pith-to-bark at breast (1.3 m) height were collected at 5-mm increments from 221 50-year-old trees, which represented 19 of initially planted 20 clones (7–19 ramets per clone). Only straight trees with no visible crown asymmetry or other stem defects, such as visible root rot, double tops or severe browsing damage, were selected for core sampling. Annual ring width data were obtained using high-frequency densitometry with a LignoStation [44]. These were cross-dated and verified by graphical inspection and using the COFECHA software [45].
The tree ring data allowed for the study of the age–diameter relationship at an annual resolution [46]. The DBH for each year was reconstructed using annual diameter increments, which were based on the measurements that were taken at the age of 50 years. For the diameter reconstruction, the tree stems were assumed to be circular so that the DBH could be calculated from the incremental cores. As a result, time-series data for the DBH of each tree were obtained for the ages of 20–50 years (Figure 1).
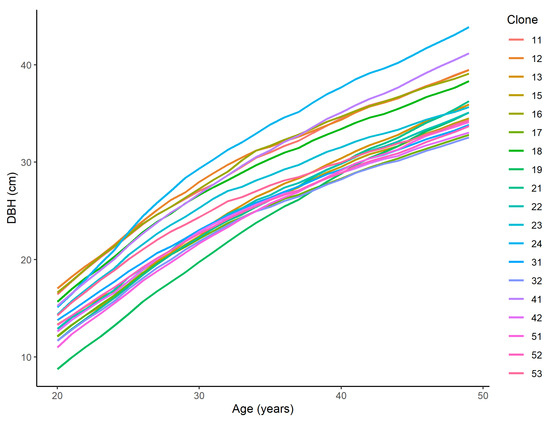
Figure 1.
The mean diameter growth trajectories of the 19 Norway spruce clones that were analysed in this study.
2.2. Modelling Approach
The clone effect on the parameters of the diameter–age relationship was investigated by applying the Chapman–Richard base equation:
where DBHiA is the DBH for the i-th clone at age A, β1 is the asymptotic diameter parameter, β2 is the rate parameter, β3 is the shape parameter and ԑiA is a normally distributed zero-expectation random error due to the DBH that was observed at age A [47]. We followed the approach of using models that had been previously fitted successfully by other researchers [48]. The preliminary analyses and previous studies have suggested that the Chapman–Richard function is a biologically reasonable selection for modelling tree growth curves [34,46,49,50].
The clone effect on the diameter–age relationship was modelled as random effects on the parameters in Equation (1) using the function:
where DBHiA and ԑiA are as defined as for Equation (1), β10, β20 and β30 are fixed effect parameters and b1i, b2i and b3i are random effect parameters for the i-th clone (, and with no correlation among these parameters). Heteroscedasticity in the error term ԑiA was not detected. The autocorrelations of the errors that were due to ring width measurements on the same trees were modelled by mixed first-order autoregressive and moving average structures (ARMA (1,1)). To remove the effects of the various variances in the different clones, we modelled different variances for each factor (clone) using the variance function [51].
Equation (2) was fitted using nonlinear mixed-effect regression with the nlme package in R software [52]. The effects of the clone on the model parameters were investigated using a common approach: eliminating the random effect parameters from the model one by one by using random effects for all parameters initially. Different combinations of parameters were tested and the best model was selected using the likelihood ratio test, Akaike’s information criterion (AIC) and the Bayesian information criterion (BIC). The fitted model was evaluated using mean bias and root mean squared error [53]. The significance of random factors in the final fitted model was evaluated by applying likelihood ratio tests of model reductions for each random effect term, which were provided by the rand function in the lmerTest package [54]. The normality of the final fitted model residuals was tested by applying the Jarque–Bera test.
2.3. Genetic Parameters
To estimate the variance components, the following model was used:
where yij is the observation of the ith tree from the jth clone, μ is the overall mean, Ci is the random effect of the cloning and ԑij is the random error. To evaluate the dynamics of the genetic parameters, (i) the broad-sense heritability (H2) of DBH for each year and (ii) the age–age genotypic correlations of DBH among the years were estimated as follows:
where and are the estimated variance components of clone and residual, respectively, and:
where and are the genotypic (clone) variances at two different ages and is the estimated genotypic covariance between the two measurements.
For the final fitted model, we adapted a formula for calculating the genotypic coefficient of variation (CVg) [55] in order to describe the extent of genetic variability among the clones for any random effect parameter:
where CVg is the genotypic coefficient of variation, is the estimated variance for the random effect parameter x and βx is the fixed effect parameter x. The CVg of DBH was calculated for each year. For comparison, the H2 and CVg of tree height at the age of 50 years was estimated.
The realised genetic gain at the age of 50 years (final harvest age) was estimated for each clone using the best linear unbiased predictions (BLUPs) from the final fitted model as a percentage of the trial mean DBH.
3. Results
3.1. The Growth Model
The model form with all three random parameters (random asymptote (b1i), random rate (b2i) and random shape (b3i)) had the lowest value of the AIC statistic (−189.152) (Table 1). Overall, the model fit was significantly improved by addition of the random rate and/or shape into the model that already contained the random effect parameter b1i compared to the anamorphic random asymptote equation (p < 0.01).

Table 1.
Parameter estimates (fixed effect parameters: β10, β20 and β30; estimated variance components: , , , ) and model statistics (AIC, Akaike’s information criterion; BIC, Bayesian information criterion; logLik, log likelihood test) of the Chapman–Richard base equation when applying different combinations of random asymptotes (β1), random rates (β2) and random shapes (β3), which were fitted to diameter at breast height from the 19 clones that were used in the study.
The residuals of the final model were distributed symmetrically around zero with an approximately even variance and did not violate the assumption of normality (p = 0.154). The model provided a good representation of the dataset (Figure 2). The distribution of the random effects did not indicate any noticeable violations of the assumption of normality. For the final fitted model, the mean bias was −0.57 cm with a root mean square error of 3.61 cm.
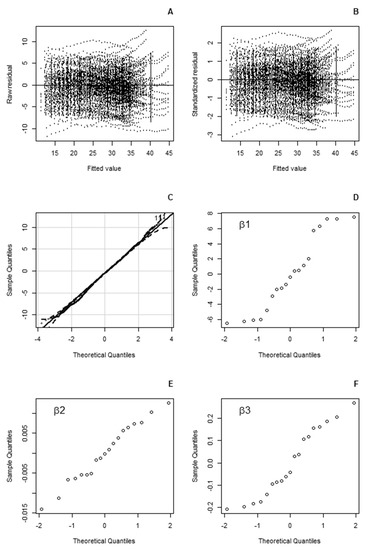
Figure 2.
Statistics of the final fitted Chapman–Richard mixed model that was applied to investigate the clone effect of the diameter–age relationship on the parameters: (A,B) plots of raw (A) and standardised (B) residuals for the final equation. The whiskers denote the 95% confidence intervals of the residuals for the classified fitted values. (C) Quantile–quantile plot of the final fitted model. (D–F) Normal plots of the estimated random effects of the asymptotic diameter parameter β1 (D), the rate parameter β2 (E) and the shape parameter β3 (F) for the final fitted model.
From the data that were used in this study, genetic variety (clone) significantly (p ≤ 0.05) affected the asymptotic DBH and the rate and shape parameters of the Chapman–Richards diameter–age model. Thus, there was a significant polymorphism among the diameter–age trajectories of the different clones.
3.2. Dynamics of Genetic Parameters
The estimated broad-sense heritability (H2) ± standard error (SE) for DBH increased from 0.19 ± 0.087 at the age of 20 years to 0.35 ± 0.131 at the age of 40 years (Figure 3). Afterwards, H2 gradually decreased and was 0.32 ± 0.123 at the age of 50 years. On the contrary, the genotypic coefficient of variation (CVg) was the highest at the age of 20 years (12.9%) and decreased to 7.8% at the age of 45 years, after which it remained stable for the following 5 years. The H2 and CVg for tree height at the age of 50 years was 0.41 ± 0.088 and 5.6%, respectively.
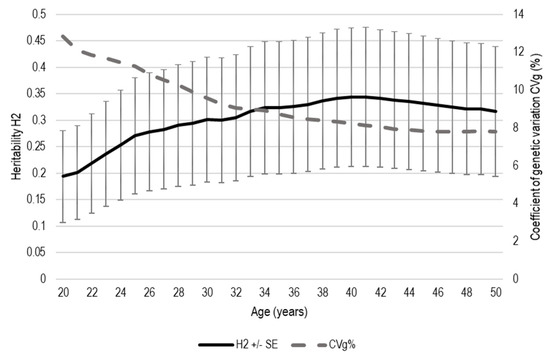
Figure 3.
Dynamics of the estimated broad-sense heritability (H2) and genotypic coefficient of variation (CVg) during the studied period (age 20–50 years) of Norway spruce clones. The whiskers denote the standard error for H2.
The estimated CVg for the DBH growth model parameters β1, β2 and β3 were 11.0, 17.1 and 11.9%, respectively. Overall, variance in the asymptotic DBH due to the clonal effects was slightly greater ( = 26.69 cm) than the within-group (within-clone) error variance ( = 23.05 cm) (Table 1). The realised genetic gains of the clones at the final harvest age varied from −6.3 to +24.0% around the trial mean (Figure 4).
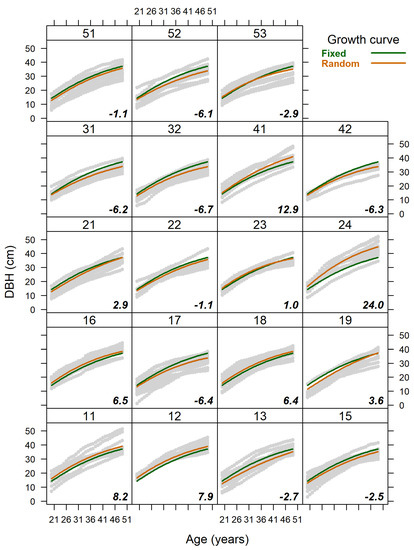
Figure 4.
Predicted trajectories of DBH growth curves for population mean (fixed), each individual clone (random) and its realised genetic gain (numbers in bold and italic, %) at the final harvest age of 50 years (45 years of breast height age) using the final fitted model. Grey dots represent the sample data for each clone.
The estimated age–age genotypic correlations (rG) were positive and mainly very strong (>0.80), although they were slightly weaker, yet still strong (>0.76), for the older trees (age 20–22 versus age 46–50 years). There was a trend of slightly stronger correlations between similar ages with increasing age. For instance, DBH between age 45 and 50 was 100% genetically correlated, while rG between ages 20 and 15 was 0.97.
4. Discussion
Growth curve fitting is a common procedure that is used to understand general biological growth trends [56] and incorporating factors that affect this curve can improve the accuracy of the function under different conditions [33,57]. These factors include any silvicultural treatment over time [58], among which clonal effects are perceived. In our study, the Chapman–Richards equation, with its sigmoid form, inflection point and asymptote, fitted the data well (Figure 2) and the function parameters were meaningful for the analysis of the response of DBH to clonal effects over time [58,59].
Applying a mixed model, we estimated the population mean response that was common to the entire clonal plantation as fixed effect parameters [34], while random effect parameters that varied around the fixed mean [60] represented the specific responses of the clone grouping variable (Table 1, Figure 4). The possibility of estimating the variance within and among the clones for the random effect parameters [51,61] was an important advantage in terms of analysing the growth modelling results from a tree breeding perspective, since this field of study widely utilises genetically determined variations in traits of interest (in our case, the model parameters) to estimate quantitative genetic parameters and breeding values [55].
Our final model fitting results showed that all three model parameters (asymptote, growth rate and shape) were significantly affected by clone. There are not many previous studies on this issue, but those that do exist have mainly explored the tree height growth response to genetic effects. For loblolly pine (Pinus taeda L.), Sabatia and Burkhart [62] found that clone significantly affected the asymptotic height and shape parameters of the Chapman–Richards height–age model, while Knowe and Foster [63] concluded that half-sib families had an effect on the asymptote and rate. Half-sib genetic varieties and provenance have been reported to only affect the asymptote of the Korf function [29,64]. In contrast, Sprinz et al. [65] only reported the effects of half-sib families on the shape parameter. In Chinese fir (Cunninghamia lanceolata (Lamb.) Hook.), height growth trajectories in stands with different provenances only differed in the asymptote [66]. A strong genetic influence on the asymptote has also been reported for Konishii fir (Cunninghamia konishii Hay.) using an application of the Weibull-based function of DBH [67].
4.1. Dynamics of Clone-Specific Diameter Growth and Its Genetic Parameters over Time
Although variance component analyses are of primary interest in quantitative genetic studies, the random effect variances in the model parameters have been rarely reported or interpreted within ecological modelling [68]. Our results of the random effects showed significant variances in all three model parameters that were determined by the genetic effects. The overall magnitude of variation in DBH among the clones was greater than that within the clones (Table 1), which indicated the great importance of random effect variance, i.e., clonal differences, for selection [61,68,69]. Moreover, the genotypic coefficients of variation for the model parameters (asymptote, growth rate and shape) ranged between 11.0 and 17.1%, which exceeded the variation in DBH at the time of final felling (7.8%) and suggested the potential for genetic improvement in the asymptotic DBH, as well as a more rapid radial growth trajectory. For DBH growth function of Konishii fir, provenance and family have been reported to account for 26% of the variation in the asymptote, but only 4% in both the rate and shape [67]. For the loblolly pine height curve, the coefficients of variation among the clones in the asymptote and shape of the Chapman–Richards function have been estimated to be 4.2 and 2.8%, respectively [70].
By comparison, the CVg for DBH in trials involving 19-year-old Norway spruce clones has been reported to vary between 13.6 and 15.9% [71]. Still, our results showed that CVg and H2 were not constant and changed over time. The estimated H2 increased from 0.19 at the age of 20 years to a peak of 0.35 at the age of 40 years. A similar trend has been observed for the narrow-sense heritability h2 of DBH in open- pollinated progenies of Norway spruce in southern Sweden, for which h2 stabilised at circa 0.22 at the cambial age of 10 years after increasing from close to zero near the pith [72]. For Scots pine full-sib families in Sweden, a trend of increasing h2 has been observed for wood quality traits and cumulative ring width, for which this parameter increased from very low to 0.25 at the age of 20 years [73]. Hannrup et al. [71] reported a H2 of 0.34–0.50 for 19-year-old Norway spruce clones, while a low H2 (< 0.14) was estimated for juvenile white spruce (Picea glauca (Moench) Voss) somatic clones 4 years after outplanting [74].
In contrast to H2, CVg decreased by almost half from 12.9% at the age of 20 years to 7.8% at the age of 45, after which it remained stable (Figure 3). Similar to descendent trend that was observed for CVg in our study, spruce clones in series of experiments in northern Germany demonstrated a steady decrease in genetic variance in height from circa 20% at the age of 3 years to a plateau of 7% after the age of 8 years [75]. Joint site data from Sweden showed that the coefficient of additive genotypic variation CVa for DBH in Norway spruce decreased from 15.45% to 11.91% at the ages of 12 and 21 years, respectively [76]. The estimated CVa showed a marked decline with age for both H and DBH (from 25–33% to 7–14%) in Silver fir (Abies alba Mill.) up to the ages of 10–15, after which they became stable [77].
In our study, H2 and CVg stabilised after the age of 40–45 years (Figure 3), which was likely due to reaching the moment of canopy closure and the intensification of inter-tree competition [78] as diameter increment is considered to be the trait that is most (first) affected by competition [79]. Canopy closure depends on the initial planting density and the increment of the trees. The onset of inter-tree competition in loblolly pine has been estimated to be after 5 years in the most densely planted plots (1.2 × 1.2 m) and after 8.6 years in the most sparsely planted plots (3.7 × 3.7 m) [80]. The latter age corresponds to circa 35% of the rotation age for managed P. taeda [81], which indicates a longer period of competition-free early growth for the wider spacing. Although canopy closure in Norway spruce progeny plots in northern Europe with conventional spacing is typically observed at the age of 10–20 years [79], the low planting density (5 × 5 m) in the study site could have delayed it substantially [82,83].
Nevertheless, we acknowledge that the exceptionally sparsely planted trial is an unusual competitive environment for plantations. Some of the commonly known risks for fast growing sparely planted Norway spruce include reduced wood density and stronger branching, which reduce timber quality [71,72,84]. Still, despite the unfavourable negative phenotypic correlations between fast growth and wood quality traits, selection for both may be possible at a clonal level [12,85]. Our study site also differed from common Norway spruce plantations in terms of its reproductive material (vegetatively propagated grafted clones), which is not commonly used as planting stock. Liziniewicz et al. [39] concluded that growth differences among different genetic varieties can be assumed to be independent of plant type, although they compared seedlings to rooted cuttings. The rootstock × scion effect has been reported as being inessential to the growth of loblolly pine, which is contrary to the genetic and site impacts [86]. The fast growth of the studied plantation indicated no potentially negative effects of cyclophysis [87,88,89,90], which has occasionally been detected in clonal trials [91]. However, we stress that our interest was in fitting the model as an analytical tool to investigate the differences in the response curve trajectories of different clones of the same propagation type with a wide range of realised genetic gains for DBH (Figure 4). Still, the clones characterise a local population and thus, had to be generalised with caution.
4.2. Age–Age Genotypic Correlations
The growth pattern of each individual tree is shaped by a combination of both its genetics and environment [92]. Still, the DBHs of individual trees are unlikely to be affected by competition at a genetic level over time from the indirect additive effect of neighbouring trees [79], which was indicated by the strong to very strong positive genotypic age–age correlations that were observed in this study (rg > 0.76).
Somewhat stronger rG at older ages have also been reported previously for various conifer tree species, which could be associated with the cumulative nature of the growth traits [93,94]. Our results corresponded well to earlier studies of growth traits in progeny trials, which showed very strong genotypic relations among similar ages, with a slight decline as the age differences increased [72,75,77,78,94].
Overall, the strong age–age correlations and clone-specific DBH growth trajectories, which were mostly without pronounced rank shifts during the studied period (Figure 1), justify the early selection for DBH. We observed that the clone-specific DBH growth curves are primarily relatively parallel to the population mean curve (Figure 4) and that there were no trends of superior clones, in terms of asymptotic DBH, having a more rapid growth rate. Nevertheless, all DBH growth curve parameters showed substantial genotypic variance (CVg ≥ 11.0%, Table 1) and separate clones (e.g., clone numbers 19, 24, 53) had obviously different growth shapes and rates (Figure 1 and Figure 5), which were likely associated with the different genetically determined growth responses of certain clones to climatic factors [95].
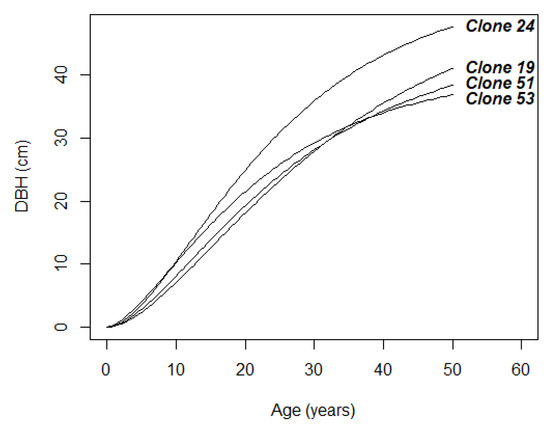
Figure 5.
Growth curves of the selected clones (19, 24, 51, 53) with markedly different DBH growth trajectories.
Thus, we argue that the selection of superior clones using early measurements of DBH could be combined and improved with information about the genetic variations in growth curve parameters when such data (e.g., increment cores) become available from long-term trials. In particular, intensive tree breeding that applies vegetative propagation would benefit from the knowledge of genotype-specific growth trajectories when a set of only a few superior clones is selected. Precise growth functions can improve the effectiveness of tree breeding, which supports the early selection of superior genetic entries using more reliable information on their expected future performance and the subsequent economic outcome of their selection [62,63]. Even small differences in the predicted growth traits can have a substantial impact on the ranking of clones [63]. The knowledge of genetic variances in function parameters can be utilised to develop and test more practically desirable and dynamic base–age–invariant functions [96] by incorporating genetic effects as modifiers for the model parameters [97], which is just as important in practical applications in forestry.
5. Conclusions
We found different growth patterns among the studied Norway spruce clones. There were significant differences between clones in terms of all three of the parameters of the Chapman–Richards function: asymptote, rate and shape. All diameter growth curve parameters demonstrated genotypic variations between the clones that were sufficient for selection with a wide range of realised genetic gains in DBH (up to +24%) that had the potential for genetic improvement. The studied clones possessed considerable heritability (H2 = 0.32) and a significant genotypic coefficient of variation (CVg = 7.8%), which tended to stabilise at the age of 40–45 years. Although the mainly very strong age–age genotypic correlations would justify selection for DBH at earlier age, we suggest that growth curve parameters are just as important for tree breeding in terms of the selection of elite clones, once the data from long-term clonal tests are available. The substantial genetic variation in growth rate, shape and asymptote suggests the potential for more precise selection using predictions for not only final dimensions, but also desirable patterns of growth trajectories. Based on this information, clone-specific genetic modifiers should be tested using dynamic base–age–invariant functions for future growth predictions in practical forestry in order to improve the prediction accuracy for genetic entries with various genetic gains.
Author Contributions
Conceptualisation, A.K. and Ā.J.; methodology, P.Z. and A.K.; formal analysis, P.Z. and J.K.; data curation, J.K.; writing—original draft preparation, P.Z.; writing—review and editing, A.K. and Ā.J.; supervision, A.K.; project administration, Ā.J. All authors have read and agreed to the published version of the manuscript.
Funding
This study was carried out as part of the European Regional Development Fund (project number 1.1.1.1/19/A/111) “Decision support tool for increased forest productivity via efficient climate-adjusted transfer of genetic gain”.
Data Availability Statement
Data are available upon request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ruotsalainen, S. Increased forest production through forest tree breeding. Scand. J. For. Res. 2014, 29, 333–344. [Google Scholar] [CrossRef]
- Jansons, Ā.; Donis, J.; Danusevičius, D.; Baumanis, I. Differential analysis for next breeding cycle for Norway spruce in Latvia. Balt. For. 2015, 21, 285–297. [Google Scholar]
- Jansson, G.; Hansen, J.K.; Haapanen, M.; Kvaalen, H.; Steffenrem, A. The genetic and economic gains from forest tree breeding programmes in Scandinavia and Finland. Scand. J. For. Res. 2017, 32, 273–286. [Google Scholar] [CrossRef]
- Ahtikoski, A.; Ahtikoski, R.; Haapanen, M.; Hynynen, J.; Kärkkäinen, K. Economic performance of genetically improved reforestation material in joint production of timber and carbon sequestration: A case study from Finland. Forests 2020, 11, 847. [Google Scholar] [CrossRef]
- Haapanen, M. Performance of genetically improved Norway spruce in one-third rotation-aged progeny trials in southern Finland. Scand. J. For. Res. 2020, 35, 221–226. [Google Scholar] [CrossRef]
- Katrevičs, J.; Džeriņa, B.; Neimane, U.; Desaine, I.; Bigača, Z. Jansons Production and profitability of low density Norway spruce (Picea abies (L.) Karst.) plantation at 50 years of age: Case study from eastern Latvia. Agron. Res. 2018, 16, 113–121. [Google Scholar] [CrossRef]
- Pfister, O.; Wallentin, C.; Nilsson, U.; Ekö, P.M. Effects of wide spacing and thinning strategies on wood quality in Norway spruce (Picea abies) stands in southern Sweden. Scand. J. For. Res. 2007, 22, 333–343. [Google Scholar] [CrossRef]
- Routa, J.; Kilpeläinen, A.; Ikonen, V.-P.; Asikainen, A.; Venäläinen, A.; Peltola, H. Effects of intensified silviculture on timber production and its economic profitability in boreal Norway spruce and Scots pine stands under changing climatic conditions. For. Int. J. For. Res. 2019, 92, 648–658. [Google Scholar] [CrossRef]
- Arhipova, N.; Gaitnieks, T.; Donis, J.; Stenlid, J.; Vasaitis, R. Butt rot incidence, causal fungi, and related yield loss in Picea abies stands of Latvia. Can. J. For. Res. 2011, 41, 2337–2345. [Google Scholar] [CrossRef]
- Allikmäe, E.; Laarmann, D.; Korjus, H. Vitality assessment of visually healthy trees in Estonia. Forests 2017, 8, 223. [Google Scholar] [CrossRef]
- Donis, J.; Kitenberga, M.; Šņepsts, G.; Dubrovskis, E.; Jansons, Ā. Factors affecting windstorm damage at the stand level in hemiboreal forests in Latvia: Case study of 2005 winter storm. Silva Fenn. 2018, 52, 10009. [Google Scholar] [CrossRef]
- Zeltiņš, P.; Katrevičs, J.; Gailis, A.; Maaten, T.; Bāders, E.; Jansons, Ā.; Zeltiņš, P.; Katrevičs, J.; Gailis, A.; Maaten, T.; et al. Effect of Stem Diameter, Genetics, and Wood Properties on Stem Cracking in Norway Spruce. Forests 2018, 9, 546. [Google Scholar] [CrossRef]
- de Groot, M.; Diaci, J.; Ogris, N. Forest management history is an important factor in bark beetle outbreaks: Lessons for the future. For. Ecol. Manag. 2019, 433, 467–474. [Google Scholar] [CrossRef]
- Rosvall, O.; Jansson, G.; Andersson, B. Predicted genetic gain from existing and future seed orchards and clone mixes in Sweden. In Proceedings of the Integrating Tree Breeding and Forestry—Proceedings of the Nordic Group for Management of Genetic Resources of Trees, Mekrijärvi, Finland, 23–27 March 2001; Haapanen, M., Mikola, J., Eds.; Finnish Forest Research Institute: Vantaa, Finland, 2002; Volume 1, pp. 23–27. [Google Scholar]
- Mullin, T.J.; Morgenstern, E.K.; Park, Y.S.; Fowler, D.P. Genetic parameters from a clonally replicated test of black spruce (Picea mariana). Can. J. For. Res. 1992, 22, 24–36. [Google Scholar] [CrossRef]
- Wu, H.X. Benefits and risks of using clones in forestry—A review. Scand. J. For. Res. 2019, 34, 352–359. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Hai, H.N.T.; Helmersson, A.; Liziniewicz, M.; Hallingbäck, H.R.; Fries, A.; Berlin, M.; Wu, H.X. Advantage of clonal deployment in Norway spruce (Picea abies (L.) H. Karst.). Ann. For. Sci. 2020, 77, 14. [Google Scholar] [CrossRef]
- Rosvall, O. Using Norway spruce clones in Swedish forestry: General overview and concepts. Scand. J. For. Res. 2019, 34, 336–341. [Google Scholar] [CrossRef]
- Liziniewicz, M.; Berlin, M. Differences in growth and areal production between Norway spruce (Picea abies L. Karst.) regeneration material representing different levels of genetic improvement. For. Ecol. Manag. 2019, 435, 158–169. [Google Scholar] [CrossRef]
- Rosvall, O. Using Norway spruce clones in Swedish forestry: Swedish forest conditions, tree breeding program and experiences with clones in field trials. Scand. J. For. Res. 2019, 34, 342–351. [Google Scholar] [CrossRef]
- Sabatia, C.O. Stand Dynamics, Growth, and Yield of Genetically Enhanced Loblolly Pine (Pinus taeda L.). Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2011. Volume 1. [Google Scholar]
- Egbäck, S.; Nilsson, U.; Nyström, K.; Högberg, K.-A.; Fahlvik, N. Modeling early height growth in trials of genetically improved Norway spruce and Scots pine in southern Sweden. Silva Fenn. 2017, 51, 5662. [Google Scholar] [CrossRef]
- Fahlvik, N.; Nyström, K.; Nystrom, K. Models for predicting individual tree height increment and tree diameter in young stands in southern Sweden. Scand. J. For. Res. 2006, 21, 16–28. [Google Scholar] [CrossRef]
- Ahtikoski, A.; Ojansuu, R.; Haapanen, M.; Hynynen, J.; Kärkkäinen, K. Financial performance of using genetically improved regeneration material of Scots pine (Pinus sylvestris L.) in Finland. New For. 2012, 43, 335–348. [Google Scholar] [CrossRef]
- Bravo, F.; Fabrika, M.; Ammer, C.; Barreiro, S.; Bielak, K.; Coll, L.; Fonseca, T.; Kangur, A.; Löf, M.; Merganičová, K.; et al. Modelling approaches for mixed forests dynamics prognosis. Research gaps and opportunities. For. Syst. 2019, 28, eR002. [Google Scholar] [CrossRef]
- Gould, P.J.; Marshall, D.D. Estimation and Application of Genetic- Gain Multipliers for Douglas-Fir Height and Diameter Growth. For. Sci. 2008, 54, 588–596. [Google Scholar]
- Rehfeldt, G.E.; Wykoff, W.R.; Hoff, R.J.; Steinhoff, R.J. Genetic gains in growth and simulated yield of Pinus monticola. For. Sci. 1991, 37, 326–342. [Google Scholar]
- Carson, S.D.; Garcia, O.; Hayes, J.D. Realized gain and prediction of yield with genetically improved Pinus radiata in New Zealand. For. Sci. 1999, 45, 186–200. [Google Scholar]
- Buford, M.A.; Burkhart, H.E. Genetic improvement effects on growth and yield of loblolly pine plantations. For. Sci. 1987, 33, 707–724. [Google Scholar] [CrossRef]
- Newton, P.F. Systematic review of yield responses of four North American conifers to forest tree improvement practices. For. Ecol. Manag. 2003, 172, 29–51. [Google Scholar] [CrossRef]
- Vergara, R.; White, T.L.; Huber, D.A.; Shiver, B.D.; Rockwood, D.L. Estimated realized gains for first-generation slash pine (Pinus elliottii var. elliottii) tree improvement in the southeastern United States. Can. J. For. Res. 2004, 34, 2587–2600. [Google Scholar] [CrossRef]
- Adams, J.P.; Matney, T.G.; Land, S.B.; Belli, K.L.; Duzan, H.W. Incorporating genetic parameters into a loblolly pine growth-and-yield model. Can. J. For. Res. 2006, 36, 1959–1967. [Google Scholar] [CrossRef]
- Adame, P.; Hynynen, J.; Cañellas, I.; del Río, M. Individual-tree diameter growth model for rebollo oak (Quercus pyrenaica Willd.) coppices. For. Ecol. Manag. 2008, 255, 1011–1022. [Google Scholar] [CrossRef]
- Subedi, N.; Sharma, M. Individual-tree diameter growth models for black spruce and jack pine plantations in northern Ontario. For. Ecol. Manag. 2011, 261, 2140–2148. [Google Scholar] [CrossRef]
- Timilsina, N.; Staudhammer, C.L. Individual tree-based diameter growth model of slash pine in Florida using nonlinear mixed modeling. For. Sci. 2013, 59, 27–37. [Google Scholar] [CrossRef]
- Xu, H.; Sun, Y.; Wang, X.; Fu, Y.; Dong, Y.; Li, Y. Nonlinear mixed-effects (NLME) diameter growth models for individual China-fir (Cunninghamia lanceolata) trees in southeast China. PLoS ONE 2014, 9, e104012. [Google Scholar] [CrossRef]
- Anderson, B.D.; Russell, M.B.; Windmuller-Campione, M.A.; Palik, B.J.; Kastendick, D.N. Development and evaluation of black spruce (Picea mariana (Miller) B.S.P.) Diameter increment models across silvicultural treatments in northern Minnesota, USA. Forests 2018, 9, 747. [Google Scholar] [CrossRef]
- Hallingbäck, H.R.; Högberg, K.A.; Säll, H.; Lindeberg, J.; Johansson, M.; Jansson, G. Optimal timing of early genetic selection for sawn timber traits in Picea abies. Eur. J. For. Res. 2018, 137, 553–564. [Google Scholar] [CrossRef]
- Liziniewicz, M.; Berlin, M.; Karlsson, B. Early assessments are reliable indicators for future volume production in Norway spruce (Picea abies L. Karst.) genetic field trials. For. Ecol. Manag. 2018, 411, 75–81. [Google Scholar] [CrossRef]
- Rosvall, O.; Bradshaw, R.H.W.; Egertsdotter, U.; Ingvarsson, P.K.; Mullin, T.J.; Wu, H. Using Norway spruce clones in Swedish forestry: Implications of clones for management. Scand. J. For. Res. 2019, 34, 390–404. [Google Scholar] [CrossRef]
- White, T.L.; Adams, W.T.; Neale, D.B. Forest Genetics; CABI Publishing: Wallingford, UK, 2007; ISBN 9780851990835. [Google Scholar]
- Buss, K. Forest ecosystem classification in Latvia. Proc. Latv. Acad. Sci. Sect. B 1997, 51, 204–218. [Google Scholar]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Spiecker, H.; Hansen, N.; Schinker, M.G. High-Frequency Densitometry-A New Method for the Rapid Evaluation of Wood Density Variations. IAWA J. 2003, 24, 231–239. [Google Scholar] [CrossRef]
- Holmes, R. Computer-Assisted Quality Control in Tree-Ring Dating and Measurement. Tree-Ring Bull. 1983, 43, 51–67. [Google Scholar]
- Rohner, B.; Bugmann, H.; Bigler, C. Estimating the age-diameter relationship of oak species in Switzerland using nonlinear mixed-effects models. Eur. J. For. Res. 2013, 132, 751–764. [Google Scholar] [CrossRef]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Bolker, B.M.; Gardner, B.; Maunder, M.; Berg, C.W.; Brooks, M.; Comita, L.; Crone, E.; Cubaynes, S.; Davies, T.; de Valpine, P.; et al. Strategies for fitting nonlinear ecological models in R, AD Model Builder, and BUGS. Methods Ecol. Evol. 2013, 4, 501–512. [Google Scholar] [CrossRef]
- Zeide, B. Analysis of Growth Equations. For. Sci. 1993, 39, 594–616. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S.; Jansa, V.; Kučera, M. Modelling individual tree diameter growth for Norway spruce in the Czech Republic using a generalized algebraic difference approach. J. For. Sci. 2017, 63, 227–238. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer Science & Business Media: Cham, Switzerland, 2000. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D. The R Core Team Nlme: Linear and Nonlinear Mixed Effects Models; R Package Version 3.1-143; 2019. Available online: https://cran.r-project.org/web/packages/nlme/nlme.pdf (accessed on 21 March 2022).
- Montgomery, D.; Peck, E.; Vining, G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef]
- Falconer, D.S.; Mackay, T.F. Introduction to Quantitative Genetics, 4th ed.; Longman Group Ltd.: London, UK, 1996. [Google Scholar]
- Savageau, M.A. Growth of complex systems can be related to the properties of their underlying determinants. Proc. Natl. Acad. Sci. USA 1979, 76, 5413–5417. [Google Scholar] [CrossRef] [PubMed]
- Ivancich, H.; Martínez Pastur, G.J.; Lencinas, M.V.; Cellini, J.M.; Peri, P.L. Proposals for Nothofagus antarctica diameter growth estimation: Simple vs. global models. J. For. Sci. 2014, 60, 307–317. [Google Scholar] [CrossRef]
- Meredith, M.P.; Stehman, S.V. Repeated measures experiments in forestry: Focus on analysis of response curves. Can. J. For. Res. 1991, 21, 957–965. [Google Scholar] [CrossRef]
- Fekedulegn, D.; Mac Siurtain, M.P.; Colbert, J.J. Parameter estimation of nonlinear growth models in forestry. Silva Fenn. 1999, 33, 327–336. [Google Scholar] [CrossRef]
- Nothdurft, A.; Kublin, E.; Lappi, J. A non-linear hierarchical mixed model to describe tree height growth. Eur. J. For. Res. 2006, 125, 281–289. [Google Scholar] [CrossRef]
- Harrison, X.A.; Donaldson, L.; Correa-Cano, M.E.; Evans, J.; Fisher, D.N.; Goodwin, C.E.D.; Robinson, B.S.; Hodgson, D.J.; Inger, R. A brief introduction to mixed effects modelling and multi-model inference in ecology. PeerJ 2018, 2018, e4794. [Google Scholar] [CrossRef] [PubMed]
- Sabatia, C.O.; Burkhart, H.E. Modeling height development of loblolly pine genetic varieties. For. Sci. 2013, 59, 267–277. [Google Scholar] [CrossRef]
- Knowe, S.A.; Foster, G.S. Application of Growth Models For Simulating Genetic Gain of Loblolly Pine. For. Sci. 1989, 35, 211–228. [Google Scholar]
- Nance, W.L.; Wells, O.O. Site index models for height growth of planted loblolly pine (Pinus taeda L.) seed sources. In Proceedings of the 16th Southern Forest Tree Improvement Conference, Blacksburg, VA, USA, 27–28 May 1981; 1981; pp. 86–96. [Google Scholar]
- Sprinz, P.T.; Talbert, C.B.; Strub, M.R. Height-age trends from an Arkansas seed source study. For. Sci. 1989, 35, 677–691. [Google Scholar] [CrossRef]
- Tang, S.; Meng, F.R.; Bourque, C.P.A. Analyzing parameters of growth and yield models for Chinese fir provenances with a linear mixed model approach. Silvae Genet. 2001, 50, 140–145. [Google Scholar]
- Der Chung, J.; Chien, C.T.; Nigh, G.; Ying, C.C. Genetic variation in growth curve parameters of Konishii fir (Cunninghamia lanceolata (Lamb.) Hook. var. konishii). Silvae Genet. 2009, 58, 1–10. [Google Scholar] [CrossRef]
- Schielzeth, H.; Nakagawa, S. Nested by design: Model fitting and interpretation in a mixed model era. Methods Ecol. Evol. 2013, 4, 14–24. [Google Scholar] [CrossRef]
- Oddi, F.J.; Miguez, F.E.; Ghermandi, L.; Bianchi, L.O.; Garibaldi, L.A. A nonlinear mixed-effects modeling approach for ecological data: Using temporal dynamics of vegetation moisture as an example. Ecol. Evol. 2019, 9, 10225–10240. [Google Scholar] [CrossRef] [PubMed]
- Sabatia, C.O.; Burkhart, H.E. Height and Diameter Relationships and Distributions in Loblolly Pine Stands of Enhanced Genetic Material. For. Sci. 2013, 59, 278–289. [Google Scholar] [CrossRef]
- Hannrup, B.; Cahalan, C.; Chantre, G.; Grabner, M.; Karlsson, B.; Le Bayon, I.; Jones, G.L.; Müller, U.; Pereira, H.; Rodrigues, J.C.; et al. Genetic Parameters of Growth and Wood Quality Traits in Picea abies. Scand. J. For. Res. 2004, 19, 14–29. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Gil, M.R.G.; Karlsson, B.; Lundqvist, S.O.; Olsson, L.; Wu, H.X. Inheritance of growth and solid wood quality traits in a large Norway spruce population tested at two locations in southern Sweden. Tree Genet. Genomes 2014, 10, 1291–1303. [Google Scholar] [CrossRef]
- Hong, Z.; Fries, A.; Wu, H.X. Age trend of heritability, genetic correlation, and efficiency of early selection for wood quality traits in Scots pine. Can. J. For. Res. 2015, 825, 817–825. [Google Scholar] [CrossRef]
- Wahid, N.; Rainville, A.; Lamhamedi, M.S.; Margolis, H.A.; Beaulieu, J.; Deblois, J. Genetic parameters and performance stability of white spruce somatic seedlings in clonal tests. For. Ecol. Manag. 2012, 270, 45–53. [Google Scholar] [CrossRef]
- Isik, K.; Kleinschmit, J.; Steiner, W. Age-age correlations and early selection for height in a clonal genetic test of Norway spruce. For. Sci. 2010, 56, 212–221. [Google Scholar] [CrossRef]
- Chen, Z.-Q. Quantitative Genetics of Norway Spruce in Sweden; Sveriges Lantbruksuniversitet: Uppsala, Sweden, 2016. [Google Scholar]
- Mihai, G.; Mirancea, I. Age trends in genetic parameters for growth and quality traits in Abies alba. IForest 2016, 9, 954–959. [Google Scholar] [CrossRef]
- Hiraoka, Y.; Miura, M.; Fukatsu, E.; Iki, T.; Yamanobe, T.; Kurita, M.; Isoda, K.; Kubota, M.; Takahashi, M. Time trends of genetic parameters and genetic gains and optimum selection age for growth traits in sugi (Cryptomeria japonica) based on progeny tests conducted throughout Japan. J. For. Res. 2019, 24, 303–312. [Google Scholar] [CrossRef]
- Jansson, G.; Kerr, R.; Dutkowski, G.; Kroon, J. Competition effects in breeding value prediction of forest trees. Can. J. For. Res. 2021, 51, 1002–1014. [Google Scholar] [CrossRef]
- Radtke, P.J.; Westfall, J.A.; Burkhart, H.E. Conditioning a distance-dependent competition index to indicate the onset of inter-tree competition. For. Ecol. Manag. 2003, 175, 17–30. [Google Scholar] [CrossRef]
- Amateis, R.L.; Burkhart, H.E. Rotation-age results from a loblolly pine spacing trial. South. J. Appl. For. 2012, 36, 11–18. [Google Scholar] [CrossRef]
- Franklin, E.C. Model relating levels of genetic variance to stand development of four north American conifers. Silvae Genet. 1979, 28, 207–212. [Google Scholar]
- Sato, Y.; Fukatsu, E.; Hiraoka, Y.; Watanabe, A.; Takahashi, M. The effect of genotype and planting density on the growth patterns and selection of local varieties of Sugi (Cryptomeria japonica). Nihon Ringakkai Shi/J. Jpn. For. Soc. 2016, 98, 45–52. [Google Scholar] [CrossRef][Green Version]
- Štícha, V.; Sharma, R.P.; Vacek, Z.; Vacek, S.; Nuhlíček, O. Timber and branch volume prediction: Effects of stand and site characteristics on dendromass and timber-to-branch volume ratio of Norway spruce in managed forests. Forests 2019, 10, 144. [Google Scholar] [CrossRef]
- Zubizarreta Gerendiain, A.; Peltola, H.; Pulkkinen, P.; Jaatinen, R.; Pappinen, A.; Kellomäki, S. Differences in growth and wood property traits in cloned Norway spruce (Picea abies). Can. J. For. Res. 2007, 37, 2600–2611. [Google Scholar] [CrossRef]
- Jayawickrama, K.J.; McKeand, S.E.; Jett, J.B. Rootstock effects on scion growth and reproduction in 8-year-old grafted loblolly pine. Can. J. For. Res. 1997, 27, 1781–1787. [Google Scholar] [CrossRef]
- Olesen, P.O. On cyclophysis and topophysis. Silvae Genet. 1978, 27, 173–178. [Google Scholar]
- Greenwood, M.S.; Hutchison, K.W. Maturation as a Developmental Process. In Clonal Forestry I; Springer: Berlin/Heidelberg, Germany, 1993; pp. 14–33. ISBN 978-3-642-84177-4. [Google Scholar]
- Viherä-Aarnio, A.; Ryynänen, L. Seed production of micropropagated plants, grafts and seedlings of birch in a seed orchard. Silva Fenn. 1994, 28, 257–263. [Google Scholar] [CrossRef]
- Wendling, I.; Trueman, S.J.; Xavier, A. Maturation and related aspects in clonal forestry-Part I: Concepts, regulation and consequences of phase change. New For. 2014, 45, 449–471. [Google Scholar] [CrossRef]
- Cannell, M.; Sheppard, L.; Cahalan, C. C effects and second generation clone performance in Picea sitchensis and Pinus contorta. Silvae Genet. 1988, 37, 15–19. [Google Scholar]
- Huston, M.; DeAngelis, D.; Post, W. New Computer Models Unify Ecological Theory. Bioscience 1988, 38, 682–691. [Google Scholar] [CrossRef]
- Johnson, G.R.; Sniezko, R.A.; Mandel, N.L. Age trends in Douglas-fir genetic parameters and implications for optimum selection age. Silvae Genet. 1998, 46, 349–358. [Google Scholar]
- Kroon, J.; Ericsson, T.; Jansson, G.; Andersson, B. Patterns of genetic parameters for height in field genetic tests of Picea abies and Pinus sylvestris in Sweden. Tree Genet. Genomes 2011, 7, 1099–1111. [Google Scholar] [CrossRef]
- Zubizarreta-Gerendiain, A.; Gort-Oromi, J.; Mehtätalo, L.; Peltola, H.; Venäläinen, A.; Pulkkinen, P. Effects of cambial age, clone and climatic factors on ring width and ring density in Norway spruce (Picea abies) in southeastern Finland. For. Ecol. Manag. 2012, 263, 9–16. [Google Scholar] [CrossRef]
- Cieszewski, C.J.; Bailey, R.L. Generalized Algebraic Difference Approach: A New Methodology for Derivation of Biologically Based Dynamic Site Equations. For. Sci. 2000, 46, 116–126. [Google Scholar]
- Diéguez-Aranda, U.; Burkhart, H.E.; Amateis, R.L. Dynamic site model for loblolly pine (Pinus taeda L.) plantations in the United States. For. Sci. 2006, 52, 262–272. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).