Integrating Habitat Quality of the Great Spotted Woodpecker (Dendrocopos major) in Forest Spatial Harvest Scheduling Problems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Forest Growth Simulations
2.3. Habitat Suitability Index Model
2.4. Economic Value
2.5. Planning Model Formulations
2.6. Management Strategies
2.7. Optimization Algorithm
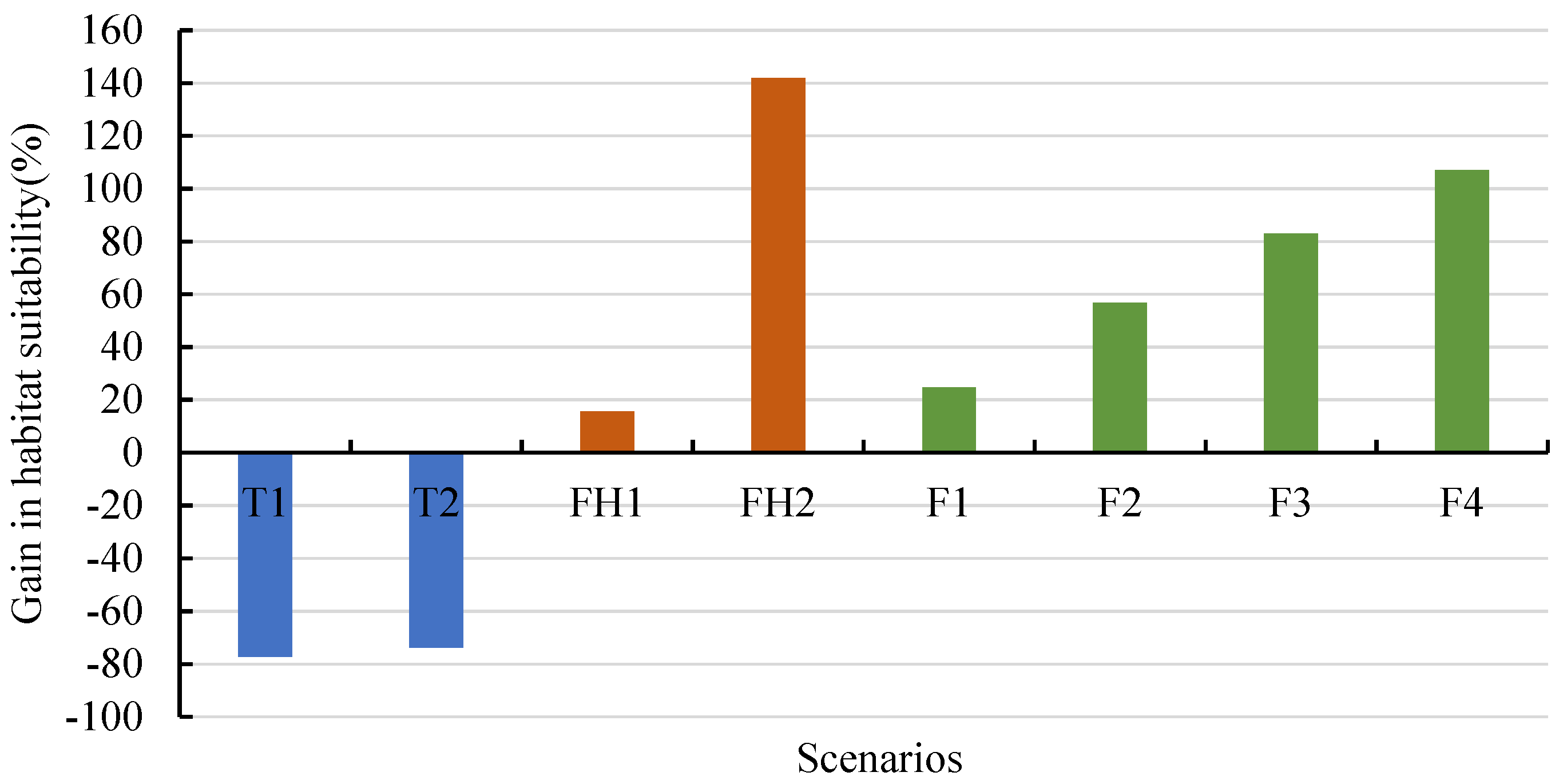
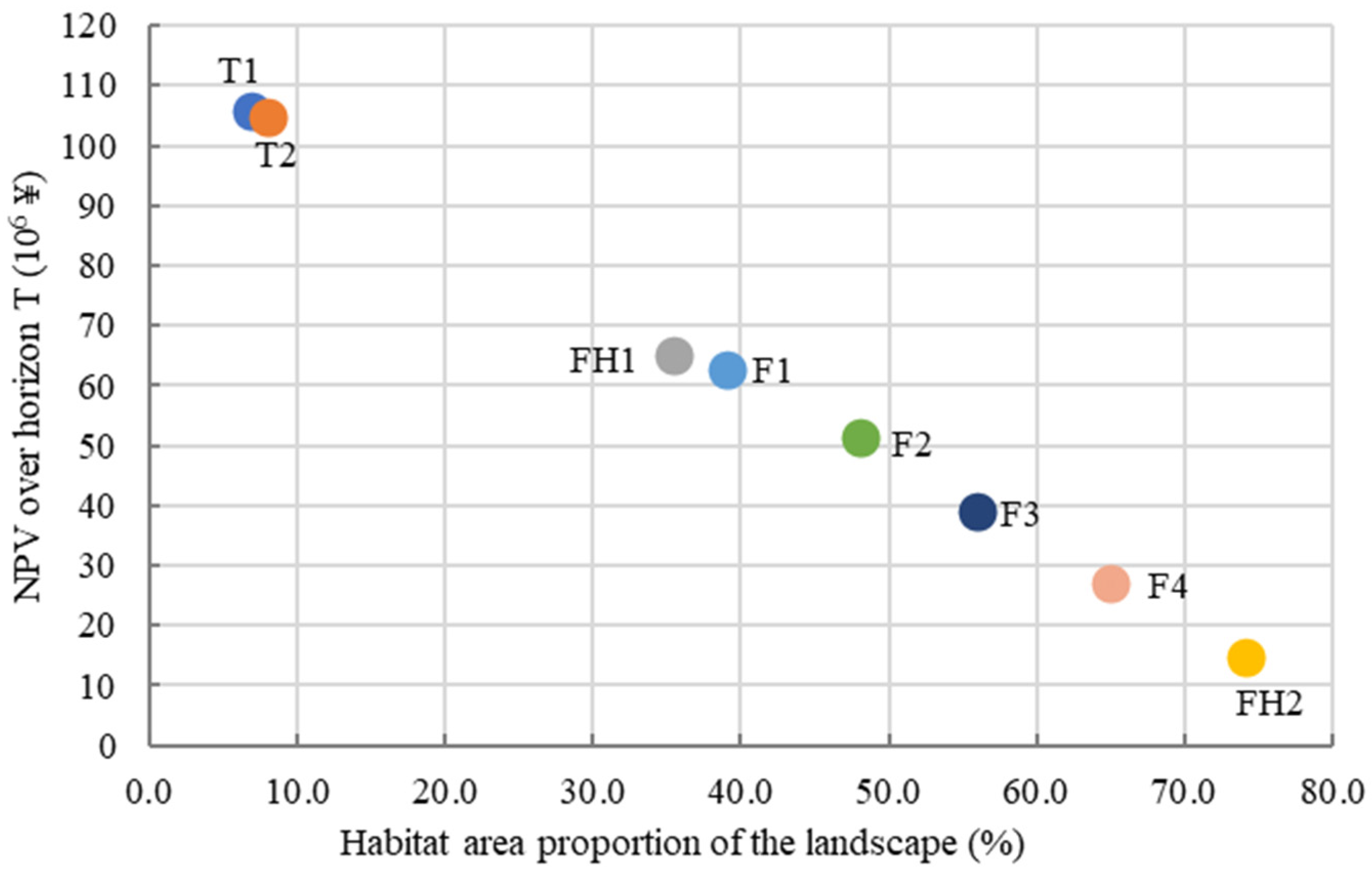
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mönkkönen, M.; Juutinen, A.; Mazziotta, A.; Miettinen, K.; Podkopaev, D.; Reunanen, P.; Salminen, H.; Tikkanen, O.P. Spatially Dynamic Forest Management to Sustain Biodiversity and Economic Returns. J. Environ. Manag. 2014, 134, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Price, J.M.; Silbernagel, J.; Nixon, K.; Swearingen, A.; Swaty, R.; Miller, N. Collaborative Scenario Modeling Reveals Potential Advantages of Blending Strategies to Achieve Conservation Goals in a Working Forest Landscape. Landsc. Ecol. 2016, 31, 1093–1115. [Google Scholar] [CrossRef]
- von Detten, R.; Hanewinkel, M. Strategies of Handling Risk and Uncertainty in Forest Management in Central Europe. Curr. For. Rep. 2017, 3, 60–73. [Google Scholar] [CrossRef]
- Tittler, R.; Messier, C.; Burton, P.J. Hierarchical Forest Management Planning and Sustainable Forest Management in the Boreal Forest. For. Chron. 2001, 77, 998–1005. [Google Scholar] [CrossRef] [Green Version]
- Fisher, B.; Edwards, D.P.; Larsen, T.H.; Ansell, F.A.; Hsu, W.W.; Roberts, C.S.; Wilcove, D.S. Cost-Effective Conservation: Calculating Biodiversity and Logging Trade-Offs in Southeast Asia. Conserv. Lett. 2011, 4, 443–450. [Google Scholar] [CrossRef]
- Nalle, D.J.; Montgomery, C.A.; Arthur, J.L.; Polasky, S.; Schumaker, N.H. Modeling Joint Production of Wildlife and Timber. J. Environ. Manag. 2004, 48, 997–1017. [Google Scholar] [CrossRef]
- Nieuwenhuis, M.; Tiernan, D. The Impact of the Introduction of Sustainable Forest Management Objectives on the Optimisation of PC-Based Forest-Level Harvest Schedules. For. Policy Econ. 2005, 7, 689–701. [Google Scholar] [CrossRef]
- Bettinger, P.; Boston, K. Habitat and Commodity Production Trade-Offs in Coastal Oregon. Socioecon. Plann. Sci. 2008, 42, 112–128. [Google Scholar] [CrossRef]
- Turner, M.G.; Gardner, R.H. Landscape Ecology in Theory and Practice: Pattern and Process, 2nd ed.; Springer: New York, NY, USA, 2015; p. 237. [Google Scholar]
- Edenius, L.; Mikusiński, G. Utility of Habitat Suitability Models as Biodiversity Assessment Tools in Forest Management. Scand. J. For. Res. 2006, 21, 62–72. [Google Scholar] [CrossRef]
- Öhman, K.; Edenius, L.; Mikusiński, G. Optimizing Spatial Habitat Suitability and Timber Revenue in Long-Term Forest Planning. Can. J. For. Res. 2011, 41, 543–551. [Google Scholar] [CrossRef] [Green Version]
- Pukkala, T.; Sulkava, R.; Jaakkola, L.; Lähde, E. Relationships between Economic Profitability and Habitat Quality of Siberian Jay in Uneven-Aged Norway Spruce Forest. For. Ecol. Manag. 2012, 276, 224–230. [Google Scholar] [CrossRef]
- Konoshima, M.; Yoshimoto, A. Balancing Timber Production and Habitat Conservation of Okinawa Rails (Gallirallus Okinawae): Application of a Harvest Scheduling Optimization Model in Subtropical Forest in Okinawa, Japan. J. Mt. Sci. 2019, 16, 2770–2782. [Google Scholar] [CrossRef]
- Bagdon, B.A.; Huang, C.-H.; Dewhurst, S. Managing for Ecosystem Services in Northern Arizona Ponderosa Pine Forests Using a Novel Simulation-to-Optimization Methodology. Ecol. Model. 2016, 324, 11–27. [Google Scholar] [CrossRef]
- Kline, J.D.; Harmon, M.E.; Spies, T.A.; Morzillo, A.T.; Pabst, R.J.; McComb, B.C.; Schnekenburger, F.; Olsen, K.A.; Csuti, B.; Vogeler, J.C. Evaluating Carbon Storage, Timber Harvest, and Habitat Possibilities for a Western Cascades (USA) Forest Landscape. Ecol. Appl. 2016, 26, 2044–2059. [Google Scholar] [CrossRef]
- Mazziotta, A.; Podkopaev, D.; Triviño, M.; Miettinen, K.; Pohjanmies, T.; Mönkkönen, M. Quantifying and Resolving Conservation Conflicts in Forest Landscapes via Multiobjective Optimization. Silva Fenn. 2017, 51, 1778. [Google Scholar] [CrossRef]
- Dupont, S.; Ikonen, V.-P.; Väisänen, H.; Peltola, H. Predicting Tree Damage in Fragmented Landscapes Using a Wind Risk Model Coupled with an Airflow Model. Can. J. For. Res. 2015, 45, 1065–1076. [Google Scholar] [CrossRef]
- Baskent, E.Z.; Keles, S. Spatial Forest Planning: A Review. Ecol. Model. 2005, 188, 145–173. [Google Scholar] [CrossRef]
- Stang, M.B.; Arce, J.E.; do Amaral Machado, S.; Belavenutti, P.H.; Fiorentin, L.D. Spatial Forest Planning for Optimized Harvest Scheduling. Floresta E Ambiente 2019, 26, e20160100. [Google Scholar] [CrossRef]
- Murray, A.T. Spatial Restrictions in Harvest Scheduling. For. Sci. 1999, 45, 45–52. [Google Scholar]
- McDill, M.E.; Rebain, S.A.; Braze, J. Harvest Scheduling with Area-Based Adjacency Constraints. For. Sci. 2002, 48, 631–642. [Google Scholar] [CrossRef]
- Irene, D.P.L.; Hoganson, H.M.; Carson, M.T.; Windmuller-Campione, M. Recognizing Spatial Considerations in Forest Management Planning. Curr. For. Rep. 2017, 3, 308–316. [Google Scholar] [CrossRef]
- Dong, L.; Lu, W.; Liu, Z. Developing Alternative Forest Spatial Management Plans When Carbon and Timber Values Are Considered: A Real Case from Northeastern China. Ecol. Model. 2018, 385, 45–57. [Google Scholar] [CrossRef]
- Cyr, G.; Raulier, F.; Fortin, D.; Pothier, D. Using Operating Area Size and Adjacency Constraints to Mitigate the Effects of Harvesting Activities on Boreal Caribou Habitat. Landsc. Ecol. 2017, 32, 377–395. [Google Scholar] [CrossRef]
- Wang, H.Z. Dynamic Simulating System for Stand Growth of Forests in Northeast China. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2012. (In Chinese). [Google Scholar]
- Dong, L.; Lu, W.; Liu, Z. Determining the Optimal Rotations of Larch Plantations When Multiple Carbon Pools and Wood Products Are Valued. For. Ecol. Manag. 2020, 474, 118356. [Google Scholar] [CrossRef]
- Drever, M.C.; Aitken, K.E.H.; Norris, A.R.; Martin, K. Woodpeckers as Reliable Indicators of Bird Richness, Forest Health and Harvest. Biol. Conserv. 2008, 141, 624–634. [Google Scholar] [CrossRef]
- Roberge, J.-M.; Angelstam, P.; Villard, M.-A. Specialised Woodpeckers and Naturalness in Hemiboreal Forests—Deriving Quantitative Targets for Conservation Planning. Biol. Conserv. 2008, 141, 997–1012. [Google Scholar] [CrossRef]
- Blanc, L.A.; Martin, K. Identifying Suitable Woodpecker Nest Trees Using Decay Selection Profiles in Trembling Aspen (Populus Tremuloides). For. Ecol. Manag. 2012, 286, 192–202. [Google Scholar] [CrossRef]
- van der Hoek, Y.; Gaona, G.V.; Martin, K. The Diversity, Distribution and Conservation Status of the Tree-Cavity-Nesting Birds of the World. Divers. Distrib. 2017, 23, 1120–1131. [Google Scholar] [CrossRef] [Green Version]
- Heilongjiang Forestry and Grassland Administration. List of Provincial Key Protected Wild Animals. Harbin: Heilongjiang Forestry and Grassland Administration. Available online: https://www.doc88.com/p-605951168974.html?s=rel&id=1 (accessed on 29 November 2021).
- Barrientos, R. Retention of Native Vegetation within the Plantation Matrix Improves Its Conservation Value for a Generalist Woodpecker. For. Ecol. Manag. 2010, 260, 595–602. [Google Scholar] [CrossRef]
- Yang, Y. Study on Habitat Selection and Habitat Assessment of Picoides major. Master’s Thesis, Beijing Forestry University, Beijing, China, 2011. (In Chinese). [Google Scholar]
- Zhao, Z. Fauna of Rare and Endangered Species of Vertebrates of Northeast China; China Forestry Publishing House: Beijing, China, 1999; pp. 428–430. (In Chinese) [Google Scholar]
- Pasinelli, G. Nest Site Selection in Middle and Great Spotted Woodpeckers Dendrocopos Medius & D. Major: Implications for Forest Management and Conservation. Biodivers. Conserv. 2007, 16, 1283–1298. [Google Scholar] [CrossRef] [Green Version]
- Hebda, G. Nesting Sites of the Great Spotted Woodpecker Dendrocopos Major L. in Poland: Analysis of Nest Cards. Pol. J. Ecol. 2009, 57, 149–158. [Google Scholar]
- Rolstad, J.; Rolstad, E.; Stokke, P.K. Feeding Habitat and Nest-Site Selection of Breeding Great Spotted Woodpeckers Dendrocopos Major. Ornis Fenn. 1995, 72, 62–71. [Google Scholar]
- Deng, W.-H.; Gao, W. Edge Effects on Nesting Success of Cavity-Nesting Birds in Fragmented Forests. Biol. Conserv. 2005, 126, 363–370. [Google Scholar] [CrossRef]
- Wiacek, J.; Polak, M.; Kucharczyk, M.; Bohatkiewicz, J. The Influence of Road Traffic on Birds during Autumn Period: Implications for Planning and Management of Road Network. Landsc. Urban Plan. 2015, 134, 76–82. [Google Scholar] [CrossRef]
- Dong, L.; Bettinger, P.; Liu, Z.; Qin, H. A Comparison of a Neighborhood Search Technique for Forest Spatial Harvest Scheduling Problems: A Case Study of the Simulated Annealing Algorithm. For. Ecol. Manag. 2015, 356, 124–135. [Google Scholar] [CrossRef]
- DB23/T 870-2004; Merchantable Volume Ratio Tables of Main Tree Species in Heilongjiang Province. Heilongjiang Forestry and Grassland Administration: Harbin, China. Available online: https://max.book118.com/html/2016/0101/32487748.shtm (accessed on 5 November 2021). (In Chinese)
- Jin, X.; Pukkala, T.; Li, F. Fine-Tuning Heuristic Methods for Combinatorial Optimization in Forest Planning. Eur. J. For. Res. 2016, 135, 765–779. [Google Scholar] [CrossRef]
- Lockwood, C.; Moore, T. Harvest Scheduling with Spatial Constraints: A Simulated Annealing Approach. Can. J. For. Res. 1993, 23, 468–478. [Google Scholar] [CrossRef]
- Bettinger, P.; Johnson, D.L.; Johnson, K.N. Spatial Forest Plan Development with Ecological and Economic Goals. Ecol. Model. 2003, 169, 215–236. [Google Scholar] [CrossRef]
- Kašpar, J.; Róbert, R.; Hlavatý, R. A Forest Planning Approach with Respect to the Creation of Overmature Reserved Areas in Managed Forests. Forests 2015, 6, 328–343. [Google Scholar] [CrossRef] [Green Version]
- Laginha Pinto Correia, D.; Raulier, F.; Filotas, É.; Bouchard, M. Stand Height and Cover Type Complement Forest Age Structure as a Biodiversity Indicator in Boreal and Northern Temperate Forest Management. Ecol. Indic. 2017, 72, 288–296. [Google Scholar] [CrossRef]
- Augustynczik, A.L.D. Habitat Amount and Connectivity in Forest Planning Models: Consequences for Profitability and Compensation Schemes. J. Environ. Manag. 2021, 283, 111982. [Google Scholar] [CrossRef] [PubMed]
- Constantino, M.; Martins, I. Branch-and-Cut for the Forest Harvest Scheduling Subject to Clearcut and Core Area Constraints. Eur. J. Oper. Res. 2018, 265, 723–734. [Google Scholar] [CrossRef]
- Yoshimoto, A.; Asante, P. Focal-Point Aggregation Under Area Restrictions through Spatially Constrained Optimal Harvest Scheduling. For. Sci. 2019, 65, 164–177. [Google Scholar] [CrossRef]
- Boston, K.; Bettinger, P. An Economic and Landscape Evaluation of the Green-up Rules for California, Oregon, and Washington (USA). For. Policy Econ. 2006, 8, 251–266. [Google Scholar] [CrossRef]
- Toth, S.F.; McDill, M.E.; Koennyue, N.; George, S. Testing the Use of Lazy Constraints in Solving Area-Based Adjacency Formulations of Harvest Scheduling Models. For. Sci. 2013, 59, 157–176. [Google Scholar] [CrossRef]
- Fahrig, L. Rethinking Patch Size and Isolation Effects: The Habitat Amount Hypothesis. J. Biogeogr. 2013, 40, 1649–1663. [Google Scholar] [CrossRef]
- Bueno, A.S.; Peres, C.A. Patch-Scale Biodiversity Retention in Fragmented Landscapes: Reconciling the Habitat Amount Hypothesis with the Island Biogeography Theory. J. Biogeogr. 2019, 46, 621–632. [Google Scholar] [CrossRef] [Green Version]
- Yemshanov, D.; Haight, R.G.; Liu, N.; Rempel, R.S.; Koch, F.H.; Rodgers, A. Balancing Large-Scale Wildlife Protection and Forest Management Goals with a Game-Theoretic Approach. Forests 2021, 12, 809. [Google Scholar] [CrossRef]
- Baskent, E.Z. A Framework for Characterizing and Regulating Ecosystem Services in a Management Planning Context. Forests 2020, 11, 102. [Google Scholar] [CrossRef] [Green Version]
- Pukkala, T. Which Type of Forest Management Provides Most Ecosystem Services? For. Ecosyst. 2016, 3, 9. [Google Scholar] [CrossRef] [Green Version]
- Selkimäki, M.; González-Olabarria, J.R.; Trasobares, A.; Pukkala, T. Trade-Offs between Economic Profitability, Erosion Risk Mitigation and Biodiversity in the Management of Uneven-Aged Abies Alba Mill. Stands. Ann. For. Sci. 2020, 77, 12. [Google Scholar] [CrossRef] [Green Version]
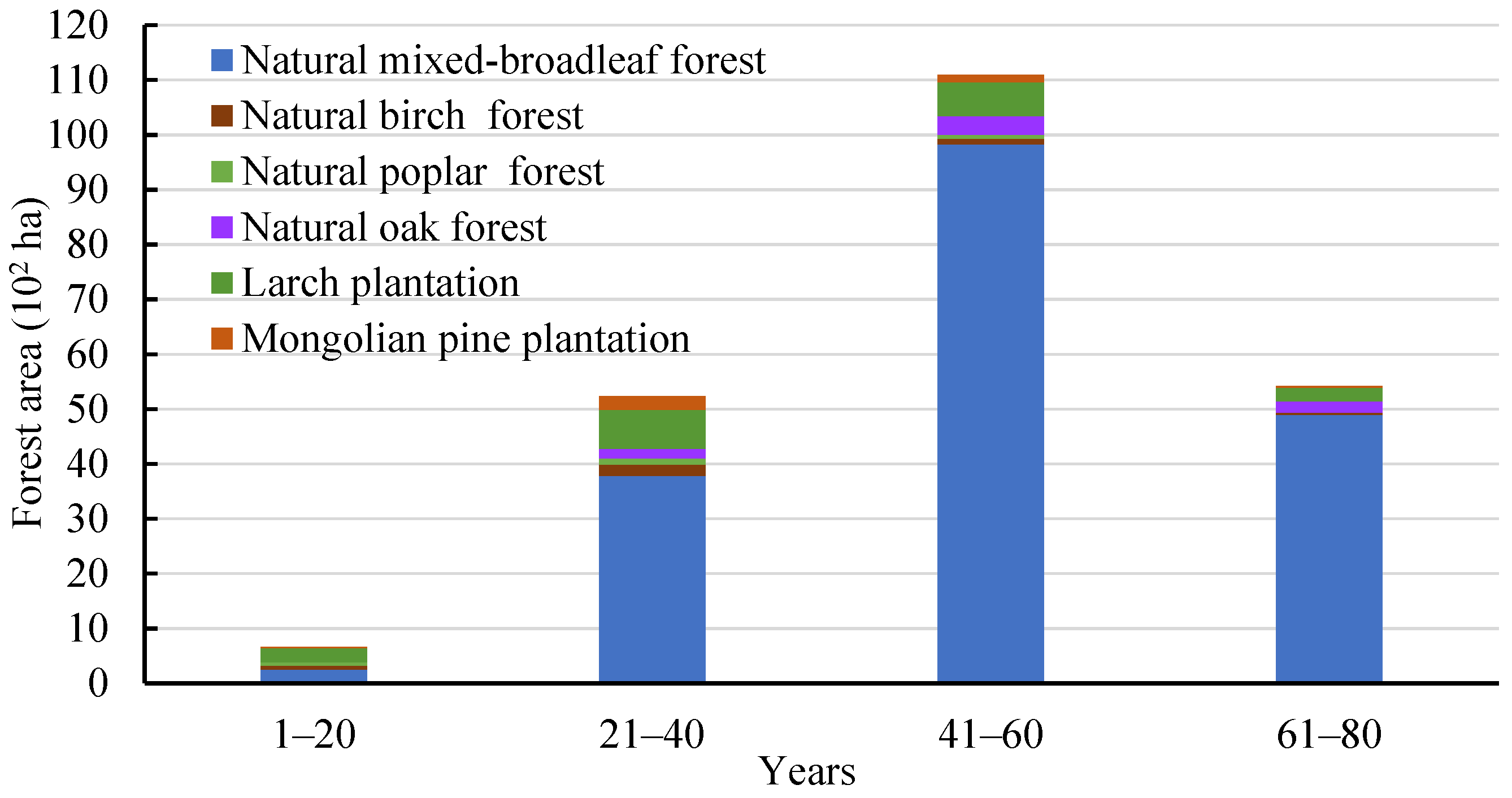
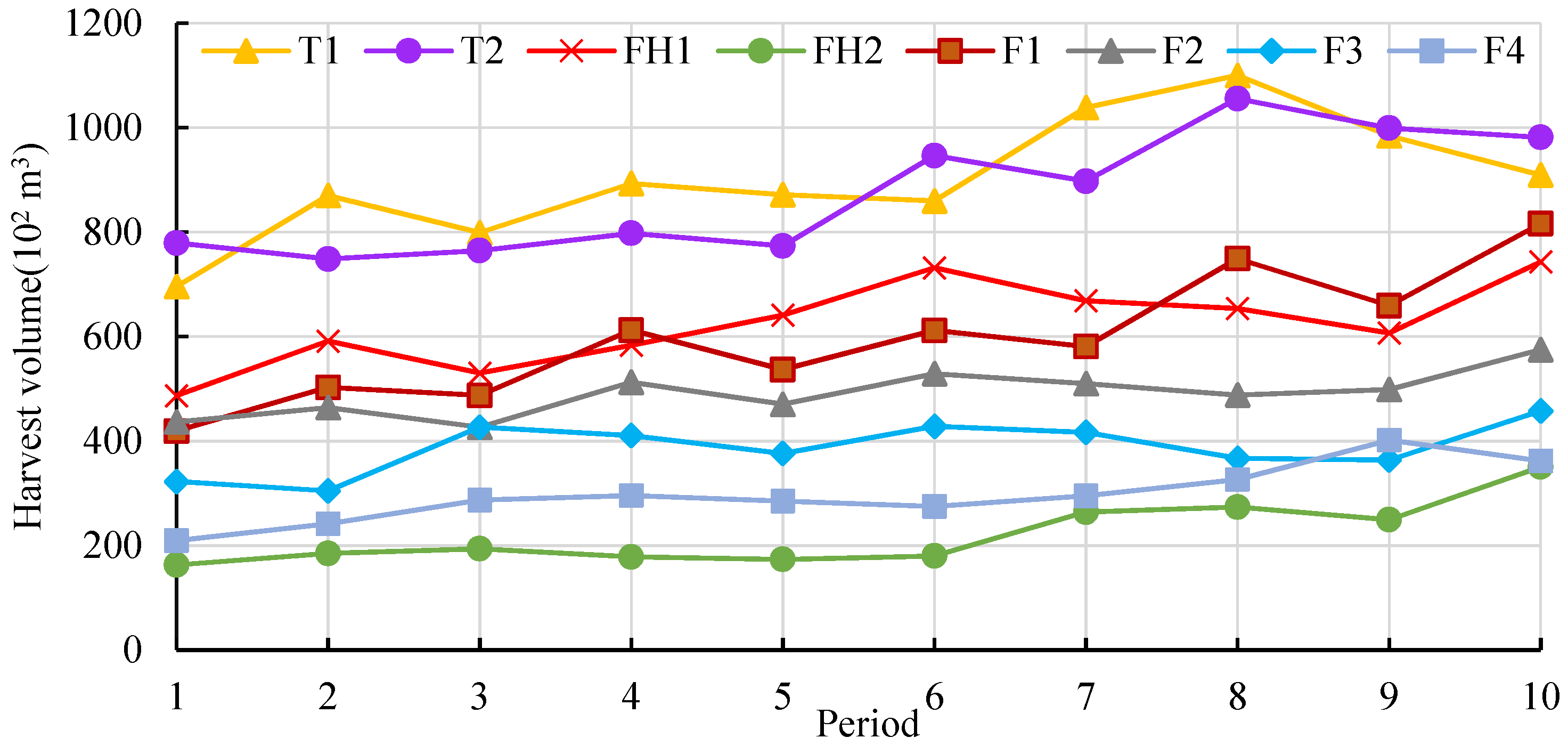
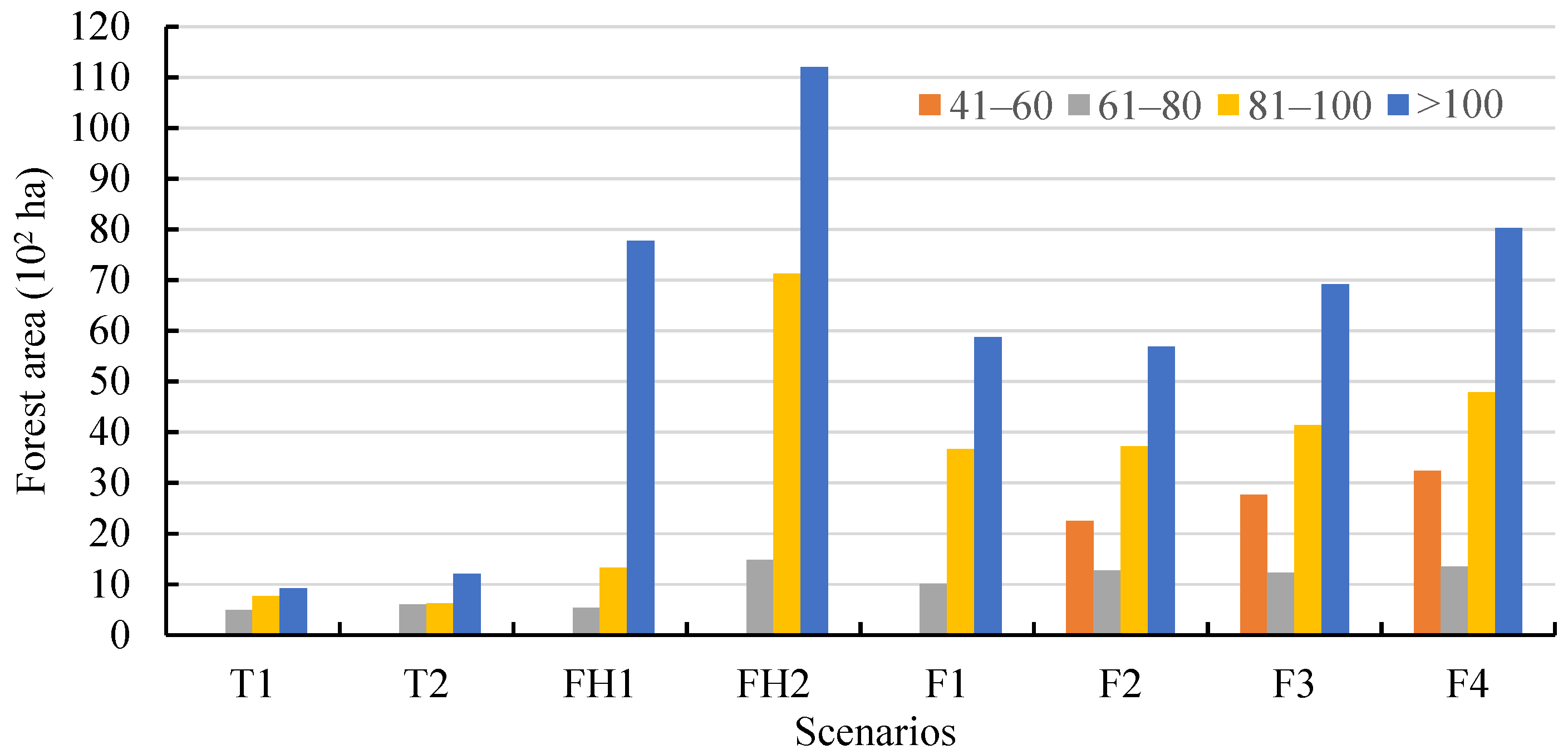
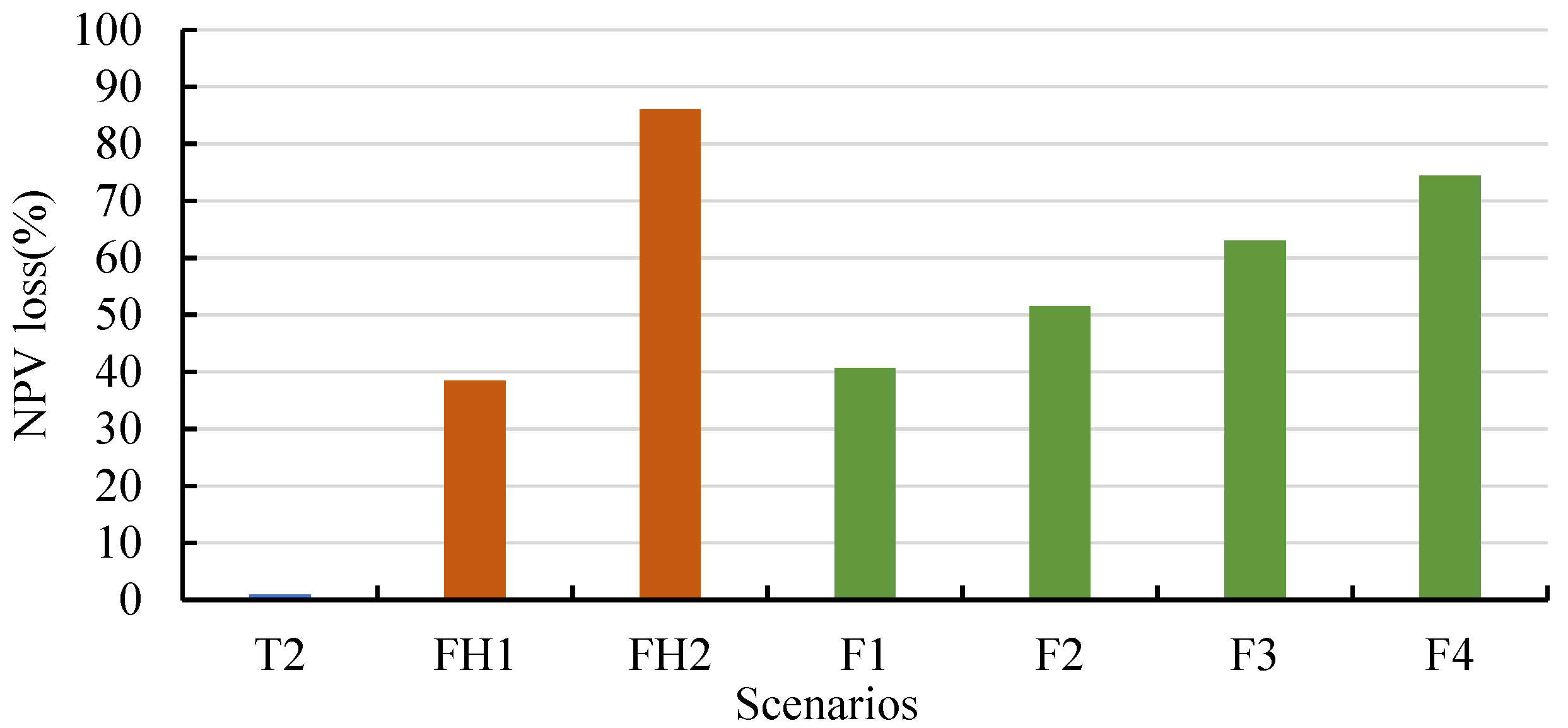
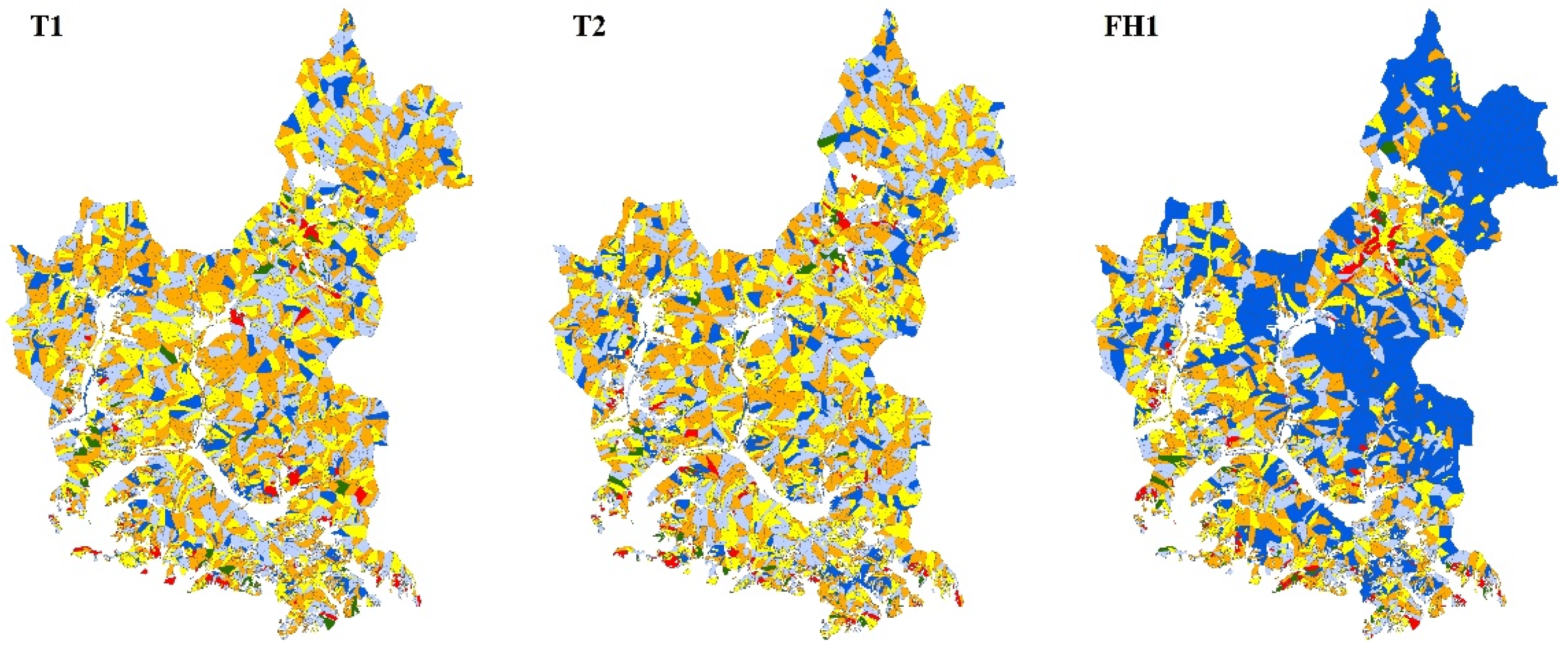
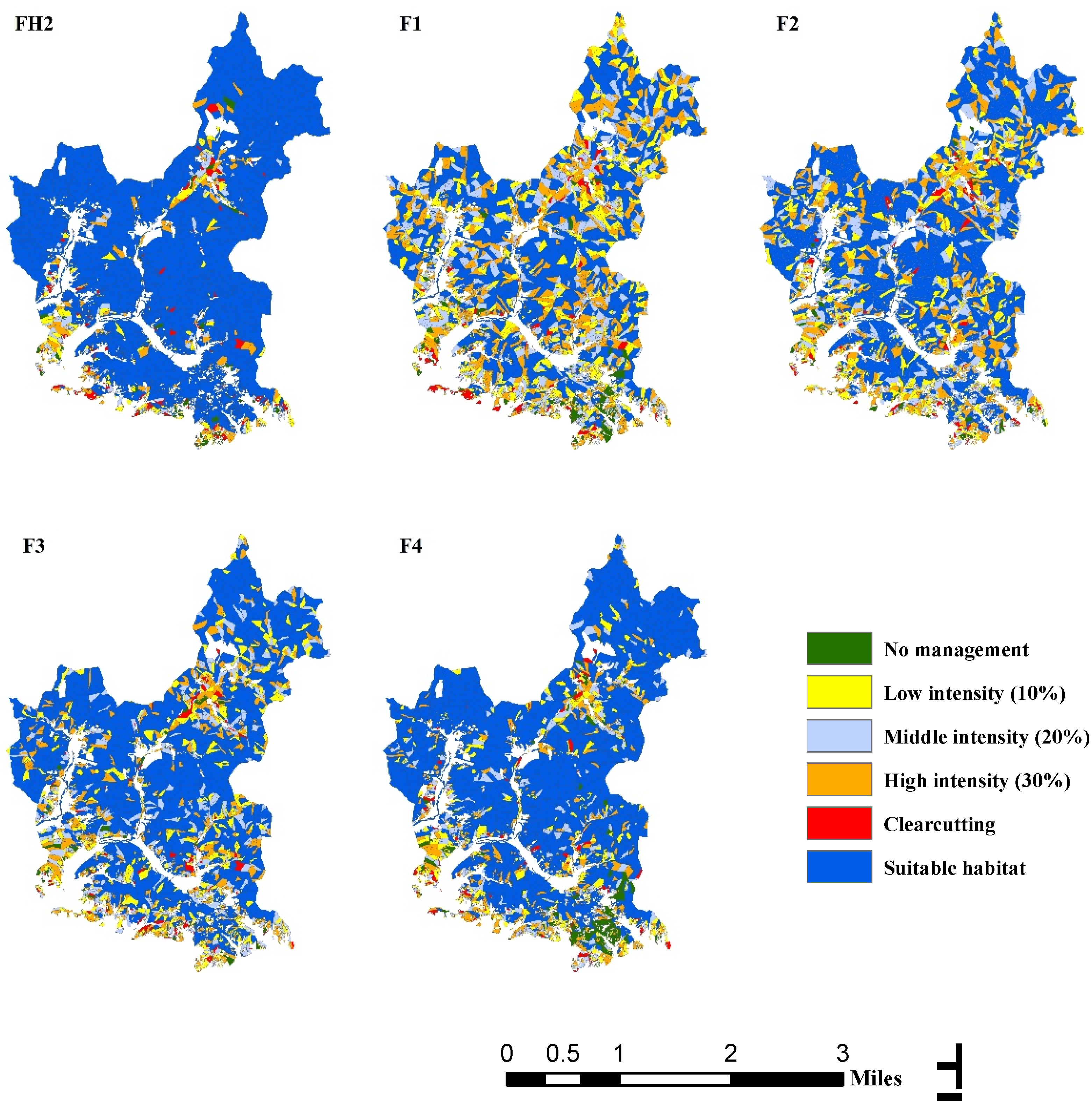
| Management Treatment | Age Limit for Forest Types 4 (Year) | Description |
|---|---|---|
| No management | NBF, NPF, LP, and MP: <21; NOF and NMBF: <41 | Any management treatments when stand age is younger than the limiting ages are strictly prohibited. |
| Low intensity 1 | NBF and NPF: ≥21; LP and MP: ≥21 and <41; NOF and NMBF: ≥41 | Can only be assigned to one of the three intensities of thinning, or no management, when stand age falls within the interval of the limiting ages. |
| Middle intensity 2 | ||
| High intensity 3 | ||
| Clearcutting | LP and MP: ≥41 | Only LP and MP can be assigned to clearcutting when stand age exceeds the limiting ages, and they can be assigned to thinning or no management, too. |
| Management Scenarios | Objective | Adjacent Constraints | Habitat Quality Constraints | Planning Formulations |
|---|---|---|---|---|
| T1 | Maximize NPV | 2 periods of green-up constraint; Umax = 40 ha. | Equations (6)–(10) | |
| T2 | Equations (6)–(11) | |||
| FH1 | HSIit ≥ HSIsuit; t = 0. | Equations (6)–(13) and (15) | ||
| FH2 | HSIit ≥ HSIsuit; t = 0, 1, 2, 3, …, 10. | Equations (6)–(13) and (15) | ||
| F1 | HSIit ≥ HSIsuit; β = 0.39 1; t = 0, 1, 2, 3, …, 10. | Equations (6)–(15) | ||
| F2 | HSIit ≥ HSIsuit; β = 0.48 2; t = 0, 1, 2, 3, …, 10. | Equations (6)–(15) | ||
| F3 | HSIit ≥ HSIsuit; β = 0.56 3; t = 0, 1, 2, 3, …, 10. | Equations (6)–(15) | ||
| F4 | HSIit ≥ HSIsuit; β = 0.65 4; t = 0, 1, 2, 3, …, 10. | Equations (6)–(15) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Dong, L.; Liu, Z. Integrating Habitat Quality of the Great Spotted Woodpecker (Dendrocopos major) in Forest Spatial Harvest Scheduling Problems. Forests 2022, 13, 525. https://doi.org/10.3390/f13040525
Chen Y, Dong L, Liu Z. Integrating Habitat Quality of the Great Spotted Woodpecker (Dendrocopos major) in Forest Spatial Harvest Scheduling Problems. Forests. 2022; 13(4):525. https://doi.org/10.3390/f13040525
Chicago/Turabian StyleChen, Ying, Lingbo Dong, and Zhaogang Liu. 2022. "Integrating Habitat Quality of the Great Spotted Woodpecker (Dendrocopos major) in Forest Spatial Harvest Scheduling Problems" Forests 13, no. 4: 525. https://doi.org/10.3390/f13040525
APA StyleChen, Y., Dong, L., & Liu, Z. (2022). Integrating Habitat Quality of the Great Spotted Woodpecker (Dendrocopos major) in Forest Spatial Harvest Scheduling Problems. Forests, 13(4), 525. https://doi.org/10.3390/f13040525






