Abstract
As spatial scale changes, the ecological processes and mechanisms that determine community patterns change. To understand these spatial effects, we established a medium-sized forest plot in an evergreen and deciduous broad-leaved mixed forest in Guilin, Guangxi, southwestern China. Here, we compared the fit of niche and neutral models to the observed species abundance distributions (SADs) at three sampling scales (10 m × 10 m, 20 m × 20 m, 50 m × 50 m). We also performed a PER-SIMPER analysis to further evaluate the relative contribution of niche and neutral processes based on taxon occurrence data. Our results showed that niche-based selection and dispersal-based neutral processes are simultaneously expressed at the 10 m × 10 m and 20 m × 20 m sampling scales. Additionally, dispersal-based neutral processes were predominant at each sampling scale. From these results, we found that the dispersal-based neutral process is the prominent driver for forest community structure in a typical karst forest environment. Ultimately, our work will be useful for future restoration and reconstruction efforts in karst forest communities, showing that environmental heterogeneity, inter-species relationships, and geographic spatial differences should be considered in these efforts.
1. Introduction
Understanding the mechanisms that drive the variation and maintenance of species diversity in ecological communities remains a fundamental question in biology. Historically, in-depth community assembly studies have gradually formed two mainstream views: niche theory and neutral theory. Niche theory can be viewed as a strictly deterministic process that connects species, communities, and environmental factors, and stipulates that the successful coexistence of multiple species lies in the differentiation of niches between species and their different suitability to the environment and resources [1,2,3]. In contrast, neutral theory can be viewed as a purely stochastic ecological process where the existence, absence, and relative abundance of species is controlled by random seeding, dispersal, ecological drift, and extinction processes [4]. In recent years, however, a growing body of research has revealed that these two conflicting perspectives may actually both contribute to better describe and understand community assembly patterns [5].
With community assembly, the species abundance distributions (SADs) describe the abundances of all species within a community, and this has been used extensively to examine the influence of niche differentiation, dispersal, density dependence, speciation, and extinction on the structure and dynamics of ecological communities [6]. Since 1932, many types of models have been used to verify mechanistic rules that explain the structure of ecological communities and reveal the effects of various ecological processes in SADs patterns [7]. Together, these models can be broadly classified into three categories according to their ecological significance: ecological niche models, neutral models, and mathematical pure statistical models. The mathematical pure statistical model is not clear in its ecological meaning, so the niche model and the neutral model are the two most important models that are used to explain the multiplicity of a species, and this model represents two ecological processes [8]. Additionally, researchers have found the relative effects of these ecological processes that determine community structure, but it is not understood how they are impacted by different sampling scales [9,10]. Specifically, the community habitat heterogeneity, species coexistence degree of individual aggregation, and movement and dispersal of organisms will increase or decrease correspondingly with the increase or decrease in sampling size. However, these factors may also create different community assemblies [11]. For example, the importance of environmental filtering is more pronounced at larger sampling scales, while the effect of interspecies competition is more pronounced at smaller sampling scales [12,13]. Some studies on tropical rain forests also show that dispersal limitation is decisive at smaller scales (0.2–50 km) [14]. Other research also suggests that the random process is the main ecological driver of different successional stages for conifer and broad-leaved mixed forest communities at moderate and large sampling scales [15,16].
Previously, many studies based on SADs explored different facets of community assembly, but most of them focused on normal landscapes, and the karst topography has not been extensively investigated [17,18]. This region is an atypical area with unique geological, environmental, and floristic conditions. The karst topography is characterized by a series of clustered peaks (i.e., steep low hills) with a common base and a funnel landscape. Additionally, tree species are often patchily distributed in their natural forests. Usually, soil layers are mainly formed by the dissolution of one or more layers of soluble bedrock, typically carbonate rock such as limestone. In these forests, long-term strong dissolution and erosion lead to interspersed distribution of bare rock and soil surfaces, which creates unique rock–soil formations with fragmented structural attributes [19]. These rare and special conditions exhibit local complex topographic positions that significantly limit the succession of karst vegetation and the development of climax communities. Here, the evergreen and deciduous broad-leaved mixed forest is regarded as the climax succession community, in a transition zone from deciduous broad-leaved forest to evergreen broad-leaved forest. In this area, the forest has not reached its true succession climax (i.e., evergreen broad-leaved forest) compared to other habitats with better soil and water conditions. Although this community has not reached its true succession climax, it still possesses a distinct community structure and contains a unique biodiversity that is remarkably different from the adjacent tropical and temperate forests [20]. Ultimately, it is a special model that will benefit studies of species coexistence mechanisms.
In this study, we explored the effect of spatial changes using these models in a karst forest community of evergreen and deciduous broad-leaved mixed trees in Guilin, Guangxi, southwestern China, with the aim of better understanding their community structure mechanism and providing a theoretical basis for the restoration and reconstruction of vegetation in this area. We established a medium-sized forest plot and compared the fit of a suite of niche and neutral theory models to the observed SADs at different sampling scales. We then performed a PER-SIMPER analysis to detect the relative importance of niche and neutral processes. Initially, we expected that the relative contribution of the niche and neutral process would vary depending on the sampling scale. Our specific hypothesis was: (i) the relative contribution of the niche and neutral process will show scale differences in the subtropical karst evergreen and deciduous broad-leaved mixed forest, and (ii) the neutral process will influence the community construction, and niche-based selection cannot be excluded at small and medium scales. By doing so, this study will further contribute to unmask the assembly processes that predominate at various spatial scales.
2. Materials and Methods
2.1. Study Area
The study region was located in the karst area of Guilin, Guangxi Zhuang Autonomous Region, China (24°59′57.23″–24°59′55.72″ N, 110°07′25.87″–110°07′18.49″ E), with altitudes that range from 100–500 m. This area belongs to the subtropical humid monsoon climate, where the annual average temperature is 18–19 °C, with the coldest monthly mean in January (8 °C). The annual frost-free period is 309 days, and the annual rainfall is 1856 mm. The rainfall distribution throughout the year is uneven, where spring and summer are humid and rainy [21]. The vegetation type in the area is known as an evergreen and deciduous broad-leaved mixed forest.
2.2. Field Sampling
Samples were collected in the karst evergreen and deciduous broad-leaved mixed forest community. Following standard ForestGeo protocols (https://forestgeo.si.edu/node/145665/, accessed on 15 May 2020), we established a fixed monitoring plot of 200 m × 100 m in the study region during the summer of 2020. All woody plants with a diameter at breast height (DBH, 1.3 m) ≥ 1 cm in the plot were enumerated and identified. We recorded their species name, height, and spatial position. Most live individuals were identified to species, but in some cases, when plant identity was uncertain, a voucher specimen was collected and labeled for subsequent identification at Flora of China (http://frps.eflora.cn, accessed on 7 July 2020). On investigation, 4562 live individual trees were documented, belonging to 53 families, 87 genera, and 103 species. Most of the tree species in the plot were unique to the karst region. Euphorbiaceae, Fabaceae, and Lamiaceae were the three most common families. The most dominant species were Cyclobalanopsis glauca (278 individuals), Mallotus philippensis (252 individuals), Boniodendron minus (88 individuals), and Zelkova schneideriana (70 individuals), respectively. For subsequent analyses, we used three sizes of subplots: 10 m× 10 m (n = 200), 20 m× 20 m (n = 50), and 50 m × 50 m (n = 8) to compare the spatial effects.
2.3. Measurement of Environmental Factors
Soil sampling was conducted in July 2020. The forest plot was divided into 200 10 m × 10 m subplots for surveying, and the subplots were further combined to obtain soil data for the 50 20 m × 20 m subplots and the 8 50 m × 50 m plots. In each 10 m × 10 m subplot, a soil sampler was used to collect soil samples at 5 random points. At each sampling point, a soil sample was collected with a depth of 0–20 cm after removing any possible organic layer. The 5 soil samples in each subplot were mixed as a test sample. We then analyzed the physical and chemical properties of each test sample by using methods that have been previously described for soil agrochemical analysis [22], including soil pH (pH), water content (SWC), organic matter (SOM), total nitrogen (TN), available nitrogen (AN), total phosphorus (TP), available phosphorus (AP), available potassium (AK), and calcium (Ca). Among them, the pH was determined in a 1:2.5 soil-to-water suspension ratio. SWC was measured as the fresh soil weight minus the oven-dried weight divided by the fresh weight. SOM was determined by wet oxidation with KCr2O7 + H2SO4 and titrated with FeSO4. TN was determined using the automatic Kjeldahl analysis method (KJELTECTM 8400, FOSS Quality Assurance Co., Ltd., Hillerød, Denmark). AN was quantified using the alkaline hydrolysis diffusion method. TP was examined by acid digestion with a H2SO4 + HClO4 solution. AP was extracted with 0.5 M Na2CO3, and it was measured using the molybdenum blue colorimetric method. AK was determined by flame photometry after extraction with ammonium acetate. For Ca determination, 0.2 g litter samples were digested with 4 mL of concentrated nitric acid heated at 120 °C, and 30% hydrogen peroxide (H2O2) was repeatedly added until the digested solution was colorless. After H2O2 digestion, the cation concentrations were measured by atomic absorption spectroscopy (TAS-990, Beijing, China).
The topographical factors included elevation, slope, and convexity. For each sample square, elevation was calculated as the average of the elevation at the four vertices of the sample square. Slope was calculated as the average of the angles between the plane and the horizontal plane formed by any three angles of the target sample square. The elevation of the target square minus the average elevation of the surrounding eight squares was used for the concavity and convexity of each sample square. For a sample square located at the edge or four corners of the sample plot, its convexity value was obtained by subtracting the average elevation of several adjacent sample squares from the elevation of the sample square [23,24].
2.4. Statistical Analyses
We used two types of models to explain and quantify the patterns and processes of the SADs: two niche models (BSM, NPM) and two neutral models (MZMM, VM) to assess the relative importance of the niche-based deterministic processes and the neutral-based stochastic processes regarding community assembly across three different spatial scales in a medium-sized forest plot (200 m × 100 m) in a typical karst forest (evergreen and deciduous broad-leaved mixed forest). A brief introduction to each fitting model is described below.
2.4.1. Niche Models
The broken stick model (BSM), proposed by MacArthur [25], is a resource allocation model. The model assumes that the total niche (total resources) in a community is equivalent to a stick equal to 1. Resources are allocated by randomly setting S−1 points on the stick and then dividing the stick into S segments, which represent the niches occupied by the S species. The model assumes that S species have similar taxonomic status and competitive abilities and appear in the community at the same time. The total number of individuals in the community is J, and the abundance of the i-th species in the model is:
The niche preemption model (NPM) assumes that the most dominant species in the community occupy k shares of the total niche, and the subdominant species occupy the remaining k shares, namely k(1–k), and so on, until the remaining resources can no longer sustain a species [26]. This model guarantees that dominant species have priority in the use of resources, and the species clearly form a hierarchy in niche occupation. Here, we let A1 represent the abundance of the most dominant species in the model, while the abundance of the i-th species in the model is:
2.4.2. Neutral Models
The metacommunity zero-sum multinomial distribution model (MZMM) assumes that the species abundance distribution at a certain point comes from the random drift of the neutral metacommunity. The model includes two parameters: the number of individuals in the sampling point (J) and the fundamental biodiversity number (θ). The log-series distribution is a special case in this model [27], so that the fitting effects of the two models are very similar. According to this model, the number of species (S) with an abundance of n at any sampling point in the metacommunity can be expressed as:
The Volkov model (VM) adds the parameter migration coefficient m to the previous metacommunity zero-sum multinomial distribution model. It also assumes that the migration coefficient m of the species from the compound community to the local community is fixed. According to this model, the number of species (S) with an abundance of n in a local community can be expressed as:
where γ represents the number of individuals migrating to the local community [28].
To test which of the above four models best fit the observed species abundance distributions, we used Akaike’s information criteria (AIC) values and K-S tests. The AIC approach is advantageous because it takes into account both the optimality of model predictions and the simplicity of the model. Generally, a lower AIC value produces a more robust fit. We also used the K-S test to judge whether there was a significant difference between the empirical distribution function of the two samples by calculating the distance (statistic D).
Further, we applied a permutation-based algorithm called PER-SIMPER [29], a distance-based computational procedure to quantify the relative contribution of each taxon to the overall average dissimilarity (OAD) between the different taxonomic assemblage groups. There were three distinct permutations based on null models where: (1) Taxon distribution is controlled only by the number and breadth of niches available in each assemblage, regardless of the dispersal potential of the taxa. Following this null hypothesis, taxon occurrences are randomly permuted to keep the species richness (i.e., row sum) of the sample sites unchanged. (2) Taxon distribution is controlled by the dispersal potential of the taxa, which simulates the migration of species between different points to retain the species’ potential dispersal capacity. Following this null hypothesis, taxon occurrences are randomly arranged under a constant taxon ubiquity (i.e., column sum). (3) Taxon distribution is controlled by a combination of the two previous models, which simulates the joint drive of the “dispersal effect” and “niche differentiation” to keep the row and column sums constant to retain most of the original information. We then generated three distinct null SIMPER profile distributions (default 1000 random permutations) that can be directly compared with empirical SIMPER profiles that sum after squaring and use logarithms to obtain the E-metric.
where γi represents the relative contribution of species group i to the overall average dissimilarity (OAD) observed between two or more sets of samples, null represents the null model matrix, and obs represents the observation matrix.
The lower the distribution on the E axis, the more similar the empirical profile to the null SIMPER profiles that correspond to the underlying permutation model. With this model, we can qualitatively judge the main driving processes for community assembly.
All statistical analyses were performed in R version 4.1.0 [30]. The standardization of taxonomic species names and the SAD model fitting were conducted using the Taxonstand and sads software packages, respectively [31,32]. The PER-SIMPER analysis was tested using the PerSIMPER function script by Gibert et al. [29].
3. Results
3.1. Patterns of Species Abundance Distributions
We estimated SADs for the evergreen and deciduous broad-leaved mixed forest by fitting neutral models (MZMM, VM) and niche models (BSM, NPM) with the varying sampling scales (Figure 1 and Table 1). At the small and medium scales (10 m × 10 m and 20 m × 20 m), all four models passed the K-S test and were within an acceptable range (p > 0.05). For AIC values, MZMM and VM were generally close to each other, and lower than the BSM and NPM. However, at the large sampling scale (50 m × 50 m), the fit of the two niche models was rejected (p < 0.05), but the neutral models still showed a high goodness of fit. These results suggest that at small and medium scales, niche-based selection and dispersal-based neutral processes could operate simultaneously. They also imply that neutral processes affect the shape of species composition and are more important than niche process building, which can be seen from the AIC information criteria and K-S test. Additionally, we conducted a redundancy analysis of species distributions and environmental factors at small and medium scales, which also indicated weak environmental forces in community construction (Appendix B).
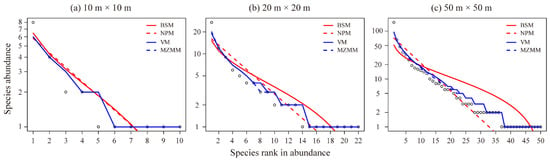
Figure 1.
Species-abundance distributions (SADs) and model fitting for the evergreen and deciduous broad-leaved mixed forest. Graphs (a–c) represent rank-abundance plots and the fitting of the four models at increasing plant sampling spatial scales (m × m). Observed values are shown as open circles, and simulated values are shown as different colored curves. Among these, the solid red line represents the fitted distribution of the BSM, the dashed red line represents the fitted distribution of the NPM, the solid blue line represents the fitted distribution of the VM, and the dashed blue line represents the fitted distribution of the MZMM.

Table 1.
Goodness of fit tests of four models for the species abundance distributions in the evergreen and deciduous broad-leaved mixed forest at different sampling scales.
3.2. The PER-SIMPER Analysis of Simulated Species Distributions
We then obtained three relative uniform distribution E values (i.e., niche- and dispersal-controlled distribution, dispersal-based controlled distribution, and niche-based controlled distribution) using the PER-SIMPER analysis at the three sampling scales (Figure 2). The E values between the niche- and dispersal-controlled distribution and the dispersal-controlled distribution were very similar, showing low E values, while the niche-controlled distribution showed a high E value, which suggests that a dispersal-controlled distribution plays a dominant role at all three sampling scales.

Figure 2.
Example of E-metric distributions resulting from the permutational SIMPER analyses for the different plot sizes of (a) 10 m × 10 m, (b) 20 m × 20 m, and (c) 50 m ×50 m. The blue boxplot represents niche-based and dispersal-based controlled distribution. The orange boxplot represents dispersal-based controlled distribution. The green boxplot represents niche-based controlled distribution.
4. Discussion
4.1. Scale Dependence of Community Assembly in Subtropical Karst Forests
In combination with spatial scale, different SADs present different ecological processes [6,33]. In this work, we determined the best-fit SADs models, and explored the mechanisms that shape SADs at three different sampling scales. Our results demonstrate that at small and medium scales, niche-based selection and dispersal-based neutral processes could operate simultaneously; however, their species abundance distributions are better explained by the neutral assumption with the different sampling scales (Table A1, Figure 2 and Figure A1). Additionally, our findings are similar to those found in other previous works. For example, Wu et al. [16] showed that species abundance structure was better explained by the neutral and niche process at smaller sampling scales. However, the neutral process became the major mechanism that maintained the SADs as the sampling area increased in two typical subtropical secondary forests. Tan et al. [8] also found that niche-based models provided a better fit at small sample sizes (10 m × 10 m, 30 m × 30 m), and that the neutral model performed better for both 60 m × 60 m and 90 m × 90 m scales in three natural forests in Northeastern China. Therefore, it is important to use various models to reveal the relative contributions of the SADs patterns with different spatial scales and to recognize that they are not mutually exclusive.
At small and medium scales, we assumed that density dependence would have a strong effect on the SADs, which would result in inter-species competition exclusion, consequently reducing interspecific density [34]. This type of competition improves species diversity by promoting niche differentiation [35,36]. Secondly, this may be constrained in a karst heterogeneous environment because limestone rock–soil structure with greater topographic variability forms more microhabitats that limit dominant species dispersal at local areas and creates opportunities for rare species to enter. Similar results were also found in earlier studies. For instance, Breugel et al. [37] showed that higher habitat heterogeneity in a community can enhance dispersal limitation. Furthermore, the interaction between neutral or niche processes that drive community dynamics is not completely exclusive, especially on different scales. Since no community is truly neutral or fully niche-based, the end of the niche-neutrality continuum only exists in theory [38,39,40]. Altogether, in this study, we find that dispersal limitation and niche processes have a combined effect at medium and small scales. Meanwhile, our findings also demonstrates that dispersal processes represented by neutral models are the main ecological processes under different spatial scales, specifically at the size of 50 m × 50 m, which has also been confirmed in other research.
4.2. The Neutral Process Plays a Dominant Role in Subtropical Karst Forests
To qualitatively identify the dominant processes in a community, we used PER-SIMPER analysis and verified the dominant role of neutral theory at different scales. Our results further show support for the unified neutral theory as a tool for understanding abundance patterns in communities. From a statistical perspective, neutral models assume that the total number of individuals in a community is relatively constant and is determined by stochastic processes, such as dispersal limitation [27]. Meanwhile, niche models assume that the total niche in the community is 1 and that it fits an abundance distribution, which does not correspond to the real situation, and is not as accurate as neutral models [41]. From an ecological perspective, as the community in this area is in its terminal succession stage, species had already reached stable coexistence, and the niche processes had been weakened. Therefore, we speculated that the corresponding effects of the neutral processes would strengthen when the effects of the niche processes declined [7]. In the karst forest environment, its habitats cause extensive fragmentation and seriously decrease the soil water-holding capacity and soil nutrient content, which may negatively impact the fruiting rate of a species, weaken species colonization ability, and limit other ecological processes [42,43]. Herrera et al. [44] also found that habitat fragmentation increases seed dispersal limitation across a landscape and may also affect subsequent demographic stages, such as seedling establishment. Together, our results show that the neutral theory plays the dominant role in shaping community structures, especially in unique environments such as the karst forest.
5. Conclusions
The dispersal-based neutral processes of plant communities in an evergreen and deciduous broad-leaved mixed forest showed a strong imprint on species distribution patterns. Due to the important role of dispersal-based neutral processes in the karst region, forest patches are important for protecting forest plant species. It is pertinent that management planning takes into account both habitat heterogeneity and the spread of species between communities, by means such as artificial introduction, for the restoration of natural vegetation in these areas. Altogether, we should use the models defined in this work to understand and predict the possible contributions made by other community assembly processes, such as interspecific relationships (i.e., competition, reciprocity, predation, parasitism, etc.), as well as the relative importance of other mechanisms.
Author Contributions
Conceptualization, Y.J. and S.L.; methodology, Y.J.; validation, Y.J., S.L. and Y.H.; formal analysis, Y.H.; investigation, Y.H. and W.N.; resources, S.L.; data curation, Y.H. and W.N.; writing—original draft preparation, Y.H. and S.L.; writing—review and editing, Y.J.; visualization, Y.H.; funding acquisition, Y.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (31860124, 32260283) and the College Students’ Innovation and Entrepreneurship Training Program (202210602012).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank numerous students from the Chinese Guangxi Normal University for their support in conducting the tough field work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Data Preparation before the PER-SIMPER Analysis
We first calculated the relative importance value (RIV) using the average function of relative density, relative basal area, and relative frequency on a percentage basis for each tree species at the three different sampling scales in a medium-sized forest plot (200 m × 100 m). We then defined two different taxonomic groups at each sampling scale through a twinspan function in the twinspanR software package [45] based on a species × plot RIVs matrix for comparison. Next, we used the analysis of similarities (ANOSIM) to statistically test whether there was a significant difference between the two different taxonomic groups (Table A1).

Table A1.
ANOSIM statistical test parameters of plant community taxonomy at different sampling scales.
Table A1.
ANOSIM statistical test parameters of plant community taxonomy at different sampling scales.
| Scale | Group | R2 | p |
|---|---|---|---|
| 10 m × 10 m | 2 | 0.026 | 0.001 *** |
| 20 m × 20 m | 2 | 0.429 | 0.001 *** |
| 50 m × 50 m | 2 | 0.538 | 0.048 * |
Note: * p < 0.05, *** p < 0.001.
Appendix B
Redundancy Analysis (RDA) Ordination between SADs and Environmental Variables
With the different sampling scales, we can infer the relative importance of habitat filtering by comparing the relative explanatory power of the environment to the varying species composition. RDA was performed based on an environmental data matrix and species-abundance matrix for the 10 m × 10 m and 20 m × 20 m scales, respectively. However, the major problem with using this method is that there are too many environmental variables that produce collinearity problems, which result in inaccurate data values. Thus, we applied the variance inflation factor (VIF) method to test the collinearity problem of 12 variables at these two scales. An environmental variable VIF value > 10 suggests that there could be a collinearity problem. Ultimately, we found the VIF value of TN exceeded 10 at the 10 m × 10 m and 20 m × 20 m sampling scales, so it was eliminated.
Additionally, the SADs patterns explained by environmental variables for these two sampling scales were quite similar regarding their first two ordination axes analyses. This combination of 11 environmental variables explained only 5.96% of the total variance in the species abundance at the 10 m × 10 m sampling scale, while the total variance explained only a small increase of 5.96% to 9.69% for the 20 m × 20 m sampling scale (Figure A1).
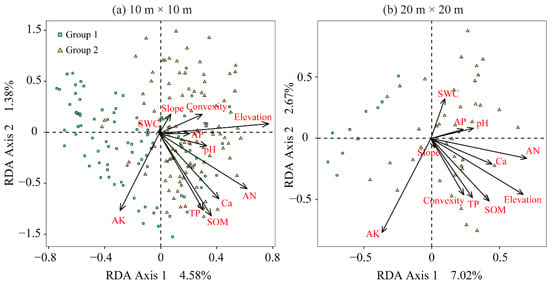
Figure A1.
Redundancy analysis RDA ordination diagram for 200 subplots and environmental variables at the 10 m × 10 m sampling scale (a) and for 50 subplots and environmental variables at the 20 m × 20 m sampling scale (b). The green solid square represents group one, and the solid orange triangle represents group two.
References
- Meszéna, G.; Gyllenberg, M.; Pásztor, L.; Metz, J.A. Competitive exclusion and limiting similarity: A unified theory. Theor. Popul. Biol. 2006, 69, 68–87. [Google Scholar] [CrossRef] [PubMed]
- Albuquerque, U.P.; Nascimento, A.L.B.D.; Chaves, L.D.S.; Feitosa, I.S.; de Moura, J.M.B.; Gonçalves, P.H.S.; da Silva, R.H.; da Silva, T.C.; Ferreira, W.S. A brief introduction to niche construction theory for ecologists and conservationists. Biol. Conserv. 2019, 237, 50–56. [Google Scholar] [CrossRef]
- Koffel, T.; Daufresne, T.; Klausmeier, C.A. From competition to facilitation and mutualism: A general theory of the niche. Ecol. Monogr. 2021, 91, e01458. [Google Scholar] [CrossRef]
- Pos, E.; Guevara, J.E.; Molino, J.; Sabatier, D.; Bánki, O.; Pitman, N.C.; Mogollón, H.F.; García-Villacorta, R.; Neill, D.; Phillips, O.L.; et al. Scaling issues of neutral theory reveal violations of ecological equivalence for dominant Amazonian tree species. Ecol. Lett. 2019, 22, 1072–1082. [Google Scholar] [CrossRef] [PubMed]
- Anceschi, N.; Hidalgo, J.; Plata, C.A.; Bellini, T.; Maritan, A.; Suweis, S. Neutral and niche forces as drivers of species selection. J. Theor. Biol. 2019, 483, 109969. [Google Scholar] [CrossRef]
- Deng, N.; Song, Q.; Ma, F.; Tian, Y. Patterns and driving factors of diversity in the shrub community in central and southern China. Forests 2022, 13, 1090. [Google Scholar] [CrossRef]
- Huang, L.; Yang, H.; An, X.; Yu, Y.; Yu, L.; Huang, G.; Liu, X.; Chen, M.; Xue, Y. Species abundance distributions patterns between Tiankeng forests and nearby Non-Tiankeng forests in southwest China. Diversity 2022, 14, 64. [Google Scholar] [CrossRef]
- Tan, L.Z.; Zhang, P.; Zhao, X.H.; Fan, C.Y.; Zhang, C.Y.; Yan, Y.; Gadow, K.V. Analysing species abundance distribution patterns across sampling scales in three natural forests in Northeastern China. iForest-Biogeosci. For. 2020, 13, 482–489. [Google Scholar] [CrossRef]
- Adler, P.B.; Fajardo, A.; Kleinhesselink, A.R.; Kraft, N.J.B. Trait-based tests of coexistence mechanisms. Ecol. Lett. 2013, 16, 1294–1306. [Google Scholar] [CrossRef]
- Fang, X.F.; Shen, G.C.; Yang, Q.S.; Liu, H.L.; Ma, Z.P.; Deane, D.C.; Wang, X.H. Habitat heterogeneity explains mosaics of evergreen and deciduous trees at local-scales in a subtropical evergreen broad-leaved forest. J. Veg. Sci. 2017, 28, 379–388. [Google Scholar] [CrossRef]
- McGill, B.J.; Etienne, R.; Gray, J.S.; Alonso, D.; Anderson, M.J.; Benecha, H.K.; Dornelas, M.; Enquist, B.; Green, J.L.; He, F.; et al. Species abundance distributions: Moving beyond single prediction theories to integration within an ecological framework. Ecol. Lett. 2007, 10, 995–1015. [Google Scholar] [CrossRef] [PubMed]
- Shipley, B.; Paine, C.E.T.; Baraloto, C. Quantifying the importance of local niche-based and stochastic processes to tropical tree community assembly. Ecology 2012, 93, 760–769. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, T.; Uriarte, M.; Kraft, N.; Shen, G.; Wang, X.; He, F. Spatially explicit metrics of species diversity, functional diversity, and phylogenetic diversity: Insights into plant community assembly processes. Annu. Rev. Ecol. Syst. 2017, 48, 329–351. [Google Scholar] [CrossRef]
- Condit, R.; Pitman, N.; Leigh, E.G.; Chave, J.; Terborgh, J.; Foster, R.B.; Núñez, P.; Aguilar, S.; Valencia, R.; Villa, G.; et al. Beta-diversity in tropical forest trees. Science 2002, 295, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Wang, B.; Li, D.; Mallik, A.U.; Xiang, W.; Ding, T.; Wen, S.; Lu, S.; Huang, F.; He, Y.; et al. Effects of topography and spatial processes on structuring tree species composition in a diverse heterogeneous tropical karst seasonal rainforest. Flora 2017, 231, 21–28. [Google Scholar] [CrossRef]
- Wu, A.; Deng, X.; He, H.; Ren, X.; Jing, Y.; Xiang, W.; Ouyang, S.; Yan, W.; Fang, X. Responses of species abundance distribution patterns to spatial scaling in subtropical secondary forests. Ecol. Evol. 2019, 9, 5338–5347. [Google Scholar] [CrossRef] [PubMed]
- Villa, P.M.; Martins, S.V.; Rodrigues, A.C.; Safar, N.V.H.; Bonilla, M.A.C.; Ali, A. Testing species abundance distribution models in tropical forest successions: Implications for fine-scale passive restoration. Ecol. Eng. 2019, 135, 28–35. [Google Scholar] [CrossRef]
- Ulrich, W.; Soliveres, S.; Thomas, A.D.; Dougill, A.J.; Maestre, F.T. Environmental correlates of species rank—Abundance distributions in global drylands. Perspect. PlantEcol. Evol. Syst. 2016, 20, 56–64. [Google Scholar] [CrossRef]
- Liu, C.N.; Huang, Y.; Wu, F.; Liu, W.J.; Ning, Y.Q.; Huang, Z.R.; Tang, S.Q.; Liang, Y. Plant adaptability in karst regions. J. Plant Res. 2021, 134, 889–906. [Google Scholar] [CrossRef]
- Du, H.; Peng, W.X.; Song, T.Q.; Zeng, F.P.; Wang, K.L.; Song, M.; Zhang, H. Spatial pattern of woody plants and their environmental interpretation in the karst forest of southwest China. Plant Biosyst. Int. J. Deal. All Asp. Plant Biol. 2015, 149, 121–130. [Google Scholar] [CrossRef]
- He, Y.; Liang, S.; Liu, R.; Jiang, Y. Beta diversity patterns unlock the community assembly of woody plant communities in the riparian zone. Forests 2022, 13, 673. [Google Scholar] [CrossRef]
- Bao, S.D. Soil Agrochemical Analysis; China Agriculture Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Harms, K.E.; Condit, R.; Hubbell, S.P.; Foster, R.B. Habitat associations of trees and shrubs in a 50-ha neotropical forest plot. J. Ecol. 2001, 89, 947–959. [Google Scholar] [CrossRef]
- Valencia, R.; Foster, R.B.; Villa, G.; Condit, R.; Svenning, J.C.; Hernández, C.; Romoleroux, K.; Losos, E.; Magård, E.; Balslev, H. Tree species distributions and local habitat variation in the Amazon: Large forest plot in eastern Ecuador. J. Ecol. 2004, 92, 214–229. [Google Scholar] [CrossRef]
- MacArthur, R.H. On the relative abundance of bird species. Proc. Natl. Acad. Sci. USA 1957, 43, 293–295. [Google Scholar] [CrossRef] [PubMed]
- Motonura, I. On the statistical treatment of communities. Zool. Mag. 1932, 44, 379–383. [Google Scholar]
- Hubbell, S.P. The Unified Neutral Theory of Biodiversity and Biogeography; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Volkov, I.; Banavar, J.R.; Hubbell, S.P.; Maritan, A. Neutral theory and relative species abundance in ecology. Nature 2003, 424, 1035–1037. [Google Scholar] [CrossRef]
- Gibert, C.; Escarguel, G.; Lyons, K. PER-SIMPER—A new tool for inferring community assembly processes from taxon occurrences. Glob. Ecol. Biogeogr. 2019, 28, 374–385. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 10 October 2021).
- Cayuela, L.; Macarro, I.; Stein, A.; Oksanen, J. Taxonstand: Taxonomic Standardization of Plant Species Names. R Package Version 2.4. 2021. Available online: https://CRAN.R-project.org/package=Taxonstand (accessed on 10 May 2021).
- Prado, P.I.; Miranda, M.D.; Chalom, A. SADs: Maximum Likelihood Models for Species Abundance Distributions. R Package Version 0.4.2. 2018. Available online: https://CRAN.R-project.org/package=sads (accessed on 16 June 2018).
- Chase, J.M. Spatial scale resolves the niche versus neutral theory debate. J. Veg. Sci. 2014, 25, 319–322. [Google Scholar] [CrossRef]
- Volkov, I.; Banavar, J.; He, F.; Hubbell, S.P.; Martin, A. Density dependence explains tree species abundance and diversity in tropical forests. Nature 2005, 438, 658–661. [Google Scholar] [CrossRef]
- Aarssen, L.W. Ecological combining ability and competitive combining ability in plants: Toward a general evolutionary theory of coexistence in systems of competition. Am. Nat. 1983, 122, 707–731. [Google Scholar] [CrossRef]
- Kim, D.; Ohr, S. Coexistence of plant species under harsh environmental conditions: An evaluation of niche differentiation and stochasticity along salt marsh creeks. J. Ecol. Environ. 2020, 44, 19. [Google Scholar] [CrossRef]
- Breugel, M.; Craven, D.; Lai, H.R.; Baillon, M.; Turner, B.L.; Hall, J.S. Soil nutrients and dispersal limitation shape compositional variation in secondary tropical forests across multiple scales. J. Ecol. 2019, 107, 566–581. [Google Scholar] [CrossRef]
- Gravel, D.; Canham, C.D.; Beaudet, M.; Messier, C. Reconciling niche and neutrality: The continuum hypothesis. Ecol. Lett. 2006, 9, 399–409. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Z.; Ellwood, M.D.F.; Ai, D.; Zhang, R.; Wang, G. Species abundance distributions as a proxy for the niche–neutrality continuum. J. Plant Ecol. 2018, 11, 445–452. [Google Scholar] [CrossRef]
- Furniss, T.J.; Larson, A.J.; Lutz, J.A. Reconciling niches and neutrality in a subalpine temperate forest. Ecosphere 2017, 8, e01847. [Google Scholar] [CrossRef]
- Matthews, T.J.; Whittaker, R.J. Fitting and comparing competing models of the species abundance distribution: Assessment and prospect. Front. Biogeogr. 2014, 6, 67–82. [Google Scholar] [CrossRef]
- Butaye, J.; Jacquemyn, H.; Honnay, O.; Hermy, M. The species pool concept applied to forests in a fragmented landscape: Dispersal limitation versus habitat limitation. J. Veg. Sci. 2002, 13, 27–34. [Google Scholar] [CrossRef]
- Lauri, L.; Riin, T.; Inga, H.; Robert, S.K.; Antonio, G.; Meelis, P. Microfragmentation concept explains non-positive environmental heterogeneity-diversity relationships. Oecologia 2013, 171, 217–226. [Google Scholar] [CrossRef]
- Herrera, J.M.; Garc’ia, D. Effects of forest fragmentation on seed dispersal and seedling establishment in ornithochorous trees. Conserv. Biol. 2010, 24, 1089–1098. [Google Scholar] [CrossRef]
- Zeleny, D. TwinspanR: Two-Way Indicator Species Analysis (and Its Modified Version) in R. R Package Version 0.22. 2021. Available online: https://github.com/zdealveindy/twinspanR (accessed on 19 February 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).