Abstract
Vegetation slope protection has been widely utilized as an eco-friendly approach for slope stability. Up to now, research on the slope protection effect of shrubs and herbaceous vegetation is more than those of trees, which can be attributed to the challenge of evaluating the slope protection effect of tree root systems that can be influenced by many factors, such as root morphology, root volume, plant spacing, and planting patterns. Therefore, this study takes tap-like tree root systems as the research object, constructs the corresponding root-soil composite model by using 3D printing technology, and carries out a series of physical model experiments on slopes supported by tap-like tree root systems, examining the anti-sliding force, slope surface displacement, sliding range, and slope cracks throughout the entire process of deformation and the damage to shallow slopes, to finally evaluate the effectiveness in the slope protection effect of tree root systems from multiple perspectives. The results indicate that: (1) the peak anti-sliding force of the slope supported by tree root systems correlates positively with the root volume and negatively with plant spacing generally, and the influence of tree plant spacing on the peak anti-sliding force is weaker than that of the root volume; (2) the displacement of slopes supported by tree root systems in the square planting pattern is generally less than that in the staggered planting pattern, and the displacement of slopes has a negative correlation with the root volume and a positive correlation with the plant spacing; (3) the sliding range of the slope supported by tree root systems is significantly reduced compared with that of the unsupported slope, and the tree root system can prevent the occurrence of slope surface cracks to a certain extent, which makes the sliding-body show better integrity. The above understanding enriches the study on the slope protection effect of the tree root system, reveals the influence of the tree root volume, plant spacing, and planting pattern (square distribution and staggered distribution) of the tap-like tree root system, and offers some guidance for the engineering application of tree slope protection in practice.
1. Introduction
In mountainous regions, shallow landslides are exceedingly prevalent and highly likely to occur. Despite the small scale of these landslides, they have the potential to evolve into debris flow over time and initiate disaster chains [1,2]. Therefore, it is a key challenge to find efficient methods to prevent and manage the occurrence of shallow landslides in mountainous regions [3,4,5,6]. According to previous studies [7,8,9,10,11], the stability of slopes in mountainous areas are inextricably related to vegetation, which primarily affects slope stability in two ways: one is to change the hydrological conditions of the slope, either by reducing the water content through root uptake and transpiration of vegetation, or by reducing the scouring of rainwater on slopes through canopy retention [12,13,14,15], but this vegetation-influenced hydrological effect will shift dramatically as the seasons change; the other is to improve the mechanical properties of the slope through soil reinforcement directly by the roots [16,17,18]. This mechanical effect of soil consolidation provided by roots is relatively stable throughout the year and is typically further enhanced by vegetation growth, which is usually considered to contribute more to the long-term stability of slopes [19,20]. As a result, various previous studies have been carried out to focus on the latter vegetation consolidation mechanism.
In terms of theoretical research on the mechanical properties of roots, some researchers have quantified the force that roots contribute to the soil [21,22,23,24,25,26,27,28,29,30,31,32,33]. For example, Wu et al. [23] and Waldron [24] believed that the root system altered the cohesiveness of the soil and proposed a vertical root system model based on the Mohr–Coulomb strength criterion, which has been gradually refined and adjusted [25,26]. It should be emphasized that this model is of great importance for quantitatively assessing the slope protection effect of vegetated roots, but because it assumes that all roots are dislodged by the force and break at the same time, the effect of the roots may be overstated [27,28]. For this reason, Pollen and Simon [27] introduced Fiber bundle models (FBMs), which are based on the fracture mechanics of composite materials in the field of materials science, to evaluate the mechanical effects of vegetation roots on slope consolidation. They believed that the roots break gradually and could be pulled out under the action of shear force [29]. However, the FBMs model undervalues the significance of the root system to some extent, which ignores the effects of variables such as root volume and root branching [30,31]. In view of this, in recent years, an extension of the FBM has been proposed; researchers have suggested root bundle models (RBMs) that can take into account the impact of the lateral roots of various diameters on the shear strength of the soil [30,32] and other researchers have proposed new energy-based FBMs (FBMs-W) [33], so as to further enhance the theoretical study of soil reinforced by vegetation roots.
In terms of experimental research on the mechanical properties of roots, previous studies have generally focused on root strength and the bond strength between the root and soil. For example, the tensile strength of the root system is frequently assessed through root tensile tests [34,35,36], and the contact strength between the roots and soil is usually determined by the In situ root pull-out test [37,38], and the shear strength of the soil containing the roots is often evaluated using direct shear tests on root-reinforced soils to determine the shear strength of soil containing roots [39,40]. Obviously, all of these mechanical parameters related to roots play a significant role in determining the stability of slopes that have been enhanced by vegetation, and research related to these parameters has greatly enhanced the ability to quantitatively evaluate the effectiveness of vegetation in stabilizing slopes. It should be pointed out that the results of experiments on the mechanical properties of vegetation roots are sensitive to the impact of vegetation species, plant growth environments, and the subjectivity of the experimenter [41,42,43,44]. As a result, the representativeness of the results obtained through the experiments should be evaluated.
In terms of the numerical simulation of the mechanical properties of vegetation roots, related research can be divided into two main groups: the first group focuses on the construction of a numerical model that contains the morphology and structure of the root system and then analyzes the various reinforcement mechanisms of the root system [45,46,47]. These studies can make up for the inability to quantitatively investigate the root mechanism in mechanical performance studies of vegetation roots due to the great diversity of root systems. However, the root system in the model must be precisely described and modeled; therefore, computational efficiency is limited to some degree. The second group is intended to reflect the reinforcing effect of the root system on soil strength by adding an extra cohesive force () [48,49,50]. These studies are equivalent to simplifying the reinforcement effect of the vegetation and applying it evenly throughout the soil, which in some ways lessens the challenge of evaluating the roots to enhance slope stability. However, it should be noted that due to the spatial randomness of the vegetation growth [51], the actual reinforcement effect of the roots on the soil is frequently non-uniform and will change due to different root densities or root morphologies [43], which deviates greatly from the numerical model.
Obviously, numerous research has been conducted and has significantly enhanced our understanding of the reinforcement mechanisms of the root system. Nevertheless, it should be mentioned that there are relatively few physical model studies on the slope protection effect of vegetation root systems, and most of previous studies mainly focuses on herbs and shrubs [52], while very few physical model experiments are conducted on trees with huge roots. In addition, most of the previous studies on vegetation root reinforcement slopes often focus on the bond effect between the root system and soil [53]; few studies have been performed on the slope protection effect under different planting methods of trees, such as plant spacing and planting patterns. In view of this, this study takes tap-like tree root systems as the research object and adopts 3D printing technology to rapidly construct the corresponding root-soil composite model. Based on the self-designed physical model experiment platform of the slope, a series of physical model experiments of the slopes with and without tree root systems are carried out, respectively, aimed at analyzing the influence of the tap-like tree root volume, plant spacing, and planting pattern on the slope protection effect, and further providing a reference for the practical application of ecological slope protection measures.
2. Materials and Methods
2.1. Study Site and Experimental Material
The study site is located in the small watershed of the Reshui River in Xide County, Liangshan Yi Autonomous Prefecture, Sichuan Province, China (Figure 1). This small watershed has undulating mountains with a high vegetation cover and is frequently struck by geological disasters that seriously threaten the lives and property of people in this area. Figure 2 shows natural slopes in the small watershed. It can be seen that there are many shallow unstable slopes, which may become the debris source in the flood season. Therefore, we focused on the shallow soil slope of the small watershed of the Reshui River and carried out a series of physical model experiments. The soil for this study was taken from the study site (Figure 1). The liquid-plastic limit test, compaction test, and direct shear test were used to determine some basic physical properties of the test soil. Its fundamental physical and mechanical properties are displayed in Table 1. Particle size analysis showed the content of the particles with a grain size less than 0.075, which made up more than 80% of the entire mass.
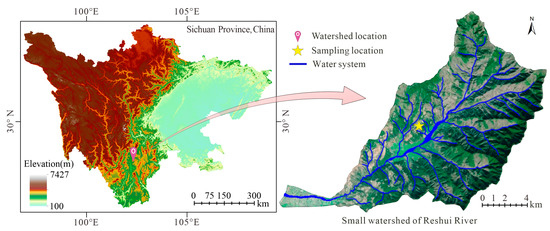
Figure 1.
Study area and sampling location of soil material in physical model experiment.

Figure 2.
Pines on slopes of the small watershed of Reshui River. (a) Photo of shallow landslides; (b) Pine trees dumped on the shallow landslide.

Table 1.
The physical mechanics of soil samples.
Due to the difference in terrain, soil conditions, regional climate, and so on, vegetation root morphologies are kaleidoscopic [54,55]. Our study aims at analyzing the influence of tap-like tree root volume, plant spaceing, and planting patterns on the slope protection effect; therefore, it is necessary to generalize the roots. In general, tree roots can be divided into three categories based on the three-dimensional morphology as depicted in Figure 3 [56]: a tap-like root system, a heart-like root system, and a plate-like root system. The tap-like root system is made up of large downward-growing primary roots and horizontally growing lateral roots, the heart-like root system consists of roots that develop from the bottom of the trunk in all directions, and the plate-like root system is composed of large lateral roots that develop horizontally from the bottom of the trunk [57]. For the sake of study, some researchers regard the root system and soil as a unit. Thus, the three types of root systems mentioned above can be generalized into three kinds of root-soil composite models [58] (Figure 3), which have been extensively employed today. Compared to the exposed pine roots in the small watershed of the Reshui River, as seen in Figure 4, this study proposes the application of the tap-like root-soil composite geometric model to characterize the morphology of the pine root system [40]. This study also uses a 3D printer and polylactic acid material and prints tap-like root-soil composites of the pine roots (Figure 4d) layer by layer. On the basis of this, a series of physical model experiments are conducted to investigate the influence of tap-like tree root systems on the slope protection effect.
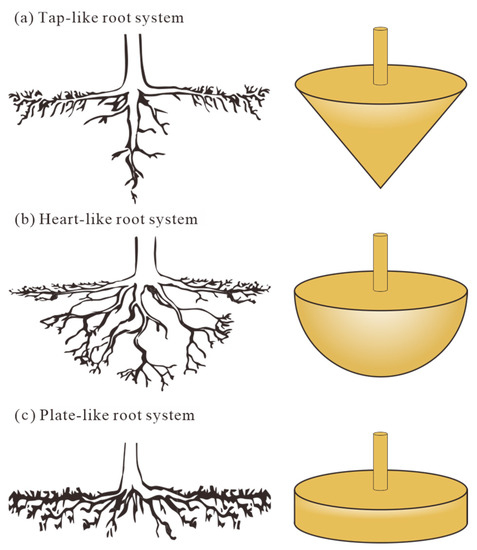
Figure 3.
Schematic diagram of root system morphologies and their corresponding geometrical models of root-soil composites. (a) Tap-like root system; (b) Heart-like root system; (c) Plate-like root system.
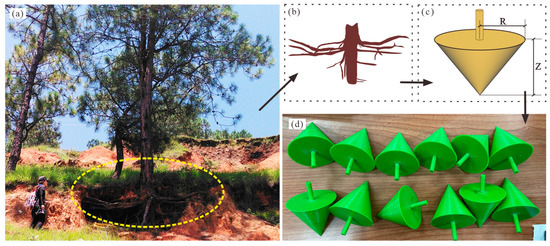
Figure 4.
Pine root morphology exposed at the site. (a) Real root system; (b) Root morphology; (c) Root-soil composite of tap-like pine tree; (d) 3D printed root-soil composite.
2.2. Physical Model Experiment System
The physical model experiment system is made up of a model box, a Canon EOS 700D high-definition camera (HDV, Canon Inc., Tokyo, Japan), a stress–strain data collecting system, and some additional apparatus, as illustrated in Figure 5 [59]. The model box is 120 cm × 50 cm × 80 cm, and a quantitative scale of 1:100 was used in this model. On the front edge of the model box, a traction motor is mounted to induce shallow landslides by pulling the sliding surface. The speed of the traction motor driving shaft is 0.15 mm/min. The anti-sliding force is measured by the tension-compression sensor on the front edge of the model box, recorded by the stress–strain data acquisition system, and transferred to the computer in real-time, with a range of −1000 N to +1000 N and an accuracy of 0.01 N. On the surface of the slope model, displacement monitoring points are placed, and the entire test is captured by an HDV in order to determine the displacement of the monitoring sites. In conclusion, the physical model experiment can acquire comprehensive monitoring data, including the anti-sliding force, the slope surface displacement, and the sliding range during the deformation and failure of the slope.
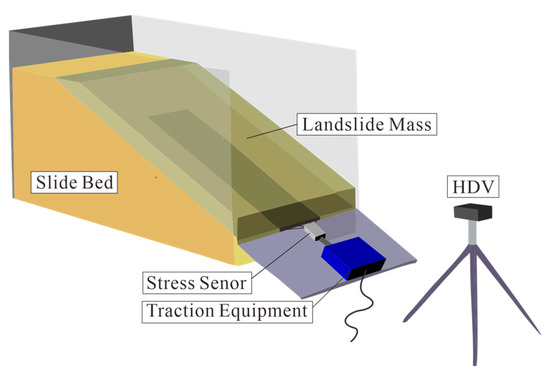
Figure 5.
Schematic diagram of the physical model experiment system.
In this work, the slide bed is filled and piled up by the test soil in order to ensure this is no deformation in this part, and the landslide mass is made by uniformly filling the sieved test soil in layers while the moisture content of the remolded soil is controlled at 18% and the slope angle is set to 30°. The thickness of the soil layer is set to 8 cm, and the chromium-plated wire mesh is laid on the preset displacement surface as the lead surface (inclination angle 30°) with a size of 16.5 cm × 64.5 cm.
2.3. Test Scheme
In order to examine the influence of the tree root volume, plant spacing, and planting pattern (square distribution and staggered distribution) on the slope protection effect, we performed one group of slope model tests without the tree root systems support and ten groups of slope model experiments with the tree root support. The specific test plan is shown in Table 2. In the physical model experiment of the slopes supported by trees, four rows of root-soil composites were organized, with three root-soil composites in each row, and displacement monitoring points were placed on the slope surface, as shown in Figure 6.

Table 2.
Test scheme.
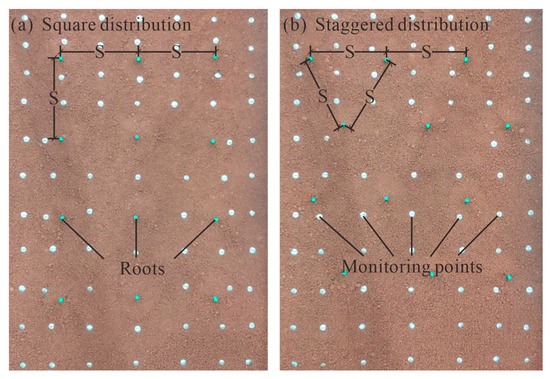
Figure 6.
Planting pattern of root-soil composites and slope displacement tracking points. (a) Square distribution; (b) Staggered distribution.
3. Results
Regarding the unsupported slope test as the reference group, the influences of root volume, plant spacing, and planting pattern on the slope protection effect were analyzed from the perspectives of the anti-sliding force, slope surface displacement, sliding range, and slope cracks, respectively.
3.1. Anti-Sliding Force
The effect of the volume of the tap-like root system on the anti-sliding force is depicted in Figure 7, which demonstrates that when the plant spacing is constant (S = 13 cm), the peak anti-sliding force generally increases with an increase in the root system volume, and this relationship holds true whether the root systems are arranged in a square or staggered pattern. To be more precise, when the root systems were arranged in a square (Figure 7a), the peak anti-sliding force of the three different volumes of root-soil composites (Set 1, 2, and 3) increased by 15.11%, 31.97%, and 68.68%, respectively, compared to the unsupported slope. When the root systems were staggered (Figure 7b), the peak anti-sliding force of the three different volumes of root-soil composites (Set 4, 5, and 6) increased by 9.14%, 15.48%, and 35.86%, respectively, compared to the unsupported slope.
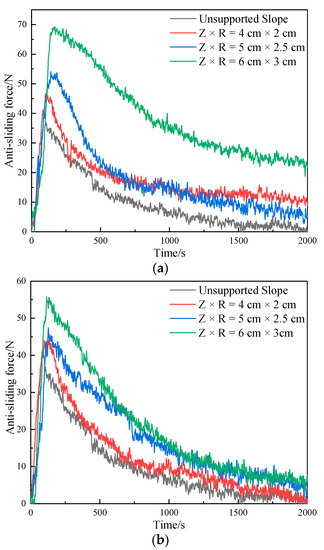
Figure 7.
Effect of volume of tap-like root system on anti-sliding force with constant plant spacing. (a) Square distribution; (b) Staggered distribution.
The effect of the plant spacing of tap-like root systems on the anti-sliding force is depicted in Figure 8, which demonstrates that the peak anti-sliding force tends to decrease with increasing planting space when the root system volume is constant (Z × R = 4 cm × 2 cm), regardless of whether the root systems are arranged in the square or staggered pattern, which is consistent with previous numerical simulation results [60]. Specifically, when the root systems were arranged in a square (Figure 8a), the peak anti-sliding force of the three different plant spacing experiments increased by 8.47%, 15.11%, and 5.32% (Set 7, 1, and 8), respectively, in comparison to the unsupported slope. When the root systems were staggered (Figure 8b), the peak anti-sliding force of the three different planting space experiments increased by 11.38%, 9.14%, and 3.21% (Set 9, 4, and 10), respectively, compared to the unsupported slope. Additionally, comparing Figure 7 and Figure 8, it can be found that the influence of the root volume on the peak anti-sliding force was often stronger than that of the plant spaceing, which should be taken into account in the actual ecological slope protection.
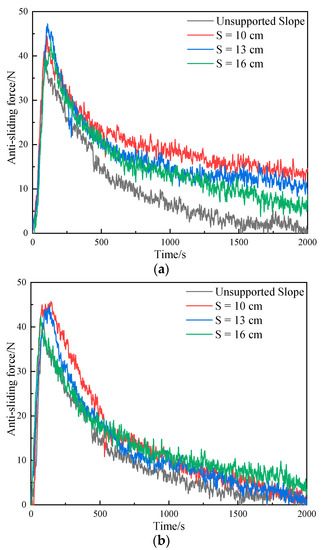
Figure 8.
Effect of plant spacing of tap-like root system on anti-sliding force with constant root volume. (a) Square distribution; (b) Staggered distribution.
The influence of the planting pattern of the tap-like root systems on the anti-sliding force is depicted in Figure 9 and Figure 10. It is clear that the square planting pattern has a more positive impact than the staggered planting pattern. Specifically, when the plant spacing is constant, the peak anti-sliding force of the root systems arranged in a square is better than that in the staggered root systems, and this advantage becomes increasingly apparent as the root volume increases. This finding is consistent with the conclusion of the previous numerical simulation studies [61]. Moreover, when the volume of the root system remains constant, the residual anti-sliding force of the slope supported by the root systems in a square is generally better than in the staggered root systems, but this advantage gradually diminishes as the plant spaceing increases.
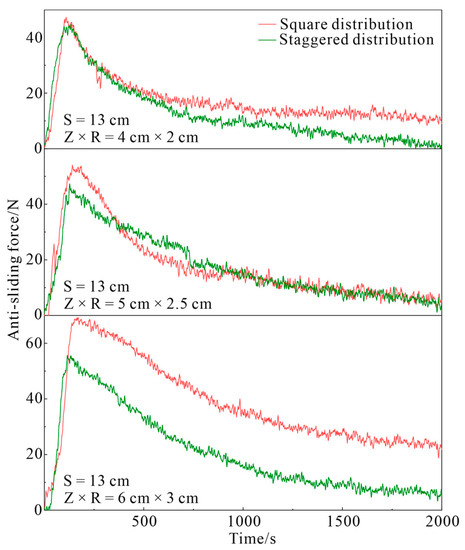
Figure 9.
Effect of planting pattern of tap-like root system on anti-sliding force with constant plant spacing.
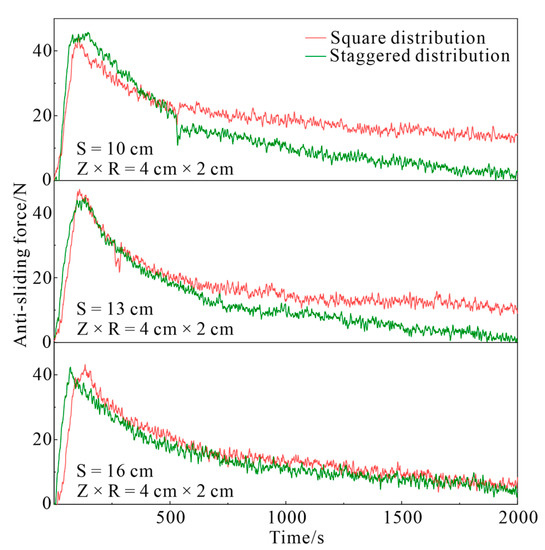
Figure 10.
Effect of planting pattern of tap-like root system on anti-sliding force with constant root volume.
3.2. Surface Displacement
Figure 6 depicts the configuration of the displacement monitoring sites for the physical model test. Through the image processing of a series of photographs captured by an HDV throughout the experiment, the variation curve of the slope surface displacement with time under various test conditions may be recorded. Consequently, the following conclusions can be drawn:
When the plant spacing is constant, the influence of the tap-like root system volume and the planting pattern on the slope surface displacement is depicted in Figure 11. It can be observed that when the plant spacing is constant (S = 13 cm), the larger the root-soil composite volume, the lower the overall slope displacement. Moreover, the overall displacement supported by root systems in the square pattern is usually smaller than that in the staggered pattern. It should be noted that when the root-soil composite volume is minimal (Z × R = 4 cm × 2 cm), regardless of whether the root systems are arranged in a square pattern or staggered pattern, the sliding range of the slopes supported by the tree root systems is bigger than that of the unsupported slope at the beginning of the experiment, but with the root systems gradually playing the role of slope stabilization, the sliding range of the slope with a tree root systems support is gradually controlled in the middle and latter stages of the experiment and is ultimately slightly smaller than that of the unsupported slope. When the volume of the root-soil composite was greater (Z × R = 6 cm × 3 cm), the sliding range of the slope supported by the tree root systems was always less than that of the unsupported slope.
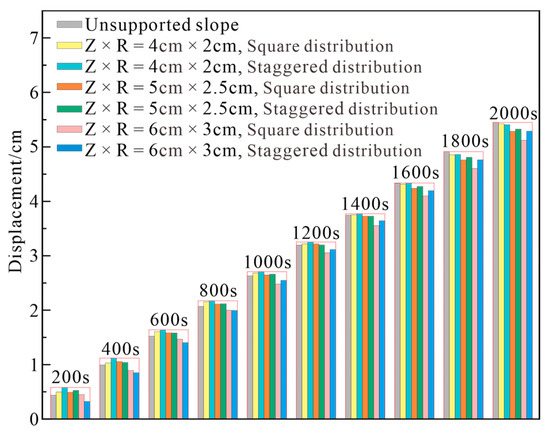
Figure 11.
Effect of volume and planting pattern of tap-like root system on slope surface displacement with constant plant spacing.
When the volume of the tap-like root-soil composite remains constant, the impact of the tap-like root system plant spacing and planting pattern on the slope surface displacement is depicted in Figure 12. It can be seen that when the volume of the composite is certain (Z × R = 4 cm × 2 cm), the smaller the plant spacing, the smaller the overall slope displacement, and the overall displacement supported by the root systems in a square pattern are than in the staggered pattern. It should be noted that when the plant spacing increases, the difference between the influences of the two planting patterns on the slope surface displacement gradually decreases.
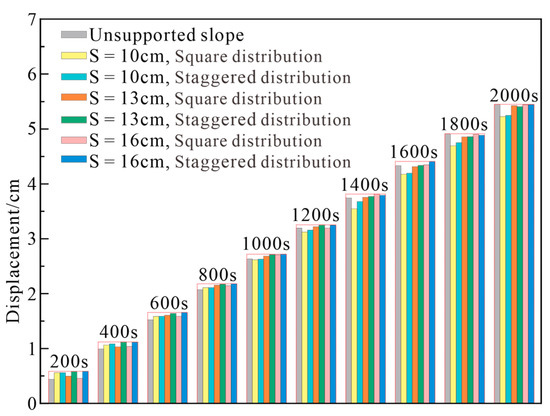
Figure 12.
Effect of plant spacing and planting pattern of tap-like root system on slope surface displacement with constant root volume.
3.3. Sliding Range and Slope Cracks
Taking the three experiments of set 0, set 3, and set 6 in Table 2 as examples, through the image processing of a series of images acquired by the HDV throughout the experiment, the sliding range and the development of the cracks can be evaluated for both slopes with and without tree root support.
Figure 13 depicts the distribution of the slope surface cracks at the end of the three mentioned experiments. It can be observed that the sliding range of the slope supported by trees has decreased significantly compared to the unsupported slope. Moreover, when the root volume and plant spacing were kept constant, the sliding range of the slope with the root systems arranged in a square was smaller than that in the staggered root systems. Specifically speaking, it can be observed that:
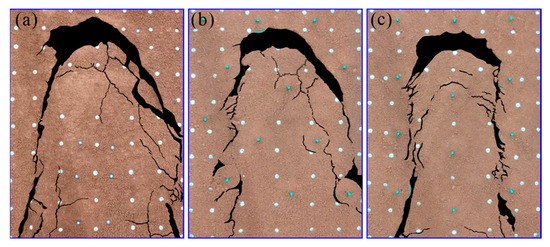
Figure 13.
Slope surface cracks at the moment of 2000 s, where (a) set 0: unsupported slope; (b) set 6: slope supported by tap-like root systems in staggered pattern; (c) set 3: slope supported by tap-like root systems in square pattern.
(1) The unsupported slope has a more obvious and extensive sliding. The perimeter of the sliding body has approached the boundary of the model box, and the slope surface cracks are widely dispersed (Figure 13a).
(2) For the slopes supported by root systems in a staggered pattern, the cracks on the right side of the slope did not extend completely to the boundary of the model box but were forced to the lower-right root-soil composite (Figure 13b). It seems that the surface cracks were limited by the root systems to some extent.
(3) For the slopes supported by root systems in a square pattern, the cracks on the slope surface were clearly confined between the root systems on both sides, and the extent of the sliding body was significantly diminished (Figure 13c).
(4) In comparison to the unsupported slope, the perimeter of the slide body of the slope supported by the tree root systems is relatively fragmented, the surface cracks are numerous and short, and the connection of cracks is poor, indicating that root systems can make the slide body of the slope exhibit greater integrity.
4. Discussion
4.1. Soil Arch Effect between Trees
The utilization of anti-slide piles is considered an effective reinforcement measure for unstable slopes. In addition to the support function that the pile itself performs, the soil arch effect between the piles is also a key role in enhancing the support function of the anti-slide pile. The soil arch effect is caused by the non-uniform displacement of the soil behind the piles and the redistribution of the stress inside the soil [62,63,64]. The generation of the soil arch effect between the piles requires two prerequisites: first, there must be an inhomogeneous displacement of the soil, and second, there must be an arch footing that can provide support (e.g., anti-slide piles that penetrate deep into the stable formation). In addition, it has been demonstrated [65,66,67] that pile spacing and pile width are two significant determining factors for the generation of the soil arch effect between the piles. Similarly, it has been also proposed that the soil arch can be generated between tree roots [68]. However, for slopes supported by trees, it is worth discussing whether the tree root systems can serve as arch footings for soil arch effects and what conditions the root-soil composite volume and tree planting space need to meet (Figure 14).
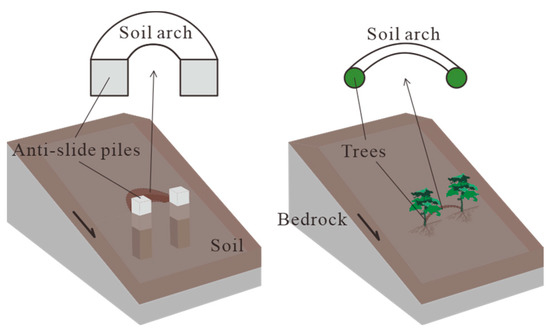
Figure 14.
Schematic diagram of soil arch under anti-slide piles and tree root systems.
4.2. Timeliness of Slope Protection Effect of Vegetation
As presented in Section 3.1, it is known that tree root systems can improve the stability of slopes by affecting the peak anti-sliding force and residual anti-sliding force to varying degrees, and with the growth of trees, the slope protection effect is gradually improved, which is consistent with earlier research that vegetation (particularly trees) can improve the stability of shallow slopes and reduce the probability of shallow landslides in the short term [69]. However, it is worth considering whether or not such vegetation protection measures can be as effective as geotechnical engineering measures (e.g., anti-slide piles and anchor bolts) in slope reinforcements over the long run. Theoretically, as the tree grows, the anti-sliding force provided by the roots will increase. However, we cannot ignore the fact that the tree canopy will also grow gradually over time. Under the wind load, the enormous tree canopy will force the tree trunk to tremble (or even uproot the whole tree), causing the soil around the root systems to become looser, inducing tension cracks to appear on the slope surface, damage the slope integrity, speed up the infiltration of rainfall water, and eventually cause slope instability [70,71,72]. Furthermore, in the long term, the roots of growing vegetation have the potential to penetrate deeply into the fractured or weathered bedrock [73], causing the weathered bedrock to break into clastic rocks, turning the bedrock into the soil and creating the ideal environment for shallow landslides [5,74]. Therefore, it is very necessary to further study the slope protection effect of vegetation on a long-term time scale in the future.
4.3. Limitations of the Current Study
In this study, there are some differences between the actual tree root systems and the tap-like tree root-soil composites created by 3D printing technology, such as the fact that the model surface roughness can neither restore the real situation nor set the friction coefficient for the contact surface between the roots and soil as in numerical simulation. Moreover, during the actual growth of the vegetation roots, the biochemical interactions between the roots and soil could have an effect on the strength of the soil surrounding the roots [75]. For example, the roots will change as the pore water pressure in the soil leads to more absorption of water from the soil and thus have an effect on the shear strength of the soil [3], but these are still challenging to be considered in the current physical experimental studies. For these reasons, it is suggested that the root-soil contact surface should be finely carved in future studies by numerical simulations and other methods, and detailed studies on the hydrological interactions between the roots and soil should be carried out.
5. Conclusions
In this study, we constructed the root-soil composite model of tap-like tree root systems using 3D printing technology, carried out a series of physical model experiments of the slope supported by the tap-like root systems with different volumes of the root, plant spacing, and planting patterns, assessed the effect of tree root systems on protecting the slope from a variety of angles, and finally attained the following insights.
(1) In comparison to the unsupported slope, the peak anti-sliding force of the slope with the tree root systems support shows an increasing trend. Moreover, the peak anti-sliding force generally increases with the root volume and decreases with the plant spacing but is more readily affected by the root volume. In addition, the slope protection effect of the tree root systems in the square planting pattern is generally better than that in the staggered planting pattern.
(2) In comparison to the unsupported slope, the slope surface displacement of the slope with tree root systems support shows a general trend of reduction. Moreover, the slope surface displacement decreases with the root volume and increases with the tree plant spacing. In addition, the displacement of the slope supported by the root systems in the square planting pattern is generally better than that in the staggered planting pattern.
(3) In comparison to the unsupported slope, the sliding range of the slope with the root system support is significantly reduced, and the root system limits the development of the slope cracks to a certain extent, which makes the sliding body show better integrity.
The present study highlights the influence of the tree root volume, plant spacing, and planting pattern (square distribution and staggered distribution) of the tap-like tree root system, enriches the study on the slope protection effect of the tree root systems, which can provide some guidance for the practical engineering application of tree slope protection. However, it should be noted that relying on ecological measures alone is often insufficient to deal with large landslides that are prone to cause significant damage. In the long run, it is necessary to combine vegetation measures and geotechnical measures for landslide hazard prevention and control, but the synergistic effect between them is still unclear [76], especially how to configure them to maximize the slope protection effect, which needs to be strengthened. In addition, the common cases of comprehensive slope stabilization nowadays are the combination of geotechnical engineering measures and herbaceous vegetation, which play the role of vegetation in controlling slope erosion, but few cases of combining geotechnical engineering measures with trees are observed.
Author Contributions
H.D. writing and original draft preparation; L.X., L.L. and H.D. conceived and designed the experiments; H.D. and H.W. performed the experiments and collected the data; L.L., M.Z. and H.D. analyzed the data; L.X. and H.L. reviewed and edited the article. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA23090402), and the National Natural Science Foundation of China (Grant Nos. 41977249 and 42090052).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hicks, D.M.; Gomez, B.; Trustrum, N.A. Erosion thresholds and suspended sediment yields, Waipaoa River Basin, New Zealand. Water Resour. Res. 2000, 36, 1129–1142. [Google Scholar] [CrossRef]
- Peng, C.; Yongming, L. Debris-flow Treatment: The Integration of Botanical and Geotechnical Methods. J. Resour. Ecol. 2013, 4, 97–104. [Google Scholar] [CrossRef]
- Liu, X.; Lan, H.; Li, L.; Cui, P. An ecological indicator system for shallow landslide analysis. Catena 2022, 214, 106211. [Google Scholar] [CrossRef]
- Phillips, C.; Hales, T.; Smith, H.; Basher, L. Shallow landslides and vegetation at the catchment scale: A perspective. Ecol. Eng. 2021, 173, 106436. [Google Scholar] [CrossRef]
- Gabet, E.J.; Dunne, T. Landslides on coastal sage-scrub and grassland hillslopes in a severe El Niño winter: The effects of vegetation conversion on sediment delivery. Geol. Soc. Am. Bull. 2002, 114, 983–990. [Google Scholar] [CrossRef]
- Bathurst, J.C.; Bovolo, C.I.; Cisneros, F. Modelling the effect of forest cover on shallow landslides at the river basin scale. Ecol. Eng. 2010, 36, 317–327. [Google Scholar] [CrossRef]
- Roering, J.J.; Marshall, J.; Booth, A.M.; Mort, M.; Jin, Q. Evidence for biotic controls on topography and soil production. Earth Planet. Sci. Lett. 2010, 298, 183–190. [Google Scholar] [CrossRef]
- Schmidt, K.M.; Roering, J.J.; Stock, J.D.; Dietrich, W.E.; Montgomery, D.R.; Schaub, T. The variability of root cohesion as an influence on shallow landslide susceptibility in the Oregon Coast Range. Can. Geotech. J. 2001, 38, 995–1024. [Google Scholar] [CrossRef]
- Hwang, T.; Band, L.E.; Hales, T.C.; Miniat, C.F.; Vose, J.M.; Bolstad, P.V.; Miles, B.; Price, K. Simulating vegetation controls on hurricane-induced shallow landslides with a distributed ecohydrological model. J. Geophys. Res. Biogeosci. 2015, 120, 361–378. [Google Scholar] [CrossRef]
- Reubens, B.; Poesen, J.; Danjon, F.; Geudens, G.; Muys, B. The role of fine and coarse roots in shallow slope stability and soil erosion control with a focus on root system architecture: A review. Trees 2007, 21, 385–402. [Google Scholar] [CrossRef]
- Löbmann, M.T.; Geitner, C.; Wellstein, C.; Zerbe, S. The influence of herbaceous vegetation on slope stability—A review. Earth-Sci. Rev. 2020, 209, 103328. [Google Scholar] [CrossRef]
- Nsengiyumva, J.B.; Luo, G.; Nahayo, L.; Huang, X.; Cai, P. Landslide Susceptibility Assessment Using Spatial Multi-Criteria Evaluation Model in Rwanda. Int. J. Environ. Res. Public Health 2018, 15, 243. [Google Scholar] [CrossRef] [PubMed]
- Schellekens, J.; Scatena, F.N.; Bruijnzeel, L.A.; Wickel, A.J. Modelling rainfall interception by a lowland tropical rain forest in northeastern Puerto Rico. J. Hydrol. 1999, 225, 168–184. [Google Scholar] [CrossRef]
- Keim, R.F.; Skaugset, A.E. Modelling effects of forest canopies on slope stability. Hydrol. Process. 2003, 17, 1457–1467. [Google Scholar] [CrossRef]
- McGuire, L.A.; Rengers, F.K.; Kean, J.W.; Coe, J.A.; Mirus, B.B.; Baum, R.L.; Godt, J.W. Elucidating the role of vegetation in the initiation of rainfall-induced shallow landslides: Insights from an extreme rainfall event in the Colorado Front Range. Geophys. Res. Lett. 2016, 43, 9084–9092. [Google Scholar] [CrossRef]
- Cohen, D.; Schwarz, M. Tree-root control of shallow landslides. Earth Surf. Dyn. 2017, 5, 451–477. [Google Scholar] [CrossRef]
- Burylo, M.; Hudek, C.; Rey, F. Soil reinforcement by the roots of six dominant species on eroded mountainous marly slopes (Southern Alps, France). Catena 2011, 84, 70–78. [Google Scholar] [CrossRef]
- Yan, Z.; Yan, C.; Wang, H. Mechanical interaction between roots and soil mass in slope vegetation. Sci. China Tech. Sci. 2010, 41, 3039–3044. [Google Scholar] [CrossRef]
- Liu, H.; Mao, Z.; Wang, Y.; Kim, J.H.; Bourrier, F.; Mohamed, A.; Stokes, A. Slow recovery from soil disturbance increases susceptibility of high elevation forests to landslides. For. Ecol. Manag. 2021, 485, 118891. [Google Scholar] [CrossRef]
- Gabet, E.J.; Dunne, T. A stochastic sediment delivery model for a steep Mediterranean landscape. Water Resour. Res. 2003, 39, 1237. [Google Scholar] [CrossRef]
- Meijer, G.J.; Muir Wood, D.; Knappett, J.A.; Bengough, G.A.; Liang, T. Analysis of coupled axial and lateral deformation of roots in soil. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 684–707. [Google Scholar] [CrossRef]
- Mao, Z. Root reinforcement models: Classification, criticism and perspectives. Plant Soil 2022, 472, 17–28. [Google Scholar] [CrossRef]
- Wu, T.H.; McKinnell, W.P.; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Waldron, L.J. The Shear Resistance of Root-Permeated Homogeneous and Stratified Soil. Soil Sci. Soc. Am. J. 1977, 41, 843–849. [Google Scholar] [CrossRef]
- Waldron, L.J.; Dakessian, S. Soil reinforcement by roots: Calculation of increased soil shear resistance from root properties. Soil Sci. 1981, 132, 427. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. The distribution and strength of riparian tree roots in relation to riverbank reinforcement. Hydrol. Process. 2001, 15, 63–79. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour. Res. 2005, 41, W07025. [Google Scholar] [CrossRef]
- Schwarz, M.; Preti, F.; Giadrossich, F.; Lehmann, P.; Or, D. Quantifying the role of vegetation in slope stability: A case study in Tuscany (Italy). Ecol. Eng. 2010, 36, 285–291. [Google Scholar] [CrossRef]
- Pollen, N. Temporal and spatial variability in root reinforcement of streambanks: Accounting for soil shear strength and moisture. Catena 2007, 69, 197–205. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. 2010, 115, F04035. [Google Scholar] [CrossRef]
- Comino, E.; Marengo, P.; Rolli, V. Root reinforcement effect of different grass species: A comparison between experimental and models results. Soil Tillage Res. 2010, 110, 60–68. [Google Scholar] [CrossRef]
- Schwarz, M.; Lehmann, P.; Or, D. Quantifying lateral root reinforcement in steep slopes—From a bundle of roots to tree stands. Earth Surf. Process. Landf. 2010, 35, 354–367. [Google Scholar] [CrossRef]
- Ji, J.; Mao, Z.; Qu, W.; Zhang, Z. Energy-based fibre bundle model algorithms to predict soil reinforcement by roots. Plant Soil 2019, 446, 307–329. [Google Scholar] [CrossRef]
- Mattia, C.; Bischetti, G.B.; Gentile, F. Biotechnical Characteristics of Root Systems of Typical Mediterranean Species. Plant Soil 2005, 278, 23–32. [Google Scholar] [CrossRef]
- Deljouei, A.; Abdi, E.; Schwarz, M.; Majnounian, B.; Sohrabi, H.; Dumroese, R.K. Mechanical Characteristics of the Fine Roots of Two Broadleaved Tree Species from the Temperate Caspian Hyrcanian Ecoregion. Forests 2020, 11, 345. [Google Scholar] [CrossRef]
- Mehtab, A.; Jiang, Y.J.; Su, L.J.; Shamsher, S.; Li, J.J.; Mahfuzur, R. Scaling the Roots Mechanical Reinforcement in Plantation of Cunninghamia R. Br in Southwest China. Forests 2020, 12, 33. [Google Scholar] [CrossRef]
- Vergani, C.; Schwarz, M.; Soldati, M.; Corda, A.; Giadrossich, F.; Chiaradia, E.A.; Morando, P.; Bassanelli, C. Root reinforcement dynamics in subalpine spruce forests following timber harvest: A case study in Canton Schwyz, Switzerland. Catena 2016, 143, 275–288. [Google Scholar] [CrossRef]
- Ruan, S.; Tang, L.; Huang, T. The Pullout Mechanical Properties of Shrub Root Systems in a Typical Karst Area, Southwest China. Sustainability 2022, 14, 3297. [Google Scholar] [CrossRef]
- Comino, E.; Druetta, A. The effect of Poaceae roots on the shear strength of soils in the Italian alpine environment. Soil Tillage Res. 2010, 106, 194–201. [Google Scholar] [CrossRef]
- Ghestem, M.; Veylon, G.; Bernard, A.; Vanel, Q.; Stokes, A. Influence of plant root system morphology and architectural traits on soil shear resistance. Plant Soil 2013, 377, 43–61. [Google Scholar] [CrossRef]
- Hales, T.C.; Cole-Hawthorne, C.; Lovell, L.; Evans, S.L. Assessing the accuracy of simple field based root strength measurements. Plant Soil 2013, 372, 553–565. [Google Scholar] [CrossRef]
- Hales, T.C.; Miniat, C.F. Soil moisture causes dynamic adjustments to root reinforcement that reduce slope stability. Earth Surf. Process. Landf. 2017, 42, 803–813. [Google Scholar] [CrossRef]
- Bischetti, G.B.; Chiaradia, E.A.; Simonato, T.; Speziali, B.; Vitali, B.; Vullo, P.; Zocco, A. Root Strength and Root Area Ratio of Forest Species in Lombardy (Northern Italy). Plant Soil 2005, 278, 11–22. [Google Scholar] [CrossRef]
- Giadrossich, F.; Schwarz, M.; Cohen, D.; Cislaghi, A.; Vergani, C.; Hubble, T.; Phillips, C.; Stokes, A. Methods to measure the mechanical behaviour of tree roots: A review. Ecol. Eng. 2017, 109, 256–271. [Google Scholar] [CrossRef]
- Lin, D.G.; Huang, B.S.; Lin, S.H. 3-D numerical investigations into the shear strength of the soil–root system of Makino bamboo and its effect on slope stability. Ecol. Eng. 2010, 36, 992–1006. [Google Scholar] [CrossRef]
- Xu, H.; Wang, X.Y.; Liu, C.N.; Chen, J.N.; Zhang, C. A 3D root system morphological and mechanical model based on L-Systems and its application to estimate the shear strength of root-soil composites. Soil Tillage Res. 2021, 212, 105074. [Google Scholar] [CrossRef]
- Dupuy, L.; Fourcaud, T.; Stokes, A. A Numerical Investigation into the Influence of Soil Type and Root Architecture on Tree Anchorage. Plant Soil 2005, 278, 119–134. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Duan, Q.; Su, C.; Yan, M.; Dong, Y. The Investigation and 3D Numerical Simulation of Herb Roots in Reinforcing Soil and Stabilizing Slope. KSCE J. Civ. Eng. 2018, 22, 4909–4921. [Google Scholar] [CrossRef]
- Temgoua, A.G.T.; Kokutse, N.K.; Kavazović, Z.; Richard, M. A 3D model applied to analyze the mechanical stability of real-world forested hillslopes prone to landslides. Ecol. Eng. 2017, 106, 609–619. [Google Scholar] [CrossRef]
- Ji, J.; Kokutse, N.; Genet, M.; Fourcaud, T.; Zhang, Z. Effect of spatial variation of tree root characteristics on slope stability. A case study on Black Locust (Robinia pseudoacacia) and Arborvitae (Platycladus orientalis) stands on the Loess Plateau, China. Catena 2012, 92, 139–154. [Google Scholar] [CrossRef]
- He, C.; Jia, S.; Luo, Y.; Hao, Z.; Yin, Q. Spatial Distribution and Species Association of Dominant Tree Species in Huangguan Plot of Qinling Mountains, China. Forests 2022, 13, 866. [Google Scholar] [CrossRef]
- Lozada, C.; Mendoza, C.; Amortegui, J.V. Physical and Numerical Modeling of Clayey Slopes Reinforced with Roots. Int. J. Civ. Eng. 2022, 20, 1115–1128. [Google Scholar] [CrossRef]
- Giadrossich, F.; Cohen, D.; Schwarz, M.; Ganga, A.; Marrosu, R.; Pirastru, M.; Capra, G.F. Large roots dominate the contribution of trees to slope stability. Earth Surf. Process. Landf. 2019, 44, 1602–1609. [Google Scholar] [CrossRef]
- Soethe, N.; Lehmann, J.; Engels, C. Root Morphology and Anchorage of Six Native Tree Species from a Tropical Montane Forest and an Elfin Forest in Ecuador. Plant Soil 2006, 279, 173–185. [Google Scholar] [CrossRef]
- Nicoll, B.C.; Berthier, S.; Achim, A.; Gouskou, K.; Danjon, F.; van Beek, L.P.H. The architecture of Picea sitchensis structural root systems on horizontal and sloping terrain. Trees 2006, 20, 701–712. [Google Scholar] [CrossRef]
- Busgen, M.; Munch, E. Structure and Life of Forest Trees; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1929. [Google Scholar]
- Stokes, A.B.; Mattheck, C.G.A. Variation of wood strength in tree roots. J. Exp. Bot. 1996, 47, 693–699. [Google Scholar] [CrossRef]
- Köstler, J.N.; Brückner, E.; Bibelriether, H. Die Wurzein der Waldbaüme Edn; Verlag Paul Parey: Hamburg, Germany, 1968; p. 280. [Google Scholar]
- Jiang, T.; Li, L.; Xue, L.; Huang, K.; Zhao, J.; Wang, L.; Wan, L.; Ding, H. Study on Synergistic Characteristics of Accumulation Landslides Supported by Arbor Species. Forests 2022, 13, 1610. [Google Scholar] [CrossRef]
- Tsige, D.; Senadheera, S.; Talema, A. Stability Analysis of Plant-Root-Reinforced Shallow Slopes along Mountainous Road Corridors Based on Numerical Modeling. Geosciences 2019, 10, 19. [Google Scholar] [CrossRef]
- Temgoua, A.G.T.; Kokutse, N.K.; Kavazović, Z. Influence of forest stands and root morphologies on hillslope stability. Ecol. Eng. 2016, 95, 622–634. [Google Scholar] [CrossRef]
- Karl, T. Theoretical Soil Mechanics; Wiley: Hoboken, NJ, USA, 1943. [Google Scholar]
- Wang, H.; Wang, P.; Qin, H.; Yue, J.; Zhang, J. Method to Control the Deformation of Anti-Slide Piles in Zhenzilin Landslide. Appl. Sci. 2020, 10, 2831. [Google Scholar] [CrossRef]
- Li, H.; Du, Q.w. Stabilizing a post-landslide loess slope with anti-slide piles in Yan’an, China. Environ. Earth Sci. 2021, 80, 739. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Xu, M. The Determination of Rational Spacing of Anti-Slide Piles and Soil Pressure on Pile Sheet Based on Soil Arching Effect. Geotech. Geol. Eng. 2022, 40, 2857–2866. [Google Scholar] [CrossRef]
- Qiao, S.; Xu, P.; Teng, J.; Sun, X. Numerical Study of Optimal Parameters on the High Filling Embankment Landslide Reinforced by the Portal Anti-Slide Pile. KSCE J. Civ. Eng. 2020, 24, 1460–1475. [Google Scholar] [CrossRef]
- Chen, G.; Zou, L.; Wang, Q.; Zhang, G. Pile-Spacing Calculation of Anti-Slide Pile Based on Soil Arching Effect. Adv. Civ. Eng. 2020, 2020, 7149379. [Google Scholar] [CrossRef]
- Bosscher, P.J.; Gray, D.H.b. Soil Arching in Sandy Slopes. J. Geotech. Geoenviron. Eng. 1986, 112, 626–645. [Google Scholar] [CrossRef]
- Reichenbach, P.; Busca, C.; Mondini, A.C.; Rossi, M. The influence of land use change on landslide susceptibility zonation: The Briga catchment test site (Messina, Italy). Environ. Manag. 2014, 54, 1372–1384. [Google Scholar] [CrossRef]
- Mitchell, S.J. Wind as a natural disturbance agent in forests: A synthesis. Forestry 2013, 86, 147–157. [Google Scholar] [CrossRef]
- Stokes, A. Strain distribution during anchorage failure of Pinus pinaster Ait. at different ages and tree growth response to wind-induced root movement. Plant Soil 1999, 217, 17–27. [Google Scholar] [CrossRef]
- Zhuang, Y.; Xing, A.; Jiang, Y.; Sun, Q.; Yan, J.; Zhang, Y. Typhoon, rainfall and trees jointly cause landslides in coastal regions. Eng. Geol. 2022, 298, 106561. [Google Scholar] [CrossRef]
- Reneau, S.L.; Dietrich, W.E. Erosion rates in the southern oregon coast range: Evidence for an equilibrium between hillslope erosion and sediment yield. Earth Surf. Process. Landf. 1991, 16, 307–322. [Google Scholar] [CrossRef]
- Milledge, D.G.; Bellugi, D.; McKean, J.A.; Densmore, A.L.; Dietrich, W.E. A multidimensional stability model for predicting shallow landslide size and shape across landscapes. J. Geophys. Res. Earth Surf. 2014, 119, 2481–2504. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.W.; Kang, Y.; So, P.S.; Ng, C.W.W.; Wong, M.H. Arbuscular mycorrhizal fungi increase the proportion of cellulose and hemicellulose in the root stele of vetiver grass. Plant Soil 2018, 425, 309–319. [Google Scholar] [CrossRef]
- Stokes, A.; Douglas, G.B.; Fourcaud, T.; Giadrossich, F.; Gillies, C.; Hubble, T.; Kim, J.H.; Loades, K.W.; Mao, Z.; McIvor, I.R.; et al. Ecological mitigation of hillslope instability: Ten key issues facing researchers and practitioners. Plant Soil 2014, 377, 1–23. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).