A Comparative Study of Shallow Machine Learning Models and Deep Learning Models for Landslide Susceptibility Assessment Based on Imbalanced Data
Abstract
1. Introduction
2. Materials
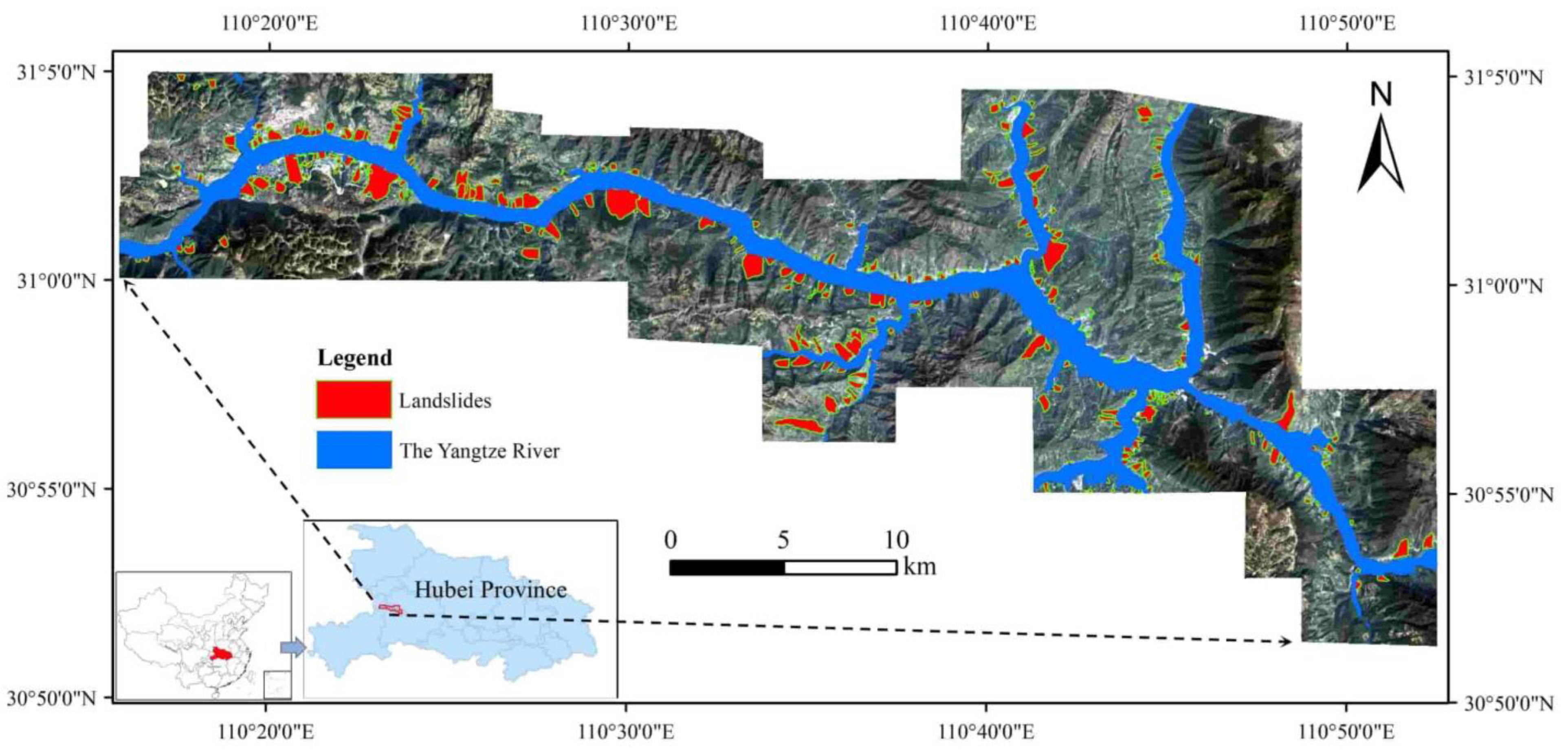
2.1. Study Area
2.2. Data Source
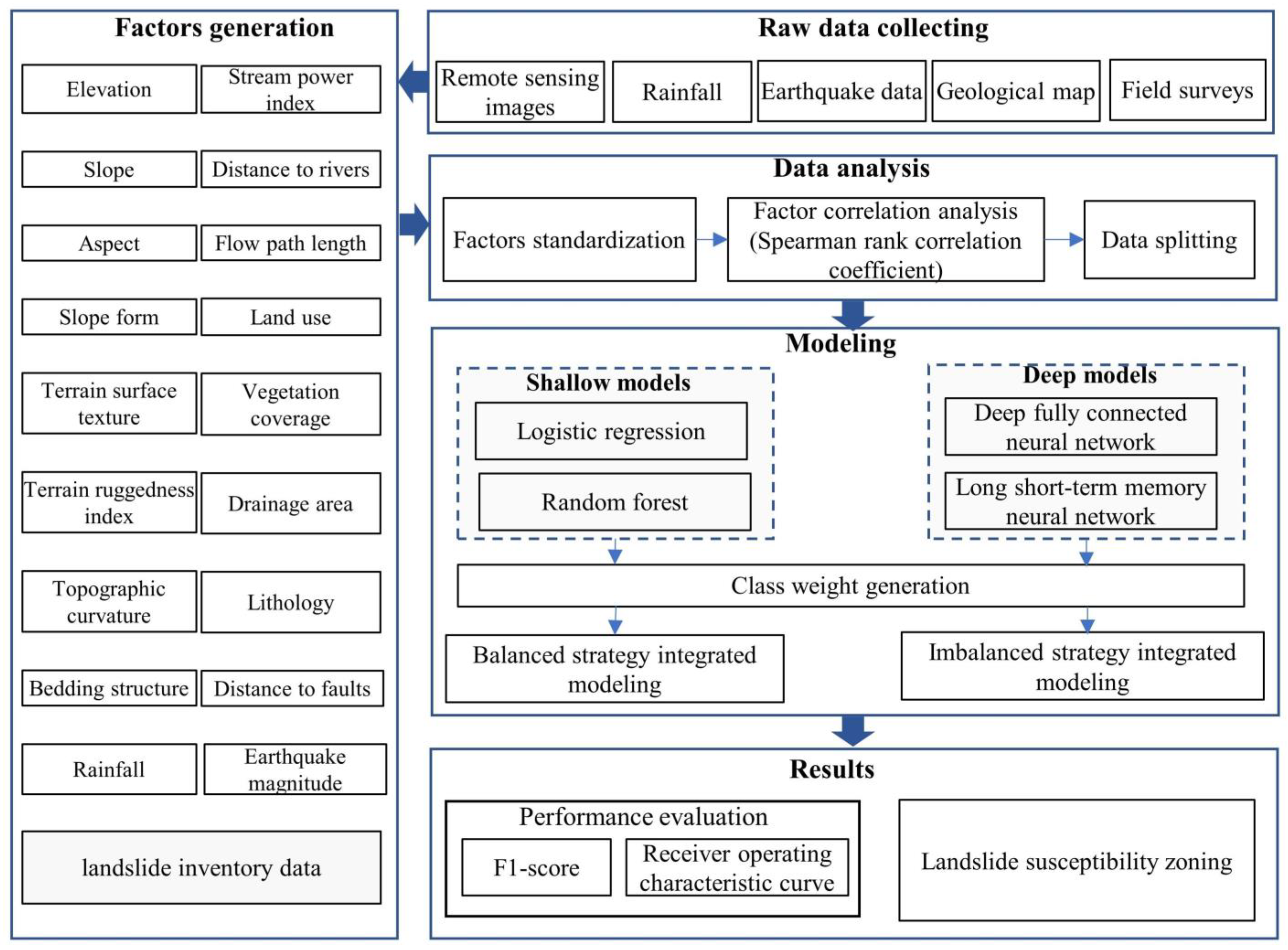
3. Methodology
3.1. Landslide Susceptibility Models
3.1.1. Logistic Regression
3.1.2. Random Forest
- (1)
- Random sample selection. Assume that the total number of samples is and there are decision trees in RF; to create subset , select samples from samples randomly; a total of sample subsets are constructed.
- (2)
- Random feature selection. Assume that the total number of features is , and features are selected from the F to form a feature subset . The optimal feature is generated from the feature subset when the decision tree splits each time.
- (3)
- Classifier voting. decision trees produce a total number of classification results. The class with the highest votes is used as the final prediction class.
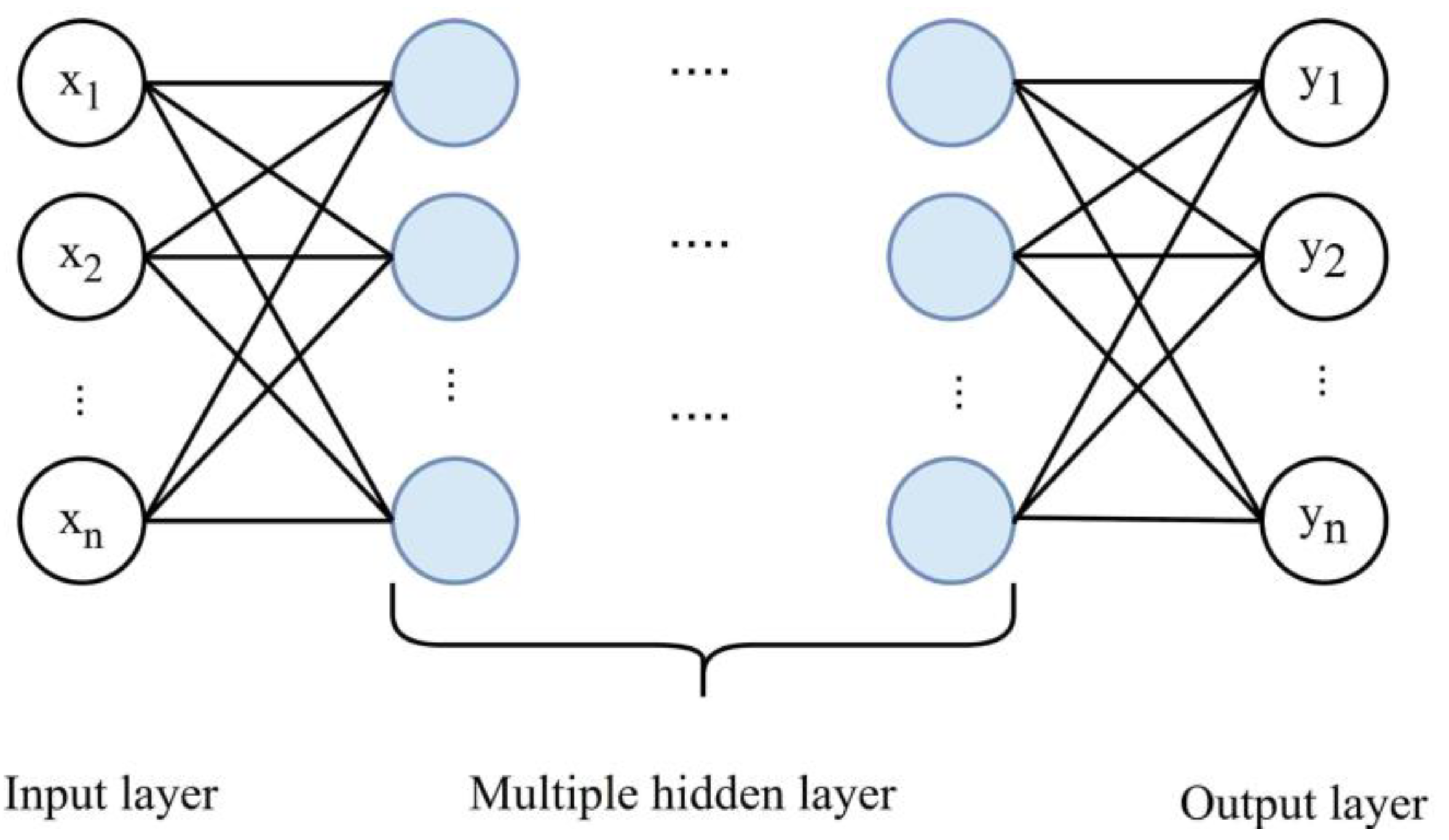
3.1.3. Deep Fully Connected Neural Network
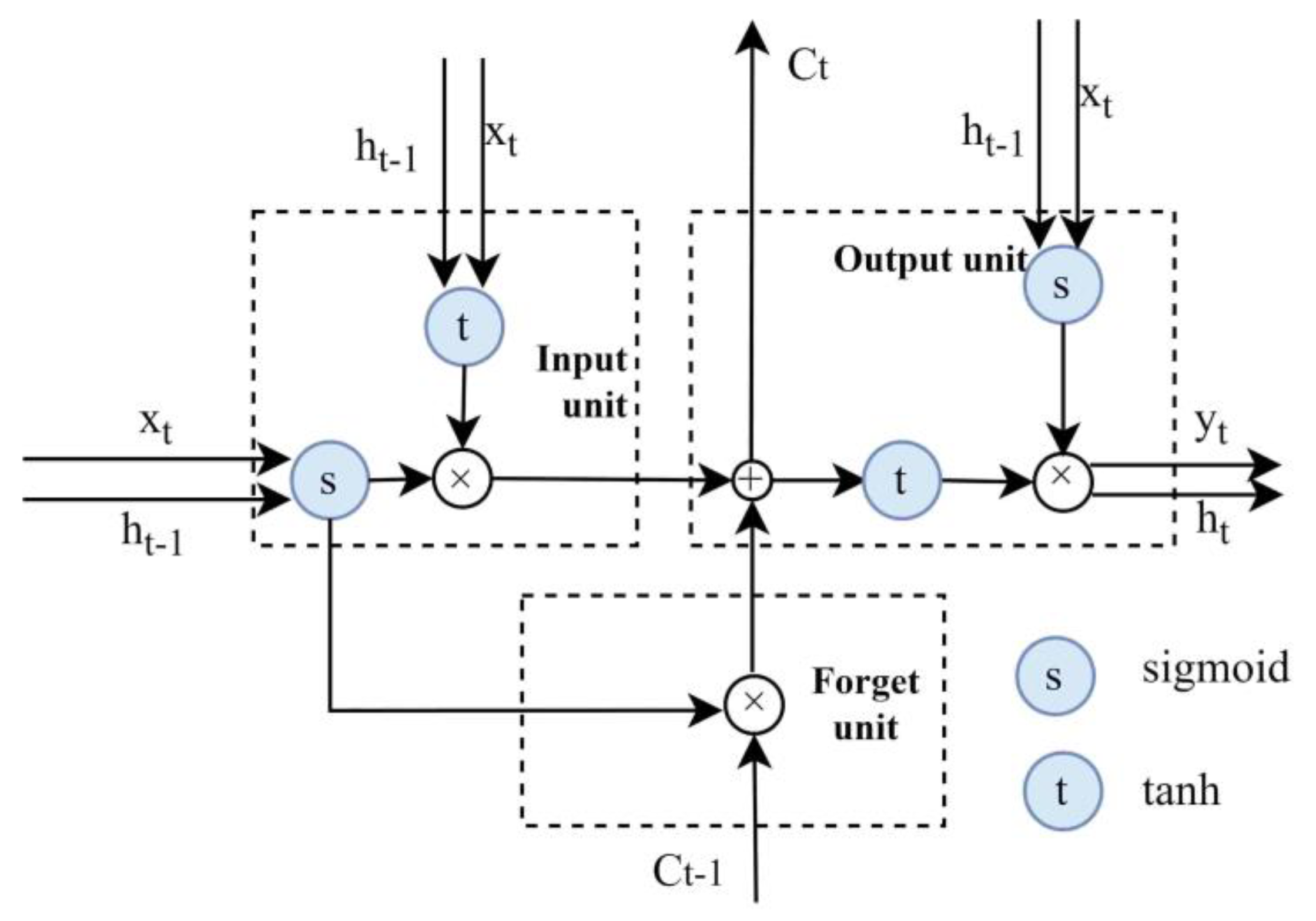
3.1.4. Long Short-Term Memory Neural Network
3.2. Landslide Influence Factors
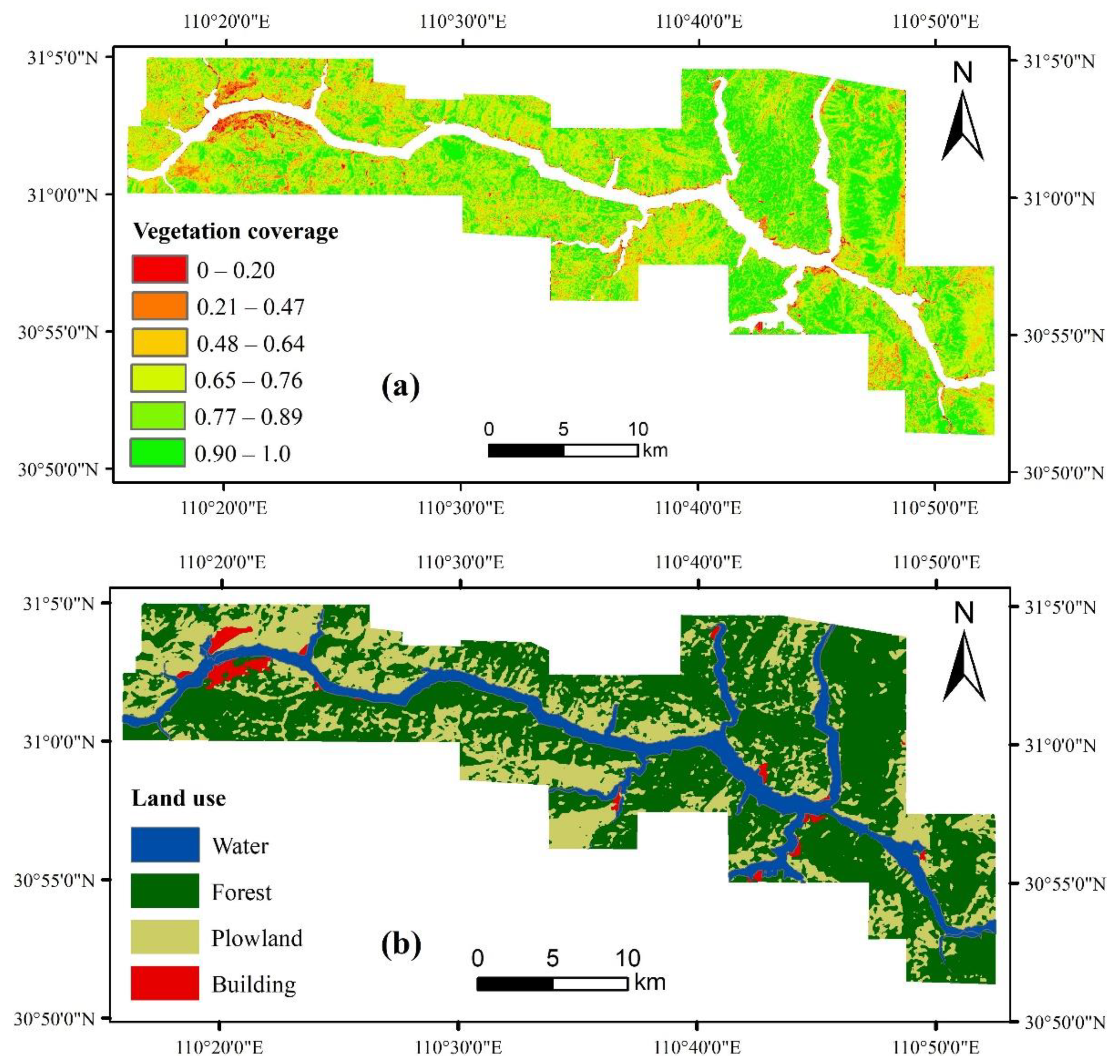
- Land cover includes land use and vegetation coverage in this study. Land use is an indicator of the intensity of human activity. In regions where human activities are violent, slope instability rises. Land uses are exacted by pixel classifications from Landsat 8 OLI images and they are then validated by a public dataset [55]. The overall validation accuracy of land use is 89.8%. To make the land use results more reliable, visual interpretation is used to correct misclassifications. Plant roots hold soil and rock in place, and absorb water in the soil at the same time. It usually exerts a positive effect on landslides [56]. The vegetation coverage is computed based on the dimidiate pixel model and normalized difference vegetation index (NDVI).
- Topography is an essential condition to control the development of landslides [56]. The slope, aspect, slope form, terrain surface texture, terrain ruggedness index, and topographic curvature are derived from the elevation. It must be noted that the bedding structures are a combination of topographic conditions and geological conditions. The bedding structures are classified into six types according to the previous literature [57].
- Hydrological conditions are also an important factor influencing the occurrence of landslides in the study area [58]. The rivers erode the riverbed on both sides, making the slope unstable. Thus, the landslides in the study area are mainly distributed on both sides of the river. Drainage area, flow path length, stream power index, and distance to rivers are used for LSA modeling.
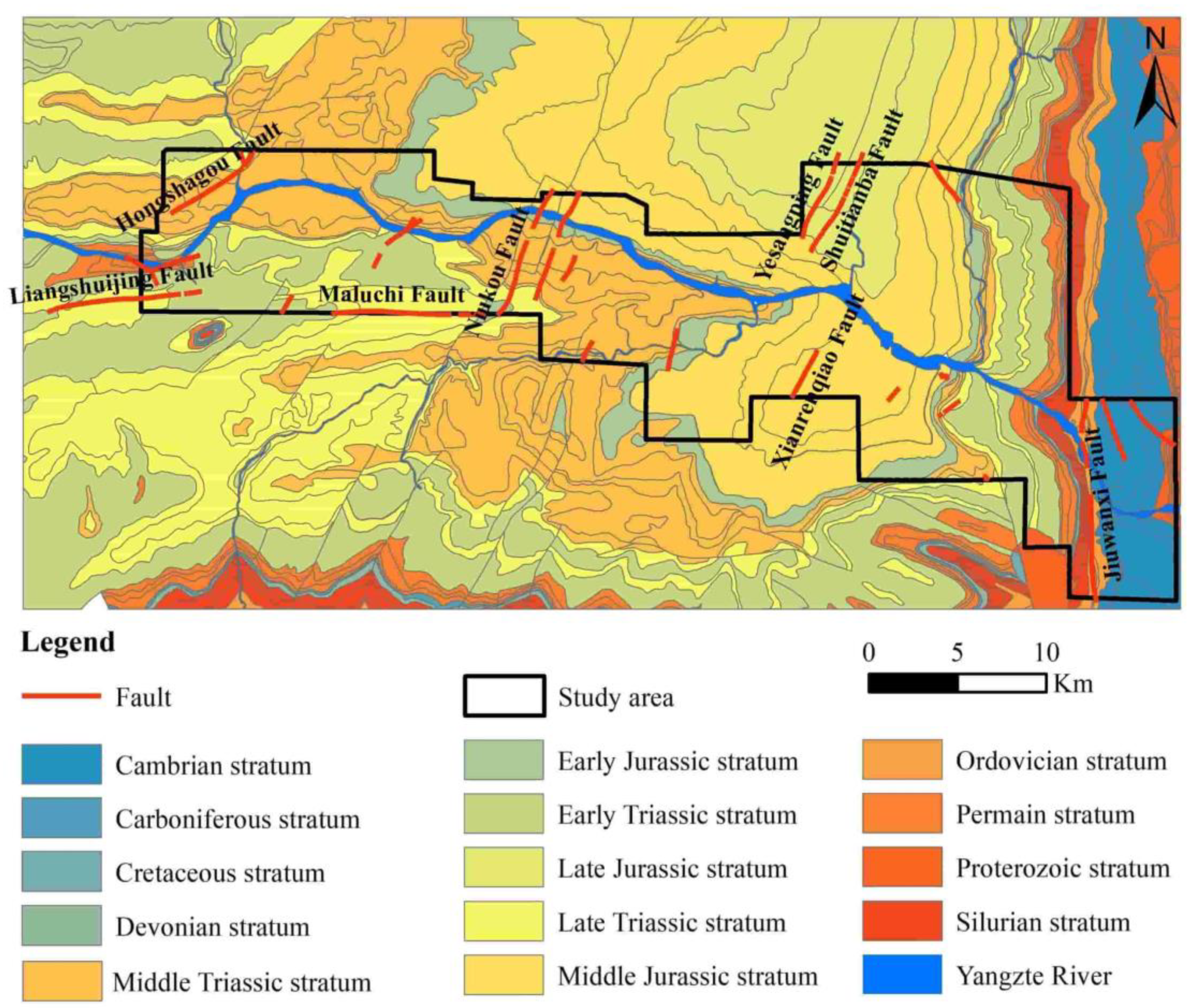
- Geological conditions play a decisive role in the development of landslides and are important internal controlling factors. The faults destroy rock formations and affect their stability [59]. The closer to the faults, the greater impact on the rock formation. The geological factors including the lithology and the faults are mainly exacted from geological maps by vectorization.
- Earthquakes squeeze and stretch the formation, causing huge deformations of the formation and resulting in drastic changes in the geological environment, and finally affect the stability of the slope [60]. The earthquake data were collected from earthquake monitoring sites and then imported into GIS software for further processing.
- Rainfall affects the water content in the soil and it is one of the main factors that trigger landslides [61,62]. Short-term heavy rainfall may lead to soil erosion, an increase in surface runoff, and a reduction in the soil’s and rock’s absorption capacity. Simultaneously, the rainfall causes fluctuations in reservoir water levels, and the static and dynamic water pressures vary accordingly, aggravating the slope further.
3.3. Spearman Rank Correlation Coefficient
3.4. Performance Evaluation
- F1-score
- 2.
- Receiver operating characteristic curve
3.5. Assessment Units
3.6. Factors Standardization
3.7. Class Weighted Strategy
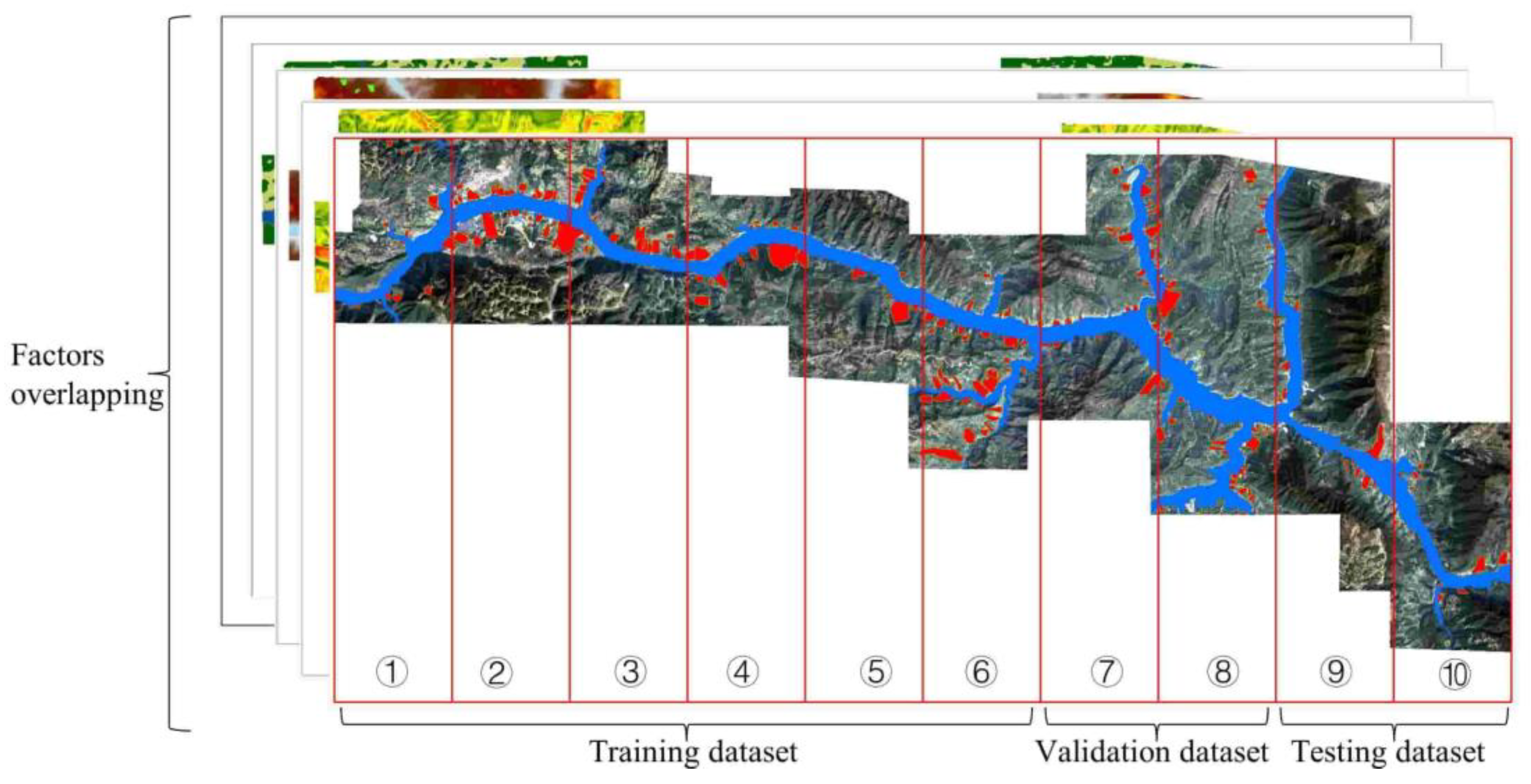
3.8. Experiment Setup
4. Results
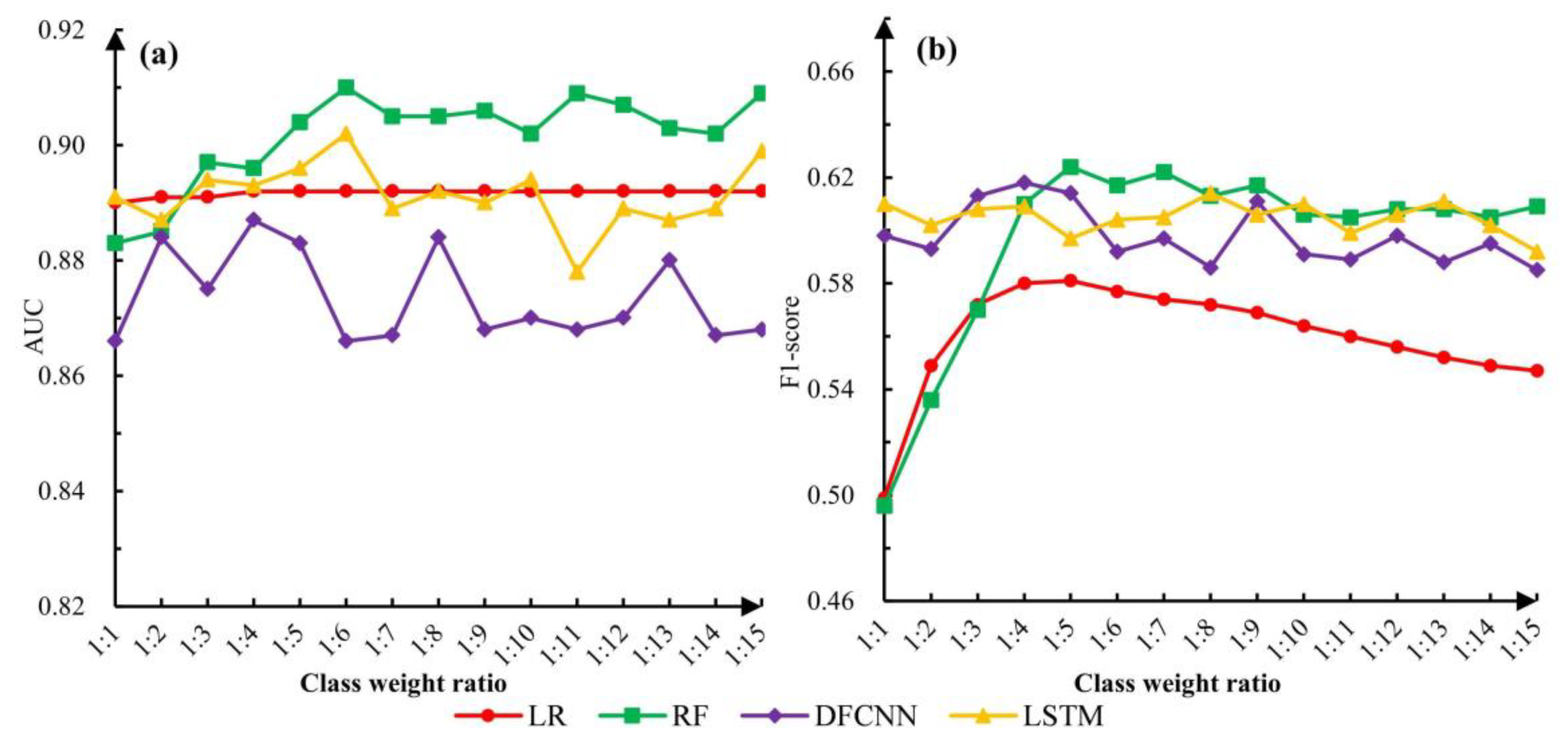
4.1. Performances of Different Class Weights
4.2. Correlations of Influence Factors
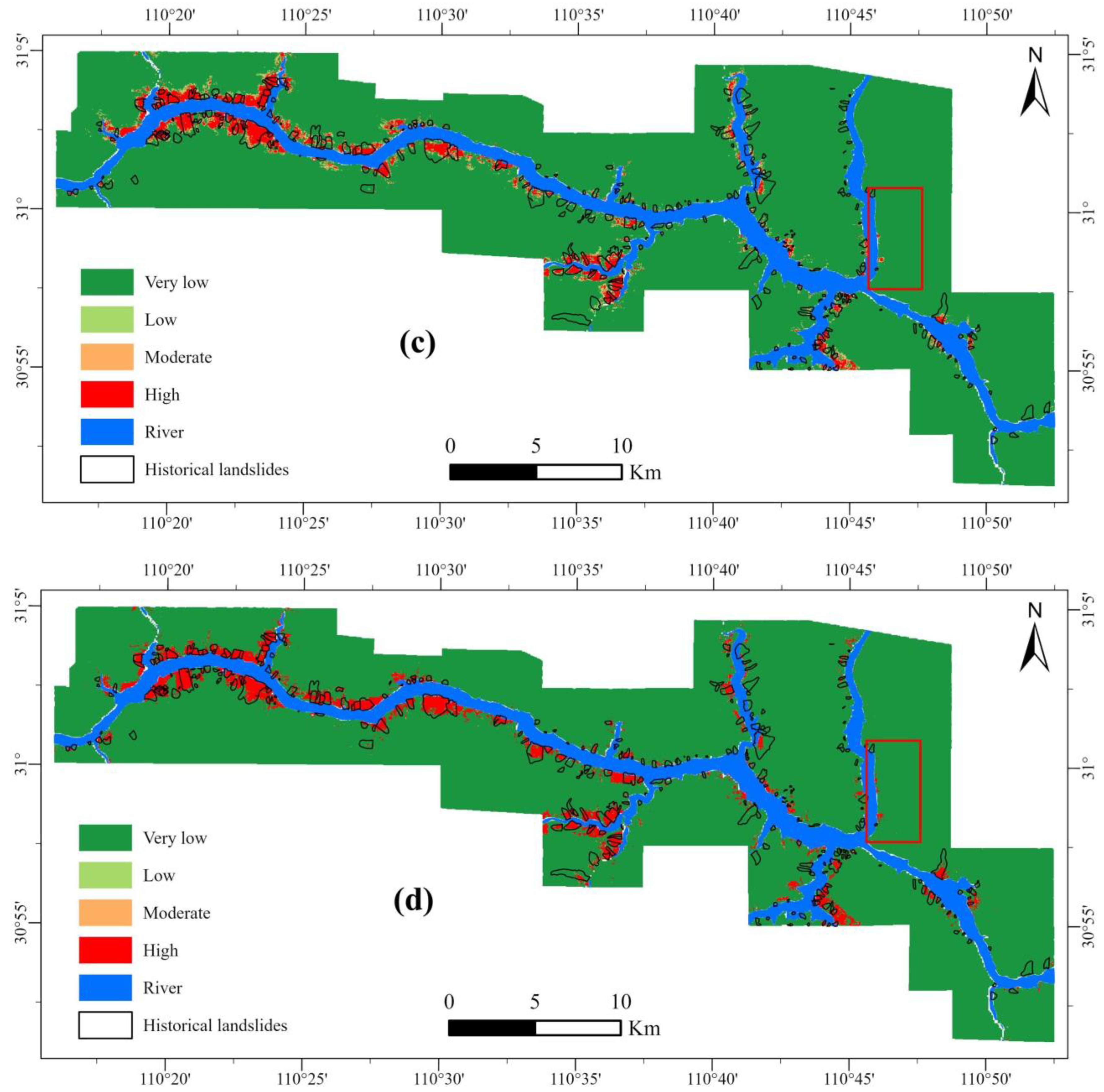
4.3. Landslide Susceptibility Results
5. Discussion
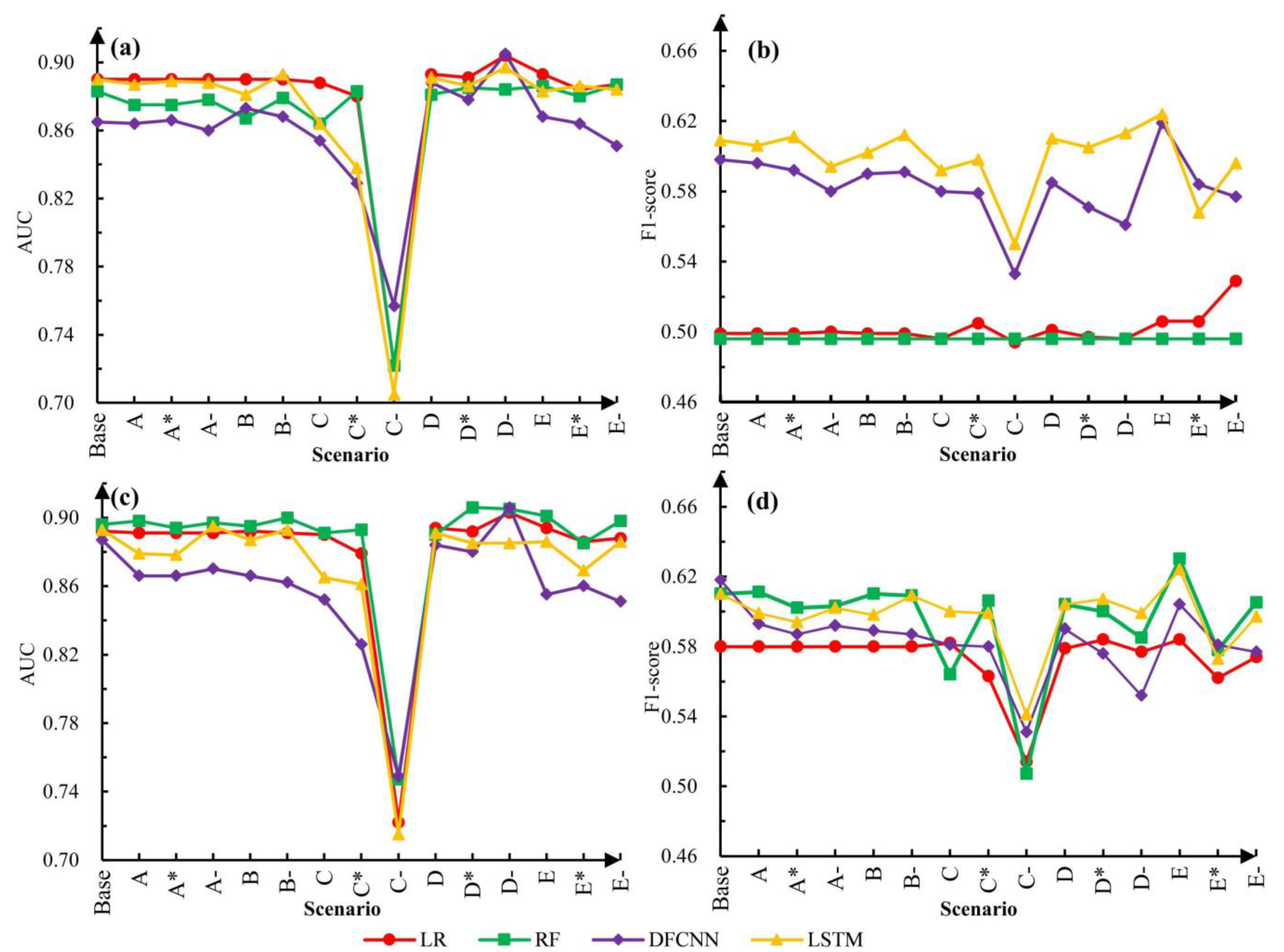
5.1. Comparison of Performances
5.2. Susceptibility Spatial Patterns
5.3. Influences of Class Weights
5.4. Model Evaluation and Factors Processing
5.5. Training Time Consumed
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Argyriou, A.V.; Teeuw, R.M.; Rust, D.; Sarris, A. GIS multi-criteria decision analysis for assessment and mapping of neotectonic landscape deformation: A case study from Crete. Geomorphology 2016, 253, 262–274. [Google Scholar] [CrossRef]
- Vahidnia, M.H.; Alesheikh, A.A.; Alimohammadi, A.; Hosseinali, F. A GIS-based neuro-fuzzy procedure for integrating knowledge and data in landslide susceptibility mapping. Comput. Geosci. 2010, 36, 1101–1114. [Google Scholar] [CrossRef]
- Cabral, V.C.; Reis, F.A.G.V. Assessment of Shallow Landslides Susceptibility Using SHALSTAB and SINMAP at Serra Do Mar, Brazil. In Understanding and Reducing Landslide Disaster Risk; Guzzetti, F., Mihalić Arbanas, S., Reichenbach, P., Sassa, K., Bobrowsky, P.T., Takara, K., Eds.; Springer: Cham, Switzerland, 2021; Volume 2, pp. 257–265. [Google Scholar] [CrossRef]
- Fernandes, N.F.; Guimarães, R.F.; Gomes, R.A.T.; Vieira, B.C.; Montgomery, D.R.; Greenberg, H. Topographic controls of landslides in Rio de Janeiro: Field evidence and modeling. Catena 2004, 55, 163–181. [Google Scholar] [CrossRef]
- Ciurleo, M.; Cascini, L.; Calvello, M. A comparison of statistical and deterministic methods for shallow landslide susceptibility zoning in clayey soils. Eng. Geol. 2017, 223, 71–81. [Google Scholar] [CrossRef]
- Lin, W.; Yin, K.; Wang, N.; Xu, Y.; Guo, Z.; Li, Y. Landslide hazard assessment of rainfall-induced landslide based on the CF-SINMAP model: A case study from Wuling Mountain in Hunan Province, China. Nat. Hazards 2021, 106, 679–700. [Google Scholar] [CrossRef]
- Melo, C.M.; Kobiyama, M.; Michel, G.P.; de Brito, M.M. The Relevance of Geotechnical-Unit Characterization for Landslide-Susceptibility Mapping with SHALSTAB. GeoHazards 2021, 2, 383–397. [Google Scholar] [CrossRef]
- Chen, W.; Li, W.; Chai, H.; Hou, E.; Li, X.; Ding, X. GIS-based landslide susceptibility mapping using analytical hierarchy process (AHP) and certainty factor (CF) models for the Baozhong region of Baoji City, China. Environ. Earth Sci. 2016, 75, 1–14. [Google Scholar] [CrossRef]
- Vilasan, R.T.; Kapse, V.S. Evaluation of the prediction capability of AHP and F-AHP methods in flood susceptibility mapping of Ernakulam district (India). Nat. Hazards 2022, 112, 1767–1793. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Wang, L.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J. A comparative study of landslide susceptibility maps using logistic regression, frequency ratio, decision tree, weights of evidence and artificial neural network. Geosci. J. 2016, 20, 117–136. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Niu, R.; Peng, L. Integration of Information Theory, K-Means Cluster Analysis and the Logistic Regression Model for Landslide Susceptibility Mapping in the Three Gorges Area, China. Remote Sens. 2017, 9, 938. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, W.; Qin, Y.; Fu, X. Geoinformation-based landslide susceptibility mapping in subtropical area. Sci. Rep. 2021, 11, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Wang, Y.; Niu, R.; Hu, Y. A Combination of Geographically Weighted Regression, Particle Swarm Optimization and Support Vector Machine for Landslide Susceptibility Mapping: A Case Study at Wanzhou in the Three Gorges Area, China. Int. J. Environ. Res. Public Health 2016, 13, 487. [Google Scholar] [CrossRef] [PubMed]
- Kainthura, P.; Sharma, N. Machine learning driven landslide susceptibility prediction for the Uttarkashi region of Uttarakhand in India. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2021, 16, 570–583. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Zhang, Y.; Xu, J.; Zhang, W. Landslide susceptibility mapping using hybrid random forest with GeoDetector and RFE for factor optimization. Geosci. Front. 2021, 12, 101211. [Google Scholar] [CrossRef]
- Dou, J.; Yamagishi, H.; Pourghasemi, H.R.; Yunus, A.P.; Song, X.; Xu, Y.; Zhu, Z. An integrated artificial neural network model for the landslide susceptibility assessment of Osado Island, Japan. Nat. Hazards 2015, 78, 1749–1776. [Google Scholar] [CrossRef]
- Pham, B.T.; Van Dao, D.; Acharya, T.D.; Van Phong, T.; Costache, R.; Van Le, H.; Nguyen, H.B.T.; Prakash, I. Performance assessment of artificial neural network using chi-square and backward elimination feature selection methods for landslide susceptibility analysis. Environ. Earth Sci. 2021, 80, 686. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Li, Z.; Zhang, H.; Zhang, W. An interpretable model for the susceptibility of rainfall-induced shallow landslides based on SHAP and XGBoost. Geocarto Int. 2022, 1–32. [Google Scholar] [CrossRef]
- Saha, S.; Roy, J.; Pradhan, B.; Hembram, T.K. Hybrid ensemble machine learning approaches for landslide susceptibility mapping using different sampling ratios at East Sikkim Himalayan, India. Adv. Space Res. 2021, 68, 2819–2840. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.; Liem, N.V.; Trinh, P.T. Comparing the prediction performance of a Deep Learning Neural Network model with conventional machine learning models in landslide susceptibility assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- Sun, D.; Gu, Q.; Wen, H.; Shi, S.; Mi, C.; Zhang, F. A Hybrid Landslide Warning Model Coupling Susceptibility Zoning and Precipitation. Forests 2022, 13, 827. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, S.; Wang, L.; Samui, P.; Chwała, M.; He, Y. Landslide Susceptibility Research Combining Qualitative Analysis and Quantitative Evaluation: A Case Study of Yunyang County in Chongqing, China. Forests 2022, 13, 1055. [Google Scholar] [CrossRef]
- Chai, J.; Zeng, H.; Li, A.; Ngai, E.W.T. Deep learning in computer vision: A critical review of emerging techniques and application scenarios. Mach. Learn. Appl. 2021, 6, 100134. [Google Scholar] [CrossRef]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A Survey of the Usages of Deep Learning for Natural Language Processing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 604–624. [Google Scholar] [CrossRef]
- Grigorescu, S.; Trasnea, B.; Cocias, T.; Macesanu, G. A survey of deep learning techniques for autonomous driving. J. Field Robot. 2020, 37, 362–386. [Google Scholar] [CrossRef]
- Esteva, A.; Chou, K.; Yeung, S.; Naik, N.; Madani, A.; Mottaghi, A.; Liu, Y.; Topol, E.; Dean, J.; Socher, R. Deep learning-enabled medical computer vision. NPJ Digit. Med. 2021, 4, 5. [Google Scholar] [CrossRef] [PubMed]
- Bera, S.; Upadhyay, V.K.; Guru, B.; Oommen, T. Landslide inventory and susceptibility models considering the landslide typology using deep learning: Himalayas, India. Nat. Hazards 2021, 108, 1257–1289. [Google Scholar] [CrossRef]
- Thi Ngo, P.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Luo, H.; He, J.; Cheung, R.W.M. AI-powered landslide susceptibility assessment in Hong Kong. Eng. Geol. 2021, 288, 106103. [Google Scholar] [CrossRef]
- Wang, W.; He, Z.; Han, Z.; Li, Y.; Dou, J.; Huang, J. Mapping the susceptibility to landslides based on the deep belief network: A case study in Sichuan Province, China. Nat. Hazards 2020, 103, 3239–3261. [Google Scholar] [CrossRef]
- Liu, R.; Yang, X.; Xu, C.; Wei, L.; Zeng, X. Comparative Study of Convolutional Neural Network and Conventional Machine Learning Methods for Landslide Susceptibility Mapping. Remote Sens. 2022, 14, 321. [Google Scholar] [CrossRef]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep learning-based landslide susceptibility mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.; Zhang, Z.; Zhang, W.; Jia, H.; Zhang, J. Landslide susceptibility mapping using multiscale sampling strategy and convolutional neural network: A case study in Jiuzhaigou region. Catena 2020, 195, 104851. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Habumugisha, J.M.; Chen, N.; Rahman, M.; Islam, M.M.; Ahmad, H.; Elbeltagi, A.; Sharma, G.; Liza, S.N.; Dewan, A.M. Landslide Susceptibility Mapping with Deep Learning Algorithms. Sustainability 2022, 14, 1734. [Google Scholar] [CrossRef]
- Wu, B.; Qiu, W.; Jia, J.; Liu, N. Landslide Susceptibility Modeling Using Bagging-Based Positive-Unlabeled Learning. IEEE Geosci. Remote Sens. Lett. 2021, 18, 766–770. [Google Scholar] [CrossRef]
- Yao, J.; Qin, S.; Qiao, S.; Liu, X.; Zhang, L.; Chen, J. Application of a two-step sampling strategy based on deep neural network for landslide susceptibility mapping. Bull. Eng. Geol. Environ. 2022, 81, 148. [Google Scholar] [CrossRef]
- Zhang, H.; Song, Y.; Xu, S.; He, Y.; Li, Z.; Yu, X.; Liang, Y.; Wu, W.; Wang, Y. Combining a class-weighted algorithm and machine learning models in landslide susceptibility mapping: A case study of Wanzhou section of the Three Gorges Reservoir, China. Comput. Geosci. 2022, 158, 104966. [Google Scholar] [CrossRef]
- Süzen, M.L.; Kaya, B.Ş. Evaluation of environmental parameters in logistic regression models for landslide susceptibility mapping. Int. J. Digit. Earth 2012, 5, 338–355. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, X.; Peng, L.; Niu, R. Landslide susceptibility mapping based on global and local logistic regression models in Three Gorges Reservoir area, China. Environ. Earth Sci. 2016, 75, 958. [Google Scholar] [CrossRef]
- Akinci, H.; Zeybek, M. Comparing classical statistic and machine learning models in landslide susceptibility mapping in Ardanuc (Artvin), Turkey. Nat. Hazards 2021, 108, 1515–1543. [Google Scholar] [CrossRef]
- Mira, J.; Sandoval, F. From Natural to Artificial Neural Computation: International Workshop on Artificial Neural Networks, Malaga-Torremolinos, Spain, 7–9 June 1995: Proceedings; Springer-Verlag: New York, USA, 1995; Volume 930, pp. 195–201. [Google Scholar]
- Chen, W.; Sun, Z.; Zhao, X.; Lei, X.; Shirzadi, A.; Shahabi, H. Performance Evaluation and Comparison of Bivariate Statistical-Based Artificial Intelligence Algorithms for Spatial Prediction of Landslides. ISPRS Int. J. Geo-Inf. 2020, 9, 696. [Google Scholar] [CrossRef]
- Akinci, H.; Kilicoglu, C.; Dogan, S. Random Forest-Based Landslide Susceptibility Mapping in Coastal Regions of Artvin, Turkey. ISPRS Int. J. Geo-Inf. 2020, 9, 553. [Google Scholar] [CrossRef]
- Akinci, H. Assessment of rainfall-induced landslide susceptibility in Artvin, Turkey using machine learning techniques. J. Afr. Earth Sci. 2022, 191, 104535. [Google Scholar] [CrossRef]
- Li, J.; Cheng, J.; Shi, J.; Huang, F. Brief Introduction of Back Propagation (BP) Neural Network Algorithm and Its Improvement. In Advances in Intelligent and Soft Computing, Proceedings of the Advances in Computer Science and Information Engineering; Jin, D., Lin, S., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2012; Volume 169, pp. 553–558. [Google Scholar]
- Wang, S.-C. Artificial Neural Network. In Interdisciplinary Computing in Java Programming; Wang, S.-C., Ed.; The Springer International Series in Engineering and Computer Science; Springer US: Boston, MA, USA, 2003; Volume 743, pp. 81–100. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; ICML: Haifa, Israel, 2010; pp. 807–814. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Moosavi, V.; Niazi, Y. Development of hybrid wavelet packet-statistical models (WP-SM) for landslide susceptibility mapping. Landslides 2016, 13, 97–114. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, W.; Wang, Q.; Wu, Y.; Yang, B. A comparative study of statistical index and certainty factor models in landslide susceptibility mapping: A case study for the Shangzhou District, Shaanxi Province, China. Arab. J. Geosci. 2015, 8, 9079–9088. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Bourenane, H.; Bouhadad, Y.; Guettouche, M.S.; Braham, M. GIS-based landslide susceptibility zonation using bivariate statistical and expert approaches in the city of Constantine (Northeast Algeria). Bull. Eng. Geol. Environ. 2015, 74, 337–355. [Google Scholar] [CrossRef]
- Peng, L.; Niu, R.; Huang, B.; Wu, X.; Zhao, Y.; Ye, R. Landslide susceptibility mapping based on rough set theory and support vector machines: A case of the Three Gorges area, China. Geomorphology 2014, 204, 287–301. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; McDonald, E.V.; Vitek, J.D. A comparison of logistic regression-based models of susceptibility to landslides in western Colorado, USA. Landslides 2014, 11, 247–262. [Google Scholar] [CrossRef]
- Tang, C.; Ma, G.; Chang, M.; Li, W.; Zhang, D.; Jia, T.; Zhou, Z. Landslides triggered by the 20 April 2013 Lushan earthquake, Sichuan Province, China. Eng. Geol. 2015, 187, 45–55. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Integration of convolutional neural network and conventional machine learning classifiers for landslide susceptibility mapping. Comput. Geosci. 2020, 139, 104470. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. Rainfall thresholds for the possible landslide occurrence in Sicily (Southern Italy) based on the automatic reconstruction of rainfall events. Landslides 2016, 13, 165–172. [Google Scholar] [CrossRef]
- Fallah-Zazuli, M.; Vafaeinejad, A.; Alesheykh, A.A.; Modiri, M.; Aghamohammadi, H. Mapping landslide susceptibility in the Zagros Mountains, Iran: A comparative study of different data mining models. Earth Sci. Inform. 2019, 12, 615–628. [Google Scholar] [CrossRef]
- Rodgers, J.L.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Gauthier, T. Detecting Trends Using Spearman’s Rank Correlation Coefficient. Environ. Forensics 2001, 2, 359–362. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, K.; Song, Y.; Jiang, W.; Zhou, J. Study on landslide susceptibility mapping based on rock–soil characteristic factors. Sci. Rep. 2021, 11, 15476. [Google Scholar] [CrossRef] [PubMed]
- Flach, P.; Kull, M. Precision-recall-gain curves: PR analysis done right. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; Volume 1, pp. 838–846. [Google Scholar]
- Pontius, R.G.; Parmentier, B. Recommendations for using the relative operating characteristic (ROC). Landsc. Ecol. 2014, 29, 367–382. [Google Scholar] [CrossRef]
- Erener, A.; Düzgün, H.S.B. Landslide susceptibility assessment: What are the effects of mapping unit and mapping method? Environ. Earth Sci. 2012, 66, 859–877. [Google Scholar] [CrossRef]
- Hussin, H.Y.; Zumpano, V.; Reichenbach, P.; Sterlacchini, S.; Micu, M.; van Westen, C.; Bălteanu, D. Different landslide sampling strategies in a grid-based bi-variate statistical susceptibility model. Geomorphology 2016, 253, 508–523. [Google Scholar] [CrossRef]
- Spiegel, M.R.; Schiller, J.J.; Srinivasan, R.A. Schaum’s Outline of Probability and Statistics, 4th ed.; McGraw-Hill Education: Los Angeles, CA, USA, 2013; pp. 75–107. [Google Scholar]
- Wang, H.; Zhang, L.; Yin, K.; Luo, H.; Li, J. Landslide identification using machine learning. Geosci. Front. 2021, 12, 351–364. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhou, Y.; Wang, F.; Wang, S.; Wang, Z.; Ji, J.; Wang, J.; Zou, W.; You, D.; Qin, G. A Novel Intelligent Method Based on the Gaussian Heatmap Sampling Technique and Convolutional Neural Network for Landslide Susceptibility Mapping. Remote Sens. 2022, 14, 2866. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Duan, G.; Peng, L. Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China. Remote Sens. 2021, 13, 238. [Google Scholar] [CrossRef]
- Wang, Y.; Song, C.; Lin, Q.; Li, J. Occurrence probability assessment of earthquake-triggered landslides with Newmark displacement values and logistic regression: The Wenchuan earthquake, China. Geomorphology 2016, 258, 108–119. [Google Scholar] [CrossRef]
- Pineda, M.C.; Viloria, J.; Martínez-Casasnovas, J.A. Landslides susceptibility change over time according to terrain conditions in a mountain area of the tropic region. Environ. Monit. Assess. 2016, 188, 255. [Google Scholar] [CrossRef]
- Hua, Y.; Wang, X.; Li, Y.; Xu, P.; Xia, W. Dynamic development of landslide susceptibility based on slope unit and deep neural networks. Landslides 2021, 18, 281–302. [Google Scholar] [CrossRef]
- Dao, D.V.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Phong, T.V.; Ly, H.; Le, T.; Trinh, P.T.; et al. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. Catena 2020, 188, 104451. [Google Scholar] [CrossRef]


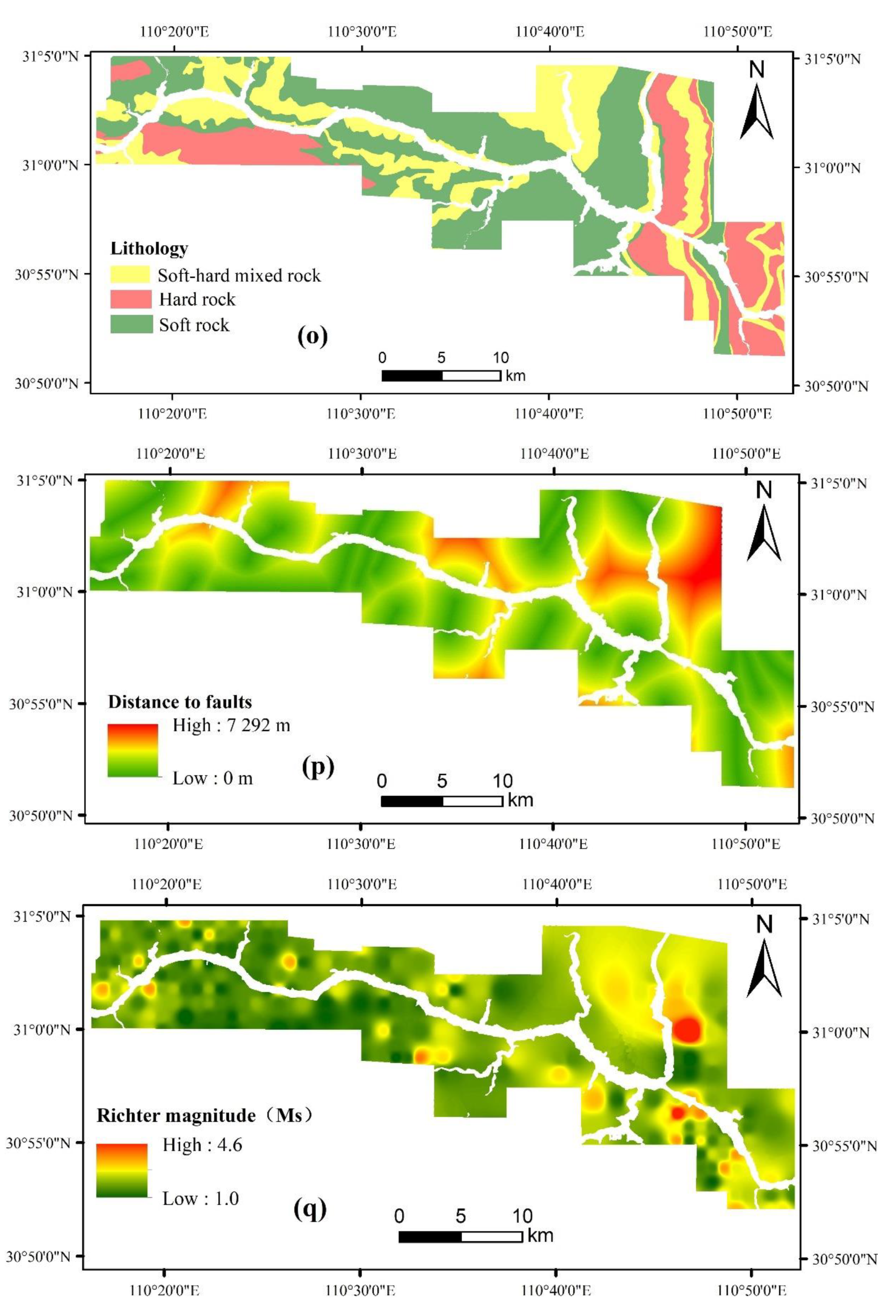







| Data Source | Type | Exaction Tools | Variable Type | Influence Factor |
|---|---|---|---|---|
| Landsat images | Land cover | Preprocessing, vegetation coverage estimation based on dimidiate pixel models, and implemented using python in ArcGIS | Continuous | Vegetation coverage |
| Preprocessing, pixel classification in QGIS | Discrete | Land use | ||
| DEM | Topography | Direct utilization | Continuous | Elevation |
| Model calculation based on the terrain analysis tool of GDAL | Continuous | Slope | ||
| Model calculation based on the terrain analysis tool of GDAL | Continuous | Aspect | ||
| Model calculation using curvature tools of SAGA | Discrete | Slope form | ||
| Model calculation using the terrain analysis tool of SAGA | Continuous | Terrain surface texture | ||
| Model calculation using the terrain analysis tool of SAGA | Continuous | Terrain ruggedness index | ||
| Model calculation using curvature tools of SAGA | Continuous | Topographic curvature | ||
| Vectorization, rasterization, and calculation based on slope and aspect in QGIS | Discrete | Bedding structure | ||
| DEM Landsat image | Hydrological | Model calculation using terrain analysis—hydrology tool of SAGA | Continuous | Drainage area |
| Model calculation using terrain analysis—hydrology tool of SAGA | Continuous | Flow path length | ||
| Model calculation using terrain analysis—hydrology tool of SAGA | Continuous | Stream power index | ||
| Model calculation based on proximity (Raster distance) tool of QGIS | Continuous | Distance to rivers | ||
| Geological map | Geological | Vectorization, rasterization, and reclassifying in QGIS | Discrete | Lithology |
| Vectorization, rasterization, and model calculation based on the proximity (raster distance) tool of QGIS | Continuous | Distance to faults | ||
| Earthquake monitoring sites | Earthquake | Model calculation using TIN interpolation in QGIS | Continuous | Earthquake magnitude |
| Rainfall data | Rainfall | Direct utilization | Continuous | Rainfall |
| Scenario | Influence Factors Removed |
|---|---|
| Base | All factors are used |
| A | Stream power index |
| A* | Drainage area |
| A- | Stream power index, drainage area |
| B | Slope form |
| B- | Slope form, drainage area |
| C | Distance to rivers |
| C* | Elevation |
| C- | Distance to rivers, elevation |
| D | Terrain ruggedness index |
| D* | Slope |
| D- | Terrain ruggedness index, slope |
| E | Rainfall |
| E* | Earthquake magnitude |
| E- | Rainfall, earthquake magnitude |
| Model | AUC | F1-Score | ||
|---|---|---|---|---|
| Imbalanced | Balanced | Imbalanced | Balanced | |
| LR | 0.89 | 0.89 | 0.50 | 0.58 |
| RF | 0.88 | 0.90 | 0.50 | 0.61 |
| DFCNN | 0.87 | 0.89 | 0.60 | 0.62 |
| LSTM | 0.89 | 0.89 | 0.61 | 0.61 |
| Model | Average Time Consumed (s) | |
|---|---|---|
| Class Balanced | Class Imbalanced | |
| LR | 1 | 1 |
| RF | 12 | 11 |
| DFCNN | 418 | 405 |
| LSTM | 765 | 761 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Song, Y.; Hao, X. A Comparative Study of Shallow Machine Learning Models and Deep Learning Models for Landslide Susceptibility Assessment Based on Imbalanced Data. Forests 2022, 13, 1908. https://doi.org/10.3390/f13111908
Xu S, Song Y, Hao X. A Comparative Study of Shallow Machine Learning Models and Deep Learning Models for Landslide Susceptibility Assessment Based on Imbalanced Data. Forests. 2022; 13(11):1908. https://doi.org/10.3390/f13111908
Chicago/Turabian StyleXu, Shiluo, Yingxu Song, and Xiulan Hao. 2022. "A Comparative Study of Shallow Machine Learning Models and Deep Learning Models for Landslide Susceptibility Assessment Based on Imbalanced Data" Forests 13, no. 11: 1908. https://doi.org/10.3390/f13111908
APA StyleXu, S., Song, Y., & Hao, X. (2022). A Comparative Study of Shallow Machine Learning Models and Deep Learning Models for Landslide Susceptibility Assessment Based on Imbalanced Data. Forests, 13(11), 1908. https://doi.org/10.3390/f13111908







