Abstract
Canopy interception is an important part of forest ecosystem hydrological processes. It is the first stage of water distribution when rainfall reaches the canopy and has an important impact on nutrient inputs and water exchange. Pinus tabulaeformis is a main tree species in the rocky mountain areas of Northern China, and it is also a primary species for artificial afforestation. In previous studies of canopy interception, applications of the revised Gash model did not take rainfall characteristics into account. Therefore, in this study, rainfall patterns were divided according to the local rainfall characteristics in the rocky mountainous areas of Northern China. Rainfall was divided into three patterns. Rain pattern A was the main rainfall type. Rainfall patterns B and C were two types of rainstorms. Next, the revised Gash model was used to simulate Pinus tabulaeformis plantations under different rainfall patterns. The results showed that the canopy interception rate of Pinus tabulaeformis plantations in this area ranged from 14.7% to 17.9%. The revised Gash model can be used to simulate Pinus tabulaeformis plantations in the rocky mountainous areas of Northern China, with good simulation results for more than 80% of the conventional rainfall patterns. Furthermore, the canopy interception effect of simulated cumulative rainfall events was better than the individual rainfall event. The simulation effect for special rainfall patterns was not good, so it is necessary to improve the model parameters or collect more rainfall samples. These results can be used to explore the applicability of the revised Gash model in Pinus tabulaeformis plantations in the rocky mountain areas of Northern China. They also demonstrate different applicability of the model under different rainfall characteristics.
1. Introduction
Forest–water interactions represent an important part of forest hydrology. Vegetation is an important regulator of large-scale water fluxes [1,2], and water fluxes indicate hydrological processes. In this context, vegetation largely impacts hydrological processes. The influence of vegetation on hydrological processes mainly occurs through canopy interception, ground cover water storage and soil water storage. Therefore, canopy interception is an important component of forest ecosystem hydrological processes. It is the first stage of water distribution when rainfall reaches the canopy, and it has an important impact on water exchange and redistribution [3], produces retention, and affects the input of nutrients. When rain comes into contact with the leaves, branches, and trunks of a forest, canopy interception begins. Some of the rain is stored and evaporated back into the atmosphere, and the residual rain reaches the ground in the forms of throughfall and stemflow [4]. Canopy interception is the difference between measured rainfall above the canopy interception and throughfall and stemflow below the canopy [5,6,7]. Previous studies have shown that canopy interception can account for 10%–50% of total precipitation [8,9,10,11]. Factors affecting canopy interception can be divided into large and small-scale factors [12]. Large-scale factors include meteorological factors, such as wind speed and exposure, rainfall intensity, available evaporation energy, and fog incidence, among others. Small-scale factors are forest characteristics, such as vegetation density, canopy cover, canopy architecture, canopy porosity, tree age, aerodynamics, and canopy roughness [13,14,15]. Stemflow is also an important part of the forest water cycle and is closely related to canopy interception [16,17,18]. Although the proportion of stemflow is small, it can be highly concentrated in the root soil. Stemflow transports a large amount of nutrients, which is a good supplement to nutrients in the soil.
When studying land–atmosphere interactions, the dynamics of the global water cycle, hydrological modeling, and the impacts of deforestation at the global scale, we need to quantify the magnitude of rainfall interception [19]; the most commonly used model is the Gash model. Nearly 100 years of attention and research have followed Horton’s [20] proposal of the concept of canopy interception [21]. The Gash model is widely used for canopy interception simulation and has had good applicability and effect in different regions and vegetation types around the world, such as the Mediterranean climate zone [22], arid and semi-arid areas [23], temperate areas [24] and tropical areas [25]. Although there have been some studies on the revised Gash model in temperate areas, there are few studies in the temperate monsoon climate zone, especially in the Rocky Mountain areas of North China. Besides, only the same simulation of all rainfall conditions has been carried out, and there is no division of rain patterns, potentially causing a large error in the simulation effect. The objective of this research is to study the applicability of the revised Gash model to a P. tabulaeformis plantation in the Rocky Mountain areas of North China under a temperate monsoon climate. The canopy interception under common and special rainfall conditions was studied by classifying rainfall patterns, thus providing a basis for the investigation of hydrological cycles.
Pinus tabulaeformis (P. tabulaeformis) is the main tree species found in the Rocky Mountain areas of Northern China. In addition to natural forests, P. tabulaeformis is also regarded as a primary species for afforestation. Some studies have used the revised Gash model to simulate canopy interception of P. tabulaeformis forests in various areas, such as the tropics [26], the Mediterranean region [27], and semi-arid and arid regions [28,29]. In this region, however, the revised Gash model has mainly been applied to simulate natural forest canopy interception. There have been few simulations of plantation forests, and there were few studies on the division of rainfall patterns. In this study, in addition to simulating the cumulative canopy interception of all rainfall events that was widely used in previous studies, canopy interception was also simulated for an individual rainfall event. The Miyun Reservoir, the largest reservoir in the region, was selected as the study area, and the revised Gash model was used to simulate P. tabulaeformis plantation forest canopy interception. The results can be used to explore the applicability of P. tabulaeformis plantations in the rocky mountain areas of Northern China. Moreover, this research creates a theoretical foundation for the investigation of ecological hydrological process and provides a scientific basis for the management of P. tabulaeformis.
2. Materials and Methods
2.1. Study Area
This study was conducted in the Miyun Reservoir (40°19′–41°38′ N, 115°25′–117°35′ E) (Figure 1), which is located to the northeast of Beijing (the capital of China), at an elevation of 205 to 700 m. It is the largest reservoir in Northern China [30], and the local vegetation is representative of the rocky mountain areas of Northern China.
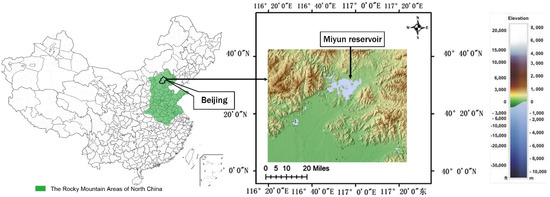
Figure 1.
Geographical location of the research region and study site.
The region has a warm temperate semi-humid continental monsoon climate, with perennial average temperatures of 9–10 °C [31]. Average annual precipitation is 669 mm, and the distribution of precipitation during the year is uneven. Overall, 80% to 85% of the annual precipitation is concentrated between July and September.
2.2. Data Sources
A sample plot was selected after investigating P. tabulaeformis plantations and excluding human disturbance in the study area (Figure 2). The sample plot included a 36-year-old afforestation P. tabulaeformis plantation with an area of 4279.3 m2 (Table 1). The average canopy density was 0.31, the average tree height was 2.72 m, and the average diameter at breast height was 11.3 cm. There were some shrubs under the plantation that were ignored. In the plot, one canopy throughfall collector with three flumes was placed on the ground (Table 2). Each flume was 2 m long and 20 cm wide. The aim of the flumes was to replace replicates of extra canopy throughfall collectors. This reduced error caused by uneven crown distribution. To represent the growth of the trees in the plot, standard trees were selected. After investigating all trees in the plot, three standard trees representing the average growth of trees were identified and selected. Stemflow from each standard tree was diverted from a plastic pipe (3 cm wide) to a collection container at the base of each tree. Each plastic pipe was stapled and sealed with caulking around the circumference of the three standard trees at a mean height of 1.3 m.

Figure 2.
The photo of measurements for canopy interception and stemflow.

Table 1.
Characteristics of the plantation in the sample plot.

Table 2.
Characteristics of different rainfall patterns.
A total of 120 rainfall events in the study area were identified from 2018 to 2021. Because the duration and intensity of minimal rainfall events during the classification process can affect the conclusions derived from classification results, rainfall events totaling less than 2 mm in 24 h were removed from the analysis. To use as many samples as possible to improve the accuracy of rain pattern classification, all 120 rainfall events observed were used in the study of rain pattern division. Of those events, some were not selected because of human disturbance, errors, or impacts of animals. Overall, 51 events not influenced were selected for simulation, which can make the results more scientific.
2.3. Methodology
2.3.1. Rain Pattern Division
There are four main methods for classifying rainfall patterns [32,33,34], including the Chicago method designed by Keifer [35], the Pilgrim–Cordery method [36], the Huff method [37] and the K-means clustering method [38]. When using the Chicago method and the Pilgrim–Cordery method, the rain peak was too sharp and thin for the area. In many rainfall events, the durations were too short, which made it difficult to use the Huff method. Therefore, the most widely used method was K-means clustering combined with discriminant analysis [39,40]. In this study, the SPSS software and the method of system clustering and fast clustering were used for analysis [41,42], Overall, 120 rainfall events from 2018 to 2021 were classified and divided into three categories by K-means clustering based on rainfall amount, rainfall duration and rainfall intensity. Values of 25 % and 75 % quantiles of each index were taken as the range of the corresponding rainfall patterns to analyze the characteristics of each rainfall pattern.
2.3.2. Descriptions of the Revised Gash Model
The original Gash model [43] presented rainfall as a series of discrete events and divided it into three phases. The first is the wetting phase, which starts at the beginning of precipitation and ends when the canopy is saturated. The second is the saturation phase, which begins when the canopy storage is exceeded and last throughout the rainfall process. The third is the drying phase, which begins at the end of rainfall and ends when the trees are completely dried. The model is based on the assumption that there is a rainfall process every day, and the canopy has sufficient time to dry between rainfall intervals. Based on this, studies have shown that the Gash model is not suitable for short vegetation types [44] and sparse canopy cases [45] in temperate latitudes.
Given the conceptual errors and limitations of applicable conditions in the original model [46], Gash et al. presented a revised version in 1995. Valente et al. improved the Gash model by scaling the average evaporation during rainfall and other parameters to the canopy coverage ratio in the study area to consider the canopy sparsity. The average evaporation of a saturated canopy was calculated using the Penman–Monteith equation. The results showed that the average evaporation in open areas was zero. The modified Gash model has the following assumptions: (i) rain falls from the canopy after it is saturated; (ii) stemflow occurs after canopy saturation; (iii) tree trunk evaporation occurs after rainfall; and (iv) the forest can be divided into areas with and without vegetation cover. Evaporation only occurs in vegetated areas, and evaporation only occurs in one-dimensional vertical space.
2.3.3. Calculation of the Revised Gash Model
Canopy interception is calculated by the function as follows [47]:
In the model, m is the number of events in which the canopy storage capacity is not filled, n is the number of events in which the canopy storage capacity is filled, j is rainfall event, Ij is canopy interception, c is closure, PG is rainfall, P′G is the amount of rainfall to fill the canopy storage capacity, E is average evaporation rate, Ec = E/c, R is average rainfall rate, q is the amount of rainfall to fill the trunk storage capacity, pt is the stemflow coefficient, ptc = pt/c, and St is the trunk storage capacity, Stc = St/c.
The amounts of rainfall to fill the canopy storage capacity (P′G) and trunk storage capacity (P’’G) were calculated as follows [48]:
S is the canopy storage capacity, Sc = S/c.
According to the sparse Gash model, stemflow (SF) and throughfall (TF) can also be calculated as follows:
The relationship between canopy interception (I), stemflow (SF) and throughfall (TF) can be described as follows:
3. Results
3.1. Rain Pattern Classification and Statistical Analysis
To characterize the characteristics of the rainfall process, three indicators were selected: average rainfall intensity (I) (mm/h), rainfall amount (P) (mm), and rainfall duration (T) (h). K-means clustering and discriminant analysis were used to divide the 120 rainfall events into categories as patterns A, B, and C (Figure 3). The discriminant analysis adopted a Fisher function, yielding the following discriminant functions:
Function 1, F1 = 0.096P − 0.028T − 0.0.034I − 1.083 (p < 0.005)
Function 2, F2 = −0.011P + 0.134T + 0.143I −1.545 (p < 0.005)
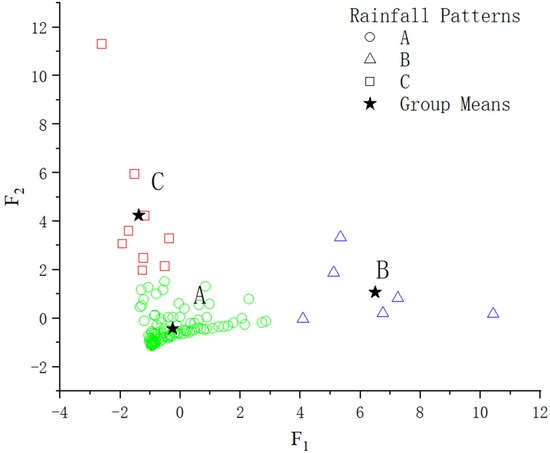
Figure 3.
Scatterplot showing rainfall discrimination and classification analysis results.
The datapoints corresponding to the three rainfall type clustering functions were clustered in three relatively concentrated areas in the scatterplot as shown in Figure 3, and the classification functions were significant (p < 0.005), which indicated that the clustering result was valid. The datapoints corresponding to each rainfall pattern were relatively discrete. Most scatter points of each rainfall pattern were concentrated, but some scatter points of each rain patterns had partial dispersion, indicating that the characteristics of each rainfall pattern changed slightly. The group points and group means of rainfall patterns A and C were closer, which were far from the group point and group mean of rain type B. It showed that the rainfall characteristics of rainfall pattern A and C were closer, and rainfall pattern B was significantly different. Some of the rainfall conditions in patterns A and C were relatively similar. However, the conditions were both significantly different from those in rainfall pattern B. According to the feature indices, the values corresponding to the first and third quantiles of the quartile, i.e., the 25th and 75th percentiles, were used to represent the range of variability for each rainfall type (Table 2). Accordingly, the characteristics of different rainfall patterns were summarized as follows: rainfall pattern A: 105 events, 87.5% of the total number of events at the station, medium duration (1.7–5.2 h), light rainfall amount (3.6–16.4 mm), light rain intensity (1.7–6.6 mm/h); rainfall pattern B: six events, 5% of the total number of events, long duration (4.5–12.8 h), heavy rainfall amount (76.6–92.8 mm), medium rain intensity (6.3–23.1 mm/h); rainfall pattern C: nine events, 7.5% of the total number of events, short duration (0.18–0.33 h), medium rainfall amount (7.0–15.4 mm), heavy rain intensity (28.7–41.2 mm/h).
3.2. Parameters Related to Canopy and Stem
Of the 120 rainfall events, throughfall and stemflow were measured for 51. The total rainfall under pattern A was 563.6 mm, the total throughfall was 452.6 mm, and stemflow was 4.01 mm. According to Equation (1), canopy interception was 106.59 mm, accounting for 18.93% of the rainfall. Under rainfall pattern B, the total rainfall was 524.4 mm, total throughfall was 390.2 mm, total stemflow was 12.19 mm, and the canopy interception was 122.01 mm, accounting for 23.27% of the rainfall. Under rainfall pattern C, total rainfall was 104.1 mm, total throughfall was 86.2 mm, total stemflow was 0.3 mm, and the canopy interception was 17.6 mm, accounting for 16.91% of the rainfall.
Figure showed that throughfall (TF) and stemflow (SF) under three rainfall patterns were linearly correlated with rainfall amount (P). The results can be described by the formula in Table 3.

Table 3.
Estimation for each rainfall pattern for TF and P.
In this study, canopy storage capacity (S) was determined using the methods of Limousin [22] andWallace [49]. Next, the residual error (Δ) of throughfall was obtained to calculate the rainfall amount of the inflection point of the equation, and the relationship between the residual TF (Δ) of TF and P was calculated. P was greater than this value and the residual TF (Δ) > 0 was used for the regression equation with corresponding throughfall. According to the relationships between TF, SF and P among the rainfall patterns, S can be calculated. For rainfall pattern A: S = 1.07 and SC = 3.44; for pattern B: S = 7.85 and SC = 25.32; for pattern C: S = 0.8 and SC = 2.56.
The trunk storage capacity (St) and stemflow coefficient (pt) were determined according to the relationship equation between stemflow (SF) and rainfall amount (P) (Table 4). Pattern A: St = 0.0283, pt = 0.0089; pattern B: St = 1.053, pt = 0.0353; pattern C: St = 0.0036, pt = 0.0081.

Table 4.
Estimation for each rainfall pattern for SF and P.
According to Equations (2) and (3) and the parameters involved, for rainfall pattern A: P′G = 4.063, P″G = 8.544; pattern B: P′G = 29.905, P″G = 71.94; pattern C: P′G = 3.029, P″G = 3.656.
3.3. Model Estimation Results
Throughfall and stemflow for the individual rainfall events and cumulative rainfall events under all three rainfall patterns were obtained from the Gash model. As seen in Figure 4, for the individual event, the predicted values of canopy interception of three rainfall patterns were generally lower than the observed values. The ratio between the difference of the predicted and observed values to the observed values were large, ranging from 0.24%–58.22%, of which most were distributed within 20%, and only a few events were greater than 40%. The average relative difference of rainfall pattern B was the lowest (14.9%); for pattern A it was 19.93%; and for pattern C it was the highest (25.54%).
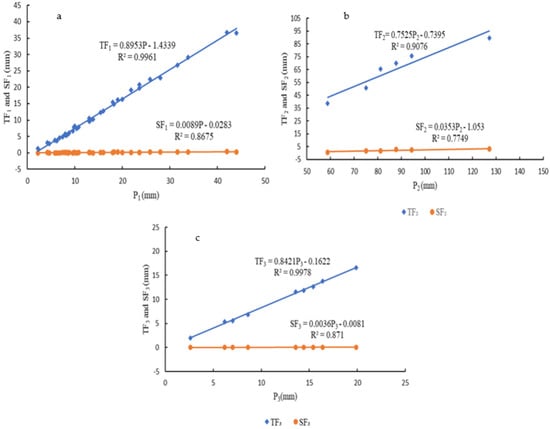
Figure 4.
Relationships between stemflow (SF), throughfall (TF), and rainfall amount (P) in the studied plot. (a): Rainfall pattern A; (b): rainfall pattern B; (c): rainfall pattern C.
When dividing the rainfall amount by the predicted or observed canopy interception, we obtained the proportion of canopy interception to rainfall (Figure 5). For rainfall pattern A, predicted cumulative canopy interception accounted for 14.9% of the total rainfall, which was 4% less than observed. For pattern B, predicted cumulative canopy interception accounted for 17.9% of the total rainfall, 5.3% less than observed. For pattern C, predicted cumulative canopy interception accounted for 14.7% of total rainfall, 2.2% less than observed. By comparing the predicted and observed values of cumulative canopy interception with the revised Gash model (Figure 6), the relative difference was greatest under rainfall pattern C. With the increase in the number of rainfall events, the relative difference under pattern A increased from 10.52% to 21.46%, pattern B increased from 8.23% to 22.5%, and pattern C increased from 3.36% to 13.06%. Compared with the simulation of an individual rainfall event, the relative difference between the cumulative predicted and observed value was generally lower with a smaller change. This demonstrated that the revised Gash model is more suitable for simulating canopy interception with accumulated rainfall. Table 5 showed cumulative observed and estimated canopy water fluxes predicted by the revised Gash model.
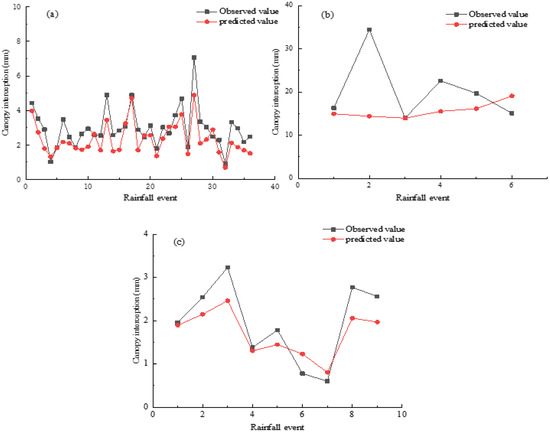
Figure 5.
Comparison of individual observed and predicted canopy interception. (a): Rainfall pattern A; (b): rainfall pattern B; (c): rainfall pattern C.
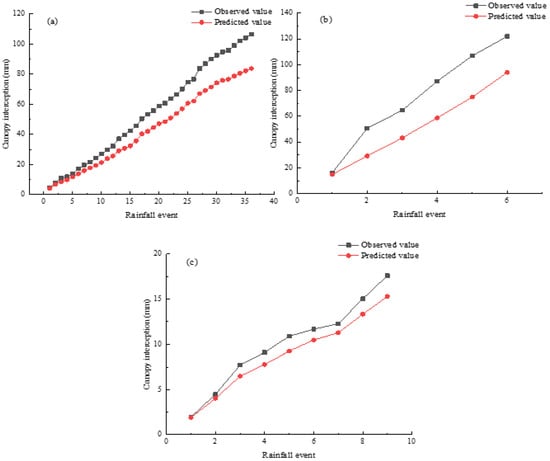
Figure 6.
Comparison of cumulative observed and predicted canopy interception. (a): Rainfall pattern A; (b): rainfall pattern B; (c): rainfall pattern C.

Table 5.
Cumulative observed and estimated canopy water fluxes predicted by the revised Gash model.
Figure 7 compares predicted and observed stemflow values for trunk saturation. Similar to canopy interception, the revised Gash model prediction of stemflow for the three rainfall patterns performed best for pattern A and worst for pattern C. The maximum difference in stemflow between predicted and observed values was 0.13 mm for pattern A, 2.68 mm for pattern B, and 0.06 mm for pattern C. For rainfall patterns A and B, the simulated values were generally lower than the measured values. However, for pattern C, simulated values were generally greater than the measured values.
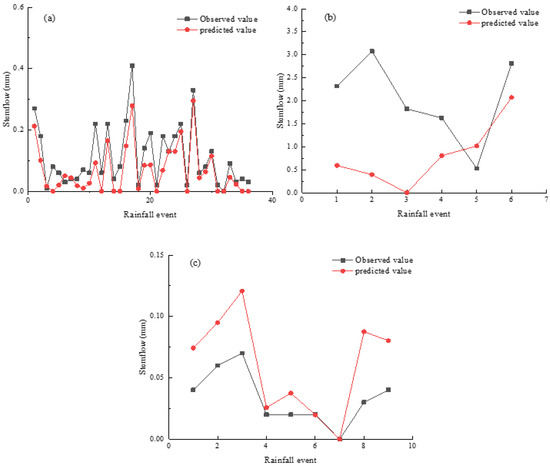
Figure 7.
Comparison of individual observed and predicted stemflow. (a): Rainfall pattern A; (b): rainfall pattern B; (c): rainfall pattern C.
Figure 8 shows that the differences between predicted and observed values for cumulative stemflow under patterns B and C were greater than 50%.
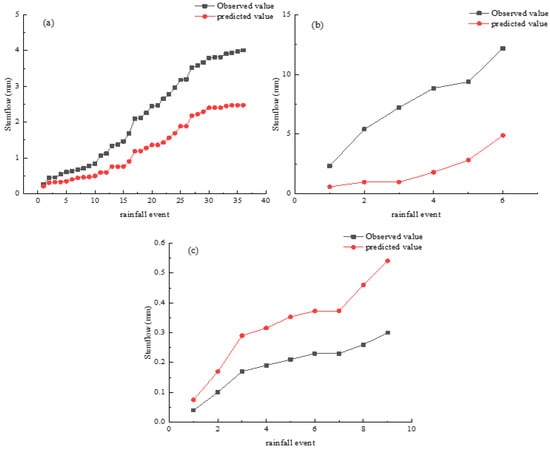
Figure 8.
Comparison of cumulative observed and predicted stemflow. (a): Rainfall pattern A; (b): rainfall pattern B; (c): rainfall pattern C.
Figure 9 shows that the simulation results for throughfall were better for rainfall patterns A and C, and predicted values were generally higher than the observed values. The effect of the model for rainfall pattern B was poor.
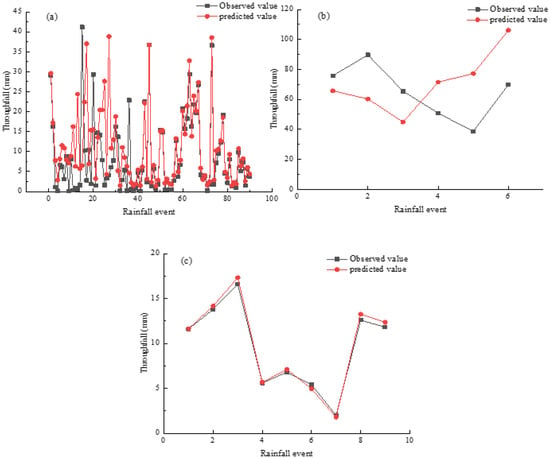
Figure 9.
Comparison of observed and predicted throughfall of studied rainfall events. (a): Rainfall pattern A; (b): rainfall pattern B; (c): rainfall pattern C.
Table 6 shows the performance metrics of the revised Gash model. According to the RMSE, CE and R, the simulated effects of patterns A and C were better than pattern B. As mentioned earlier, the error for observed and predicted of the rainfall pattern A was the minimum; therefore, the model was more suitable for simulating pattern A.

Table 6.
A comparison of the total observed/predicted canopy interception and stemflow by the revised Gash model.
4. Discussion
4.1. Rainfall Patterns and Characteristics in the Rocky Mountain Areas of Northern China
In this study, rainfall amount, rainfall intensity, and rainfall duration were used as three indicators to classify rainfall patterns. Rain in the region was divided into three patterns: A, medium duration, light rainfall intensity, and light rainfall amount; B, long duration, moderate intensity, and heavy rainfall amount; and C, short duration, heavy rain intensity, and moderate rainfall amount. Pattern A accounted for 87.5% of total rainfall events, indicating that moderate duration, light rainfall intensity events with a light rainfall amount were dominant in the rocky mountain areas of Northern China. Rainfall patterns B and C were two special types of rainfall and the main form of heavy rain. Rainfall pattern B was long in duration with high overall rainfall. Pattern C was characterized by heavy rainfall with high intensity over a short time.
Based on our previous studies about the response of runoff and sediment to rainfall in the area, rainfall pattern B had the largest contribution to surface runoff, and was the main rainfall pattern causing soil erosion. Pattern C had a great influence on runoff in certain plantations, such as Castanea mollissima and Juglandis. To increase the production of these economic plantations, little other coverage was reserved on the surface, so the surface soil was not sufficient to withstand a short period of heavy rainfall amount and erosion occurred.
4.2. Parameters of Revised Gash Model
Canopy storage capacity (S) is one parameter in the revised Gash model, and is also the basis for accurate model estimation of canopy interception [50,51]. Depending on how it is calculated and the characteristics of the three rainfall patterns, canopy storage capacity may vary, so this study did not calculate the overall canopy storage capacity of a P. tabulaeformis plantation, and instead carried out separate calculations. Canopy storage capacity values under rainfall patterns A, B, and C were S1 = 1.07, S2 = 7.85, and S3 = 0.8. The values of S1 and S3 of this study were similar to the ranges (0.25–3 mm) reported by Deguchi (2006) [52] and Llorens et al. (1997) [53] in their studies carried out in the southeast of Toyota within a temperate marine monsoon climate, and in Eastern Pyrenees Spain within a Mediterranean climate, respectively. However, S2 was much higher than the value they obtained. After excluding calculation and human errors, this may be because pattern B was long-duration with a heavy rainfall amount, and rainfall during the rainy season in the region occurred relatively frequently. Therefore, there was a shorter interval between two rainfall events compared to the other two rainfall patterns. Before the next rainfall event occurred, the evaporation process was short, and therefore, the canopy may not have completely dried, which may have caused the error. This result proved that the simulation accuracy of the revised Gash model can be improved by calculating the canopy storage capacity of each pattern separately.
4.3. Simulation Results of the Revised Gash Model
Canopy interception of a P. tabulaeformis plantation was simulated based on each rainfall pattern. The predicted canopy interception and throughfall values of the revised Gash model for an individual rainfall event and a cumulative rainfall event in the rainy season were generally close to the observed values. The differences were small, but the relative difference of stemflow was large, which was related to the hydrothermal patterns in the region. The rainy season in the area is summer, and because of the high temperature, evapotranspiration is higher than other seasons. In this sense, the high evapotranspiration and the rapid canopy drying generally restricted the possible simulation error to some extent. The predicted values for rainfall interception in this study were slightly lower than the measured values, similar to the results of the studies of Shi (2010) [24], Liang (2014) [47] and Wang (2013) [54], which may be related to climatic conditions such as high rainfall frequency and high intensity rainfall in the wet season.
When simulating canopy interception of an individual rainfall event under three rainfall patterns, although the relative difference for some events was greater than 40%, the relative difference of most events was less than 20%, indicating that the revised Gash model can be used for simulating an individual rainfall event. Relative differences greater than 40% were mainly observed under patterns B and C, indicating that the model is more suitable for simulating pattern A. The long duration of rainfall events and high rainfall in pattern B may not allow the canopy to dry between events, which not only affects the calculation of canopy interception capacity, but also affects the predicted values. Rainfall pattern C was short-term with low canopy interception, so the relative difference was large.
The simulated stemflow effects of pattern A were better than those for patterns B and C. For patterns A and B, the predicted values were generally less than the observed values. For pattern C, the predicted values were greater than the observed. This may be because pattern C was of short duration but heavy, which is generally accompanied by severe weather such as strong winds. Therefore, the stemflow would be affected by wind while moving down along the trunk until reaching the ground, resulting in lower values than those under normal conditions. The revised Gash model did not take this into account, so the simulation values were higher.
Throughfall was calculated based on predicted canopy interception and stemflow. The revised Gash model had a better simulated effect under rainfall patterns A and C, and predicted values were generally higher than the observed values. Differences from pattern B were high, and the relationship between the predicted and observed values was irregular.
In this study, the revised Gash model was also used to simulate the cumulative canopy interception and stemflow during the rainy season. Canopy interception accounted for 14.7%–17.9% of total rainfall amount and predicted values were less than the observed. This may be because simulated atmospheric rainfall was not enough to saturate the canopy, and canopy interception was expressed as canopy closure c multiplied by the atmospheric rainfall without considering the influence of evaporation. In reality, some rainfall falling on the canopy reaches the surface without the canopy achieving saturation, and this was ignored in the model. When the canopy is saturated by atmospheric rainfall, canopy interception is composed of canopy humidification, evaporation during rainfall, evaporation after rainfall ends, and stem interception and its evaporation. Similarly, rainfall reaching the ground from the canopy was not considered, so that predicted value was lower than the observed value.
Because stemflow was low, the relative difference of predicted stemflow was greater than that of the predicted canopy interception, so the simulated cumulative canopy interception was better. Due to the characteristics of rainfall pattern C mentioned above, the relationship between observed and predicted differed from those in patterns A and B, which also impacted simulation accuracy.
Compared with an individual rainfall event, the revised Gash model for cumulative rainfall events had less difference and higher fit for simulating canopy interception and stemflow.
5. Conclusions
In this study, rainfall in the rocky mountain areas of Northern China was divided into three patterns. Pattern A was the main rainfall type and represented more than 80% of all rainfall events. It was characterized by medium duration, light rainfall amount and light rain intensity. Patterns B and C were two types of rainstorms. Pattern B rainfall was long in duration, heavy and medium in intensity. Pattern C was short in duration, medium rainfall with heavy intensity.
The revised Gash model was used to simulate canopy interception under the three rainfall patterns. For an individual rainfall event, the simulation effect of rainfall pattern A was better than that of patterns B and C, and the simulation effect of pattern B was the worst. The simulation results for cumulative rainfall events were similar to those for the individual rainfall event, with the best effect for pattern A. The effect of simulating cumulative rainfall events was better than that for an individual rainfall event. In the simulation of individual and cumulative stemflow, the simulation results of rainfall patterns A and B were better, the results for rainfall pattern C were poorer, and the effect of cumulative rainfall events was better than that of an individual event. The errors of throughfall for the three rainfall patterns calculated by the revised Gash model were relatively low.
The canopy interception rate of a P. tabulaeformis plantation ranged from 14.7% to 17.9% in the rocky mountain areas of Northern China. This was lower than other tree species.
In conclusion, the revised Gash model can be used to simulate P. tabulaeformis plantations in the rocky mountain areas of Northern China, and more than 80% of the conventional rainfall patterns had good simulation results. Rainfall patterns B and C had lower probabilities of occurrence. The number of samples collected was small and the changes were large; therefore, the simulation effect was poor. More samples should be collected for further research.
Author Contributions
Y.Q.: Data curation; investigation; writing—original draft; writing—review and editing. C.S.: Conceptualization; supervision. T.Z.: Supervision. J.L.: Funding acquisition. B.B.: Supervision. G.L.: Resources. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ecological Benefits of Projects for Sand Control and Sandstorm Disaster Emergency Monitoring in Beijing (2018007-JC05, 2017006-JC02).
Data Availability Statement
Not applicable.
Acknowledgments
This research was supported by Ecological Benefits of Projects for Sand Control and Sandstorm Disaster Emergency Monitoring in Beijing (2018007-JC05, 2017006-JC02). The support from Beijing Water Source Forest Protection Forest Experiment Station is appreciated.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study.
References
- Delire, C.; de Noblet-Ducoudré, N.; Sima, A.; Gouirand, I. Vegetation dynamics enhancing long-term climate variability confirmed by two models. J. Clim. 2011, 24, 2238–2257. [Google Scholar] [CrossRef]
- Murray, S.J.; Foster, P.N.; Prentice, I.C. Future global water resources with respect to climate change and water withdrawals as estimated by a dynamic global vegetation model. J. Hydrol. 2012, 448–449, 14–29. [Google Scholar] [CrossRef]
- Fleischbein, K.; Wilcke, W.; Goller, R.; Boy, J.; Valarezo, C.; Zech, W.; Knoblich, K. Rainfall interception in a lower montane forest in Ecuador: Effects of canopy properties. Hydrol. Processes 2005, 19, 1355–1371. [Google Scholar] [CrossRef]
- Sadeghi, S.M.M.; Attarod, P.; Van Stan, J.T.; Pypker, T.G. The importance of considering rainfall partitioning in afforestation initiatives in semiarid climates: A comparison of common planted tree species in Tehran, Iran. Sci. Total Environ. 2016, 568, 845–855. [Google Scholar] [CrossRef]
- Lloyd, C. Spatial variability of throughfall and stemflow measurements in Amazonian rainforest. Agric. For. Meteorol. 1988, 42, 63–73. [Google Scholar] [CrossRef]
- Mahendrappa, M.K. Partitioning of rain water and chemicals into throughfall and stemflow in different forest stands. For. Ecol. Manag. 1990, 30, 65–72. [Google Scholar] [CrossRef]
- Tobon, M.; Bouten, C.W.; Serink, J. Gross rainfall and its portioning into throughfall, stemflow and evaporation of intercepted water in four forest ecosystems in western Amazionia. J. Hydrol. 2000, 237, 40–57. [Google Scholar]
- Johnson, R.C. The interception, throughfall and stemflow in a forest highland in Scotland and the comparison with other upland forests in the UK. J. Hydrol. 1990, 118, 281–287. [Google Scholar] [CrossRef]
- Rowe, L.K. Rainfall interception by an evergreen beech forest, Nelson, New Zealand. J. Hydrol. 1983, 66, 143–158. [Google Scholar] [CrossRef]
- Li, X.; Xiao, Q.; Niu, J. Process-based rainfall interception by small trees in Northern China: The effect of rainfall traits and crown structure characteristics. Agric. For. Meteorol. 2016, 218, 65–73. [Google Scholar] [CrossRef]
- Llorens, P.; Domingo, F. Rainfall partitioning by vegetation under Mediterranean conditions: A review of studies in Europe. J. Hydrol. 2007, 335, 37–54. [Google Scholar] [CrossRef]
- Deng, J.F. Fitting the revised Gash analytical model of rainfall interception to Mongolian Scots pines in Mu Us Sandy Land, China. Trees For. People 2020, 1, 100007. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests: Not seeing the soil for the trees. Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
- Roth, B.E.; Slatton, K.C.; Cohen, M. On the potential for high-resolution LiDAR to improve rainfall interception estimates in forest ecosystems. Front. Ecol. Environ. 2007, 5, 421–428. [Google Scholar] [CrossRef]
- Li, X.Y.; Liu, L.Y.; Gao, S.Y.; Ma, Y.J.; Yang, Z.P. Stemflow in three shrubs and its effect on soil water enhancement in semiarid loess region of China. Agric. For. Meteorol. 2008, 148, 1501–1507. [Google Scholar] [CrossRef]
- Llorens, P.; Latron, J.; Carlyle-Moses, D.E.; Nathe, K.; Chang, J.L.; Nanko, K.; Iida, S.; Levia, D.F. Stemflow infiltration areas into forest soils around American beech (Fagus grandifolia Ehrh.) trees. Ecohydrology 2021, 15, 2369. [Google Scholar] [CrossRef]
- Pinos, J.; Latron, J.; Levia, D.F.; Llorens, P. Drivers of the circumferential variation of stemflow inputs on the boles of Pinus sylvestris L. (Scots pine). Ecohydrology 2021, 14, 2438. [Google Scholar] [CrossRef]
- Hanchi, A.; Rapp, M. Stemflow determination in forest stands. For. Ecol. Manag. 1997, 3, 231–235. [Google Scholar] [CrossRef]
- Zheng, C.L.L.; Jia, L. Global canopy rainfall interception loss derived from satellite earth observations. Ecohydrology 2020, 13, 2. [Google Scholar] [CrossRef]
- Horton, E.R. Rainfall Interception. MWR 1919, 47, 603–623. [Google Scholar] [CrossRef]
- Cui, Y.K.; Zhao, P.; Yan, B.Y.; Xie, H.J.; Yu, P.T.; Wan, W.; Fan, W.J.; Hong, Y. Developing the Remote Sensing-Gash Analytical Model for Estimating Vegetation Rainfall Interception at Very High Resolution: A Case Study in the Heihe River Basin. Remote Sens. 2014, 9, 661. [Google Scholar] [CrossRef]
- Limousin, J.M.; Rambal, S.; Ourcival, J.M.; Joffre, R. Modeling rainfall interception in a Mediterranean Quercus ilex ecosystem: Lesson from a through-fall exclusion experiment. J. Hydrol. 2008, 357, 57–66. [Google Scholar] [CrossRef]
- Sadeghi, S.M.M.; Attarod, P.; Stan, G.T.V.; Pypker, T.G.; Dunkerley, D. Efficiency of the reformulated Gash’s interception model in semiarid afforestations. Agric. For. Meteorol. 2015, 201, 76–85. [Google Scholar] [CrossRef]
- Shi, Z.J.; Wang, Y.H.; Xu, L.H. Fraction of incident rainfall within the canopy of a pure stand of Pinus armandiiith revised Gash model in the Liupan Mountains of China. J. Hydrol. 2010, 2, 1–7. [Google Scholar]
- Cuartas, L.A.; Tomasella, J.; Nobre, A.D.; Hodnett, M.G.; Waterloo, M.J.; Munera, J.C. Interception water-partitioning dynamics for a pristine rainforest in central Amazonia: Marked differences between normal and dry years. Agric. For. Meteorol. 2007, 145, 69–83. [Google Scholar] [CrossRef]
- Bolanos-Sanchez, C.; Prado-Hernandez, J.V.; Silvan-Cardenas, J.L.; Vazquez-Pena, M.A.; Madrigal-Gomez, J.M.; Martinez-Ruiz, A. Estimating Rainfall Interception of Pinus hartwegii and Abies religiosa Using Analytical Models and Point Cloud. Forests 2021, 12, 866. [Google Scholar] [CrossRef]
- Eliades, M.; Bruggeman, A.; Djuma, H.; Christou, A.; Rovanias, K.; Lubczynski, M.W. Testing three rainfall interception models and different parameterization methods with data from an open Mediterranean pine forest. Agric. For. Meteorol. 2022, 313, 108755. [Google Scholar] [CrossRef]
- Attarod, P.; Sadeghi, S.M.M.; Pypker, T.G.; Bagheri, H.; Bagheri, M.; Bayramzadeh, V. Needle-leaved trees impacts on rainfall interception and canopy storage capacity in an arid environment. New For. 2015, 46, 339–355. [Google Scholar] [CrossRef]
- Seyed, M.M.S.; Pedram, A.; Thomas, G.P.; David, D. Is canopy interception increased in semiarid tree plantations? Evidence from a field investigation in Tehran, Iran. Turk. J. Agric. For. 2014, 38, 792–806. [Google Scholar]
- Gong, W.F.; Liu, T.D.; Duan, X.Y.; Sun, Y.X.; Zhang, Y.Y.; Tong, X.Y.; Qiu, Z.X. Estimating the Soil Erosion Response to Land-Use Land-Cover Change Using GIS-Based RUSLE and Remote Sensing: A Case Study of Miyun Reservoir, North China. Water 2022, 14, 742. [Google Scholar] [CrossRef]
- Wang, X.; Hao, G.L.; Yang, Z.F.; Liang, P.Y.; Cai, Y.P.; Li, C.H.; Sun, L.; Zhu, J. Variation analysis of streamflow and ecological flow for the twin rivers of the Miyun Reservoir Basin in northern China from 1963 to 2011. Sci. Total Environ. 2015, 536, 739–749. [Google Scholar] [CrossRef] [PubMed]
- Yin, Q.; Wang, Y.; Xie, Y.; Liu, A. Characteristics of intra-strom temporal pattern over China. Adv. Water Sci. 2014, 25, 617–624. (In Chinese) [Google Scholar]
- Zhen, F.; Bian, F.; Lu, J.; Tan, C.; Xu, X. Effects of rainfall patterns on hillslope erosion with longitudinal ridge in typical black soil region of northeast China. Trans. Chin. Soc. Agric. Mach. 2016, 47, 90–97. (In Chinese) [Google Scholar]
- Zhou, Z.; Wang, L.; Wang, X.; Ma, H.; Li, M. Rainfall characteristics and their effects on slope erosion in western loess hilly region. Bull. Soil Water Conserv. 2014, 34, 24–27. (In Chinese) [Google Scholar]
- Keifer, C.J.; Chu, H.H. Synthetic storm pattern for drainage design. J. Hydraul. Div. ASCE 1957, 83, 1–25. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Cordery, I. Rainfall temporal patterns for design floods. J. Hydraul. Div. 1975, 101, 81–95. [Google Scholar] [CrossRef]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Yen, B.C.; Chow, C.T. Design hyetographs for small drainage structures. ASCE J. Hydraul. Div. 1980, 106, 1055–1076. [Google Scholar] [CrossRef]
- Fang, H.Y.; Cai, Q.G.; Chen, H.; Li, Q.Y. Effect of rainfall regime and slope on runoff in a gullied loess region on the loess plateau in China. Environ. Manag. 2008, 42, 402–411. [Google Scholar] [CrossRef]
- Wu, L.; Wang, Y.; Wang, C.; Wang, Y.; Wang, B. Effect of rainfall patterns on hillslope soil erosion in rocky mountain area of north China. Trans. Chin. Soc. Agric. Eng. 2017, 33, 157–164. (In Chinese) [Google Scholar]
- Zhang, J.J.; Sun, Z.B.; Chen, S.J. A pattern classification of the mean pentad circulations at 500 mb level over East Asia. Acta Meteorol. Sin. 1984, 42, 311–319. [Google Scholar]
- Ye, H.Z. Establishment and selection of regionalized Gauss-Markov hyetograph. Resour. Sci. 2004, 26, 44–53. [Google Scholar]
- Gash, J.H.C. An analytical model of rainfall interception in forest. Q. J. R. Meteorol. Soc. 1979, 105, 43–55. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Bruijnzeel, L.A. Modelling rainfall interception by vegetation of variable density using an adapted analytical model. J. Hydrol. 2001, 247, 239–262. [Google Scholar] [CrossRef]
- Lankreijer, H.; Hendriks, M.J.; Klaassen, W. A comparison of models simulating rainfall interception of forests. Agric. For. Meteorol. 1993, 64, 187–199. [Google Scholar] [CrossRef]
- Teklehaimonot, Z.; Jarvis, P.G. Modelling of rainfall interception loss on agroforestry systems. Agric. Sys. 1991, 14, 65–80. [Google Scholar] [CrossRef]
- Wen, J.L. Short Communication. Simulation of gash model to rainfall interception of Pinus tabulaeformis. For. Syst. 2014, 23, 300–303. [Google Scholar]
- Valente, F.; David, J.J.M.; Gash, J.H.C. Modeling interception loss for two sparse eucalypt and pine forests in central Portugal using reformulated Rutter and Gash analytical models. J. Hydrol. 1997, 190, 141–162. [Google Scholar] [CrossRef]
- Wallance, J.; McJannet, D. On interception modeling of a lowland coastal rainforest in northern Queensland Australia. J. Hydrol. 2006, 329, 477–488. [Google Scholar] [CrossRef]
- Wang, Y.P.; Wang, L. Modeling canopy rainfall interception of a replanted Robinia pseudoacacia forest in the Loess Plateau. Acta Ecol. Sin. 2012, 32, 5445–5453. [Google Scholar] [CrossRef]
- Liu, S. Estimation of rainfall storage capacity in the canopies of cypress wetlands and slash pine uplands in North Central Florida. J. Hydrol. 1998, 207, 32–41. [Google Scholar] [CrossRef]
- Deguchi, A.; Hattori, S.; Park, H.T. The influence of seasonal changes in canopy structure on interception loss: Application of the revised Gash model. J. Hydrol. 2006, 318, 80–102. [Google Scholar] [CrossRef]
- Llorens, P.; Poch, R.; Latron, J. Rainfall interception by a Pinus sylventris forest patch overgrown in a Mediterranean moun tainous abandoned area. J. Hydrol. 1997, 199, 331–345. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Q.F.; Shao, M.A.; Wang, Q.J. Rainfall Interception in a Robinia pseudoacacia Forest Stand: Estimates Using Gash’s Analytical Model. J. Hydrol. Eng. 2013, 18, 474–479. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).