A Static Pulling Test Is a Suitable Method for Comparison of the Loading Resistance of Silver Birch (Betula pendula Roth.) between Urban and Peri-Urban Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Sample Trees
2.1.1. Forest Sites
2.1.2. Urban Sites
2.2. Static Pulling Tests
2.3. Data Processing and Analysis
3. Results and Discussion
3.1. Comparison of Aspen and Birch
3.2. Comparison of Urban and Forest Birch Trees
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Egidi, G.; Salvati, L.; Vinci, S. The long way to tipperary: City size and worldwide urban population trends, 1950–2030. Sustain. Cities Soc. 2020, 60, 102148. [Google Scholar] [CrossRef]
- Gulsrud, N.M.; Nielsen, A.B.; Bastrup-Birk, A.; Olafsson, A.S.; Lier, M.; Fischer, C.; Zalkauskas, R.; Hedblom, M.; Sievanen, T.; Nordh, H.; et al. Urban Forests in a European Perspective: What Can the National Forest Inventory Tell Us. In Proceedings of the Workshop for Practitioners and Researchers”, Brussels, Belgium, 15 March 2018; Department of Geosciences and Natural Resource Management, University of Copenhagen: København, Denmark, 2018. [Google Scholar]
- Stone, B.; Rodgers, M.O. Urban form and thermal efficiency: How the design of cities influences the urban heat island effect. J. Am. Plan. Assoc. 2001, 67, 186–198. [Google Scholar] [CrossRef]
- Livesley, S.J.; McPherson, E.G.; Calfapietra, C. The Urban Forest and Ecosystem Services: Impacts on Urban Water, Heat, and Pollution Cycles at the Tree, Street, and City Scale. J. Environ. Qual. 2016, 45, 119–124. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; McBride, J.; Zhou, J.; Sun, Z. The urban forest in Beijing and its role in air pollution reduction. Urban For. Urban Green. 2005, 3, 65–78. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, J.; Xie, J.; Zhang, M. Empirical study on recreation suitability evaluation of suburban forest park—A case study of Baiyun forest park in Lishui city, China. Appl. Ecol. Environ. Res. 2019, 17, 3499–3512. [Google Scholar] [CrossRef]
- Kenney, W.A. A strategy for Canada’s urban forests. For. Chron. 2003, 79, 785–789. [Google Scholar] [CrossRef]
- Nowak, D.J.; Dwyer, J.F. Understanding the Benefits and Costs of Urban Forest Ecosystems. In Handbook of Urban and Community Forestry in the Northeast; Kuser, J.E., Ed.; Springer: Boston, MA, USA; New York, NY, USA, 2000; pp. 11–25. [Google Scholar]
- Czaja, M.; Kołton, A.; Muras, P. The complex issue of urban trees-stress factor accumulation and ecological service possibilities. Forests 2020, 11, 932. [Google Scholar] [CrossRef]
- Hunt, A.; Watkiss, P. Climate change impacts and adaptation in cities: A review of the literature. Clim. Chang. 2011, 104, 13–49. [Google Scholar] [CrossRef] [Green Version]
- Seidl, R.; Thom, D.; Kautz, M.; Martin-benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, J.; et al. Forest disturbances under climate change. Nat. Clim. Chang. 2017, 7, 395–402. [Google Scholar] [CrossRef] [Green Version]
- Solecki, W.; Marcotullio, P.J. Climate Change and Urban Biodiversity Vulnerability. In Urbanization, Biodiversity and Ecosystem Services: Challenges and Opportunities: A Global Assessment; Elmqvist, T., Fragkias, M., Goodness, J., Guneralp, B., Marcotullio, P.J., McDonald, R.I., Parnell, S., Schewenius, M., Sendstad, M., Seto, K.C., et al., Eds.; Springer Opem: Dordrecht The Netherlands; Heidelberg, Germany; New York, NY, USA; London, UK, 2013; pp. 453–459. ISBN 9789400770881. [Google Scholar]
- Sani, L.; Lisci, R.; Moschi, M.; Sarri, D.; Rimediotti, M.; Vieri, M.; Tofanelli, S.; Tofanelli, S. Preliminary experiments and verification of controlled pulling tests for tree stability assessments in Mediterranean urban areas. Biosyst. Eng. 2012, 112, 218–226. [Google Scholar] [CrossRef]
- James, K.R.; Haritos, N.; Ades, P.K. Mechanical stability of trees under dynamic loads. Am. J. Bot. 2006, 93, 1522–1530. [Google Scholar] [CrossRef]
- Nicoll, B.C.; Ray, D. Adaptive growth of tree root systems in response to wind action and site conditions. Tree Physiol. 1996, 16, 891–898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peltola, H.; Ikonen, V.P.; Gregow, H.; Strandman, H.; Kilpeläinen, A.; Venäläinen, A.; Kellomäki, S. Impacts of climate change on timber production and regional risks of wind-induced damage to forests in Finland. For. Ecol. Manag. 2010, 260, 833–845. [Google Scholar] [CrossRef]
- Ståhl, E.G. Changes in wood and stem properties of Pinus sylvestris caused by provenance transfer. Silva Fenn. 1998, 32, 163–172. [Google Scholar] [CrossRef] [Green Version]
- Giambastiani, Y.; Preti, F.; Errico, A.; Sani, L. On the tree stability: Pulling tests and modelling to assess the root anchorage. Procedia Environ. Sci. Eng. Manag. 2017, 4, 207–218. [Google Scholar]
- Moffat, A.; Nisbet, T.; Nicoll, B. Environmental Effects of Stump and Root Harvesting; Forestry Commission: Edinburgh, Scotland, 2011. [Google Scholar]
- Weltecke, K.; Gaertig, T. Influence of soil aeration on rooting and growth of the Beuys-trees in Kassel, Germany. Urban For. Urban Green. 2012, 11, 329–338. [Google Scholar] [CrossRef]
- Lindsey, P.; Bassuk, N. Specifying soil volumes to meet the water needs of mature urban street trees and trees in containers. J. Arboric. 1991, 17, 141–149. [Google Scholar] [CrossRef]
- Stubbs, C.J.; Cook, D.D.; Niklas, K.J. A general review of the biomechanics of root anchorage. J. Exp. Bot. 2019, 70, 3439–3451. [Google Scholar] [CrossRef] [PubMed]
- Hekkala, A.M.; Tarvainen, O.; Tolvanen, A. Dynamics of understory vegetation after restoration of natural characteristics in the boreal forests in Finland. For. Ecol. Manag. 2014, 330, 55–66. [Google Scholar] [CrossRef]
- Kowarik, I.; von der Lippe, M.; Cierjacks, A. Prevalence of alien versus native species of woody plants in Berlin differs between habitats and at different scales. Preslia 2013, 85, 113–132. [Google Scholar]
- Putz, F.E.; Coley, P.D.; Lu, K.; Montalvo, A.; Aiello, A. Uprooting and snapping of trees: Structural determinants and ecological censequences. Can. J. For. Res. 1983, 13, 1011–1020. [Google Scholar] [CrossRef]
- Halme, P.; Purhonen, J.; Marjakangas, E.L.; Komonen, A.; Juutilainen, K.; Abrego, N. Dead wood profile of a semi-natural boreal forest-implications for sampling. Silva Fenn. 2019, 53, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Rich, R.L.; Frelich, L.E.; Reich, P.B. Wind-throw mortality in the southern boreal forest: Effects of species, diameter and stand age. J. Ecol. 2007, 95, 1261–1273. [Google Scholar] [CrossRef]
- Petrokas, R.; Baliuckas, V.; Manton, M. Successional categorization of european hemi-boreal forest tree species. Plants 2020, 9, 1381. [Google Scholar] [CrossRef] [PubMed]
- Dyderski, M.K.; Paź, S.; Frelich, L.E.; Jagodziński, A.M. How much does climate change threaten European forest tree species distributions? Glob. Chang. Biol. 2018, 24, 1150–1163. [Google Scholar] [CrossRef]
- Kneeshaw, D.; Bergeron, Y. Canopy Gap Characteristics and Tree Replacement in the Southeastern Boreal Forest. Ecology 1998, 79, 783–794. [Google Scholar] [CrossRef]
- Urban Forestry in the Nordic and Baltic Countries; Sander, H.; Randrup, T.B. (Eds.) Estonian Agricultural University, Department of Forestry, Forest Research Institute: Tallinn, Estonia; Copenhagen, Denmark, 1998; p. 77. [Google Scholar]
- Atkinson, M.D. Betula pendula Roth (B. Verrucosa Ehrh.) and B. Pubescens Ehrh. J. Ecol. 1992, 80, 837–870. [Google Scholar] [CrossRef]
- Caudullo, G.; Commission, E.; Rigo, D. De Populus tremula in Europe: Distribution, habitat, usage and threats. In European Atlas of Forest Tree Species; San-Miguel-Ayanz, J., de Rigo, D., Caudullo, G., Houston Durrant, T., Mauri, A., Eds.; Off. EU.: Luxembourg, 2016; p. 148. [Google Scholar]
- Esseen, P.A.; Ehnström, B.; Ericson, L.; Sjöberg, K. Boreal forests. In Boreal Ecosystems and Landscapes: Structures, Processes and Conservation of Biodiversity; Hansson, Ed.; Ecological Bulletins; Munksgaard: Copenhagen, Denmark, 1997; Volume 46, pp. 16–47. [Google Scholar]
- Peltola, H.; Kellomäki, S.; Hassinen, A.; Granander, M. Mechanical stability of Scots pine, Norway spruce and birch: An analysis of tree-pulling experiments in Finland. For. Ecol. Manag. 2000, 143–153. [Google Scholar] [CrossRef]
- Čakša, L.; Šēnhofa, S.; Šņepsts, G.; Elferts, D.; Liepa, L.; Jansons, Ā. Effect of stem snapping on aspen timber assortment recovery in hemiboreal forests. Forests 2021, 12, 28. [Google Scholar] [CrossRef]
- Krišāns, O.; Matisons, R.; Kitenberga, M.; Donis, J.; Rust, S.; Elferts, D.; Jansons, Ā. Wind resistance of eastern Baltic silver birch (Betula pendula Roth.) suggests its suitability for periodically waterlogged sites. Forests 2021, 12, 21. [Google Scholar] [CrossRef]
- Jankovska, I.; Donis, J.; Straupe, I.; Panagopoulos, T.; Kupfere, L. Assessment of forest recreation accessibility in Latvia. Fresenius Environ. Bull. 2013, 22, 2145–2151. [Google Scholar]
- Liepiņš, J.; Lazdiņš, A.; Liepiņš, K. Equations for estimating above- and belowground biomass of Norway spruce, Scots pine, birch spp. and European aspen in Latvia. Scand. J. For. Res. 2018, 33, 58–70. [Google Scholar] [CrossRef]
- Lygis, V.; Bakys, R.; Gustiene, A.; Burokiene, D.; Matelis, A.; Vasaitis, R. Forest self-regeneration following clear-felling of dieback-affected Fraxinus excelsior: Focus on ash. Eur. J. For. Res. 2014, 133, 501–510. [Google Scholar] [CrossRef]
- Veinberga, M.; Zigmunde, D. Aesthetics and Ecology in Planning of Urban Green Spaces of Latvia. Sci. J. Latv. Univ. Agric. 2016, 8, 43–52. [Google Scholar]
- Rydberg, D.; Falck, J. Designing the urban forest of tomorrow: Pre-commercial thinning adapted for use in urban areas in sweden. Arboric. J. 1998, 22, 147–171. [Google Scholar] [CrossRef]
- Belda, M.; Holtanová, E.; Halenka, T.; Kalvová, J. Climate classification revisited: From Köppen to Trewartha. Clim. Res. 2014, 59, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Jaagus, J.; Briede, A.; Rimkus, E.; Remm, K. Precipitation pattern in the Baltic countries under the influence of large-scale atmospheric circulation and local. Int. J. Climatol. 2010, 30, 705–720. [Google Scholar] [CrossRef] [Green Version]
- LEGMC Latvian Environment, Geology and Meteorology Centre. Available online: https://klimats.meteo.lv/klimats/latvijas_klimats/ (accessed on 19 January 2016).
- Lizuma, L. An Analysis of a Long-Term Meteorological Data Series in Riga. Folia Geogr. 2000, 7, 53–61. [Google Scholar]
- Samariks, V.; Krisans, O.; Donis, J.; Silamikele, I.; Katrevics, J.; Jansons, A. Cost-benefit analysis of measures to reduce windstorm impact in pure Norway Spruce (Picea abies L. Karst.) stands in Latvia. Forests 2020, 11, 576. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J.; de Rigo, J.; Caudullo, D.; Durrant, G.; Mauri, T.; Tinner, A.; Ballian, W.; Beck, D.; Birks, P.; Eaton, H.; et al. European Atlas of Forest Tree Species; Publications Office of the European Union: Luxembourg, 2016. [Google Scholar]
- Dahlhausen, J.; Rötzer, T.; Biber, P.; Uhl, E.; Pretzsch, H. Urban climate modifies tree growth in Berlin. Int. J. Biometeorol. 2018, 62, 795–808. [Google Scholar] [CrossRef]
- Climate-Data. Available online: https://en.climate-data.org/europe/germany/baden-wuerttemberg/karlsruhe-2143/ (accessed on 14 December 2021).
- Climate-Data. Available online: https://en.climate-data.org/europe/germany/hamburg/hamburg-69/ (accessed on 14 December 2021).
- Krisans, O.; Saleniece, R.; Rust, S.; Elferts, D.; Kapostins, R.; Jansons, A.; Matisons, R. Effect of Bark-Stripping on Mechanical Stability of Norway Spruce. Forests 2020, 11, 357. [Google Scholar] [CrossRef] [Green Version]
- Krisans, O.; Matisons, R.; Rust, S.; Burnevica, N.; Bruna, L.; Elferts, D.; Kalvane, L.; Jansons, A. Presence of root rot reduces stability of norway spruce (Picea abies): Results of static pulling tests in Latvia. Forests 2020, 11, 416. [Google Scholar] [CrossRef] [Green Version]
- Detter, A.; Richter, K.; Rust, C.; Rust, S. Aktuelle Untersuchungen zum Primärversagen von grünem Holz-Current studies on primary failure in green wood. In Proceedings of the Conference Deutsche Baumpflegetage, Augsburg, Germany, 5–7 May 2015; pp. 156–167. [Google Scholar]
- Detter, A.; Rust, S.; Rust, C.; Maybaum, G. Determining strength limits for standing tree stems from bending tests. Proceedings of 18th International Nondestructive Testing and Evaluation of Wood Symposium, Madison, WI, USA, 24–27 September 2013; pp. 24–27. [Google Scholar]
- Rust, S.; Detter, A. Experimental test of non-destructive methods to assess the anchorage of urban trees. In Proceedings of the 21st international nondestructive testing and evaluation of wood symposium, Freiburg, Germany, 24–27 September 2019. [Google Scholar]
- James, K.; Hallam, C.; Spencer, C. Measuring tilt of tree structural root zones under static and wind loading. Agric. For. Meteorol. 2013, 168, 160–167. [Google Scholar] [CrossRef]
- Brudi, E.; van Wassenaer, P. Trees and statics: Non-destructive failure analysis. In Proceedings of the Tree Structure and Mechanics Conference: How Trees Stand up and Fall down; ISA: Savannah, GA, USA, October 2001; pp. 53–70. [Google Scholar]
- Smiley, E.T.; Coder, K. Tree Structure and Mechanics Conference Proceedings: How Trees Stand up and Fall down; Kim, D., Ed.; ISA: Champaign, IL, USA, 2002. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 20 May 2019).
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Bartoń, K. MuMIn: Multi-Model Inference. Available online: https://cran.r-project.org/web/packages/MuMIn/index.html (accessed on 24 November 2020).
- Detter, A.; Van Wassenaer, P.; Rust, S. Stability recovery in London plane trees 8 years after primary anchorage failure. Arboric. Urban For. 2019, 45, 279–288. [Google Scholar] [CrossRef]
- Nykänen, M.L.; Peltola, H.; Quine, C.; Kellomäki, S.; Broadgate, M. Factors affecting snow damage of trees with particular reference to European conditions. Silva Fenn. 1997, 31, 193–213. [Google Scholar] [CrossRef] [Green Version]
- Hauer, R.J.; Wang, W.; Dawson, J.O. Ice storm damage to urban trees. J. Arboric. 1993, 19, 187–194. [Google Scholar]
- Samariks, V.; Brizga, D.; Rūba, J.; Seipulis, A.; Jansons, Ā. Root-plate characteristics of common aspen in hemiboreal forests of Latvia: A case study. Forests 2021, 12, 32. [Google Scholar] [CrossRef]
- Szoradova, A.; Praus, L.; Kolarik, J. Evaluation of the root system resistance against failure of urban trees using principal component analysis. Biosyst. Eng. 2013, 115, 244–249. [Google Scholar] [CrossRef]
- Laapas, M.; Lehtonen, I.; Venäläinen, A.; Peltola, H.M. The 10-year return levels of maximum wind speeds under frozen and unfrozen soil forest conditions. Climate 2019, 7, 62. [Google Scholar] [CrossRef] [Green Version]
- Dupuy, L.; Fourcaud, T.; Stokes, A. A numerical investigation into the influence of soil type and root architecture on tree anchorage. Plant Soil 2005, 278, 119–134. [Google Scholar] [CrossRef]
- Samariks, V.; Īstenais, N.; Seipulis, A.; Miezīte, O.; Krišāns, O.; Jansons, Ā. Root-soil plate characteristics of silver birch on wet and dry mineral soils in Latvia. Forests 2021, 12, 20. [Google Scholar] [CrossRef]
- DesRochers, A.; Lieffers, V.J. The coarse-root system of mature Populus tremuloides in declining stands in Alberta, Canada. J. Veg. Sci. 2001, 12, 355–360. [Google Scholar] [CrossRef]
- Ennos, A.R. The mechanics of root anchorage. Adv. Bot. Res. 2000, 33, 133–157. [Google Scholar] [CrossRef]
- Taylor, A.M.; Gartner, B.L.; Morrell, J.J. Heartwood formation and natural durability—A review. Wood Fiber Sci. 2002, 34, 587–611. [Google Scholar]
- Dahle, G.A.; James, K.R.; Kane, B.; Grabosky, J.C.; Detter, A. A review of factors that affect the static load-bearing capacity of urban trees. Arboric. Urban For. 2017, 43, 89–106. [Google Scholar] [CrossRef]
- Niklas, K.J.; Spatz, H.C. Worldwide correlations of mechanical properties and green wood density. Am. J. Bot. 2010, 97, 1587–1594. [Google Scholar] [CrossRef]
- Nakagawa, S.; Johnson, P.C.D.; Schielzeth, H. The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. J. R. Soc. Interface 2017, 14, 20170213. [Google Scholar] [CrossRef] [Green Version]
- Pokorny, J.; O’Brien, J.; Hauer, R.; Johnson, G.; Albers, J.; Bedker, P.; Mielke, M. Urban Tree Risk Management: A Community Guide to Program Design and Implementation; McGuinness, B., Ed.; The U.S. Department of Agriculture: St. Paul, MN, USA, 1992. [Google Scholar]
- Silapachote, P.; Srisuphab, A.; Sirilertworakul, V.; Anekwiroj, P. Spectral Analysis of Dynamic Wind Loads on Trees. In Proceedings of the IEEE Region 10 Annual International Conference, Proceedings/TENCON, Jeju, Korea, 28–31 October 2018; pp. 593–598. [Google Scholar]
- Miller, R.W.; Hauer, R.J.; Werner, L.P. Urban Forestry: Planning and Managing Urban Greenspaces, 3rd ed.; Robert, W.M., Richard, J.H., Werner, L.P., Eds.; Waveland Press: Long Grove, IL, USA, 2015. [Google Scholar]
- Ghani, M.A.; Stokes, A.; Fourcaud, T. The effect of root architecture and root loss through trenching on the anchorage of tropical urban trees (Eugenia grandis Wight). Trees 2009, 23, 197–209. [Google Scholar] [CrossRef]
- Korhonen, A.; Siitonen, J.; Kotze, D.J.; Immonen, A.; Hamberg, L. Stand characteristics and dead wood in urban forests: Potential biodiversity hotspots in managed boreal landscapes. Landsc. Urban Plan. 2020, 201, 103855. [Google Scholar] [CrossRef]
- Sharon, E.M. Tree failures, risk and reasonableness. A commonsense approach. Arboric. J. 1989, 13, 193–209. [Google Scholar] [CrossRef]
- Groot, A.; Cortini, F. The effect of the interaction of tree slenderness and relative height with ring width on wood density in Abies balsamea and Picea glauca. Wood Sci. Technol. 2017, 51, 175–194. [Google Scholar] [CrossRef]
- Sinacore, K.; Hall, J.S.; Potvin, C.; Royo, A.A.; Ducey, M.J.; Ashton, M.S. Unearthing the hidden world of roots: Root biomass and architecture differ among species within the same guild. PLoS ONE 2017, 12, e0185934. [Google Scholar] [CrossRef] [PubMed]
- Lüttge, U.; Buckeridge, M. Trees: Structure and function and the challenges of urbanization. Trees 2020, 34, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Detter, V.A.; Rust, S. Aktuelle Untersuchungsergebnisse zu Zugversuchen, Findings of recent research on the pulling test method. Jahrb. Baumpflege 2013, 17, 87–100. [Google Scholar]
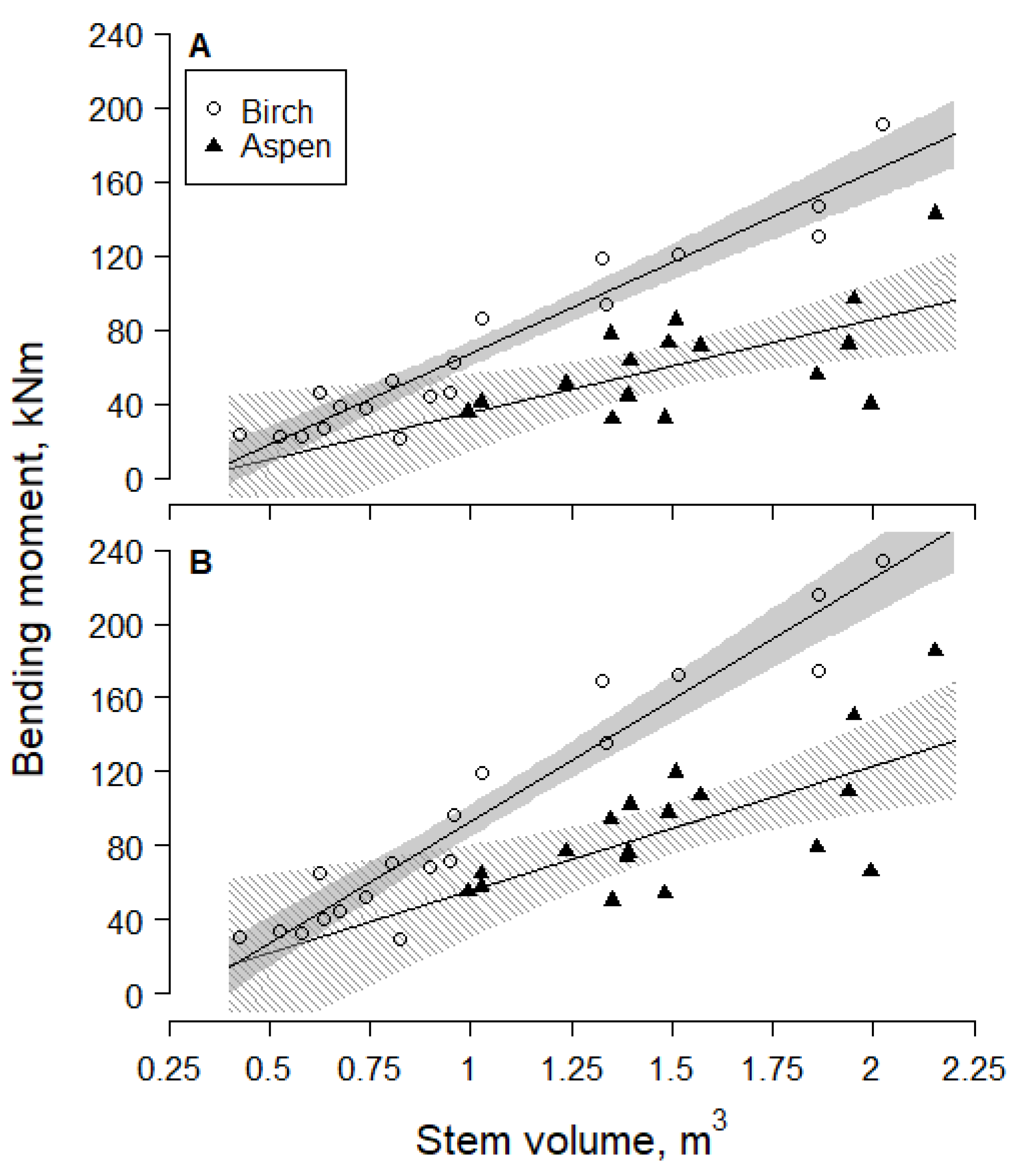
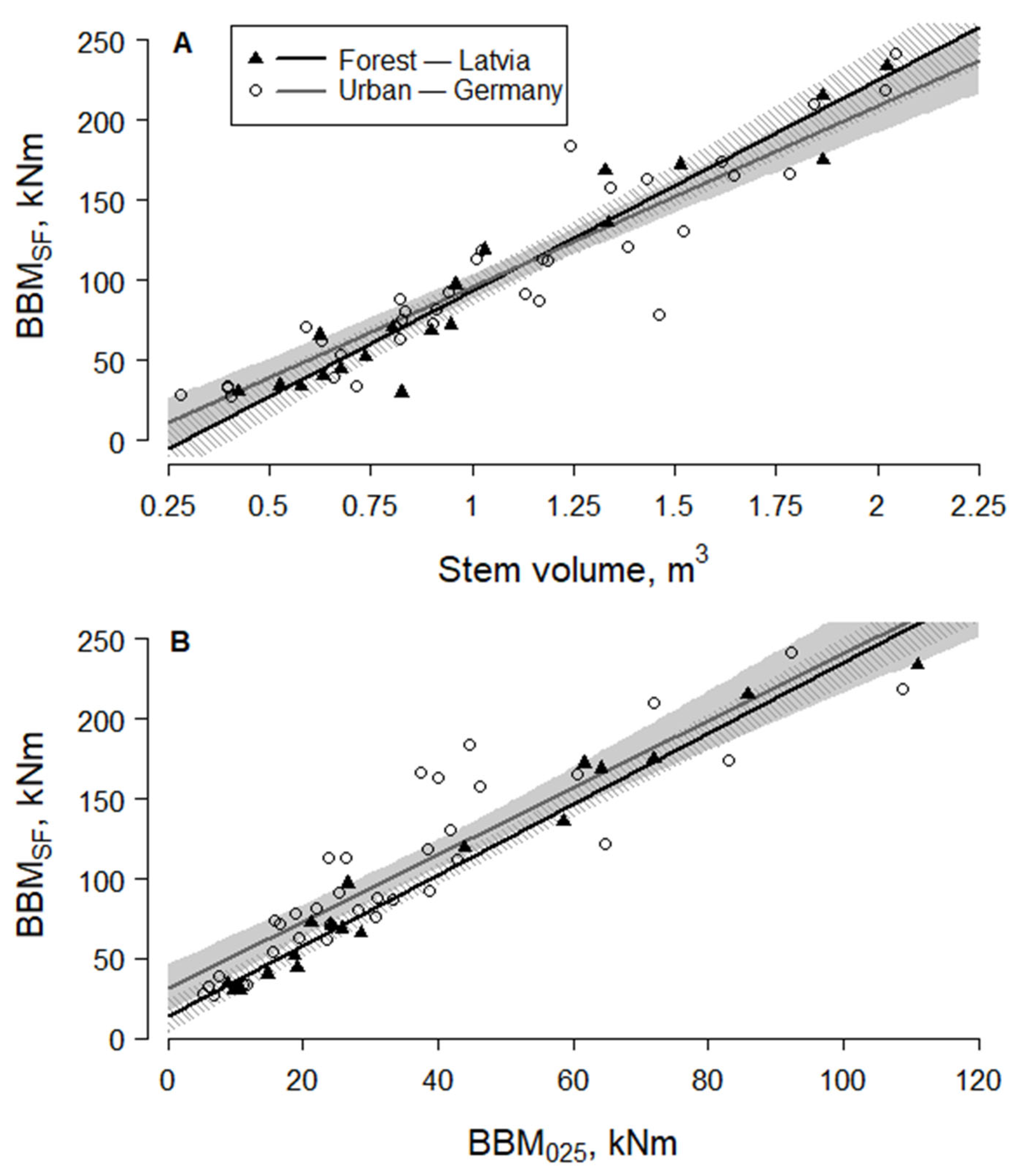
| Site No. | Composition (%) | N | DBH (cm) | H (m) | Vstem (m3) | Root Depth (m) | GWCsoil (%) | Soil Density (kg m−3) |
|---|---|---|---|---|---|---|---|---|
| Aspen | ||||||||
| 1 | A(100) | 6 | 33.8 ± 3.8 | 36.0 ± 1.8 | 1.55 ± 0.39 | 0.60 * | 11.1 ± 3.3 | 1144 ± 36 |
| 2 | A(90), B(10) | 2 | 31.3 ± 2.2 | 32.3 ± 4.4 | 1.19 ± 0.32 | 0.75 * | 8.7 ± 1.2 | 1146 ± 58 |
| 3 | A(80), B(20) | 6 | 34.4 ± 4.4 | 32.6 ± 1.0 | 1.46 ± 0.41 | - | 17.0 ± 5.6 | 1009 ± 128 |
| 4 | A(80), B(20) | 4 | 35.8 ± 4.1 | 34.5 ± 2.4 | 1.66 ± 0.46 | 0.64 ± 0.19 | 13.5 ± 5.3 | 1058 ± 104 |
| Birch | ||||||||
| 5 | B(90), G(10) | 10 | 25.5 ± 1.8 | 29.1 ± 1.3 | 0.67 ± 0.10 | 0.85 ± 0.10 | 5.9 ± 1.2 | 969 ± 31 |
| 6 | B(90), P(20) | 9 | 35.0 ± 3.9 | 32.8 ± 1.3 | 1.43 ± 0.32 | 0.84 ± 0.10 | 7.4 ± 0.7 | 1014 ± 38 |
| Karlsruhe | - | 21 | 37.9 ± 3.6 | 19.9 ± 1.4 | 1.07 ± 0.20 | - | - | - |
| Hamburg | - | 14 | 38.9 ± 4.2 | 18.8 ± 1.5 | 1.08 ± 0.30 | - | - | - |
| Site No. | BBMPF (kNm) | BBMSF (kNm) | BBMDIF (kNm) | MOE (GPa) | Stem Breakage, N |
|---|---|---|---|---|---|
| Aspen | |||||
| 1 | 56.0 ± 24.2 | 89.7 ± 34.9 | 33.7 ± 11.1 | 9.5 ± 2.4 | 5 |
| 2 | 36.6 ± 9.6 | 54.0 ± 7.6 | 17.5 ± 2.0 | 7.4 ± 0.2 | 1 |
| 3 | 75.0 ± 39.2 | 106.0 ± 47.7 | 31.1 ± 9.4 | 8.1 ± 0.9 | 6 |
| 4 | 59.4 ± 32.3 | 84.1 ± 37.8 | 24.7 ± 14.1 | 8.7 ± 1.2 | 1 |
| Birch | |||||
| 5 | 33.5 ± 8.3 | 46.9 ± 11.6 | 13.4 ± 4.2 | 13.9 ± 2.3 | 0 |
| 6 | 110.9 ± 34.0 | 154.3 ± 40.8 | 43.4 ± 9.6 | 15.7 ± 2.8 | 0 |
| Karlsruhe | - | 102.3 ± 25.5 | - | 7.5 ± 2.3 | 0 |
| Hamburg | - | 107.7 ± 36.0 | - | 9.6 ± 1.1 | 0 |
| BBMPF | BBMSF | BBMDIF | MOE | |||||
|---|---|---|---|---|---|---|---|---|
| Predictors | Est. | p-Value | Est. | p-Value | Est. | p-Value | Est. | p-Value |
| Intercept | −19.15 | 0.33 | −18.7 | 0.44 | 1.01 | 0.90 | 8.63 | <0.001 |
| Vstem | 52.52 | <0.001 | 70.76 | <0.001 | 17.88 | <0.01 | ||
| Species | −9.82 | 0.68 | −8.29 | 0.78 | 2.12 | 0.85 | 6.12 | <0.001 |
| Vstem by species | 43.71 | 0.01 | 50.51 | 0.01 | 6.10 | 0.42 | ||
| Random Effects | ||||||||
| σ2 | 312.47 | 448.78 | 54.45 | 7.33 | ||||
| τ00 | 78.29 | 168.87 | 36.84 | 0.13 | ||||
| ICC | 0.20 | 0.27 | 0.40 | 0.02 | ||||
| N site | 6 | 6 | 6 | 6 | ||||
| Observations | 37 | 37 | 37 | 37 | ||||
| Marginal R2 | 0.76 | 0.76 | 0.48 | 0.56 | ||||
| Conditional R2 | 0.81 | 0.83 | 0.69 | 0.57 | ||||
| F-Value | p-Value | |
|---|---|---|
| Stem volume | 386.71 | <0.001 |
| Location (urban or peri-urban forest) | 0.05 | 0.81 |
| Stem volume by location interaction | 1.99 | 0.16 |
| R2 | 0.88 | |
| Model overall significance, p-value | <0.001 | |
| BBM025 | 350.73 | <0.001 |
| Urban or peri-urban forest | 4.38 | 0.04 |
| BBM025 by location interaction | 0.27 | 0.60 |
| R2 | 0.87 | |
| Model overall significance, p-value | <0.001 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krišāns, O.; Čakša, L.; Matisons, R.; Rust, S.; Elferts, D.; Seipulis, A.; Jansons, Ā. A Static Pulling Test Is a Suitable Method for Comparison of the Loading Resistance of Silver Birch (Betula pendula Roth.) between Urban and Peri-Urban Forests. Forests 2022, 13, 127. https://doi.org/10.3390/f13010127
Krišāns O, Čakša L, Matisons R, Rust S, Elferts D, Seipulis A, Jansons Ā. A Static Pulling Test Is a Suitable Method for Comparison of the Loading Resistance of Silver Birch (Betula pendula Roth.) between Urban and Peri-Urban Forests. Forests. 2022; 13(1):127. https://doi.org/10.3390/f13010127
Chicago/Turabian StyleKrišāns, Oskars, Linda Čakša, Roberts Matisons, Steffen Rust, Didzis Elferts, Andris Seipulis, and Āris Jansons. 2022. "A Static Pulling Test Is a Suitable Method for Comparison of the Loading Resistance of Silver Birch (Betula pendula Roth.) between Urban and Peri-Urban Forests" Forests 13, no. 1: 127. https://doi.org/10.3390/f13010127
APA StyleKrišāns, O., Čakša, L., Matisons, R., Rust, S., Elferts, D., Seipulis, A., & Jansons, Ā. (2022). A Static Pulling Test Is a Suitable Method for Comparison of the Loading Resistance of Silver Birch (Betula pendula Roth.) between Urban and Peri-Urban Forests. Forests, 13(1), 127. https://doi.org/10.3390/f13010127








