Temporal Dynamics of Root Reinforcement in European Spruce Forests
Abstract
:1. Introduction
2. Materials and Methods
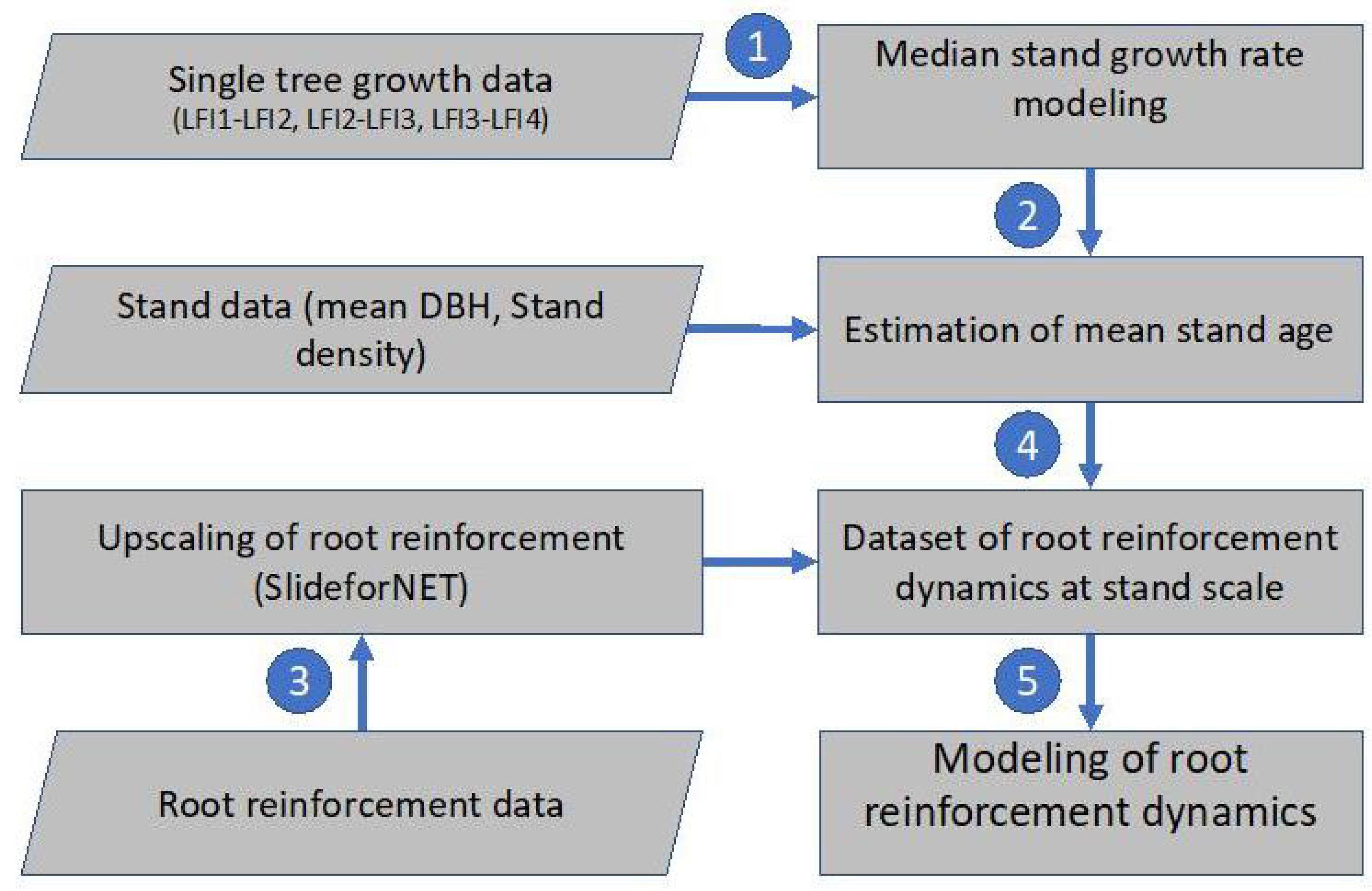
2.1. Workflow and Methodological Approaches
2.2. Data Sources
2.3. Stem Diameter Growth Modelling
2.4. Estimation of Mean Stand Age
2.5. Upscaling of Root Reinforcement
2.6. Model for the Temporal Dynamics of Root Reinforcement after Disturbances
3. Results
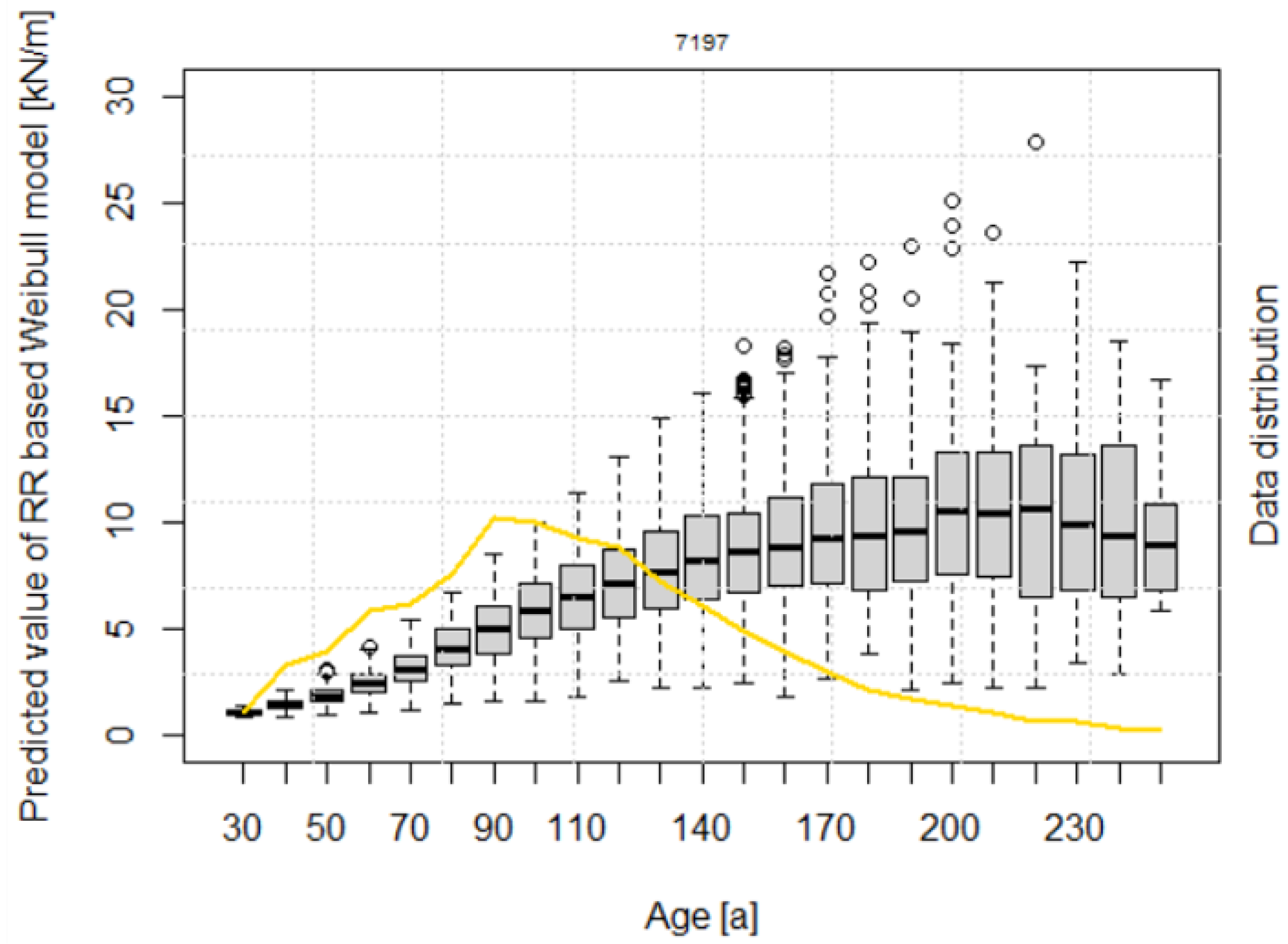
3.1. Modeling of Growth Rate
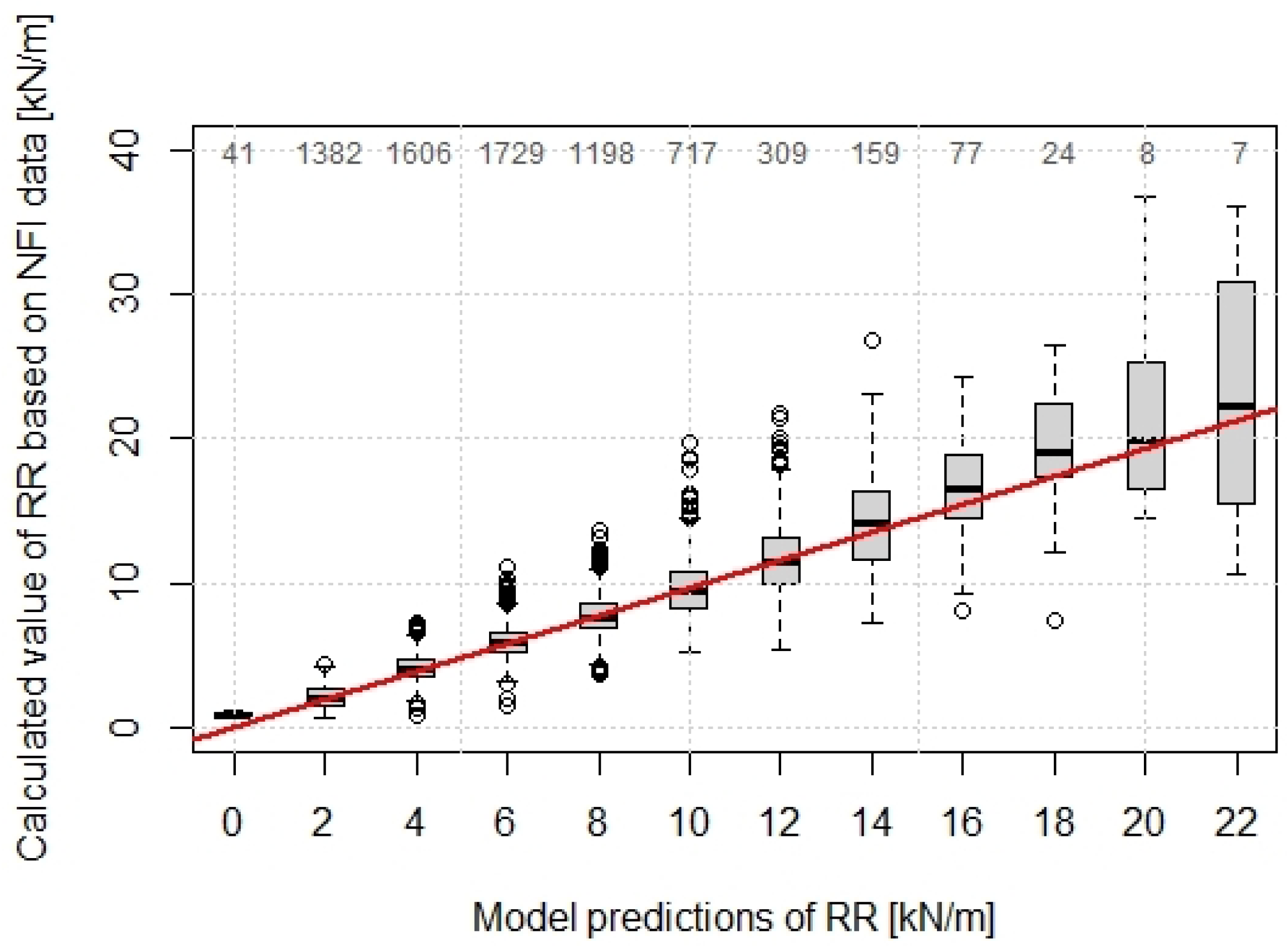
3.2. Calculation of Root Reinforcement
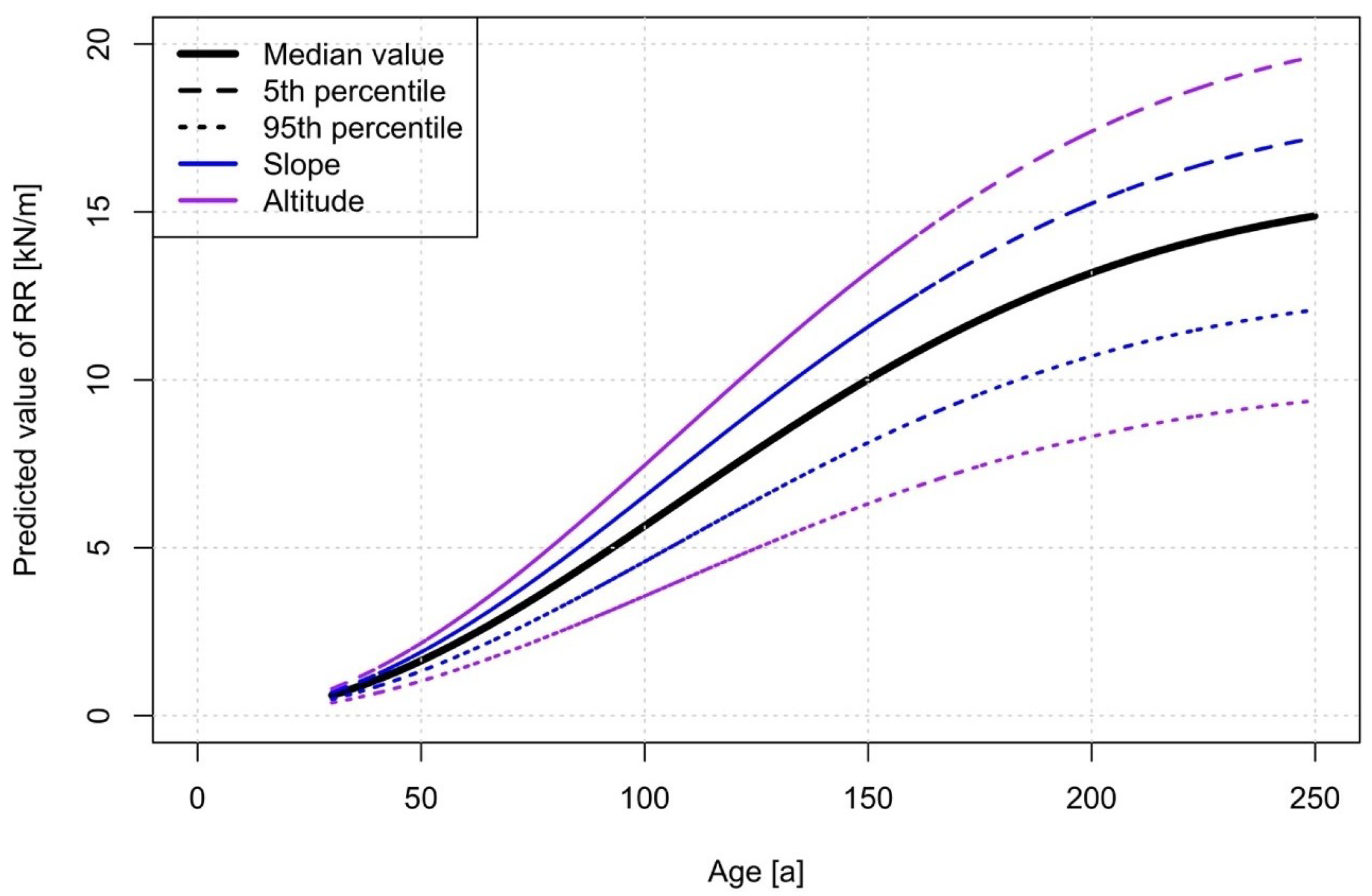
3.3. Modelling Root Reinforcement Dynamic
4. Discussion
4.1. Comparison of the Two Growth Rate Models
4.2. Correlation between Mean DBH and Stand Age
4.3. Upscaling of Root Reinforcement
4.4. Root Reinforcement Dynamics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DBH | Diameter on Breast Height |
| NFI | National Forestry Inventory |
| NLM | Nonlinear Model |
| LM | Linear Model |
| QMD | Quadratic Mean Diameter |
| RBMw | Root Bundle Model Weibull |
| RR | Root Reinforcement |
| SDI | Stand Density Index |
References
- Moos, C.; Bebi, P.; Schwarz, M.; Stoffel, M.; Sudmeier-Rieux, K.; Dorren, L. Ecosystem-based disaster risk reduction in mountains. Earth Sci. Rev. 2018, 177, 497–513. [Google Scholar] [CrossRef]
- Seidl, R.; Thom, D.; Kautz, M.; Martin-Benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, J.; et al. Forest disturbances under climate change. Nat. Clim. Chang. 2017, 7, 395–402. [Google Scholar] [CrossRef] [PubMed]
- Vergani, C.; Giadrossich, F.; Buckley, P.; Conedera, M.; Pividori, M.; Salbitano, F.; Rauch, H.; Lovreglio, R.; Schwarz, M. Root reinforcement dynamics of European coppice woodlands and their effect on shallow landslides: A review. Earth Sci. Rev. 2017, 167, 88–102. [Google Scholar] [CrossRef]
- Sidle, R.C. A conceptual model of changes in root cohesion in response to vegetation management. J. Environ. Qual. 1991, 20, 43–52. [Google Scholar] [CrossRef]
- Saito, H.; Murakami, W.; Daimaru, H.; Oguchi, T. Effect of forest clear-cutting on landslide occurrences: Analysis of rainfall thresholds at Mt. Ichifusa, Japan. Geomorphology 2017, 276, 1–7. [Google Scholar] [CrossRef]
- Rengers, F.K.; McGuire, L.A.; Oakley, N.S.; Kean, J.W.; Staley, D.M.; Tang, H. Landslides after wildfire: Initiation, magnitude, and mobility. Landslides 2020, 17, 2631–2641. [Google Scholar] [CrossRef]
- Bebi, P.; Bast, A.; Ginzler, C.; Rickli, C.; Schöngrundner, K.; Graf, F. Waldentwicklung und flachgründige Rutschungen: Eine grossflächige GIS-Analyse. Schweiz. Z. Forstwes. 2019, 170, 318–325. [Google Scholar] [CrossRef]
- Sidle, R.; Ochiai, H. Processes, prediction, and land use. In Water Resources Monograph; American Geophysical Union: Washington, DC, USA, 2006. [Google Scholar]
- Kim, J.; Kim, Y.; Jeong, S.; Hong, M. Rainfall-induced landslides by deficit field matric suction in unsaturated soil slopes. Environ. Earth Sci. 2017, 76, 1–17. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Z.; He, S. Modeling the landslide-generated debris flow from formation to propagation and run-out by considering the effect of vegetation. Landslides 2021, 18, 43–58. [Google Scholar] [CrossRef]
- O’loughlin, C.; Watson, A. Root-wood strength deterioration in radiata pine after clearfelling. NZJ For. Sci. 1979, 9, 284–293. [Google Scholar]
- Preti, F. Forest protection and protection forest: Tree root degradation over hydrological shallow landslides triggering. Ecol. Eng. 2013, 61, 633–645. [Google Scholar] [CrossRef]
- Vergani, C.; Schwarz, M.; Soldati, M.; Corda, A.; Giadrossich, F.; Chiaradia, E.A.; Morando, P.; Bassanelli, C. Root reinforcement dynamics in subalpine spruce forests following timber harvest: A case study in Canton Schwyz, Switzerland. Catena 2016, 143, 275–288. [Google Scholar] [CrossRef]
- Gehring, E.; Conedera, M.; Maringer, J.; Giadrossich, F.; Guastini, E.; Schwarz, M. Shallow landslide disposition in burnt European beech (Fagus sylvatica L.) forests. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Schwarz, M.; Preti, F.; Giadrossich, F.; Lehmann, P.; Or, D. Quantifying the role of vegetation in slope stability: A case study in Tuscany (Italy). Ecol. Eng. 2010, 36, 285–291. [Google Scholar] [CrossRef]
- Ammann, M. Schutzwirkung Abgestorbener Bäume Gegen Naturgefahren; ETHZ: Zürich, Switzerland, 2006. [Google Scholar]
- Zhu, J.; Wang, Y.; Wang, Y.; Mao, Z.; Langendoen, E.J. How does root biodegradation after plant felling change root reinforcement to soil? Plant Soil 2020, 446, 211–227. [Google Scholar] [CrossRef]
- Vergani, C.; Werlen, M.; Conedera, M.; Cohen, D.; Schwarz, M. Investigation of root reinforcement decay after a forest fire in a Scots pine (Pinus sylvestris) protection forest. For. Ecol. Manag. 2017, 400, 339–352. [Google Scholar] [CrossRef]
- Dazio, E.; Conedera, M.; Schwarz, M. Impact of different chestnut coppice managements on root reinforcement and shallow landslide susceptibility. For. Ecol. Manag. 2018, 417, 63–76. [Google Scholar] [CrossRef]
- Ziemer, R. Roots and the stability of forested slopes. In Proceedings of the International Symposium on Erosion and Sediment Transport in Pacific Rim Steeplands, Christchurch, New Zealand, 25–31 January 1981; pp. 343–361. [Google Scholar]
- Schwarz, M.; Cohen, D.; Or, D. Spatial characterization of root reinforcement at stand scale: Theory and case study. Geomorphology 2012, 171, 190–200. [Google Scholar] [CrossRef]
- Lier, M.; Schuck, A.; Fischer, C.; Moffat, A.; Linser, S. Maintenance and appropriate enhancement of protective functions in forest management (notably soil and water). In State of Europe’s Forests 2020; UNECE: Geneva, Switzerland, 2020. [Google Scholar]
- Brändli, U.; Abegg, M.; Allgaier Leuch, B. Schweizerisches Landesforstinventar: Ergebnisse der Vierten Erhebung 2009–2017. (Results of the Fourth Swiss National Forest Inventory 2009–2017); Swiss Federal Research Institute for Forest, Snow and Landscape Research, Birmensdorf (ZH) and Federal Office for the Environment (FOEN): Bern, Switzerland, 2020. [Google Scholar]
- Büchsenmeister, R. Waldinventur 2007/09: Betriebe und Bundesforste nutzen mehr als den Zuwachs. BFW Praxisinf. 2011, 24, 6–9. [Google Scholar]
- Hlásny, T.; Barka, I.; Roessiger, J.; Kulla, L.; Trombik, J.; Sarvašová, Z.; Bucha, T.; Kovalčík, M.; Čihák, T. Conversion of Norway spruce forests in the face of climate change: A case study in Central Europe. Eur. J. For. Res. 2017, 136, 1013–1028. [Google Scholar] [CrossRef]
- Thiele, J.C.; Nuske, R.S.; Ahrends, B.; Panferov, O.; Albert, M.; Staupendahl, K.; Junghans, U.; Jansen, M.; Saborowski, J. Climate change impact assessment—A simulation experiment with Norway spruce for a forest district in Central Europe. Ecol. Model. 2017, 346, 30–47. [Google Scholar] [CrossRef]
- Scherrer, D.; Ascoli, D.; Conedera, M.; Fischer, C.; Maringer, J.; Moser, B.; Nikolova, P.S.; Rigling, A.; Wohlgemuth, T. Canopy Disturbances Catalyse Tree Species Shifts in Swiss Forests. Ecosystems 2021. [Google Scholar] [CrossRef]
- Mäkinen, H.; Nöjd, P.; Kahle, H.P.; Neumann, U.; Tveite, B.; Mielikäinen, K.; Röhle, H.; Spiecker, H. Radial growth variation of Norway spruce (Picea abies (L.) Karst.) across latitudinal and altitudinal gradients in central and northern Europe. For. Ecol. Manag. 2002, 171, 243–259. [Google Scholar] [CrossRef]
- Schelhaas, M.J.; Hengeveld, G.M.; Heidema, N.; Thürig, E.; Rohner, B.; Vacchiano, G.; Vayreda, J.; Redmond, J.; Socha, J.; Fridman, J.; et al. Species-specific, pan-European diameter increment models based on data of 2.3 million trees. For. Ecosyst. 2018, 5, 1–19. [Google Scholar] [CrossRef]
- Schwarz, M.; Giadrossich, F.; Cohen, D. Modeling root reinforcement using a root-failure Weibull survival function. Hydrol. Earth Syst. Sci. 2013, 17, 4367–4377. [Google Scholar] [CrossRef]
- Brassel, P.; Brändli, U.B.; la Neige et le Paysage (Birmensdorf) Institut Fédéral de Recherches sur la Forêt; des Forêts et du Paysage Suisse Office Fédéral de l’Environnement. Swiss National Forest Inventory: Methods and Models of the Second Assessment; WSL: Birmensdorf, Switzerland, 2001. [Google Scholar]
- Fischer, C.; Traub, B. Swiss National Forest Inventory-Methods and Models of the Fourth Assessment; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Lanz, A.; Abegg, M.; Braendli, U.B.; Camin, P.; Cioldi, F.; Ginzler, C.; Fischer, C. National Forest Inventories; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Reineke, L.H. Perfection a stand-density index for even-aged forest. J. Agric. Res. 1933, 46, 627–638. [Google Scholar]
- Schütz, J.P.; Zingg, A. Improving estimations of maximal stand density by combining Reineke’s size-density rule and the yield level, using the example of spruce (Picea abies (L.) Karst.) and European Beech (Fagus sylvatica L.). Ann. For. Sci. 2010, 67, 507. [Google Scholar] [CrossRef]
- Vacchiano, G.; Derose, R.J.; Shaw, J.D.; Svoboda, M.; Motta, R. A density management diagram for Norway spruce in the temperate European montane region. Eur. J. For. Res. 2013, 132, 535–549. [Google Scholar] [CrossRef]
- Vergani, C.; Chiaradia, E.; Bassanelli, C.; Bischetti, G. Root strength and density decay after felling in a Silver Fir-Norway Spruce stand in the Italian Alps. Plant Soil 2014, 377, 63–81. [Google Scholar] [CrossRef]
- Moos, C.; Bebi, P.; Graf, F.; Mattli, J.; Rickli, C.; Schwarz, M. How does forest structure affect root reinforcement and susceptibility to shallow landslides? Earth Surf. Process. Landf. 2016, 41, 951–960. [Google Scholar] [CrossRef]
- Ryter, U. Wachstum der Fichte in Hochlagenaufforstungen im Berner Oberland; Abteilung Naturgefahren des Kantons: Bern, Switzerland, 2015. [Google Scholar]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Giadrossich, F.; Schwarz, M.; Cohen, D.; Cislaghi, A.; Vergani, C.; Hubble, T.; Phillips, C.; Stokes, A. Methods to measure the mechanical behaviour of tree roots: A review. Ecol. Eng. 2017, 109, 256–271. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Mak, T.K. Heteroscedastic regression models with non-normally distributed errors. J. Stat. Comput. Simul. 2000, 67, 21–36. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X.; Zeng, W.; Wang, J.; Meng, J. Development of a mixed-effects individual-tree basal area increment model for oaks (Quercus spp.) considering forest structural diversity. Forests 2019, 10, 474. [Google Scholar] [CrossRef]
- Krejza, J.; Cienciala, E.; Světlík, J.; Bellan, M.; Noyer, E.; Horáček, P.; Štěpánek, P.; Marek, M.V. Evidence of climate-induced stress of Norway spruce along elevation gradient preceding the current dieback in Central Europe. Trees 2021, 35, 103–119. [Google Scholar] [CrossRef]
- Panayotov, M.; Kulakowski, D.; Tsvetanov, N.; Krumm, F.; Barbeito, I.; Bebi, P. Climate extremes during high competition contribute to mortality in unmanaged self-thinning Norway spruce stands in Bulgaria. For. Ecol. Manag. 2016, 369, 74–88. [Google Scholar] [CrossRef]
- Biging, G.S.; Dobbertin, M. A comparison of distance-dependent competition measures for height and basal area growth of individual conifer trees. For. Sci. 1992, 38, 695–720. [Google Scholar]
- Vitali, V.; Brang, P.; Cherubini, P.; Zingg, A.; Nikolova, P.S. Radial growth changes in Norway spruce montane and subalpine forests after strip cutting in the Swiss Alps. For. Ecol. Manag. 2016, 364, 145–153. [Google Scholar] [CrossRef]
- Uhl, E. Variabilität des Zuwachsverhaltens unter-und zwischenständiger Bäume nach Freistellung, ein Beitrag zur Baumart Fichte (Picea abies (L.) KARST.). DVFFA Ertragskunde Jahrestag. 2009, 2009, 61–68. [Google Scholar]
- Pretzsch, H.; Dieler, J. The dependency of the size-growth relationship of Norway spruce (Picea abies [L.] Karst.) and European beech (Fagus sylvatica [L.]) in forest stands on long-term site conditions, drought events, and ozone stress. Trees 2011, 25, 355–369. [Google Scholar] [CrossRef]
- Van Kuijk, M.; Anten, N.; Oomen, R.; Van Bentum, D.; Werger, M. The limited importance of size-asymmetric light competition and growth of pioneer species in early secondary forest succession in Vietnam. Oecologia 2008, 157, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Eidgenössische Anstalt für das forstliche Versuchswesen. Ertragstafeln Fichte. Tables de Production; WSL: Birmensdorf, Switzerland, 1983. [Google Scholar]
- Stöcker, G. Wachstumsdynamik der Fichte (Picea abies [L.] KARSTEN) in naturnahen Fichtenwald-Ökosystemen des Nationalparks Hochharz 1. Regenerations-und Wachstumsphase. Forstwiss. Cent. Ver. Mit Tharandter Forstl. Jahrb. 2001, 120, 187–202. [Google Scholar] [CrossRef]
- Ammann, P.L. Untersuchung der Natürlichen Entwicklungsdynamik in Jungwaldbeständen-Biologische Rationalisierung der Waldbaulichen Produktion bei Fichte, Esche, Bergahorn und Buche. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2004. [Google Scholar]
- Schelhaas, M.; Fedorkov, A.; Jorritsma, I.; van der Sluis, T.; Slim, P.; Zlotnitsky, A. Towards Sustainable Forestry in the Pechora Basin: Results of a Simulation Study; Cluster B: Biodiversity, Land Use & Forestry Modeling; Technical Report; Alterra: Wageningen, The Netherlands, 2005. [Google Scholar]
- Simmler, K. Dendrochronological Study of the Structure and Dynamics in a Subalpine Spruce-Larch Stand in Davos (Switzerland). Master’s Thesis, ETH Zurich, Zürich, Switzerland, 2017. [Google Scholar]
- Kindermann, G.E.; Kristöfel, F.; Neumann, M.; Rössler, G.; Ledermann, T.; Schueler, S. 109 years of forest growth measurements from individual Norway spruce trees. Sci. Data 2018, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Castagneri, D.; Storaunet, K.O.; Rolstad, J. Age and growth patterns of old Norway spruce trees in Trillemarka forest, Norway. Scand. J. For. Res. 2013, 28, 232–240. [Google Scholar] [CrossRef]
- Laio, F.; D’Odorico, P.; Ridolfi, L. An analytical model to relate the vertical root distribution to climate and soil properties. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Abellán, A.; Calvet, J.; Vilaplana, J.M.; Blanchard, J. Detection and spatial prediction of rockfalls by means of terrestrial laser scanner monitoring. Geomorphology 2010, 119, 162–171. [Google Scholar] [CrossRef]
- Mao, Z.; Saint-André, L.; Bourrier, F.; Stokes, A.; Cordonnier, T. Modelling and predicting the spatial distribution of tree root density in heterogeneous forest ecosystems. Ann. Bot. 2015, 116, 261–277. [Google Scholar] [CrossRef]
- Abegg, M.; Brändli, U.B.; Cioldi, F.; Fischer, C.; Herold, A.; Meile, R.; Rösler, E.; Speich, S.; Traub, B. Ergebnistabellen und Karten der LFI-Erhebungen 1983–2017 (LFI1, LFI2, LFI3, LFI4); Eidgenössische Forschungsanstalt für Wald, Schnee und Landschaft WSL: Birmensdorf, Switzerland, 2020. [Google Scholar] [CrossRef]



| Coefficient | Value | Std Error | Error t-Value | p-Value |
|---|---|---|---|---|
| Slope x1 | −9.631 | <0.001 | ||
| Altitude x2 | −8.267 | <0.001 | ||
| Aspect x3 | 0.751 | 0.452 | ||
| SDI x4 | −21.438 | <0.001 | ||
| Slope y1 | 8.550 | <0.001 | ||
| Altitude y2 | 9.502 | <0.001 | ||
| Aspect y3 | −0.771 | 0.441 | ||
| SDI y4 | 19.523 | <0.001 | ||
| c_1 | 39.694 | <0.001 | ||
| c_2 | −33.740 | <0.001 |
| Coefficient | Value | Std Error | Error t-Value | p-Value |
|---|---|---|---|---|
| Slope x1 | −7.543 | < | ||
| Altitude x2 | −7.299 | < | ||
| Aspect x3 | −0.406 | 0.6848 | ||
| SDI x4 | −20.400 | <0.001 | ||
| Slope y1 | 2.343 | 0.0191 | ||
| Altitude y2 | 2.449 | 0.0144 | ||
| Aspect y3 | 0.264 | 0.7919 | ||
| SDI y4 | 11.249 | <0.001 | ||
| c | 37.885 | <0.001 | ||
| c | −8.996 | <0.001 |
| Coefficient | Value | Std Error | Error t-Value | p-Value |
|---|---|---|---|---|
| Slope x1 | −7.553 | |||
| Altitude x2 | −7.339 | |||
| SDI x4 | −20.429 | <0.001 | ||
| Slope y1 | 2.355 | 0.0186 | ||
| Altitude y2 | 2.466 | 0.0137 | ||
| SDI y4 | 11.272 | <0.001 | ||
| c_1 | 40.411 | <0.001 | ||
| c_2 | −9.455 | <0.001 |
| Coefficient | Value | Std Error | Error t-Value | p-Value |
|---|---|---|---|---|
| −0.06986 | 0.0027 | −25.98 | <0.001 | |
| −0.0085 | 0.0002 | −39.38 | <0.001 | |
| lambda | 150.04 | 2.7191 | 55.18 | <0.001 |
| k | 2.017 | 0.0293 | 68.79 | <0.001 |
| s_1 | 27.87 | 0.5932 | 46.99 | <0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flepp, G.; Robyr, R.; Scotti, R.; Giadrossich, F.; Conedera, M.; Vacchiano, G.; Fischer, C.; Ammann, P.; May, D.; Schwarz, M. Temporal Dynamics of Root Reinforcement in European Spruce Forests. Forests 2021, 12, 815. https://doi.org/10.3390/f12060815
Flepp G, Robyr R, Scotti R, Giadrossich F, Conedera M, Vacchiano G, Fischer C, Ammann P, May D, Schwarz M. Temporal Dynamics of Root Reinforcement in European Spruce Forests. Forests. 2021; 12(6):815. https://doi.org/10.3390/f12060815
Chicago/Turabian StyleFlepp, Gianluca, Roger Robyr, Roberto Scotti, Filippo Giadrossich, Marco Conedera, Giorgio Vacchiano, Christoph Fischer, Peter Ammann, Dominik May, and Massimiliano Schwarz. 2021. "Temporal Dynamics of Root Reinforcement in European Spruce Forests" Forests 12, no. 6: 815. https://doi.org/10.3390/f12060815
APA StyleFlepp, G., Robyr, R., Scotti, R., Giadrossich, F., Conedera, M., Vacchiano, G., Fischer, C., Ammann, P., May, D., & Schwarz, M. (2021). Temporal Dynamics of Root Reinforcement in European Spruce Forests. Forests, 12(6), 815. https://doi.org/10.3390/f12060815








