NutSpaFHy—A Distributed Nutrient Balance Model to Predict Nutrient Export from Managed Boreal Headwater Catchments
Abstract
1. Introduction
2. Materials and Methods
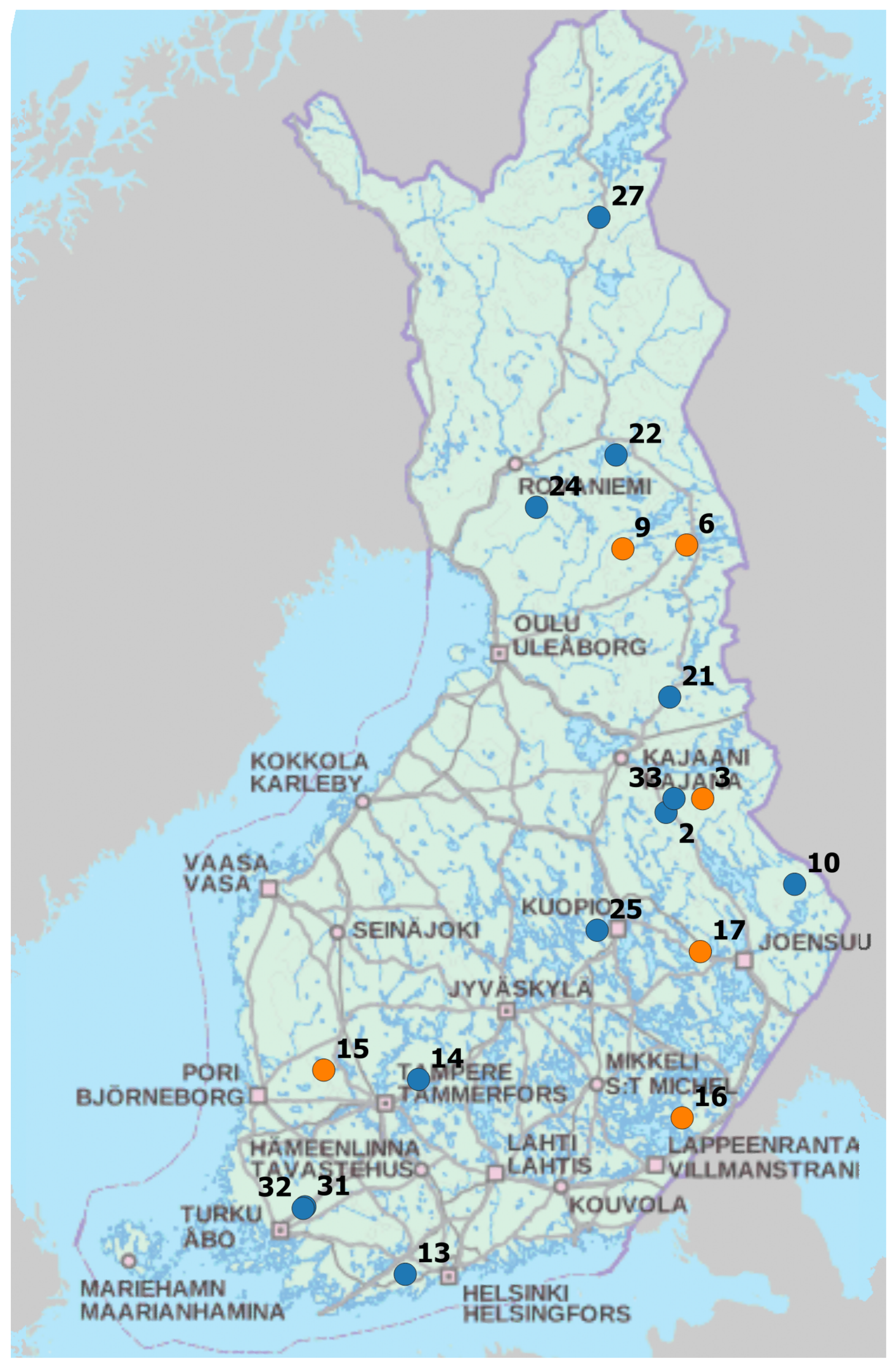
2.1. Field Data
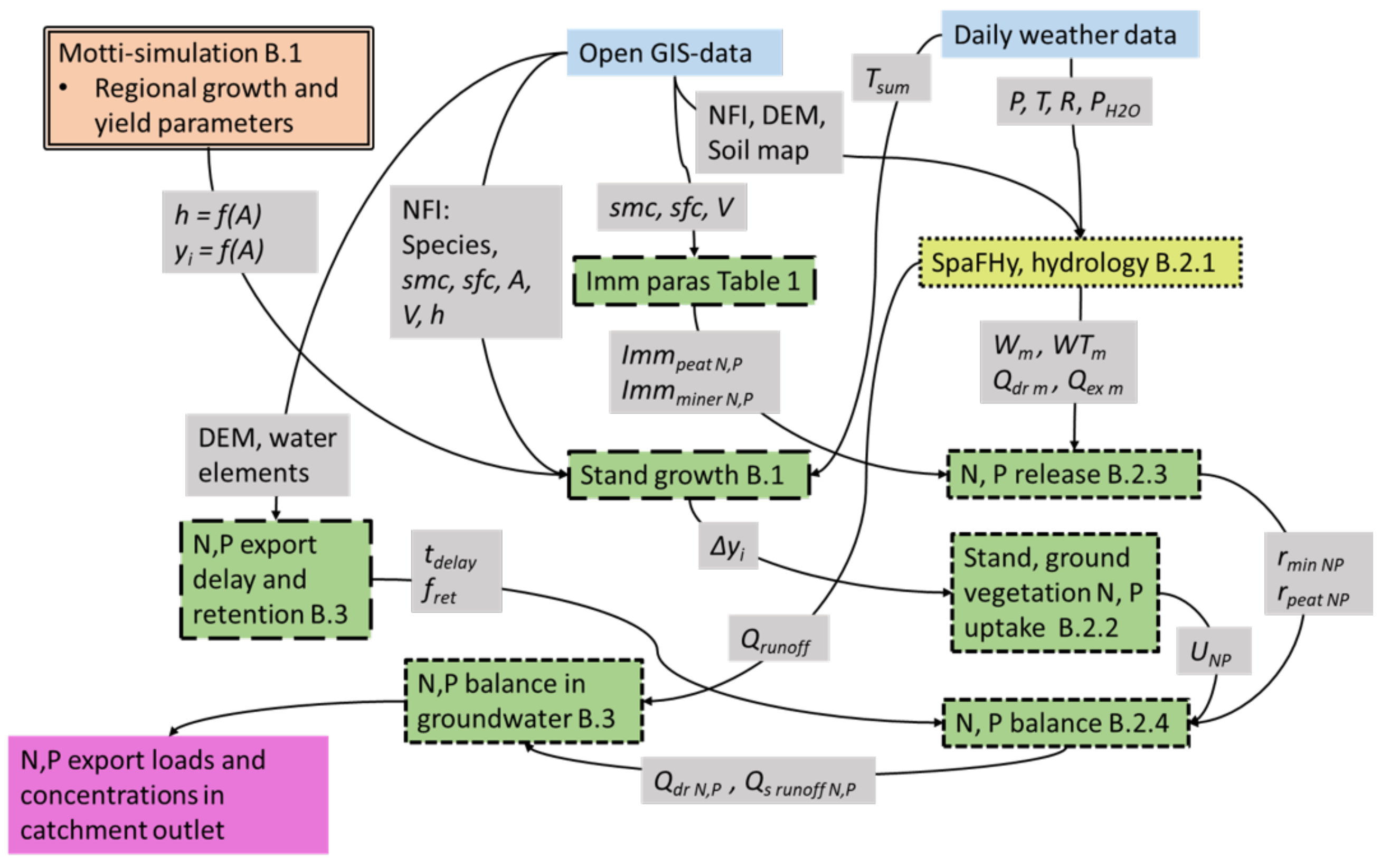
2.2. Model Description
2.3. Calibration
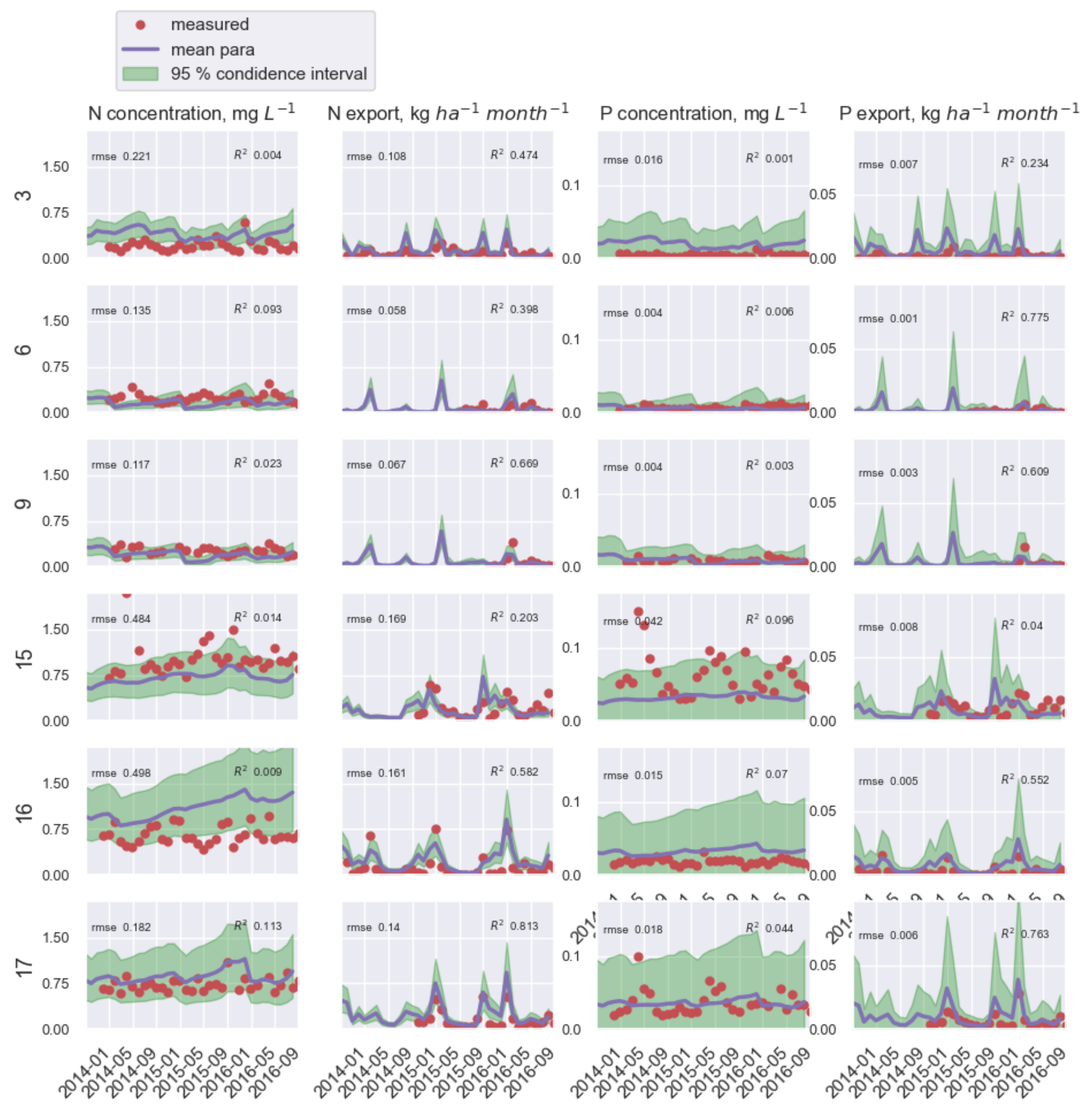
2.4. Model Testing
2.5. Application to Clear-Cut Scenario
3. Results
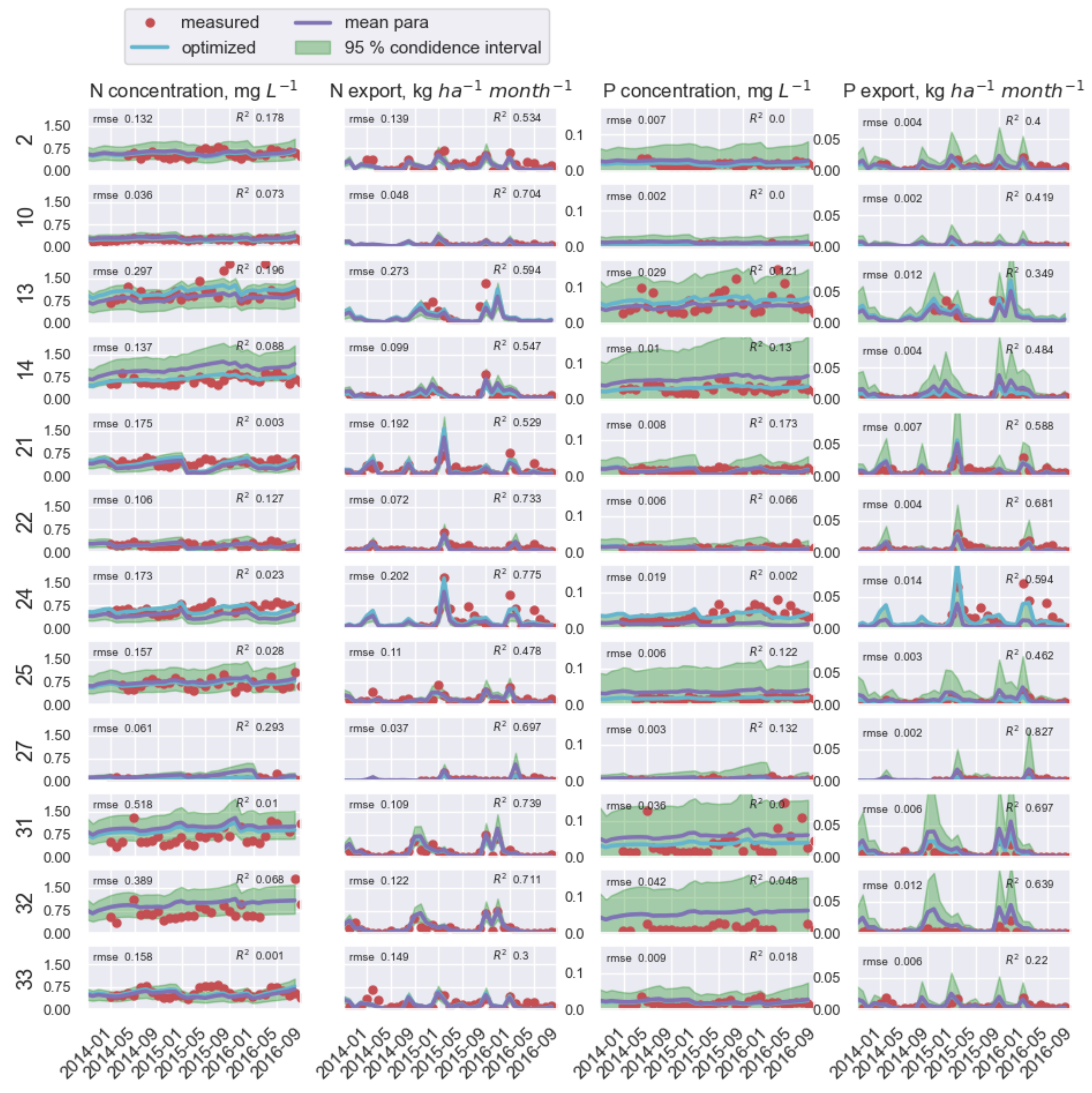
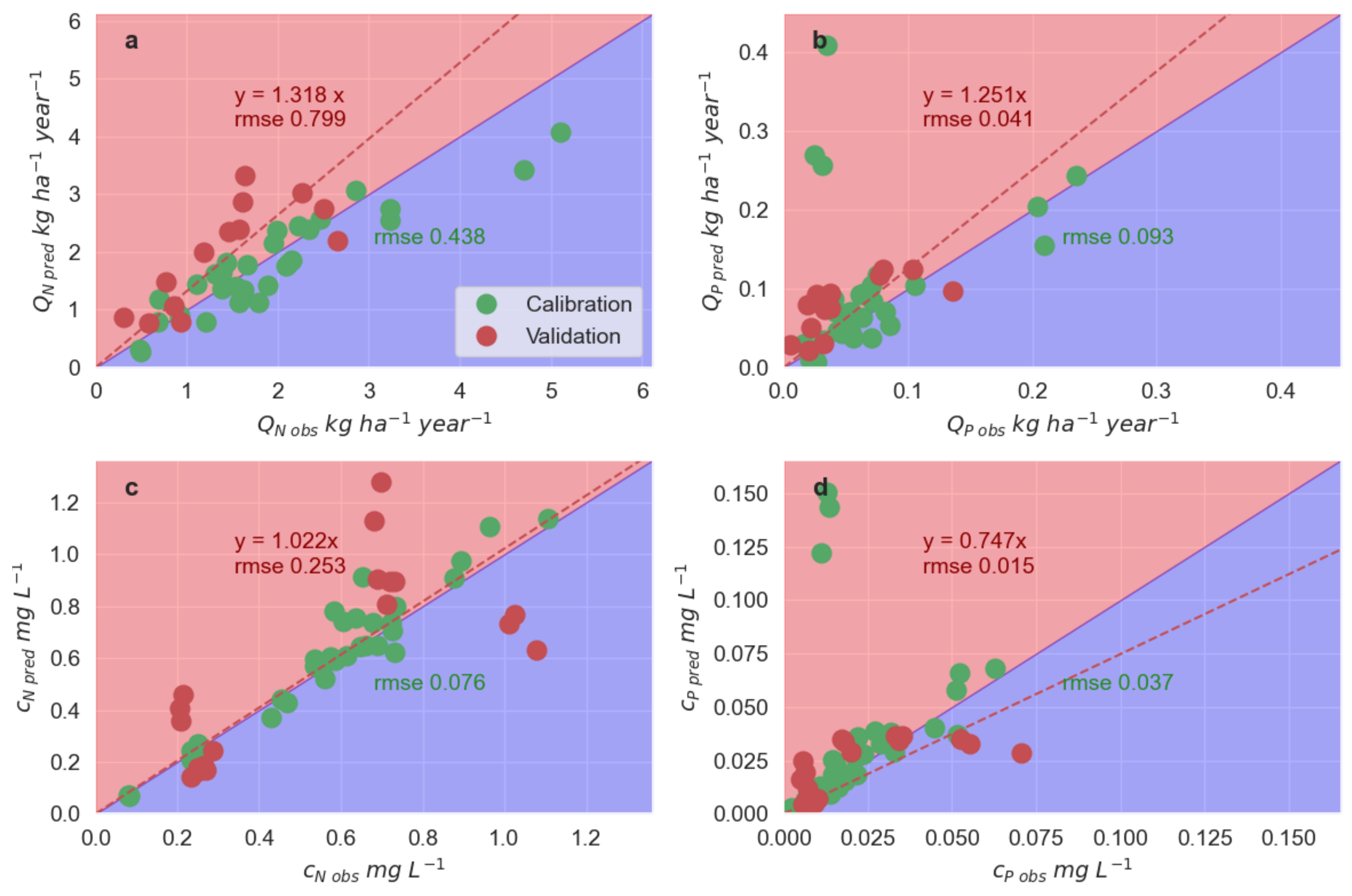
3.1. Model Calibration and Immobilization Parameters
3.2. N and P Concentration and Export Load
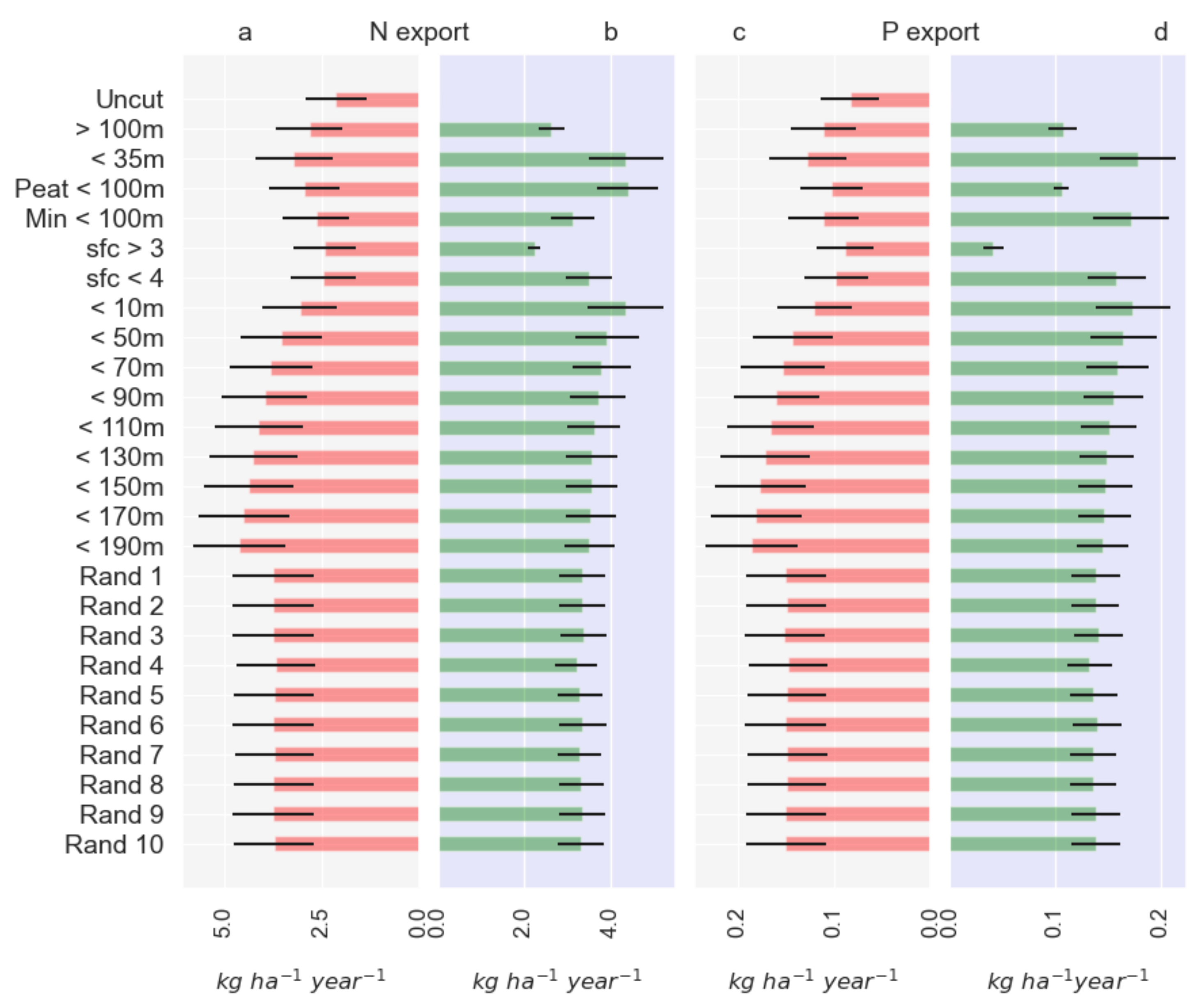
3.3. NutSpaFHy Application
4. Discussion
4.1. Model Requirements
4.2. Evaluation of Model Structure
4.3. Model Performance at Study Catchments
4.4. Nutrient Export from Different Harvesting Scenarios
4.5. Potential for Forest Management Planning
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Sites and stand | |
| A | Stand age, years |
| Relative height growth performance, m m−1 | |
| Index age, years | |
| Observed stand age in a grid cell, years | |
| h | Stand height, m |
| h at , m | |
| Observed stand mean height (m) in the grid cell | |
| Mean stand height predicted by a priori computed parameters | |
| at age , m | |
| Observed leaf area index, m2 m−2 | |
| Height growth parameter, calculated a priori | |
| Height growth parameter, calculated a priori | |
| Stand yield parameter, calculated a priori | |
| Stand yield parameter, calculated a priori | |
| Site main class, class variable (mineral soil, fen, bog, open peatland) | |
| Site fertility class, class variable (fertility dcreases from to ) | |
| Duration of the simulation, years | |
| V | Stand volume, m3 ha−1 |
| Stand volume at the end of simulation, m3 ha−1 | |
| y | Stand yield, m3 ha−1 |
| Stand yield at index age , m3 ha−1 | |
| Stand yield between time points, m3 ha−1 | |
| Weather data | |
| Precipitation, mm day−1, FMI data | |
| Vapor pressure, hPa, FMI data | |
| R | Global radiation, W m−2, FMI data |
| T | Air temperature, C, FMI data |
| Temperature sum, degree-days | |
| Monthly temperature sum, degree-days | |
| Water and nutrient variables | |
| Catchment area, m2 | |
| B | Parameter in peat respiration model |
| Content of N, P in the forest stand, kg ha−1 | |
| N, P concentrations in leaf mass, kg kg−1 | |
| N, P concentration in ground vegetation component i, mg g−1 | |
| Observed monthly mean N,P concentration in runoff water, mg L−1 | |
| Predicted monthly mean N,P concentration in runoff water, mg L−1 | |
| Concentration of N,P in soil organic matter in mineral soils, kg kg−1 | |
| Concentration of C in soil organic matter in mineral soils, kg kg−1 | |
| Peat N,P concentration, kg kg−1 | |
| Conversion factor from g m−2 h−1 to kg ha−1 day−1 | |
| Conversion factor from CO2 to C | |
| Conversion factor from kg ha−1 month−1 to kg grid-cell−1 month −1 | |
| Conversion factor from m s−1 to m month −1 | |
| Peat depth, m | |
| Distance to receiving water body, m | |
| N and P retention factor, kg kg−1 | |
| Moisture restriction function for mineal soil respiration | |
| Biomass in ground vegetation i, kg ha−1 | |
| Groundwater N and P storage in catchment, kg | |
| Groundwater storage in catchment, m3 | |
| i | Ground vegetation component: dwarf shrub, herbs and sedges, |
| mosses, Sphagna | |
| N, P immobilization in decomposition, peatlands, kg kg−1 | |
| N, P immobilization in decomposition, mineral soil, kg kg−1 | |
| Saturated hydraulic conductivity, m s−1 | |
| leaf longevity, years | |
| b, k, Stand nutrient content parameters from [13] | |
| Soil porosity, m3 m−3 | |
| Peat bulk density, kg m−3 | |
| reference rate of heterotrophic respiration | |
| kg ha−1 month−1 | |
| Heterotrophic respiration from mineral soil, | |
| kg CO2 ha−1 month−1 | |
| Release of N,P in the organic matter decomposition, kg ha−1 month−1 | |
| Heterotrophic respiration from peat soil, kg CO2 ha−1 month−1 | |
| Heterotrophic respiration from peat soil in reference temperature, | |
| kg CO2 ha−1 month−1 | |
| Release of N,P in the peat decomposition, kg ha−1 month−1 | |
| N, P retranslocation before litterfall in ground vegetation | |
| component i, kg kg−1 | |
| Number of days in month | |
| N, P retranslocation before litterfall, kg kg−1 | |
| s | Slope parameter in the calibration process |
| Temperature sensitivity parameter | |
| Water flux down from root layer, m month−1 | |
| N, P flux down from root layer, kg ha−1 month−1 | |
| N, P flux down from root layer, delayed with | |
| Water flux from soil to surface runoff, m month−1 | |
| N, P flux from soil to surface runoff, kg ha−1 month−1 | |
| N, P outflux from catchment with groundwater, kg month−1 | |
| Outflux of N and P from the catchment, kg month−1 | |
| Runoff from catchment, m month−1 | |
| N, P flux with runoff from catchment, kg ha−1 month−1 | |
| Runoff from catchment, m month−1 | |
| N, P flux with surface runoff, kg ha−1 month−1 | |
| Specific leaf area, m2 kg−1 | |
| Mean water flow path slope, m m−1 | |
| Turnover rate in ground vegetation component i, years−1 | |
| Soil temperature, C | |
| Soil temperature where = 0, C | |
| Reference soil temperature, C | |
| Time delay from to stream, months | |
| Monthly uptake of N,P, kg ha−1 month−1 | |
| Total N, P uptake of stand and ground vegetation, kg ha−1 | |
| Uptake of N, P to compensate the nutrient lost in litterfall, kg ha−1 | |
| N, P uptake by ground vegetation, kg ha −1 | |
| Stand net uptake of N, P, kg ha−1 | |
| Ground vegetation uptake of N, P to compensate the nutrient | |
| lost in litterfall, kg ha−1 year−1 | |
| Ground vegetation N,P net uptake, kg ha−1 | |
| Monthly mean water content in root layer, m3 m−3 | |
| Monthly mean water table, m |
Appendix A. Catchment Properties
| Calibration | ||||||||||
| 2 | 0.88 | 0.17 | 0.22 | 0.03 | 0.03 | 0.46 | 0.09 | 0.03 | 0.55 | 0.00 |
| 10 | 0.94 | 0.02 | 0.35 | 0.11 | 0.00 | 0.23 | 0.25 | 0.00 | 0.48 | 0.02 |
| 13 | 0.83 | 0.02 | 0.03 | 0.00 | 0.01 | 0.03 | 0.02 | 0.19 | 0.55 | 0.01 |
| 14 | 0.82 | 0.05 | 0.04 | 0.00 | 0.01 | 0.12 | 0.01 | 0.25 | 0.63 | 0.00 |
| 21 | 0.82 | 0.06 | 0.22 | 0.00 | 0.02 | 0.24 | 0.06 | 0.02 | 0.67 | 0.00 |
| 22 | 0.89 | 0.02 | 0.17 | 0.06 | 0.02 | 0.16 | 0.08 | 0.01 | 0.73 | 0.00 |
| 24 | 0.84 | 0.05 | 0.39 | 0.09 | 0.04 | 0.30 | 0.16 | 0.00 | 0.45 | 0.00 |
| 25 | 0.81 | 0.10 | 0.13 | 0.00 | 0.02 | 0.19 | 0.04 | 0.25 | 0.43 | 0.00 |
| 27 | 0.89 | 0.00 | 0.02 | 0.02 | 0.02 | 0.03 | 0.00 | 0.00 | 0.09 | 0.17 |
| 31 | 0.85 | 0.00 | 0.05 | 0.00 | 0.00 | 0.03 | 0.02 | 0.12 | 0.77 | 0.03 |
| 32 | 0.90 | 0.00 | 0.08 | 0.00 | 0.00 | 0.03 | 0.05 | 0.06 | 0.65 | 0.06 |
| 33 | 0.84 | 0.06 | 0.24 | 0.00 | 0.01 | 0.28 | 0.05 | 0.06 | 0.64 | 0.00 |
| Test | ||||||||||
| 3 | 0.89 | 0.03 | 0.14 | 0.00 | 0.02 | 0.15 | 0.02 | 0.06 | 0.76 | 0.01 |
| 6 | 0.88 | 0.01 | 0.33 | 0.04 | 0.01 | 0.27 | 0.09 | 0.00 | 0.62 | 0.00 |
| 9 | 0.85 | 0.01 | 0.15 | 0.15 | 0.00 | 0.22 | 0.08 | 0.00 | 0.69 | 0.00 |
| 15 | 0.88 | 0.01 | 0.32 | 0.02 | 0.00 | 0.17 | 0.19 | 0.02 | 0.48 | 0.11 |
| 16 | 0.88 | 0.03 | 0.39 | 0.00 | 0.02 | 0.33 | 0.09 | 0.05 | 0.51 | 0.00 |
| 17 | 0.83 | 0.13 | 0.19 | 0.00 | 0.03 | 0.31 | 0.02 | 0.19 | 0.45 | 0.01 |
Appendix B. Description of NutSpaFHy
Appendix B.1. Regional Scale Growth and Yield
Appendix B.2. Grid-Cell Water and Nutrient Balance
Appendix B.2.1. Soil Moisture and Water Flux from Rooting Zone to Groundwater
Appendix B.2.2. Nutrient Uptake
| i | |||||
|---|---|---|---|---|---|
| Dwarf shrubs | 12.0 | 1.0 | 0.2 | 0.5 | 0.5 |
| Herbs, sedges | 18.0 | 2.0 | 1.0 | 0.5 | 0.5 |
| Upland mosses | 12.5 | 1.4 | 0.3 | 0 | 0 |
| Sphagna | 6.0 | 1.4 | 0.3 | 0 | 0 |
Appendix B.2.3. Nutrient Release
Appendix B.2.4. Nutrient Balance
Appendix B.3. Nutrient Export
References
- Laurén, A.; Palviainen, M.; Page, S.; Evans, C.; Urzainki, I.; Hökkä, H. Nutrient Balance as a Tool for Maintaining Yield and Mitigating Environmental Impacts of Acacia Plantation in Drained Tropical Peatland—Description of Plantation Simulator. Forests 2021, 12, 312. [Google Scholar] [CrossRef]
- Finér, L.; Lepistö, A.; Karlsson, K.; Räike, A.; Härkönen, L.; Huttunen, M.; Joensuu, S.; Kortelainen, P.; Mattsson, T.; Piirainen, S.; et al. Drainage for forestry increases N, P and TOC export to boreal surface waters. Sci. Total Environ. 2021, 762, 144098. [Google Scholar] [CrossRef] [PubMed]
- Sponseller, R.A.; Gundale, M.J.; Futter, M.; Ring, E.; Nordin, A.; Näsholm, T.; Laudon, H. Nitrogen dynamics in managed boreal forests: Recent advances and future research directions. Ambio 2016, 45, 175–187. [Google Scholar] [CrossRef] [PubMed]
- Palviainen, M.; Finér, L.; Laurén, A.; Launiainen, S.; Piirainen, S.; Mattsson, T.; Starr, M. Nitrogen, Phosphorus, Carbon, and Suspended Solids Loads from Forest Clear-Cutting and Site Preparation: Long-Term Paired Catchment Studies from Eastern Finland. Ambio 2014, 43, 218–233. [Google Scholar] [CrossRef] [PubMed]
- Nieminen, M. Export of dissolved organic carbon, nitrogen and phosphorus following clear-cutting of three Norway spruce forests growing on drained peatlands in southern Finland. Silva Fenn. 2004, 38, 123–132. [Google Scholar] [CrossRef]
- Ide, J.; Finér, L.; Laurén, A.; Piirainen, S.; Launiainen, S. Effects of clear-cutting on annual and seasonal runoff from a boreal forest catchment in eastern Finland. For. Ecol. Manag. 2013, 304, 482–491. [Google Scholar] [CrossRef]
- Kreutzweiser, D.P.; Hazlett, P.W.; Gunn, J.M. Logging impacts on the biogeochemistry of boreal forest soils and nutrient export to aquatic systems: A review. Environ. Rev. 2008, 16, 157–179. [Google Scholar] [CrossRef]
- Laurén, A.; Finér, L.; Koivusalo, H.; Kokkonen, T.; Karvonen, T.; Kellomäki, S.; Mannerkoski, H.; Ahtiainen, M. Water and nitrogen processes along a typical water flowpath and streamwater exports from a forested catchment and changes after clear-cutting: A modelling study. Hydrol. Earth Syst. Sci. 2005, 9, 657–674. [Google Scholar] [CrossRef]
- Ahtiainen, M.; Huttunen, P. Long term effects of forestry managements on water quality and loading in brooks. Boreal Environ. Res. 1999, 4, 101–114. [Google Scholar]
- Kortelainen, P.; Saukkonen, S.; Mattsson, T. Leaching of nitrogen from forested catchments in Finland. Glob. Biogeochem. Cycles 1997, 11, 627–638. [Google Scholar] [CrossRef]
- Sarkkola, S.; Koivusalo, H.; Laurén, A.; Kortelainen, P.; Mattsson, T.; Palviainen, M.; Piirainen, S.; Starr, M.; Finér, L. Trends in hydrometeorological conditions and stream water organic carbon in boreal forested catchments. Sci. Total Environ. 2009, 408, 92–101. [Google Scholar] [CrossRef] [PubMed]
- D’Arcy, P.; Carignan, R. Influence of catchment topography on water chemistry in southeastern Québec Shield lakes. Can. J. Fish. Aquat. Sci. 1997, 54, 2215–2227. [Google Scholar] [CrossRef]
- Palviainen, M.; Finér, L. Estimation of nutrient removals in stem-only and whole-tree harvesting of Scots pine, Norway spruce, and birch stands with generalized nutrient equations. Eur. J. For. Res. 2012, 131, 945–964. [Google Scholar] [CrossRef]
- Palviainen, M.; Finér, L.; Mannerkoski, H.; Piirainen, S.; Starr, M. Responses of ground vegetation species to clear-cutting in a boreal forest: Aboveground biomass and nutrient contents during the first 7 years. Ecol. Res. 2005, 20, 652–660. [Google Scholar] [CrossRef]
- Futter, M.; Ring, E.; Högbom, L.; Entenmann, S.; Bishop, K. Consequences of nitrate leaching following stem-only harvesting of Swedish forests are dependent on spatial scale. Environ. Pollut. 2010, 158, 3552–3559. [Google Scholar] [CrossRef]
- Palviainen, M.; Finér, L.; Laurén, A.; Högbom, L. A method to estimate the impact of clear-cutting on nutrient concentrations in boreal headwater streams. Ambio 2015, 44, 521–531. [Google Scholar] [CrossRef]
- Kenttämies, K. A method for calculating nutrient loads from forestry: Principles and national applications in Finland. Int. Ver. Für Theor. Und Angew. Limnol. Verhandlungen 2006, 29, 1591–1594. [Google Scholar] [CrossRef]
- Palviainen, M.; Laurén, A.; Launiainen, S.; Piirainen, S. Predicting the export and concentrations of organic carbon, nitrogen and phosphorus in boreal lakes by catchment characteristics and land use: A practical approach. Ambio 2016, 45, 933–945. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, J.; Marttila, H.; Launiainen, S.; Lepistö, A.; Kløve, B. Combined use of satellite image analysis, land-use statistics, and land-use-specific export coefficients to predict nutrients in drained peatland catchment. Sci. Total Environ. 2021, 779, 146419. [Google Scholar] [CrossRef] [PubMed]
- Whitehead, P.G.; Wilson, E.; Butterfield, D. A semi-distributed Integrated Nitrogen model for multiple source assessment in Catchments (INCA): Part I—model structure and process equations. Sci. Total Environ. 1998, 210, 547–558. [Google Scholar] [CrossRef]
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Giesler, R.; Högberg, M.; Högberg, P. Soil chemistry and plants in Fennoscandian boreal forest as exemplified by a local gradient. Ecology 1998, 79, 119–137. [Google Scholar] [CrossRef]
- Seibert, J.; Stendahl, J.; Sørensen, R. Topographical influences on soil properties in boreal forests. Geoderma 2007, 141, 139–148. [Google Scholar] [CrossRef]
- Rodhe, A.; Seibert, J. Wetland occurrence in relation to topography: A test of topographic indices as moisture indicators. Agric. For. Meteorol. 1999, 98, 325–340. [Google Scholar] [CrossRef]
- Laudon, H.; Kuglerová, L.; Sponseller, R.A.; Futter, M.; Nordin, A.; Bishop, K.; Lundmark, T.; Egnell, G.; Ågren, A.M. The role of biogeochemical hotspots, landscape heterogeneity, and hydrological connectivity for minimizing forestry effects on water quality. Ambio 2016, 45, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Kuglerová, L.; Ågren, A.; Jansson, R.; Laudon, H. Towards optimizing riparian buffer zones: Ecological and biogeochemical implications for forest management. For. Ecol. Manag. 2014, 334, 74–84. [Google Scholar] [CrossRef]
- Lidberg, W.; Nilsson, M.; Ågren, A. Using machine learning to generate high-resolution wet area maps for planning forest management: A study in a boreal forest landscape. Ambio 2020, 49, 475–486. [Google Scholar] [CrossRef]
- Ring, E.; Ågren, A.; Bergkvist, I.; Finér, L.; Johansson, F.; Högbom, L. A Guide to Using Wet Area Maps in Forestry; Skogforsk Arbetsrapport 1051-2020; Skogforsk: Uppsala, Sweden, 2020; p. 36. [Google Scholar]
- Launiainen, S.; Guan, M.; Salmivaara, A.; Kieloaho, A.J. Modeling boreal forest evapotranspiration and water balance at stand and catchment scales: A spatial approach. Hydrol. Earth Syst. Sci. 2019, 23, 3457–3480. [Google Scholar] [CrossRef]
- Näykki, T.; Kyröläinen, H.; Witick, A.; Mäkinen, I.; Pehkonen, R.; Väisänen, T.; Sainio, P.; Luotola, M. Laatusuositukset ympäristöhallinnon vedenlaaturekistereihin vietävälle tiedolle: Vesistä tehtävien analyyttien määritysrajat, mittausepävarmuudet sekä säilytysajat ja-tavat (Quality Recommendations for Data Entered into the Environmental Administration’s Water Quality Registers: Quantification Limits, Measurement Uncertainties, Storage Times and Methods Associated with Analytes Determined from Waters). Available online: https://helda.helsinki.fi/handle/10138/40920 (accessed on 6 June 2021).
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Salminen, H.; Lehtonen, M.; Hynynen, J. Reusing legacy FORTRAN in the MOTTI growth and yield simulator. Comput. Electron. Agric. 2005, 49, 103–113. [Google Scholar] [CrossRef]
- Muukkonen, P.; Mäkipää, R. Empirical biomass models of understorey vegetation in boreal forests according to stand and site attributes. Boreal Environ. Res. 2005, 11, 355–369. [Google Scholar]
- Laurén, A.; Palviainen, M.; Launiainen, S.; Leppä, K.; Stenberg, L.; Urzainki, I.; Nieminen, M.; Laiho, R.; Hökkä, H. Drainage and Stand Growth Response in Peatland Forests—Description, Testing, and Application of Mechanistic Peatland Simulator SUSI. Forests 2021, 12, 293. [Google Scholar] [CrossRef]
- Pumpanen, J.; Ilvesniemi, H.; Hari, P. A Process-Based Model for Predicting Soil Carbon Dioxide Efflux and Concentration. Soil Sci. Soc. Am. J. 2003, 67, 402–413. [Google Scholar] [CrossRef]
- Ojanen, P.; Minkkinen, K.; Alm, J.; Penttilä, T. Soil–atmosphere CO2, CH4 and N2O fluxes in boreal forestry-drained peatlands. For. Ecol. Manag. 2010, 260, 411–421. [Google Scholar] [CrossRef]
- Heikkinen, K.; Karppinen, A.; Karjalainen, S.; Postila, H.; Hadzic, M.; Tolkkinen, M.; Marttila, H.; Ihme, R.; Kløve, B. Long-term purification efficiency and factors affecting performance in peatland-based treatment wetlands: An analysis of 28 peat extraction sites in Finland. Ecol. Eng. 2018, 117, 153–164. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J.; Freer, J.E.; Lamb, R. A history of TOPMODEL. Hydrol. Earth Syst. Sci. 2021, 25, 527–549. [Google Scholar] [CrossRef]
- Kreutzer, K.; Butterbach-Bahl, K.; Rennenberg, H.; Papen, H. The complete nitrogen cycle of an N-saturated spruce forest ecosystem. Plant Biol. 2009, 11, 643–649. [Google Scholar] [CrossRef]
- Kortelainen, P.; Mattsson, T.; Finér, L.; Ahtiainen, M.; Saukkonen, S.; Sallantaus, T. Controls on the export of C, N, P and Fe from undisturbed boreal catchments, Finland. Aquat. Sci. 2006, 68, 453–468. [Google Scholar] [CrossRef]
- Brookshire, E.N.J.; Valett, H.M.; Thomas, S.A.; Webster, J.R. Coupled Cycling of Dissolved Organic Nnitrogen AND Carbon in a Forest Stream. Ecology 2005, 86, 2487–2496. [Google Scholar] [CrossRef]
- Stedmon, C.A.; Markager, S.; Tranvik, L.; Kronberg, L.; Slätis, T.; Martinsen, W. Photochemical production of ammonium and transformation of dissolved organic matter in the Baltic Sea. Mar. Chem. 2007, 104, 227–240. [Google Scholar] [CrossRef]
- Tahovska, K.; Kaňa, J.; Barta, J.; Oulehle, F.; Richter, A.; Santruckova, H. Microbial N immobilization is of great importance in acidified mountain spruce forest soils. Soil Biol. Biochem. 2013, 59, 58–71. [Google Scholar] [CrossRef]
- Chertov, O.; Komarov, A.; Nadporozhskaya, M.; Bykhovets, S.; Zudin, S. ROMUL—A model of forest soil organic matter dynamics as a substantial tool for forest ecosystem modeling. Ecol. Model. 2001, 138, 289–308. [Google Scholar] [CrossRef]
- Berg, B.; McClaugherty, C. Plant Litter. Decomposition, Humus Formation, Carbon Sequestration; Springer: Berlin, Germany, 2003. [Google Scholar] [CrossRef]
- Jackson-Blake, L.; Dunn, S.; Helliwell, R.; Skeffington, R.; Stutter, M.; Wade, A. How well can we model stream phosphorus concentrations in agricultural catchments? Environ. Model. Softw. 2014, 64. [Google Scholar] [CrossRef]
- Janes-Bassett, V.; Davies, J.; Rowe, E.C.; Tipping, E. Simulating long-term carbon nitrogen and phosphorus biogeochemical cycling in agricultural environments. Sci. Total Environ. 2020, 714, 136599. [Google Scholar] [CrossRef] [PubMed]
- Kaila, A.; Sarkkola, S.; Laurén, A.; Ukonmaanaho, L.; Koivusalo, H.; Xiao, L.; O’Driscoll, C.; Asam, Z.u.Z.; Tervahauta, A.; Nieminen, M. Phosphorus export from drained Scots pine mires after clear-felling and bioenergy harvesting. For. Ecol. Manag. 2014, 325, 99–107. [Google Scholar] [CrossRef]
- Kaila, A.; Laurén, A.; Sarkkola, S.; Koivusalo, H.; Ukonmaanaho, L.; O’Driscoll, C.; Xiao, L.; Asam, Z.u.Z.; Nieminen, M. Effect of clear-felling and harvest residue removal on nitrogen and phosphorus export from drained Norway spruce mires in southern Finland. Boreal Environ. Res. 2015, 20, 693–706. [Google Scholar]
- Koskinen, M.; Tahvanainen, T.; Sarkkola, S.; Menberu, M.W.; Laurén, A.; Sallantaus, T.; Marttila, H.; Ronkanen, A.K.; Parviainen, M.; Tolvanen, A.; et al. Restoration of nutrient-rich forestry-drained peatlands poses a risk for high exports of dissolved organic carbon, nitrogen, and phosphorus. Sci. Total Environ. 2017, 586, 858–869. [Google Scholar] [CrossRef]
- Mäkisara, K.; Katila, M.; Peräsaari, J.; Tomppo, E. The Multi-Source National Forest Inventory of Finland–Methods and Results 2013. Available online: https://jukuri.luke.fi/handle/10024/532147 (accessed on 6 June 2021).
- Laine-Kaulio, H.; Backnäs, S.; Karvonen, T.; Koivusalo, H.; McDonnell, J.J. Lateral subsurface stormflow and solute transport in a forested hillslope: A combined measurement and modeling approach. Water Resour. Res. 2014, 50, 8159–8178. [Google Scholar] [CrossRef]
- Warsta, L.; Karvonen, T.; Koivusalo, H.; Paasonen-Kivekäs, M.; Taskinen, A. Simulation of water balance in a clayey, subsurface drained agricultural field with three-dimensional FLUSH model. J. Hydrol. 2013, 476, 395–409. [Google Scholar] [CrossRef]
- Laurén, A.; Heinonen, J.; Koivusalo, H.; Sarkkola, S.; Tattari, S.; Mattsson, T.; Ahtiainen, M.; Joensuu, S.; Kokkonen, T.; Finér, L. Implications of Uncertainty in a Pre-treatment Dataset when Estimating Treatment Effects in Paired Catchment Studies: Phosphorus Loads from Forest Clear-cuts. Water Air Soil Pollut. 2009, 169, 251–261. [Google Scholar] [CrossRef]
- Lundin, L. Effects on hydrology and surface water chemistry of regeneration cuttings in peatland forests. Int. Peat J. 1999, 9, 118–126. [Google Scholar]
- Laiho, R.; Laine, J. Nitrogen and phosphorus stores in Peatlands drained for forestry in Finland. Scand. J. For. Res. 1994, 9, 251–260. [Google Scholar] [CrossRef]
- Laiho, R.; Laine, J. Changes in mineral element concentrations in peat soils drained for forestry in Finland. Scand. J. For. Res. 1995, 10, 218–224. [Google Scholar] [CrossRef]
- Laine, J.; Vanha-Majamaa, I. Vegetation ecology along a trophic gradient on drained pine mires in southern Finland. Ann. Bot. Fenn. 1992, 29, 213–233. [Google Scholar]
- Tamminen, P. Kangasmaan ravinnetunnusten ilmaiseminen ja viljavuuden alueellinen vaihtelu Etelä-Suomessa. Folia For. 1991, 777, 40. [Google Scholar]
- Fabrika, M.; Pretzsch, H. Forest Ecosystem Analysis and Modelling; Faculty of Forestry, Department of Forest Management and Geodesy, Technical University in Zvolen: Zvolen, Slovakia, 2013; pp. 1–620. [Google Scholar]
- Hynynen, J.; Ojansuu, R.; Hökkä, H.; Siipilehto, J.; Salminen, H.; Haapala, P. Models for predicting stand development in MELA system. Finn. For. Res. Inst. Res. Pap. 2002, 835, 1–116. [Google Scholar]
- Äijälä, O.; Koistinen, A.; Sved, J.; Vanhatalo, K.; Väisänen, P. Metsänhoidon suositukset. Metsätalouden Kehittämiskeskus Tapion Julkaisuja. Available online: http://www.xn--metsinen-3za.fi/tietopankin-lahteet/ (accessed on 6 June 2021).
- Nanang, D.M.; Nunifu, T. Selecting a functional form for anamorphic site index curve estimation. For. Ecol. Manag. 1999, 118, 211–221. [Google Scholar] [CrossRef]
- Eerikäinen, K. A Site Dependent Simultaneous Growth Projection Model for Pinus kesiya Plantations in Zambia and Zimbabwe. For. Sci. 2002, 48, 518–529. [Google Scholar]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A., Jr.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 1–415. [Google Scholar] [CrossRef]
- Bragazza, L.; Limpens, J.; Gerdol, R.; Grosvernier, P.; Hájek, M.; Hájek, T.; Hajkova, P.; Hansen, I.; Iacumin, P.; Kutnar, L.; et al. Nitrogen concentration and δ15N signature of ombrotrophic Sphagnum mosses at different N deposition levels in Europe. Glob. Chang. Biol. 2005, 11, 106–114. [Google Scholar] [CrossRef]
- Mälkönen, E. Growth, suppression, death, and self-pruning of branches of Scots pine in southern and central Finland. Commun. Inst. For. Fenn. 1974, 838, 1–87. [Google Scholar]
- Skopp, J.; Jawson, M.D.; Doran, J.W. Steady-State Aerobic Microbial Activity as a Function of Soil Water Content. Soil Sci. Soc. Am. J. 1990, 54, 1619–1625. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X.; Shen, S.S.P.; Zeng, Q.C.; Dickinson, R.E. Time Scales of Land Surface Hydrology. J. Hydrometeorol. 2006, 7, 868–879. [Google Scholar] [CrossRef]
- Koivusalo, H.; Kokkonen, T.; Laurén, A.; Ahtiainen, M.; Karvonen, T.; Mannerkoski, H.; Penttinen, S.; Seuna, P.; Starr, M.; Finér, L. Parameterisation and application of a hillslope hydrological model to assess impacts of a forest clear-cutting on runoff generation. Environ. Model. Softw. 2006, 21, 1324–1339. [Google Scholar] [CrossRef]
- Greve, M.; Tiberg, E. Nordic Reference Soils: 1. Characterisation and Classification of 13 Typical Nordic Soils; 2. Sorption of 2,4-D, Atrazine and Glyphosate; TemaNord (København), Nordic Council of Ministers: Copenhagen, Denmark, 1998. [Google Scholar]
| P | V | |||||||
|---|---|---|---|---|---|---|---|---|
| Calibration catchments | ||||||||
| 2 p | 167 | 1118 | 674 | 156 | 0.88 | 1.94 | 70 | 0.42 |
| 10 p | 74 | 1145 | 668 | 88 | 0.94 | 1.65 | 123 | 0.48 |
| 13 m | 436 | 1454 | 661 | 148 | 0.83 | 5.50 | 105 | 0.05 |
| 14 m | 154 | 1283 | 606 | 165 | 0.82 | 2.82 | 86 | 0.09 |
| 21 m | 1053 | 1043 | 807 | 96 | 0.82 | 3.37 | 86 | 0.28 |
| 22 m | 1560 | 942 | 600 | 61 | 0.89 | 5.82 | 218 | 0.25 |
| 24 m | 1719 | 968 | 623 | 51 | 0.84 | 1.49 | 89 | 0.53 |
| 25 m | 1072 | 1261 | 626 | 142 | 0.81 | 3.00 | 104 | 0.23 |
| 27 m | 1373 | 942 | 600 | 25 | 0.89 | 3.91 | 235 | 0.04 |
| 31 m | 31 | 1425 | 574 | 137 | 0.85 | 3.43 | 32 | 0.05 |
| 32 m | 37 | 1439 | 583 | 145 | 0.90 | 2.45 | 51 | 0.08 |
| 33 m | 51 | 1118 | 674 | 130 | 0.84 | 2.18 | 215 | 0.30 |
| Test catchments | ||||||||
| 3 p | 72 | 1106 | 731 | 166 | 0.89 | 4.36 | 226 | 0.17 |
| 6 p | 49 | 878 | 697 | 74 | 0.88 | 3.96 | 351 | 0.37 |
| 9 p | 75 | 898 | 731 | 62 | 0.85 | 3.02 | 403 | 0.31 |
| 15 m | 1455 | 1287 | 667 | 108 | 0.88 | 1.53 | 126 | 0.34 |
| 16 m | 505 | 1366 | 646 | 152 | 0.88 | 2.05 | 49 | 0.42 |
| 17 m | 1966 | 1275 | 665 | 140 | 0.83 | 1.97 | 52 | 0.33 |
| Scenario | Distance, m | Clear-Cut Area, ha | Harvested V, m3 | Mean Harvested V, m3 ha −1 |
|---|---|---|---|---|
| Uncut | - | - | - | - |
| >100 m | >100 | 41 | 9066 | 211 |
| <35 m | <35 | 43 | 6955 | 168 |
| Peat <100 m | <100 | 30 | 4977 | 168 |
| Min <100 m | <100 | 27 | 4979 | 184 |
| sfc 4,5,6 | no limit | 21 | 3032 | 144 |
| sfc 1,2,3 | no limit | 15 | 3035 | 196 |
| <10 m | <10 | 34 | 5582 | 166 |
| <50 m | <50 | 60 | 10,298 | 174 |
| <70 m | <70 | 73 | 12,775 | 174 |
| <90 m | <90 | 82 | 14,445 | 175 |
| <110 m | <110 | 91 | 16,118 | 177 |
| <130 m | <130 | 99 | 17,802 | 179 |
| <150 m | <150 | 105 | 19,154 | 181 |
| <170 m | <170 | 112 | 20,471 | 183 |
| <190 m | <190 | 118 | 21,692 | 184 |
| Rand 1 ...10 | no limit | 80 | 15,000 | 188 |
| Variable | ||||
|---|---|---|---|---|
| 0.652 () | 0.894 () | 0.846 () | 0.882 () | |
| 0.282 (p 0.013) | - | - | - | |
| −0.150 (p 0.009) | - | - | - | |
| - | 0.284 (p 0.038) | - | - | |
| 0.607 | 0.301 | 0.031 | 0.0 | |
| 0.019 | 0.019 | 0.070 | 0.054 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lauren, A.; Guan, M.; Salmivaara, A.; Leinonen, A.; Palviainen, M.; Launiainen, S. NutSpaFHy—A Distributed Nutrient Balance Model to Predict Nutrient Export from Managed Boreal Headwater Catchments. Forests 2021, 12, 808. https://doi.org/10.3390/f12060808
Lauren A, Guan M, Salmivaara A, Leinonen A, Palviainen M, Launiainen S. NutSpaFHy—A Distributed Nutrient Balance Model to Predict Nutrient Export from Managed Boreal Headwater Catchments. Forests. 2021; 12(6):808. https://doi.org/10.3390/f12060808
Chicago/Turabian StyleLauren, Annamari (Ari), Mingfu Guan, Aura Salmivaara, Antti Leinonen, Marjo Palviainen, and Samuli Launiainen. 2021. "NutSpaFHy—A Distributed Nutrient Balance Model to Predict Nutrient Export from Managed Boreal Headwater Catchments" Forests 12, no. 6: 808. https://doi.org/10.3390/f12060808
APA StyleLauren, A., Guan, M., Salmivaara, A., Leinonen, A., Palviainen, M., & Launiainen, S. (2021). NutSpaFHy—A Distributed Nutrient Balance Model to Predict Nutrient Export from Managed Boreal Headwater Catchments. Forests, 12(6), 808. https://doi.org/10.3390/f12060808







