Abstract
Laser scanning via LiDAR is a powerful technique for collecting data necessary for Digital Terrain Model (DTM) generation, even in densely forested areas. LiDAR observations located at the ground level can be separated from the initial point cloud and used as input for the generation of a Digital Terrain Model (DTM) via interpolation. This paper proposes a quantitative analysis of the accuracy of DTMs (and derived slope maps) obtained from LiDAR data and is focused on conditions common to most forestry activities (rough, steep terrain with forest cover). Three interpolation algorithms were tested: Inverse Distance Weighted (IDW), Natural Neighbour (NN) and Thin-Plate Spline (TPS). Research was mainly focused on the issue of point data density. To analyze its impact on the quality of ground surface modelling, the density of the filtered data set was artificially lowered (from 0.89 to 0.09 points/m2) by randomly removing point observations in 10% increments. This provides a comprehensive method of evaluating the impact of LiDAR ground point density on DTM accuracy. While the reduction of point density leads to a less accurate DTM in all cases (as expected), the exact pattern varies by algorithm. The accuracy of the LiDAR-derived DTMs is relatively good even when LiDAR sampling density is reduced to 0.40–0.50 points/m2 (50–60 % of the initial point density), as long as a suitable interpolation algorithm is used (as IDW proved to be less resilient to density reductions below approximately 0.60 points/m2). In the case of slope estimation, the pattern is relatively similar, except the difference in accuracy between IDW and the other two algorithms is even more pronounced than in the case of DTM accuracy. Based on this research, we conclude that LiDAR is an adequate method for collecting morphological data necessary for modelling the ground surface, even when the sampling density is significantly reduced.
1. Introduction
A Digital Elevation Model (DEM) is defined by the U.S. Geological Survey as a “digital cartographic representation of the elevation of the land at regularly spaced intervals in x and y directions, with z-values referenced to a common vertical datum” [1] (p. 805). Usually, a DEM models the elevation of the ground surface devoid of any vegetation or man-made structures (also referred to as the bare-earth surface). To highlight that the modelling of this bare-earth surface is the focus of our research, we have opted to use the term Digital Terrain Model (DTM). In other words, the term DTM should be understood as referring to a specific case of surface, which is that of the bare-earth (so after vegetation and other obstacles have been removed).
LiDAR (Light Detection and Ranging) is a mapping technique developed in the 1980s, which has since become the preferred method for collecting morphological data necessary for the creation of large-scale DTMs [2]. It is therefore widely used in research, education and management of both private and public resources. As far as forestry is concerned, LiDAR (also called laser scanning) provides a two-fold advantage over most other geo-spatial technologies. Firstly, a LiDAR data set will contain points distributed across the vertical structure of the forest. Thus, a 3-dimensional representation of forest ecosystems is obtained [3], which allows for fresh insights by offering a new perspective on forest structure and processes [4]. Secondly, laser pulses have the ability, limited though it may be, to cross the canopy and reach the ground level [5]. Thus, for land covered with forest vegetation, LiDAR is among the few data sources that allow the collection of accurate ground data for DTM generation.
LiDAR data also provide the means to accurately estimate structural parameters of tree stands, such as: tree height [6,7], diameter at breast height (DBH) [4], basal area, timber volume [8,9], stand density [10,11] or the shape and distribution of forest gaps [12]. Laser scanning can also be an important asset in monitoring the health of vegetation [13,14,15] or in the adoption of sustainable management practices for forest resources, with lower costs relative to traditional methods of data collection such as in-field inventories [16].
The ability of Airborne Laser Scanning (ALS) to map the ground surface covered by forest vegetation also enables the generation of high-quality ground surface models (DTMs), which provide data necessary for the design forest road networks, allow the mapping of existing forest roads or aid in planning logging operations [17]. Furthermore, since a DTM of the forest ecosystem is generally a necessary input for estimating certain structural parameters [18,19,20,21], the accuracy of the DTM will influence the reliability of those estimations [22].
A significant number of variables is known to influence the accuracy of LiDAR-derived DTMs. Three of the most important factors to consider are: LiDAR sampling density [23], morphological complexity of the ground surface and land cover [24]. Of these, the sampling density can be treated as an operational parameter of the survey. Furthermore, the desired LiDAR sampling density is an important factor to consider during the planning phase, as it is responsible for a significant part of the total cost involved in data collection [25].
Increasing the sampling density of LiDAR data is achieved by: lowering the flight altitude of the sensor platform, reducing the scan angle, covering the area of interest multiple times, using a more sophisticated LiDAR sensor with a high pulse repetition rate or any combination thereof. All of the above involve increased costs, lowered efficiency or both. Furthermore, higher density data sets also mean higher post-survey costs, as they require more data storage capacity, processing power and personnel. It is therefore necessary to establish the degree to which LiDAR sampling density influences the quality of derivables such as DTMs or slope maps. If no pattern is identified between DTM accuracy and point density reduction up to a certain threshold, then the case could be made that more LiDAR data is not always beneficial.
Numerous studies have compared the relative performance of interpolation algorithms for DTM generation. While some studies are concerned with the establishment of theoretical models for DTM accuracy [1,26,27,28], most papers are empirical in nature. In these cases, real-world elevation data is collected over one or more test areas and a series of interpolation algorithms are tested, by comparing interpolated DTMs with reference elevation data. In some cases, mathematically-generated surfaces are tested, rather than natural ones [29,30].
In the past, the main sources of elevation data used for research were: points extracted from contour lines on topographical maps [31,32], digital stereo-matching [1] or topographical ground surveys [33,34]. In the last few decades, with the larger availability of modern data collection technologies, the focus has shifted to methods such as GNSS (Global Navigational Satellite Systems) surveys [35] or laser scanning.
Of the numerous interpolation algorithms, some have been more widely tested, such as:
- Inverse Distance Weighted (IDW), probably the most popular interpolation algorithm [1,29,30,31,32,33,34,35,36,37,38].
- Kriging [30,32,35] and its variants: Universal Kriging (UK) [29,31] or Ordinary Kriging (OK) [37].
- Triangular Irregular Network (TIN) interpolation [23,36,37].
- Radial Basis Functions (RBF), also called spline-based interpolators; common algorithms of this type are spline [34,35,37], MultiQuadratic (MQ) [31,32], Regularised Spline with Tension (RST) [32] or Thin-Plate Spline (TPS) [30,33,39].
Given the wide range of natural conditions, data collection methods and interpolation algorithms, it is no wonder that there is little consensus with regards to the performance of algorithms for DTM interpolation. Therefore, in an attempt to further understand the issues involved, most papers look at various external factors that might explain the observed variations of DTM accuracy. Factors usually taken into account can be characterized as: surface-, cover-, data- or processing-specific. Surface-specific factors take into consideration the morphological conditions of the test area [1,23,32,35,40]; common examples are the ground slope [2,36], the Coefficient of Variation (CV) of elevation values [37] or the Surface Roughness [41]—in other words, indices that attempt to describe the topographical complexity of the ground surface. In terms of cover-specific factors, past research has looked in some detail to vegetation (density, species composition and so on) [34,36,40]. In other cases, landcover classes are taken into account in a general manner [2,23]. A common data-specific factor, regardless of the data collection method, is the density of sampled locations [1,31,32,33,37]. With LiDAR data collection, another data-specific factor taken into account by past research is the off-nadir angle at which points were recorded [36,40]. Finally, by processing-specific factors we refer to the variables involved in the process by which raw, unprocessed elevation data is used to generate a continuous model of the ground surface, such as a DTM. When data collection is done by laser scanning, commonly analyzed factors are the choice of ground filtering algorithm [5,41] or the DTM resolution [32,37,39].
On the other hand, comparatively few papers have examined the effect of LiDAR sample density (or spacing) in a comprehensive manner [31]. A typical comprehensive approach to this issue is to simulate conditions of lower ground point density by artificially removing random samples from the initial point cloud, in percentage increments. For example, [42] report that data sets reduced by 95% see an increase of only 8 cm in terms of Root Mean Square Error (RMSE) when compared to data sets reduced by 50%, with no obvious advantage to any of the algorithms tested. However, the scale at which this analysis was carried out is unknown, as the resolution used for DTM generation is not reported. A similar study reports a dependence of accuracy degradation on DTM resolution: if for a 5 m DTM resolution the LiDAR data set could be reduced to 50% density without significant effects, the density could be reduced by as much as 90% for a DTM resolution of 30 m [43].
Using a similar approach for LiDAR data reduction, [38] find that even as much as a 50% reduction of sampling density does not significantly degrade DTM accuracy. However, DTMs have a relatively coarse resolution of 5 m and only a single interpolation algorithm is tested (Inverse Distance Weighted). Meanwhile, [37] report stable DTM accuracies up to 70% of the initial point density, with Inverse Distance Weighted having a worse performance at the highest DTM resolution (0.5 m). Reported RMSE values are around 0.10–0.15 m at 0.5 m resolution and around 0.15–0.20 m at 1 m resolution, with generally small variations as LiDAR point density is gradually reduced.
With this paper, we propose a quantitative analysis of LiDAR-derived DTM accuracy as dependent on LiDAR sampling density, for the case of topographically-complex terrain with dense forest cover. The main objective of the study is to determine the degree to which the decrease of LiDAR sampling density negatively impacts the DTM accuracy. By random removal of LiDAR ground points, our aim is to roughly simulate a flight campaign whose data collection parameters (such as flight altitude or pulse repetition rate) would produce a lower density point cloud. Three interpolation algorithms were tested, in order to establish what significance the choice of algorithm has on this issue. To summarize, the main question that lead to this analysis is the following: is more LiDAR data always beneficial for DTM generation (cost considered)?
2. Materials and Methods
2.1. Study Area
The chosen test site is a forested area of about 1.6 km2 located in a mountainous region of Vâlcea County in Romania (Figure 1), generally following the Bora River valley which flows from SW to NE, discharging into the Vidra storage reservoir just to the South of the study site. The most recent forest management plan indicates that the forest composition consists of a mixture of spruce (around 90%) and pine (less than 10%). The predominant tree stand age is around 85–95 years, with younger stands of about 55–75 years present in a smaller proportion. The area is characterized by a high density of forest cover, as the forest management plan estimates an average canopy density of approximately 0.8. The average canopy cover density was also estimated from the LiDAR data using the approach implemented in the FUSION LIDAR processing software. This involves the overlay of a grid network over the point cloud; the proportion of LiDAR observations whose distance to the ground surface is above a threshold is then determined for each cell of the grid network. In this case, the threshold was set to 2 m, with the assumption that points located less than 2 m above the ground could potentially indicate objects such as boulders, fallen tree trunks or understory vegetation, while points above that threshold are indicative of the presence of canopy cover. Since the optimal cell size for canopy density estimation should be larger than the projection of a typical tree crown, the cell size in this case was set to 15 m. The average canopy density for the study area was estimated at approximately 78%, which is in accordance with the forest management plan.
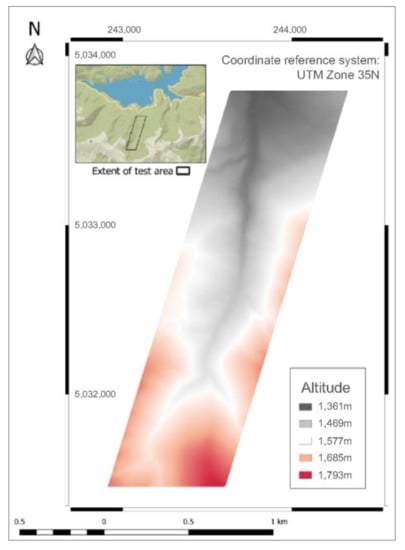
Figure 1.
Location of test area.
Morphologically, the area is characterized by steep slopes and a high surface roughness, typical of the Latoriței Mountains of which it is part of. The elevation has a range of approximately 400 m, from approximately 1360 m in the southern parts of the area up to just under 1800 m in the northern parts. The average ground slope is approximately 26 degrees.
2.2. Laser Scanner Data
Morphological data was collected using Airborne Laser Scanning (ALS) in 2012. This mapping technology involves the installation of a laser scanner system on an airborne platform in order to efficiently cover vast areas of land. The laser scanner used is a full-wave Riegl LMS-Q560, mounted on a DA42 MPP airplane. The main technical parameters of this laser scanner and of the flight campaign have been detailed previously so will not be reproduced here [39].
Part of the area was covered twice by the airborne platform, from different directions. Because of this, the resulting point cloud has a relatively high initial point density of 5.13 points m−2, as parts of the study site have effectively been scanned twice. Initial data processing was carried out by the data provider, but this processing did not include the classification (or labelling) of point data. Therefore, the provided data set is a cloud that contains unlabeled points. Figure 2 shows the spatial and frequency distribution of the LiDAR point cloud. The spatial representation clearly shows that the middle part of the test area was surveyed twice, therefore the higher point density when compared to the northern/southern edges of the site. The representation also highlights the areas of overlap between flight strips, as narrow bands of higher point density. The irregularity of the point cloud density is also evidenced by the distribution of values, which is bimodal: with one peak at approximately 2.25 points/m2 (due to the lower density areas at the edges of the test site and another peak at approximately 5.85 points/m2 (due to the areas of overlap between flight directions).
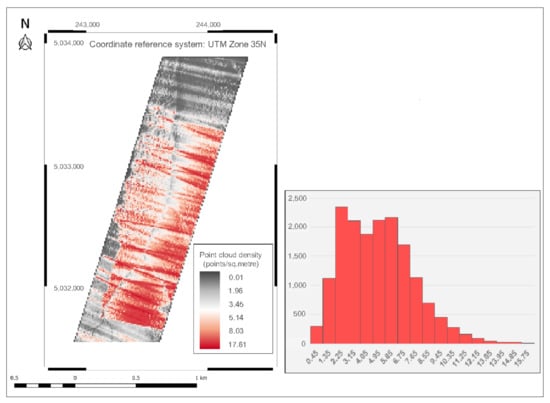
Figure 2.
Spatial and frequency distribution of the initial LiDAR point cloud. The point density grid was generated at a 10 m resolution, to reduce the amount of noise.
For our purposes, there are two classes into which observations have to be separated: (1) non-ground points, which are caused by various objects and obstacles blocking the laser pulse from reaching the ground surface and (2) ground points, when enough of the laser pulse’s energy reaches the ground surface. Given the high canopy density of the study area, the vast majority of non-ground points are likely due to vegetation blocking the laser pulses from reaching the ground.
Therefore, the first processing step we carried out was the ground filtering [44]. The purpose of this is the identification non-ground points so they can be removed from the data set, leaving only ground points suitable for DTM interpolation. This procedure was carried out in a combined manner, with both automatic and manual steps. The automatic filtering was done using lasground, a LiDAR filtering algorithm that is part of the LasTools software suite developed by rapidlasso GmbH. The result of this automatic procedure was then manually checked, by traversing a visual representation of the resulting point cloud in 20 m wide strips. User subjectivity is inherent to the manual correction, but this process can still help in correcting the relatively few points that have been obviously mislabeled.
The result of ground filtering is therefore a subset of the initial point cloud. This we can assume only contains (inevitable errors aside) those LiDAR points that are either at the ground level or very close to it. 87% of observations were removed in this step, leaving a reduced set of ground points with an average density of 0.89 points m−2 (a reduction of 85% from the initial point density). Figure 3 shows the spatial and frequency distribution of the filtered point cloud containing only ground observations.
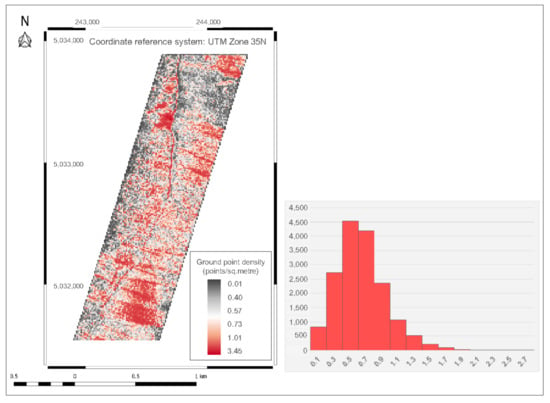
Figure 3.
Spatial and frequency distribution of the filtered ground point cloud. The point density grid was generated at a 10 m resolution, to reduce the amount of noise.
The spatial pattern shown here mostly follows that of the initial point density, as expected. A couple of areas located towards the northern part of study area have a noticeably higher ground point density than their surroundings due to the reduced canopy cover. The spatial distribution of ground points is not only affected by the flight pattern of the surveying platform, but also by the variation of the canopy cover. It is therefore expected to show a highly irregular spatial distribution, as is the case here. The statistical distribution of ground point density has a slight positive skew, with a long tail to the right (likely due to the small areas of open terrain, where the ground point density is significantly higher than average).
2.3. Interpolation Algorithms
As previously discussed, the result of LiDAR data collection is a data structure consisting of discrete observations (a cloud of points). On the other hand, a ground model is a continuous surface that expresses the variation of elevation values over a given area. The process through which a continuous surface is obtained from a set of discrete samples is called interpolation [45] and over the years numerous algorithms for it have been developed [46]. In general terms, interpolation methods aim to establish a weighting function to predict values at unsampled locations, based upon measured values in the same general vicinity.
Three interpolation algorithms were tested in this study. In order of increasing complexity, they are: Inverse Distance Weighted or IDW [47], Natural Neighbour or NN [48] and Thin-Plate Spline or TPS [49]. IDW and NN are somewhat similar, in that they are local interpolators: they estimate values by considering the k-closest sampled locations, with no predicted values outside the range of sampled values. On the other hand, TPS is part of a class of algorithms usually referred to as spline-based or Radial Basis Functions (RBF). These aim to generate a surface of minimal tension, in order to reduce the effect of inherent measurement errors of samples [33]. TPS is a global interpolator: all known values contribute to each predicted value and predictions do not always fall within the range of sampled values.
All interpolations were carried out in SAGA GIS version 2.3.2. The parameter values presented below were chosen based on past research and after visual inspection of DTMs generated using various parameter values:
- For Inverse Distance Weighted: maximum search distance: 40 m (if no observations are within this distance of a grid cell, that cell will not be assigned an elevation value; a high value was used for this parameter to ensure that generated DTMs will have no gaps), maximum points: 8 (if more than 8 points are within the maximum search distance, then only the 8 closest will be used for prediction), weighting function: inverse distance to a power (power was set to the commonly used value of 2; in other words, the weight assigned to an observation decreases with the square of the distance between that observation and the location where a prediction is made).
- For Natural Neighbour: method: Sibson (usually has no significant effect on the interpolation results), minimum weight: 0 (the minimum weight that can be assigned to observations; a positive value ensures that no extrapolation is carried out).
- For Thin-Plate Spline: search range: global (any observations can be used for a prediction, of course with a bias for closer observations), maximum number of nearest points: 8 (the number of nearest observations taken into account for prediction), direction: all directions (does not constrain the selection of closest observations along specific directions such as in quadrants).
Further technical details relating to the operation of these three algorithms (and the process of interpolation in general) can be found in [39].
A general rule-of-thumb regarding the scale at which DTMs should be interpolated is to choose a spatial resolution that is close to the average ground point spacing [37]. Since the average point spacing of our filtered point cloud is about 1.06 meters, all DTM interpolation was carried out at 1 m resolution.
2.4. Prediction vs. Validation Data
An independent data set is required in order to evaluate the accuracy of ground models obtained by interpolation. Since the ground conditions of the test site do not permit carrying out a topographical survey in safety conditions, we instead relied on the established method that previous research refers to as cross-validation [50] or true validation [1,51].
More specifically, we relied on a type of cross-validation called the split-sample method [33,38,52,53] or sometimes the jack-knife procedure [40]. This approach involves the separation of data into two subsets: (1) a prediction data set, which contains the majority of initial samples and (2) a validation data set, which contains a small proportion of the original data. In this manner, since the samples chosen for validation are not used for prediction, they can act as a faux-independent data set to estimate accuracy.
When determining the proportion between validation and prediction samples, two guiding principles are usually taken into account [22]. First, the validation data set should contain a high enough number of samples so that the accuracy estimation is statistically significant. On the other hand, the validation data set should be small enough that the integrity of prediction data is not affected. A survey of past research on the interpolation and accuracy of DTMs highlights that there is no consensus with regard to the proportion between prediction and validation data. The proportion of data used for validation ranges from 0.1 [40] to 10% [30], with most reported values in the 3–5% range [1,22].
Taking these issues into account, and also considering the specifics of our data (with LiDAR points numbering in the millions), we chose a 95/5% split between prediction and validation data. In other words, 95% of observations (approximately 1 mil. points) in the filtered point cloud are used for interpolation, while the other 5% (n = 52,358) are validation points randomly extracted from the initial data set and used for estimating the accuracy of DTMs. Validation data has a point density of approximately 0.03 points/m2. In other words, given that the resolution of interpolated DTMs is 1 m, around 3% of DTM cell values should contain a validation point. It is reasonable to assume that the validation points can thus ensure a sufficient statistical reliability of estimated accuracy.
2.5. Artificial Reduction of Density
The main purpose of this study is to analyze the effect of LiDAR point density on DTM accuracy. Therefore, a way to perform a controlled variation of density is required. This was done by reducing the point cloud density in 10%increments. Starting from the prediction data set (consisting of 95% of initial ground points, as previously discussed), k-percent of ground points are randomly selected and removed, where k is a multiple of 10. In other words, 10 point clouds of varying point densities are obtained, with the final one containing 10% of the initial observations (and a point density of 0.09 points/m2).
If one wants to ensure that the spatial characteristics of a set of discrete observations is preserved, random sampling is the preferred method for reducing point density. As previously mentioned, our goal was to roughly simulate a LiDAR data set collected at a lower point density and the effect this has on the accuracy of DTM interpolation. Because of this, grid-based thinning (which is usually the desirable method of sampling density reduction, as it makes the spatial distribution of points more homogeneous and therefore better suited for DTM generation) would go against our stated goal. This is even more significant in the case of DTM generations for forestry applications, as the density of LiDAR ground points is usually highly heterogeneous due to the variations of canopy cover. Thus, random removal of observations ensures that the initial heterogeneity of ground point data is preserved for the most part, so that DTM accuracy is not overestimated.
Since our aim was to test the effect that LiDAR sampling density has on DTM accuracy for three interpolation algorithms, 30 DTMs were therefore analyzed. A secondary objective was to estimate the degree to which the prediction of a derivative of DTM (such as slope) is affected by the lowered ground point density, so 30 slope maps were also generated from these DTMs.
2.6. Accuracy of Elevation and Slope Estimates
For each validation point i, two elevation values (or Z-values) are known: the Z-value as obtained from ALS data collection (which for simplification is considered correct), and the Z-value of the DTM—more explicitly, the elevation value associated to the DTM cell in which validation point i is located. Using these values, the vertical error for point i can be determined [54]:
where E(i) is the vertical error (or residual value), ZDTM(i) is the elevation value of the raster cell in which point i is located and ZALS(i) is the measured elevation for point i. The accuracy of an interpolated DTM can then be estimated by aggregating the error values for each of the n validation points.
E(i) = ZDTM(i) − ZALS(i)
The average signed elevation error is not a particularly useful summary statistic, beyond signaling any consistent bias of elevation values. Given that the average of signed elevation errors should be around zero if errors are truly random, any significant distance from zero would indicate a negative/positive prediction bias. Error values were therefore converted to absolute (unsigned) values and common summary statistics were calculated, such as: mean unsigned error, Root Mean Square Error (RMSE), standard deviation or the 95th percentile of error values.
In terms of slope estimation errors, the procedure is somewhat similar. However, the validation points do not have a slope value to be taken as reference, so they cannot be used for estimating the accuracy of slope maps. Therefore, the only option is to choose an initial slope map as a baseline to which all other slope maps are compared. This slope map is generated from a DTM interpolated using all ground points (so before the separation of the data set into prediction and validation subsets). Subsequent slope maps are then overlaid with it, and errors are determined on a cell-by-cell basis as the difference between the values of the two raster models. Slope errors are then converted into absolute values and summary statistics are calculated, as previously explained.
For an alternative perspective on DTM accuracy, a pair of threshold values for elevation error and slope error were established and the number of validation points over those thresholds was determined. For elevation, the thresholds were set at 0.25 and 0.50 m, while for slope they were set at 5 and 10 degrees.
It is worth mentioning that, given the lack of external (truly independent) validation data, reported values should be interpreted as an expression of the relative accuracy of elevation and slope estimations across interpolation algorithms and point densities, not as absolute measures of prediction accuracy. In other words, any systematic errors (for e.g., due to the measurement error inherent to the laser scanner) will affect in an equal measure both the prediction and the validation points. These types of errors cannot therefore be evaluated in the absence of external data.
A graphical representation of the general workflow detailed in this section is presented in Figure 4.
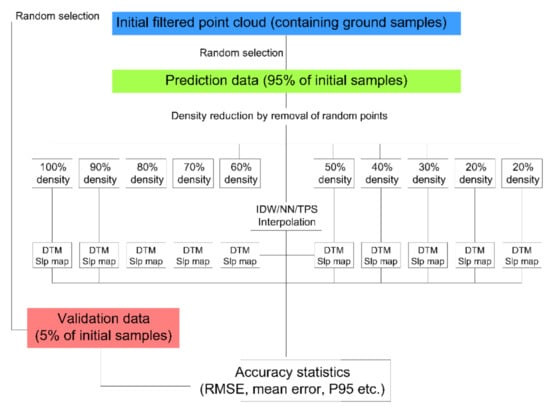
Figure 4.
General research workflow.
3. Results
3.1. Elevation Error of Interpolated DTMs
The effect of LiDAR sampling density on the accuracy of ground surface interpolation was analyzed for three algorithms, by artificially reducing the initial point density in 10% increments. Summary statistics for elevation errors (residuals) are presented in Table 1.

Table 1.
DTM accuracy at various point densities.
The results show that in all cases mean signed errors are very close to zero, so there is no significant bias (consistent over/under-estimation) of prediction. In the case of IDW interpolation, most of the statistics reveal a similar pattern: a relatively consistent degradation of DTM accuracy as point density decreases. By contrast, accuracy indicators for DTMs interpolated using NN or TPS are either: (1) relatively stable across different density values (for e.g., in the case of the standard deviation of unsigned errors, P95 or RMSE) or (2) have an erratic variation that does not offer any real insight (like in the case of the maximum elevation error). The indicator that seems to be more sensitive to the accuracy degradation induced by the reduction of point density is the mean unsigned error. Therefore, it is presented in graphical form rather than tabular, in order to better highlight our findings (Figure 5). The vertical bars shown in Figure 5 represent the 95% confidence interval of the calculated means; they are very small due to the high number of observations (although they naturally increase as elevation error values get higher, at the lowest point densities).
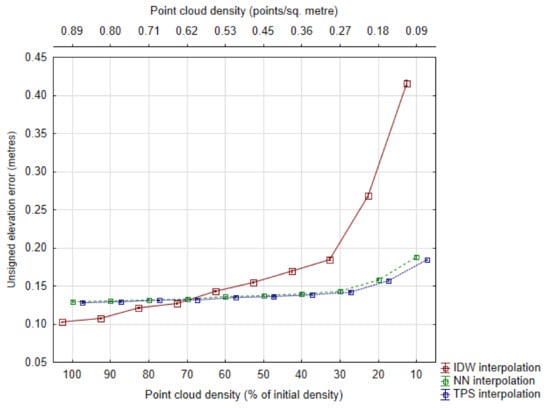
Figure 5.
Mean unsigned elevation error as a measure of DTM accuracy, across different point densities. Whiskers represent the 95% confidence interval of mean values. Points are horizontally offset for clarity.
The statistics presented, in particular the mean unsigned error highlight two issues in particular. Firstly, regardless of interpolation algorithm, the reduction of sampling density is associated with a relatively consistent degradation of DTM accuracy. Secondly, IDW interpolation is affected to a higher degree than the other two methods. In fact, in the case of NN or TPS interpolation, overall DTM accuracy is relatively stable until point density drops below 0.30 points/m2 (around 30–40% of the initial point density).
Another perspective from which we analyzed the overall DTM accuracy is by establishing a pair of thresholds (0.25 and 0.50 m) and then quantifying the number of validation points with elevation errors that exceed those values. Errors over 0.25 m (Figure 6) and especially those over 0.50 m (Figure 7), highlight the following:
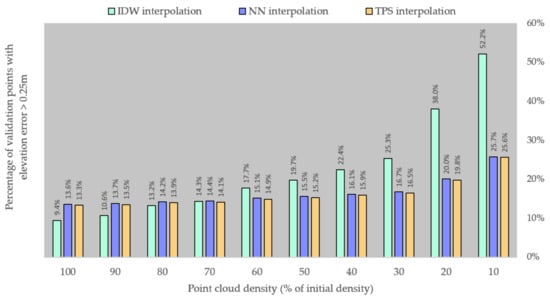
Figure 6.
Percentage of validation points with an elevation error over 0.25 m.
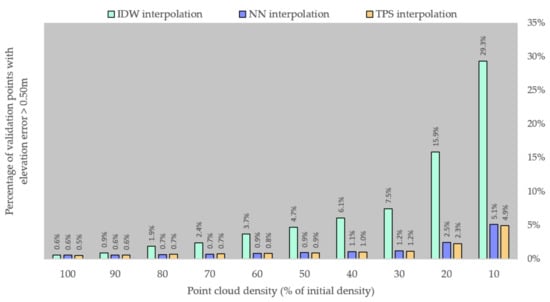
Figure 7.
Percentage of validation points with an elevation error over 0.50 m.
- DTMs interpolated using NN or TPS are very similar in terms of accuracy, with a slight advantage to TPS at all point densities.
- NN/TPS interpolation has a relatively stable rate of accuracy degradation, with errors over 0.25 m doubling over the range of point densities; meanwhile, errors over 0.50 m had an eight-fold increase over that same range.
- DTMs interpolated using IDW have similar accuracies at the higher point densities, but fall behind the other two algorithms after point density is reduced to less than 0.60 points/m2 (60–70% of the initial density).
- The issue described above is due to IDW’s significantly faster rate of accuracy degradation as point density is reduced: errors over 0.25 m increase almost five-fold between the initial and the final point density, while errors over 0.50 m increase approximately 48 times over that range (from approximately 0.6% of the validation points having errors over 0.50 m at the initial point density of 0.89 points/m2, to approximately 52.2% of the validation points at the final point density of 0.09 points/m2).
3.2. Accuracy of Slope Prediction
The accuracy of slope maps was estimated by comparison with a reference slope map. A raster of slope errors was obtained by calculating the arithmetical difference between the cell values of the two raster slope maps. These error values were than aggregated to estimate the overall accuracy of each slope map (Table 2). Mean signed errors show that, in the case of slope maps generated from IDW DTMs, a consistent bias is present regardless of point density. Values of around minus 3 to minus 4 degrees for the mean signed error highlight a relatively significant under-estimation of ground slope. This tendency is not present in the case of the other two interpolation algorithms, for which the mean signed error is very close to zero regardless of sampling density.

Table 2.
Slope prediction accuracy at various point densities.
Similar to DTM accuracy, the mean unsigned slope error appears to highlight the clearest pattern of evolution across point densities, so it is presented in graphical form, rather than tabular (Figure 8). The whiskers shown in Figure 8 represent the 95% confidence interval of the calculated means and are very small due to the high number of observations (although they naturally increase as slope error values get higher, at the lowest point densities).
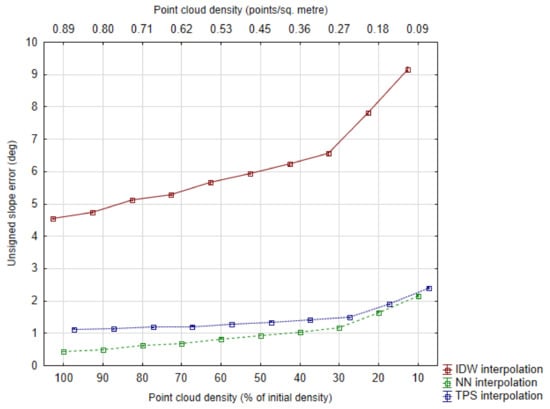
Figure 8.
Mean unsigned elevation error as a measure of slope map accuracy, across different point densities. Whiskers represent the 95% confidence interval of mean values. Points are horizontally offset for clarity.
The situation highlighted in Figure 8 shows that, in terms of slope prediction, IDW is not up to par with the other two algorithms. If in terms of elevation error IDW is close to the other two algorithms (or even more accurate) at higher point densities (Figure 5), in the case of slope estimation the difference is significant, regardless of point density. An example to illustrate this point: the best RMSE value for a slope map derived from an IDW DTM (at a density of 0.89 points/m2) is 6.47 degrees. Meanwhile, the worst RMSE values for slope maps derived from NN or TPS DTMs are about two times lower: 3.02 and 3.37 degrees, respectively.
Another way we looked at the accuracy of ground slope prediction is by quantifying the amount of raster slope map cells with an error crossing over certain thresholds. Chosen thresholds are at 5 degrees (Figure 9) and 10 degrees (Figure 10) slope error. It is apparent that DTMs obtained by IDW interpolation are much less suited for slope prediction, regardless of point density. For example, the highest percentage of slope prediction errors over 5 degrees for NN (approximately 8.3% of validation points, at a ground point density of 0.09 points/m2) is four times better than the lowest amount of slope prediction errors for IDW (approximately 32.9% of validation points, at the initial ground point density of 0.89 points/m2). When looking at the second threshold (slope prediction errors over 10 degrees), the differences are even more pronounced: for IDW the number of slope errors increases from approximately 11.9% to 38.2% of validation points as point density decreases; meanwhile the percentage of slope errors for NN/TPS does not go over 1.5 points/m2. IDW aside, NN and TPS have relatively similar accuracies for slope prediction (just like in the case of elevation prediction), but in the case of slope errors NN seems to have a slightly better performance when compared with TPS. And in a pattern similar to that described for the elevation accuracy of DTMs, slope maps derived DTMs interpolated using these two algorithms have a relatively stable general accuracy, even at reduced densities of 0.3–0.4 points/m2.
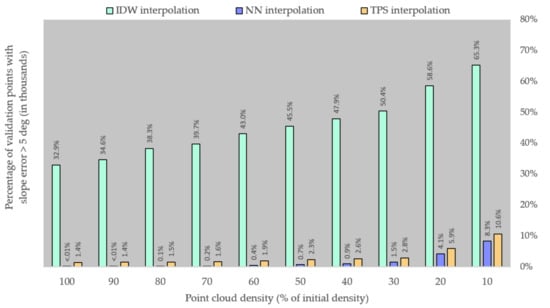
Figure 9.
Number of validation points with a slope error over the 5-degree threshold.
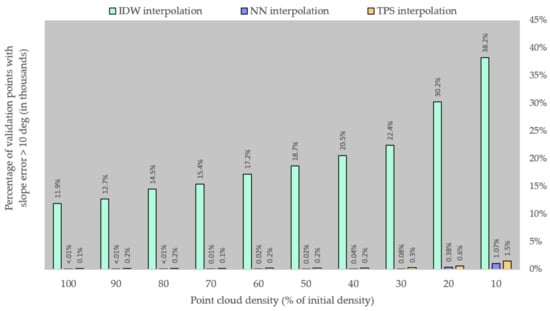
Figure 10.
Number of validation points with a slope error over the 10-degree threshold.
Overall, DTMs interpolated using Natural Neighbour seem to offer a more accurate basis for slope prediction regardless of point density, but the differences with DTMs interpolated using Thin-Plate Spline are not significant. On the other hand, slope prediction has a faster rate of degradation after point density falls below 30% for each algorithm (0.27 ground points/m2).
3.3. Processing Time
Two advantages of working with a LiDAR data set of reduced sampling density are lower storage requirements and faster processing. To highlight the gains in terms of computing requirements, we determined the time it took to generate the DTMs for the three interpolation algorithms (Table 3). All processing was carried out on the same machine, a mid-range PC equipped with an AMD 4-core processor at 3.2 GHz and 12 GB of RAM.

Table 3.
Processing time for DTM generation.
As expected, the processing time consistently decreases with the reduction of point density. In the case of IDW or NN, which are relatively fast methods in general, the gains are on the order of fractions of minutes, so not significant. However, for a resource-intensive algorithm like TPS, the processing time decreases from over 38 min to less than 4. This is expected, as TPS interpolation requires the generation of spline functions that take into account all data points at once. Therefore, any reduction in terms of observations will have a direct impact on the time needed to calculate those functions.
4. Discussion
Research has long since established that a connection exists between DTM accuracy and sample density [1,55]. Furthermore, studies have also shown that the rate of DTM accuracy degradation is higher as sample densities are progressively reduced [55]. While in the cited study the factor that is varied is the spatial resolution of DTMs, a larger DTM cell size (lower resolution) is roughly analogous to a decreased density of sampled points.
The three algorithms that were tested as part of this research show different rates of accuracy degradation as LiDAR sampling density decreases. In other words, in areas where a lower point density is expected to occur (for example in the case of dense canopy cover), the quality of the DTM will depend to a larger extent on the choice of interpolation algorithm. This is in accordance with past research [31,38,56].
The results show that Inverse Distance Weighted (IDW) has a slightly better performance than the other two algorithms at the higher sampling densities (between 0.89 and 0.62 points/m2). However, as density is reduced below 0.62 points/m2 (representing 70% of the initial density), IDW has a faster rate of accuracy degradation (highlighted by its significantly higher RMSE values) than Natural Neighbour or Thin-Plate Spline (Table 1). This could be due to IDW being a local interpolator, which cannot estimate local peaks or troughs whose elevation is outside the interval of sampled elevation values [1]. In other words, IDW might be especially sensitive to the reduction in sampling density and might offer an explanation for IDW’s contrasting performance in past research. For example, some studies conclude that IDW fares just as well, if not better, at DTM generation when compared to algorithms like Kriging or Radial Basis Functions [31,32,37,40]. In fact, [40] cite the high point density as a likely explanation for IDW providing a more accurate DTM than Kriging or Spline. On the other hand, some studies establish that IDW interpolation has poorer performance than other methods [1,33,34,35]. This disparity could be caused by the interaction between the complexity of the ground surface and the sampling density. All interpolation algorithms are affected by these two factors, but it appears that IDW is influenced to a larger extent by this combination of high topographical complexity (numerous local points of inflection of the ground surface) and lower sampling density. This warrants further research into the correlation between ground surface roughness, sampling density and DTM accuracy when using IDW for interpolation.
The relatively poorer performance of IDW in terms of slope estimation is likely due to error compounding. Since slope maps are primary derivatives of DTMs, any elevation errors will carry over to the slope prediction. In fact, a derivative like slope should be more sensitive to the quality of the DTM than altitude itself [31]. This is a likely explanation for the larger disparities between algorithm performance in terms of slope prediction accuracy (Figure 8), as opposed to elevation prediction accuracy (Figure 5). However, the fact that IDW is significantly worse at predicting slope variation at all point densities is not easily explained and requires further research.
As previously discussed, Thin-Plate Spline (TPS) interpolation applies a degree of smoothing to the generated surface, so it was expected to provide a better representation of elevation even when sampling density decreases. Past research indicates that the smoothing effect could actually improve the accuracy of elevation data, especially under deciduous canopy cover where sampled locations tend to be clustered together [23]. The relatively good performance of TPS reported in this paper is therefore in accordance with previously published research: [33] find that TPS has better accuracy than IDW, while [30] report that TPS interpolation is more accurate than both Kriging or IDW. Other studies, while not testing TPS specifically, find that other RBF (or spline-based) interpolation algorithms are suited for LiDAR-derived DTM generation [34,35].
To our knowledge, the Natural Neighbour (NN) interpolation algorithm is not a very popular choice as far as comparative studies of DTM interpolation go. Nevertheless, in the few papers where it was included in analysis, NN appears to fare better than most of the other algorithms tested. For example, [36] tested NN along numerous other algorithms, including IDW, Nearest Neighbour or TIN, among others. The focus of the cited study is DTM generation in dense mountain forest environments, with results indicating a relatively good performance for Natural Neighbour. Our analysis, carried out in similar conditions, is in accordance.
When considering the RMSE values reported in this paper, especially in relation to DTM accuracies from studies carried out on planar surfaces of open ground, the challenging terrain conditions of our study area have to be taken into account. Past research has shown that both the presence of dense vegetation [22,36,57] and rugged terrain [1,2,23] are significant factors that pose a challenge to the accuracy of LiDAR-derived DTMs.
With regards to the random removal of observations as the means for density reduction, it is worth pointing out that this approach is generally suited for research purposes, in accordance with our main purpose of simulating a LiDAR flight campaign leading to a lower density point cloud. In practice, if the aim is to reduce the point cloud after data processing, grid-based thinning is more adequate. In this approach, a grid system is overlaid with the point cloud and for each cell a point is randomly selected to be kept, with the rest being eliminated. The cell size is chosen depending on the desired final point density. In this way, the density reduction will lead to a more homogeneous spatial distribution of observations and the user can ensure that the most valuable observations (the isolated ones) are not randomly removed from the data set. This approach would likely go towards reducing one of the disadvantages of LiDAR data collection in forested areas, which is the highly irregular spatial distribution of ground observations due to variations of the canopy cover. In other words, it is assumed that a more accurate DTM would be generated from a reduced data set using this method.
A natural next step for this study would be the development and validation of an empirical model to estimate RMSE values for DTMs/slope maps based on LiDAR point density, for similar terrain conditions. Such a model would allow users to start with a desired DTM accuracy and determine the minimum LiDAR sampling density to aim for, in order to achieve a high enough density of ground points for DTM interpolation.
In other words, a model that would provide an a priori cost estimate (expressed as a decrease of DTM or slope prediction accuracy) due to a reduction of LiDAR sampling density.
5. Conclusions
The main purpose of this paper was to determine the degree to which a lower density LiDAR point cloud can still provide an accurate representation of the ground’s surface in the form a DTM, for the specific case of rough terrain with a dense forest cover. To achieve this, LiDAR data was collected over a test area located in a mountainous area. 5% of the initial ground points were separated from the data set for validation purposes (n = 52,358). The density of the remaining ground points was reduced from its initial value of 0.89 points/m2 down to 0.09 points/m2, in 10% increments by gradual removal of observations (random stratified sampling). The resulting point clouds, of varying point density, were the input for DTM interpolation, using three interpolation algorithms: Inverse Distance Weighted and Thin-Plate Spline. Thirty DTMs were thus obtained (10 for each interpolation algorithm, interpolated from point clouds of decreasing density) and their accuracy was analyzed, from the perspective of both elevation and slope determination errors.
The degree to which LiDAR sampling density can be reduced without significant loss of DTM accuracy varies depending on factors such as: the initial sampling density, the scale (or spatial resolution) at which the ground surface is modelled, the morphological complexity of the terrain, the algorithm used for interpolation and the intended applications for the DTM product and its derivatives. Our research shows that, even in the challenging case of highly rugged mountainous terrain, a certain degree of point density reduction was achievable without sacrificing the accuracy of the DTM. In practice, such a density reduction could be intentional (for gains in terms of surveying costs, processing time and storage capacity), but a reduced point density could also be taken into account as an operational parameter, before the LiDAR survey campaign is carried out. Planning the data collection campaign in order to reach a (potentially unnecessary) high sampling density across the object surface will inevitably lead to significant over-sampling in areas of open-ground or lower canopy density, where the laser pulses are not hindered from reaching the ground surface.
With regards to the estimation of various forest parameters, some studies find that past a certain LiDAR sampling density, the accuracy of predictions does not significantly change [58]. Therefore, when acquiring LiDAR data that will be utilized for multiple applications, each potential usage should be taken into account when determining point density requirements.
Author Contributions
Conceptualization, M.C. and A.C.; methodology, M.C.; software processing, M.C.; writing-original draft preparation, M.C.; writing—review and editing, M.C. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend their gratitude towards the National Institute for Research and Development in Forestry (INCDS) “Marin Drăcea” for kindly providing access to the ALS data used in this study. The authors express their sincere appreciation to the anonymous reviewers, whose insightful comments and suggestions helped improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aguilar, F.J.; Agüera, F.; Aguilar, M.A.; Carvajal, F. Effects of terrain morphology, sampling density, and interpolation methods on grid DEM accuracy. Photogramm. Eng. Remote Sens. 2005, 71, 805–816. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Jensen, J.; Raber, G.; Tullis, J.; Davis, B.A.; Thompson, G.; Schuckman, K. An evaluation of lidar-derived elevation and terrain slope in leaf-off conditions. Photogramm. Eng. Remote Sens. 2005, 71, 817–823. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geog. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Maguya, A.S.; Junttila, V.; Kauranne, T. Adaptive algorithm for large scale dtm interpolation from lidar data for forestry applications in steep forested terrain. ISPRS J. Photogramm. Remote Sens. 2013, 85, 74–83. [Google Scholar] [CrossRef]
- Hyde, P.; Dubayah, R.; Walker, W.; Blair, J.B.; Hofton, M.; Hunsaker, C. Mapping forest structure for wildlife habitat analysis using multi-sensor (LiDAR, SAR/InSAR, ETM+, Quickbird) synergy. Remote Sens. Environ. 2006, 102, 63–73. [Google Scholar] [CrossRef]
- Moe, K.; Owari, T.; Furuya, N.; Hiroshima, T. Comparing Individual Tree Height Information Derived from Field Surveys, LiDAR and UAV-DAP for High-Value Timber Species in Northern Japan. Forests 2020, 11, 223. [Google Scholar] [CrossRef]
- Yoga, S.; Bégin, J.; Daigle, G.; Riopel, M.; St-Onge, B. A Generalized Lidar-Based Model for Predicting the Merchantable Volume of Balsam Fir of Sites Located along a Bioclimatic Gradient in Quebec, Canada. Forests 2018, 9, 166. [Google Scholar] [CrossRef]
- Hill, A.; Breschan, J.; Mandallaz, D. Accuracy Assessment of Timber Volume Maps Using Forest Inventory Data and LiDAR Canopy Height Models. Forests 2014, 5, 2253–2275. [Google Scholar] [CrossRef]
- Chen, L.; Chiang, T.; Teo, T. Fusion of LIDAR data and high resolution images for forest canopy modelling. In Proceedings of the 26th Asian Conference on Remote Sensing, Hanoi, Vietnam, 7–11 November 2005. [Google Scholar]
- Lee, A.C.; Lucas, R.M. A LiDAR-derived canopy density model for tree stem and crown mapping in Australian forests. Remote Sens. Environ. 2007, 111, 493–518. [Google Scholar] [CrossRef]
- Means, J.E.; Means, J.E.; Acker, S.A.; Fitt, O.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting Forest Stand Characteristics with Airborne Laser Scanning LIDAR. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1372. [Google Scholar]
- Vastaranta, M.; Kantola, T.; Lyytikäinen-Saarenmaa, P.; Holopainen, M.; Kankare, V.; Wulder, M.A.; Hyyppä, J.; Hyyppä, H. Area-based mapping of defoliation of scots pine stands using airborne scanning LiDAR. Remote Sens. 2013, 5, 1220–1234. [Google Scholar] [CrossRef]
- Barnes, C.; Balzter, H.; Barrett, K.; Eddy, J.; Milner, S.; Suárez, J. Individual tree crown delineation from airborne laser scanning for diseased larch forest stands. Remote Sens. 2017, 9, 231. [Google Scholar] [CrossRef]
- Solberg, S.; Næsset, E.; Lange, H.; Bollandsås, O.M. Remote sensing of forest health. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36. [Google Scholar]
- Rubén Fernández de Villarán, S.J.; Domingo-Santos, J.M. The role of gis and lidar as tools for sustainable forest management. GIS Overv. Appl. 2018, 1, 124–148. [Google Scholar]
- Wulder, M.A.; Bater, C.W.; Coops, N.C.; Hilker, T.; White, J.C. The role of LiDAR in sustainable forest management. For. Chron. 2008, 84, 807–826. [Google Scholar] [CrossRef]
- Chen, W.; Hu, X.; Chen, W.; Hong, Y.; Yang, M. Airborne LiDAR remote sensing for individual tree forest inventory using trunk detection-aided mean shift clustering techniques. Remote Sens. 2018, 10, 1078. [Google Scholar] [CrossRef]
- Lindberg, E.; Hollaus, M. Comparison of methods for estimation of stem volume, stem number and basal area from airborne laser scanning data in a hemi-boreal forest. Remote Sens. 2012, 4, 1004–1023. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Assessment of Individual Tree Detection and Canopy Cover Estimation using Unmanned Aerial Vehicle based Light Detection and Ranging (UAV-LiDAR) Data in Planted Forests. Remote Sens. 2019, 11, 908. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; She, G. Estimating forest structural parameters using canopy metrics derived from airborne LiDAR data in subtropical forests. Remote Sens. 2017, 9, 940. [Google Scholar] [CrossRef]
- Bater, C.W.; Coops, N.C. Evaluating error associated with lidar-derived DEM interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Bresnahan, P. Accuracy of airborne LiDAR-derived elevation. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Mills, J.P.; Delgado, J.; Aguilar, M.A.; Negreiros, J.G.; Pérez, J.L. Modelling vertical error in LiDAR-derived digital elevation models. ISPRS J. Photogramm. Remote Sens. 2010, 65, 103–110. [Google Scholar] [CrossRef]
- Raber, G.T.; Jensen, J.R.; Hodgson, M.E.; Tullis, J.A.; Davis, B.A.; Berglund, J. Impact of LiDAR nominal post-spacing on DEM accuracy and flood zone delineation. Photogramm. Eng. Remote Sens. 2007, 73, 793–804. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Mills, J.P. Accuracy assessment of lidar-derived digital elevation models. Photogramm. Rec. 2008, 23, 148–169. [Google Scholar] [CrossRef]
- Kraus, K.; Karel, W.; Briese, C.; Mandlburger, G. Local accuracy measures for digital terrain models. Photogramm. Rec. 2006, 21, 342–354. [Google Scholar] [CrossRef]
- Hu, P.; Liu, X.; Hu, H. Accuracy assessment of digital elevation models based on approximation theory. Photogramm. Eng. Remote Sens. 2009, 75, 49–56. [Google Scholar] [CrossRef]
- Zimmerman, D.; Pavlik, C.; Ruggles, A.; Armstrong, M.P. An experimental comparison of ordinary and universal kriging and inverse distance weighting. Math. Geol. 1999, 31, 375–390. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y. A Fast Global Interpolation Method for Digital Terrain Model Generation from Large LiDAR-Derived Data. Remote Sens. 2019, 11, 1324. [Google Scholar] [CrossRef]
- Chaplot, V.; Darboux, F.; Bourennane, H.; Leguédois, S.; Silvera, N.; Phachomphon, K. Accuracy of interpolation techniques for the derivation of digital elevation models in relation to landform types and data density. Geomorphology 2006, 77, 126–141. [Google Scholar] [CrossRef]
- Weng, Q. An Evaluation of Spatial Interpolation Accuracy of Elevation data. In Progress in Spatial Data Handling; Riedl, A., Kainz, W., Elmes, G.A., Eds.; Springer: Berlin, Germany, 2006; pp. 805–824. [Google Scholar]
- Erdogan, S. A comparison of interpolation methods for producing digital elevation models at the field scale. Earth Surf. Process. Landf. 2009, 34, 366–376. [Google Scholar] [CrossRef]
- Ismail, Z.; Abdul Khanan, M.F.; Omar, F.Z.; Abdul Rahman, M.Z.; Mohd Salleh, M.R. Evaluating Error of LiDar Derived DEM Interpolation for Vegetation Area. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 42. [Google Scholar] [CrossRef]
- Arun, P.V. A comparative analysis of different DEM interpolation methods. Egypt. J. Remote Sens. Space Sci. 2013, 16, 133–139. [Google Scholar]
- Stereńczak, K.; Ciesielski, M.; Balazy, R.; Zawiła-Niedźwiecki, T. Comparison of various algorithms for DTM interpolation from LIDAR data in dense mountain forests. Eur. J. Remote Sens. 2016, 49, 599–621. [Google Scholar] [CrossRef]
- Guo, Q.; Li, W.; Yu, H.; Alvarez, O. Effects of topographic variability and lidar sampling density on several DEM interpolation methods. Photogramm. Eng. Remote Sens. 2010, 76, 701–712. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Peterson, J.; Chandra, S. The effect of LiDAR data density on DEM accuracy. In Proceedings of the International Congress on Modelling and Simulation (MODSIM07), Christchurch, New Zealand, 10–13 December 2007; Oxley, L., Kulasiri, D., Eds.; Modelling and Simulation Society of Australia and New Zealand Inc.: Christchurch, New Zealand, 2007; pp. 1363–1369. [Google Scholar]
- Cățeanu, M.; Ciubotaru, A. Accuracy of Ground Surface Interpolation from Airborne Laser Scanning (ALS) Data in Dense Forest Cover. ISPRS Int. J. Geo-Inf. 2020, 9, 224. [Google Scholar] [CrossRef]
- Su, J.; Bork, E. Influence of vegetation, slope, and lidar sampling angle on DEM accuracy. Photogramm. Eng. Remote Sens. 2006, 72, 1265–1274. [Google Scholar] [CrossRef]
- Cățeanu, M.; Arcadie, C. ALS for terrain mapping in forest environments: An analysis of lidar filtering algorithms. EARSeL eProceedings 2017, 16, 9–20. [Google Scholar]
- Anderson, E.S.; Thompson, J.A.; Austin, R.E. LIDAR density and linear interpolator effects on elevation estimates. Int. J. Remote Sens. 2005, 26, 3889–3900. [Google Scholar] [CrossRef]
- Anderson, E.S.; Thompson, J.A.; Crouse, D.A.; Austin, R.E. Horizontal resolution and data density effects on remotely sensed LIDAR-based DEM. Geoderma 2006, 132, 406–415. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons, Ltd.: Chichester, UK, 2007; pp. 37–38. [Google Scholar]
- Mitas, L.; Mitasova, H. Spatial interpolation. Geogr. Inf. Syst. Princ. Tech. Manag. Appl. 1999, 1, 481–492. [Google Scholar]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 23rd National Conference of the Association for Computing Machinery, Princeton, NJ, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Sibson, R. A brief description of natural neighbour interpolation. In Interpreting Multivariate Data; Barnett, V., Ed.; Wiley: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Donato, G.; Belongie, S. Approximate thin plate spline mappings. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2002; pp. 21–31. [Google Scholar]
- Davis, B.M. Uses and abuses of cross-validation in geostatistics. Math. Geol. 1987, 19, 241–248. [Google Scholar] [CrossRef]
- Voltz, M.; Webster, R. A comparison of kriging, cubic splines and classification for predicting soil properties from sample information. J. Soil Sci. 1990, 41, 473–490. [Google Scholar] [CrossRef]
- Declercq, F.A.N. Interpolation methods for scattered sample data: Accuracy, spatial patterns, processing time. Cartogr. Geogr. Inf. Syst. 1996, 23, 128–144. [Google Scholar] [CrossRef]
- Smith, S.L.; Holland, D.A.; Longley, P.A. Quantifying Interpolation Errors in Urban Airborne Laser Scanning Models. Geogr. Anal. 2005, 37, 200–224. [Google Scholar] [CrossRef]
- Li, Z. On the measure of digital terrain model accuracy. Photogramm. Rec. 1988, 12, 873–877. [Google Scholar] [CrossRef]
- Maceachren, A.M.; Davidson, J.V. Sampling and isometric mapping of continuous geographic surfaces. Am. Cartogr. 1987, 14, 299–320. [Google Scholar] [CrossRef]
- Lazzaro, D.; Montefusco, L.B. Radial basis functions for the multivariate interpolation of large scattered data sets. J. Comput. Appl. Math. 2002, 140, 521–536. [Google Scholar] [CrossRef]
- Sterenczak, K.; Moskalik, T. Use of LIDAR-based digital terrain model and single tree segmentation data for optimal forest skid trail network. iForest-Biogeosci. For. 2014, 8, 661. [Google Scholar] [CrossRef]
- Treitz, P.; Lim, K.; Woods, M.; Pitt, D.; Nesbitt, D.; Etheridge, D. LiDAR Sampling Density for Forest Resource Inventories in Ontario, Canada. Remote Sens. 2012, 4, 830–848. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).