Modelling the Tree Height, Crown Base Height, and Effective Crown Height of Pinus koraiensis Plantations Based on Knot Analysis
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. Data Collection
3.2. Model Development
3.2.1. Data Screening
3.2.2. Basic Model Selection
3.2.3. Mixed-Effects Model Development
- To construct a mixed-effects model based on a basic model, we first needed to determine the categorical variables. All single-level models consider the corresponding levels to be categorical random-effects variable.
- The random parameters in the Richards model were determined. The NLMIXED module of the Statistical Analysis System (SAS 9.2) [34] software was used to fit the single-level effective crown height and crown base height hybrid model, and random combinations of different random parameters were considered to determine the best nonlinear hybrid model.
- The variance-covariance random-effect structure generally adopts the generalized positive definite matrix D; this matrix mainly reflects the differences among the tree samples and can be expressed as follows:where is the variance in random parameter , is the variance in random parameter , is the variance in random parameter , is the covariance between random parameters and , is the covariance between random parameters and , and is the covariance between the random parameters and .
- The intragroup variance-covariance structure, A, is determined. To determine the within-group variance structure, the heteroscedasticity and autocorrelation problems must be solved. The variance structure of the residuals must be considered. Therefore, the intragroup variance-covariance can be expressed as follows:where refers to the residual variance value of the observed object and is the -dimensional unit matrix describing the change.
3.3. Model Evaluation
3.4. Time and Intensity of Artificial Pruning
4. Results and Analysis
4.1. Tree Height Model Selection
4.2. Effective Crown Height Model Selection
4.3. Crown Base Height Model Selection
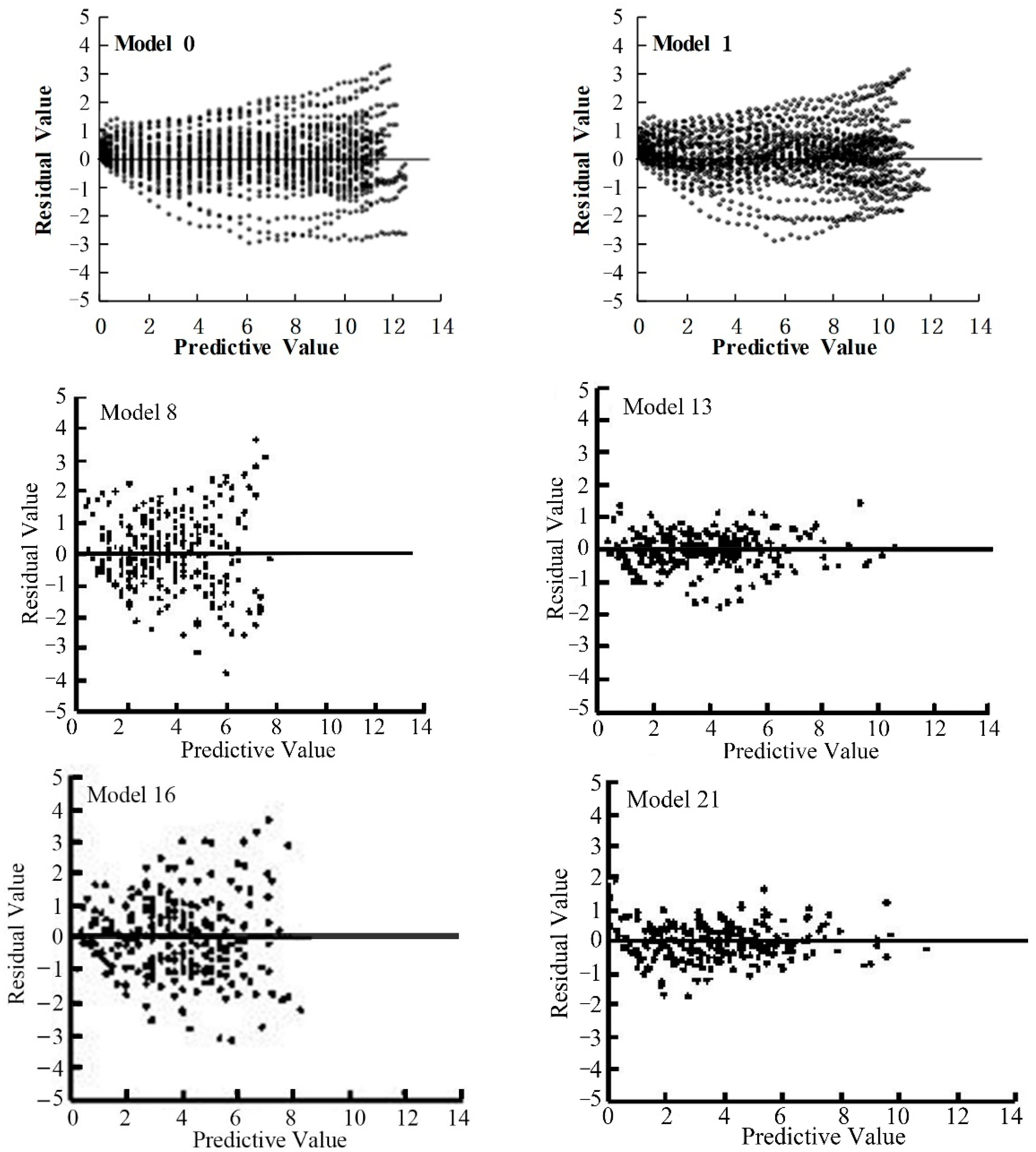
4.4. Model Evaluation
4.5. Estimations of the Time and Intensity of Artificial Pruning
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pretzsch, H. Tree growth as affected by stem and crown structure. Trees 2021, 35, 947–960. [Google Scholar] [CrossRef]
- Xiao, Y.; Jokela, E.J.; White, T.L. Species differences in crown structure and growth performance of juvenile loblolly and slash pine. For. Ecol. Manag. 2003, 174, 295–313. [Google Scholar] [CrossRef]
- Fahey, T.D.; Cahill, J.M.; Snellgrove, T.A. Lumber and Veneer Recovery from Intensively Managed Young-Growth Douglas-Fir; Research Station Research Paper; United States Department of Agriculture: Washington, DC, USA, 1991; 89p. [Google Scholar]
- Jozsa, L.A.; Middleton, G.R. A Discussion of Wood Quality Attributes and Their Practical Implications; SP-34; Forintek Canada Corp, Western Laboratory: Vancouver, BC, Canada, 1994; 42p. [Google Scholar]
- Kuprevicius, A.; Auty, D.; Achim, A.; Caspersen, J.P. Quantifying the influence of live crown ratio on the mechanical properties of clear wood. Forestry 2014, 87, 449–458. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, H.; Sharma, R.P.; Pang, L.F.; Wang, G.X. A generalized nonlinear mixed-effects height to crown base model for Mongolian oak in northeast China. For. Ecol. Manag. 2017, 384, 34–43. [Google Scholar] [CrossRef]
- Garber, S.M.; Monserud, R.A.; Maguire, D.A. Crown recession patterns in three conifer species of the Northern Rocky Mountains. For. Sci. 2008, 54, 633–646. [Google Scholar]
- Kleine, M. Sortentafeln fur Buche in Osterreich. Centralbl. Ges. Forstw 1986, 103, 15–36. [Google Scholar]
- Oliver, C.D.; Larson, B.C. Forest Stand Dynamics, 1st ed.; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Liu, Q.; Xie, L.; Dong, L.; Li, F. Dynamic simulation of the multilayer crown net photosynthetic rate and determination of the functional crown for larch (Larix olgensis) trees. New For. 2021, 52, 1011–1035. [Google Scholar] [CrossRef]
- Ow, L.F.; Ghosh, S.; Sim, E.K. Mechanical injury and occlusion: An urban, tropical perspective. Urban. For. Urban. Gree 2013, 12, 255–261. [Google Scholar] [CrossRef]
- Jia, W.; Chen, D. Nonlinear mixed-eff ects height to crown base and crown length dynamic models using the branch mortality technique for a Korean larch ( Larix olgensis ) plantations in northeast China. J. For. Res. 2019, 30, 2095–2109. [Google Scholar] [CrossRef]
- Fujimori, T. Dynamics of crown structure and stem growth based on knot analysis of a hinoki cypress. For. Ecol. Manag. 1993, 56, 57–68. [Google Scholar] [CrossRef]
- Rijal, B.; Weiskittel, A.R.; Kershaw, J.A.T. Development of height to crown base models for hirteen tree species of the North American Acadian Region. For. Chron. 2012, 88, 60–73. [Google Scholar] [CrossRef]
- Duan, G.S.; Li, X.D.; Feng, Y. Generalized nonlinear mixed-effects crown base height model of Larix principis-rupprechtii natural secondary forests. J. Nanjing For. Univ. 2018, 42, 170–176. [Google Scholar]
- Li, F.R.; Wang, Z.F.; Wang, B.S. Dynamic study on effective crown of larch plantation. J. Northeast. For. Univ. 1996, 24, 1–8. [Google Scholar]
- Geng, L.; Li, M.Z.; Fan, W.Y. Individual Tree Structure Parameters and Effective Crown of the Stand Extraction Base on Airborn LiDAR Data. Sci. Silvae Sin. 2018, 54, 62–71. [Google Scholar]
- Liu, X.; Hao, Y.S.; Widagdo, F.R.A.; Xie, L.; Dong, L.; Li, F. Predicting Height to Crown Base of Larix olgensis in Northeast China Using UAV-LiDAR Data and Nonlinear Mixed Effects Models. Remote Sens. 2021, 13, 1834. [Google Scholar] [CrossRef]
- Hann, D.W.; Hanus, M.L. Evaluation of nonspatial approaches and equation forms used to predict tree crown recession. Can. J. For. Res. 2004, 34, 1993–2003. [Google Scholar] [CrossRef]
- Koehler, A. A method of studying knot formation. For. J. 1936, 34, 1062–1063. [Google Scholar]
- Koide, R. Study on pruning. 4. Process of branch death upwards and its fall. J. Jpn. For. Soc. 1941, 23, 1–15. (In Japanese) [Google Scholar]
- Maguire, D.A.; Hann, D.W. A stem dissection technique for dating branch mortality and reconstructing past crown recession. For. Sci. 1987, 33, 858–871. [Google Scholar]
- Kershaw, J.A.; Maguire, D.A.; Hann, D.W. Longevity and duration of radial growth in Douglas-fir branches. Can. J. For. Res. 1990, 20, 1690–1695. [Google Scholar] [CrossRef]
- Shao, G. Study on individual tree growth model for Korean pine plantations. J. Northeast. Fore. Univ. 1985, 3, 38–46. (In Chinese) [Google Scholar]
- Gao, H.; Bi, H.; Li, F. Modelling conifer crown profiles as nonlinear conditional quantiles: An example with planted Korean pine in northeast China. For. Ecol. Manag. 2017, 398, 101–115. [Google Scholar] [CrossRef]
- Jin, X. Dissertation for the Degree of Doctor Forests Planning Model Based on Heuristics Algorithm of Mengjiagang Farm. Ph.D. Dissertation, Northeast Forestry University, Harbin, China, 2014. [Google Scholar]
- Li, F. Forest Mensuration, 4th ed.; China Forestry Press: Beijing, China, 2019; pp. 164–165. ISBN 978-7-5219-0182-5. [Google Scholar]
- Jia, W.; Cui, C.; Li, F. Knot Attributes of Korean Pine Plantation Based on Mixed Effect Model. Chin. J. Appl. Ecol. 2018, 29, 33–43. [Google Scholar]
- Menéndez-Miguélez, M.; Ruiz-Peinado, R.; Del Río, M.; Calama, R. Improving tree biomass models through crown ratio patterns and incomplete data sources. Eur. J. For. Res. 2021, 140, 675–689. [Google Scholar] [CrossRef]
- Trincado, G.; Burkhart, H.E. A framework for modeling the dynamics of firstorder branches and spatial distribution of knots in loblolly pine trees. Can. J. For. Res. 2009, 39, 566–579. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, Z.; Hein, S.; Zeng, J.; Schuler, J.; Guo, J.; Guo, W.; Zeng, J. Effect of Planting Density on Knot Attributes and Branch Occlusion of Betula alnoides under Natural Pruning in Southern China. Forests 2015, 6, 1343–1361. [Google Scholar] [CrossRef]
- Lowell, E.C.; Maguire, D.A.; Briggs, D.G. Effects of Silviculture and Genetics on Branch/Knot Attributes of Coastal Pacific Northwest Douglas-Fir and Implications for Wood Quality—A Synthesis. Forests 2014, 5, 1717–1736. [Google Scholar] [CrossRef]
- Cao, Q.V.; Jing, W. Calibrating Fixed- and Mixed-Effects Taper Equations. For. Ecol. Manag. 2011, 262, 671–673. [Google Scholar] [CrossRef]
- SAS Institute, Inc. SAS/STAT 14.2. User’s Guide; SAS Institute, Inc.: Cary, NC, USA, 2016. [Google Scholar]
- Sun, S. Study on Size Prediction of the Knot for Pinus Sylvestris Plantation and Pruning Technology. Master’s Thesis, Northeast Forestry University, Harbin, China, 2015. [Google Scholar]
- Roberts, S.D.; Dean, T.J.; Evans, D.L. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manag. 2005, 213, 54–70. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Q. Effects of pruning intensity on nonstructural carbohydrates of Populus alba × P. talassica in the arid desert region of Northwest China. J. For. Res. 2021, 32, 823–830. [Google Scholar] [CrossRef]
- Barry, K.M.; Hall, M.F.; Mohammed, C.L. The effect of time and site on incidence and spread of pruning-related decay in plantation-grown Eucalyptus nitens. Can. J. For. Res. 2005, 35, 495–502. [Google Scholar] [CrossRef][Green Version]
- Danescu, A.; Ehring, A.; Bauhus, J.; Albrecht, A.; Hein, S. Modelling discoloration and duration of branch occlusion following green pruning in Acer pseudoplatanus and Fraxinus excelsior. For. Ecol. Manag. 2015, 335, 87–98. [Google Scholar] [CrossRef]
- Wiseman, D.; Smethurst, P.; Pinkard, L.; Wardlaw, T.; Beadle, C.; Hall, M.; Baillie, C.; Mohammed, C. Pruning and fertiliser effects on branch size and decay in two Eucalyptus nitens plantations. For. Ecol. Manage. 2006, 225, 123–133. [Google Scholar] [CrossRef]
- Metzler, B. Quantitative assessment of fungal colonization in Norway spruce after green pruning. Eur. J. For. Pathol. 1997, 27, 1–10. [Google Scholar] [CrossRef]
- Li, Y. Research of Larch Plantations Pruning. Master’s Thesis, Northeast Forestry University, Harbin, China, 2011. [Google Scholar]
- Rubio, A.; Camarero, J.J.; Gordaliza, G.G.; Cerioni, M.; Montes, M.; Gil, L. Competition overrides climate as trigger of growth decline in a mixed Fagaceae Mediterranean rear-edge forest. Ann. Forest. Sci. 2020, 77, 94. [Google Scholar] [CrossRef]
- Antos, J.A.; Parish, R.; Nigh, G.D. Effects of neighbours on crown length of Abies lasiocarpa and Picea engelmannii in two old-growth stands in British Columbia. Can. J. For. Res. 2010, 40, 638–647. [Google Scholar] [CrossRef]


| Variable Symbol | Description |
|---|---|
| HT | Tree height (m) |
| HEC | Height of the effective tree crown (m) |
| HBC | Height of the tree crown base (m) |
| ECL | Length of the effective tree crown (m) |
| CL | Length of the living crown (m) |
| RCL | Ratio of the crown length |
| RB | Age at the time of the birth of the knot (a) |
| RBC | Age at the time the knot stopped growing (a) |
| RBD | Age at the time of death of the knot (a) |
| RBO | Age at the time when the knot was occluded (a) |
| Variable | Sample Size | Min | Max | Mean | Std (Standard Deviation) | Coefficient of Variation (CV%) | ||
|---|---|---|---|---|---|---|---|---|
| Fitting dataset | Plot variable | Age (a) | 10 | 37 | 47 | 40.9 | 3.60 | 8.81 |
| Density (trees·hm−2) | 10 | 650 | 1533 | 991.1 | 296.45 | 29.91 | ||
| Elevation (m) | 10 | 201.5 | 262.8 | 242.5 | 18.73 | 7.72 | ||
| Tree variable | DBH (cm) | 50 | 12.5 | 27.3 | 20.5 | 3.52 | 17.16 | |
| HT (m) | 50 | 9.5 | 16.1 | 12.5 | 1.30 | 10.39 | ||
| CL (m) | 50 | 1.9 | 9.9 | 6.3 | 1.65 | 26.38 | ||
| CW (m) | 50 | 1.4 | 3.7 | 2.3 | 0.63 | 26.71 | ||
| H/D | 50 | 0.4 | 1.0 | 0.6 | 11.36 | 18.20 | ||
| RB | 1445 | 1 | 30.0 | 11.6 | 5.79 | 50.10 | ||
| RBC | 1445 | 7 | 46.0 | 21.8 | 6.34 | 29.03 | ||
| RBD | 1320 | 9 | 49.0 | 27.6 | 6.93 | 25.16 | ||
| RBO | 95 | 16 | 46.0 | 31.8 | 6.19 | 19.49 | ||
| Validation dataset | Plot variable | Age (a) | 2 | 32 | 37 | 34.5 | 3.54 | 10.25 |
| Density (trees·hm−2) | 2 | 1467 | 1650 | 1558.5 | 129.40 | 8.30 | ||
| Elevation (m) | 2 | 194.6 | 222.6 | 208.6 | 19.80 | 9.49 | ||
| Tree variable | DBH (cm) | 2 | 12.3 | 19.5 | 16.1 | 2.50 | 15.58 | |
| HT (m) | 2 | 9.6 | 11.3 | 10.3 | 0.58 | 5.64 | ||
| CL (m) | 2 | 3.5 | 6.6 | 5.3 | 0.88 | 16.70 | ||
| CW (m) | 2 | 1.3 | 2.4 | 1.7 | 0.35 | 20.64 | ||
| H/D | 2 | 0.5 | 0.8 | 0.7 | 0.10 | 14.85 | ||
| RB | 290 | 1 | 20 | 9.8 | 4.92 | 50.06 | ||
| RBC | 290 | 8 | 33 | 18.3 | 4.88 | 26.73 | ||
| RBD | 282 | 11 | 36 | 24.5 | 6.13 | 25.08 | ||
| RBO | 7 | 24 | 36 | 30.6 | 4.39 | 14.36 | ||
| Model Form | Random Effects Considered | Number of Simulations | AIC | BIC | −2LL | LL | LRT | p |
|---|---|---|---|---|---|---|---|---|
| 0 | None | 4 | 5142.7 | 5164.9 | 5134.7 | −2567.35 | - | - |
| 1 | b1 | 5 | 5034.4 | 5032.4 | 5024.4 | −2512.2 | 110.3 | <0.0001 |
| 2 | b2 | 5 | 5039.3 | 5037.2 | 5029.3 | −2514.65 | - | - |
| 3 | b3 | 5 | 5060.3 | 5058.4 | 5050.3 | −2525.15 | - | - |
| 4 | b1, b2 | 7 | 5029.4 | 5026.6 | 5015.4 | −2507.7 | 9.0 | 0.0111 |
| 5 | b1, b3 | 7 | 5031.6 | 5028.8 | 5017.6 | −2508.8 | - | - |
| 6 | b2, b3 | 7 | 5103.1 | 5100.3 | 5089.1 | −2544.55 | - | - |
| 7 | b1, b2, b3 | 10 | - | - | - | - | - | - |
| Model Form | Random Effects Considered | Number of Simulations | AIC | BIC | −2LL | LL | LRT | p |
|---|---|---|---|---|---|---|---|---|
| 8 | None | 4 | 899.6 | 914.3 | 891.6 | −445.8 | - | - |
| 9 | b1 | 5 | 686.0 | 695.6 | 676.0 | −338.0 | ||
| 10 | b2 | 5 | 679.7 | 689.3 | 669.7 | −334.9 | 221.9 | <0.005 |
| 11 | b3 | 5 | 683.8 | 693.3 | 673.8 | −336.9 | ||
| 12 | b1, b2 | 7 | 658.7 | 672.1 | 644.7 | −322.4 | ||
| 13 | b1, b3 | 7 | 650.8 | 664.2 | 636.8 | −318.4 | 32.9 | <0.005 |
| 14 | b2, b3 | 7 | 848.7 | 862.1 | 834.7 | −417.4 | ||
| 15 | b1, b2, b3 | - | - | - | - | - | - | - |
| Model Form | Random Effects Considered | Number of Simulations | AIC | BIC | −2LL | LL | LRT | p |
|---|---|---|---|---|---|---|---|---|
| 16 | None | 4 | 911.2 | 925.8 | 903.2 | −451.6 | - | |
| 17 | b1 | 5 | 713.1 | 722.7 | 703.1 | −351.55 | 200.1 | <0.005 |
| 18 | b2 | 5 | 718.8 | 728.4 | 708.8 | −354.4 | ||
| 19 | b3 | 5 | 743.9 | 753.4 | 733.9 | −366.95 | ||
| 20 | b1, b2 | 7 | 735.8 | 749.2 | 721.8 | −360.9 | ||
| 21 | b1, b3 | 7 | 703.8 | 717.2 | 689.8 | −344.9 | 13.3 | <0.005 |
| 22 | b2, b3 | 7 | 848.1 | 861.5 | 834.1 | −417.05 | ||
| 23 | b1, b2, b3 | - | - | - | - | - | - | - |
| Model | Response Variable | a1 | a2 | a3 | Covariance-Structure D | Ri | Ra2 | RMSE | RSS |
|---|---|---|---|---|---|---|---|---|---|
| Model 0 | HT | 15.4674 | 0.0622 | 2.5315 | - | - | 0.9496 | 0.9283 | 0.6573 |
| Model 1 | HT | 15.5153 | 0.0619 | 2.5239 | 0.8047 | 0.9529 | 0.8971 | 0.6351 | |
| Model 4 | HT | 15.5400 | 0.0618 | 2.5213 | 0.7979 | 0.9534 | 0.8930 | 0.6311 | |
| Model 8 | HEC | 10.5977 | 0.0716 | 4.2887 | - | - | 0.7132 | 1.1335 | 367.4293 |
| Model 10 | HEC | 12.1014 | 0.0687 | 4.5563 | 0.3754 | 0.9286 | 0.5656 | 91.4864 | |
| Model 13 | HEC | 11.4905 | 0.0726 | 4.7620 | 0.2743 | 0.9390 | 0.5225 | 77.2625 | |
| Model 16 | HBC | 10.9893 | 0.0593 | 5.0751 | - | - | 0.7015 | 1.1562 | 382.3540 |
| Model 17 | HBC | 9.7940 | 0.0717 | 6.6491 | 0.4407 | 0.9156 | 0.6149 | 108.1239 | |
| Model 21 | HBC | 9.2716 | 0.0792 | 7.8990 | 0.3683 | 0.9349 | 0.5402 | 82.5704 |
| Model | Response Variable | ME | MAE% | p |
|---|---|---|---|---|
| Model 1 | HT | −0.3301 | 0.1773 | 0.9893 |
| Model 13 | HEC | 0.4196 | 0.2936 | 0.9227 |
| Model 21 | HBC | 0.1363 | 0.2926 | 0.9466 |
| AGE (y) | HT (m) | HEC (m) | HBC (m) | ECL (m) | CL (m) | Difference (m) |
|---|---|---|---|---|---|---|
| 1 | 0.02 | 0.00 | 0.00 | 0.02 | 0.02 | 0.00 |
| 2 | 0.08 | 0.00 | 0.00 | 0.07 | 0.08 | 0.00 |
| 3 | 0.19 | 0.01 | 0.00 | 0.18 | 0.19 | 0.01 |
| 4 | 0.36 | 0.03 | 0.00 | 0.33 | 0.35 | 0.02 |
| 5 | 0.58 | 0.06 | 0.01 | 0.51 | 0.57 | 0.05 |
| 6 | 0.84 | 0.12 | 0.02 | 0.72 | 0.81 | 0.09 |
| 7 | 1.14 | 0.20 | 0.05 | 0.95 | 1.09 | 0.15 |
| 8 | 1.48 | 0.30 | 0.08 | 1.17 | 1.40 | 0.22 |
| 9 | 1.84 | 0.43 | 0.12 | 1.40 | 1.72 | 0.31 |
| 10 | 2.23 | 0.60 | 0.19 | 1.63 | 2.04 | 0.41 |
| 11 | 2.63 | 0.78 | 0.26 | 1.85 | 2.37 | 0.52 |
| 12 | 3.05 | 1.00 | 0.36 | 2.05 | 2.69 | 0.64 |
| 13 | 3.47 | 1.23 | 0.47 | 2.24 | 3.00 | 0.76 |
| 14 | 3.91 | 1.49 | 0.60 | 2.42 | 3.31 | 0.89 |
| 15 | 4.34 | 1.76 | 0.75 | 2.58 | 3.59 | 1.01 |
| 16 | 4.78 | 2.05 | 0.92 | 2.73 | 3.86 | 1.14 |
| 17 | 5.21 | 2.35 | 1.10 | 2.86 | 4.11 | 1.25 |
| 18 | 5.64 | 2.66 | 1.29 | 2.98 | 4.34 | 1.36 |
| 19 | 6.06 | 2.97 | 1.51 | 3.09 | 4.55 | 1.46 |
| 20 | 6.47 | 3.29 | 1.73 | 3.19 | 4.74 | 1.56 |
| Frequency | AGE (y) | HT (m) | HBC (m) | HEC (m) | Intensity (m) | Interval (y) | Crown Length Ratio before Pruning (%) | Crown Length Ratio after Pruning (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 15 | 4.34 | 0.75 | 1.76 | 1.01 | 0 | 0.83 | 0.59 |
| 2 | 20 | 6.47 | 1.76 | 3.29 | 1.52 | 5 | 0.73 | 0.49 |
| 3 | 26 | 8.38 | 3.29 | 5.13 | 1.85 | 6 | 0.61 | 0.39 |
| 4 | 32 | 10.54 | 5.13 | 6.71 | 1.57 | 6 | 0.51 | 0.36 |
| 5 | 39 | 12.13 | 6.71 | 8.08 | 1.37 | 7 | 0.45 | 0.33 |
| 6 | 46 | 13.24 | 8.08 | 9.01 | 0.93 | 7 | 0.39 | 0.32 |
| 7 | 53 | 14.01 | 9.01 | 9.61 | 0.60 | 7 | 0.36 | 0.31 |
| 8 | 59 | 14.46 | 9.61 | 9.95 | 0.34 | 6 | 0.34 | 0.31 |
| 9 | 63 | 14.69 | 9.95 | 10.11 | 0.16 | 4 | 0.32 | 0.31 |
| 10 | 66 | 14.83 | 10.11 | 10.20 | 0.09 | 3 | 0.32 | 0.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Liu, Z.; Jia, W.; Li, D. Modelling the Tree Height, Crown Base Height, and Effective Crown Height of Pinus koraiensis Plantations Based on Knot Analysis. Forests 2021, 12, 1778. https://doi.org/10.3390/f12121778
Zhu W, Liu Z, Jia W, Li D. Modelling the Tree Height, Crown Base Height, and Effective Crown Height of Pinus koraiensis Plantations Based on Knot Analysis. Forests. 2021; 12(12):1778. https://doi.org/10.3390/f12121778
Chicago/Turabian StyleZhu, Wancai, Zhaogang Liu, Weiwei Jia, and Dandan Li. 2021. "Modelling the Tree Height, Crown Base Height, and Effective Crown Height of Pinus koraiensis Plantations Based on Knot Analysis" Forests 12, no. 12: 1778. https://doi.org/10.3390/f12121778
APA StyleZhu, W., Liu, Z., Jia, W., & Li, D. (2021). Modelling the Tree Height, Crown Base Height, and Effective Crown Height of Pinus koraiensis Plantations Based on Knot Analysis. Forests, 12(12), 1778. https://doi.org/10.3390/f12121778






