Non-Destructive Assessment of the Elastic Properties of Low-Grade CLT Panels
Abstract
:1. Introduction
2. Materials and Methods
2.1. Transverse Vibration Tests
2.1.1. Description of the CLT Panels
2.1.2. Test Setup
2.2. Identification of CLT Panels’ Dynamic Properties
- Select the impulse responses to be used for the extraction of modal parameters. The impulse responses relate an arbitrary impact point to an acceleration response reference point;
- Define a maximum limit for the order of the model or system. The model order corresponds to the number of poles to be identified in the system and is equal to twice the number of vibration modes to be considered;
- Construct the Hankel matrices. These matrices contain different arrays of impulse responses;
- Calculate the poles and modal participation factors for different model orders. These calculations must be done because the proper model order is not known a priori. One of the essential steps in this stage is to calculate a series of coefficients through a least-squares approximation. These coefficients are stored in a “companion matrix”, whose eigenvalues and eigenvectors allow us to calculate the poles and modal participation factors. Finally, from these poles and factors, the dynamic properties of the system can be estimated, i.e., its resonant frequencies, damping ratios, and modal shapes;
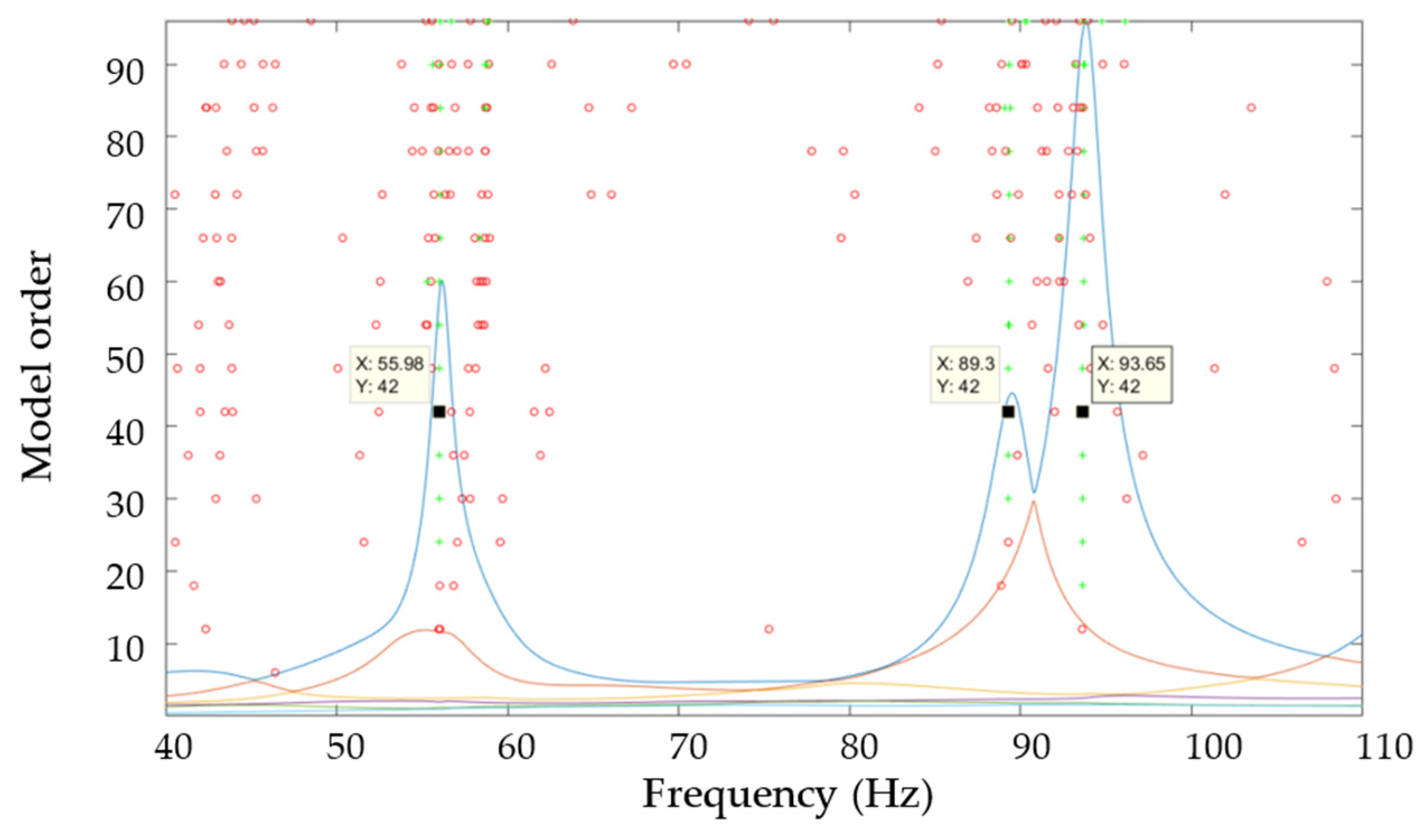
- Construct a stabilization diagram based on the estimates of poles and modal participation factors for the different model orders analyzed in the previous point. A typical stabilization diagram has a horizontal axis of frequencies and a vertical axis of model orders. Therefore, for a given model order value, the obtained poles are plotted along the frequency axis. If two poles at an order n and n + 1 of the model are within certain defined limits of frequency and damping, they are called “stable”;
- Select from the stabilization diagram the set of stable poles of interest. Finally, the frequencies and modal shapes of the system under study are obtained from these stable poles and their respective modal participation factors.
2.3. Estimation of CLT Panels’ Elastic Properties
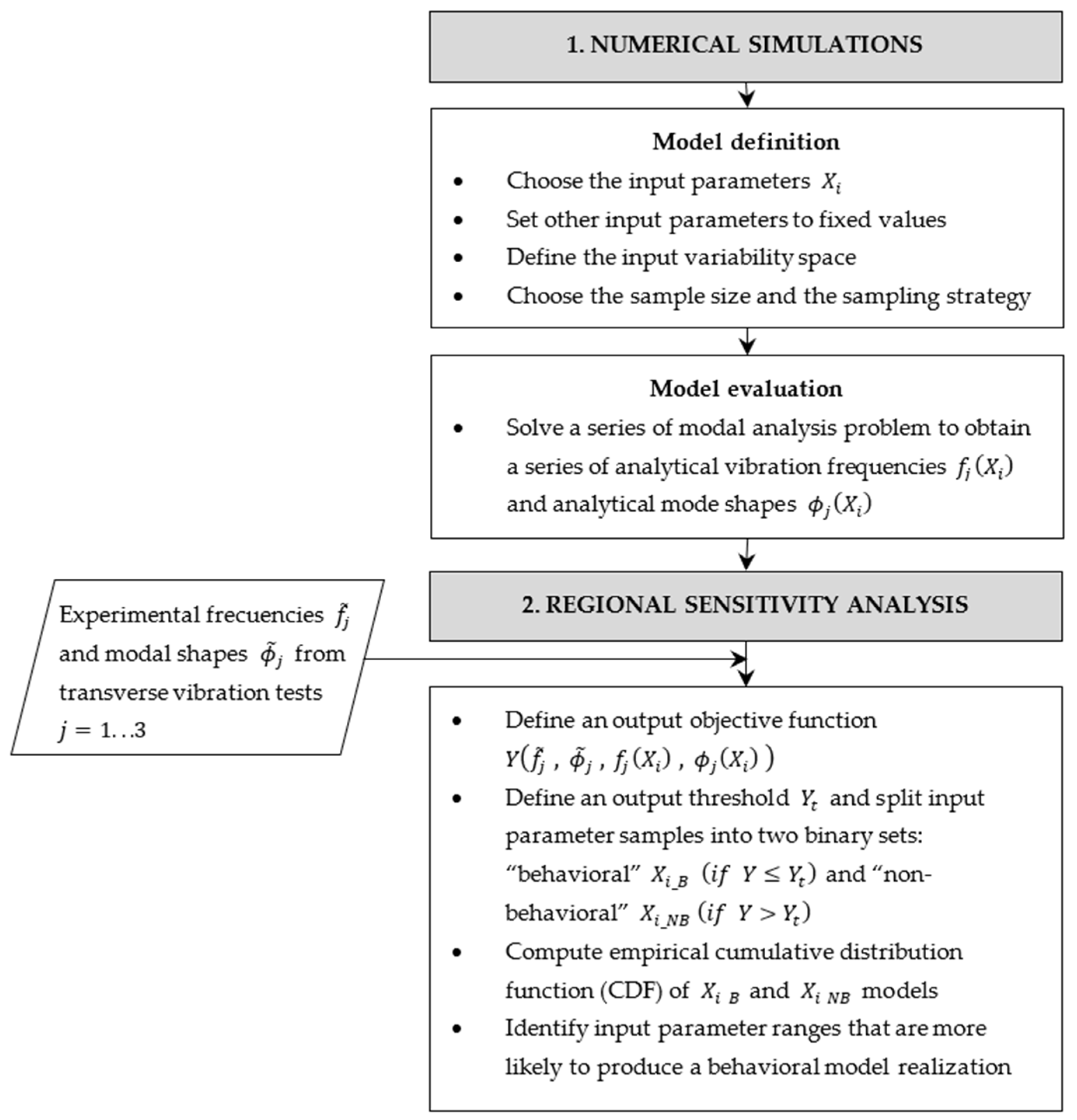
2.3.1. Numerical Simulations
2.3.2. Regional Sensitivity Analysis
- Step 1: Apply a first objective function, , shown in Equation (1), which is expressed as the average relative differences between the measured and calculated frequencies. The threshold value chosen for this function is , which is compatible with the typical differences found by other researchers [23]. Therefore, B models will be filtered in this first stage as those generating vibration frequencies with less than 5% differences concerning the experimentally measured frequencies. This first filtering stage ensures that the B models have experimentally calibrated elastic property values at the global level of the panel;
- Step 2: Apply to the B models filtered in the previous stage a second objective function , shown in Equation (2), expressed as the average Normalized Modal Difference (NMD) between the measured versus calculated modal shapes. Physically, NMD represents the fraction, on average, by which each degree of freedom (DOF) differs between two modal shapes. Besides, NMD can also be written in terms of another more popular modal shape correlation index called Modal Assurance Criterion (MAC). Thus, for example, if each DOF had an average error of 10%, the MAC and NMD values would be 0.99 and 0.1, respectively. Detailed analytical expressions of MAC and NMD can be found in [14]. According to [2], a MAC value greater than 0.95, or its corresponding NMD value less than 0.2, indicates a good correlation between two modal shapes associated with a CLT panel. Therefore, the threshold value chosen for this function is . In summary, this second filtering stage ensures that the B models have modal shapes similar to those measured experimentally at the global level;
- Step 3: Apply a third objective function to the B models filtered in step 2. This function , unlike the functions and , should have a strong emphasis on the local variability of the elastic properties. Therefore, it is convenient that is expressed in terms of the modal shapes’ DOFs that deviate most from specific ideal reference values. A suitable indicator for this type of spatial error distribution is the Coordinate Modal Assurance Criterion (COMAC). COMAC measures the correlation at each DOF averaged over a set of paired experimental–numerical modal shapes. In each DOF, the COMAC values can vary between 0 and 1, where 1 implies perfect correlation. Detailed analytical expressions of COMAC can be found in [14]. The calculation procedure of the function is shown in Figure 9.
3. Results and Discussion
3.1. Experimental Dynamic Properties of the CLT Panels
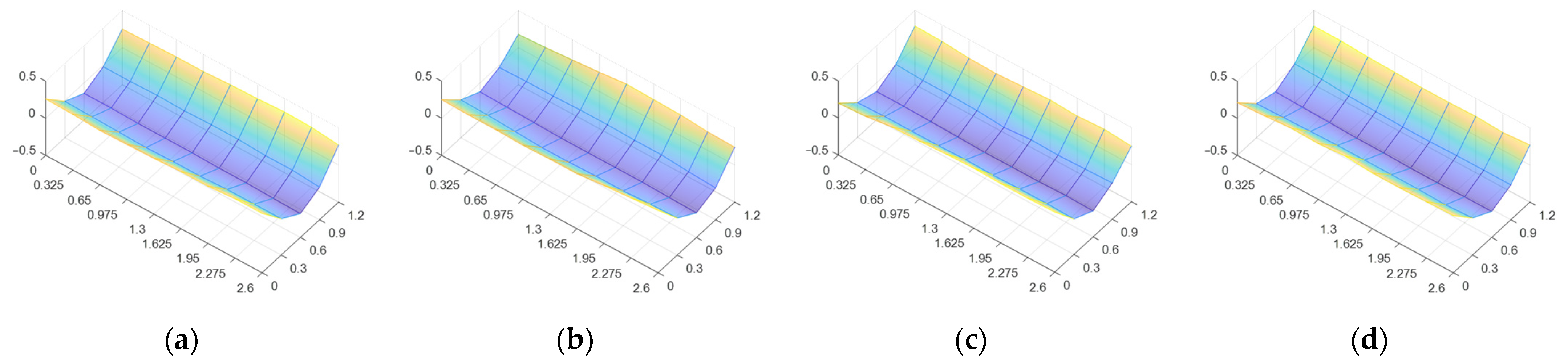
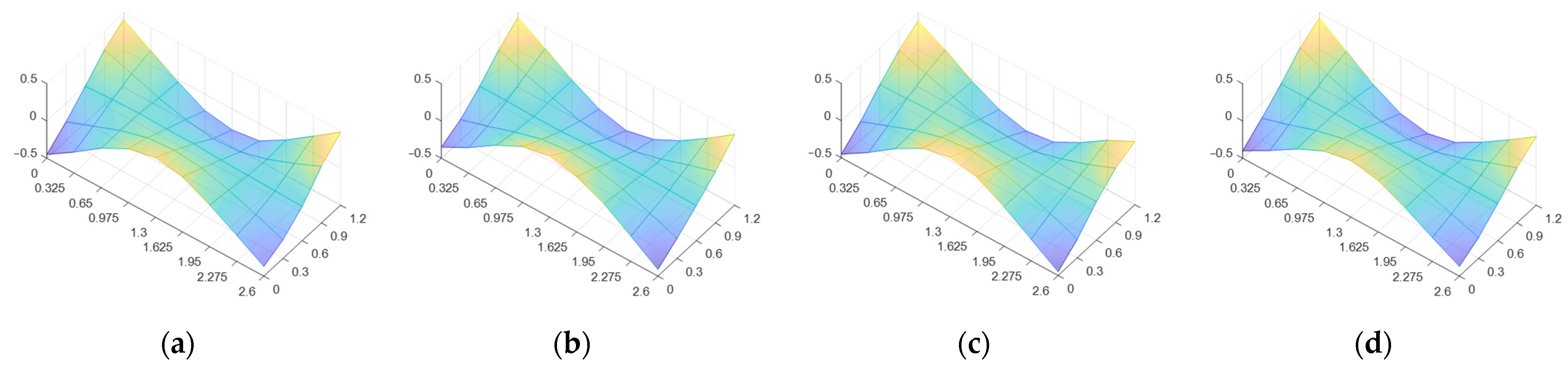
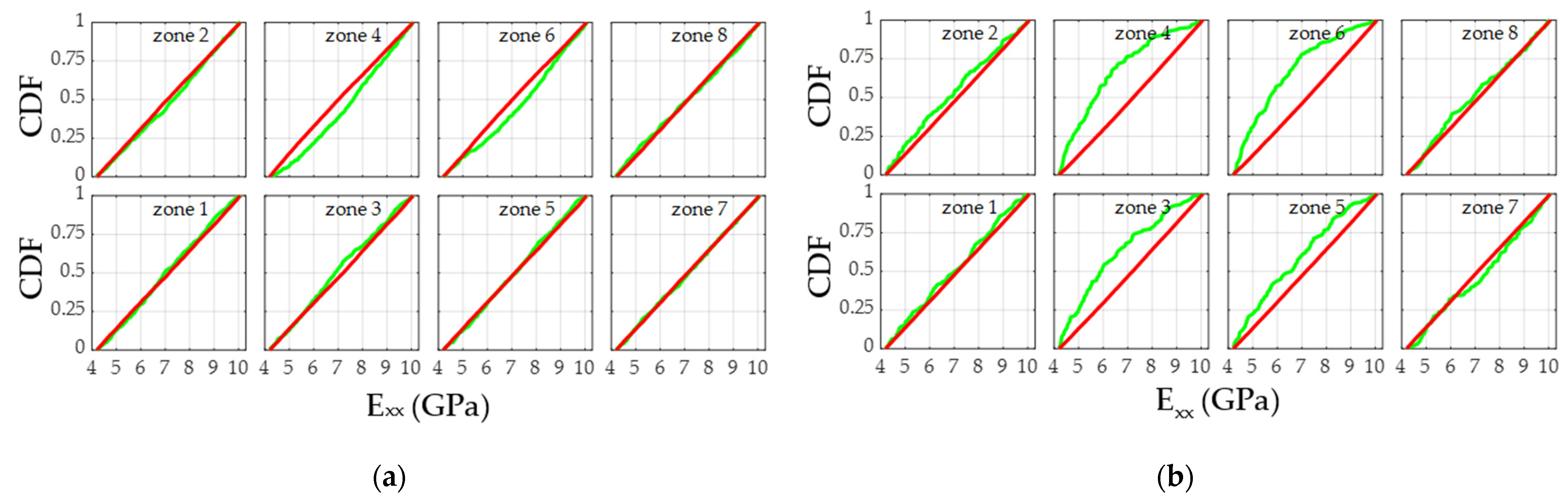
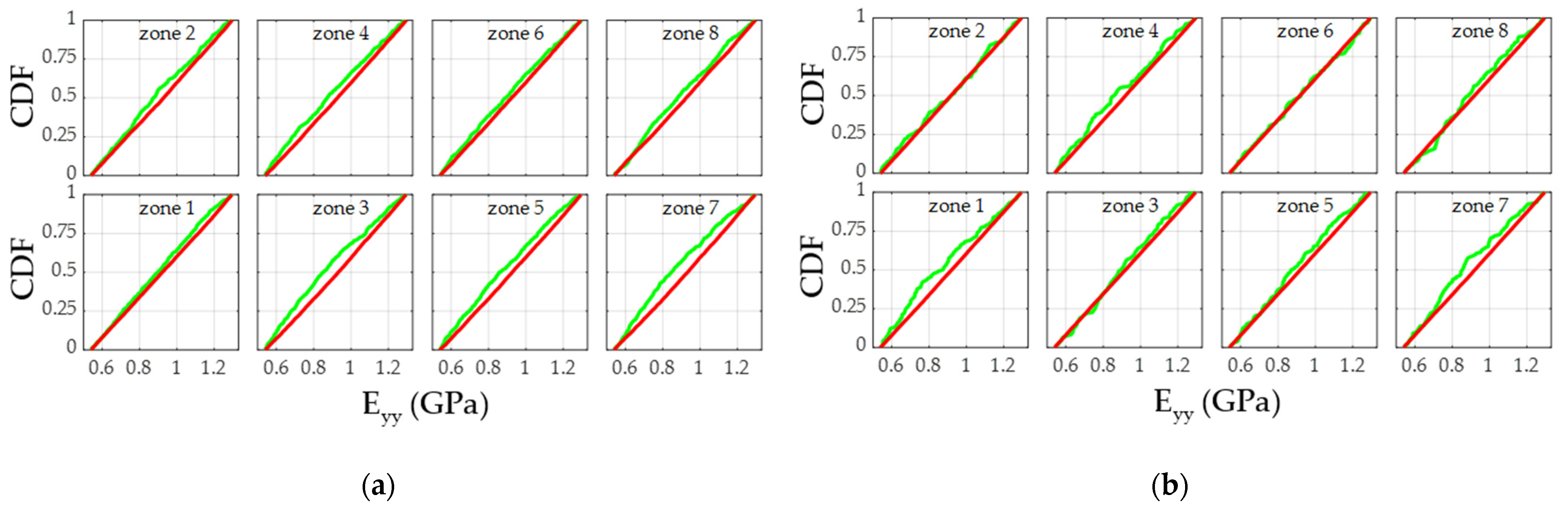
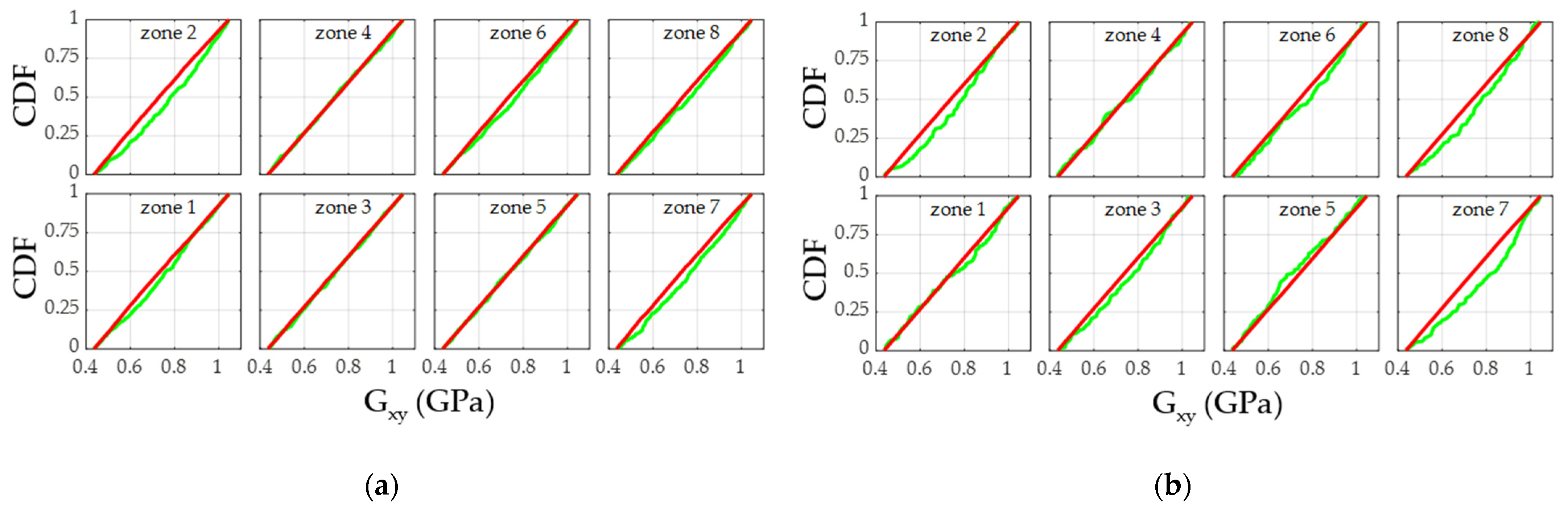
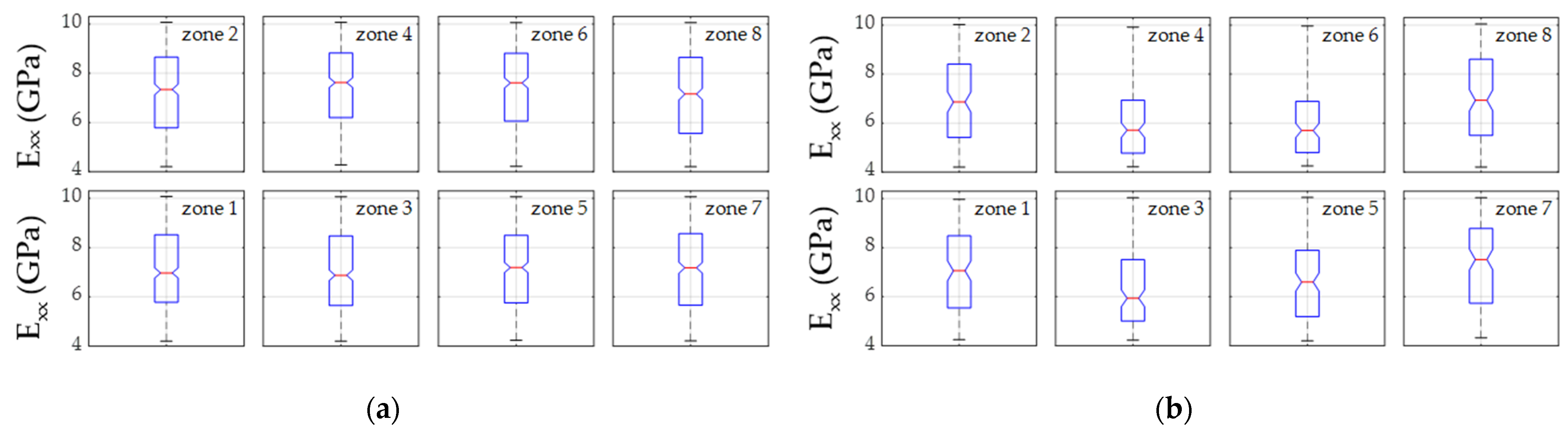
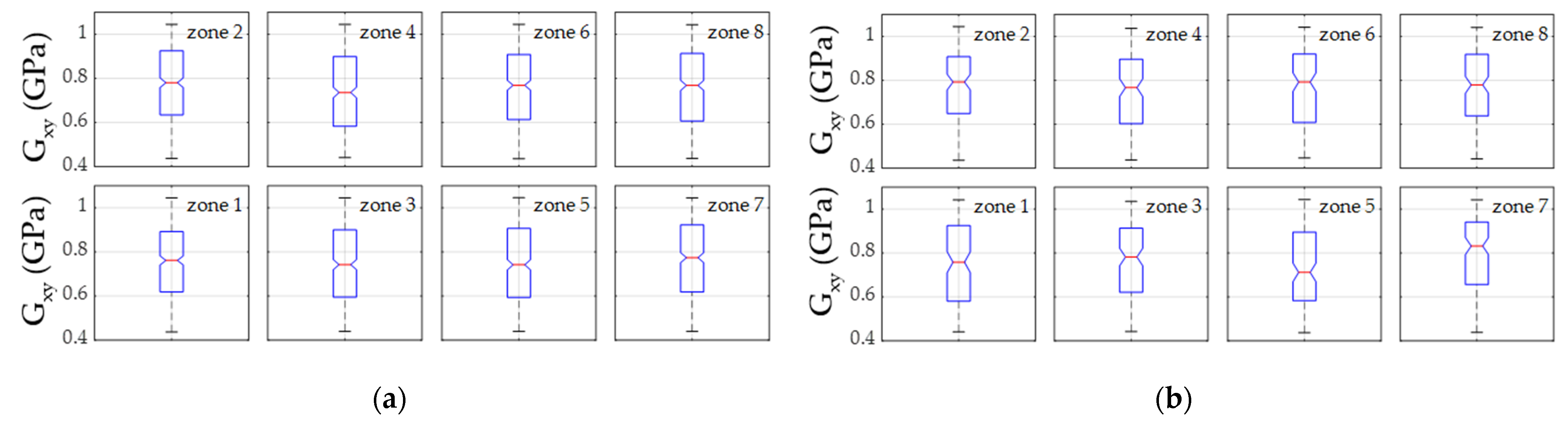
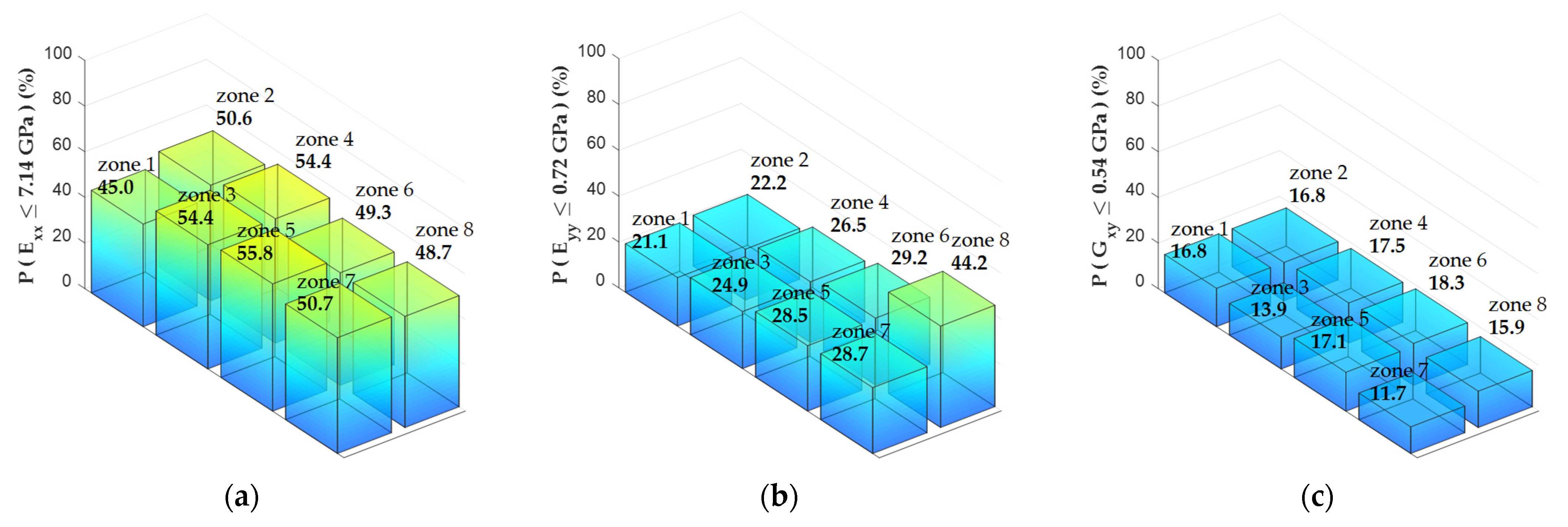
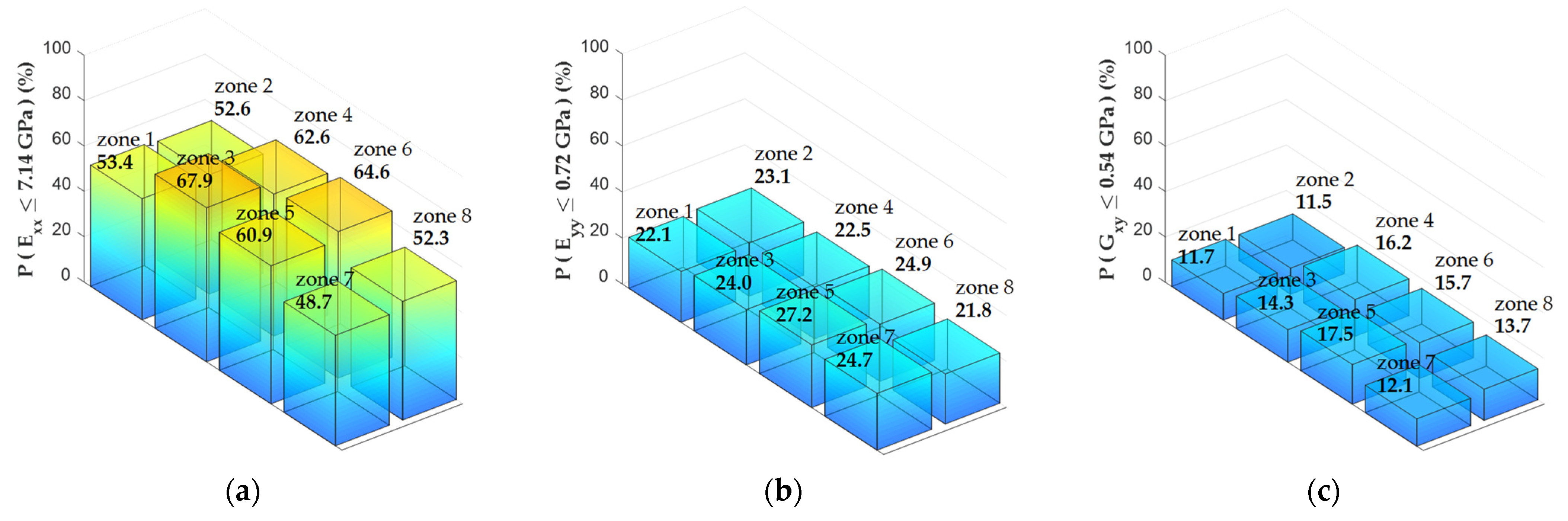
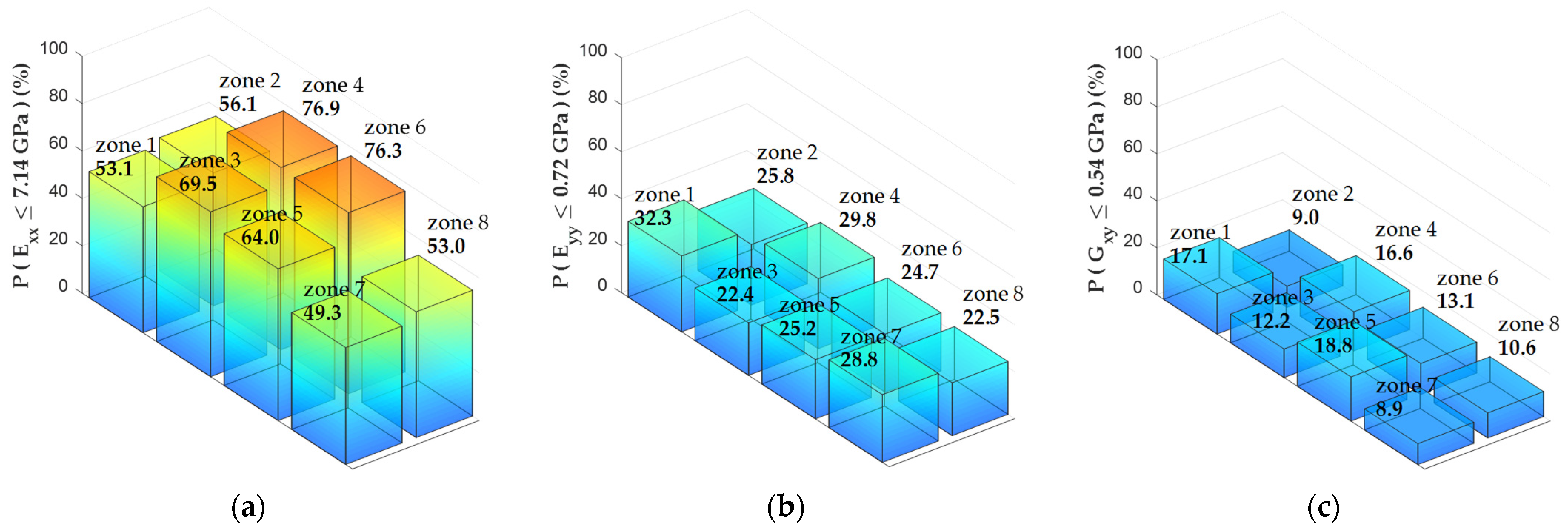
3.2. Local Variability of the Elastic Properties
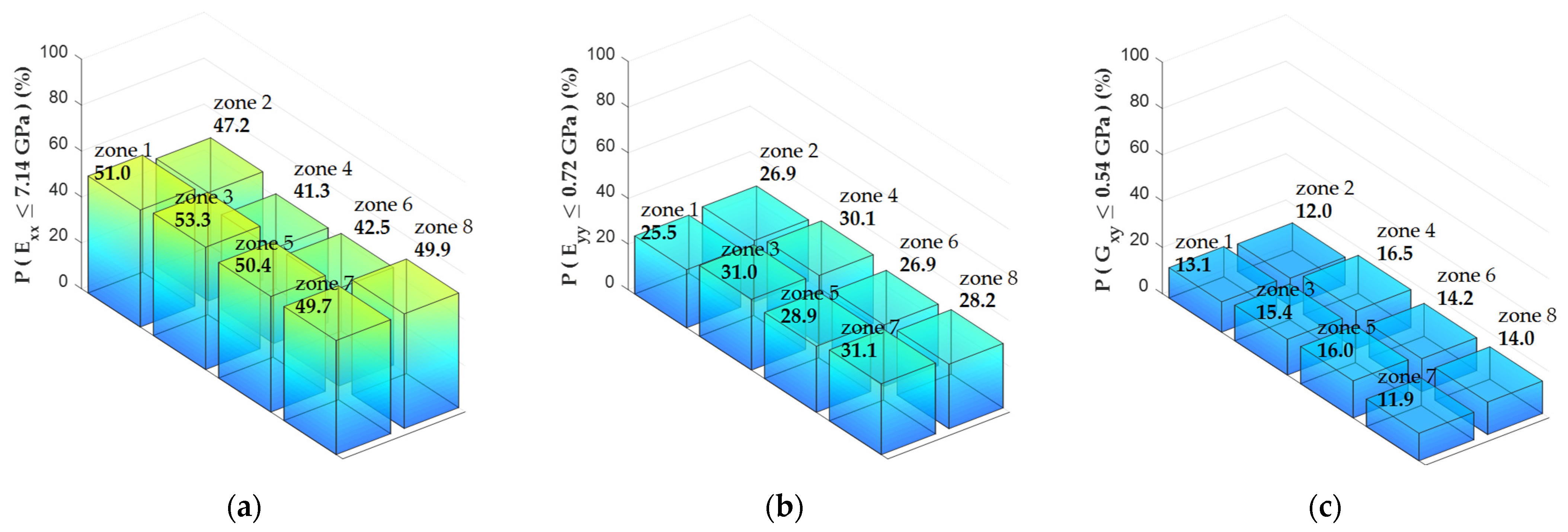
3.3. Applications for Structural Quality Control of CLT Panels
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ross, R.J. Wood Handbook: Wood as an Engineering Material; General Technical Report FPL-GTR-190; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010.
- Gsell, D.; Feltrin, G.; Schubert, S.; Steiger, R.; Motavalli, M. Cross-Laminated Timber Plates: Evaluation and Verification of Homogenized Elastic Properties. J. Struct. Eng. 2007, 133, 132–138. [Google Scholar] [CrossRef]
- Steiger, R.; Gülzow, A.; Czaderski, C.; Howald, M.T.; Niemz, P. Comparison of Bending Stiffness of Cross-Laminated Solid Timber Derived by Modal Analysis of Full Panels and by Bending Tests of Strip-Shaped Specimens. Eur. J. Wood Prod. 2012, 70, 141–153. [Google Scholar] [CrossRef] [Green Version]
- Lukacs, I.; Björnfot, A.; Tomasi, R. Strength and Stiffness of Cross-Laminated Timber (CLT) Shear Walls: State-of-the-Art of Analytical Approaches. Eng. Struct. 2019, 178, 136–147. [Google Scholar] [CrossRef]
- Bodig, J.; Jayne, B. Mechanics of Wood and Wood Composites, 1st ed.; Krieger Publishing Company: Melbourne, FL, USA, 1982. [Google Scholar]
- EU. Eurocode 5 Design of Timber Structures. Part 1-1: General Common Rules and Rules for Buildings; EN 1995-1-1; CEN: Brussels, Belgium, 2006. [Google Scholar]
- Kreuzinger, H. Plate and Shell Structures. A Model for Common Calculation Tools. Bauen Mit Holz 1999, 1, 34–39. [Google Scholar]
- Zhou, J.; Chui, Y.H.; Gong, M.; Hu, L. Elastic Properties of Full-Size Mass Timber Panels: Characterization Using Modal Testing and Comparison with Model Predictions. Compos. Part B-Eng. 2017, 112, 203–212. [Google Scholar] [CrossRef]
- Bos, F.; Casagrande, S.B. On-Line Non-Destructive Evaluation and Control of Wood-Based Panels by Vibration Analysis. J. Sound Vib. 2003, 268, 403–412. [Google Scholar] [CrossRef]
- Zhang, L.; Tiemann, A.; Zhang, T.; Gauthier, T.; Hsu, K.; Mahamid, M.; Moniruzzaman, P.K.; Ozevin, D. Nondestructive Assessment of Cross-Laminated Timber Using Non-Contact Transverse Vibration and Ultrasonic Testing. Eur. J. Wood Prod. 2021, 79, 335–347. [Google Scholar] [CrossRef]
- Ross, R.J. Nondestructive Evaluation of Wood, 2nd ed.; General Technical Report FPL-GTR-238; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2015.
- Ross, R.J.; Geske, E.; Larson, G.; Murphy, J. Transverse Vibration Nondestructive Testing Using a Personal Computer; Research Paper FPL-RP-502; U.S. Department of Agriculture, Forest Service. Forest Products Laboratory: Madison, WI, USA, 1991.
- Murphy, J. Transverse Vibration of a Simply Supported Beam with Symmetric Overhang of Arbitrary Length. J. Test. Eval. 1997, 25, 522–524. [Google Scholar]
- Maia, N.M.M.; Silva, J.M.M. Theoretical and Experimental Modal Analysis, 1st ed.; Research Studies Press Ltd.: Baldock, Hertfordshire, UK, 1997. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures, 1st ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Brincker, R.; Ventura, C. Introduction to Operational Modal Analysis, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Gülzow, A.; Gsell, D.; Steiger, R. Zerstörungsfreie Bestimmung elastischer Eigenschaften quadratischer 3-schichtiger Brettsperrholzplattenmit symmetrischem Aufbau. Holz Roh Werkst. 2008, 66, 19–37. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Chui, Y.H.; Gong, M.; Hu, L. Simultaneous Measurement of Elastic Constants of Full-Size Engineered Wood-Based Panels by Modal Testing. Holzforschung 2016, 70, 673–682. [Google Scholar] [CrossRef]
- Zhou, J.; Chui, Y.H.; Niederwestberg, J.; Gong, M. Effective Bending and Shear Stiffness of Cross-Laminated Timber by Modal Testing: Method Development and Application. Compos. Part B-Eng. 2020, 198, 108225. [Google Scholar] [CrossRef]
- Damme, B.V.; Schoenwald, S.; Zemp, A. Modeling the Bending Vibration of Cross-Laminated Timber Beams. Eur. J. Wood Prod. 2017, 75, 985–994. [Google Scholar] [CrossRef]
- Santoni, A.; Schoenwald, S.; Van Damme, B.; Fausti, P. Determination of the Elastic and Stiffness Characteristics of Cross-Laminated Timber Plates from Flexural Wave Velocity Measurements. J. Sound Vib. 2017, 400, 387–401. [Google Scholar] [CrossRef]
- Giaccu, G.F.; Meloni, D.; Concu, G.; Valdes, M.; Fragiacomo, M. Use of the Cantilever Beam Vibration Method for Determining the Elastic Properties of Maritime Pine Cross-Laminated Panels. Eng. Struct. 2019, 200, 109623. [Google Scholar] [CrossRef]
- Faircloth, A.; Brancheriau, L.; Karampour, H.; So, S.; Bailleres, H.; Kumar, C. Experimental Modal Analysis of Appropriate Boundary Conditions for the Evaluation of Cross-Laminated Timber Panels for an In-Line Approach. For. Prod. J. 2021, 71, 161–170. [Google Scholar] [CrossRef]
- Kawrza, M.; Furtmüller, T.; Adam, C.; Maderebner, R. Parameter Identification for a Point-Supported Cross Laminated Timber Slab Based on Experimental and Numerical Modal Analysis. Eur. J. Wood Prod. 2021, 79, 317–333. [Google Scholar] [CrossRef]
- NCh1198:2014. Madera-Construcciones en Madera—Cálculo. Instituto Nacional de Normalización Chile. 2014. Available online: http://normastecnicas.minvu.cl/ (accessed on 10 October 2021).
- Guan, C.; Zhang, H.; Wang, X.; Miao, H.; Zhou, L.; Liu, F. Experimental and Theoretical Modal Analysis of Full-Sized Wood Composite Panels Supported on Four Nodes. Materials 2017, 10, 683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vold, H.; Kundrat, J.; Rocklin, G.T.; Russell, R. A Multi-Input Modal Estimation Algorithm for Mini-Computers. SAE Trans. 1982, 91, 815–821. [Google Scholar]
- Brandt, A. Notes on Using the ABRAVIBE Toolbox for Experimental Modal Analysis. 2013. Available online: https://blog.abravibe.com/2013/06/21/notes-on-using-the-abravibe-toolbox-for-experimental-modal-analysis-14/ (accessed on 1 October 2021).
- Brandt, A. The ABRAVIBE Toolbox for Teaching Vibration Analysis and Structural Dynamics. In Proceedings of the Special Topics in Structural Dynamics, Volume 6; Allemang, R., De Clerck, J., Niezrecki, C., Wicks, A., Eds.; Springer: New York, NY, USA, 2013; pp. 131–141. [Google Scholar]
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with uncertainty in model updating for damage assessment: A review. Mech. Syst. Signal. Proc. 2015, 56–57, 123–149. [Google Scholar] [CrossRef] [Green Version]
- Opazo-Vega, A.; Rosales-Garces, V.; Oyarzo-Vera, C. Non-Destructive Assessment of the Dynamic Elasticity Modulus of Eucalyptus nitens Timber Boards. Materials 2021, 14, 269. [Google Scholar] [CrossRef]
- Computers and Structures Inc. ETABS—Integrated Analysis, Design and Drafting of Building Systems. Available online: https://www.csiamerica.com/products/etabs (accessed on 10 October 2021).
- Muñoz, J.; Peña, D. Evaluation of CLT Mechanical Properties by Experimental Modal Analysis. Bachelor’s Thesis, University of Bío-Bío, Concepcion, Chile, 2020. (In Spanish). [Google Scholar]
- Navarrete, A. Experimental Study of Structural Adhesives for Chilean Cross-Laminated Timber Panels. Bachelor’s Thesis, University of Bío-Bío, Concepcion, Chile, 2019. (In Spanish). [Google Scholar]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Modell. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Chichester, UK, 2008; pp. 3–31. [Google Scholar]
- Young, P.C.; Spear, R.C.; Hornberger, G.M. Modeling badly defined systems: Some further thoughts. In Proceedings of the SIMSIG Conference, Canberra, Australia, 4–8 September 1978; pp. 24–32. [Google Scholar]
- Spear, R.; Hornberger, G. Eutrophication in Peel Inlet. 2. Identification of Critical Uncertainties via Generalized Sensitivity Analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Duvnjak, I.; Damjanović, D.; Bartolac, M.; Skender, A. Mode Shape-Based Damage Detection Method (MSDI): Experimental Validation. Appl. Sci. 2021, 11, 4589. [Google Scholar] [CrossRef]
- Pianosi, F.; Sarrazin, F.; Wagener, T. A Matlab toolbox for Global Sensitivity Analysis. Environ. Modell. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons: Chichester, UK, 2004; pp. 151–161. [Google Scholar]
- Minitab. Getting Started with Minitab 19. 2019. Available online: https://www.minitab.com/en-us/support/documents/ (accessed on 10 September 2021).
- Chou, Y.-M.; Polansky, A.M.; Mason, R.L. Transforming Non-Normal Data to Normality in Statistical Process Control. J. Qual. Technol. 1998, 30, 133–141. [Google Scholar] [CrossRef]
- Pot, G.; Collet, R.; Olsson, A.; Viguier, J.; Oscarsson, J. Structural Properties od Douglas Fir Sawn Timber—Significance of Distance to Pith for Yield in Strength Classes. In Proceedings of the World Conference of Timber Engineering (WCTE), Santiago, Chile, 9–12 August 2021. [Google Scholar]
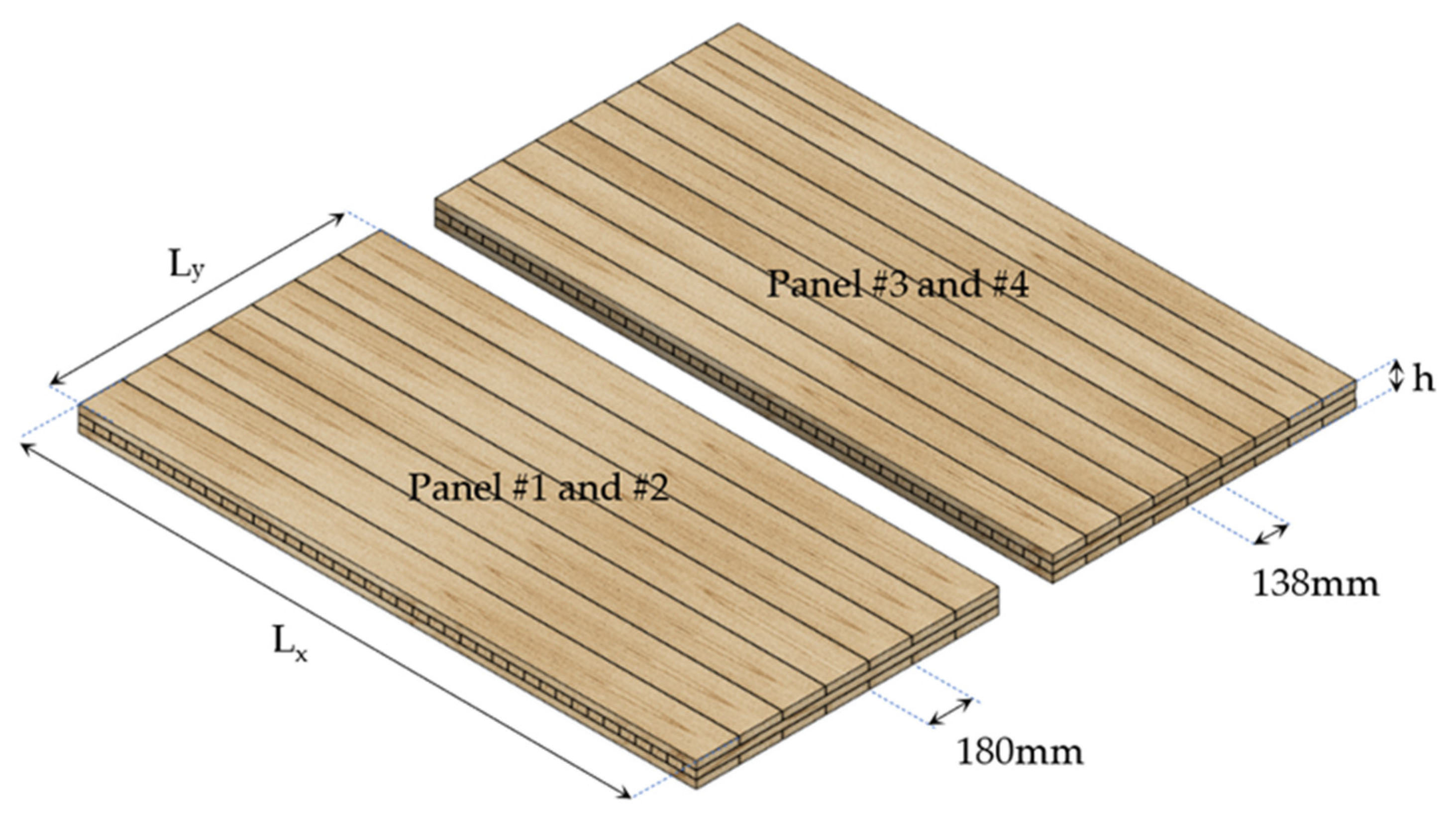









| Panel # | Ly (mm) | Lx (mm) | h (mm) | Density (kg/m3) | Moisture Content (%) |
|---|---|---|---|---|---|
| 1 | 1196.3 | 2596.0 | 96.3 | 451.9 | 11.2 |
| 2 | 1196.7 | 2580.3 | 96.1 | 457.1 | 12.8 |
| 3 | 1196.8 | 2598.0 | 96.9 | 441.7 | 12.2 |
| 4 | 1196.8 | 2596.3 | 96.8 | 442.3 | 11.1 |
| Panel # | |||
|---|---|---|---|
| 1 | 56.06 (0.11%) | 89.30 (0.04%) | 93.69 (0.05%) |
| 2 | 56.12 (0.09%) | 91.83 (0.10%) | 95.75 (0.06%) |
| 3 | 51.74 (0.11%) | 93.76 (0.11%) | 96.40 (0.06%) |
| 4 | 49.61 (0.13%) | 92.52 (0.08%) | 96.98 (0.05%) |
| Panel # | Number of Simulations | Number of B Models | Number of NB Models | Mean Value of the Objective Functions in B Models | ||
|---|---|---|---|---|---|---|
| 1 | 2400 | 440 | 1960 | 0.032 | 0.165 | 9.27 |
| 2 | 2400 | 203 | 2197 | 0.033 | 0.163 | 9.73 |
| 3 | 2400 | 418 | 1982 | 0.036 | 0.183 | 4.29 |
| 4 | 2400 | 132 | 2268 | 0.041 | 0.182 | 5.81 |
| Panel # | Elastic Property | Zone 1 | Zone 2 | Zone 3 | Zone 4 | Zone 5 | Zone 6 | Zone 7 | Zone 8 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Exx | N (0.44) | N (0.16) | I (0.02) | C (<0.001) | N (0.49) | C (<0.001) | N (0.93) | N (0.46) |
| 1 | Eyy | N (0.12) | C (0.004) | C (<0.001) | I (0.01) | C (0.002) | N (0.19) | C (<0.001) | I (0.04) |
| 1 | Gxy | I (0.03) | C (<0.001) | N (0.74) | N (0.90) | N (0.71) | I (0.04) | C (0.003) | I (0.09) |
| 4 | Exx | N (0.59) | N (0.27) | C (<0.001) | C (<0.001) | C (0.002) | C (<0.001) | N (0.28) | N (0.32) |
| 4 | Eyy | I (0.03) | N (0.89) | N (0.68) | N (0.21) | N (0.45) | N (0.86) | I (0.03) | N (0.47) |
| 4 | Gxy | N (0.28) | I (0.03) | N (0.28) | N (0.81) | N (0.28) | N (0.19) | C (0.001) | I (0.03) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Opazo-Vega, A.; Benedetti, F.; Nuñez-Decap, M.; Maureira-Carsalade, N.; Oyarzo-Vera, C. Non-Destructive Assessment of the Elastic Properties of Low-Grade CLT Panels. Forests 2021, 12, 1734. https://doi.org/10.3390/f12121734
Opazo-Vega A, Benedetti F, Nuñez-Decap M, Maureira-Carsalade N, Oyarzo-Vera C. Non-Destructive Assessment of the Elastic Properties of Low-Grade CLT Panels. Forests. 2021; 12(12):1734. https://doi.org/10.3390/f12121734
Chicago/Turabian StyleOpazo-Vega, Alexander, Franco Benedetti, Mario Nuñez-Decap, Nelson Maureira-Carsalade, and Claudio Oyarzo-Vera. 2021. "Non-Destructive Assessment of the Elastic Properties of Low-Grade CLT Panels" Forests 12, no. 12: 1734. https://doi.org/10.3390/f12121734
APA StyleOpazo-Vega, A., Benedetti, F., Nuñez-Decap, M., Maureira-Carsalade, N., & Oyarzo-Vera, C. (2021). Non-Destructive Assessment of the Elastic Properties of Low-Grade CLT Panels. Forests, 12(12), 1734. https://doi.org/10.3390/f12121734








