Abstract
Forest fire risk has increased globally during the previous decades. The Mediterranean region is traditionally the most at risk in Europe, but continental countries like Serbia have experienced significant economic and ecological losses due to forest fires. To prevent damage to forests and infrastructure, alongside other societal losses, it is necessary to create an effective protection system against fire, which minimizes the harmful effects. Forest fire probability mapping, as one of the basic tools in risk management, allows the allocation of resources for fire suppression, within a fire season, from zones with a lower risk to those under higher threat. Logistic regression (LR) has been used as a standard procedure in forest fire probability mapping, but in the last decade, machine learning methods such as fandom forest (RF) have become more frequent. The main goals in this study were to (i) determine the main explanatory variables for forest fire occurrence for both models, LR and RF, and (ii) map the probability of forest fire occurrence in Eastern Serbia based on LR and RF. The most important variable was drought code, followed by different anthropogenic features depending on the type of the model. The RF models demonstrated better overall predictive ability than LR models. The map produced may increase firefighting efficiency due to the early detection of forest fire and enable resources to be allocated in the eastern part of Serbia, which covers more than one-third of the country’s area.
1. Introduction
Forest fires, as global phenomena, present numerous forms of threats to many countries around the world, from Canada and Siberia through to Indonesia, Australia, Africa, and the Amazonia. Although statistics show that the frequency of fires, alongside the total burnt area, have been decreasing from year to year globally [1], several regions will experience larger and more intense fires [2,3,4]. The Mediterranean region is traditionally the most at risk in Europe [5], but in recent years, forest fires have also become an important issue in Central Europe [6]. Among other European countries, Serbia experienced increased fire activity during the last two decades [7].
The increasing risk and associated damage caused by fires are usually linked to climate changes [8]. Considering the current climate scenario [9], which predicts an average temperature rise of 4–6 °C by the end of this century [10,11], and a decrease in total rainfall with an uneven distribution throughout the year in the south of Europe featuring long periods of drought in summer, an increased risk of forest fire is expected in Europe [5]. The greatest changes in Europe are expected in the transition between the Mediterranean and Euro-Siberian regions [12], where the Balkan Peninsula is situated. The most dominant oak and beech forest may be replaced by evergreen Mediterranean vegetation [13,14], which is more prone to forest fire. Therefore, a further increase in forest fire risk can be expected due to changes in the fuel type.
Aside from the direct damage in terms of wood loss, which is obvious and easy to quantify, many other risks may appear following forest fires, due to the slow process of regeneration, especially in conifer forests [15]. Secondary pests, such as bark (Coleoptera: Curculionidae: Scolytinae) and ambrosia beetles (Coleoptera: Buprestidae) and diseases, that attack physiologically weakened trees may reach an outbreak population level and affect a much larger area than forest fire alone [16]. To minimize the harmful effects of forest fires, it is necessary to create an effective protection system against fire. According to San-Miguel-Ayanz [17], forest fire risk is defined as the probability of a fire happening and its consequences. Therefore, any increase in fire probability or its consequences directly results in an increase in fire risk. Our research has focused on forest fire occurrence probability mapping as a component of the future system for forest fire risk assessment. Forest fire probability mapping is a basic tool in risk management [18,19] and allows the allocation of resources for fire suppression, within a fire season, from zones with a lower risk to those under higher threat. Also, in the long run, mapping fire occurrence probability is a very valuable tool in forest management planning that improves forest resilience to fire through the implementation of various types of fire preventive silvicultural measures [20,21,22,23].
Among traditional methods, logistic regression (LR) is the most common when dealing with binary outcomes, like the presence or absence of fire [24]. Conversely, machine learning (ML) methods, as a form of artificial intelligence, are widely used in wildfire science and management, with more than 300 articles published on this topic since the 1990s [25]. Random forest (RF) belongs to the decision trees branch of the same group of ML methods [26]. Our study had the following objectives: (1) to map the probability of forest fire occurrence in Eastern Serbia based on LR and RF; (2) to determine the main explanatory variables for forest fire occurrence for both models.
2. Materials and Methods
2.1. Study Area
The study area is in the eastern and southern parts of Serbia (Figure 1). It has a total land area of 30,235.5 km2. Broadleaved, conifer, and mixed forest cover 12,587.5, 170.7, 340.6 km2, respectively. Natural grasslands, transitional woodland-shrub, and sparsely vegetated areas cover 925.7, 2949.5, and 48.0 km2, respectively, while other areas represent agricultural, urban, or other non-wood areas. The elevation ranges from 28 to 2169 m. It has been observed that durations of extremely hot weather last longer and periods of extremely cold weather are shortened compared to the reference period of 1960–1990 [27]. These trends of extreme temperature conditions are most pronounced in the summer season [27]. A decrease in spring precipitation has been detected over the central and eastern parts of Serbia [28]. The annual quantity of rainfall is often insufficient, and droughts are evident in eastern and south-eastern parts of Serbia [28]. Scenarios where the monthly quantity of precipitation falls in only a few days of the month are expected to become more frequent, which will lead to more extreme weather events such as floods and droughts [29]. Serbia has two peaks in its fire season [30]. The first peak occurs in March, which is associated with 25% of the annual burnt area, while the second and largest peak appears in August [31]. In August 2012, more than 40 large fires were recorded, including two fires that were more than 1000 ha in size [32]. More than 16,000 ha of forest land were destroyed in 2007, with the value of the wood lost was estimated at 40 million euros [33].
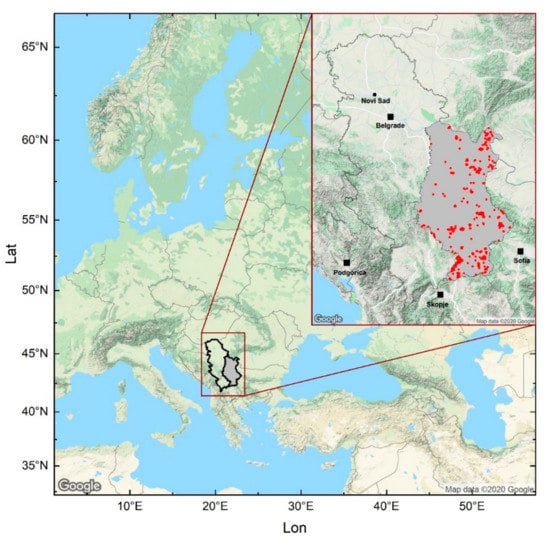
Figure 1.
The geographic position of study area, Eastern Serbia, is marked in gray (latitudes 42.27–44.82° N and longitudes 20.90–23.01° E) with the layer of forest fire hotspots obtained by NASA’s Fire Information for Resource Management System (FIRMS) (MODIS fire hotspot) for the period of 2001–2018.
2.2. Data Preparation
2.2.1. Dependent Variable
Data regarding the fire location were obtained from NASA’s Fire Information for Resource Management System (FIRMS), which distributes near real-time fire products from Moderate Resolution Imaging Spectroradiometer (MODIS) from the Terra and Aqua platforms with a spatial resolution of 1 km (https://firms.modaps.eosdis.nasa.gov). Each position of a MODIS-identified active fire represents the center of a 1 × 1 km pixel that is labeled by the algorithm as containing one or more fires inside the pixel. Only fire pixels with a confidence higher than 80% for the period from January 2001 to December 2018 were considered for further analysis, because in certain cases the product underestimates the occurrence of fire [34].
2.2.2. Independent Variables
Independent variables were grouped into four categories: topography, vegetation, anthropogenic factors, and climate. Specific variables within categories were selected based on previous studies on forest fire occurrence [24,34,35,36,37,38,39]. Detailed information on preselected variables is presented in Table 1.

Table 1.
Independent variables considered for forest fire occurrence models with codes, units, source and calculated variable inflation factors (VIFs).
Topographic parameters, elevation, slope, and aspect, were derived from the digital elevation model (DEM) with a precision of 3 arcsec previously downloaded from the United States Geological Survey (http://landsat.usgs.gov//landsatcollections.php). Average values of elevation, slope, and dominant aspect were calculated for each polygon in a 1 × 1 km grid using ArcGIS software (ESRI, Redlands, CA, USA). Obtained values of the slope and dominant aspect were divided into classes according to Carmo et al. [35], while elevations were divided into classes of 200 m (Figure 2).
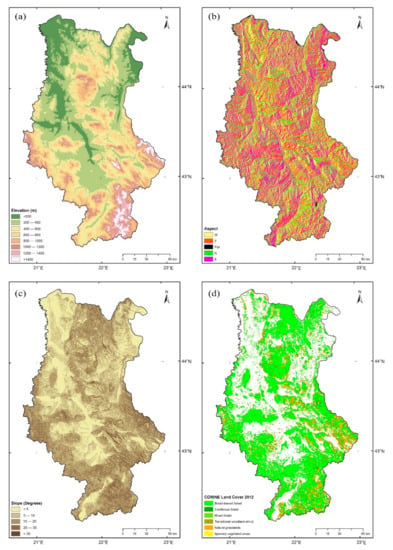
Figure 2.
Categorical predictors related to forest fire in Eastern Serbia. (a) Classes of elevation; (b) aspect classes; (c) slope categories; (d) land cover categories obtained by CORINE 2012.
Vegetation and land cover data were obtained from the CORINE 2012 data set (https://land.copernicus.eu/pan-european/corine-land-cover/clc-2012). The vector layer was intersected with polygon grid data. Objects in this vector layer were filtered for the following CORINE 2012 land cover classes (CLCs): broad-leaved forest (BF), coniferous forest (CF), mixed forest (MF), natural grasslands (NG), transitional woodland-shrub (TWS), and sparsely vegetated areas (SVA) (Figure 2). Intersecting the polygon grid data with the polygon CLC layer filtered this way, a new polygon layer with a table of attributes containing a polygon grid Object ID, CLC class ID with its description, and an area of CLC class that falls into the respective grid polygon were generated.
Data on drought code (DC), as a component of the Canadian Forest Fire Weather Index [40], were obtained from the Republic Hydrometeorological Service of Serbia (http://www.meteoalarm.rs/eng/fwi_osm.php) as tables with coordinates of meteorological stations with values on the drought code for each day in the observed period (2012–2018). Each of these tables was then converted into a spatial point layer with points representing meteorological stations and a respective table of attributes with values of the drought code. The layer was then used for interpolation using the ordinary kriging method [41], resulting in raster layers whose pixels represent values of drought code. This way, we were able to calculate zonal statistics of drought code for each day and each polygon of a grid layer for raster layers that represent the observed period. Finally, average values for each cell in the grid cells were calculated based on all of the drought code data for the observed period.
Layers of roads, populated places, railroads, and agricultural land were used for the calculation of the distance from each object of a 1 × 1 km grid to the nearest object of the respective layer, so the attribute table of the generated point and polygon grid layer was extended with distances to the nearest populated place, road, railway and agricultural land (https://www.openstreetmap.org).
Population data were obtained from a raster dataset available for download in GeoTIFF format at the Center for International Earth Science Information Network (CIESIN), Columbia University (http://dx.doi.org/10.7927/H4639MPP). The sum of the number of people per polygon grid was also calculated by a zonal statistic tool.
At the end of the GIS portion of the analysis, Boolean values (Yes/No) were assigned to the elements of the grid by using the Spatial Join tool. Values of Yes were assigned to the elements for which the historical wildfire(s) occurred, and values of No were assigned to those for which it did not.
Each cell with at least one historical record of a fire event from 2001 to 2018 was classified as a fire cell and coded as one (1). In total, 429 cells were selected as a fire cell for Eastern Serbia. The use of binary LR alongside RF classification assumes that the predicted variable is dichotomous. Therefore, necessary non-fire cells were sampled based on the propensity score matching (PSM) method [42] and coded as zero (0). In general, a propensity score analysis reduces the effect of confounding in observational (nonrandomized) studies and can be used for matching, stratification, inverse probability of treatment weighting, and covariate adjustment, all based on the propensity score [43]. Thus, PSM forms matched sets with equal ratio of treated and untreated subjects [44], in our case, of fire and non-fire cells, who share a similar value of propensity score. Matching without replacement [45] was applied for the selection of non-fire cells in this study. Namely, non-fire cells can be selected only once as a match for a given fire cell. Among greedy and optimal matching procedures of PSM, the latter was used in this study. Both approaches choose the same sets of controls for the overall matched samples, but optimal matching does a better job of minimizing the difference in propensity score value within each pair [46]. PSM was conducted in the R package ‘MatchIt’ v 3.02 [47].
As it was important to avoid the selection of non-fire cells in the vicinity of the fire cells, because of the similar environmental conditions, we tested distances among created pairs of cells. The distance between pairs of fire and non-fire cells varied from 2.2 to 268.1 km, with an average of 134.2 km. Additionally, to validate the created models, whole paired samples were randomly divided into two equal subsamples, training and validation, with the same number of fire and non-fire cells [24,39,48,49].
One of the basic assumptions that must be met before applying LR is the absence of high correlations (multicollinearity) among the explanatory variables (predictors) included in the model. Explanatory variables were checked for multicollinearity by the variance inflation factor (VIF) and Spearman’s rho correlation [50]. Only variables with VIF ≤ 10 and a Spearman’s rho coefficient lower than 0.7 [51] were considered for model building.
2.2.3. Forest Fire Occurrence Frequency across Categorical Predictors
Forest fire distribution across categorical predictors was analyzed for all events in the 15 years. Observed versus expected frequencies were analyzed and compared. Observed frequencies represented the number of forest fires that occurred within the explanatory variable category, while the expected frequencies were represented by the surface covered by the respective variable category in the study area [24]. Comparisons between observed and expected frequencies were based on chi-square statistics [52] at a significance level of 0.001. Mean values were calculated for each class of categorical predictors, and histograms were created accordingly.
2.3. Modeling Procedures
Based on collected and generated data, the model of probabilities for forest fire occurrences was generated for each cell of the polygon grid for the territory of Eastern Serbia.
2.3.1. LR Models
The algorithm obtained by the LR calculates the conditional probability of the fire event occurring from one or more input variables [53]. Also, LR can be used for estimating the contribution and significance of each variable by the Wald test [54], and afterwards can select a combination of variables that can be introduced in more complex models [55]. To estimate forest fire occurrence probability in Eastern Serbia by LR, the following equation was applied:
with “Pi” as the probability of the forest fire occurrence, “α” as a constant, “β” as a coefficient from regression, and “X” as original values of variables.
2.3.2. RF Models
This method uses a large number of decision trees, which produce their predictions and combine them into a single, more accurate, prediction [56]. RF has gained popularity in recent years, as it has been proven to perform better than LR according to several studies [39,57,58]. Specifically, it considerably outperforms LR in the accuracy measured, as well as the Brier score and area under curve (AUC) [59,60,61], on large and diverse datasets. Thus, considering the similarity of forest fire probability prediction to other risk-assessment applications, we considered RF as a strongly supported model of choice worth investigation. Similar to LR, the RF method is also good at handling both categorical and continuous types of explanatory variables.
The method proposed by Ye et al. and Genuer et al. [37,62] was applied for the variable selection. Each variable was included in the model N − 1 times, where N represents the number of variables considered as a predictor. RF models were run 16 times and an additional variable was excluded in each iteration. The variable importance obtained from each iteration was used for the calculation of relative variable importance, which represents an average value for a specific variable ranked from 0 to 1. All variables were scored from 1 to 16, according to the average importance. The variable with the highest average importance was scored as 1, and the variable with the lowest importance was scored as 16. Then, a RF model with each of the 15 highest ranked variables was generated for comparison with LR models. RF analyses were conducted by the default value of mtry (4), which represents the number of variables at each split and the 100 trees in the forest (ntree).
2.4. Model Validation
Model evaluation was conducted by a receiver operating curve (ROC) analysis, calculating the proportion of fire cells, classified as fire (sensitivity), and non-fire cells, classified as non-fire (specificity), for the obtained models. A ROC curve plots the values that represent sensitivity versus values that represent 1—specificity for the range of possible cut points [63]. AUC values between 0.5–0.7 indicate poor precision, values between 0.7–0.8 indicate acceptable precision, values between 0.8–0.9 indicate excellent precision, and values higher than 0.9 indicate outstanding model precision [63]. Additional evaluation of the models was conducted by 2 × 2 classification tables based on the overall accuracy. Thus, the tables are a result of the cross-classification of the dichotomous outcome variable, whose values are derived from the predicted and observed probabilities. Also, to compare the predictive capacity of the models produced, the distribution of fire cells of the validation group across classes of forest fire occurrence probability was analyzed. Due to the limited size of data, the k-fold cross-validation (CV) method was also applied to compare obtained models. Analysis was conducted in the R package ‘Caret’ v 6.0–86 [64] using “glm” and “rf” methods for LR and RF, respectively. ROC analysis, accuracy, and Kappa values obtained from CV were used to compare models, with k-value set as 10.
To designate each cell as fire or non-fire, an optimal cutoff point must first be defined. For the models selected by the LR and RF procedures, based on the ROC analysis and prediction accuracy obtained under the training subsets, the optimal cutoff point was determined by the sensitivity equals specificity method [65] using the easyROC web-tool [66]. Then, the estimated probability for each cell was compared to the optimal cutoff point. If the estimated probability for the particular cell exceeded the optimal cutoff point, then that cell was designated as a fire cell. Conversely, if the estimated probability was lower than the optimal cutoff point, a particular cell was designated as a non-fire cell. Cutoff values were applied within selected models to both training and validation subsets.
2.5. Variable Importance Analysis
The quantification of variable importance is used for variable selection in many applied studies. To assess the importance of individual variables selected by the LR procedure, Wald statistics were applied to the models [67]. Variable importance in RF classification could be assessed by the permutation importance indices [68] or by the Gini impurity function for a classification problem [69]. For RF, the variable importance measures are summed across all trees in the forest and scaled in the same manner so that the most important variable has a value of 1.
2.6. Mapping Forest Fire Occurrence Probability
Forest fire occurrence probability calculated by the LR or RF models for fire cells and non-fire cells was used to map the forest fire occurrence probability in Eastern Serbia in ArcGIS 10.2. According to Nhongo et al. [34], the produced map was classified into five categories: very low (0.01−0.20), low (0.21−0.40), medium (0.41−0.60), high (0.61−0.80), and very high (0.81−1.00).
All statistical analyses related to LR and RF were conducted using the software Statistica 13 (TIBCO Software Inc., Palo Alto, CA, USA).
3. Results
3.1. Forest Fire Occurrence Frequency
Forest fire distributions across the categorical explanatory variables are displayed in Figure 3. An almost normal distribution of forest fires was recorded across elevation classes, with higher frequencies at elevations between 200 and 1000 (with a less pronounced peak in the class of 600−800 m), and with lower frequencies below and above this range (Figure 3a). The frequencies of forest fire across elevation classes highly correspond to surface area covered by the respective classes (χ2 =39.83, p < 0.001). This connection was not significant between forest fire occurrence and aspect classes (χ2 = 1.11, p < 0.774). Regarding aspect, the highest frequencies of fires occurred on southern aspects, then almost equally eastern and western aspects, while the lowest frequency was recorded on northern aspects (Figure 3b). The highest frequency of forest fire was recorded on the slopes with an inclination between 10° and 19.99°, then between 5° and 9.99°, while the lowest frequency was recorded at the lowest inclination (0−4.99°). No fire was recorded at the highest inclination of over 30° (Figure 3c). Forest fires were influenced by slope (χ2 = 47.54, p < 0.001). Also, land cover type had a significant influence on forest fire occurrence (χ2 = 107.89, p < 0.001). More than 55% of forest fires occurred in broad-leaved forests, and almost 29% and 14% occurred in the transitional woodland-shrubs and natural grasslands respectively, while less than 2% of forest fires occurred in the mixed forest and coniferous forests. No forest fire was recorded in the sparsely vegetated area (Figure 3d).
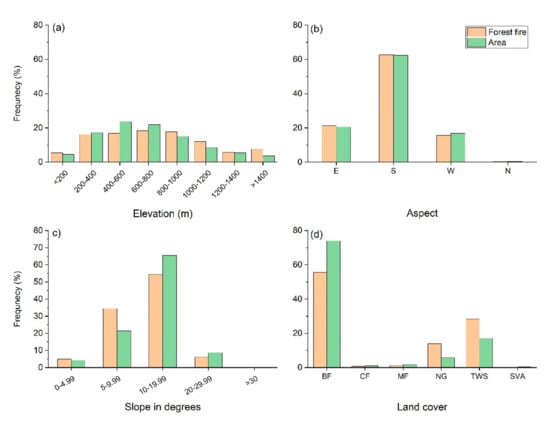
Figure 3.
Frequencies of forest fires and areas covered by categorical variables: (a) elevation classes, (b) aspect classes (exposure), (c) slope degree classes, and (d) vegetation classes obtained from CORINE land cover 2012 that are present in Eastern Serbia: BF: broad-leaved forest; CF: coniferous forest; MF: mixed forest; NG: natural grasslands; TWS: transitional woodland-shrubs, and SVA: sparsely vegetated areas.
3.2. Models of Forest Fire Occurrence
In the first step, the total forested area (TFA) variable was excluded for further analysis due to the high correlation (R = 0.84) with distance agricultural land (DAgL), as displayed in Figure S1 (see the Supplementary Materials). The remaining 16 explanatory variables met the conditions of VIF ≤ 10 and were considered for the future models. After several iterations, the final models were created by LR and RF procedure for 15 variables. The highest impact on fire probability had a drought code, followed by distance to municipality, distance to water, distance to railway, and distance to arable land, while a relative contribution of mixed forest had the lowest impact in the RF model. Also, in the LR models, the highest impact on fire probability had a drought code, while a relative contribution of coniferous forest had the lowest impact on forest fire occurrence (Table 2).

Table 2.
Explanatory variable importance evaluation based on Wald statistics for linear regression (LR) and Gini impurity for random forest (RF) models.
The overall prediction accuracy of the LR and RF models, calculated by using an optimal cut-off value, was 86.7 and 87.7%, respectively (Table 3). Moreover, the LR and RF models display AUC values of 94.2% and 94.5%, respectively, affirming a high predictive power (Figure 4b).

Table 3.
Classification tables for the training and validation sets of data based on LR and RF models, with applied cut off values, according to the sensitivity equals specificity method.
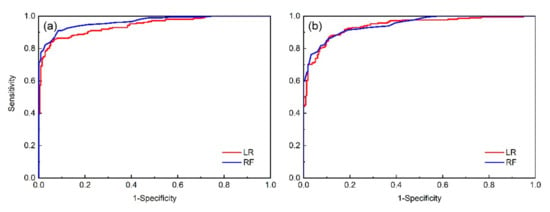
Figure 4.
Receiver operating curve (ROC) for LR and RF models: (a) training data set, (b) validation data set.
3.3. Relative Importance of Variables
In the LR models, drought code was the most important variable for fire occurrences, followed by the distance to rail and agricultural land. Conversely, the lowest importance of the forest fire occurrence was associated with the contribution of coniferous and mixed forest, and also aspect classes (Table 2). In the RF models, drought code was the most important variable followed by the distances to municipality, water, rail, and arable land. Similarly, to the LR models, contribution of mixed and coniferous forest as well as aspect classes had the lowest impact on the RF models (Table 2). Interestingly, distance to municipality was recognized by RF as very important model variable, while in the LR models this variable did not have a statistically significant effect on model performance.
3.4. Spatial Modeling of Probability of Fire Occurrence
Zones with a very high probability of forest fire occurrence were situated in the southeastern part of the study area in both models and vary from 19.7% (LR) to 18.9% (RF) of the forested area. Zones with a very low probability of forest fire occurrence were situated in the northwestern part of the study area and range from 21.1% (LR) to 22.2% (RF) of the forested area (Figure 5).
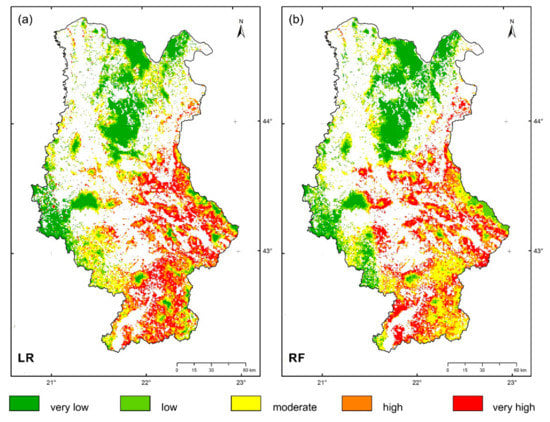
Figure 5.
Maps of forest fire probability based on (a) LR models, (b) RF models.
3.5. Model Validation
LR models performed better in the very low fire distribution class, compared to the RF models, identifying lower forest fire incidence in the validation set of data. On the other hand, RF models performed better in high and very high classes than LR models, identifying a higher number of forest fire events in the same set of data (Table 4). If the two lowest classes (low and very low) classes are compared among models, then there is a very slight difference between the LR and RF models (e.g., 23.3% vs. 23.7%, respectively). On the other hand, the RF models classified 58.6% of forest fire events in the two higher classes (high and very high), while the LR models classified 54.0% in the same classes of the validation set of data. The overall prediction accuracy of the LR and RF models, based on 10-fold cross validation, was 86.5 (kappa = 0.7296) and 91.7% (kappa = 0.8345), respectively. Moreover, the LR and RF models display AUC values of 92.4% and 97.5%, respectively, after 10-fold cross validation.

Table 4.
Forest fire distribution (%) across different probability classes based on LR and RF models for the validating set of data.
4. Discussion
There has been a huge gap in forest fire risk assessment in Serbia without any system for forest fire risk assessment at the national or even regional scale [70]. Within this study, the first step has been made on that course by producing maps with forest fire occurrence probability that cover more than one-third of the state territory. To map the forest fire probability in Eastern Serbia, the area that has been the most affected by forest fires in the past [32], two different methods were applied, LR and RF. Both methods have been widely used in forest fire risk assessment within the past few decades, with the dominance of LR at the beginning of this century [24,35,50,55,71], while the RF method has prevailed since the last decade [25,37,58,60,70]. The RF models had slightly better performance than the LR models in the training and validation sets. Better performance of the RF models over the LR models in fire occurrence prediction is consistent with similar studies in our region [72,73] and other regions [39,58]. The LR models shift performance from outstanding in training data sets to excellent in validation data sets, while in the RF procedure this shift is less pronounced according to applied model classification [63]. Based on the results obtained within this study and literature survey, we can strongly recommend the use of the RF method for the forest fire occurrence mapping of the entire territory of Serbia.
The propensity-score matching method was used to select non-fire events for known fire events. This method was adopted from the field of medical sciences [74,75,76,77], like many others, and it was used for the first time in natural hazard risk assessment by Hudson et al. [78] for evaluating the effectiveness of flood damage mitigation measures. We used this method for the first time in forest fire risk assessment to pair historical fire event data obtained from the NASA FIRMS with non-fire events using elevation as matching criteria.
Elevation had a significant and positive effect on forest fire occurrence probability, with higher frequencies observed between 200 and 1000 m. The fire season is shorter at higher elevations due to snow melting later, leading to a lower fire frequency [79]. Also, a higher relative humidity due to a decrease in temperature of 1 °C per 100 m rise in elevation reduces chances for fuel ignition [80]. However, the rapid decrease in fire frequency at altitudes over 1000 m, observed by Ramón González et al. [71], was not recorded in our study. It is more likely that climate changes will influence a positive effect of the elevation on forest fire frequency in the future, as has already been shown by Schwartz et al. [81]. Southern, intermediate slopes between 5° and 20° experienced increased fire activity in our study due to the lower moisture of combustible material being exposed to the sun radiation more than other aspects with milder and steeper slopes [34,81,82]. All topographical features strongly affect vegetation and its burn ability [83]. Forest fire frequency was much higher in the broad-leaved forests than in the coniferous forests. The negative effect of the distance to water on forest fire occurrence probability may be linked to the NASA sensor’s ability to detect only larger forest fires, while a smaller fire is suppressed easily when it is in the vicinity of the water bodies and the early phase of development are thereby not detected. Conifers cover less than 1% of the study area and were scattered in the higher mountains within the bigger broad-leaved forest complex and therefore were lesser exposed to anthropogenic activity, explaining the negative effect of its proportion on fire activity. Transitional woodland-shrubs are usually situated in the zone between forests and agricultural or arable land. Both types of land cover are connected to spring and autumn burning activity, and therefore transitional woodland-shrubs had increased fire frequency. Forests near human settlements and infrastructures that are densely populated are more prone to small fires due to negligence and/or accidental ignitions [84], while distant locations are prone to often larger, but less frequent, forest fires [85]. Therefore, an expected decrease in the population density in rural areas in the southern part of the study area [86] may result in lower fire activity in the future. Conversely, the expansion of urbanized areas and road cover with an associated increase in population density due to migration from south to north can be expected to lead to higher fire activity in the northern part of the study area.
Zones with the highest probability for forest fire occurrence are located in the southeastern part of the study area in all models, which correspond to the more pronounced drought periods during summer [27,28]. A higher drought code (higher temperature and lack of precipitation) leads to the lower moisture of fuel and makes an area more susceptible to ignition. It is well known that higher temperatures [87] reduce fuel moisture, making the fuels highly susceptible to ignition. Additionally, a study by Chang et al. [88] described low precipitation as a determinant factor for ignition. Drought code was the most important variable, followed by anthropogenic features, in both the LR and RF models. These results were consistent with other studies on determinant factors for the occurrence of wildfire where climatic and anthropogenic predictors had a higher influence on the fire occurrence probability [70,89,90,91,92]. All those models were efficiently applied at a smaller scale (such as national parks or protected areas), while our models showed similar efficacy at a larger scale. The produced maps can be used by firefighting services for strategic and operative planning. Defined zones with higher forest fire occurrence probability, in the southeast of the study area, should be intensively monitored during the fire season, especially during the second peak in August [30], when the largest forest fires can be expected [31]. Intense monitoring allows early detection of forest fires and leads to rapid response. All of these measures, along with enhanced equipment for fire suppression, can significantly decrease the burnt area in Eastern Serbia. Also, silvicultural measures that reduce fire risk [23] can be applied under zones with a higher forest fire occurrence probability according to the created maps. Thus, in the fire prone zone, less flammable tree species [93] should be selected for afforestation. Additionally, to prevent the transfer of ground fire to the crown, the introduction of silvicultural measures, such as pruning of the lower branches, should be obligatory in order to reduce fire hazard in the vulnerable zones. Other fuel reduction treatments, such as thinning, prescribed burning, and fuel breaks, can be useful tools to achieve these objectives at the landscape level [20,21].
5. Conclusions
The overall accuracy of the RF models was higher than those of the LR models. Both types of model identified drought code and anthropogenic features as the most important forest fire predictors. The models displayed a very high predictive ability, but the RF models were slightly more efficient and could be recommended for forest fire occurrence mapping in the eastern part of Serbia. The obtained maps could improve the efficacy of forest fire suppression in the study area in several ways. First, the fire probability map could be used for position optimization of the devices used in the early detection of forest fires. Also, firefighting resource allocation could be planned and applied in a manner consistent with the fire frequency. Finally, forest management planning and silvicultural measures should be adapted in terms of the forest fire risk reduction, based on the obtained maps.
Supplementary Materials
The following are available online at https://www.mdpi.com/1999-4907/12/1/5/s1: Figure S1: Correlation plot for all preselected variables based on Spearman’s rho coefficient; Table S1: Tables of contingency for training and validation sets of data for the tested random forest models.
Author Contributions
Conceptualization: S.M.; methodology: S.M. and S.D.M.; validation: D.P., L.G., and P.K.; formal analysis of Logistic Rregression: S.D.M., and D.P.; formal analysis of Random Forest: S.M., and P.K. investigation: S.M. and S.D.M.; resources: N.M.; data curation: N.M. and L.G.; writing—original draft preparation: S.M.; writing—review and editing: N.M., D.P., and L.G.; visualization: S.D.M. and N.M.; supervision: S.M. and P.K.; project administration: S.D.M.; funding acquisition: S.M. and S.D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Agriculture, Forestry and Water Management of the Republic of Serbia-Forest Directorate (contract: 401-00-1713/2019-10) and by the Ministry of Education, Science and Technological Development of the Republic of Serbia (contract: 451-03-68/2020-14/200015).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Doerr, S.H.; Santín, C. Global trends in wildfire and its impacts: Perceptions versus realities in a changing world. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2016, 371, 20150345. [Google Scholar] [CrossRef] [PubMed]
- Flannigan, M.D.; Krawchuk, M.A.; de Groot, W.J.; Wotton, B.M.; Gowman, L.M. Implications of changing climate for global wildland fire. Int. J. Wildl. Fire 2009, 18, 483–507. [Google Scholar] [CrossRef]
- Flannigan, M.; Cantin, A.S.; de Groot, W.J.; Wotton, M.; Newbery, A.; Gowman, L.M. Global wildland fire season severity in the 21st century. Ecol. Manag. 2013, 294, 54–61. [Google Scholar] [CrossRef]
- Moritz, M.A.; Batllori, E.; Bradstock, R.A.; Gill, A.M.; Handmer, J.; Hessburg, P.F.; Leonard, J.; McCaffrey, S.; Odion, D.C.; Schoennagel, T.; et al. Learning to coexist with wildfire. Nature 2014, 515, 58–66. [Google Scholar] [CrossRef]
- Turco, M.; Rosa-Cánovas, J.J.; Bedia, J.; Jerez, S.; Montávez, J.P.; Llasat, M.C.; Provenzale, A. Exacerbated fires in Mediterranean Europe due to anthropogenic warming projected with non-stationary climate-fire models. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef]
- Feurdean, A.; Vannière, B.; Finsinger, W.; Warren, D.; Connor, S.C.; Forrest, M.; Liakka, J.; Panait, A.; Werner, C.; Andrič, M.; et al. Fire hazard modulation by long-term dynamics in land cover and dominant forest type in eastern and central Europe. Biogeosciences 2020, 17, 1213–1230. [Google Scholar] [CrossRef]
- Costa, H.; de Rigo, D.; Libertà, G.; Durrant, T.; San-Miguel-Ayanz, J. European Wildfire Danger and Vulnerability in a Changing Climate: Towards Integrating Risk Dimensions; Publications Office of the European Union: Luxembourg, 2020; ISBN 978-92-76-16898-0.
- Moritz, M.A.; Parisien, M.-A.; Batllori, E.; Krawchuk, M.A.; van Dorn, J.; Ganz, D.J.; Hayhoe, K. Climate change and disruptions to global fire activity. Ecosphere 2012, 3, art49. [Google Scholar] [CrossRef]
- Räisänen, J.; Hansson, U.; Ullerstig, A.; Döscher, R.; Graham, L.P.; Jones, C.; Meier, H.E.M.; Samuelsson, P.; Willén, U. European climate in the late twenty-first century: Regional simulations with two driving global models and two forcing scenarios. Clim. Dyn. 2004, 22, 13–31. [Google Scholar] [CrossRef]
- Schär, C.; Vidale, P.L.; Lüthi, D.; Frei, C.; Häberli, C.; Liniger, M.A.; Appenzeller, C. The role of increasing temperature variability in European summer heatwaves. Nature 2004, 427, 332–336. [Google Scholar] [CrossRef]
- Fronzek, S.; Carter, T.R.; Jylhä, K. Representing two centuries of past and future climate for assessing risks to biodiversity in Europe. Glob. Ecol. Biogeogr. 2012, 21, 19–35. [Google Scholar] [CrossRef]
- Thuiller, W.; Lavorel, S.; Araújo, M.B.; Sykes, M.T.; Prentice, I.C. Climate change threats to plant diversity in Europe. Proc. Natl. Acad. Sci. USA 2005, 102, 8245–8250. [Google Scholar] [CrossRef] [PubMed]
- Brewer, S.; Cheddadi, R.; de Beaulieu, J.L.; Reille, M. The spread of deciduous Quercus throughout Europe since the last glacial period. Ecol. Manag. 2002, 156, 27–48. [Google Scholar] [CrossRef]
- Hernández, L.; Sánchez de Dios, R.; Montes, F.; Sainz-Ollero, H.; Cañellas, I. Exploring range shifts of contrasting tree species across a bioclimatic transition zone. Eur. J. Res. 2017, 136, 481–492. [Google Scholar] [CrossRef]
- Brovkina, O.; Stojanović, M.; Milanović, S.; Latypov, I.; Marković, N.; Cienciala, E. Monitoring of post-fire forest scars in Serbia based on satellite Sentinel-2 data. Geomat. Nat. Hazards Risk 2020, 11, 2315–2339. [Google Scholar] [CrossRef]
- Krawchuk, M.A.; Meigs, G.W.; Cartwright, J.M.; Coop, J.D.; Davis, R.; Holz, A.; Kolden, C.; Meddens, A.J.H. Disturbance refugia within mosaics of forest fire, drought, and insect outbreaks. Front. Ecol. Env. 2020, 18, 235–244. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J. Methodologies for the Evaluation of Forest Fire Risk: From Long-Term (Static) to Dynamic Indices. Corso Cult. Ecol. 2002, 117, 117. [Google Scholar]
- San-Miguel-Ayanz, J.; Carlson, J.D.; Alexander, M.; Tolhurst, K.; Morgan, G.; Sneeuwjagt, R.; Dudley, M. Current Methods to Assess Fire Danger Potential; World Scientific: Singapore, 2003; pp. 21–61. [Google Scholar]
- Mohammadi, F.; Bavaghar, M.P.; Shabanian, N. Forest Fire Risk Zone Modeling Using Logistic Regression and GIS: An Iranian Case Study. Small-Scale 2014, 13, 117–125. [Google Scholar] [CrossRef]
- Agee, J.K.; Bahro, B.; Finney, M.A.; Omi, P.N.; Sapsis, D.B.; Skinner, C.N.; van Wagtendonk, J.W.; Phillip-Weatherspoon, C. The use of shaded fuelbreaks in landscape fire management. Ecol. Manag. 2000, 127, 55–66. [Google Scholar] [CrossRef]
- Agee, J.K.; Skinner, C.N. Basic principles of forest fuel reduction treatments. Ecol. Manag. 2005, 211, 83–96. [Google Scholar] [CrossRef]
- Fernandes, P.M. Fire-smart management of forest landscapes in the Mediterranean basin under global change. Landsc. Urban. Plan. 2013, 110, 175–182. [Google Scholar] [CrossRef]
- Khabarov, N.; Krasovskii, A.; Obersteiner, M.; Swart, R.; Dosio, A.; San-Miguel-Ayanz, J.; Durrant, T.; Camia, A.; Migliavacca, M. Forest fires and adaptation options in Europe. Reg. Env. Chang. 2016, 16, 21–30. [Google Scholar] [CrossRef]
- Catry, F.X.; Rego, F.C.; Bação, F.L.; Moreira, F. Modeling and mapping wildfire ignition risk in Portugal. Int. J. Wildl. Fire 2009, 18, 921–931. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.P.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M.D. A review of machine learning applications in wildfire science and management. arXiv 2020, arXiv:2003.00646v1. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Malinovic-Milicevic, S.; Radovanovic, M.M.; Stanojevic, G.; Milovanovic, B. Recent changes in Serbian climate extreme indices from 1961 to 2010. Appl. Clim. 2016, 124, 1089–1098. [Google Scholar] [CrossRef]
- Luković, J.; Bajat, B.; Blagojević, D.; Kilibarda, M. Spatial pattern of recent rainfall trends in Serbia (1961–2009). Reg. Env. Chang. 2014, 14, 1789–1799. [Google Scholar] [CrossRef]
- Mimić, G.; Mihailović, D.T.; Kapor, D. Complexity analysis of the air temperature and the precipitation time series in Serbia. Appl. Clim. 2017, 127, 891–898. [Google Scholar] [CrossRef]
- Milomir, V. Forest Fire: Manual for Forest Engineers and Technicians; Level of Thesis; Faculty of Forestry University of Belgrade: Belgrade, Serbia, 1992. [Google Scholar]
- San-Miguel-Ayanz, J.; Durrant, T.; Boca, R.; Libertà, G.; Branco, A.; de Rigo, D.; Ferrari, D.; Maianti, P.; Artes, T.; Oom, D.; et al. Forest Fires in Europe, Middle East and North Africa 2018; Publications Office of the European Union: Luxembourg, 2019; ISBN 978-92-76-12591-4.
- Schmuck, G.; San-Miguel-Ayanz, J.; Camia, A.; Durrant, T.; Boca, R.; Libertà, G.; Schulte, E. Forest fires in Europe Middle East and North Africa 2012. Sci. Tech. Res. Ser. 2013, 10–30. [Google Scholar]
- Goldstein, E. Serbia’s Potential For. Sustainable Growth And Shared Prosperity Systematic Country Diagnostic Report; World Bank: Washington, DC, USA, 2015. [Google Scholar]
- Nhongo, E.J.S.; Fontana, D.C.; Guasselli, L.A.; Bremm, C. Probabilistic modelling of wildfire occurrence based on logistic regression, Niassa Reserve, Mozambique. Geomat. Nat. Hazards Risk 2019, 10, 1772–1792. [Google Scholar] [CrossRef]
- Carmo, M.; Moreira, F.; Casimiro, P.; Vaz, P. Land use and topography influences on wildfire occurrence in northern Portugal. Landsc. Urban. Plan. 2011, 100, 169–176. [Google Scholar] [CrossRef]
- Konkathi, P.; Shetty, A.; Kolluru, V.; Yathish, P.; Pruthviraj, U. Static Fire Risk Index for the Forest Resources of Karnataka. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 6716–6719. [Google Scholar]
- Ye, T.; Wang, Y.; Guo, Z.; Li, Y. Factor contribution to fire occurrence, size, & burn probability in a subtropical coniferous forest in East China. PLoS ONE 2017, 12. [Google Scholar] [CrossRef]
- Jaafari, A.; Gholami, D.M.; Zenner, E.K. A Bayesian modeling of wildfire probability in the Zagros Mountains, Iran. Ecol. Inf. 2017, 39, 32–44. [Google Scholar] [CrossRef]
- Guo, F.; Su, Z.; Wang, G.; Sun, L.; Lin, F.; Liu, A. Wildfire ignition in the forests of southeast China: Identifying drivers and spatial distribution to predict wildfire likelihood. Appl. Geogr. 2016, 66, 12–21. [Google Scholar] [CrossRef]
- van Wagner, C.E.; Forest, P.; Station, E.; Ontario, C.R.; Francais, R.U.E.; Davis, H.J. Development and Structure of the Canadian Forest Fire Weather Index System; Canadian Forestry Service: Ottawa, ON, Canada, 1987. [Google Scholar]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Austin, P.C. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivar. Behav. Res. 2011, 46, 399–424. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. Am. Stat. 1985, 39, 33–38. [Google Scholar] [CrossRef]
- Rosenbaum, P.R. Observational Studies; Springer: Berlin/Heidelberg, Germany, 2002; pp. 1–17. [Google Scholar]
- Gu, X.S.; Rosenbaum, P.R. Comparison of Multivariate Matching Methods: Structures, Distances, and Algorithms. J. Comput. Graph. Stat. 1993, 2, 405–420. [Google Scholar] [CrossRef]
- Ho, D.E.; Imai, K.; King, G.; Stuart, E.A. Matching as nonparametric preprocessing for reducing model dependence in parametric causal inference. Polit. Anal. 2007, 15, 199–236. [Google Scholar] [CrossRef]
- Chuvieco, E.; González, I.; Verdú, F.; Aguado, I.; Yebra, M. Prediction of fire occurrence from live fuel moisture content measurements in a Mediterranean ecosystem. Int. J. Wildl. Fire 2009, 18, 430. [Google Scholar] [CrossRef]
- Vilar del Hoyo, L.; Isabel, M.P.M.; Vega, F.J.M. Logistic regression models for human-caused wildfire risk estimation: Analysing the effect of the spatial accuracy in fire occurrence data. Eur. J. Res. 2011, 130, 983–996. [Google Scholar] [CrossRef]
- Midi, H.; Sarkar, S.K.; Rana, S. Collinearity diagnostics of binary logistic regression model. J. Interdiscip. Math. 2010, 13, 253–267. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Sokal, R.; Rohlf, F. Biometry: The principles and practice of statistics in biological research. J. R. Stat. Soc. Ser. A 2012, 133. [Google Scholar] [CrossRef]
- Bisquert, M.M.; Sánchez, J.M.; Caselles, V. Fire danger estimation from MODIS Enhanced Vegetation Index data: Application to Galicia region (north-west Spain). Int. J. Wildl. Fire 2011, 20, 465–473. [Google Scholar] [CrossRef]
- Martínez, J.; Vega-Garcia, C.; Chuvieco, E. Human-caused wildfire risk rating for prevention planning in Spain. J. Environ. Manag. 2009, 90, 1241–1252. [Google Scholar] [CrossRef] [PubMed]
- Bisquert, M.; Caselles, E.; Snchez, J.M.; Caselles, V. Application of artificial neural networks and logistic regression to the prediction of forest fire danger in Galicia using MODIS data. Int. J. Wildl. Fire 2012, 21, 1025–1029. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Guo, F.; Wang, G.; Su, Z.; Liang, H.; Wang, W.; Lin, F.; Liu, A. What drives forest fire in Fujian, China? Evidence from logistic regression and Random Forests. Int. J. Wildl. Fire 2016, 25, 505–519. [Google Scholar] [CrossRef]
- Chen, M.-M.; Chen, M.-C. Modeling Road Accident Severity with Comparisons of Logistic Regression, Decision Tree and Random Forest. Information 2020, 11, 270. [Google Scholar] [CrossRef]
- Caruana, R.; Niculescu-Mizil, A. An Empirical Comparison of Supervised Learning Algorithms. In Proceedings of the ACM International Conference Proceeding Series; ACM Press: New York, NY, USA, 2006; Volume 148, pp. 161–168. [Google Scholar]
- Couronné, R.; Probst, P.; Boulesteix, A.L. Random forest versus logistic regression: A large-scale benchmark experiment. BMC Bioinform. 2018, 19, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Kaitlin, K.; Smith, T.; Sadler, B. Random Forest vs. Logistic Regression: Binary Classification for Heterogeneous Datasets. SMU Data Sci. Rev. 2018, 1, 9. [Google Scholar]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression, 3rd ed.; Wiley: Hoboken, NJ, USA, 2013; ISBN 9781118548387. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28. [Google Scholar] [CrossRef]
- López-Ratón, M.; Rodríguez-Álvarez, M.X.; Suárez, C.C.; Sampedro, F.G. OptimalCutpoints: An R Package for Selecting Optimal Cutpoints in Diagnostic Tests. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Goksuluk, D.; Korkmaz, S.; Zararsiz, G.; Karaagaoglu, A.E. EasyROC: An. interactive web-tool for roc curve analysis using r language environment. R J. 2016, 8, 2. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; Chuvieco, E.; Koutsias, N. Modelling long-term fire occurrence factors in Spain by accounting for local variations with geographically weighted regression. Nat. Hazards Earth Syst. Sci. 2013, 13, 311–327. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984; ISBN 0412048418. [Google Scholar]
- Nembrini, S.; König, I.R.; Wright, M.N. The revival of the Gini importance? Bioinformatics 2018, 34, 3711–3718. [Google Scholar] [CrossRef]
- Gigović, L.; Pourghasemi, H.R.; Drobnjak, S.; Bai, S. Testing a new ensemble model based on SVM and random forest in forest fire susceptibility assessment and its mapping in Serbia’s Tara National Park. Forests 2019, 10. [Google Scholar] [CrossRef]
- Ramón González, J.; Palahí, M.; Trasobares, A.; Pukkala, T. A fire probability model for forest stands in Catalonia (north-east Spain). Ann. Sci. 2006, 63, 169–176. [Google Scholar] [CrossRef]
- Mallinis, G.; Petrila, M.; Mitsopoulos, I.; Lorenţ, A.; Neagu, Ş.; Apostol, B.; Gancz, V.; Popa, I.; Goldammer, J.G. Geospatial Patterns and Drivers of Forest Fire Occurrence in Romania. Appl. Spat. Anal. Policy 2019, 12, 773–795. [Google Scholar] [CrossRef]
- Šturm, T.; Podobnikar, T. A probability model for long-term forest fire occurrence in the Karst forest management area of Slovenia. Int. J. Wildl. Fire 2017, 26, 399. [Google Scholar] [CrossRef]
- Pourhoseingholi, M.A.; Baghestani, A.R.; Vahedi, M. How to control confounding effects by statistical analysis. Gastroenterol. Hepatol. Bed Bench 2012, 5, 79–83. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Greene, T. A Weighting Analogue to Pair Matching in Propensity Score Analysis. Int. J. Biostat. 2013, 9, 215–234. [Google Scholar] [CrossRef]
- Deb, S.; Austin, P.C.; Tu, J.V.; Ko, D.T.; Mazer, C.D.; Kiss, A.; Fremes, S.E. A Review of Propensity-Score Methods and Their Use in Cardiovascular Research. Can. J. Cardiol. 2016, 32, 259–265. [Google Scholar] [CrossRef]
- Yan, H.; Karmur, B.S.; Kulkarni, A.V. Comparing Effects of Treatment: Controlling for Confounding. Clin. Neurosurg. 2020, 86, 325–331. [Google Scholar] [CrossRef]
- Hudson, P.; Botzen, W.J.W.; Kreibich, H.; Bubeck, P.H.; Aerts, J.C.J. Evaluating the effectiveness of flood damage mitigation measures by the application of propensity score matching. Nat. Hazards Earth Syst. Sci. 2014, 14, 1731–1747. [Google Scholar] [CrossRef]
- Heyerdahl, E.K.; Brubaker, L.B.; Agee, J.K. Spatial controls of historical fire regimes: A multiscale example from the interior west, USA. Ecology 2001, 82, 660–678. [Google Scholar] [CrossRef]
- Rogeau, M.P.; Armstrong, G.W. Quantifying the effect of elevation and aspect on fire return intervals in the Canadian Rocky Mountains. Ecol. Manag. 2017, 384, 248–261. [Google Scholar] [CrossRef]
- Schwartz, M.W.; Butt, N.; Dolanc, C.R.; Holguin, A.; Moritz, M.A.; North, M.P.; Safford, H.D.; Stephenson, N.L.; Thorne, J.H.; van Mantgem, P.J. Increasing elevation of fire in the Sierra Nevada and implications for forest change. Ecosphere 2015, 6, art121. [Google Scholar] [CrossRef]
- Everett, R.L.; Schellhaas, R.; Keenum, D.; Spurbeck, D.; Ohlson, P. Fire history in the ponderosa pine/Douglas-fir forests on the east slope of the Washington Cascades. Ecol. Manag. 2000, 129, 207–225. [Google Scholar] [CrossRef]
- Castro, R.; Chuvieco, E. Modeling forest fire danger from geographic information systems. Geocarto Int. 1998, 13, 15–23. [Google Scholar] [CrossRef]
- Curt, T.; Fréjaville, T.; Lahaye, S. Modelling the spatial patterns of ignition causes and fire regime features in southern France: Implications for fire prevention policy. Int. J. Wildl. Fire 2016, 25, 785–796. [Google Scholar] [CrossRef]
- Zumbrunnen, T.; Pezzatti, G.B.; Menéndez, P.; Bugmann, H.; Bürgi, M.; Conedera, M. Weather and human impacts on forest fires: 100 years of fire history in two climatic regions of Switzerland. Ecol. Manag. 2011, 261, 2188–2199. [Google Scholar] [CrossRef]
- Petrić, J.; Maričić, T.; Basarić, J. The population conundrums and some implications for urban development in Serbia. Spatium 2012, 314, 7–14. [Google Scholar] [CrossRef]
- Fried, J.S.; Gilless, J.K.; Riley, W.J.; Moody, T.J.; Simon de Blas, C.; Hayhoe, K.; Moritz, M.; Stephens, S.; Torn, M. Predicting the effect of climate change on wildfire behavior and initial attack success. Clim. Chang. 2008, 87, 251–264. [Google Scholar] [CrossRef]
- Chang, Y.; He, H.S.; Hu, Y.; Bu, R.; Li, X. Historic and current fire regimes in the Great Xing’an Mountains, northeastern China: Implications for long-term forest management. Ecol. Manag. 2008, 254, 445–453. [Google Scholar] [CrossRef]
- Sadori, L.; Masi, A.; Ricotta, C. Climate-driven past fires in central Sicily. Plant Biosyst. Int. J. Deal. All Asp. Plant Biol. 2015, 149, 166–173. [Google Scholar] [CrossRef]
- Kalabokidis, K.; Palaiologou, P.; Gerasopoulos, E.; Giannakopoulos, C.; Kostopoulou, E.; Zerefos, C. Effect of Climate Change Projections on Forest Fire Behavior and Values-at-Risk in Southwestern Greece. Forests 2015, 6, 2214–2240. [Google Scholar] [CrossRef]
- Varela, V.; Vlachogiannis, D.; Sfetsos, A.; Karozis, S.; Politi, N.; Giroud, F. Projection of Forest Fire Danger due to Climate Change in the French Mediterranean Region. Sustainability 2019, 11, 4284. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Avand, M.; Al-Ansari, N.; Du, T.D.; Hai-Yen, H.P.; van Phong, T.; Nguyen, D.H.; van Le, H.; Mafi-Gholami, D.; et al. Performance evaluation of machine learning methods for forest fire modeling and prediction. Symmetry 2020, 12, 1022. [Google Scholar] [CrossRef]
- Xanthopoulos, G.; Calfapietra, C.; Fernandes, P. Fire Hazard and Flammability of European Forest Types. In Post-Fire Management and Restoration of Southern European Forests; Moreira, F., Arianoutsou, M., Corona, P., de las Heras, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 24, pp. 79–92. ISBN 978-94-007-2207-1. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).