Estimation of Future Changes in Aboveground Forest Carbon Stock in Romania. A Prediction Based on Forest-Cover Pattern Scenario
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
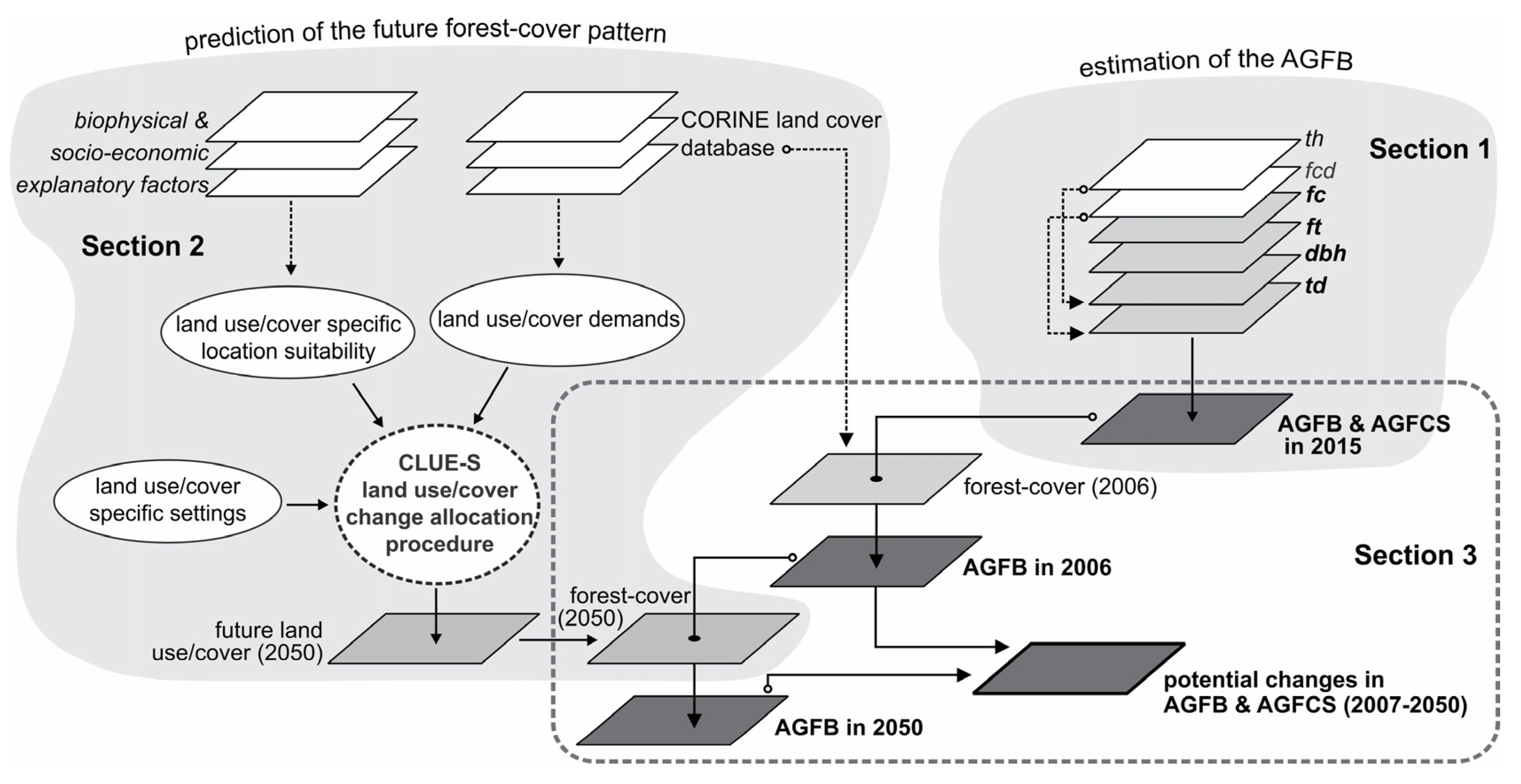
2.2. The Methodology Used to Predict Future Potential Changes in Aboveground Forest Carbon Stock
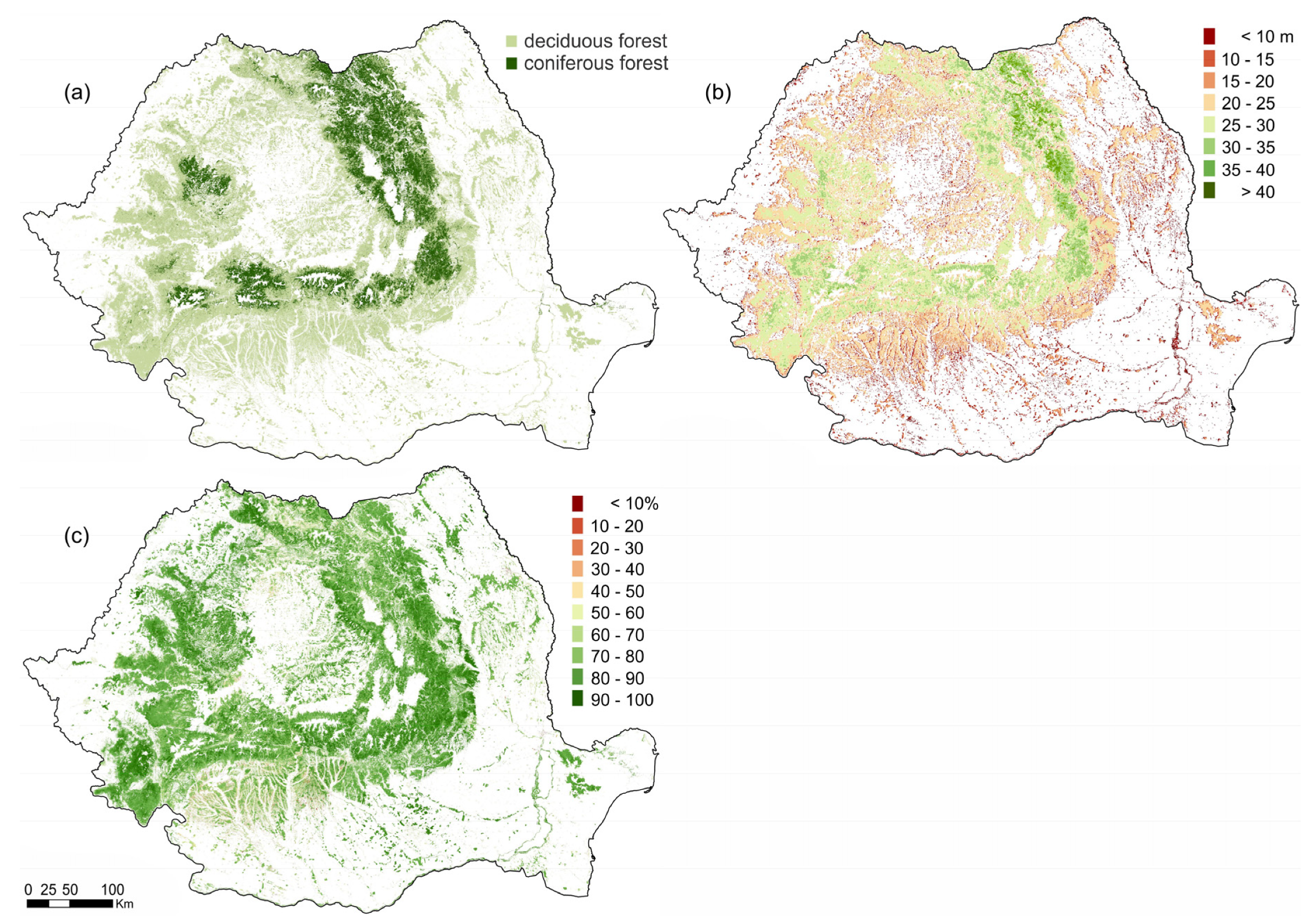
2.2.1. The Estimation of AGFB in 2015
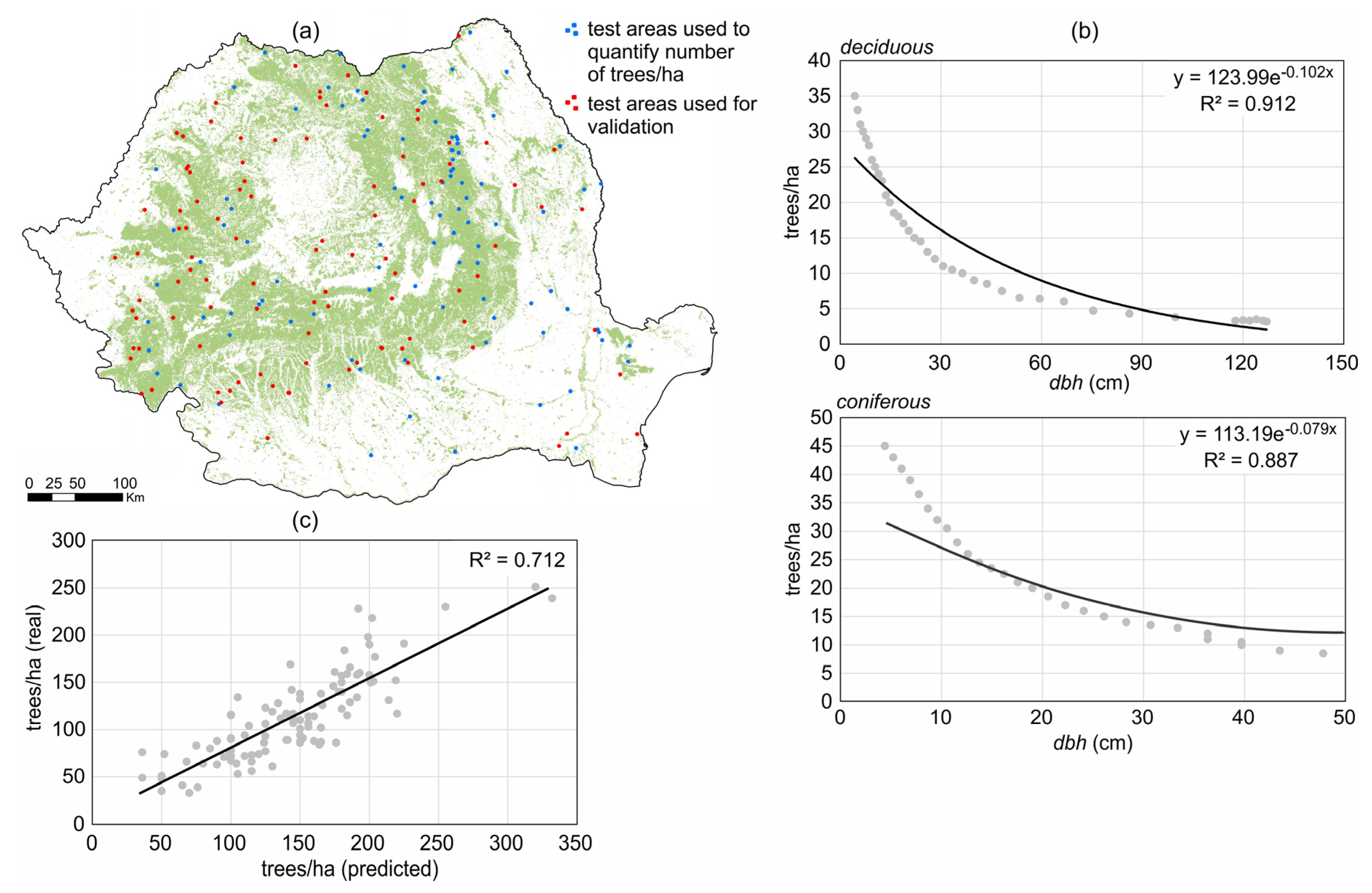
Biomass Equations
The Estimation of td
2.2.2. The Estimation of Aboveground Forest Carbon Stock
2.2.3. Modeling Forest-Cover Pattern Change
2.2.4. Integrating the Forest-Cover Pattern Change Scenario and AGFB Model to Assess Future Potential Change in AGFCS
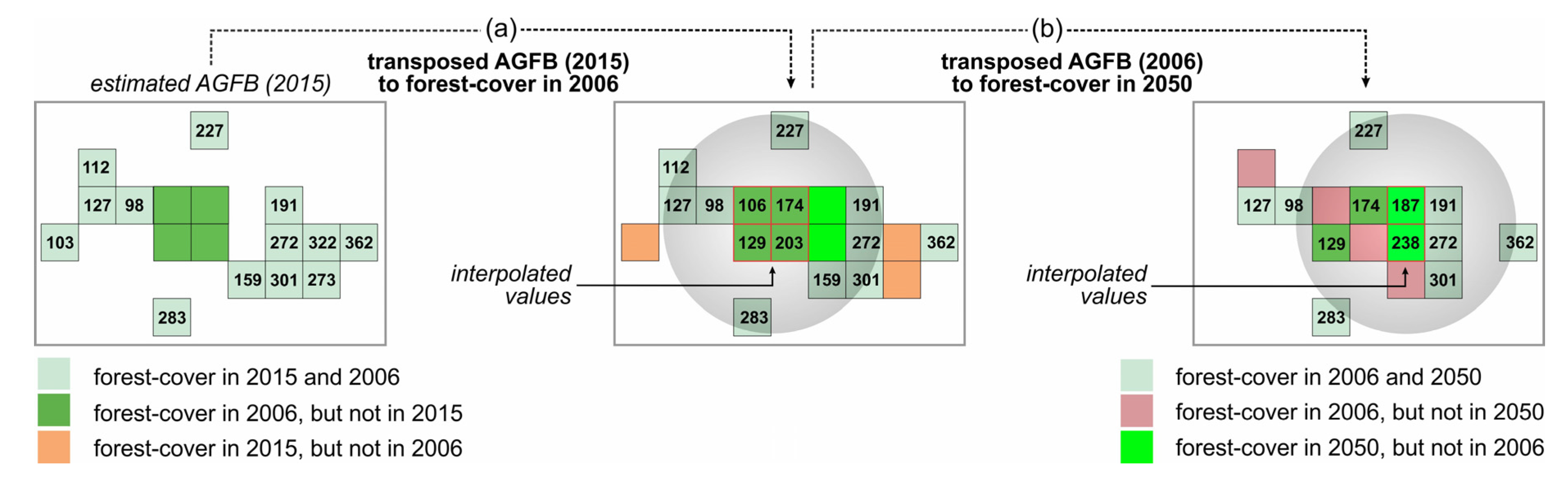
2.3. The Uncertainties of AGFB Model and Methodology Used to Transpose the Estimated Values into the Forest-Cover Pattern Scenario
3. Results
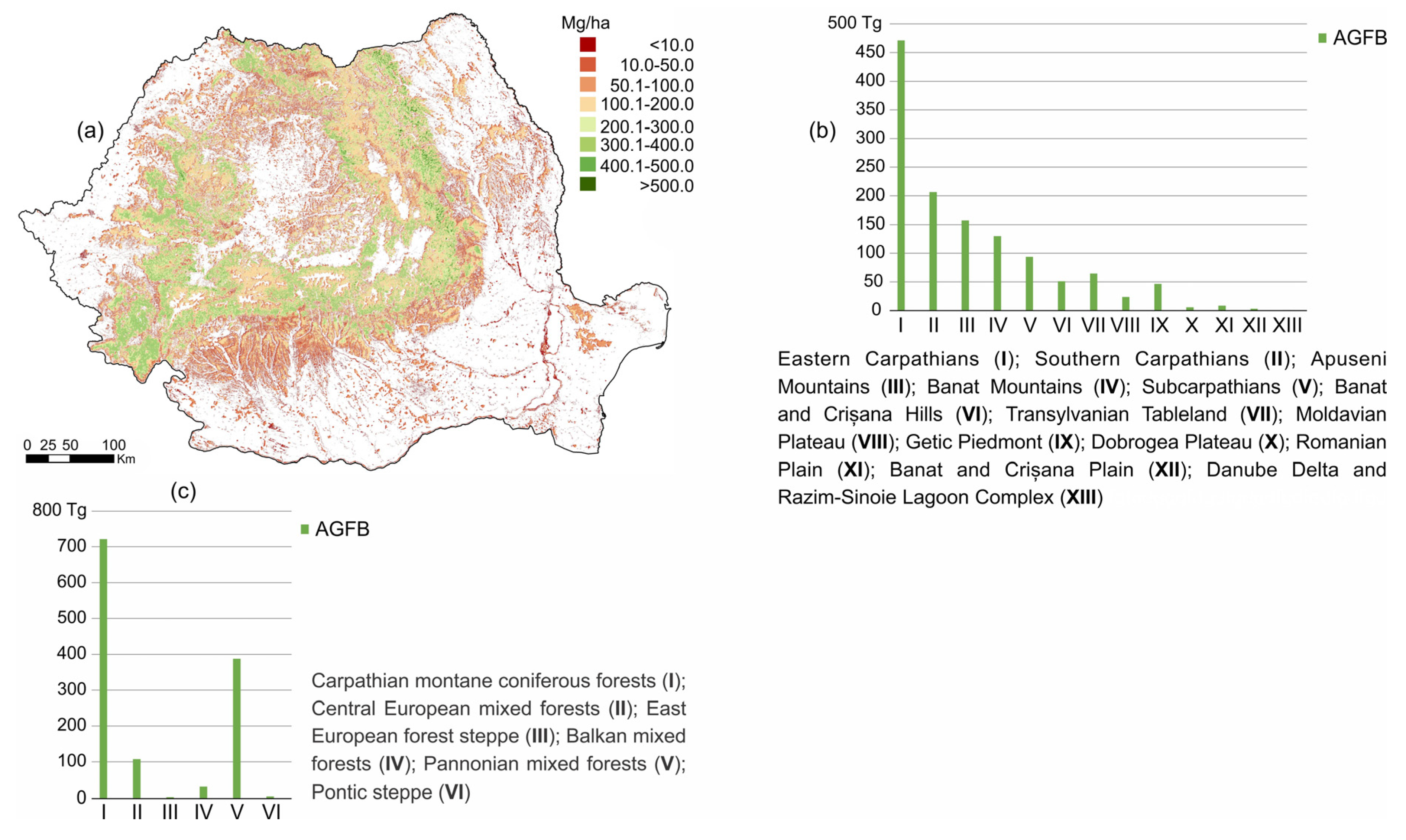
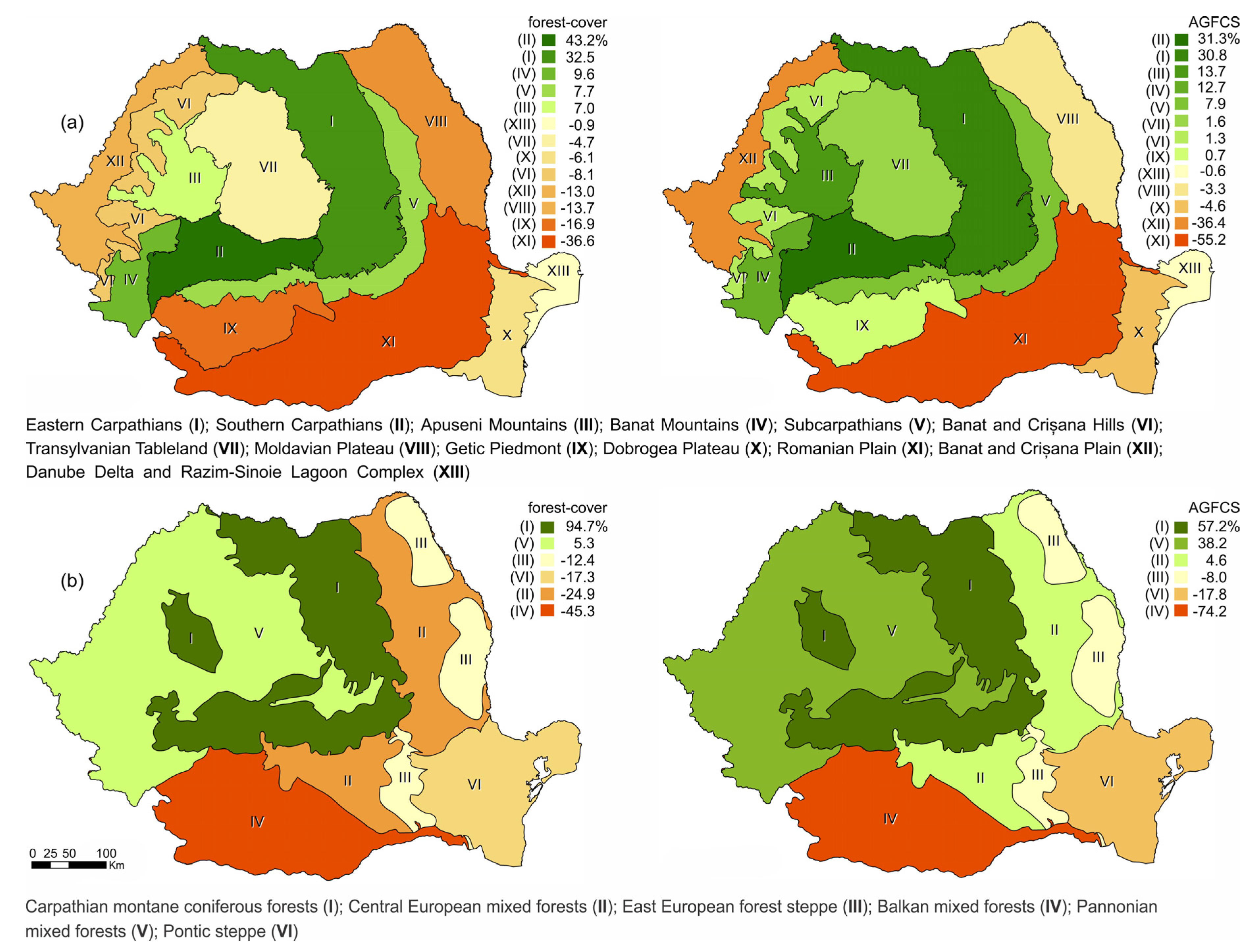
3.1. The Estimated AGFB in 2015. Transposing the Values into the Forest-Cover Map for 2006
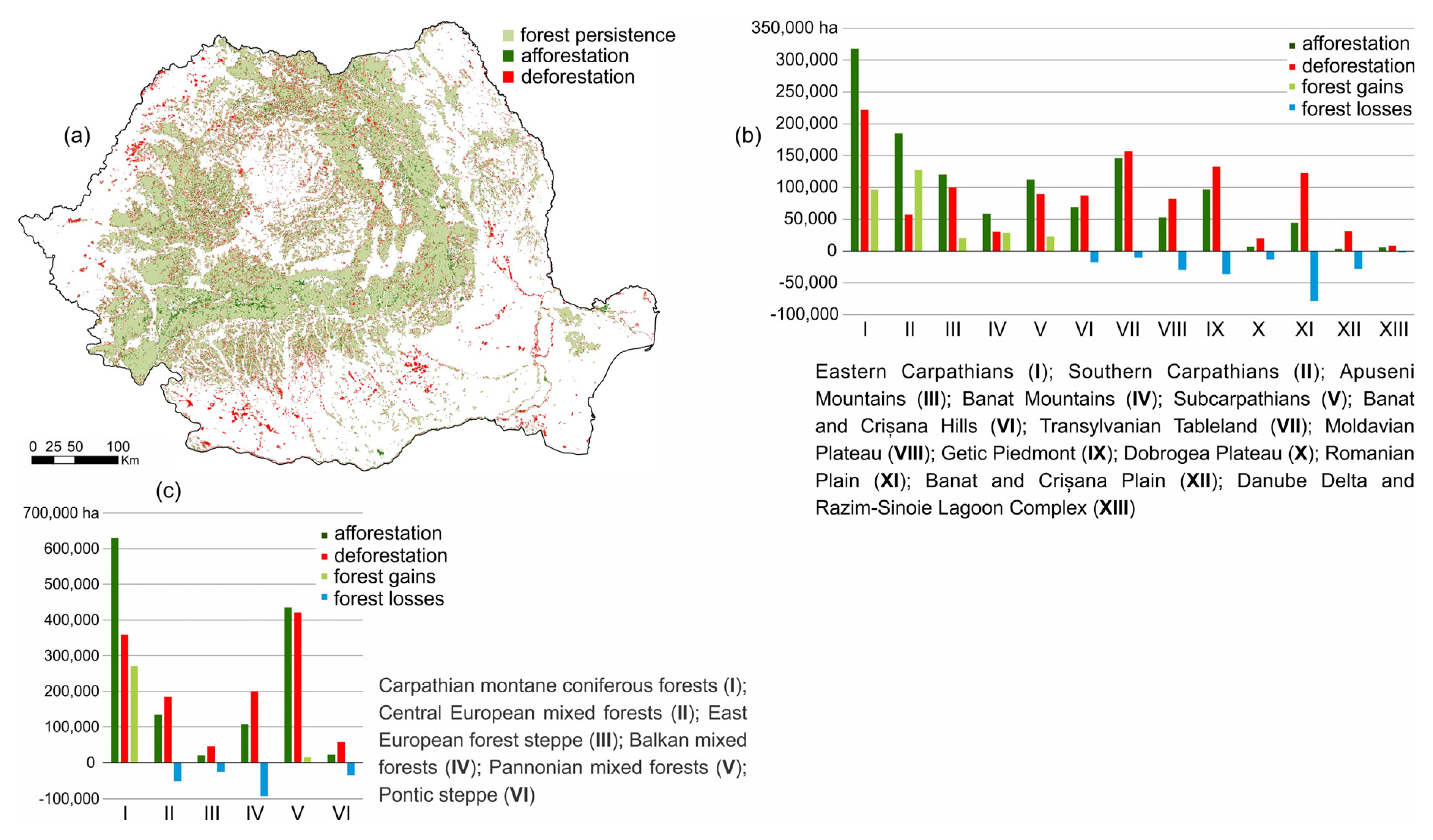
3.2. Predicted Forest-Cover Pattern Change
3.3. The Projected Potential Changes in AGFCS Quantity Up to 2050
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hofmann, D.J.; Butler, J.H.; Dlugokencky, E.J.; Elkins, J.W.; Masarie, K.; Montzka, S.A.; Tans, P. The role of carbon dioxide in climate forcing from 1979 to 2004: Introduction of the Annual Greenhouse Gas Index. Tellus 2006, 58B, 614–619. [Google Scholar] [CrossRef]
- Dixon, R.K.; Brown, S.; Houghton, R.A. Carbon pools and flux of global forest ecosystems. Science 1994, 263, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Field, C.; Lobell, D.B.; Peters, H.A.; Chiariello, N.R. Feedbacks of Terrestrial Ecosystems to Climate Change. Annu. Rev. Environ. Resour. 2007, 32, 29. [Google Scholar] [CrossRef]
- Teobaldelli, M.; Somogyi, Z.; Migliavacca, M.; Usoltsev, V.A. Generalized functions of biomass expansion factors for conifers and broadleaved by stand age, growing stock and site index. For. Ecol. Manag. 2009, 257, 1004–1013. [Google Scholar] [CrossRef]
- Kumar, R.; Nandy, S.; Agarwal, R.; Kushwaha, S.P.S. Forest cover dynamics analysis and prediction modeling using logistic regression model. Ecol. Indic. 2014, 45, 444–455. [Google Scholar] [CrossRef]
- Brown, S.; Sathaye, J.; Cannell, M.; Kauppi, P.E. Mitigation of carbon emission to the atmosphere by forest management. Commonw. For. Rev. 1996, 75, 80–91. [Google Scholar]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe, Silva Fennica Monographs 4; The Finnish Society of Forest Science: Tampere, Finland, 2005. [Google Scholar]
- Cairns, M.A.; Brown, S.; Helmer, E.H.; Baumgardner, G.A. Root biomass allocation in the world’s upland forests. Oecologia 1997, 111, 1–11. [Google Scholar] [CrossRef]
- Bi, H.; Turner, J.; Lambert, M.J. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees-Struct. Funct. 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Barredo, J.I.; Miguel, J.S.; Caudullo, G.; Busetto, L. A European Map of Living Forest Biomass and Carbon Stock. Executive Report; Joint Research Centre of the European Commission: Ispra, Italy, 2012. [Google Scholar] [CrossRef]
- Houghton, R.; Hall, F.; Goetz, S. Importance of biomass in the global carbon cycle. J. Geophys. Res. Biogeosci. 2009, 114, G2. [Google Scholar] [CrossRef]
- Climate Change. The IPCC Scientific Assessment; Houghton, J.T., Jenkins, G.J., Ephraums, J.J., Eds.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Lamlom, S.H.; Savidge, R.A. A reassessment of carbon content in wood: Variation within and between 41 North American species. Biomass Bioenergy 2003, 25, 381–388. [Google Scholar] [CrossRef]
- CEOS Land Product Validation Subgroup. Available online: https://lpvs.gsfc.nasa.gov/Biomass/AGB_home.html (accessed on 16 June 2020).
- Wilkes, P.; Disney, M.; Vicari, M.B.; Calders, K.; Burt, A. Estimating urban above ground biomass with multi-scale LiDAR. Carbon Balance Manag. 2018, 13, 10. [Google Scholar] [CrossRef] [PubMed]
- Basuki, T.M.; Skidmore, A.K.; van Laake, P.E.; van Duren, I.; Hussin, Y.A. The Potential of Spectral Mixture Analysis to Improve the Estimation Accuracy of Tropical Forest Biomass. Geocarto Int. 2012, 27, 329–345. [Google Scholar] [CrossRef]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; FAO Forestry Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1997; Volume 134, p. 55. [Google Scholar]
- Brown, S. Measuring carbon in forests: Current status and future challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
- Somogyi, Z.; Cienciala, E.; Makipaa, R.; Muukkonen, P.; Lehtonen, A.; Weiss, P. Indirect methods of largescale forest biomass estimation. Eur. J. Res. 2007, 126, 197–207. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Dong, J.R.; Kaufmann, R.K.; Myneni, R.B.; Tucker, C.J.; Kauppi, P.E.; Liski, J.; Buermann, W.; Alexeyev, V.; Hughes, M.K. Remote sensing estimates of boreal and temperate forest woody biomass: Carbon pools, sources and sinks. Remote Sens. Environ. 2003, 84, 393–410. [Google Scholar] [CrossRef]
- Calders, K.; Raumonen, P.; Herold, M. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Dassot, M.; Colin, A.; Santenoise, P.; Fournier, M.; Constant, T. Terrestrial laser scanning for measuring the solid wood volume, including branches, of adult standing trees in the forest environment. Comput. Electron. Agric. 2012, 89, 86–93. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar Detection of Individual Tree Size in Tropical Forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Mohd Zaki, N.A.; Abd Latif, Z.; Suratman, M.N.; Zainal, M.Z. Aboveground Biomass and Carbon Stocks Modelling using Non-Linear Regression Model. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2016; Volume 37. [Google Scholar] [CrossRef]
- Goetz, S.J.; Baccini, A.; Laporte, N.T.; Johns, T.; Walker, W.; Kellndorfer, J.; Houghton, R.A.; Sun, M. Mapping and monitoring carbon stocks with satellite observations: A comparison of methods. Carbon Balance Manag. 2009, 4, 2. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. For. Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar] [CrossRef]
- Schmitt, M.D.C.; Grigal, D.F. Generalized biomass estimation equation for Betula papyrifera Marsh. Can. J. For. Res. 1981, 11, 837–840. [Google Scholar] [CrossRef]
- Wirth, C.; Schumacher, J.; Schulze, E.-D. Generic biomass functions for Norway spruce in central Europe—A metaanalysis approach toward prediction and uncertainty estimation. Tree Physiol. 2004, 24, 121–139. [Google Scholar] [CrossRef]
- Duncanson, L.; Huang, W.; Johnson, K.; Swatantran, A.; McRoberts, R.E.; Dubayah, R. Implications of allometric model selection for county-level biomass mapping. Carbon Balance Manag. 2017, 12, 18. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Vashum, K.T.; Jayakumar, S. Methods to Estimate Above-Ground Biomass and Carbon Stock in Natural Forests—A Review. J. Ecosyst. Ecogr. 2012, 2. [Google Scholar] [CrossRef]
- Tan, K.; Piao, S.; Peng, C.; Fang, J. Satellite-based estimation of biomass carbon stocks for northeast China’s forests between 1982 and 1999. For. Ecol. Manag. 2007, 240, 114–121. [Google Scholar] [CrossRef]
- Avitabile, V.; Herold, M.; Heuvelink, G.B.M.; Lewis, S.L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Ashton, P.S.; Banin, L.; Bayol, N.; et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Chang. Biol. 2016, 22, 1406–1420. [Google Scholar] [CrossRef]
- Avitabile, V.; Camia, A. An assessment of forest biomass maps in Europe using harmonized national statistics and inventory plots. For. Ecol. Manag. 2018, 409, 489–498. [Google Scholar] [CrossRef]
- Cartus, O.; Kellndorfer, J.; Walker, W.; Bishop, J.; Franco, C.; Santos, L.; Michel Fuentes, J.M. A national, detailed map of forest aboveground carbon stocks in Mexico. Remote Sens. 2014, 6, 5559–5588. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using lidar remote sensing at La Selva, Costa Rica. J. Geophys. Res. 2010, 15, 1–17. [Google Scholar]
- Rodríguez-Veiga, P.; Saatchi, S.; Tansey, K.; Balzter, H. Magnitude, spatial distribution and uncertainty of forest biomass stocks in Mexico. Remote Sens. Environ. 2016, 183, 265–281. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Brovkina, O.; Novotny, J.; Cienciala, E.; Zemek, F.; Russ, R. Mapping forest aboveground biomass using airborne hyperspectral and LiDAR data in the mountainous conditions of Central Europe. Ecol. Eng. 2017, 100, 219–230. [Google Scholar] [CrossRef]
- Muukkonen, P. Generalized allometric volume and biomass equations for some tree species in Europe. Eur. J. For. Res. 2007, 126, 157–166. [Google Scholar] [CrossRef]
- FRA (Global Forest Resources Assessment). Global Forest Resources Assessment 2015; Desk Reference; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015. [Google Scholar]
- Blujdea, V.N.B.; Pilli, R.; Dutca, I.; Ciuvat, L.; Abrudan, I.V. Allometric biomass equations for young broadleaved trees in plantations in Romania. For. Ecol. Manag. 2012, 264, 172–184. [Google Scholar] [CrossRef]
- Dutcă, I.; Abrudan, I.V.; Stăncioiu, P.T.; Blujdea, V. Biomass conversion and expansion factors for young Norway Spruce (Picea abies (L.) Karst) trees planted on non-forest lands in Romania. NBHA 2010, 38, 286–292. [Google Scholar]
- Stancioiu, P.T.; O’Hara, K.L. Leaf area and growth efficiency of regeneration in mixed species, multiaged forests of the Romanian Carpathians. For. Ecol. Manag. 2006, 222, 55–66. [Google Scholar] [CrossRef]
- Kucsicsa, G.; Dumitrică, C.; Dumitrașcu, M.; Grigorescu, I.; Vrînceanu, A. Estimation of Above-Ground Forest Biomass in Romania, Ecological and Geographical Problems of Transition to a Green Economy in the Countries and Regions of the CIS; Conference Book: Minsk, Belarus, 2019; pp. 145–151. [Google Scholar]
- Le Page, Y.; Hurtt, G.; Thomson, A.M.; Bond-Lamberty, B.; Patel, P.; Wise, M.; Calvin, K.V.; Kyle, P.; Clarke, L.; Edmonds, J.; et al. Sensitivity of climate mitigation strategies to natural disturbances. Environ. Res. Lett. 2013, 8, 1–6. [Google Scholar] [CrossRef]
- Lambin, E.F. Modelling Deforestation Processes, A Review; EUR 15744 EN, TREES Series B: Research Report No. 1; Joint Research Centre, Institute for Remote Sensing Applications: Ispra, Italy; European Space Agency, Luxembourg, Office for Official Publications of the European Community: Luxembourg, 1994; p. 128. [Google Scholar]
- Veldkamp, A.; Fresco, L.O. CLUE: A conceptualmodel to study the conversion of land use and its effects. Ecol. Model. 1996, 85, 253–270. [Google Scholar] [CrossRef]
- Verburg, P.H.; Veldkamp, A. Projecting land use transitions at forest fringes in the Philippines at two spatial scales. Landsc. Ecol. 2004, 19, 77–98. [Google Scholar] [CrossRef]
- Forest Europe. UNECE. FAO. State of Europe’s Forests 2011. Status and Trends in Sustainable Forest Management in Europe; Ministerial Conference on the Protection of Forests in Europe, Liaison Unit Oslo: Zvolen, Slovakia, 2011. [Google Scholar]
- Griffiths, P.; Kuemmerle, T.; Kennedy, R.E.; Abrudan, I.V.; Knorn, J.; Hostert, P. Using annual time-series of Landsat images to assess the effects of forest restitution in postsocialist Romania. Remote Sens. Environ. 2012, 118, 199–214. [Google Scholar] [CrossRef]
- Hanganu, J.; Constantinescu, A. Land cover changes in Romania based on Corine land cover inventory 1990–2012. Rev. Roum. Géogr. Rom. J. Geogr. 2015, 59, 111–116. [Google Scholar]
- Kucsicsa, G.; Popovici, E.-A.; Bălteanu, D.; Grigorescu, I.; Dumitrașcu, M.; Mitrică, B. Future land use/cover changes in Romania: Regional simulations based on CLUE-S model and CORINE land cover database. Landsc. Ecol. Eng. 2019, 15, 75–90. [Google Scholar] [CrossRef]
- Petrişor, A.I. Using CORINE data to look at deforestation in Romania: Distribution & possible consequences. Urbanism 2015, 6, 83–90. [Google Scholar]
- Popovici, E.-A.; Bălteanu, D.; Kucsicsa, G. Assessment of changes in Land–Use and Land–Cover pattern in Romania using Corine Land Cover database. Carpathian J. Earth Environ. Sci. 2013, 8, 195–208. [Google Scholar]
- Kucsicsa, G.; Popovici, A.-E.; Bălteanu, D.; Dumitrașcu, M.; Grigorescu, I.; Mitrică, B. Assessing the potential future forest cover change in Romania, predicted using scenario-based modelling. Environ. Model. Assess. 2019, 1–21. [Google Scholar] [CrossRef]
- Bălteanu, D.; Popovici, E.A. Land use changes and land degradation in post–socialist Romania. Rev. Roum. Géogr. Rom. J. Geogr. 2010, 54, 95–105. [Google Scholar]
- European Environmental Agency (EEA). Copernicus Land Monitoring Service—CORINE Land Cover 2006. Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc-2006 (accessed on 12 February 2019).
- European Environment Agency. DMEER: Digital Map of European Ecological Regions. 2003. Available online: https://www.eea.europa.eu/data-and-maps/data/digital-map-of-european-ecological-regions (accessed on 17 June 2019).
- NIS (National Institute of Statistics). Romanian Statistical Yearbook; National Institute of Statistics: Bucharest, Romania, 2019; p. 711. [Google Scholar]
- Gurung, A.B.; Bokwa, A.; Chełmicki, W.; Elbakidze, M.; Hirschmugl, M.; Hostert, P.; Ibisch, P.; Kozak, J.; Kuemmerle, T.; Matei, E.; et al. Global change research in the Carpathian Mountain region. Mt. Res. Dev. 2009, 29, 282–288. [Google Scholar] [CrossRef][Green Version]
- Veen, P.; Fanta, J.; Raev, I.; Biris, I.-A.; de Smidt, J.; Maes, B. Virgin forests in Romania and Bulgaria: Results of two national inventory projects and their implications for protection. Biodivers. Conserv. 2010, 19, 1805–1819. [Google Scholar] [CrossRef]
- Geacu, S.; Dumitrașcu, M.; Maxim, I. The evolution of the natural protected areas network in Romania. Rev. Rom. Géogr. Rom. J. Geogr. 2012, 56, 33–41. [Google Scholar]
- Abrudan, I.V.; Marinescu, V.; Ionescu, O.; Ioras, F.; Horodnic, S.A.; Sestras, R. Developments in the Romanian Forestry and its Linkages with other Sectors. Not. Bot. Horti Agrobot. Cluj-Napoca 2009, 37, 14–21. [Google Scholar] [CrossRef]
- Strimbu, B.M.; Hickey, G.M.; Strimbu, V.G. Forest conditions and management under rapid legislation change in Romania. For. Chron. 2005, 81, 350–358. [Google Scholar] [CrossRef]
- Kissling-Näf, I.; Bisang, K. Rethinking recent changes of forest regimes in Europe through property-rights theory and policy analysis. For. Policy Econ. 2001, 3, 99–111. [Google Scholar] [CrossRef]
- Lerman, Z.; Csaki, C.; Feder, G. Evolving farm structures and land-use patterns in former socialist countries. Q. J. Int. Agric. 2004, 43, 309–335. [Google Scholar]
- Turnock, D. Ecoregion-based conservation in the Carpathians and the land use implications. Land Use Policy 2002, 19, 47–63. [Google Scholar] [CrossRef]
- Bălteanu, D.; Felciuc, M.; Dumitraşcu, M.; Grigorescu, I. Environmental changes in the Maramureş Mountains Natural Park. In Sustainable Development in Mountain Regions, Southestern Europe; Zhelezov, G., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 335–348. Available online: http://link.springer.com/book/10.1007/978-3-319-20110-8 (accessed on 24 April 2018). [CrossRef]
- Griffiths, P.; Müller, D.; Kuemmerle, T.; Hostert, P. Agricultural land change in the Carpathian ecoregion after the breakdown of socialism and expansion of the European Union. Environ. Res. Lett. 2013, 8. [Google Scholar] [CrossRef]
- Munteanu, C.; Kuemmerle, T.; Boltižiar, M.; Butsic, V.; Gimmi, U.; Halada, L.; Kaim, D.; Király, G.; Konkoly-Gyuró, É.; Kozak, J.; et al. Forest and agricultural land change in the Carpathian region—A metaanalysis of long-term patterns and drivers of change. Land Use Policy 2014, 38, 685–697. [Google Scholar] [CrossRef]
- Kucsicsa, G.; Dumitrică, C. Spatial modelling of deforestation in Romanian Carpathian Mountains using GIS and Logistic Regression. J. Mt. Sci. 2019, 16, 1005–1022. [Google Scholar] [CrossRef]
- Knorn, J.; Kuemmerle, T.; Radeloff, V.C.; Szabo, A.; Mîndrescu, M.; Keeton, W.S.; Abrudan, I.; Griffiths, P.; Gancz, V.; Hostert, P. Forest restitution and protected area effectiveness in post-socialist Romania. Biol. Conserv. 2012, 146, 204–212. [Google Scholar] [CrossRef]
- Dutcă, I.; Abrudan, I.V. Estimation of forest land–cover change in Romania, between 1990 and 2006. Bull. Transilv. Univ. Bras. 2010, 3, 33–36. [Google Scholar]
- Kucsicsa, G.; Bălteanu, D. The influence of man-induced land-use change on the upper forest limit in the Romanian Carpathians. Eur. J. For. Res. 2020. [Google Scholar] [CrossRef]
- Posea, G.; Badea, L. România, Harta Unităţilor de Relief (Regionarea Geomorfologică). Ed; Ştiinţifică şi Enciclopedică: Bucharest, Romania, 1984. [Google Scholar]
- Marklund, L.G. Biomass functions for Norway spruce (Picea abies (L.) Karst.) in Sweden. Rapp. -Sver. Lantbr. Inst. foer Skogstaxering (Sweden) 1987, 43, 1–127. [Google Scholar]
- Marklund, L.G. Biomassafunktioner for tall, gran och björk i Sverige. Sveriges lantbruksuniversitet. Inst. för skogstaxering 1988, 45, 1–73. [Google Scholar]
- Pastor, J.; Aber, J.D.; Melillo, J.M. Biomass prediction using generalized allometric regressions for some northeast tree species. For. Ecol. Manag. 1984, 7, 265–274. [Google Scholar] [CrossRef]
- Näslund, M. Skogsförsöksanstaltens Gallringsförsök i Tallskog. Meddelanden Från Statens Skogsförsökanstalt; Bsselte ab.: Stockholm, Sweden, 1937; Volume 29, pp. 1–169. [Google Scholar]
- Verburg, P.H.; Soepboer, W.; Limpiada, R.; Espaldon, M.V.O.; Sharifa, M.; Veldkamp, A. Land use change modelling at the regional scale: The CLUE–S model. Environ. Manag. 2002, 30, 391–405. [Google Scholar] [CrossRef]
- Menard, S. Applied Logistic Regression Analysis, 2nd ed.; Series: Quantitative Applications in the Social Sciences; Sage Publications: London, UK, 2002. [Google Scholar]
- Verburg, P.H.; Overmars, K.P. Combining top–down and bottom–up dynamics in land use modeling: Exploring the future of abandoned farmlands in Europe with the Dyna–CLUE model. Landsc. Ecol. 2009, 24, 1167–1181. [Google Scholar] [CrossRef]
- van Vliet, J.; Bregtb, A.K.; Hagen-Zankerc, A. Revisiting Kappa to account for change in the accuracy assessment of land-use change models. Ecol. Model. 2011, 222, 1367–1375. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scale. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Philip, G.M.; Watson, D.F. A Precise Method for Determining Contoured Surfaces. APPEA J. 1982, 22, 205–212. [Google Scholar] [CrossRef]
- Weber, D.D.; Englund, E.J. Evaluation and comparison of spatial interpolators II. Math. Geol. 1984, 26, 589–603. [Google Scholar] [CrossRef]
- Nagelkerke, N.J.D. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Popovici, E.-A.; Kucsicsa, G.; Bălteanu, D.; Grigorescu, I.; Mitrică, B.; Dumitrașcu, M.; Damian, N. Past and future land use/cover flows related to agricultural lands in Romania. An assessment using CLUE-S Model and CORINE Land Cover Database. Carpathian J. Earth Environ. Sci. 2018, 13, 613–628. [Google Scholar] [CrossRef]
- Henning, L.; Korhonen, K.T.; Lanz, A.; Riedel, T. Final Report, Specific Contract n. 17 “Use of National Forest Inventories Data to Estimate Biomass in the European Forests” in the Context of the “Framework Contract for the Provision of Forest Data and Services in Support to the European Forest Data Centre”, 15 April 2016; Joint Research Centre of the European Commission: Ispra, Italy, 2016. [Google Scholar]
- Scarlat, N.; Blujdea, V.N.; Dallemand, J.-F. Assessment of the availability of agricultural and forest residues for bioenergy production in Romania. Biomass Bioenergy 2011, 35, 1995–2005. [Google Scholar] [CrossRef]
- Rosillo-Calle, F.; Furdato, P.; Rezende, M.E.A.; Hall, D.O. The Charcoal Dilemma: Finfing Sustainable Solutions for Brazilian Industry; Intermediate Technology Publications: London, UK, 1996. [Google Scholar]
- Bouriaud, O.; Don, A.; Janssens, I.A.; Marin, G.; Schulze, E.-D. Effects of forest management on biomass stocks in Romanian beech forests. For. Ecosyst. 2019, 6, 19. [Google Scholar] [CrossRef]
- MCPFE (Ministerial Conference on the Protection of Forests in Europe). State of Europe’s Forests 2011–Status and Trends in Sustainable Forest Management in Europe; FOREST EUROPE: Oslo, Norway, 2011. [Google Scholar]
- Dumitraşcu, M.; Mocanu, I.; Mitrică, B.; Dragotă, C.; Grigorescu, I.; Dumitrică, C. The assessment of socio-economic vulnerability to drought in Southern Romania (Oltenia Plain). Int. J. Disaster Risk Reduct. 2018, 27, 142–154. [Google Scholar] [CrossRef]
- NIS (National Institute of Statistics). Tempo Online, Baza de Date Statistice. 2011. Available online: http://statistici.insse.ro:8077/tempo-online/#/pages/tables/insse-table (accessed on 20 March 2019).
- Prăvălie, R.; Peptenatu, D.; Sirodoev, I. The impact of climate change on the dynamics of agricultural systems in south-western Romania. Carpathian J. Earth Environ. Sci. 2013, 8, 175–186. [Google Scholar]
- Sima, M.; Popovici, E.A.; Bălteanu, D.; Micu, D.M.; Kucsicsa, G.; Dragotă, C.; Grigorescu, I. A farmer-based analysis of climate change adaptation options of agriculture in the Bărăgan Plain, Romania. Earth Perspect. 2015, 2, 5. [Google Scholar] [CrossRef]
- Vospernik, S.; Monserud, R.A.; Sterba, H. Do individual-tree growth models correctly represent height:diameter ratios of Norway spruce and Scots pine? For. Ecol. Manag. 2010, 260, 1735–1753. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumitrașcu, M.; Kucsicsa, G.; Dumitrică, C.; Popovici, E.-A.; Vrînceanu, A.; Mitrică, B.; Mocanu, I.; Șerban, P.-R. Estimation of Future Changes in Aboveground Forest Carbon Stock in Romania. A Prediction Based on Forest-Cover Pattern Scenario. Forests 2020, 11, 914. https://doi.org/10.3390/f11090914
Dumitrașcu M, Kucsicsa G, Dumitrică C, Popovici E-A, Vrînceanu A, Mitrică B, Mocanu I, Șerban P-R. Estimation of Future Changes in Aboveground Forest Carbon Stock in Romania. A Prediction Based on Forest-Cover Pattern Scenario. Forests. 2020; 11(9):914. https://doi.org/10.3390/f11090914
Chicago/Turabian StyleDumitrașcu, Monica, Gheorghe Kucsicsa, Cristina Dumitrică, Elena-Ana Popovici, Alexandra Vrînceanu, Bianca Mitrică, Irena Mocanu, and Paul-Răzvan Șerban. 2020. "Estimation of Future Changes in Aboveground Forest Carbon Stock in Romania. A Prediction Based on Forest-Cover Pattern Scenario" Forests 11, no. 9: 914. https://doi.org/10.3390/f11090914
APA StyleDumitrașcu, M., Kucsicsa, G., Dumitrică, C., Popovici, E.-A., Vrînceanu, A., Mitrică, B., Mocanu, I., & Șerban, P.-R. (2020). Estimation of Future Changes in Aboveground Forest Carbon Stock in Romania. A Prediction Based on Forest-Cover Pattern Scenario. Forests, 11(9), 914. https://doi.org/10.3390/f11090914





