Use of Bayesian Modeling to Determine the Effects of Meteorological Conditions, Prescribed Burn Season, and Tree Characteristics on Litterfall of Pinus nigra and Pinus pinaster Stands
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Experimental Design
2.3. Prescribed Burning
2.4. Litterfall Biomass
2.5. Data Analysis
3. Results
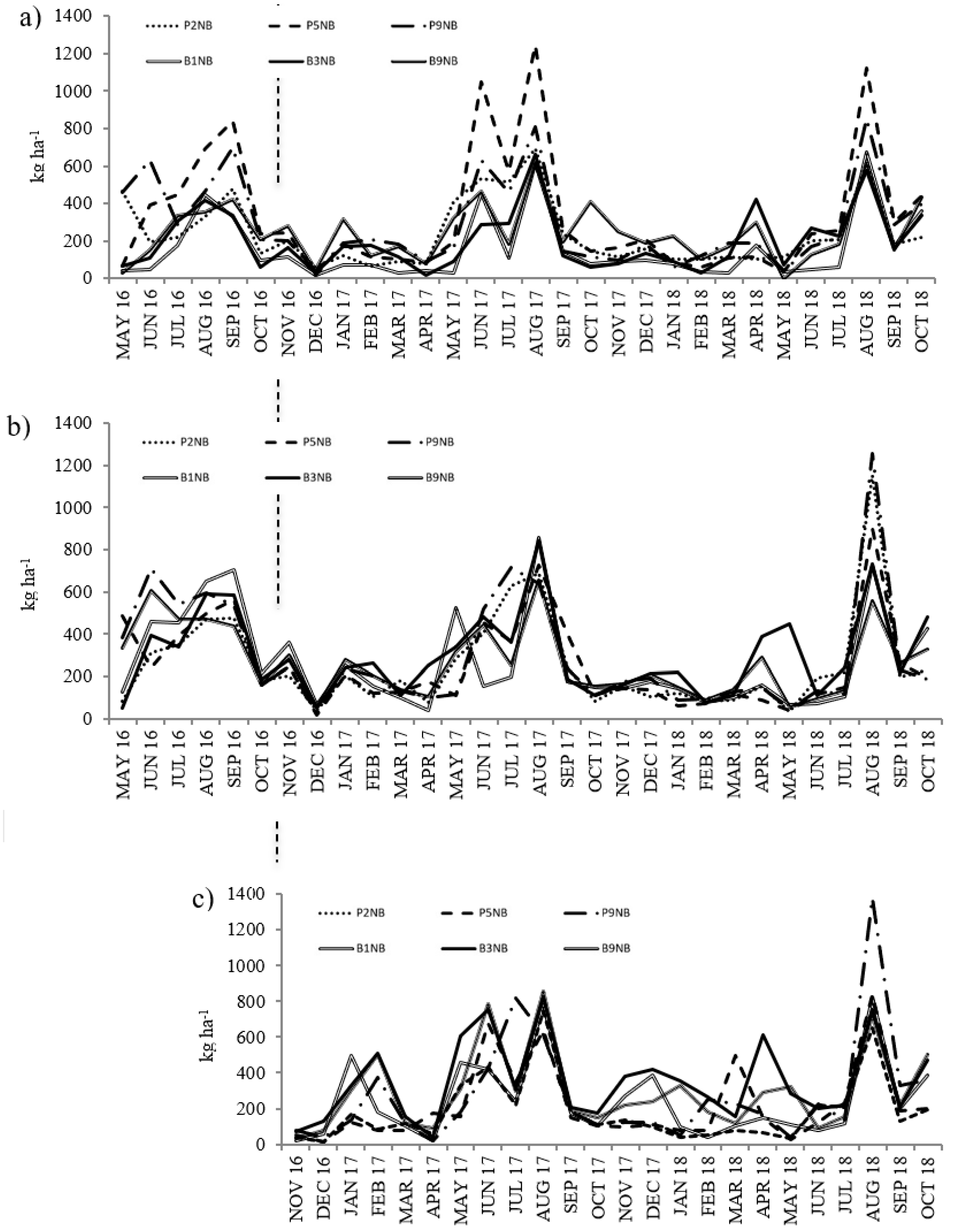
3.1. Litterfall
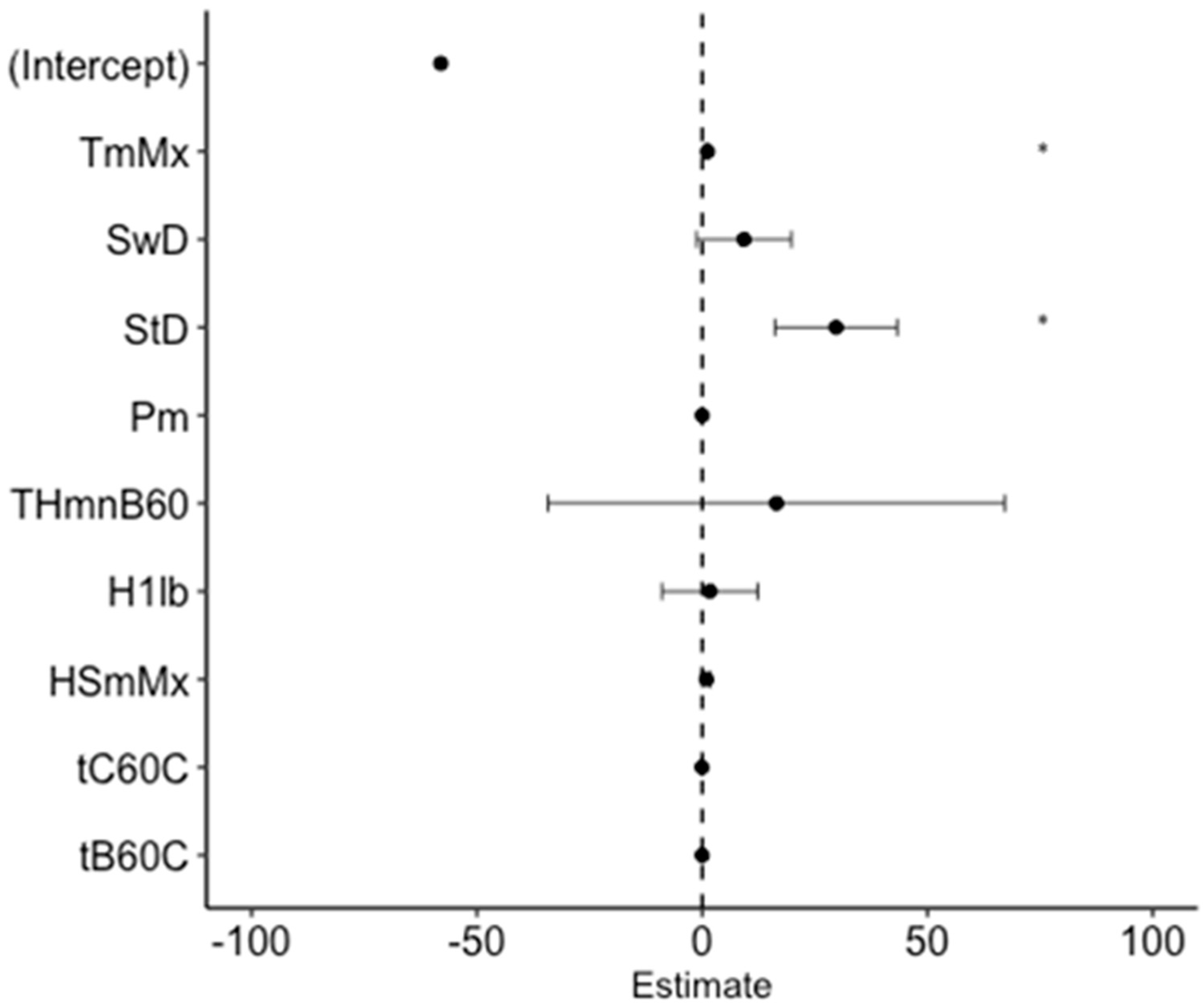
3.2. Bayesian Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moriondo, M.; Good, P.; Durao, R.; Bindi, M.; Giannakopoulos, C.; Corte-Real, J. Potential impact of climate change on fire risk in the Mediterranean area. Clim. Res. 2006, 31, 85–95. [Google Scholar] [CrossRef]
- Agee, J.K.; Skinner, C.N. Basic principles of forest fuel reduction treatments. For. Ecol. Manag. 2005, 211, 83–96. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Botelho, H.S. A review of prescribed burning effectiveness in fire hazard reduction. Int. J. Wildland Fire 2003, 12, 117–128. [Google Scholar] [CrossRef]
- Harmon, M.E. Survival of trees after low-intensity surface fires in Great Smoky Mountains National Park. Ecology 1984, 65, 796–802. [Google Scholar] [CrossRef]
- Lado-Monserrat, L.; Lidón, A.; Bautista, I. Erratum to: Litterfall, litter decomposition and associated nutrient fluxes in Pinus halepensis: Influence of tree removal intensity in a Mediterranean forest. Eur. J. For. Res. 2016, 135, 203–214. [Google Scholar] [CrossRef]
- Roig, S.; del Río, M.; Canellas, I.; Montero, G. Litter fall in Mediterranean Pinus pinaster Ait. stands under different thinning regimes. For. Ecol. Manag. 2005, 206, 179–190. [Google Scholar] [CrossRef]
- Sayer, E.J. Using experimental manipulation to assess the roles of leaf litter in the functioning of forest ecosystems. Biol. Rev. 2006, 81, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Kunhamu, T.K.; Kumar, B.M.; Viswanath, S. Does thinning affect litterfall, litter decomposition, and associated nutrient release in Acacia mangium stands of Kerala in peninsular India? Can. J. For. Res. 2009, 39, 792–801. [Google Scholar] [CrossRef]
- Hansen, K.; Vesterdal, L.; Schmidt, I.K.; Gundersen, P.; Sevel, L.; Bastrup-Birk, A.; Pedersen, L.B.; Bille-Hansen, J. Litterfall and nutrient return in five tree species in a common garden experiment. For. Ecol. Manag. 2009, 257, 2133–2144. [Google Scholar] [CrossRef]
- Kurz, C.; Coûteaux, M.M.; Thiéry, J.M. Residence time and decomposition rate of Pinus pinaster needles in a forest floor from direct field measurements under a Mediterranean climate. Soil Biol. Biochem. 2000, 32, 1197–1206. [Google Scholar] [CrossRef]
- Pausas, J.G.; Carceller, F.; Vallejo, V.R. El desfronde en bosques de Pinus sylvestris L. en relación con las características climáticas. Ecología 1994, 8, 167–176. [Google Scholar]
- Blanco, J.; Imbert, J.; Castillo, F. Influence of site characteristics and thinning intensity on litterfall production in two Pinus sylvestris L. forests in the western Pyrenees. For. Ecol. Manag. 2006, 237, 342–352. [Google Scholar] [CrossRef]
- Santa-Regina, I.S.; Tarazona, T. Nutrient return to the soil through litterfall and throughfall under beech and pine stands of Sierra de la Demanda, Spain. Arid Soil Res. Rehabil. 2000, 14, 239–252. [Google Scholar] [CrossRef]
- Wieder, R.K.; Wright, S.J. Tropical forest litter dynamics and dry season irrigation on Barro Colorado Island, Panamá. Ecology 1995, 76, 1971–1979. [Google Scholar] [CrossRef]
- Gracia, C.A.; Sabaté, S.; López, B.; Sánchez, B. Presente y futuro del bosque mediterráneo: Balance de carbono, gestión y cambio global. In Aspectos Funcionales de los Ecosistemas Mediterráneos; AEET-CSIC Press: Granada, Spain, 2001; pp. 351–372. [Google Scholar]
- Zhang, H.; Yuan, W.; Dong, W.; Liu, S. Seasonal patterns of litterfall in forest ecosystem worldwide. Ecol. Complex. 2014, 20, 240–247. [Google Scholar] [CrossRef]
- García-Plé, C.; Vanrell, P.; Morey, M. Litter fall and decomposition in a Pinus halepensis forest on Mallorca. J. Veg. Sci. 1995, 6, 17–22. [Google Scholar] [CrossRef]
- Catry, F.X.; Rego, F.; Moreira, F.; Fernandes, P.M.; Pausas, J.G. Post-fire tree mortality in mixed forests of central Portugal. For. Ecol. Manag. 2010, 260, 1184–1192. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Rigolot, E. The fire ecology and management of maritime pine (Pinus pinaster Ait.). For. Ecol. Manag. 2007, 241, 1–13. [Google Scholar] [CrossRef]
- Fulé, P.Z.; Ribas, M.; Gutiérrez, E.; Vallejo, R.; Kaye, M.W. Forest structure and fire history in an old Pinus nigra forest, eastern Spain. For. Ecol. Manag. 2008, 255, 1234–1242. [Google Scholar] [CrossRef]
- Pausas, J.G.; Llovet, J.; Rodrigo, A.; Vallejo, R. Are wildfires a disaster in the Mediterranean basin?—A review. Int. J. Wildland Fire 2009, 17, 713–723. [Google Scholar] [CrossRef]
- Piqué, M.; Domènech, R. Effectiveness of mechanical thinning and prescribed burning on fire behavior in Pinus nigra forests in NE Spain. Sci. Total Environ. 2018, 618, 1539–1546. [Google Scholar] [CrossRef] [PubMed]
- Tapias, R.; Gil, L.; Fuentes-Utrilla, P.; Pardos, J.A. Canopy seed banks in Mediterranean pines of south-eastern Spain: A comparison between Pinus halepensis Mill., P. pinaster Ait., P. nigra Arn. and P. pinea L. J. Ecol. 2001, 89, 629–638. [Google Scholar] [CrossRef]
- Lawes, M.J.; Richards, A.; Dathe, J.; Midgley, J.J. Bark thickness determines fire resistance of selected tree species from fire-prone tropical savanna in north Australia. Plant Ecol. 2011, 212, 2057–2069. [Google Scholar] [CrossRef]
- Romero, C. Bark structure and functional ecology. In Bark: Use, Management, and Commerce in Africa; Cunningham, A.B., Campbell, B.M., Luckert, K.M., Eds.; Advances in Economic Botany: New York, NY, USA, 2007; Volume 17, pp. 5–25. [Google Scholar]
- Helms, J.A. Summer photosynthesis of ponderosa pine in its natural habitat. Photosynthetica 1970, 4, 234–253. [Google Scholar]
- Wyant, J.G.; Omi, P.N.; Laven, R.D. Fire induced tree mortality in a Colorado ponderosa pine/Douglas-fir stand. For. Sci. 1986, 32, 49–59. [Google Scholar] [CrossRef]
- Elmqvist, T.; Folke, C.; Nystrom, M.; Peterson, G.; Bengtsson, J.; Walker, B.; Norberg, J. Response diversity, ecosystem change, and resilience. Front. Ecol. Environ. 2003, 1, 488–494. [Google Scholar] [CrossRef]
- Espinosa, J.; Madrigal, J.; De La Cruz, A.C.; Guijarro, M.; Jimenez, E.; Hernando, C. Short-term effects of prescribed burning on litterfall biomass in mixed stands of Pinus nigra and Pinus pinaster and pure stands of Pinus nigra in the Cuenca Mountains (Central-Eastern Spain). Sci. Total Environ. 2018, 618, 941–951. [Google Scholar] [CrossRef]
- Espinosa, J.; Palheiro, P.; Loureiro, C.; Ascoli, D.; Esposito, A.; Fernandes, P.M. Fire-severity mitigation by prescribed burning assessed from fire-treatment encounters in maritime pine stands. Can. J. For. Res. 2019, 49, 1–7. [Google Scholar] [CrossRef]
- Mirra, I.M.; Oliveira, T.M.; Barros, A.M.; Fernandes, P.M. Fuel dynamics following fire hazard reduction treatments in blue gum (Eucalyptus globulus) plantations in Portugal. For. Ecol. Manag. 2017, 398, 185–195. [Google Scholar] [CrossRef]
- Hare, R.C. The contribution of bark to fire resistance of southern trees. J. For. 1965, 4, 248–251. [Google Scholar] [CrossRef]
- Seifert, T.; Meincken, M.; Odhiambo, B.O. The effect of surface fire on tree ring growth of Pinus radiata trees. Ann. For. Sci. 2017, 74, 34. [Google Scholar] [CrossRef]
- Rozas, V.; Pérez-de-Lis, G.; García-González, I.; Arévalo, J.A. Contrasting effects of wildfire and climate on radial growth of Pinus canariensis on windward and leeward slopes on Tenerife, Canary Islands. Trees 2011, 25, 895–905. [Google Scholar] [CrossRef]
- Madrigal, J.; Souto-García, J.; Calama, R.; Guijarro, M.; Picos, J.; Hernando, C. Resistance of Pinus pinea L. bark to fire. Int. J. Wildland Fire 2019, 28, 342–353. [Google Scholar] [CrossRef]
- Espinosa, J.; Madrigal, J.; Pando, V.; de la Cruz, A.C.; Guijarro, M.; Hernando, C. The effect of low intensity prescribed burns in two seasons litterfall biomass and nutrient content. Int. J. Wildland Fire 2020. [Google Scholar] [CrossRef]
- Clark, J.S. Why environmental scientists are becoming Bayesians. Ecol. Lett. 2005, 8, 2–14. [Google Scholar] [CrossRef]
- AEMET. Weather Data from Cañizares Station (Cuenca-Spain) 1997–2018; State Meteorological Agency of Spanish Government (AEMET): Madrid, Spain, 2018.
- Plaza-Álvarez, P.; Lucas-Borja, M.; Sagra, J.; Moya, D.; Fontúrbel, T.; De las Heras, J. Soil respiration changes after prescribed fires in Spanish black pine (Pinus nigra Arn. ssp. salzmannii) monospecific and mixed forest stands. Forests 2017, 8, 248. [Google Scholar] [CrossRef]
- Scott, J.H.; Burgan, R.E. Standard Fire Behavior Fuel Models: A Comprehensive Set for Use with Rothermel’s Surface Fire Spread Model; US Department of Agriculture: Fort Collins, CO, USA; Forest Service; Rocky Mountain Station: Vancouver, BC, Canada, 2005; 72p.
- Vega, J.A. Efectos del Fuego Prescrito Sobre el Suelo en Pinares de Pinus pinaster Ait. de Galicia. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2001; 417p. [Google Scholar]
- Ukonmaanaho, L.; Pitman, R.; Bastrup-Birk, A.; Breda, N.; Rautio, P. Part XIII: Sampling and Analysis of Litterfall. In Manual on Methods and Criteria for Harmonized Sampling, Assessment, Monitoring and Analysis of the Effects of Air Pollution on Forests; UNECE ICP Forests Programme Co-Ordinating Centre, Ed.; Thünen Institute for Forests Ecosystems: Eberswalde, Germany, 2016; 15p. [Google Scholar]
- Cosandey-Godin, A.; Krainski, E.T.; Worm, B.; Flemming, J.M. Applying Bayesian spatiotemporal models to fisheries bycatch in the Canadian Arctic. Can. J. Fish. Aquat. Sci. 2014, 72, 186–197. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Geisser, S.; Eddy, W.F. A predictive approach to model selection. J. Am. Stat. Assoc. 1979, 74, 153–160. [Google Scholar] [CrossRef]
- Vehtari, A.; Lampinen, J. Bayesian model assessment and comparison using cross-validation predictive densities. Neural Comput. 2002, 14, 2439–2468. [Google Scholar] [CrossRef]
- Gelman, A.; Shalizi, C.R. Philosophy and the practice of Bayesian statistics. Br. J. Math. Stat. Psychol. 2013, 66, 8–38. [Google Scholar] [CrossRef] [PubMed]
- Spiegelhalter, D.; Best, N.G.; Carlin, B.P.; Van der Linde, A. Bayesian measures of model complexity and fit. Qual. Control Appl. Stat. 2003, 48, 431–432. [Google Scholar] [CrossRef]
- Van Der Linde, A. DIC in variable selection. Stat. Neerl. 2005, 59, 45–56. [Google Scholar] [CrossRef]
- Watanabe, S. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J. Mach. Learn. Res. 2010, 11, 3571–3594. [Google Scholar]
- Li, L.; Qiu, S.; Zhang, B.; Feng, C.X. Approximating cross-validatory predictive evaluation in Bayesian latent variable models with integrated IS and WAIC. Stat. Comput. 2016, 26, 881–897. [Google Scholar] [CrossRef]
- Pettit, L.I. The conditional predictive ordinate for the normal distribution. J. R. Stat. Soc. Ser. B 1990, 52, 175–184. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Roos, M.; Held, L. Sensitivity analysis in Bayesian generalized linear mixed models for binary data. Bayesian Anal. 2011, 6, 259–278. [Google Scholar] [CrossRef]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar] [CrossRef]
- Qiao, H.; Soberón, J.; Peterson, A.T. No silver bullets in correlative ecological niche modelling: Insights from testing among many potential algorithms for niche estimation. Methods Ecol. Evol. 2015, 6, 1126–1136. [Google Scholar] [CrossRef]
- Berg, B.; Meentemeyer, V. Litter fall in some European coniferous forests as dependent on climate: A synthesis. Can. J. For. Res. 2001, 31, 292–301. [Google Scholar] [CrossRef]
- Agren, G.; Knecht, M. Simulation of soil carbon and nutrient development under Pinus sylvestris and Pinus contorta. For. Ecol. Manag. 2001, 141, 117–129. [Google Scholar] [CrossRef]
- ICP Forests Database. The International Co-Operative Programme on Assessment and Monitoring of Air Pollution Effects on Forests, Level II Plots. Data Accessed for 2005–2014. Available online: http://icp-forests.net/page/data-requests (accessed on 9 August 2020).
- Martínez-Alonso, C.; Valladares, F.; Camarero, J.J.; Arias, M.L.; Serrano, M. The uncoupling of secondary growth, cone and litter production by intradecadal climatic variability in a Mediterranean Scots pine forest. For. Ecol. Manag. 2007, 253, 19–29. [Google Scholar] [CrossRef]
- Wareing, P.F.; Thompson, A.G. Rapid effects of red light on hormone levels. In Light and Plant Development; Smith, H., Ed.; Butterworths: London, UK, 1975; pp. 85–94. [Google Scholar]
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2018; 32p. [Google Scholar]
- Bueis, T.; Bravo, F.; Pando, V.; Turrión, M.B. Influencia de la densidad del arbolado sobre el desfronde y su reciclado en pinares de repoblación del norte de España. Bosque (Valdivia) 2017, 38, 401–407. [Google Scholar] [CrossRef][Green Version]
- Espinosa, J.; Rodríguez de Rivera, O.; Madrigal, J.; Guijarro, M.; Hernando, C. Predicting potential cambium damage and fire resistance in Pinus nigra Arn. ssp. salzmannii. For. Ecol. Manag. 2020, 474, 118372. [Google Scholar] [CrossRef]
- Tapias, R.; Climent, J.; Pardos, J.A.; Gil, L. Life histories of Mediterranean pines. Plant Ecol. 2004, 171, 53–68. [Google Scholar] [CrossRef]
- Tiscar, P.A.; Linares, J.C. Pinus nigra subsp. salzmannii forests from Southeast Spain: Using structure and process information to guide management. In Pine Forests: Types, Threats and Management; Frisiras, C.T., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2011. [Google Scholar]
- Gashaw, M.; Michelsel, A.; Friis, I.; Jensen, M.; Demissew, S.; Woldu, Z. Post-fire regeneration strategies and tree bark resistance to heating in frequently burning tropical savanna woodlands and grasslands in Ethiopia. Nord. J. Bot. 2002, 22, 19–33. [Google Scholar] [CrossRef]
- Van Mantgem, P.; Schwartz, M. Bark heat resistance of small trees in Californian mixed conifer forests: Testing some model assumptions. For. Ecol. Manag. 2003, 78, 341–352. [Google Scholar] [CrossRef]
- Hernando, C.; Guijarro, M. Temperature Regime in Pinus pinaster and P. halepensis Trunks, Proceedings of the III International Conference on Forest Fire Research and 14th Conference on Fire and Forest Meteorology; Viegas, D.X., Ed.; ADAI: Luso-Coimbra, Portugal, 1998; pp. 801–813. [Google Scholar]
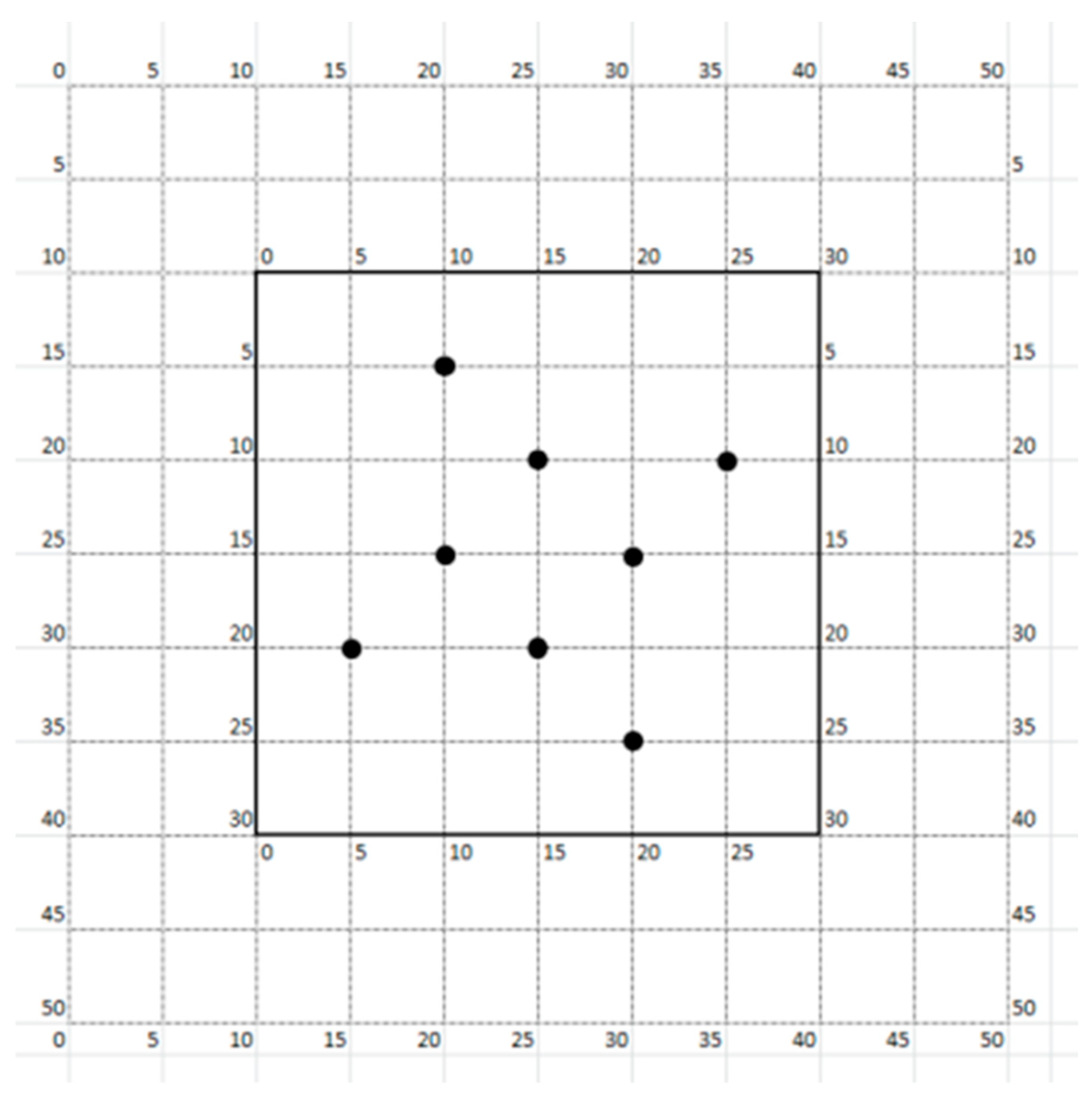
| -- | El Pozuelo | Beteta |
|---|---|---|
| Coordinates—Longitude | 40°33′36″ N | 40°33′06″ N |
| Coordinates—Latitude | 002°15′56″ W | 002°06′32″ W |
| Main species | Pinus nigra (100%) | Pinus nigra (89 ± 11%) Pinus pinaster (11 ± 11%) |
| pH of topsoil * | 7.3 (clay texture) | 6.9 (loamy-sand texture) |
| Elevation | 1015 ± 5 m a.s.l. | 1232 ± 74 m a.s.l. |
| Slope | 3–8% | 3–10% |
| Stand density | 627 ± 238 trees ha−1 | 1286 ± 339 trees ha−1 |
| Stand basal area | 25.4 ± 9.7 m2 ha−1 | 36.6 ± 10.7 m2 ha−1 |
| Dominant tree height | 18.6 ± 0.8 m | 17.0 ± 1.6 m |
| Tree height | 12.2 ± 2.0 m | 13.2 ± 2.7 m |
| First live branch | 6.4 ± 1.8 m | 8.2 ± 2.5 m |
| Diameter at breast height (DBH) | 19.8 ± 2.6 cm | 18.8 ± 4.1 cm |
| Bark thickness | 1.7 ± 0.3 cm | 1.7 ± 0.4 cm |
| Main understory vegetation | Cistus laurifolius L.; Genista scorpius Sibth. & Sm. ex Boiss; Prunus spinosa L.; Arrhenatherum bulbosum (Willd.) C.Presl; Bupleurum rigidum L. | Genista scorpius Sibth. & Sm. ex Boiss.; Rosa canina L. |
| Fuel Model ** | TU1 | TU1 |
| S | PT | Dt | Pn | Pp | Ht | H1lb | D60 | D130 | THMxB60 | THMnB60 |
|---|---|---|---|---|---|---|---|---|---|---|
| -- | -- | Trees ha−1 | % | % | m | m | cm | cm | cm | cm |
| Mixed * | NB | 563 (74) | 93 (4) | 7 (4) | 11.5 (3.2) | 5.1 (1.9) | 19.7 (3.8) | 18.7 (3.7) | 1.82 (0.58) | 0.99 (0.37) |
| Mixed * | SB | 881 (227) | 89 (8) | 11 (8) | 12.3 (0.8) | 7.1 (0.6) | 21.3 (1.0) | 19.8 (1.0) | 2.49 (0.13) | 1.34 (0.18) |
| Mixed ** | AB | 437 (110) | 85 (20) | 15 (20) | 12.9 (2.1) | 6.9 (2.4) | 22.6 (2.9) | 21.0 (2.8) | 2.43 (0.21) | 1.17 (0.19) |
| Pure * | NB | 1456 (507) | 100 (0) | 0 (0) | 10.1 (3.2) | 6.1 (3.3) | 15.1 (1.7) | 13.8 (1.6) | 1.64 (0.10) | 0.92 (0.09) |
| Pure * | SB | 1215 (209) | 100 (0) | 0 (0) | 12.7 (0.8) | 7.5 (1.3) | 20.0 (1.9) | 18.2 (2.0) | 2.46 (0.18) | 1.23 (0.20) |
| Pure ** | AB | 1274 (335) | 100 (0) | 0 (0) | 14.1 (2.2) | 9.4 (1.6) | 21.9 (4.9) | 20.0 (4.4) | 2.71 (0.24) | 1.45 (0.23) |
| -- | -- | Mixed | Mixed | Pure | Pure |
|---|---|---|---|---|---|
| PT | -- | SB | AB | SB | AB |
| T | °C | 21.5 (1.2) | 11.9 (0.4) | 20.4 (1.5) | 12.0 (0.9) |
| RH | % | 47.7 (5.3) | 67.0 (1.3) | 32.7 (2.3) | 43.5 (0.8) |
| WS | m s−1 | 0.8 (0.6) | 0.3 (0.3) | 0.8 (0.1) | 0.1 (0.1) |
| RS | m min−1 | 0.6 (0.1) | 0.6 (0.24) | 0.8 (0.1) | 0.7 (0.0) |
| HSmMx | cm | 70 (41) | 34 (11) | 160 (16) | 59 (26) |
| HSmMn | cm | 16 (9) | 5 (5) | 40 (18) | 4 (3) |
| TmMxB | °C | 209 (200) | 126 (118) | 279 (208) | 94 (108) |
| TmMxC | °C | 51 (80) | 49 (11) | 41 (45) | 40 (13) |
| TMxB | °C | 787 (--) | 605 (--) | 755 (--) | 702 (--) |
| TMxC | °C | 521 (--) | 77 (--) | 315 (--) | 75 (--) |
| TRMxB40 | % | 93 (7) | 93 (0) | 100 (0) | 91 (11) |
| TRMxC40 | % | 33 (31) | 76 (4) | 31 (10) | 45 (9) |
| TRMxB60 | % | 82 (89 | 60 (8) | 96 (8) | 57 (26) |
| TRMxC60 | % | 16 (15) | 18 (10) | 11 (4) | 5 (8) |
| tB40B | s | 562 (1057) | 179 (163) | 617 (550) | 301 (657) |
| tC40C | s | 284 (212) | 47 (128) | 666 (545) | 7 (15) |
| tB60B | s | 404 (1121) | 134 (91) | 369 (524) | 174 (268) |
| tC60C | s | 170 (120) | 6 (12) | 251 (206) | 2 (0) |
| -- | Abbreviation | Variable | Unit | Variables Selected |
|---|---|---|---|---|
| Meteorological variables | TmMx | Mean maximum temperature | °C | * |
| TmMn | Mean minimum temperature | °C | - | |
| Pm | Monthly precipitation | mm | * | |
| SwD | Days with snow | days | * | |
| StD | Days with storm | days | * | |
| WS | Mean maximum wind speed | m s−1 | - | |
| Stand and tree trait variables | THMxB60 | Maximum bark thickness at 60 cm from the base | cm | - |
| THMnB60 | Minimum bark thickness at 60 cm from the base | cm | * | |
| H1lb | Height at which first live branch appears | m | * | |
| Fire prescription and behavior variables | HSmMx | Mean maximum scorch height | cm | * |
| HSmMn | Mean minimum scorch height | cm | - | |
| TmMxB | Mean maximum bark temperature | °C | - | |
| TmMxC | Mean maximum cambium temperature | °C | - | |
| tB40C | Time which temperature is higher than 40 °C in bark-surface | s | - | |
| tC40C | Time which temperature is higher than 40 °C in cambium | s | - | |
| tB60C | Time which temperature is higher than 60 °C in bark-surface | s | * | |
| tC60C | Time which temperature is higher than 60 °C in cambium | s | * |
| S | PT | May 2016–April 2017 | May 2017–April 2018 | May 2018–October 2018 |
|---|---|---|---|---|
| -- | -- | kg ha−1 | kg ha−1 | kg ha−1 |
| Mixed | NB | 3171 | 3537 | 1965 |
| Mixed | SB | 3257 | 2991 | 1879 |
| Pure | NB | 1989 | 2585 | 1504 |
| Pure | SB | 3482 | 3120 | 1762 |
| S | PT | November 2016–October 2017 | November 2017–October 2018 | -- |
| -- | -- | kg ha−1 | kg ha−1 | -- |
| Mixed | NB | 3532 | 2726 | -- |
| Mixed | AB | 2732 | 2640 | -- |
| Pure | NB | 2393 | 2376 | -- |
| Pure | AB | 3629 | 3495 | -- |
| -- | Variables | Type of Effect | Mean | Standard Deviation | 0.025quant | 0.975quant |
|---|---|---|---|---|---|---|
| Meteorological variables | TmMx | Fixed | 1.1701 | 0.119 | 0.9363 | 1.4036 |
| SwD | Fixed | 9.6835 | 5.2434 | −0.6092 | 19.9739 | |
| StD | Fixed | 29.3036 | 6.7296 | 16.087 | 42.5045 | |
| Pm | Fixed | 0.0004 | 0.0191 | −0.0372 | 0.0379 | |
| Stand and tree trait variables | Stand | Random | 1.00 × 10−3 | 3.50 × 10−3 | 0.00 | 6.90 × 10−3 |
| THMnB60 | Fixed | 8.4226 | 25.4134 | −41.2572 | 58.459 | |
| H1lb | Fixed | 2.2874 | 5.1195 | −7.7954 | 12.309 | |
| Fire prescription and behavior variables | Treatment | Random | 1.02 × 10−2 | 5.44 × 10−2 | 0.00 | 7.10 × 10−2 |
| HSmMx | Fixed | 0.8115 | 0.4748 | −0.1175 | 1.7459 | |
| tC60C | Fixed | −0.0511 | 0.0403 | −0.1302 | 0.0279 | |
| tB60C | Fixed | −0.015 | 0.0500 | −0.1135 | 0.0827 | |
| -- | Intercept | -- | −44.616 | 92.7082 | −228.3046 | 129.4254 |
| -- | Precision for the Gaussian observations | -- | 0.00 | 0.00 | 0.00 | 0.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinosa, J.; Rodríguez De Rivera, Ó.; Madrigal, J.; Guijarro, M.; Hernando, C. Use of Bayesian Modeling to Determine the Effects of Meteorological Conditions, Prescribed Burn Season, and Tree Characteristics on Litterfall of Pinus nigra and Pinus pinaster Stands. Forests 2020, 11, 1006. https://doi.org/10.3390/f11091006
Espinosa J, Rodríguez De Rivera Ó, Madrigal J, Guijarro M, Hernando C. Use of Bayesian Modeling to Determine the Effects of Meteorological Conditions, Prescribed Burn Season, and Tree Characteristics on Litterfall of Pinus nigra and Pinus pinaster Stands. Forests. 2020; 11(9):1006. https://doi.org/10.3390/f11091006
Chicago/Turabian StyleEspinosa, Juncal, Óscar Rodríguez De Rivera, Javier Madrigal, Mercedes Guijarro, and Carmen Hernando. 2020. "Use of Bayesian Modeling to Determine the Effects of Meteorological Conditions, Prescribed Burn Season, and Tree Characteristics on Litterfall of Pinus nigra and Pinus pinaster Stands" Forests 11, no. 9: 1006. https://doi.org/10.3390/f11091006
APA StyleEspinosa, J., Rodríguez De Rivera, Ó., Madrigal, J., Guijarro, M., & Hernando, C. (2020). Use of Bayesian Modeling to Determine the Effects of Meteorological Conditions, Prescribed Burn Season, and Tree Characteristics on Litterfall of Pinus nigra and Pinus pinaster Stands. Forests, 11(9), 1006. https://doi.org/10.3390/f11091006






