Compression Properties and Its Prediction of Wood-Based Sandwich Panels with a Novel Taiji Honeycomb Core
Abstract
1. Introduction
2. Experimental Programs
2.1. Test Materials and Properties
2.2. Test Methods
3. Theoretical Analysis and Prediction
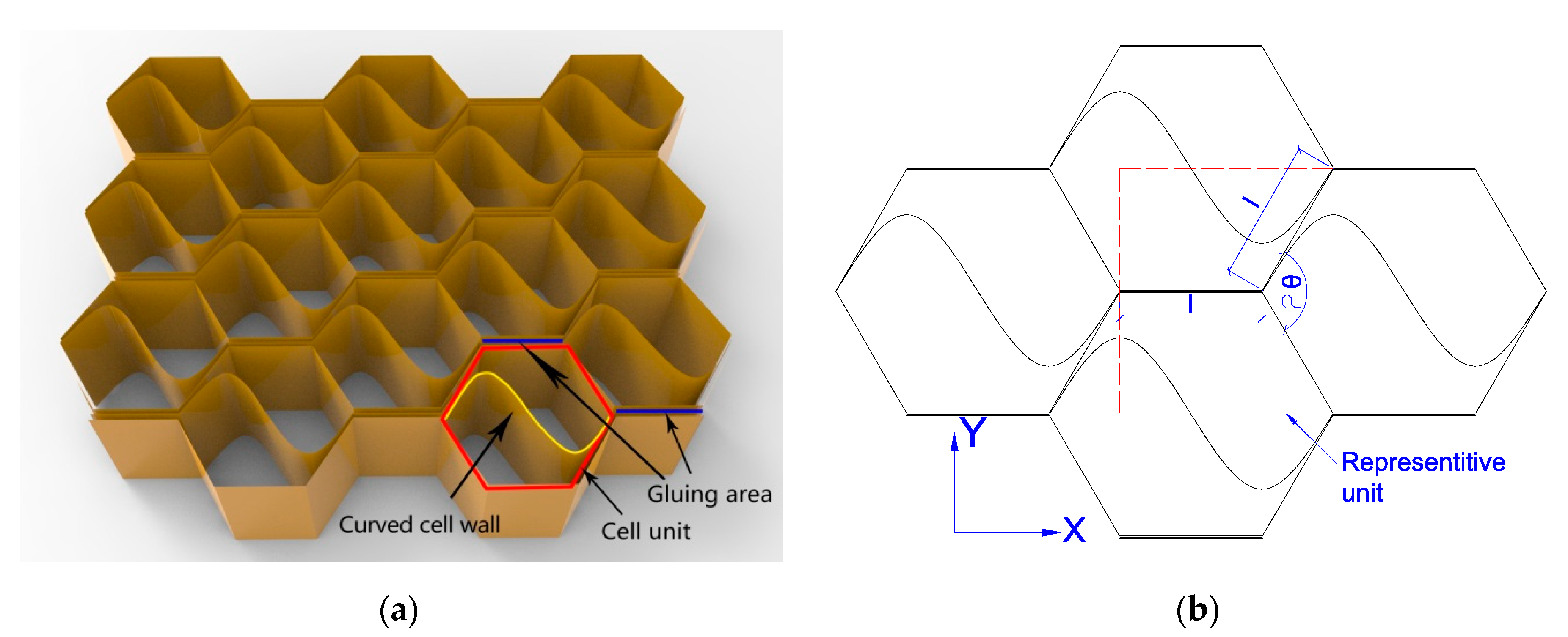
3.1. Strength Calculation of the Taiji Honeycomb
3.2. Modulus Calculation of the Taiji Honeycomb
4. Result and Discussion
4.1. Deformation and Failure Process
4.2. Strength Comparison between the Theoretical Calculation and Measured Results
4.3. Modulus Comparison between the Theoretical Calculation and Measured Results
4.4. The Effect of the Structure Parameters on the Compression Properties
4.5. Comparison between Taiji the Honeycomb and Traditional Hexagonal Honeycomb
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zou, N.; Liang, L.P. Research advances on formaldehyde emission of wood-based panels. Sichuan For. Explor. Des. 2018, 2, 80–86. [Google Scholar]
- Wang, Z.G.; Li, Z.D.; Zhou, W.; Hui, D. On the influence of structural defects for honeycomb structure. Compos. Part B 2018, 142, 183–192. [Google Scholar] [CrossRef]
- Maslej, M.; Smardzewski, J. Experimental testing of elastic properties of LayWood pyramidal cores. BioResources 2019, 14, 9686–9703. [Google Scholar]
- Smardzewski, J.; Gajęcki, A.; Wojnowska, M. Investigation of elastic properties of paper honeycomb panels with rectangular cells. BioResources 2019, 14, 1435–1451. [Google Scholar]
- Smardzewski, J. Wooden sandwich panels with prismatic core—energy absorbing capabilities. Compos. Struct. 2019, 230, 111535. [Google Scholar] [CrossRef]
- Hao, J.X.; Wu, X.F.; Liu, W.J. Bending property of sandwich beam based on layer-wise first-order theory. J. Build. Mater. 2014, 17, 1049–1053. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Smardzewski, J.; Wojciechowski, K.W. Response of wood-based sandwich beams with three-dimensional lattice core. Compos. Struct. 2019, 216, 340–349. [Google Scholar] [CrossRef]
- Hao, J.X.; Wu, X.F.; Liu, W.J. Modeling and verification of sandwich beam with wooden skin and honeycomb core subjected to transverse loading. Sci. Silvaesinicae 2014, 50, 128–137. [Google Scholar]
- Wu, X.F.; Xu, J.Y.; Hao, J.X. Calculating elastic constants of binderlessbamboo-wood sandwich composite. BioResources 2015, 10, 4473–4484. [Google Scholar] [CrossRef]
- Meng, F.C.; Cheng, C.; Hu, D.Y.; Song, J. Deformation behaviors of three-dimensional graphene honeycombs under out-of-plane compression: Atomistic simulations and predictive modeling. J. Mech. Phys. Solids 2017, 109, 241–251. [Google Scholar] [CrossRef]
- Zhang, Z.; Kutana, A.; Yang, Y.; Krainyukova, N.V.; Penev, E.S.; Yakobson, B.I. Nanomechanics of carbon honeycomb cellular structures. Carbon 2017, 113, 26–32. [Google Scholar] [CrossRef]
- Daniel, I.M.; Abot, J.L. Fabrication, testing and analysis of composite sandwich beams. Compos. Sci. Technol. 2000, 60, 2455–2463. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.G.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide; Butterworth-Heinemann: London, UK, 2000. [Google Scholar]
- Minakuchi, S.; Okabe, Y.; Takeda, N. Segment-wise model for theoretical simulation of barely visible indentation damage in composite sandwich beams: Part1-Fourmulation. Compos. Part A Appl. Sci. Manuf. 2008, 39, 133–144. [Google Scholar] [CrossRef]
- Caprino, G.; Durante, M.; Leone, C.; Lopresto, V. The effect of shear on the local indentation and failure of sandwich beams with polymeric foam core loaded in flexure. Compos. Part B Eng. 2015, 71, 45–51. [Google Scholar] [CrossRef]
- Lim, T.S.; Lee, C.S.; Lee, D.G. Failure modes of foam core sandwich beams under static and impact loads. J. Compos. Mater. 2004, 38, 1639–1662. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, N. Investigation of elastic moduli of kraft paper honeycomb core sandwich panels. Compos. Part B 2012, 43, 2107–2114. [Google Scholar] [CrossRef]
- Hao, J.X.; Wu, X.F.; Oporto, G.; Liu, W.J.; Wang, J.X. Structural analysis and strength-to-weight optimization of wood-based sandwich composite with honeycomb core under three-point flexural test. Eur. J. Wood Prod. 2020. [Google Scholar] [CrossRef]
- Wang, D.M.; Bai, Z.Y. Mechanical property of paper honeycomb structure under dynamic compression. Mater. Des. 2015, 77, 59–64. [Google Scholar] [CrossRef]
- Słonina, M.; Dziurka, D.; Smardzewski, J. Experimental research and numerical analysis of the elastic properties of paper cell cores before and after impregnation. Materials 2020, 13, 2058. [Google Scholar] [CrossRef]
- Peliński, K.; Smardzewski, J. Experimental testing of elastic properties of paper and WoodEpox in honeycomb panels. BioResources 2019, 14, 2977–2994. [Google Scholar]
- Si, L.L. Study on the mechanical properties of wood material enhanced paper honeycomb core composite boards. For. Mach. Woodwork. Equip. 2012, 40, 25–28. [Google Scholar]
- Hao, J.X.; Wu, X.F.; Oporto, G.; Wang, J.X.; Dahle, G.; Nan, N. Deformation and failure behavior of wooden sandwich composite with Taiji honeycomb core under three-point bending. Materials 2018, 11, 2325. [Google Scholar] [CrossRef] [PubMed]
- ASTM D 1037-06a. Standard Test Methods for Evaluating Properties of Wood-Base Fiber and Particle Panel Materials; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Dahle, G.A. Influence of bark on the mapping of mechanical strain using digital image correlation. Wood Sci. Technol. 2017, 51, 1469–1477. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Instability; McGraw-Hill Publishing Company: New York, NY, USA, 1961. [Google Scholar]
- Wang, Z.; Liu, J.; Hui, D. Mechanical behaviors of inclined cell honeycomb structure subjected to compression. Compos. Part B 2017, 110, 307–314. [Google Scholar] [CrossRef]









| Material | Thickness (mm) | Density (g/cm3) | Moisture Content (%) | Bending Strength (MPa) | Bending Modulus (MPa) |
|---|---|---|---|---|---|
| MDF | 3.18 | 0.88 | 5.4 | 28.9 | 5399.9 |
| PLY* | 3.18 | 0.69 | 5.6 | 88.2 | 20,578.0 |
| PLY* | 6.35 | 0.68 | 5.4 | 64.2 | 13,598.7 |
| Material | Thickness (mm) | Moisture Content (%) | Tensile Strength (MPa) | Tensile Modulus (MPa) |
|---|---|---|---|---|
| Kraft paper | 0.178 | 5.4 | 13.2 | 453.02 |
| Group | Honeycomb | Code | Effective Replicate No. | Surface Sheet (A) | Core Thickness (B) (mm) | Loading Speed (C) (mm/min) |
|---|---|---|---|---|---|---|
| 1 | Taiji | A1B1C1 | 5 for strength 3 for modulus | 3.18 mm MDF (A1) | 15.9 (B1) | 0.5 (C1) |
| 2 | Taiji | A1B2C1 | 4 for strength 3 for modulus | 3.18 mm MDF (A1) | 25.4 (B2) | 0.5 (C1) |
| 3 | Taiji | A1B3C1 | 3 for strength 3 for modulus | 3.18 mm MDF (A1) | 34.9 (B3) | 0.5 (C1) |
| 4 | Taiji | A2B2C1 | 5 for strength 5 for modulus | 3.18 mm PLY (A2) | 25.4 (B2) | 0.5 (C1) |
| 5 | Taiji | A3B2C1 | 3 for strength 3 for modulus | 6.35 mm PLY (A3) | 25.4 (B2) | 0.5 (C1) |
| 6 | Taiji | A3B2C2 | 3 for strength 3 for modulus | 6.35 mm PLY (A3) | 25.4 (B2) | 1.5 (C2) |
| 7 | Taiji | A3B2C3 | 3 for strength 3 for modulus | 6.35 mm PLY (A3) | 25.4 (B2) | 2.5 (C3) |
| 8 | Hexagonal | A1B2C1 | 4 for strength 5 for modulus | 3.18 mm MDF (A1) | 25.4 (B2) | 0.5 (C1) |
| Group | Code | Surface Sheet (A) | Core Thickness (B) (mm) | Loading Speed (C) (mm/min) | Measured Value (MPa) | Standard Deviation (MPa) | Predicted Value (MPa) |
|---|---|---|---|---|---|---|---|
| 1 | A1B1C1 | 3.18mm MDF (A1) | 15.9 (B1) | 0.5 (C1) | 0.24 | 0.03 | 0.22 |
| 2 | A1B2C1 | 3.18mm MDF (A1) | 25.4 (B2) | 0.5 (C1) | 0.23 | 0.02 | 0.22 |
| 3 | A1B3C1 | 3.18mm MDF (A1) | 34.9 (B3) | 0.5 (C1) | 0.21 | 0.11 | 0.22 |
| 4 | A2B2C1 | 3.18mm PLY (A2) | 25.4 (B2) | 0.5 (C2) | 0.21 | 0.03 | 0.22 |
| 5 | A3B2C1 | 6.35mm PLY (A3) | 25.4 (B2) | 0.5 (C1) | 0.23 | 0.01 | 0.22 |
| 6 | A3B2C2 | 6.35mm PLY (A3) | 25.4 (B2) | 1.5 (C2) | 0.23 | 0.01 | 0.22 |
| 7 | A3B2C3 | 6.35mm PLY (A3) | 25.4 (B2) | 2.5 (C3) | 0.24 | 0.04 | 0.22 |
| Group | Code | Surface Sheet (A) | Core Thickness (B) (mm) | Loading Speed (C) (mm/min) | Measured Value (MPa) | Standard Deviation (MPa) | Predicted Value (MPa) |
|---|---|---|---|---|---|---|---|
| 1 | A1B1C1 | 3.18mm MDF (A1) | 15.9 (B1) | 0.5 (C1) | 23.00 | 3.13 | 26.04 |
| 2 | A1B2C1 | 3.18 mm MDF (A1) | 25.4 (B2) | 0.5 (C1) | 22.32 | 2.02 | 26.04 |
| 3 | A1B3C1 | 3.18 mm MDF (A1) | 34.9 (B3) | 0.5 (C1) | 24.83 | 1.60 | 26.04 |
| 4 | A2B2C1 | 3.18 mm PLY (A2) | 25.4 (B2) | 0.5 (C2) | 21.11 | 3.54 | 26.04 |
| 5 | A3B2C1 | 6.35 mm PLY (A3) | 25.4 (B2) | 0.5 (C1) | 24.38 | 4.87 | 26.04 |
| 6 | A3B2C2 | 6.35 mm PLY (A3) | 25.4 (B2) | 1.5 (C2) | 22.04 | 3.07 | 26.04 |
| 7 | A3B2C3 | 6.35 mm PLY (A3) | 25.4 (B2) | 2.5 (C3) | 22.35 | 3.45 | 26.04 |
| The Effect of Core Thickness on the Compression Strength. | ||||||
| Variance Source | Sum of Squares | Degree of Freedom | Mean Squares | F Value | p Value | F Critical Value |
| Between group | 0.0023 | 2 | 0.0012 | 1.45 | 0.29 | F0.05= 4.26 |
| Internal group | 0.0073 | 9 | 0.0008 | |||
| Sum | 0.0096 | 11 | ||||
| The Effect of Core Thickness on the Compression Modulus. | ||||||
| Variance Source | Sum of Squares | Degree of Freedom | Mean Squares | F Value | p Value | F Critical Value |
| Between group | 10.12 | 2 | 5.06 | 0.53 | 0.61 | F0.05= 5.14 |
| Internal group | 57.27 | 6 | 9.54 | |||
| Sum | 67.39 | 8 | ||||
| The Effect of Surface Sheets on the Compression Strength. | ||||||
| Variance Source | Sum of Squares | Degree of Freedom | Mean Squares | F Value | p Value | F Critical Value |
| Between group | 0.0016 | 2 | 0.0008 | 1.03 | 0.40 | F0.05= 4.26 |
| Internal group | 0.0069 | 9 | 0.0008 | |||
| Sum | 0.0085 | 11 | ||||
| The Surface Sheets on the Compression Modulus. | ||||||
| Variance Source | Sum of Squares | Degree of Freedom | Mean Squares | F Value | p value | F critical value |
| Between group | 20.05 | 2 | 10.02 | 0.37 | 0.70 | F0.05= 4.46 |
| Internal group | 217.63 | 8 | 27.20 | |||
| Sum | 237.68 | 10 | ||||
| The Loading Speed on the Compression Strength. | ||||||
| Variance Source | Sum of Squares | Degree of Freedom | Mean Squares | F Value | p Value | F Critical Value |
| Between group | 0.0003 | 2 | 0.0002 | 0.15 | 0.86 | F0.05= 5.14 |
| Internal group | 0.0061 | 6 | 0.0010 | |||
| Sum | 0.0064 | 8 | ||||
| The Loading Speed on the Compression Modulus. | ||||||
| Variance Source | Sum of Squares | Degree of Freedom | Mean Squares | F Value | p Value | F Critical Value |
| Between group | 9.65 | 2 | 4.82 | 0.13 | 0.88 | F0.05= 5.14 |
| Internal group | 224.07 | 6 | 37.35 | |||
| Sum | 233.72 | 8 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, J.; Wu, X.; Oporto-Velasquez, G.; Wang, J.; Dahle, G. Compression Properties and Its Prediction of Wood-Based Sandwich Panels with a Novel Taiji Honeycomb Core. Forests 2020, 11, 886. https://doi.org/10.3390/f11080886
Hao J, Wu X, Oporto-Velasquez G, Wang J, Dahle G. Compression Properties and Its Prediction of Wood-Based Sandwich Panels with a Novel Taiji Honeycomb Core. Forests. 2020; 11(8):886. https://doi.org/10.3390/f11080886
Chicago/Turabian StyleHao, Jingxin, Xinfeng Wu, Gloria Oporto-Velasquez, Jingxin Wang, and Gregory Dahle. 2020. "Compression Properties and Its Prediction of Wood-Based Sandwich Panels with a Novel Taiji Honeycomb Core" Forests 11, no. 8: 886. https://doi.org/10.3390/f11080886
APA StyleHao, J., Wu, X., Oporto-Velasquez, G., Wang, J., & Dahle, G. (2020). Compression Properties and Its Prediction of Wood-Based Sandwich Panels with a Novel Taiji Honeycomb Core. Forests, 11(8), 886. https://doi.org/10.3390/f11080886







