2. Background and Experimental Methods
Currently, there are several known models for canopy rainfall retention during rainfall (excluding stem flow which is no more than 10% of the total interception). The most common models are those of Horton, Merrian, Jackson, Gash, Fan [
1,
2,
3,
4,
5,
6] (
Table 1).
In the present study, the authors carried out a number of experiments including the artificial creation of droplets on leaf surface of individual branches, determination of the maximum mass of water retained and calculation of the leaf surface area of the analyzed samples, determination of the maximum size of droplets and their edge angles, and the determination of the empirical dependencies of the leaf surface area of individual tree species on the maximum mass of water retained.
The Gash and Fan models are considered to be the most modern methods for estimating canopy rainfall interception. For an actual interception of 33.2% of the total amount of precipitation in a single rainfall event, the Gash model estimated an interception ratio of 35.9% and the Fan model estimated a ratio of 53.6%.
The common feature of all models is that they rely on empirical observations of net rainfall rather than on physical modeling of moisture retention on leaf surfaces. None of the models use the objective values of the droplet mass on the lamina and the leaf surface area, which the authors of this study managed to obtain by artificial sprinkling of the branches and weighing of the branches, followed by estimation of the leaf area.
Peak rainfall flood discharges form small watercourses in the forest zone; these are determined by rainfall input to the watershed surface, various losses, slope runoff formation and its transformation into runoff hydrograph at the outlet [
8]. The most significant initial losses are rainfall interception by the canopies of coniferous and deciduous trees, as well as rainfall interception loss by evaporation off the leaf surface of the canopies.
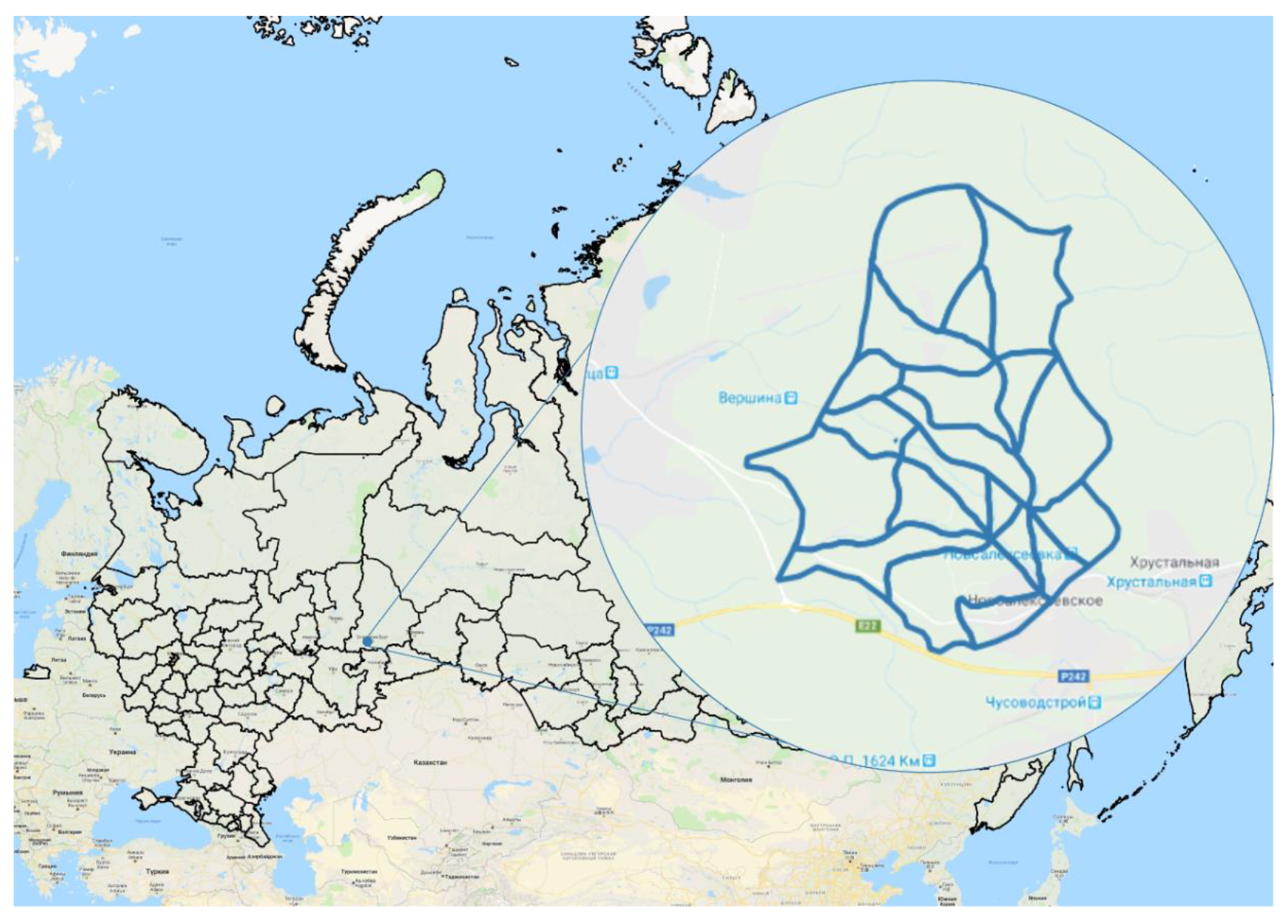
In order to estimate the spatial distribution of rainfall intercepted by the canopies of coniferous tree stands, a set of experimental, cartographic and laboratory studies were performed, as well as meteorological observations for the estimation of water retention on the phytomass of forest-forming species of the Middle Urals. The forest watershed of the Reshetka river, which is near the village of Novoalekseevskoe (watershed area F = 32.0 km
2) was chosen as the experimental site. The watershed, which is located in the Sverdlovsk Region is 31 km west of the Ekaterinburg weather station and is equipped with the Roshydromet observation station, which has been operating since 1946 up to the present day (
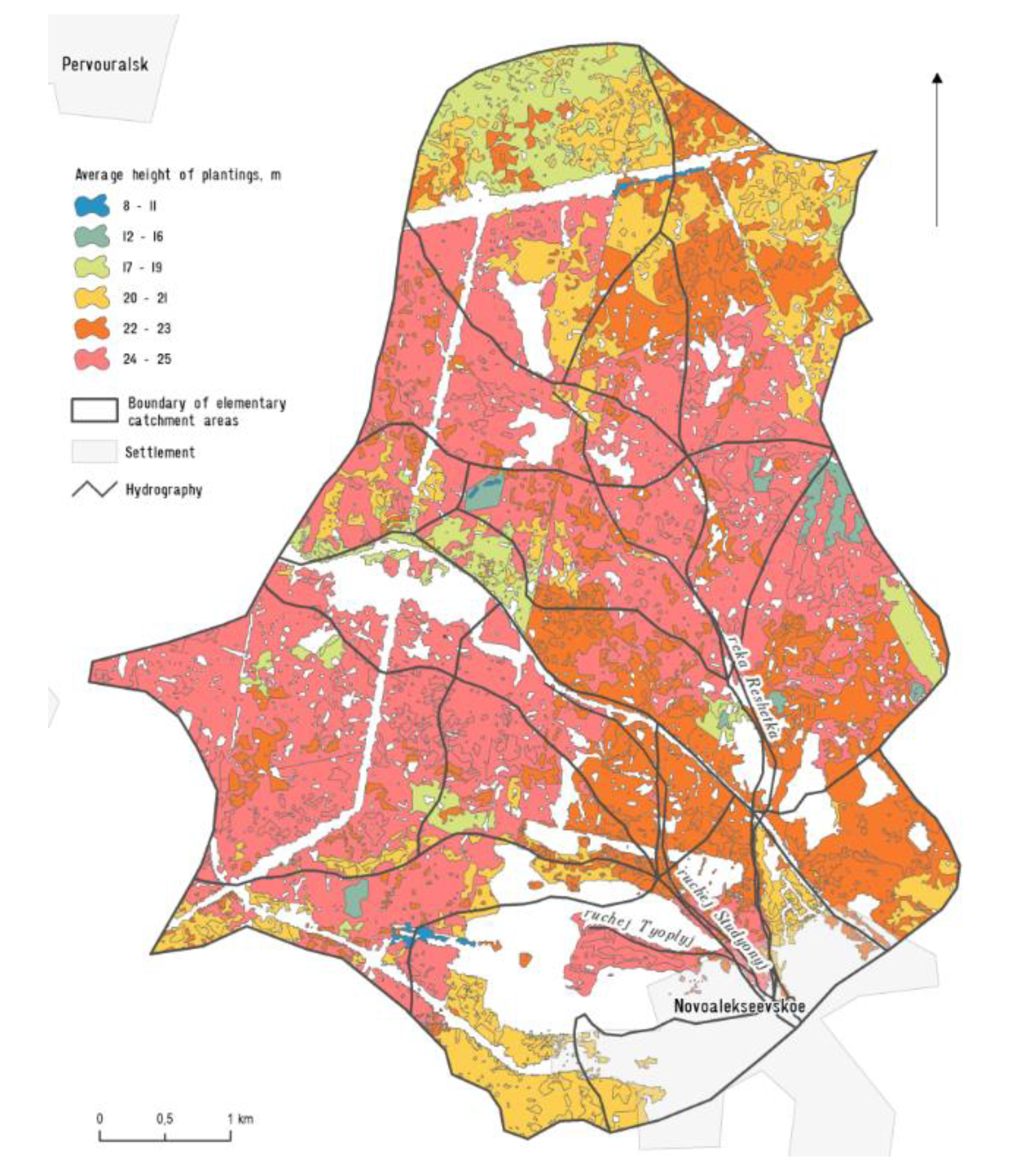
Figure 1). The main hydrographic characteristics of the watershed are: weighted-average watershed slope 33.1%; forest cover 82% (72% of which is pine, 8% is birch, and 2% is other tree species (spruce, aspen, linden, etc.); the lake percentage is 0%; swampiness is 0%; and the average tree height is 22 m. Tree species in the studied area belong to the spring-summer-autumn-green phenotype with a period of winter-spring dormancy. Vegetation lasts from the second decade of May to the first decade of October. The green mass of deciduous trees reaches its maximum growth by the end of the first decade of July. During this time, the leaf surface area is maximal and this period corresponds to the period of maximum rainfall frequency. Field and desktop research was carried out within the reference watershed to clarify the forest stand characteristics (height and species composition) and hydrographic work was also undertaken. Methods of estimating precipitation losses from the tree canopies during periods of rainfall of various intensities were developed and tested.
Liquid (rainfall or condensation) is retained on the tree leaf surface in droplet form and the retention is due to the surface energy at the phase boundaries between “solid” and “gas” and “liquid”.
Because most of the liquid precipitation is retained by coniferous and leaf surfaces, the first task to be solved was to determine the biometric indices of trees:
leaf mass per 1 ha (F1, t/ha)
leaf area index (ratio of leaf area to unit ground surface area) (LAI, ha/ha)
leaf area (total leaf or needle surface area per unit ground area) (LA, ha)
number and average size of leaves and needles.
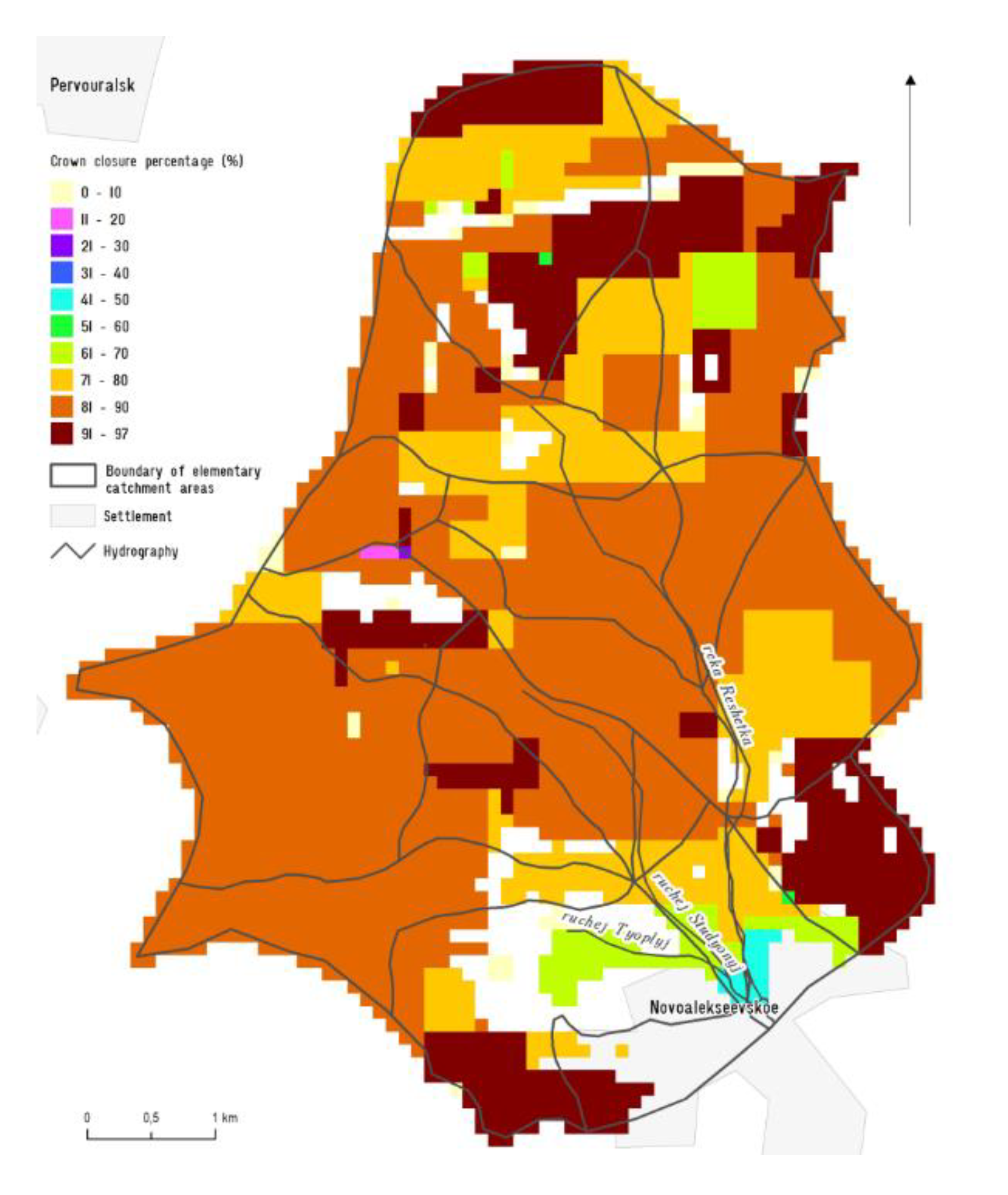
The forest site-quality class, trunk timber reserves and the degree of canopy cover were taken into account.
The approach proposed by Utkin et.al [
9] was used for estimating the average size of needles and leaves. This involves taking representative samples of needles and leaves (100 units), and their measuring them by automated means (scanning of images and subsequent measurements of area, length, width by AutoCAD). Based on the measurements, the statistical parameters (average, the coefficient of variation (Cv), and the coefficient of asymmetry (Cs)) of the needle and leave size of the analyzed species were determined (
Table 2).
Table 2 presents the previous results for deciduous species in [
10] as well as the new results for coniferous species.
The phytomass values of leaves and needles are determined on the basis of growth charts and tables of the biological productivity of tree stands [
11], and the results of field-forest studies on the surface area of forest plants obtained with the use of experimental data [
9], as well as space images and large-scale maps. A site-quality class is determined on the basis of field studies (data on the height and age of a stand) using Orlov’s tables.
Using the databases and empirical dependencies established by A.I. Utkin and others [
9] (
Table 2), LAI was determined on the basis of the phytomass value (F1, t/ha) of stand species as LAI = f (F1).
The total leaf surface area (LA, ha) is defined as:
where
S is the area of the forest plot (ha), and
k is the stand density (in unit fractions).
The stand density and its site-quality class of the model watershed of the Reshetka river were determined on the basis of field surveys, using Orlov’s tables.
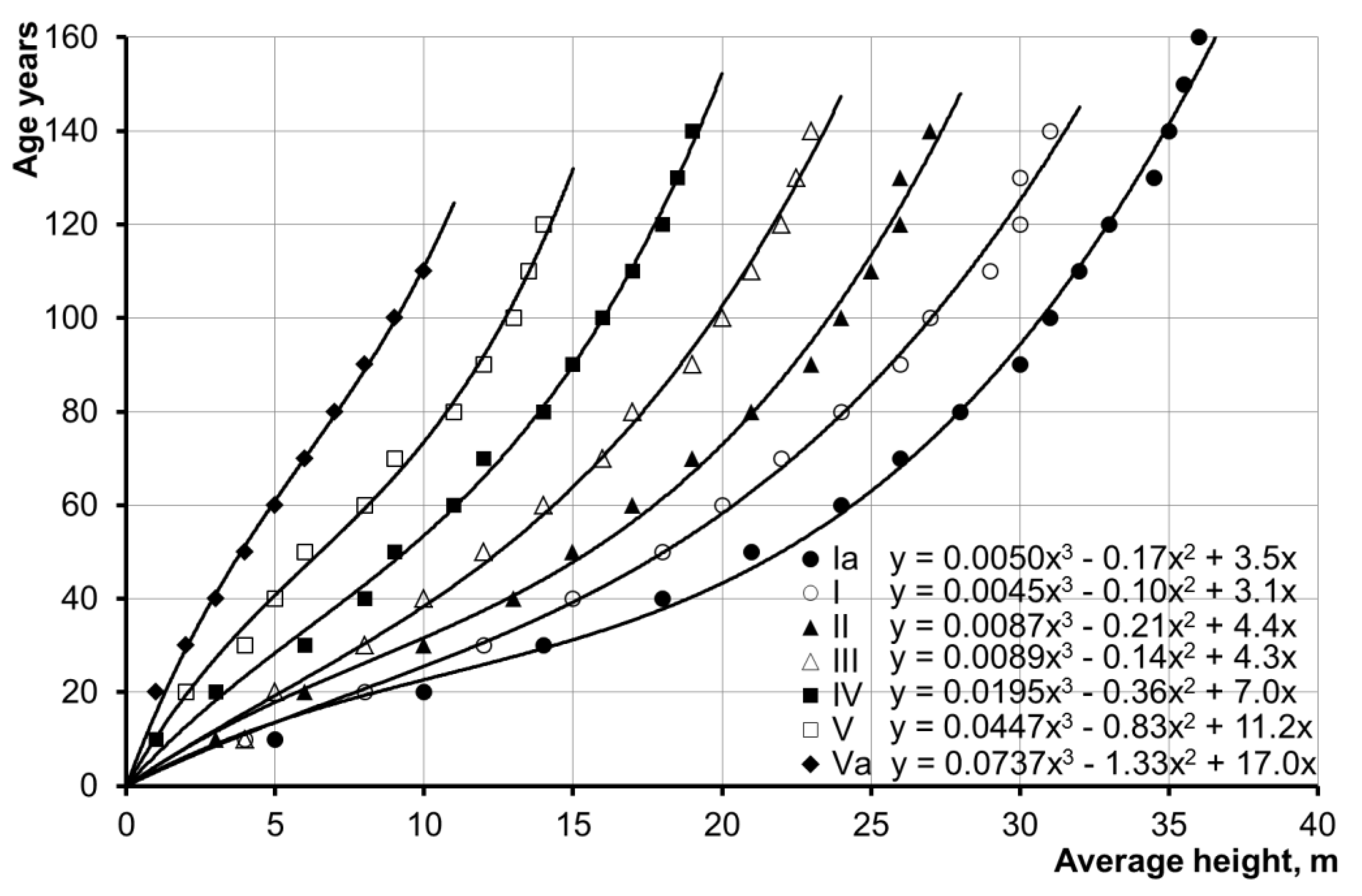
The phytomass value (F1, t/ha) for watershed areas with different species composition has been determined depending on their age and a site-quality class. Orlov’s tables were put into analytical form, and the estimation of forest age of a certain site-quality class was made on the basis of stand height data (
Figure 2). The obtained dependencies, which are built on the basis of the site-quality class tables of Orlov, are used in Russia for forest taxation work. However, they are in good agreement with the data obtained for Scots pine presented by Cieszewski et al. in 2007 [
12].
According to the fieldwork materials, the prevailing site-quality class for the model watershed is II. On the basis of works by Shvidenko et al. [
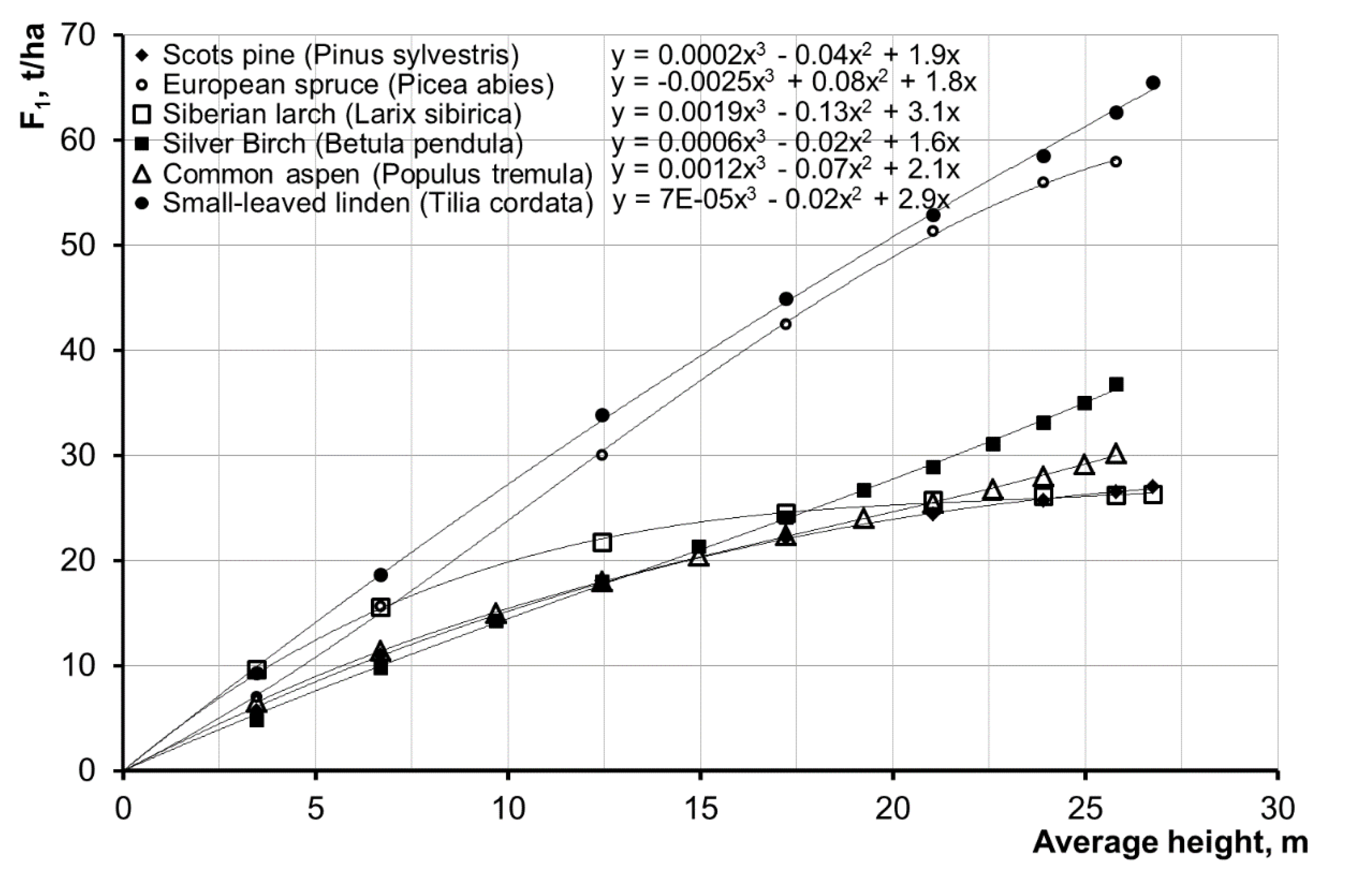
11], the relationship between the phytomass value (green mass and the mass of branches) (F1, t/ha) and the average height of tree stands of different species composition with the site-quality class II was determined analytically. Pine stands prevail in the watershed area of the Reshetka river whereas the share of spruce is insignificant (not more than 10% of the total area of coniferous plantations). Among deciduous species, birch and aspen prevail. Forests where the share of deciduous or coniferous trees is not less than 25% are considered as a mix of deciduous or coniferous forests. On the basis of these ratios, the dependency of phytomass on the average height of tree stands was estimated (
Figure 3). The presented dependences are characterized as high quality (determination coefficient
R2 more than 0.95 in each cases).
As can be seen, for the considered watershed under conditions where the tree stands are composed of rather homogeneous species, the dependencies of F
1 values on the forest average height are very similar and can be described with a single equation in the form:
where H is the tree height.
Taking into account the above-mentioned dependencies of tree height on age (
Figure 2), the estimating equation for F
1 for site-quality class II is:
where H is the tree height.
Equation (2) is preferable to use in the calculations, since it directly relates the height of the trees to the value F
1. There is no need to evaluate the site-quality class. According to Eichhorn’s rule, the total production volume of a given tree species at a given stand height should be identical for all site classes. Eichhorn [
14] originally discovered that the volume of crop trees in lightly thinned stands of European silver fir (Abies alba Mill.) is a function only of stand height (e.g., irrespective of age and basal area). This was subsequently confirmed for other tree species.
Experiments on Maximum Rainfall Retention by the Canopies of Tree Stands. Modeling of Rainfall Interception by Conifer Needles
In order to estimate the water retention value, a set of experiments on artificial sprinkling of parts of tree canopies (branches) was carried out. The research focused on the study of nine deciduous and coniferous species growing in the watershed area, e.g., birch, aspen, lime tree, pine and fir, in the period of their maximum green mass growth (the end of June 2018). Branches were selected from different parts of the canopies of the analyzed tree species to be sprinkled and weighed in order to determine the moisture mass. The age of the trees range from 40 to 60 years old and the height range from 16 to 20 m. From each tree, 10–20 branches weighing from 0.4 to 5.0 kg were used. Natural branch weight was determined under dry weather conditions and was accurate within 5 g (with the use of accuracy class III scales, OKP 42 7451, GOST 29329-92 with a permissible measurement error of +/− 5g, the error in measuring water mass on the leaves at the moment of maximum retention did not exceed 11.1% with the average being 4.3%). Then, a branch was artificially sprinkled until the maximum mass was stabilized. The maximum moisture retention value was determined on the basis of the difference between the mass of the branch under dry and wet conditions.
Leaf surface area was calculated as follows: the number of leaves on the analyzed branch was counted manually, then a sample set of 50 leaves from different parts of the branch was formed, and the average leaf area of the analyzed sample set was calculated (with a measurement error of no more than 2 mm
2). The statistical error of determining the area did not exceed 3%. The area and vein length were measured for each leaf in a sample set, followed by the calculation of the statistical parameters. Only the area and length were measured for conifer needles and the average value was used for calculations (
Table 2).
The observations made under natural and laboratory conditions showed that water retention by the tree canopy only occurs due to droplets and wetting branches (no more than 10% of total water retention).
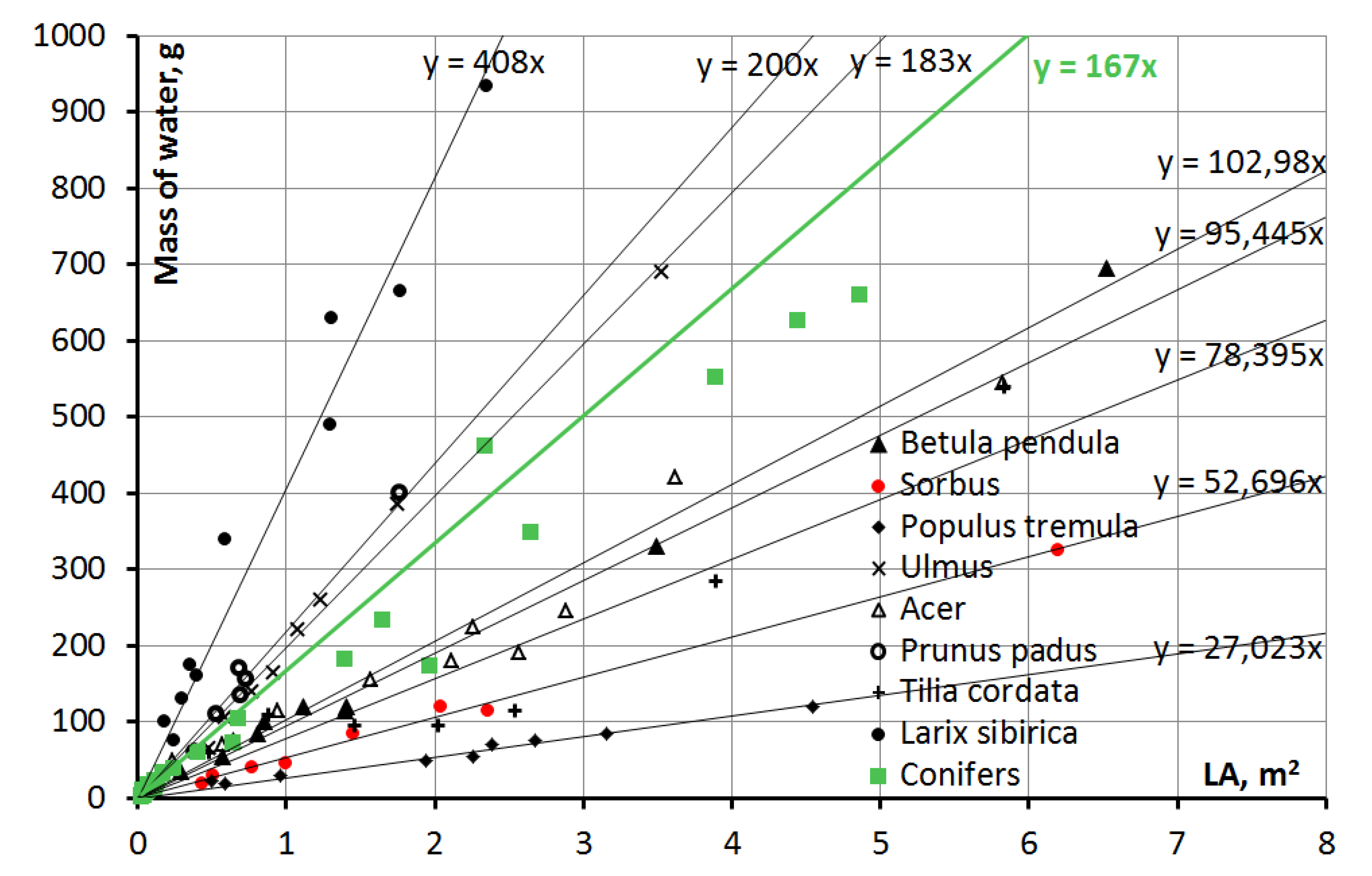
Based on the experiments on artificial sprinkling of different-sized branches, the empirical dependency of maximum rainfall retention on leaf surface area was obtained (
Figure 4).
The dependencies are characterized by good quality (with correlation coefficients greater than 0.9 in all cases: Larix sibirica, Tilia cordata = 0.97; Conifers, Prunus padus, Sorbus, Populus tremula = 0.98; Ulmus, Betula pendula, Acer = 0.99) and grouped into separate bundles. The dependency analysis led us to conclude that specific water retention of deciduous trees (the first coefficient showing the mass of water per 1 m2 of the leaf surface) is determined by the leaf venation type of the analyzed species. Leaves with pinnately-netted venation have larger retention values as compared to leaves with pennate venation.
In order to confirm this assumption, the vein length of the leaf samples was measured by means of computer programs (AutoCAD 2007). The obtained measurement results were published in scientific papers by Klimenko et al. [
10,
15] (
Table 3 shows previously published data on deciduous species and new data on coniferous species). The average leaf vein density and its correlation to a specific moisture retention for a given species was determined by the total length of visible veins and “normal” (average for the representative sample) leaf area. The dependency is considered to be of good quality (correlation coefficient 0.89).
The Sentinel-2A satellite image captured on the 5 June, 2018 was used as the source of spatial data. The choice of the date and season stems from the fact that the first half of May is the period prior to active growth of deciduous phytomass, hence it is the best possible time to use the image to determine the share of coniferous trees in the tree stand structure. Only spectral channels with spatial resolution of 10 m (near infrared, red, green) were used for classification. The blue channel was excluded because it is strongly influenced by atmospheric conditions.
Data processing was performed with the use of the licensed software package ArcGIS 10.4 and ToolBox application. Sentinel-2A satellite was launched as a part of the Copernicus program by the European Space Agency in June 2015. (ESA Introducing Sentinel-2,
http://www.esa.int/Our_Activities/Observing_the_Earth/Copernicus/ Sentinel-2/Introducing_Sentinel-2). This satellite is equipped with an optoelectronic spectral sensor for remote surveying of the Earth with a resolution from 10 to 60 m in the visible, near infrared and short-wave infrared spectral zones, including 13 spectral channels. It also allows repeated surveys every five days and makes a 290 km wide swath. The remote sensing data are actively used in mapping and monitoring of forest species composition [
16].
To create a training set of samples, the original image of the synthesis of channels “red colors” (8-4-3; near IR, red, green) was used. Training samples were collected using the toolbar “Image Classification” of the ArcGIS 10.4 software product (ESRI (Environmental Systems Research Institute, licensed version) and four classes for forest cover and five classes for non-forest areas were identified (
Figure 5). From 5 to 15 training samples were selected from different parts of the image for each class. The estimation of class separability by spectral features was carried out using scattering diagrams. After receiving the training set of samples, a signature file containing the distribution of pixel intensity for each class was created.
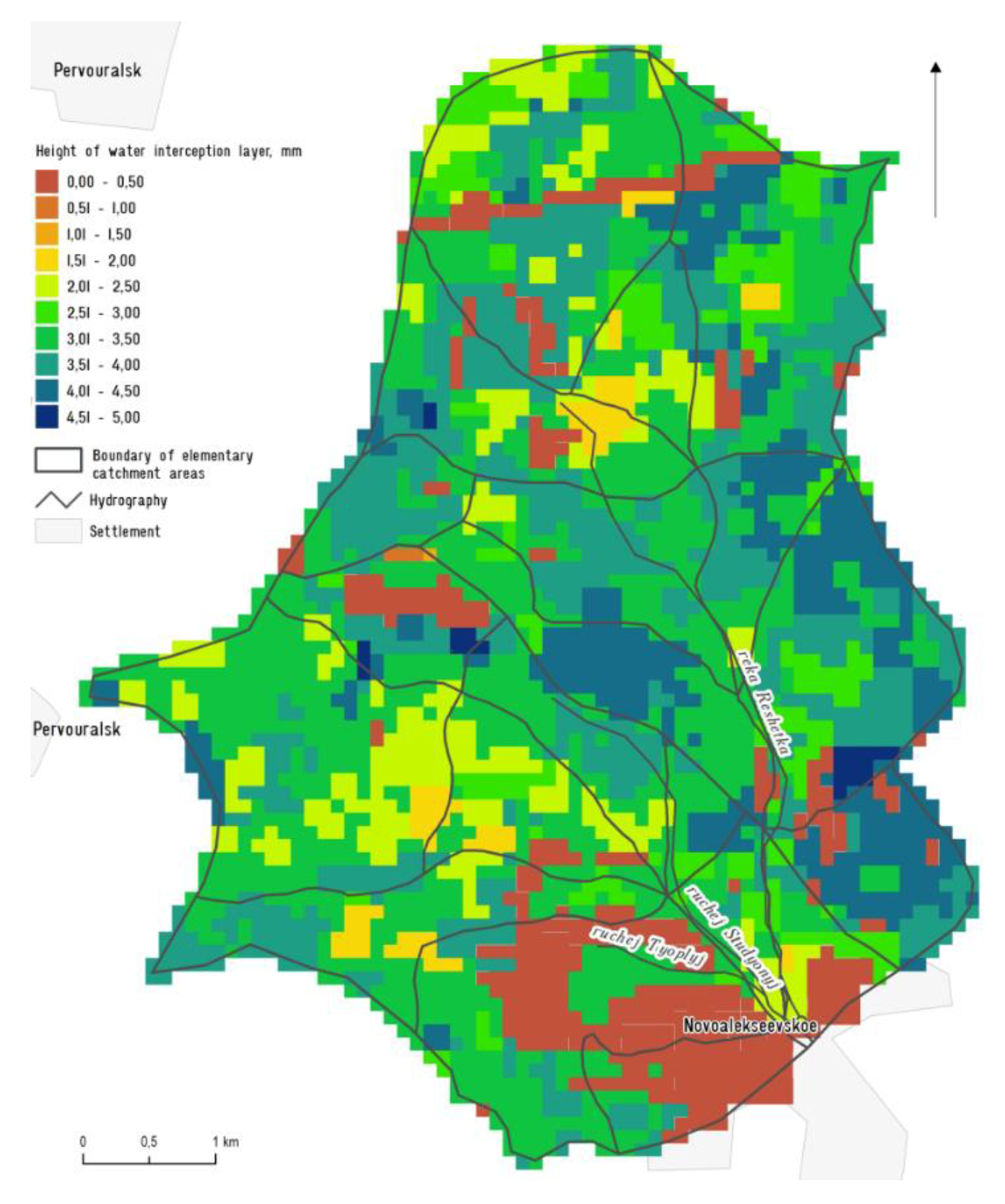
In order to estimate the depth of precipitation distributed in space h (mm) and irrecoverably retained by tree canopies, the following ratio, which proceeded from the dependencies presented in
Figure 3 is used:
where k is the stand density, and γ is specific water retention (water mass (kg) per 1 m
2 of leaf surface area LA). The specific water retention value γ for forest-forming species is calculated as the weighted average proceeding from the share of species in the watershed area, based on empirical dependencies:
γ = 167 for coniferous stands, γ = 92.7 for deciduous stands, γ = 108 for mixed deciduous stands, and γ = 151 for mixed coniferous stands.
4. Discussion
The issues related to estimating canopy rainfall retention have been investigated by various authors. However, most research is devoted to precipitation losses for long periods, and few studies focus on precipitation interception in a single rainfall event.
The most important regularities of rainfall redistribution under the forest canopy were revealed at the beginning of the 20th century in the studies of Ebermeyer, Hoppe, Nesterov, Okhlyabinin, and others [
1]. The retention of precipitation by vegetation cover and its subsequent evaporation are directly related to the size and properties of the wetted surface. The studies of different authors show that significant differences in maximum canopy water retention. According to Bele [
19,
20], spruce stands can intercept up to 3.6 mm in a single rainfall event. Rakhmanov [
21] determined that the water retention capacity for coniferous stands (spruce, fir) is between 2–4 mm (in some cases up to 6–8 mm).
Total interception is dependent on the age, composition, and volume of the area of the leaf surface and the amount of precipitation. Light rains (0.5–1.5 mm) are completely intercepted by tree stand canopies, and the maximum moisture retention capacity of high-density coniferous trees is 10–12 mm [
22].
Point estimates of the layer of single rainfall interception found in this study differ slightly from the results obtained earlier. The difference stems from the fact that the authors carried out artificial sprinkling of tree species to understand the hydrological processes, and the volume of the moisture retention was determined by weight. In other studies, these values were determined by making observations of net and gross rainfalls, which results in a number of uncertainties related to the choice of precipitation measurement points under the canopies of individual trees.
In recent years, research to determine moisture retention values for such species as Ulmus processra, Platanus×acerifolia and Corymbia maculata per leaf surface area has been covered by Baptista et al. (2018) [
23]. It was found that the interception value is determined by the leaf surface area and precipitation intensity. Thus, methods similar to those of the authors of this study were used to determine the leaf surface area. However, mapping the interception storage capacity mapping of the whole river watershed has never been carried out before.
The initial rainfall interception layer can reach 5.9 mm in forest-covered areas. With the change in age and site-quality class of natural tree stands, the precipitation interception layer can be as high as 5–8 mm per ha or even more. Due to the uneven distribution of forest-forming species in the watershed area, the amount of precipitation actually falling under the canopy differs significantly from the amount of precipitation falling on the canopy. This was the first case in the world where mapping of the spatial distribution of precipitation losses by canopies was carried out.
5. Conclusions
This article contains the published experimental data regarding the conservation of rainfall by coniferous species (compared to Klimenko et al. [
10], whose data only applied to deciduous tree species). Mapping methods for experimental mapping for experimental catchment were used.
Based on a series of experiments on artificial sprinkling of tree species, the maximum values for the specific moisture retention on the leaf surface area were determined.
Leaf surface area was determined for the “normal” leaf surface in a representative sample (statistical parameters of the leaf area, i.e., average, coefficients of variation and asymmetry were determined for the sample). The number of leaves on the experimental branch was determined manually. Statistical errors for determining the total area did not exceed 11%. The error for determining the mass of moisture retained were 4.3%.
The values obtained for the characteristics of the layer of precipitation retained by canopies were visualized on maps. Such maps were based on the methodology developed by the authors and can be used to calculate the elements pertaining to the water balance in mixed forest areas, including the maximum rainfall discharge from forest watershed. In addition, taking into account the fact that rain precipitation retained by canopies is only consumed by evaporation, this method of estimating the spatial distribution of rainfall losses can be used to estimate monthly amounts of liquid precipitation as corrections to daily rainfall values.
Based on the experiments on artificial branch sprinkling, the parameters for the dependency of the leaf surface area (LA, m2) on the maximum mass of retained water (m, d) were established. On the basis of the dependencies and the data on the leaf surface area of the estimated watersheds, it is possible to calculate the interception value during a rainfall as well as evaporation losses from the canopy area distributed in space.
The observations of the precipitation under coniferous canopies (by four rain gauges) and in open areas (by one rain gauge) in October 2017 confirmed the calculated water retention values [
15]. According to the data provided by M-99 field rain gauges, spruce canopies (80 years, site-quality class II) intercept 2–4 mm of rainfall. Meteorological observations need to be continued along with the involvement of rain recorders (pluviographs).
The method developed by the authors for estimating and mapping irrecoverable rainfall losses by tree canopies can be used in modeling the flood runoff of small rivers in the Ural forest zone. Taking into account the value of irrecoverable precipitation losses from the stand canopies allows us to considerably increase the accuracy of flood flow calculations for small rivers using genetic methods.