Mortality in Forested Ecosystems: Suggested Conceptual Advances
Abstract
1. Introduction
2. The Nature of Mortality
3. Mortality as a Continuum
4. Describing Mortality Statistically
5. Causes of Mortality
6. Modelling Mortality
7. Conclusions
8. Patents
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Input Model
Appendix A.2. Scaling Model
Appendix A.3. Cause Model
Appendix A.4. Multi-Agent Hemlock Mortality Model
References
- Franklin, J.F.; Shugart, H.H.; Harmon, M.E. Tree death as an ecological process. Bioscience 1987, 37, 550–556. [Google Scholar] [CrossRef]
- Lancaster, K.F.; Leak, W.B. A Silvicultural Guide for White Pine in the Northeast; General Technical Report 41; Department of Agriculture, Forest Service, Northeastern Forest Experiment Station: Broomall, PA, USA, 1978; pp. 1–13.
- Kerr, G.; Haufe, J. Thinning Practice: A Silvicultural Guide; Forestry Commission: Bristol, UK, 2011; pp. 1–54.
- Prestemon, J.P.; Wear, D.N.; Stewart, F.J.; Holmes, T.P. Wildfire, timber salvage, and the economics of expediency. For. Policy. Econ. 2006, 8, 312–322. [Google Scholar] [CrossRef]
- Breshears, D.D.; Cobb, N.S.; Rich, P.M.; Price, K.P.; Allen, C.D.; Balice, R.G.; Romme, W.H.; Kastens, J.H.; Floyd, M.L.; Belnap, J.; et al. Regional vegetation die-off in response to global-change-type drought. Proc. Natl. Acad. Sci. USA 2005, 102, 15144–15148. [Google Scholar] [CrossRef] [PubMed]
- Hogg, E.H.; Brandt, J.P.; Michaelian, M. Impacts of a regional drought on the productivity, dieback, and biomass of western Canadian aspen forests. Can. J. For. Res. 2008, 38, 1373–1384. [Google Scholar] [CrossRef]
- Van Mantgem, P.J.; Stephenson, N.L.; Byrne, J.C.; Daniels, L.D.; Franklin, J.F.; Fulé, P.Z.; Harmon, M.E.; Larson, A.J.; Smith, J.M.; Taylor, A.H.; et al. Widespread increase of tree mortality rates in the western United States. Science 2009, 323, 521–524. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.T.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Carnicer, J.; Coll, M.; Ninyerola, M.; Pons, X.; Sanchez, G.; Penuelas, J. Widespread crown condition decline, food web disruption, and amplified tree mortality with increased climate change-type drought. Proc. Natl. Acad. Sci. USA 2011, 108, 1474–1478. [Google Scholar] [CrossRef]
- Michaelian, M.; Hogg, E.H.; Hall, R.J.; Arsenault, E. Massive mortality of aspen following severe drought along the southern edge of the Canadian boreal forest. Glob. Chang. Boil. 2010, 17, 2084–2094. [Google Scholar] [CrossRef]
- Peng, C.; Ma, Z.; Lei, X.; Zhu, Q.; Chen, H.; Wang, W.; Liu, S.; Li, W.; Fang, X.; Zhou, X. A drought-induced pervasive increase in tree mortality across Canada’s boreal forests. Nat. Clim. Chang. 2011, 1, 467–471. [Google Scholar] [CrossRef]
- Williams, A.P.; Allen, C.D.; Macalady, A.K.; Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Swetnam, T.W.; Rauscher, S.A.; Seager, R.; Grissino-Mayer, H.D.; et al. Temperature as a potent driver of regional forest drought stress and tree mortality. Nat. Clim. Chang. 2012, 3, 292–297. [Google Scholar] [CrossRef]
- Allen, C.D.; Breshears, D.D.; McDowell, N.G. On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 2015, 6, 1–55. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Stehman, S.V.; Schroeder, T.A.; Bell, D.M.; Masek, J.G.; Huang, C.; Meigs, G.W. Forest disturbance in the conterminous United States from 1985–2012, The emerging dominance of forest decline. For. Ecol. Manag. 2016, 360, 242–252. [Google Scholar] [CrossRef]
- Orwig, D.A.; Foster, D.R.; Mausel, D.L. Landscape patterns of hemlock decline in New England due to the introduced hemlock woolly adelgid. J. Biogeogr. 2002, 29, 1475–1487. [Google Scholar] [CrossRef]
- Meddens, A.J.; Hicke, J.A.; Ferguson, C.A. Spatiotemporal patterns of observed bark beetle-caused tree mortality in British Columbia and the western United States. Ecol. Appl. 2012, 22, 1876–1891. [Google Scholar] [CrossRef]
- Herms, D.A.; McCullough, D.G. Emerald ash borer invasion of North America, history, biology, ecology, impacts, and management. Annu. Rev. Èntomol. 2014, 59, 13–30. [Google Scholar] [CrossRef] [PubMed]
- Perry, K.; Herms, D.; Klooster, W.; Smith, A.; Hartzler, D.; Coyle, D.; Gandhi, K. Downed coarse woody debris dynamics in ash (Fraxinus spp.) stands invaded by emerald ash borer (Agrilus planipennis Fairmaire). Forests 2018, 9, 191. [Google Scholar] [CrossRef]
- Meentemeyer, R.K.; Rank, N.E.; Shoemaker, D.A.; Oneal, C.B.; Wickland, A.C.; Frangioso, K.M.; Rizzo, D.M. Impact of sudden oak death on tree mortality in the Big Sur ecoregion of California. Boil. Invasions 2007, 10, 1243–1255. [Google Scholar] [CrossRef]
- Schlarbaum, S.E.; Hebard, F.; Spaine, P.C.; Kamalay, J.C. Three American tragedies, chestnut blight, butternut canker, and Dutch elm disease. In Exotic Pests of Eastern Forests Conference Proceedings1997 April 8–10; Britton, K.O., Ed.; US Forest Service and Tennessee Exotic Pest Plant Council: Nashville, TN, USA, 1998; pp. 45–54. [Google Scholar]
- La Porta, N.; Capretti, P.; Thomsen, I.M.; Kasanen, R.; Hietala, A.M.; Von Weissenberg, K. Forest pathogens with higher damage potential due to climate change in Europe. Can. J. Plant Pathol. 2008, 30, 177–195. [Google Scholar] [CrossRef]
- Westerling, A.L.; Hidalgo, H.G.; Cayan, D.R.; Swetnam, T.W. Warming and earlier spring increase western US forest wildfire activity. Science 2006, 313, 940–943. [Google Scholar] [CrossRef]
- Brando, P.M.; Balch, J.K.; Nepstad, D.C.; Morton, D.C.; Putz, F.E.; Coe, M.T.; Silvério, D.; Macedo, M.N.; Davidson, E.A.; Nóbrega, C.C.; et al. Abrupt increases in Amazonian tree mortality due to drought–fire interactions. Proc. Natl. Acad. Sci. USA 2014, 111, 6347–6352. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.; Baker, D.B.; Zeng, H.; Henkel, T.K.; Chambers, J.Q. Assessing hurricane-induced tree mortality in US Gulf Coast forest ecosystems. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Masek, J.G.; Huang, C.; Wolfe, R.; Cohen, W.; Hall, F.; Kutler, J.; Nelson, P. North American forest disturbance mapped from a decadal Landsat record. Remote. Sens. Environ. 2008, 112, 2914–2926. [Google Scholar] [CrossRef]
- Hartmann, H.; Schuldt, B.; Sanders, T.G.; Macinnis-Ng, C.; Boehmer, H.J.; Allen, C.D.; Bolte, A.; Crowther, T.W.; Hansen, M.C.; Medlyn, B.E.; et al. Monitoring global tree mortality patterns and trends. Report from the VW symposium ‘Crossing scales and disciplines to identify global trends of tree mortality as indicators of forest health’. New Phytol. 2018, 217, 984–987. [Google Scholar] [CrossRef] [PubMed]
- Harmon, M.E.; Franklin, J.F.; Swanson, F.J.; Sollins, P.; Lattin, J.D.; Anderson, N.H.; Gregory, S.V.; Cline, S.P.; Aumen, N.G.; Sedell, J.R.; et al. The ecology of coarse woody debris in temperate ecosystems. Adv. Ecol. Res. 1986, 15, 133–302. [Google Scholar]
- Bamber, R.K. Heartwood, its function and formation. Wood Sci. Technol. 1976, 10, 1–8. [Google Scholar] [CrossRef]
- Sobrado, M.A. Cost-benefit relationships in deciduous and evergreen leaves of tropical dry forest species. Funct. Ecol. 1991, 5, 608. [Google Scholar] [CrossRef]
- Eamus, D.; Myers, B.; Duff, G.; Williams, R. A cost-benefit analysis of leaves of eight Australian savanna tree species of differing leaf life-span. Photosynthetica 2000, 36, 575–586. [Google Scholar] [CrossRef]
- Villar, R.; Merino, J. Comparison of leaf construction costs in woody species with differing leaf life-spans in contrasting ecosystems. New Phytol. 2001, 151, 213–226. [Google Scholar] [CrossRef]
- Marchin, R.; Zeng, H.; Hoffmann, W. Drought-deciduous behavior reduces nutrient losses from temperate deciduous trees under severe drought. Oecologia 2010, 163, 845–854. [Google Scholar] [CrossRef]
- Mäkinen, H. Growth, suppression, death, and self-pruning of branches of Scots pine in southern and central Finland. Can. J. For. Res. 1999, 29, 585–594. [Google Scholar] [CrossRef]
- Kint, V.; Hein, S.; Campioli, M.; Muys, B. Modelling self-pruning and branch attributes for young Quercus robur L. and Fagus sylvatica L. trees. For. Ecol. Manag. 2010, 260, 2023–2034. [Google Scholar] [CrossRef]
- Shugart, H.H. A Theory of Forest Dynamics, the Ecological Implications of Forest Succession Models; Springer: New York, NY, USA; Berlin/Heidelberg, Germany; Tokyo, Japan, 1984; Volume 278, pp. 1–278. [Google Scholar]
- Zhu, K.; Woodall, C.W.; Ghosh, S.; Gelfand, A.E.; Clark, J.S. Dual impacts of climate change, forest migration and turnover through life history. Glob. Chang. Boil. 2013, 20, 251–264. [Google Scholar] [CrossRef]
- Duvigneaud, P.; Denaeyer-De Smet, S. Biological cycling of minerals in temperate deciduous forests. In Analysis of Temperate Forest Ecosystems; Reichle, D.E., Ed.; Springer: Berlin/Heidelberg, Germany, 1973; Volume 1, pp. 199–225. [Google Scholar]
- Beck, C.B. The appearance of gymnospermous structure. Boil. Rev. 1970, 45, 379–399. [Google Scholar] [CrossRef]
- Chapman, C.R.; Morrison, D. Impacts on the Earth by asteroids and comets, assessing the hazard. Nature 1994, 367, 33–40. [Google Scholar] [CrossRef]
- Pickett, S.T.; White, P.S. The Ecology of Natural Disturbance and Patch Dynamics; Academic Orlando: Orlando, FL, USA, 1985; pp. 1–472. [Google Scholar]
- Bormann, F.H.; Likens, G.E. Catastrophic disturbance and the steady state in northern hardwood forests, A new look at the role of disturbance in the development of forest ecosystems suggests important implications for land-use policies. Am. Sci. 1979, 67, 660–669. [Google Scholar]
- Lutz, J.A.; Halpern, C.B. Tree mortality during early forest development, a long-term study of rates, causes, and consequences. Ecol. Monogr. 2006, 76, 257–275. [Google Scholar] [CrossRef]
- Farinella, P.; Foschini, L.; Froeschlé, C.; Gonczi, R.; Jopek, T.J.; Longo, G.; Michel, P. Probable asteroidal origin of the Tunguska Cosmic Body. Astron. Astrophys. 2001, 377, 1081–1097. [Google Scholar] [CrossRef]
- Collins, B.D.; Dunne, T. Effects of forest land management on erosion and revegetation after the eruption of Mount St. Helens. Earth Surf. Process. Landforms 1988, 13, 193–205. [Google Scholar] [CrossRef]
- Harmon, M.E.; Pabst, R.J. The Long-Term Effects of Wind Disturbance on a Sitka Spruce-Western Hemlock Forest. Forests 2019, 10, 119. [Google Scholar] [CrossRef]
- Manion, P.D. Tree Disease Concepts; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1981; pp. 1–399. [Google Scholar]
- Lieutier, F. Mechanisms of resistance in conifers and bark beetle attack strategies. In Mechanisms and Deployment of Resistance in Trees to Insects; Wagner, M.R., Clancy, K.M., Lieutier, F., Paine, T.D., Eds.; Springer: Dordrecht, The Netherlands, 2002; pp. 31–77. [Google Scholar]
- Shore, T.L.; Safranyik, L.; Hawkes, B.C.; Taylor, S.W. Effects of the mountain pine beetle on lodgepole pine stand structure and dynamics. In The Mountain Pine Beetle, a Synthesis of Biology, Management and Impacts on Lodgepole Pine; Safranyik, L., Wilson, B., Eds.; Canadian Forest Service: Victoria, BC, Canada, 2006; pp. 94–114. [Google Scholar]
- Solheim, H.; Safranyik, L. Pathogenicity to Sitka spruce of Ceratocystis rufipenni and Leptographium abietinum blue-stain fungi associated with the spruce beetle. Can. J. For. Res. 1997, 27, 1336–1341. [Google Scholar] [CrossRef]
- Anderegg, L.D.; Anderegg, W.R.; Berry, J.A. Not all droughts are created equal, translating meteorological drought into woody plant mortality. Tree Physiol. 2013, 33, 672–683. [Google Scholar] [CrossRef] [PubMed]
- Metcalf, C.J.E.; McMahon, S.E.; Clark, J.S. Overcoming data sparseness and parametric constraints in modeling of tree mortality, a new nonparametric Bayesian model. Can. J. For. Res. 2009, 39, 1677–1687. [Google Scholar] [CrossRef]
- Clark, J.S.; Bell, D.M.; Hersh, M.H.; Nichols, L. Climate change vulnerability of forest biodiversity, climate and resource tracking of demographic rates. Glob. Chang. Boil. 2011, 17, 1834–1849. [Google Scholar] [CrossRef]
- Monserud, R.A. Simulation of forest tree mortality. For. Sci. 1976, 22, 438–444. [Google Scholar]
- Lines, E.R.; Coomes, D.A.; Purves, D.W. Influences of forest structure, climate and species composition on tree mortality across the eastern US. PLoS ONE 2010, 5, e13212. [Google Scholar] [CrossRef]
- Hamilton, D.A., Jr. Extending the range of applicability of an individual tree mortality model. Can. J. For. Res. 1990, 20, 1212–1218. [Google Scholar] [CrossRef]
- Woodall, C.W.; Grambsch, P.L.; Thomas, W. Applying survival analysis to a large-scale forest inventory for assessment of tree mortality in Minnesota. Ecol. Model. 2005, 189, 199–208. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. Modeling individual tree mortality for Austrian forest species. For. Ecol. Manag. 1999, 113, 109–123. [Google Scholar] [CrossRef]
- Wyckoff, P.H.; Clark, J.S. Predicting tree mortality from diameter growth, a comparison of maximum likelihood and Bayesian approaches. Can. J. Forest. Res. 2000, 30, 156–167. [Google Scholar] [CrossRef]
- Temesgen, H.; Mitchell, S.J. An individual-tree mortality model for complex stands of southeastern British Columbia. West. J. Appl. For. 2005, 20, 101–109. [Google Scholar] [CrossRef]
- Eid, T.; Tuhus, E. Models for individual tree mortality in Norway. For. Ecol. Manag. 2001, 154, 69–84. [Google Scholar] [CrossRef]
- Reinhardt, E.D.; Keane, R.E.; Brown, J.K. Modeling fire effects. Int. J. Wildland Fire 2001, 10, 373. [Google Scholar] [CrossRef]
- Rich, R.L.; Frelich, L.E.; Reich, P.B. Wind-throw mortality in the southern boreal forest, Effects of species, diameter and stand age. J. Ecol. 2007, 95, 1261–1273. [Google Scholar] [CrossRef]
- Bell, D.M.; Bradford, J.B.; Lauenroth, W.K. Scale dependence of disease impacts on quaking aspen (Populus tremuloides) mortality in the southwestern United States. Ecology 2015, 96, 1835–1845. [Google Scholar] [CrossRef] [PubMed]
- van Mantgem, P.J.; Falk, D.A.; Williams, E.C.; Das, A.J.; Stephensen, N.L. The influence of pre-fire growth patterns on post-fire tree mortality for common conifers in western US parks. Int. J. Wildland Fire 2020. [Google Scholar] [CrossRef]
- Bell, D.M.; Pabst, R.J.; Shaw, D. Tree growth declines and mortality were associated with a parasitic plant during warm and dry climatic conditions in a temperate coniferous forest ecosystem. Glob. Chang. Boil. 2019, 26, 1714–1724. [Google Scholar] [CrossRef]

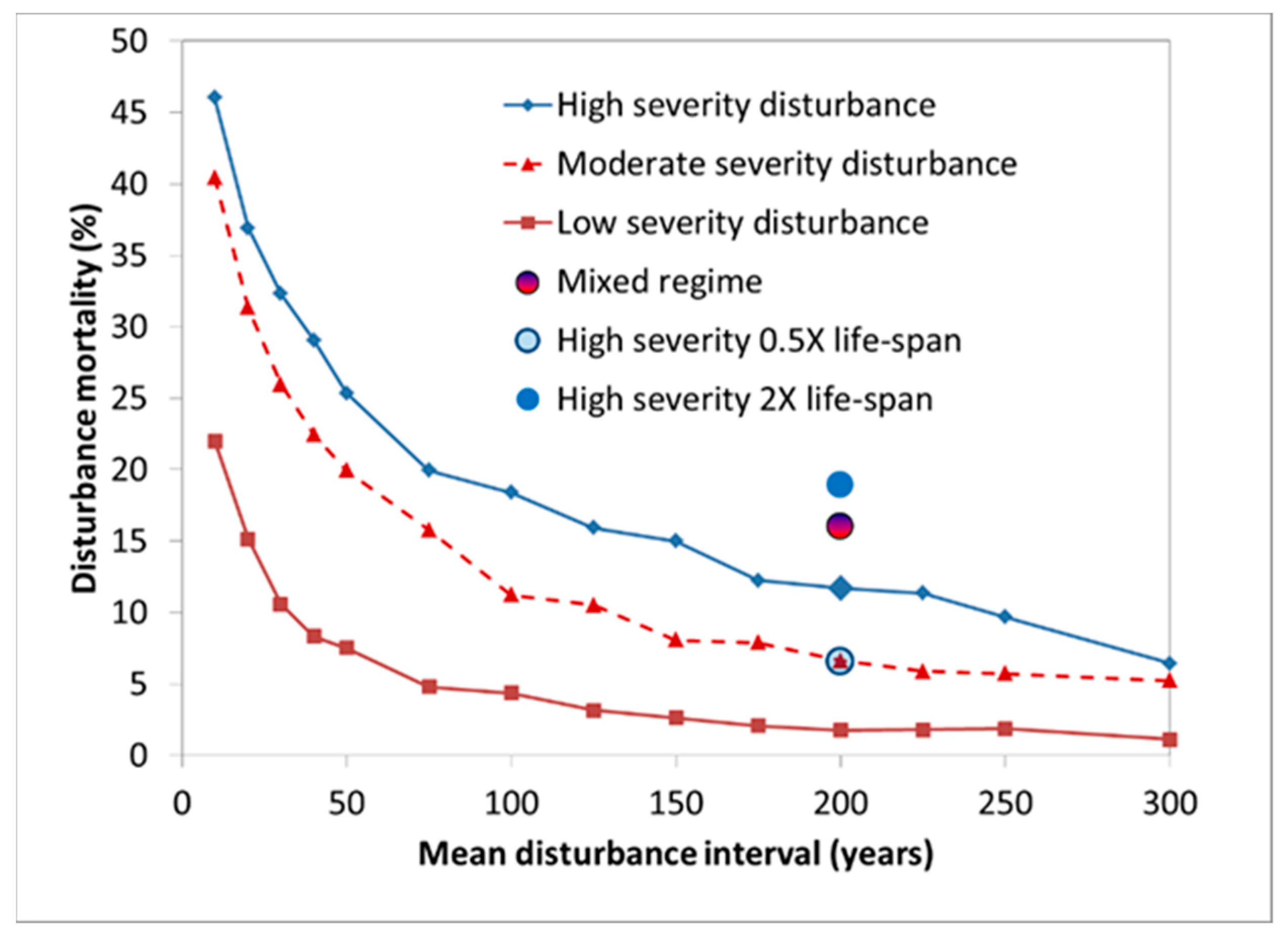
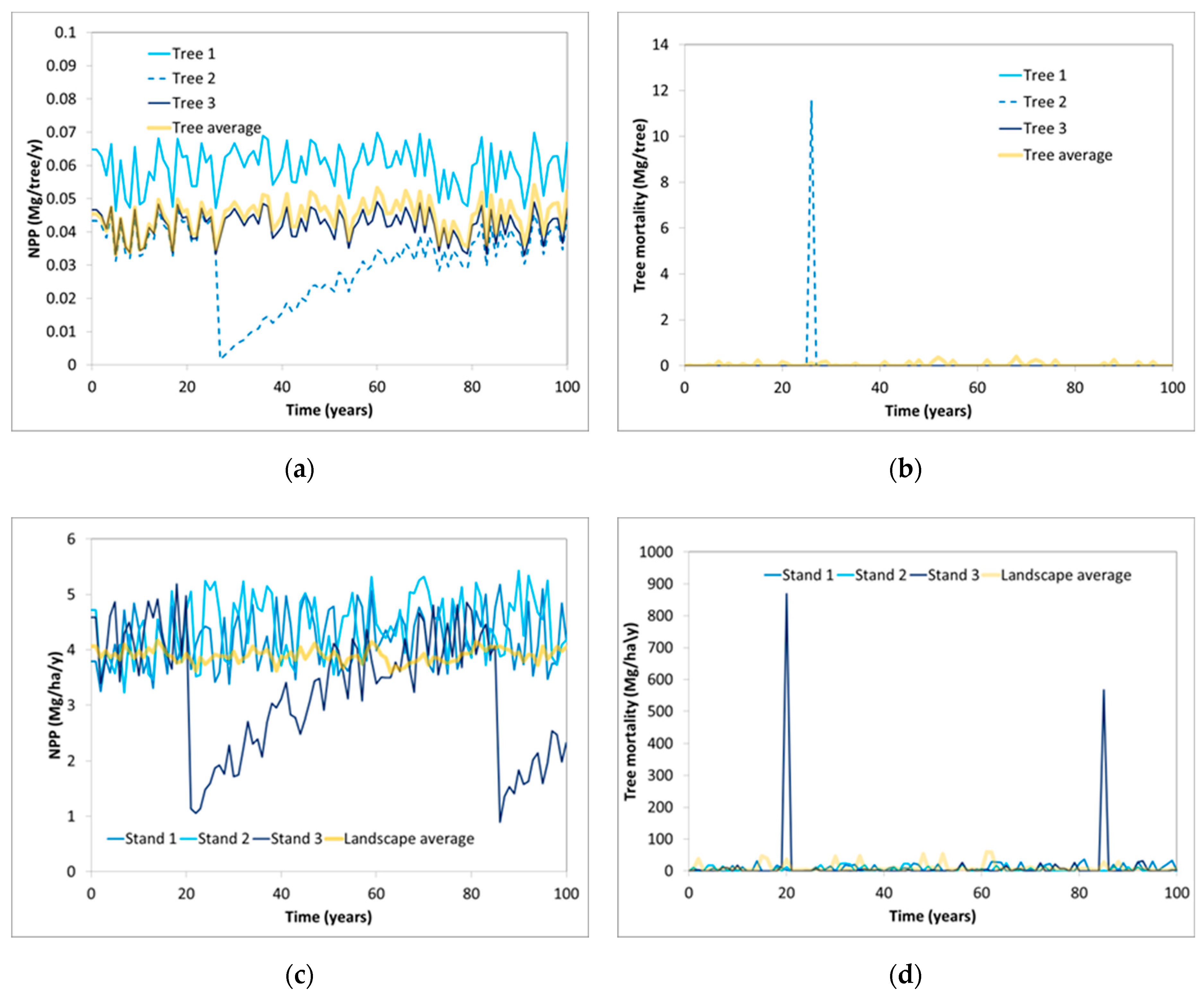

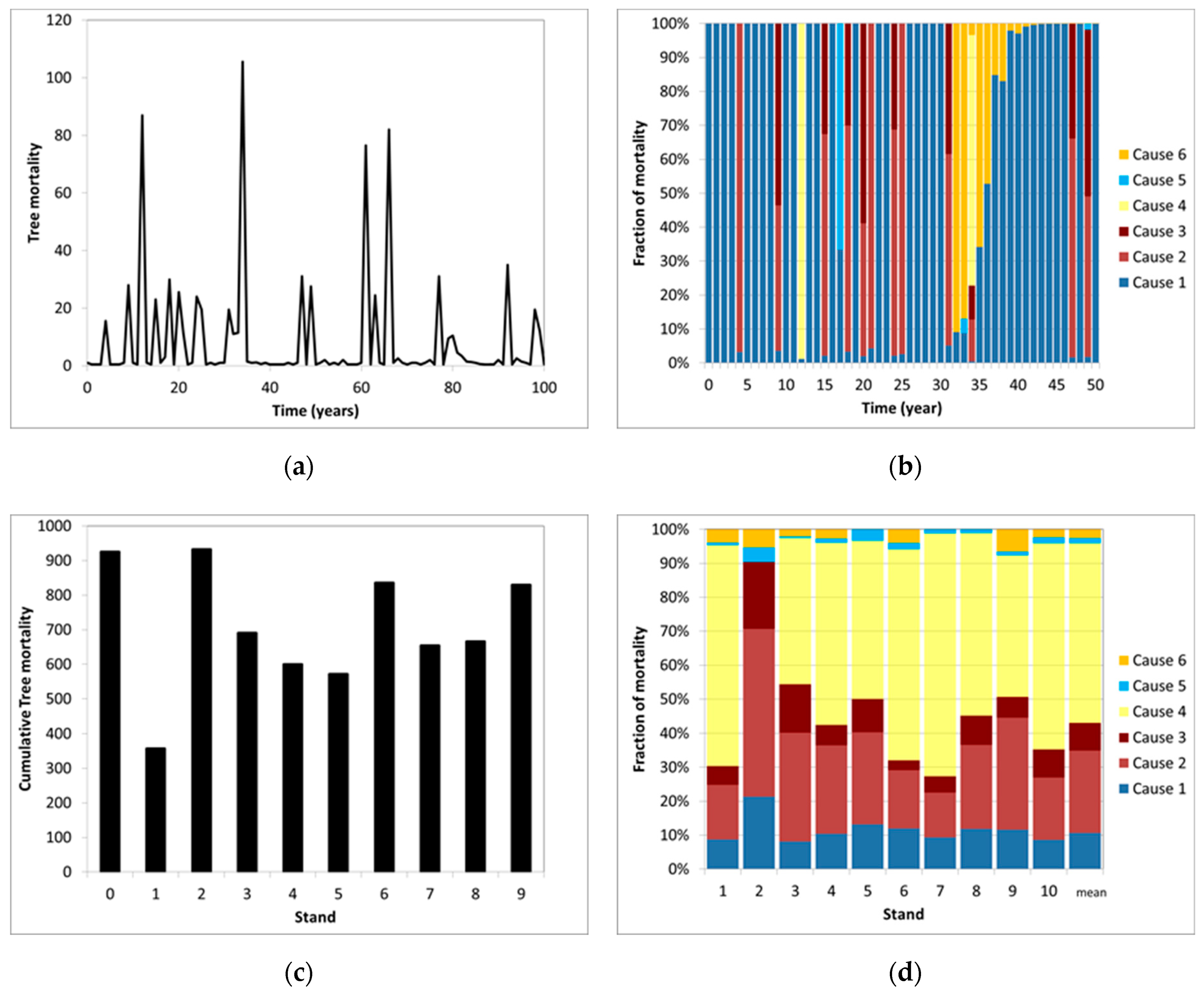
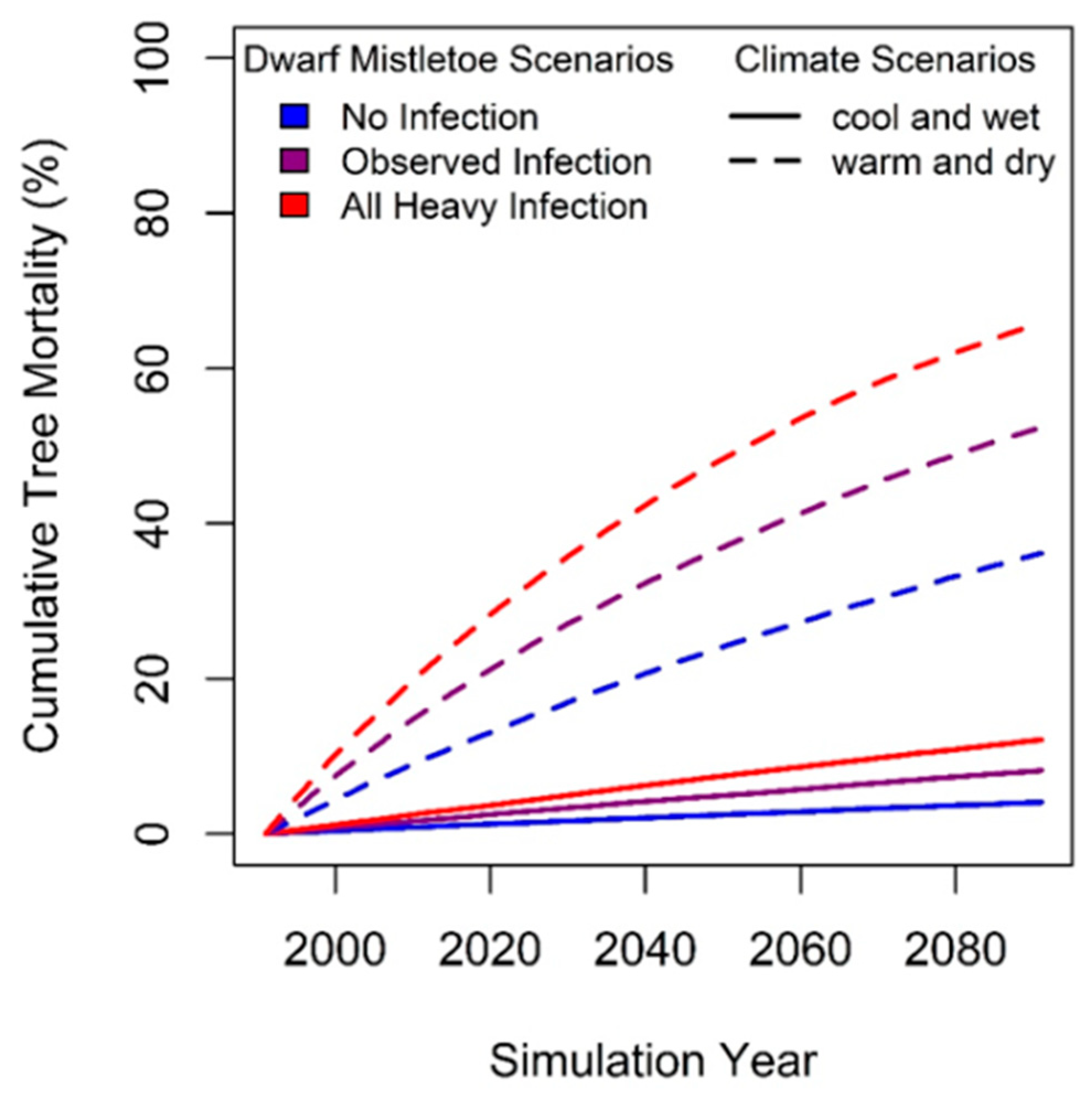
| Parameter | Description |
|---|---|
| Frequency | Number of events in a period of time defined by mean and variation |
| Regularity | Nature of the period between events (i.e., regular versus random versus aggregated) |
| Extent | Area impacted by the event, best represented by a frequency distribution |
| Aggregation | Degree events are spatially aggregated, independent, or regularly spaced |
| Severity | Proportion of either population or mass impacted by mortality agent |
| Species selectivity | Degree mortality agent is species-specific versus non-specific |
| Target size | Degree mortality agent impacts different tree sizes (height, diameter) |
| Interdependence | Degree mortality agent depends on previous mortality event by either same or different agents. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harmon, M.E.; Bell, D.M. Mortality in Forested Ecosystems: Suggested Conceptual Advances. Forests 2020, 11, 572. https://doi.org/10.3390/f11050572
Harmon ME, Bell DM. Mortality in Forested Ecosystems: Suggested Conceptual Advances. Forests. 2020; 11(5):572. https://doi.org/10.3390/f11050572
Chicago/Turabian StyleHarmon, Mark E., and David M. Bell. 2020. "Mortality in Forested Ecosystems: Suggested Conceptual Advances" Forests 11, no. 5: 572. https://doi.org/10.3390/f11050572
APA StyleHarmon, M. E., & Bell, D. M. (2020). Mortality in Forested Ecosystems: Suggested Conceptual Advances. Forests, 11(5), 572. https://doi.org/10.3390/f11050572





