Combined Analyses of Phenotype, Genotype and Climate Implicate Local Adaptation as a Driver of Diversity in Eucalyptus microcarpa (Grey Box)
Abstract
1. Introduction
2. Materials and Methods
2.1. Trial Design and Trait Measurements
2.2. Phenotypic Analysis
2.2.1. Genetic Variance
2.2.2. Genetic Trait–Trait Correlations
2.2.3. Climate Associations
2.3. Genotype-Phenotype Analysis
2.3.1. Genotyping
2.3.2. Genotype–Phenotype Associations
2.4. Genotype-Phenotype-Climate Analysis
3. Results
3.1. Genetic Variation Within Quantitative Traits
3.2. Genetic Trait–Trait Correlations
3.3. Climate Associations with Quantitative Trait Variation
3.4. Genotype–Phenotype Associations
3.5. Genotype–Phenotype-Climate Associations
4. Discussion
4.1. Evidence of Genetic Variance and Climate Adaptation
4.2. Linking Genotype and Phenotype
4.3. Conservation and Restoration under Climate Change
5. Conclusions
Supplementary Materials
Data Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Neale, D.B.; Kremer, A. Forest tree genomics: Growing resources and applications. Nat. Rev. Genet. 2011, 12, 111–122. [Google Scholar] [CrossRef] [PubMed]
- Petit, R.J.; Hampe, A. Some evolutionary consequences of being a tree. Annu. Rev. Ecol. Evol. Syst. 2006, 37, 187–214. [Google Scholar] [CrossRef]
- Matusick, G.; Ruthrof, K.X.; Brouwers, N.C.; Dell, B.; Hardy, G.S.J. Sudden forest canopy collapse corresponding with extreme drought and heat in a mediterranean-type eucalypt forest in southwestern Australia. Eur. J. For. Res. 2013, 132, 497–510. [Google Scholar] [CrossRef]
- Klein, T.; Cahanovitc, R.; Sprintsin, M.; Herr, N.; Schiller, G. A nation-wide analysis of tree mortality under climate change: Forest loss and its causes in Israel 1948–2017. For. Ecol. Manag. 2019, 432, 840–849. [Google Scholar] [CrossRef]
- Andrew, M.E.; Ruthrof, K.X.; Matusick, G.; Hardy, G.E.S.J. Spatial configuration of drought disturbance and forest gap creation across environmental gradients. PLoS ONE 2016, 11, e0157154. [Google Scholar] [CrossRef]
- Hall, A.A.G.; Gherlenda, A.N.; Hasegawa, S.; Johnson, S.N.; Cook, J.M.; Riegler, M. Anatomy of an outbreak: The biology and population dynamics of a Cardiaspina psyllid species in an endangered woodland ecosystem. Agric. For. Entomol. 2015, 17, 292–301. [Google Scholar] [CrossRef]
- Wearne, L.J.; Morgan, J.W. Recent forest encroachment into subalpine grasslands near Mount Hotham, Victoria, Australia. Arct. Antarct. Alp. Res. 2001, 33, 369–377. [Google Scholar] [CrossRef]
- Aitken, S.N.; Bemmels, J.B. Time to get moving: Assisted gene flow of forest trees. Evol. Appl. 2016, 9, 271–290. [Google Scholar] [CrossRef]
- Prober, S.M.; Byrne, M.; McLean, E.H.; Steane, D.A.; Potts, B.M.; Vaillancourt, R.E.; Stock, W.D. Climate-adjusted provenancing: A strategy for climate-resilient ecological restoration. Front. Ecol. Evol. 2015, 3, 65. [Google Scholar] [CrossRef]
- Mahony, C.R.; MacLachlan, I.R.; Lind, B.M.; Yoder, J.B.; Wang, T.; Aitken, S.N. Evaluating genomic data for management of local adaptation in a changing climate: A lodgepole pine case study. Evol. Appl. 2019, 13, 116–131. [Google Scholar] [CrossRef]
- Steane, D.A.; Potts, B.M.; McLean, E.; Prober, S.M.; Stock, W.D.; Vaillancourt, R.E.; Byrne, M. Genome-wide scans detect adaptation to aridity in a widespread forest tree species. Mol. Ecol. 2014, 23, 2500–2513. [Google Scholar] [CrossRef] [PubMed]
- Jordan, R.; Hoffmann, A.A.; Dillon, S.K.; Prober, S.M. Evidence of genomic adaptation to climate in Eucalyptus microcarpa: Implications for adaptive potential to projected climate change. Mol. Ecol. 2017, 26, 6002–6020. [Google Scholar] [CrossRef] [PubMed]
- Holliday, J.A.; Aitken, S.N.; Cooke, J.E.K.; Fady, B.; González-Martínez, S.C.; Heuertz, M.; Heuertz, M.; Jaramillo-Correa, J.P.; Lexer, C.; Staton, M.; et al. Advances in ecological genomics in forest trees and applications to genetic resources conservation and breeding. Mol. Ecol. 2016, 26, 706–717. [Google Scholar] [CrossRef] [PubMed]
- Supple, M.A.; Bragg, J.G.; Broadhurst, L.M.; Nicotra, A.B.; Byrne, M.; Andrew, R.L.; Widdup, A.; Aitken, N.C.; Borevitz, J.O. Landscape genomic prediction for restoration of a Eucalyptus foundation species under climate change. eLife 2018, 7, e31835. [Google Scholar] [CrossRef]
- Ingvarsson, P.K.; Bernhardsson, C. Genome-wide signatures of environmental adaptation in European aspen (Populus tremula) under current and future climate conditions. Evol. Appl. 2019, 13, 132–142. [Google Scholar] [CrossRef]
- Sork, V.L.; Aitken, S.N.; Dyer, R.J.; Eckert, A.J.; Legendre, P.; Neale, D.B. Putting the landscape into the genomics of trees: Approaches for understanding local adaptation and population responses to changing climate. Tree Genet. Genomes 2013, 9, 901–911. [Google Scholar] [CrossRef]
- Dillon, S.; McEvoy, R.; Baldwin, D.S.; Rees, G.N.; Parsons, Y.; Southerton, S. Characterisation of adaptive genetic diversity in environmentally contrasted populations of Eucalyptus camaldulensis Dehnh. (River Red Gum). PLoS ONE 2014, 9, e103515. [Google Scholar] [CrossRef]
- Yeaman, S.; Hodgins, K.A.; Lotterhos, K.E.; Suren, H.; Nadeau, S.; Degner, J.C.; Nurkowski, K.A.; Smets, P.; Wang, T.; Gray, L.K.; et al. Convergent local adaptation to climate in distantly related conifers. Science 2016, 353, 23–26. [Google Scholar] [CrossRef]
- Kremer, A.; Potts, B.M.; Delzon, S. Genetic divergence in forest trees: Understanding the consequences of climate change. Funct. Ecol. 2014, 28, 22–36. [Google Scholar] [CrossRef]
- McKown, A.D.; Guy, R.D.; Klápště, J.; Geraldes, A.; Friedmann, M.; Cronk, Q.C.B.; El-Kassaby, Y.A.; Mansfield, S.D.; Douglas, C.J. Geographical and environmental gradients shape phenotypic trait variation and genetic structure in Populus trichocarpa. New Phytol. 2014, 201, 1263–1276. [Google Scholar] [CrossRef]
- Vitasse, Y.; Lenz, A.; Kollas, C.; Randin, C.F.; Hoch, G.; Körner, C. Genetic vs. non-genetic responses of leaf morphology and growth to elevation in temperate tree species. Funct. Ecol. 2014, 28, 243–252. [Google Scholar] [CrossRef]
- Costa e Silva, J.; Potts, B.M.; Dutkowski, G.W. Genotype by environment interaction for growth of Eucalyptus globulus in Australia. Tree Genet. Genomes 2006, 2, 61–75. [Google Scholar] [CrossRef]
- Bansal, S.; Harrington, C.A.; Gould, P.J.; St Clair, J.B. Climate-related genetic variation in drought-resistance of Douglas-fir (Pseudotsuga menziesii). Glob. Chang. Biol. 2015, 21, 947–958. [Google Scholar] [CrossRef] [PubMed]
- McLean, E.H.; Prober, S.M.; Stock, W.D.; Steane, D.A.; Potts, B.M.; Vaillancourt, R.E.; Byrne, M. Plasticity of functional traits varies clinally along a rainfall gradient in Eucalyptus tricarpa. Plant Cell Environ. 2014, 37, 1440–1451. [Google Scholar] [CrossRef] [PubMed]
- Holliday, J.A.; Ritland, K.; Aitken, S.N. Widespread, ecologically relevant genetic markers developed from association mapping of climate-related traits in Sitka spruce (Picea sitchensis). New Phytol. 2010, 188, 501–514. [Google Scholar] [CrossRef] [PubMed]
- De Villemereuil, P.; Gaggiotti, O.E.; Mouterde, M.; Till-Bottraud, I. Common garden experiments in the genomic era: New perspectives and opportunities. Heredity 2016, 116, 249–254. [Google Scholar] [CrossRef]
- Rellstab, C.; Gugerli, F.; Eckert, A.J.; Hancock, A.M.; Holderegger, R. A practical guide to environmental association analysis in landscape genomics. Mol. Ecol. 2015, 24, 4348–4370. [Google Scholar] [CrossRef]
- De Kort, H.; Vandepitte, K.; Bruun, H.H.; Closset-Kopp, D.; Honnay, O.; Mergeay, J. Landscape genomics and a common garden trial reveal adaptive differentiation to temperature across Europe in the tree species Alnus glutinosa. Mol. Ecol. 2014, 23, 4709–4721. [Google Scholar] [CrossRef]
- Eckert, A.J.; Bower, A.D.; Wegrzyn, J.L.; Pande, B.; Jermstad, K.D.; Krutovsky, K.V.; Clair, J.B.S.; Neale, D.B. Association genetics of coastal Douglas fir (Pseudotsuga menziesii var. menziesii, Pinaceae). I. Cold-hardiness related traits. Genetics 2009, 182, 1289–1302. [Google Scholar] [CrossRef]
- Williams, J.E.; Brooker, I. Eucalypts: An introduction. In Eucalypt Ecology; Williams, J.E., Woinarski, J., Eds.; Cambridge University Press: Cambridge, UK, 1997; pp. 1–15. [Google Scholar]
- Prober, S.M.; Potts, B.M.; Bailey, T.; Byrne, M.; Dillon, S.; Harrison, P.A.; Hoffmann, A.A.; Jordan, R.; McLean, E.H.; Steane, D.A.; et al. Climate adaptation and ecological restoration in eucalypts. Proc. R. Soc. Victoria 2016, 128, 40–53. [Google Scholar] [CrossRef]
- Butt, N.; Pollock, L.J.; McAlpine, C.A. Eucalypts face increasing climate stress. Ecol. Evol. 2013, 3, 5011–5022. [Google Scholar] [CrossRef]
- Hughes, L. Climate change and Australia: Key vulnerable regions. Reg. Environ. Chang. 2011, 11, 189–195. [Google Scholar] [CrossRef]
- Aitken, S.N.; Yeaman, S.; Holliday, J.A.; Wang, T.; Curtis-McLane, S. Adaptation, migration or extirpation: Climate change outcomes for tree populations. Evol. Appl. 2008, 1, 95–111. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, E.K.; Mazanec, R.A.; Krauss, S.L. Provenance variation of ecologically important traits of forest trees: Implications for restoration. J. Appl. Ecol. 2007, 44, 583–593. [Google Scholar] [CrossRef]
- Gauli, A.; Vaillancourt, R.E.; Bailey, T.G.; Steane, D.A.; Potts, B.M. Evidence for local climate adaptation in early-life traits of Tasmanian populations of Eucalyptus pauciflora. Tree Genet. Genomes 2015, 11, 104. [Google Scholar] [CrossRef]
- Rawal, D.S.; Kasel, S.; Keatley, M.R.; Nitschke, C.R. Climatic and photoperiodic effects on flowering phenology of select eucalypts from south-eastern Australia. Agric. For. Meteorol. 2015, 214, 231–242. [Google Scholar] [CrossRef]
- Slatyer, R. Altitudinal variation in the photosynthetic characteristics of Snow Gum, Eucalyptus pauciflora Sieb. ex Spreng. III Temperature response of material grown in contrasting thermal environments. Aust. J. Plant Physiol. 1977, 4, 301–312. [Google Scholar] [CrossRef]
- Drake, J.E.; Aspinwall, M.J.; Pfautsch, S.; Rymer, P.D.; Reich, P.B.; Smith, R.A.; Crous, K.Y.; Tissue, D.T.; Ghannoum, O.; Tjoelker, M.G. The capacity to cope with climate warming declines from temperate to tropical latitudes in two widely distributed Eucalyptus species. Glob. Chang. Biol. 2015, 21, 459–472. [Google Scholar] [CrossRef]
- Steane, D.A.; McLean, E.H.; Potts, B.M.; Prober, S.M.; Stock, W.D.; Stylianou, V.M.; Vaillancourt, R.E.; Byrne, M. Evidence for adaptation and acclimation in a widespread eucalypt of semi-arid Australia. Biol. J. Linn. Soc. 2017, 121, 484–500. [Google Scholar] [CrossRef]
- Atlas of Living Australia [Internet]. Available online: http://www.ala.org.au (accessed on 30 January 2017).
- Bean, A.R. Taxonomic and nomenclatural notes on the Eastern grey boxes (Eucalyptus ser. Moluccanae Chippendale, Myrtaceae) and the reinstatement of Eucalyptus woollsiana R.T.Baker. Austrobaileya 2009, 8, 25–34. [Google Scholar]
- Falconer, D.S.; Mackay, T.C. Introduction to Quantitative Genetics, 4th ed.; Pearson: London, UK, 1996. [Google Scholar]
- Eldridge, K.; Davidson, J.; Harwood, C.E.; van Wyk, G. Eucalypt Domestication and Breeding; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Bush, D.; Kain, D.; Matheson, C.; Kanowski, P. Marker-based adjustment of the additive relationship matrix for estimation of genetic parameters—An example using Eucalyptus cladocalyx. Tree Genet. Genomes 2011, 7, 23–35. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Found. Stat. Comput.: Vienna, Austria, 2018; [Internet]; Available online: https://www.r-project.org/ (accessed on 25 July 2015).
- Bates, D.; Mächler, M.; Bolker, B.M.; Walker, S.C. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67. [Google Scholar] [CrossRef]
- Butler, D.; Cullis, B.; Gilmour, A.; Gogle, B. ASReml-R Reference Manual, Release 3. Technical Series QE02001; Queensland Department of Primary Industries: Brisbane, Australia, 2009.
- White, I. The R Pin Function [Internet]. 2013. Available online: http://www.homepages.ed.ac.uk/iwhite/asreml (accessed on 1 December 2016).
- Whitlock, M.C. Evolutionary inferences from, QST. Mol. Ecol. 2008, 17, 1885–1896. [Google Scholar] [CrossRef] [PubMed]
- Lewontin, R.; Krakauer, J. Distribution of gene frequency as a test of the theory of the selective neutrality of polymorphisms. Genetics 1973, 74, 175–195. [Google Scholar]
- Dabney, A.; Storey, J.D. Qvalue: Q-Value Estimation for False Discovery Rate Control. R Package Version 1.43.0 [Internet]. 2015. Available online: https://bioconductor.riken.jp/packages/3.0/bioc/html/qvalue.html (accessed on 1 December 2016).
- Reisinger, A.; Kitching, R.L.; Chiew, F.; Hughes, L.; Newton, P.C.D.; Schuster, S.S.; Tait, A.; Whetton, P. Australasia. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the fifth Assessment Report of the Intergovernmental Panel on Climate Change; Barros, V.R., Field, C.B., Dokken, D.J., Mastrandrea, M.D., Mach, K.J., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1371–1438. [Google Scholar]
- Lenth, R.V. Least-squares means: The R package lsmeans. J. Stat. Softw. 2016, 69. [Google Scholar] [CrossRef]
- Lê, S.; Josse, J.; Husson, F. FactoMineR: An R package for multivariate analysis. J. Stat. Softw. 2008, 25, 1–18. [Google Scholar] [CrossRef]
- Jordan, R.; Dillon, S.K.; Prober, S.M.; Hoffmann, A.A. Landscape genomics reveals altered genome wide diversity within revegetated stands of Eucalyptus microcarpa (Grey Box). New Phytol. 2016, 212, 992–1006. [Google Scholar] [CrossRef]
- Tiffin, P.; Ross-Ibarra, J. Advances and limits of using population genetics to understand local adaptation. Trends Ecol. Evol. 2014, 29, 673–680. [Google Scholar] [CrossRef]
- Foll, M.; Gaggiotti, O. A genome-scan method to identify selected loci appropriate for both dominant and codominant markers: A Bayesian perspective. Genetics 2008, 180, 977–993. [Google Scholar] [CrossRef]
- Excoffier, L.; Hofer, T.; Foll, M. Detecting loci under selection in a hierarchically structured population. Heredity 2009, 103, 285–298. [Google Scholar] [CrossRef]
- Beaumont, M.A.; Nichols, R.A. Evaluating loci for use in the genetic analysis of population structure. Proc. R. Soc. B Biol. Sci. 1996, 263, 1619–1626. [Google Scholar]
- Antao, T.; Lopes, A.; Lopes, R.J.; Beja-Pereira, A.; Luikart, G. LOSITAN: A workbench to detect molecular adaptation based on a FST-outlier method. BMC Bioinform. 2008, 9, 323. [Google Scholar] [CrossRef] [PubMed]
- Günther, T.; Coop, G. Robust identification of local adaptation from allele frequencies. Genetics 2013, 195, 205–220. [Google Scholar] [CrossRef] [PubMed]
- Coop, G.; Witonsky, D.; Di Rienzo, A.; Pritchard, J.K. Using environmental correlations to identify loci underlying local adaptation. Genetics 2010, 185, 1411–1423. [Google Scholar] [CrossRef]
- Myburg, A.A.; Grattapaglia, D.; Tuskan, G.A.; Hellsten, U.; Hayes, R.D.; Grimwood, J.; Jenkins, J.; Lindquist, E.; Tice, H.; Bauer, D. The genome of Eucalyptus grandis. Nature 2014, 510, 356–362. [Google Scholar] [CrossRef]
- Lotterhos, K.E.; Whitlock, M.C. The relative power of genome scans to detect local adaptation depends on sampling design and statistical method. Mol. Ecol. 2015, 24, 1031–1046. [Google Scholar] [CrossRef]
- Excoffier, L.; Laval, G.; Schneider, S. Arlequin (version 3.0): An integrated software package for population genetics data analysis. Evol. Bioinforma. 2005, 1, 47–50. [Google Scholar] [CrossRef]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R. The Sequence Alignment/Map format and SAMtools. Bioinformatics 2009, 25, 2078–2079. [Google Scholar] [CrossRef]
- Blischak, P.D.; Kubatko, L.S.; Wolfe, A.D. Accounting for genotype uncertainty in the estimation of allele frequencies in autopolyploids. Mol. Ecol. Resour. 2016, 16, 742–754. [Google Scholar] [CrossRef]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.R.; Bender, D.; Maller, J.; Sklar, P.; De Bakker, P.I.; Daly, M.J.; et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef]
- Bradbury, P.J.; Zhang, Z.; Kroon, D.E.; Casstevens, T.M.; Ramdoss, Y.; Buckler, E.S. TASSEL: Software for association mapping of complex traits in diverse samples. Bioinformatics 2007, 23, 2633–2635. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. COANCESTRY: A program for simulating, estimating and analysing relatedness and inbreeding coefficients. Mol. Ecol. Resour. 2011, 11, 141–145. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Triadic IBD coefficients and applications to estimating pairwise relatedness. Genet. Res. 2007, 89, 135–153. [Google Scholar] [CrossRef] [PubMed]
- House, S.M. Reproductive biology of eucalypts. In Eucalypt Ecology; Williams, J.E., Woinarski, J., Eds.; Cambridge University Press: Cambridge, UK, 1997; pp. 30–55. [Google Scholar]
- Lynch, M.; Ritland, K. Estimation of pairwise relatedness with molecular markers. Genetics 1999, 152, 1753–1766. [Google Scholar] [PubMed]
- TAIR. The Arabidopsis Information Resource (TAIR) [Internet]. 2017. Available online: https://www.arabidopsis.org (accessed on 1 March 2017).
- Yoon, S.-K.; Park, E.-J.; Choi, Y.-I.; Bae, E.-K.; Kim, J.-H.; Park, S.-Y.; Kang, K.S.; Lee, H. Response to drought and salt stress in leaves of poplar (Populus alba × Populus glandulosa): Expression profiling by oligonucleotide microarray analysis. Plant Physiol. Biochem. 2014, 84, 158–168. [Google Scholar] [CrossRef] [PubMed]
- Yanhui, C.; Xiaoyuan, Y.; Kun, H.; Meihua, L.; Jigang, L.; Zhaofeng, G.; Zhiqiang, L.; Yunfei, Z.; Xiaoxiao, W.; Xiaoming, Q.; et al. The MYB transcription factor superfamily of Arabidopsis: Expression analysis and phylogenetic comparison with the rice MYB family. Plant Mol. Biol. 2006, 60, 107–124. [Google Scholar] [CrossRef]
- Silva-Junior, O.B.; Grattapaglia, D. Genome-wide patterns of recombination, linkage disequilibrium and nucleotide diversity from pooled resequencing and single nucleotide polymorphism genotyping unlock the evolutionary history of Eucalyptus grandis. New Phytol. 2015, 208, 830–845. [Google Scholar] [CrossRef]
- Steane, D.A.; Conod, N.; Jones, R.C.; Vaillancourt, R.E.; Potts, B.M. A comparative analysis of population structure of a forest tree, Eucalyptus globulus (Myrtaceae), using microsatellite markers and quantitative traits. Tree Genet. Genomes 2006, 2, 30–38. [Google Scholar] [CrossRef]
- White, T.L.; Adams, W.T.; Neale, D.B. Forest Genetics; CAB International: Oxfordshire, UK, 2007. [Google Scholar]
- Alberto, F.J.; Aitken, S.N.; Alía, R.; González-Martínez, S.C.; Hänninen, H.; Kremer, A.; Lefèvre, F.; Lenormand, T.; Yeaman, S.; Whetten, R.; et al. Potential for evolutionary responses to climate change—Evidence from tree populations. Glob. Chang. Biol. 2013, 19, 1645–1661. [Google Scholar] [CrossRef]
- Merchant, A.; Callister, A.; Arndt, S.; Tausz, M.; Adams, M. Contrasting physiological responses of six Eucalyptus species to water deficit. Ann. Bot. 2007, 100, 1507–1515. [Google Scholar] [CrossRef]
- Niinemets, Ü. Global-scale climatic controls of leaf dry mass per area, density and thickness in trees and shrubs. Ecology 2001, 82, 453–469. [Google Scholar] [CrossRef]
- Eckert, A.J.; Wegrzyn, J.L.; Liechty, J.D.; Lee, J.M.; Cumbie, W.P.; Davis, J.M.; Goldfarb, B.; Loopstra, C.A.; Palle, S.R.; Quesada, T.; et al. The evolutionary genetics of the genes underlying phenotypic associations for loblolly pine (Pinus taeda, Pinaceae). Genetics 2013, 195, 1353–1372. [Google Scholar] [CrossRef] [PubMed]
- Lind, B.M.; Menon, M.; Bolte, C.E.; Faske, T.M.; Eckert, A.J. The genomics of local adaptation in trees: Are we out of the woods yet? Tree Genet. Genomes 2018, 14, 29. [Google Scholar] [CrossRef]
- Le Corre, V.; Kremer, A. The genetic differentiation at quantitative trait loci under local adaptation. Mol. Ecol. 2012, 21, 1548–1566. [Google Scholar] [CrossRef] [PubMed]
- Boyle, E.A.; Li, Y.I.; Pritchard, J.K. An expanded view of complex traits: From polygenic to omnigenic. Cell 2017, 169, 1177–1186. [Google Scholar] [CrossRef] [PubMed]
- Rajora, O.P.; Eckert, A.J.; Zinck, J.W.R. Single-locus versus multilocus patterns of local adaptation to climate in Eastern White Pine (Pinus strobus, Pinaceae). PLoS ONE 2016, 11, e0158691. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, A.; Griffin, P.; Dillon, S.; Catullo, R.; Rane, R.; Byrne, M.; Jordan, R.; Oakeshott, J.; Weeks, A.; Joseph, L.; et al. A framework for incorporating evolutionary genomics into biodiversity conservation and management. Clim. Chang. Responses 2015, 2, 1. [Google Scholar] [CrossRef]
- Kremer, A.; Ronce, O.; Robledo-Arnuncio, J.J.; Guillaume, F.; Bohrer, G.; Nathan, R.; Bridle, J.R.; Gomulkiewicz, R.; Klein, E.K.; Ritland, K.; et al. Long-distance gene flow and adaptation of forest trees to rapid climate change. Ecol. Lett. 2012, 15, 378–392. [Google Scholar] [CrossRef]
- Hoffmann, A.A.; Sgrò, C.M.; Kristensen, T.N. Revisiting adaptive potential, population size, and conservation. Trends Ecol. Evol. 2017, 32, 506–517. [Google Scholar] [CrossRef]
- Lienert, J. Habitat fragmentation effects on fitness of plant populations—A review. J. Nat. Conserv. 2004, 12, 53–72. [Google Scholar] [CrossRef]
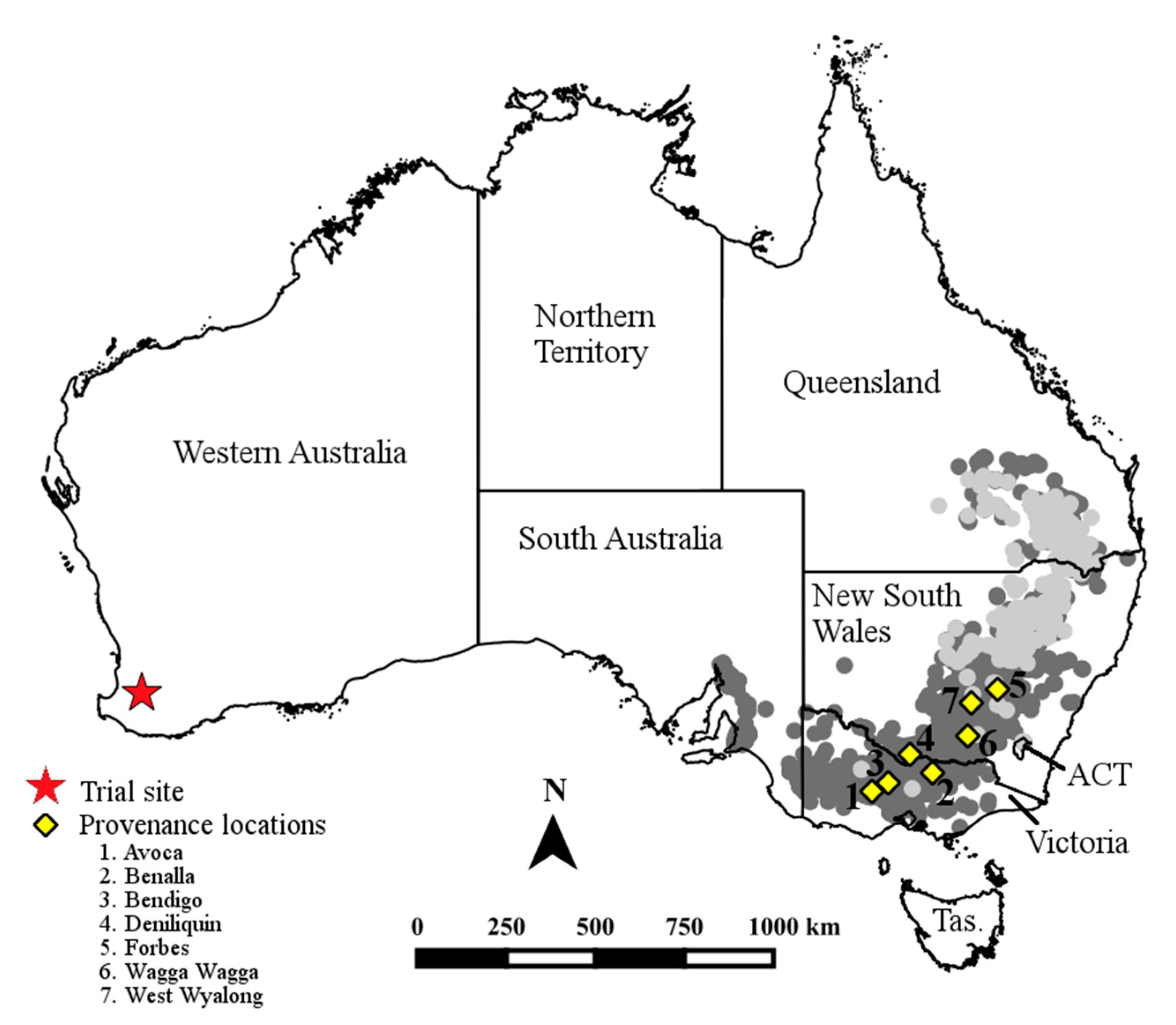
| Number of Samples (n) | Aridity Index (Ratio) 1 | Precipitation (mm) | Temperature (°C) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Site | State | DBH | Height | Leaf Traits | Genotyped | Mean Annual | Maximum Month | Annual (Bio12) | Summer | Winter | Driest Period (Bio14) | Wettest Period (Bio13) | Annual Mean (Bio01) | Max. Month Abs. Mean Max. | Warmest Period Max. (Bio05) |
| Avoca | Vic | 251 | 65 | 62 | 58 | 0.740 | 1.797 | 529 | 103 | 176 | 6 | 14 | 13.7 | 43 | 28.8 |
| Benalla | Vic | 289 | 69 | 67 | 58 | 0.698 | 1.745 | 550 | 108 | 174 | 7 | 16 | 15.4 | 44 | 30.9 |
| Bendigo | Vic | 240 | 75 | 71 | 66 | 0.640 | 1.613 | 489 | 88 | 154 | 5 | 13 | 14.4 | 44 | 29.9 |
| Deniliquin | NSW | 250 | 71 | 64 | 60 | 0.394 | 0.989 | 374 | 85 | 109 | 5 | 10 | 15.6 | 46 | 31.5 |
| Forbes | NSW | 245 | 69 | 63 | 57 | 0.479 | 1.017 | 556 | 158 | 134 | 8 | 13 | 16.8 | 45 | 33.1 |
| Wagga Wagga | NSW | 243 | 73 | 66 | 61 | 0.487 | 1.189 | 489 | 110 | 133 | 7 | 12 | 16.4 | 45 | 33 |
| West Wyalong | NSW | 226 | 74 | 66 | 62 | 0.427 | 1.010 | 466 | 124 | 113 | 7 | 12 | 16.4 | 45 | 32.8 |
| Total | 1744 | 496 | 459 | 422 | |||||||||||
| Minimum | 0.394 | 0.989 | 374 | 85 | 109 | 5 | 10 | 13.7 | 43 | 28.8 | |||||
| Maximum | 0.740 | 1.797 | 556 | 158 | 176 | 8 | 16 | 16.8 | 46 | 33.1 | |||||
| Trial site | WA | 0.796 | 2.445 | 587 | 42 | 307 | 2 | 24 | 15.2 | 45 | 30.6 | ||||
| Trait | Abbreviation | Units | Family Level | Provenance Level | ||||
|---|---|---|---|---|---|---|---|---|
| h2 | SE | QST | SE | |||||
| Growth traits | ||||||||
| Diameter at breast height | DBH | cm | 0.318 | 0.226 | 0.094 | 0.065 | ||
| Height | Height | m | 0.210 | 0.137 | 0.431 | 0.190 | * | |
| Size Ratio | Size Ratio | height:DBH | 0.106 | 0.080 | 0.165 | 0.162 | ||
| Leaf traits | ||||||||
| Leaf area | Area | cm2 | 0.155 | 0.169 | 0.467 | 0.220 | * | |
| Leaf length | Length | cm | 0.144 | 0.100 | 0.483 | 0.226 | * | |
| Leaf weight | Weight | g | 0.235 | 0.102 | 0.224 | 0.145 | ||
| Leaf thickness | Thickness | mm | 0.193 | 0.098 | 0.205 | 0.147 | ||
| Specific leaf area | SLA | mm2 mg−1 | 0.373 | 0.116 | 0.182 | 0.115 | ||
| Leaf density | Density | mg mm−3 | 0.000 | - | - | - | ||
| Growth Traits | Leaf Traits | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| DBH | Height | Size Ratio | Area | Length | Weight | Thickness | SLA | ||
| Growth traits | |||||||||
| DBH | 0.88 * | −0.97 * | −0.20 * | −0.08 | −0.03 | −0.18 | −0.15 | ||
| Height | 0.93 * | −0.75 * | −0.30 * | −0.56 * | 0.16 | −0.34 * | −0.35 * | ||
| Size Ratio | 0.35 | 0.81 | −0.35 | −0.16 | −0.55 * | −0.42 * | −0.15 | ||
| Leaf traits | |||||||||
| Area | 0.76 | 0.53 | 0.04 | 0.72 * | 0.97 * | 0.46 * | −0.36 * | ||
| Length | 0.40 | 0.32 | 0.38 | 0.79 * | 0.84 * | 0.38 * | −0.36 * | ||
| Weight | 0.92 * | 0.56 | −0.01 | 0.95 * | 0.59 | 0.70 * | −0.77 * | ||
| Thickness | −0.37 | −0.22 | 0.22 | −0.74 | −0.50 | −0.76 | −0.98 * | ||
| SLA | 0.16 | 0.19 | 0.06 | 0.70 | 0.93 * | 0.34 | −0.38 | ||
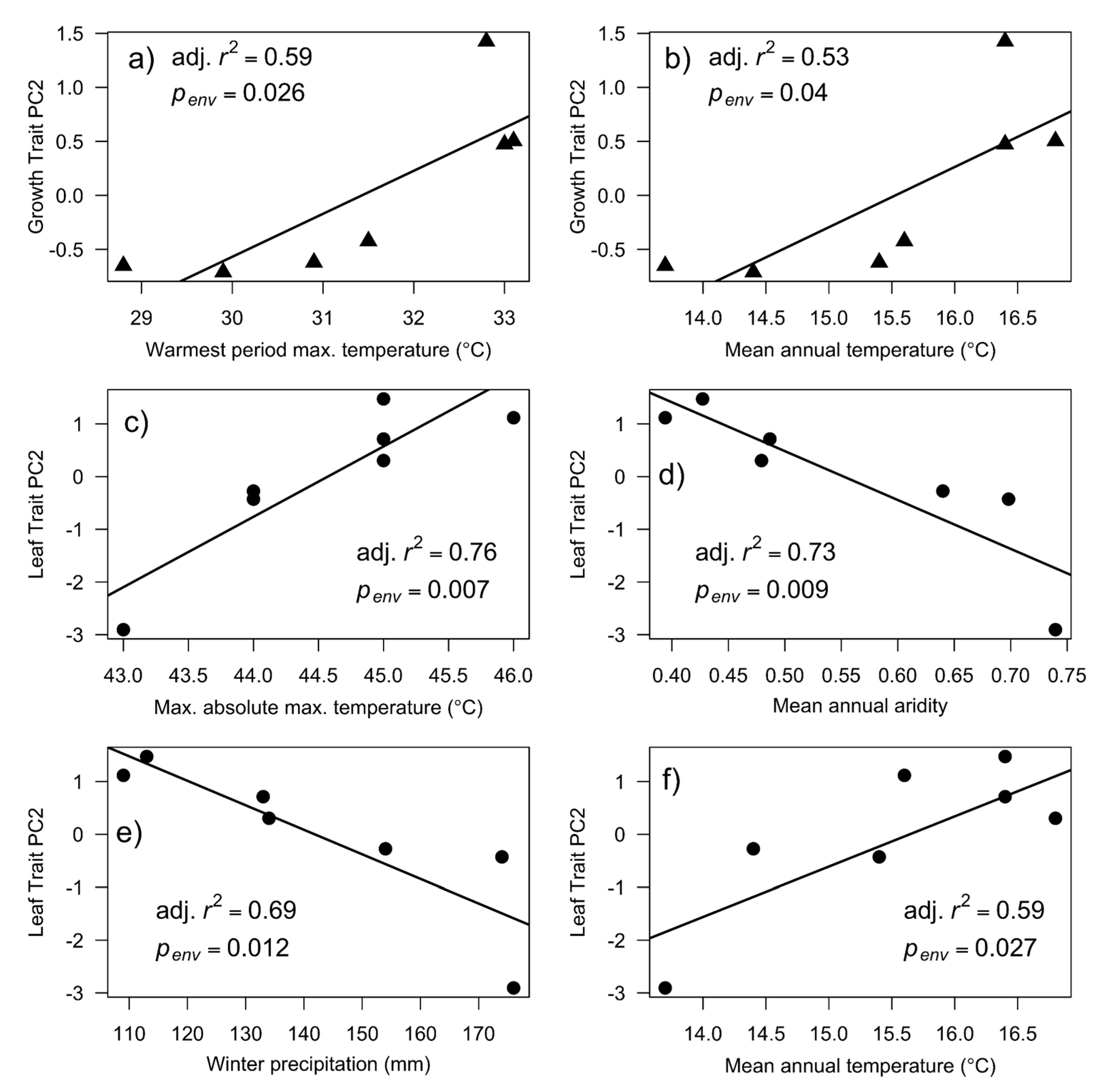
| Trait | Environment | (a) Trait ~ Environment | (b) Trait ~ Lat. + Long. + Environment | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Adj. r2 | Assoc. | Fenv [1,5] | penv | qenv | Adj. r2 | Assoc. | Fenv [1,3] | penv | qenv | |||
| Growth traits | ||||||||||||
| PC2 | Warmest period max. temp. | 0.59 | + | 9.7 | 0.026 | 0.13 | 0.56 | + | 0.1 | 0.831 | 0.811 | |
| PC2 | Mean annual temp. | 0.53 | + | 7.7 | 0.040 | 0.15 | 0.56 | − | 0.1 | 0.835 | 0.811 | |
| Leaf traits | ||||||||||||
| PC2 | Max. abs. mean max. temp. | 0.76 | + | 20.1 | 0.007 | 0.13 | 0.69 | + | 7.4 | 0.073 | 0.400 | |
| PC2 | Mean annual aridity | 0.73 | − | 17.1 | 0.009 | 0.13 | 0.71 | − | 8.4 | 0.063 | 0.400 | |
| PC2 | Winter precipitation | 0.69 | − | 14.6 | 0.012 | 0.13 | 0.81 | − | 13.8 | 0.034 | 0.400 | |
| PC2 | Max. aridity | 0.63 | − | 11.1 | 0.021 | 0.13 | 0.58 | − | 4.7 | 0.119 | 0.575 | |
| PC2 | Warmest period max. temp. | 0.62 | + | 10.6 | 0.022 | 0.13 | 0.70 | + | 7.9 | 0.067 | 0.400 | |
| PC2 | Mean annual temp. | 0.59 | + | 9.5 | 0.027 | 0.13 | 0.74 | + | 9.4 | 0.055 | 0.400 | |
| PC3 | Summer precipitation | 0.52 | − | 7.6 | 0.040 | 0.15 | 0.26 | − | 2.5 | 0.215 | 0.811 | |
| PC2 | Summer precipitation | −0.17 | + | 0.1 | 0.732 | 0.61 | 0.88 | − | 23.1 | 0.017 | 0.385 | |
| PC2 | Driest period prec. | −0.17 | + | 0.1 | 0.742 | 0.61 | 0.87 | − | 22.7 | 0.018 | 0.385 | |
| PC2 | Annual precipitation | 0.13 | − | 1.9 | 0.231 | 0.43 | 0.77 | − | 11.4 | 0.043 | 0.400 | |
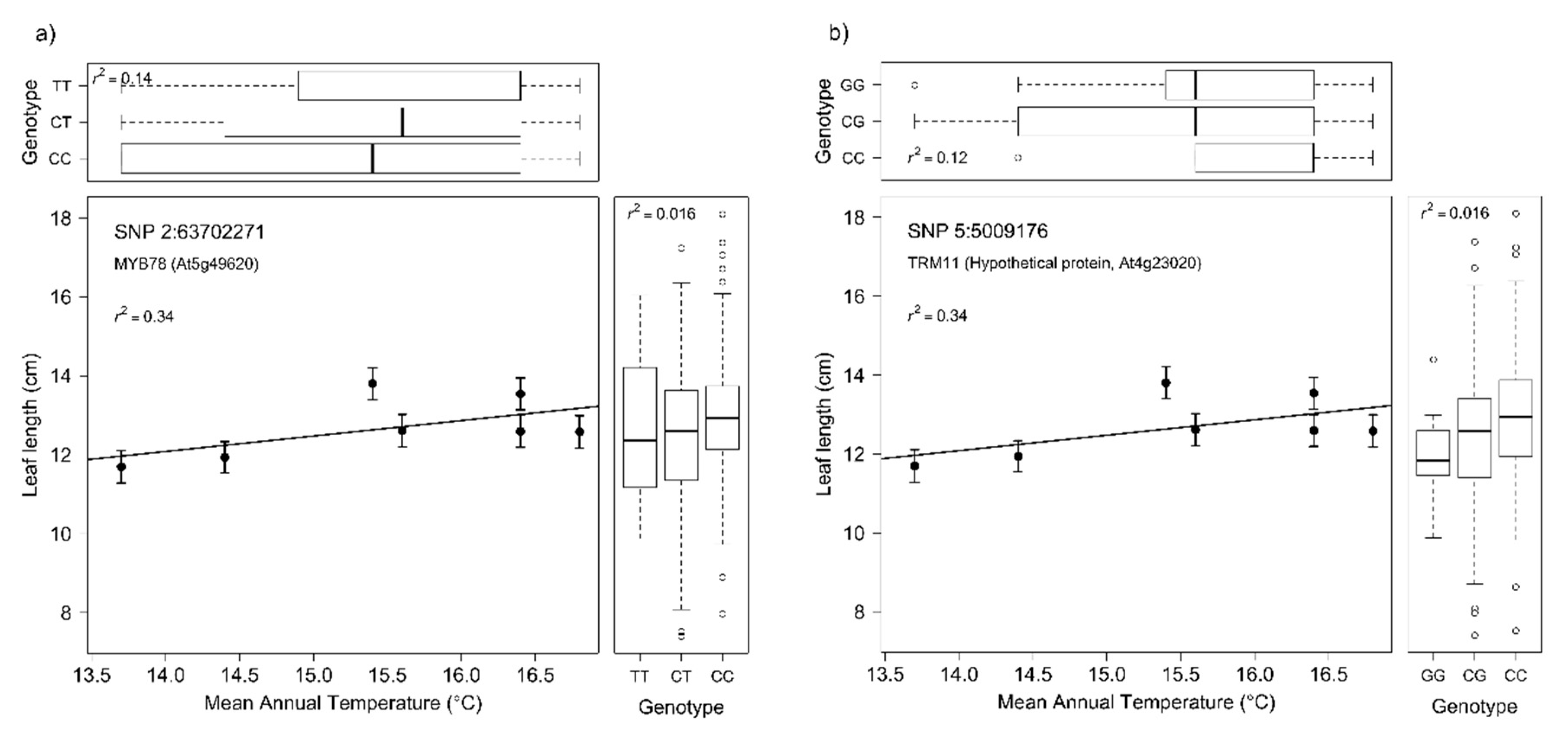
| MLM (Indv. Kinship) | MLM (Avg. Kinship) | Eucalyptus grandis (v1.1) Gene Information (+/−2000 bp) | Best TAIR10 Gene Orthologue | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Trait Marker | p | r2 | p | r2 | Name | Gene Effect | Name | Symbol | Definition | |
| DBH | ||||||||||
| 3:59841756 | 0.043 | 0.019 | 0.049 | 0.019 | Eucgr.C03147 | synonymous | AT3G13980.1 | |||
| Size Ratio | ||||||||||
| 10:29282238 | 0.023 | 0.012 | 0.015 | 0.014 | Eucgr.J02333 | synonymous | AT3G27150.1 | Galactose oxidase/kelch repeat superfamily protein | ||
| 10:29282238 | 0.023 | 0.012 | 0.015 | 0.014 | Eucgr.J02334 | upstream | AT5G14170.1 | CHC1 | SWIB/MDM2 domain superfamily protein | |
| 2:58822368 | 0.060 | 0.009 | 0.044 | 0.010 | Eucgr.B03399 | downstream | AT1G27150.1 | Tetratricopeptide repeat (TPR)-like superfamily protein | ||
| Leaf area | ||||||||||
| 4:30801453 | 0.069 | 0.013 | 0.037 | 0.016 | Eucgr.D01681 | synonymous, intron | AT1G64660.1 | ATMGL, MGL | methionine gamma-lyase | |
| 11:4085447 | 0.052 | 0.016 | 0.044 | 0.017 | Eucgr.K00355 | downstream | AT5G38280.1 | PR5K | PR5-like receptor kinase | |
| Leaf length | ||||||||||
| 2:63702271 | 0.036 | 0.016 | 0.002 | 0.030 | Eucgr.B03985 | missense | AT5G49620.1 | AtMYB78, MYB78 | myb domain protein 78 | |
| 4:30801453 | 0.012 | 0.021 | 0.004 | 0.026 | Eucgr.D01681 | synonymous, intron | AT1G64660.1 | ATMGL, MGL | methionine gamma-lyase | |
| 5:5009176 | 0.030 | 0.016 | 0.130 | 0.009 | Eucgr.E00527 | missense | AT4G23020.1 | |||
| Leaf weight | ||||||||||
| 5:4625458 | 0.028 | 0.017 | 0.027 | 0.017 | Eucgr.E00491 | upstream | AT3G60890.2 | ZPR2 | protein binding | |
| Leaf thickness | ||||||||||
| 5:4625458 | 0.006 | 0.023 | 0.007 | 0.023 | Eucgr.E00491 | upstream | AT3G60890.2 | ZPR2 | protein binding | |
| SLA | ||||||||||
| 5:4625458 | 0.024 | 0.018 | 0.017 | 0.020 | Eucgr.E00491 | upstream | AT3G60890.2 | ZPR2 | protein binding | |
| 11:4085447 | 0.020 | 0.021 | 0.015 | 0.022 | Eucgr.K00355 | downstream | AT5G38280.1 | PR5K | PR5-like receptor kinase | |
| Leaf density | ||||||||||
| 5:4625458 | 0.102 | 0.010 | 0.042 | 0.014 | Eucgr.E00491 | upstream | AT3G60890.2 | ZPR2 | protein binding | |
| 6:39617441 | 0.086 | 0.014 | 0.044 | 0.018 | Eucgr.F02999 | synonymous | AT1G22610.1 | C2 calcium/lipid-binding plant phosphoribosyltransferase family protein | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jordan, R.; Prober, S.M.; Hoffmann, A.A.; Dillon, S.K. Combined Analyses of Phenotype, Genotype and Climate Implicate Local Adaptation as a Driver of Diversity in Eucalyptus microcarpa (Grey Box). Forests 2020, 11, 495. https://doi.org/10.3390/f11050495
Jordan R, Prober SM, Hoffmann AA, Dillon SK. Combined Analyses of Phenotype, Genotype and Climate Implicate Local Adaptation as a Driver of Diversity in Eucalyptus microcarpa (Grey Box). Forests. 2020; 11(5):495. https://doi.org/10.3390/f11050495
Chicago/Turabian StyleJordan, Rebecca, Suzanne M. Prober, Ary A. Hoffmann, and Shannon K. Dillon. 2020. "Combined Analyses of Phenotype, Genotype and Climate Implicate Local Adaptation as a Driver of Diversity in Eucalyptus microcarpa (Grey Box)" Forests 11, no. 5: 495. https://doi.org/10.3390/f11050495
APA StyleJordan, R., Prober, S. M., Hoffmann, A. A., & Dillon, S. K. (2020). Combined Analyses of Phenotype, Genotype and Climate Implicate Local Adaptation as a Driver of Diversity in Eucalyptus microcarpa (Grey Box). Forests, 11(5), 495. https://doi.org/10.3390/f11050495






